1 Introduction

Many liquids of engineering importance have nonlinear relationship between stress and shear rate, and hence, their flow behavior cannot be predicted through the usual Newton’s law of viscosity. Some examples of these fluids are molten plastics, gelatin, polymers, dyes, paints, bloods, multi-grade oils, shampoos, fruit juices and honey. An important characteristic of these fluids is the retention of a fading memory of their flow history, which is termed as elasticity. Apart from viscosity, the viscoelastic fluids exhibit normal stress effects attributed to the fluid elasticity. These fluids have certain amount of energy stored in the form of strain energy which is responsible for the partial elastic recovery upon the removal of stress. One of the popular models of viscoelastic fluids is the upper-convected Maxwell (UCM) fluid model which explains the influence of fluid memory in view of the fluid relaxation time. In the past, the boundary layer flows of UCM fluid have been given special attention by the research community. For instance, Sadeghy et al. [1] investigated the two-dimensional flow of Maxwell fluid over a flat plate in a calm fluid. They discussed a comparative study of different numerical and analytical approaches for solving the developed nonlinear problem. Later, Kumari and Nath [2] analyzed buoyancy effects on Maxwell fluid flow in the region of stagnation point. They developed numerical approximations by finite difference method and observed that fluid velocity near the plate has inverse relation with the viscoelastic fluid parameter. Abel et al. [3] examined the Maxwell fluid flow adjacent to a stretchable surface utilizing a numerical technique. Hayat et al. [4] analyzed melting effects in Maxwell fluid flow near a stagnation point on a deforming surface. Shateyi [5] introduced a numerical method for tackling the Maxwell fluid flow with mass transfer. Recently, several interesting contributions regarding the flow analysis of Maxwell fluid are made [6–14].

Radiative heat transfer has special significance in engineering processes such as solar power technology, nuclear power plant, satellites and space vehicles; in combustion applications such as fires, furnaces, IC engines; and in solar radiation buildings. The concept of nonlinear radiation flux for laminar flow was first introduced by Rahman and El-tayeb [15]. They considered the nanofluid flow due to nonlinearly deforming surface using nonlinear Rosseland heat flux. Pantokratoras and Fang [16] examined heat transfer mechanism for laminar flow past a constantly moving radiative plate utilizing nonlinear radiative flux term. In another paper, Pantokratoras and Fang [17] analyzed the well-known Blasius flow subject to nonlinear radiation flux. Stagnation-point flow of Maxwell fluid subject to nonlinear thermal radiation was investigated by Mushtaq et al. [18]. Cortell [19] analyzed onset of the nonlinear radiation flux effects flow developed by quadratic deforming surface. Recently, various researchers discussed the nonlinear radiation flux aspect under different situations [20–25].

Here, our main objective is to discuss the non-aligned stagnation-point flow of an electrically conducting Maxwell fluid past a stretchable boundary considering nonlinear thermal radiation and heat source effects. The present study is an extension of the work reported by Abel et al. [3]. The present attempt is important to determine the onset of viscoelasticity and magnetic field on the heat transfer rate which is of fundamental interest in many extrusion processes. In recent past, some interesting numerical/analytical approaches for tackling MHD boundary layer equations have been proposed [26–40]. In the next section, we present the problem formulation. Section 3 deals with the description of numerical method and results. In Sect. 4, the conclusions of the present work are reported.

2 Basic equations

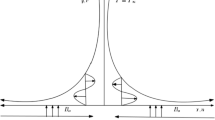
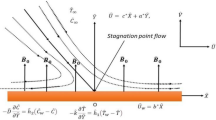
Consider a Maxwell fluid flow past a stretchable surface residing along the x-axis. Let the flow far from the sheet be characterized by \(u = bx,\,v = - by\), where \(b\) denotes the intensity of the stagnation flow. The velocity components at the surface are \(u = a(x + c),\,v = 0\), where \(a > 0\) denotes the rate of stretching and \(c\) indicates the point of stretching origin. It means that the axis of stretching and the free stream are not aligned in general. Magnetic field with uniform strength \(B_{0}\) acts normal to the stretching boundary, and induced magnetic field is ignored by assuming low magnetic Reynolds number. Let \(T_{w}\) be the constant temperature of the stretching boundary which is assumed to be larger than ambient temperature \(T_{\infty }\). Relevant equations which govern the laminar flow and radiative heat transfer of UCM fluid are expressed below [5, 25]:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(1)
$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + \lambda_{1} \left( {u^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }} + 2uv\frac{{\partial^{2} u}}{\partial x\partial y}} \right) = U_{\infty } \frac{{dU_{\infty } }}{dx} + \nu \frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\sigma B_{0}^{2} }}{\rho }\left( {u - U_{\infty } + \lambda_{1} v\frac{\partial u}{\partial y}} \right),$$
(2)
$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{\partial }{\partial y}\left( {\alpha + \frac{{16\sigma^{*} }}{{3\rho C_{p} k^{*} }}T^{3} } \right)\frac{\partial T}{\partial y} + Q\left( {T - T_{\infty } } \right),$$
(3)

where the coordinate x extends along the surface and y is normal to it. \(u\) and \(v\) denote the fluid velocities in x- and y-directions, respectively, \(\lambda_{1}\) is the fluid relaxation time, \(\nu\) stands for kinematic viscosity, \(\rho\) represents the fluid density, \(\sigma\) denotes the fluid electrical conductivity, \(C_{p}\) is the specific heat capacity, \(\sigma^{*}\) and \(k^{*}\) denote the Stefan–Boltzmann constant and the mean absorption coefficient, respectively, and \(Q\) is heat source/sink parameter. The boundary conditions for problem under consideration are [40]:

$$\begin{aligned} & u = U_{w} (x) = a(x + c),v = 0,T = T_{w} \quad at\;y = 0, \\ & u = U_{\infty } (x) = bx,v = - by,T \to T_{\infty } \quad as\;y \to \infty . \\ \end{aligned}$$
(4)

Consider the following transformations:

$$\eta = y\sqrt {\frac{a}{\nu }} ,\quad u = axf^{\prime } (\eta ) + bch(\eta ),\quad v = - \sqrt {\nu a} f(\eta ).$$
(5)

Equation (1) is satisfied identically in view of (5). Making use of variables (5) in Eq. (2) and then equating like powers of \(x\) and \(x^{0}\), we arrive at the following coupled ordinary differential equations:

$$f^{\prime \prime \prime } - f^{\prime 2} + ff^{\prime \prime } + De\left( {2ff^{\prime } f^{\prime \prime } - f^{2} f^{\prime \prime \prime } } \right) + M\left( {\gamma - f^{\prime } + Deff^{\prime \prime } } \right) + \gamma^{2} = 0,$$
(6)
$$h^{\prime \prime } + fh^{\prime } - hf^{\prime } + De\left( {2hff^{\prime \prime } - f^{2} h^{\prime \prime } } \right) + M\left( {Defh^{\prime } - h} \right) = 0.$$
(7)

In order to find similar form of Eq. (3), we define a non-dimensional temperature as \(\theta (\eta ) = (T - T_{\infty } )/(T_{w} - T_{\infty } )\). Thus, we have \(T = T_{\infty } (1 + (\theta_{w} - 1)\theta )\), where \(\theta_{w} = T_{w} /T_{\infty }\). So first term on the right-hand side of Eq. (3) can be written as \(\alpha \tfrac{\partial }{\partial y}\left[ {1 + Rd\left( {1 + \left( {\theta_{w} - 1} \right)\theta } \right)^{3} \tfrac{\partial T}{\partial y}} \right]\) in which \(Rd = 16\sigma^{*} T_{\infty }^{3} /3kk^{*}\) denotes the radiation parameter. This expression can be further reduced to \(\tfrac{{a(T_{w} - T_{\infty } )}}{Pr}\left[ {1 + Rd\left( {1 + \left( {\theta_{w} - 1} \right)\theta } \right)^{3} \theta^{\prime } } \right]^{\prime }\) where \(Pr = \nu /\alpha\) denotes the Prandtl number. Equation (8) in non-dimensional form is given below:

$$\frac{1}{Pr}\left[ {\left( {1 + Rd\left( {1 + \left( {\theta_{w} - 1} \right)\theta } \right)^{3} } \right)\theta^{\prime } } \right]^{\prime } + f\theta^{\prime } + S\theta = 0.$$
(8)

In Eqs. (6)–(8), \(De = \lambda_{1} a\) is the viscoelastic fluid parameter (also referred to as Deborah number), \(\gamma = b/a\) the stretching rates ratio, \(S = Q/a\) the heat source/sink parameter, and \(M = \sigma B_{0}^{2} /\rho a\) the magnetic field parameter. The transformed conditions are:

$$\begin{aligned} & f(0) = 0,\quad f^{\prime } (0) = 1,\quad h(0) = 1,\quad \theta (0) = 1, \\ & f^{\prime } (\infty ) \to \gamma ,\quad h(\infty ) \to 0,\quad \theta (\infty ) \to 0. \\ \end{aligned}$$
(9)

Quantity of practical interest here is the local Nusselt number \(Nu_{x}\) defined as follows:

$$Nu_{x} = \frac{{xq_{w} }}{{k\left( {T_{w} - T_{\infty } } \right)}},$$
(10)

where \(q_{w} = - k\left( {\partial T/\partial y} \right)_{y = 0} + \left( {q_{r} } \right)_{y = 0}\) is the wall heat flux. Now using dimensionless quantities from Eq. (5) in Eq. (10), one obtains

$$Re_{x}^{ - 1/2} Nu_{x} = - \left[ {1 + Rd\theta_{w}^{3} } \right]\theta^{\prime } (0),$$
(11)

where \({Re}_{x} = U_{w} x/\nu\) is the local Reynolds number.

3 Numerical method

A standard shooting approach using fifth-order Runge–Kutta (RK5) method is implemented for finding approximations of the differential Eqs. (6)–(8) subject to the conditions (9). RK method is generally a preferred integration technique since it uses derivative information at the midpoint of stepping interval. It acquires advantages of faster convergence and simple implementation of the methods for initial value problems. Fifth-order refers to the magnitude of the error term in RK method. The present fifth-order RK method also works with adaptive step size which makes it computationally efficient than the usual Euler method or finite difference schemes. Substituting \(y_{1} = f,y_{2} = f^{\prime } ,y_{3} = f^{\prime \prime } ,y_{4} = h,y_{5} = h^{\prime } ,y_{6} = \theta ,y_{7} = \theta^{\prime }\), we obtain first-order system comprising of seven ordinary differential equations given below:

$$\begin{aligned} & y_{1}^{\prime } = y_{2} ;\quad y_{1} (0) = 0 \\ & y_{2}^{\prime } = y_{3} ;\quad y_{2} (0) = 1 \\ & y_{3}^{\prime } = \frac{{y_{2}^{2} - y_{1} y_{3} - 2\left( {De} \right)y_{1} y_{2} y_{3} - M\left( {\gamma - y_{2} + \left( {De} \right)y_{1} y_{3} } \right) - \gamma^{2} }}{{1 - Dey_{1}^{2} }};\quad y_{3} (0) = s_{1} \\ & y_{4}^{\prime } = y_{5} ;\quad y_{4} (0) = 0 \\ & y_{5}^{\prime } = \frac{{y_{4} y_{2} - y_{1} y_{5} - 2\left( {De} \right)y_{1} y_{4} y_{2} + M\left( {y_{4} - \left( {De} \right)y_{1} y_{5} } \right)}}{{1 - Dey_{1}^{2} }};\quad y_{5} (0) = s_{2} \\ & y_{6}^{\prime } = y_{7} ;\quad y_{6} (0) = 1 \\ & y_{7}^{\prime } = \frac{{ - Pry_{1} y_{7} - PrSy_{6} - 3\left( {Rd} \right)y_{7}^{2} \left( {\theta_{w} - 1} \right)\left( {1 + \left( {\theta_{w} - 1} \right)y_{6} } \right)^{2} }}{{1 + Rd\left( {1 + \left( {\theta_{w} - 1} \right)y_{6} } \right)^{3} }};\quad y_{7} (0) = s_{3} \\ \end{aligned}$$
(12)

To solve the system (12), guesses for the initial slopes \([f^{\prime \prime } (0) = s_{1} ,h^{\prime } (0) = s_{2} ,\theta^{\prime } (0) = s_{3} ]\) are made and then integration is performed through RK5. The values of these slopes are iteratively estimated through Newton’s method until the far-field conditions \(f^{\prime } (\infty ),h(\infty )\) and \(\theta (\infty )\) are satisfied. The error tolerance was taken as \(10^{ - 6}\), and integrations at different \(\eta_{\hbox{max} }\) were performed in order to ensure that solutions become independent of the domain size.

4 Results and discussion

To validate our findings, we made a comparison of present computational results with those of Abel et al. [3] for a limiting situation (see Table 1). This comparison is found to be very good for all the considered Deborah numbers. Moreover, the results obtained through shooting method are also consistent with those obtained by bvp4c of MATLAB.

Table 1 Comparison of numerical values of \(f^{\prime \prime } (0)\) with Abel et al. [3] for different values of \(De\) with \(M = \gamma = 0 \,\)
Full size table

Figure 1 includes a sample of streamlines at two different values of c. Fig. 2 shows the curves of \(f^{\prime}\) for varying Deborah number \(De\). The results are computed at different values of stretching rates ratio parameter \(\gamma\), which compares the free stream velocity with the velocity of the stretching surface. We observe that \(f^{\prime}\) is a decreasing function of \(De\) when \(\gamma < 1\), i.e., when free stream moves slower than the stretching surface. However, when free stream velocity is larger than the stretching velocity \((\gamma > 1)\), the velocity field \(f^{\prime}\) appears to increase upon increasing \(De\). Irrespective of the value of parameter \(\gamma\), the profiles tend to the free stream at shorter distances from the bounding surface, indicating that boundary layer thickness decreases upon increasing the Deborah number \(De\). Deborah number compares the duration of fluid memory (known as fluid relaxation time) to the time of observation. Naturally, the material has a viscous-like response if Deborah number is small, that is, if the relaxation time is small in comparison with the observation time scale. However, when relaxation time is large (or large Deborah number), the elastic effect is dominant compared to viscous effect and the materials response is solid-like.

Fig. 1
figure 1

Streamlines for \(De = \gamma = 0.5\) with \(c = 0\) (left) and \(c = - 1\) (right)

Full size image

Figure 3 shows the effects of Hartman number \(M\) on the velocity field \(f^{\prime}\) at various values of stretching rates ratio parameter \(\gamma\). For any value of \(\gamma\), the profiles are tilted toward the boundary when \(M\) is incremented. It means that momentum boundary layer thickness is reduced due to the inclusion of magnetic force term. This opposition to the momentum transport is brought by Lorentz force due to the application of magnetic field.

Fig. 2
figure 2

Profiles of velocity field \(f^{\prime }\) for various values of Deborah number \(De\)

Full size image

In Fig. 4, we include the effects of Deborah number \(De\) and Hartman number \(M\) on the non-alignment function \(h\). We see that magnitude of \(h\) reduces upon increasing either the effects of magnetic field strength or the viscoelasticity. Further, the variation in function \(h\) with \(M\) and \(De\) is found to be qualitatively similar for any value of stretching rates ratio parameter \(\gamma\).

Fig. 3
figure 3

Profiles of velocity field \(f^{\prime }\) for different values of magnetic field parameter \(M\)

Full size image

Figure 5 portrays the effects of heat source/sink parameter \(S\) on temperature distribution. Naturally, the larger the heat source \(S\), the greater the temperature and the thermal boundary layer thickness. For sufficiently large \(S\), fluid temperature becomes greater than that of the bounding surface. As a result, we expect a reverse heat flow between the fluid and the stretching sheet.

Fig. 4
figure 4

Effects of Hartman number \(M\) and Deborah number \(De\) on non-alignment function \(h\)

Full size image

The effects of temperature ratio parameter \(\theta_{w}\) on temperature \(\theta\) are depicted in Fig. 6. It is a well-known fact that thermal penetration depth is dependent on the fluid thermal diffusivity. In the current situation, thermal diffusivity has the form \(\alpha + 16\sigma^{*} T^{3} /3\rho c_{p} k^{*}\) as depicted in Eq. (3). This expression gives the sum of classical thermal diffusivity and temperature-dependent term attributed to the radiation effect. Note that the thermal diffusivity is temperature dependent which suggests that thermal boundary layer thickness would vary inside the boundary layer as the temperature changes. Thus, one anticipates that thermal boundary layer thickness will be smaller far from the boundary because free stream temperature is smaller than the wall temperature. As \(\theta_{w}\) increases, the second term in the expression of thermal diffusivity increases. This leads to the thickening of thermal boundary layer and, hence, an obvious reduction in wall temperature gradient. Consequently, wall temperature gradient approaches zero value when wall-to-ambient temperature ratio is sufficiently large. Fig. 7 shows that temperature θ increases for increasing values of radiation parameter Rd. Wall temperature gradient \(\theta^{\prime } (0)\) against the temperature ratio parameter \(\theta_{w}\) is shown in Fig. 8. We observe that \(\theta^{\prime } (0)\) is inversely proportional to the wall-to-ambient temperature ratio.

Fig. 5
figure 5

Temperature profiles for different values of \(S\)

Full size image
Fig. 6
figure 6

Temperature profiles for different values of temperature ratio parameter \(\theta_{w}\)

Full size image
Fig. 7
figure 7

Temperature profiles for different values of radiation parameter \(Rd\)

Full size image
Fig. 8
figure 8

Effect of Deborah number \(De\) on temperature gradient \(\theta^{\prime } (0)\)

Full size image

Computational results of local Nusselt number \(Re_{x}^{ - 1/2} Nu_{x}\) for various parametric values are included in Table 2. It is evident that wall heat flux in viscous fluid is large in comparison with the viscoelastic fluid. Both stretching rates ratio parameter \(\gamma\) and heat source/sink parameter \(S\) accelerate the heat transfer from the stretching wall. The value of \(Re_{x}^{ - 1/2} Nu_{x}\) is negative when \(S = 1\). This is because of the reverse heat flow near the wall as explained earlier through Fig. 4. We also conclude that heat transfer rate decreases upon increasing the magnetic field intensity.

Table 2 Numerical values of local Nusselt number for different values of \(\gamma ,\,S\) and \(M\) with \(\Pr = 7,\,Rd = 0.5\) and \(\theta_{w} = 1.2\)
Full size table

5 Concluding remarks

In this article, we discussed the non-aligned MHD stagnation-point flow of Maxwell fluid bounded by deformable surface. Heat transfer with nonlinear radiation flux and heat source/sink is explored. The key aspects of this research are outlined below:

  • Hydrodynamic boundary layer becomes thinner when either magnetic field parameter \(M\) or Deborah number \(De\) is increased.

  • Hydrodynamic boundary layer thickness is a decreasing function of stretching rates ratio parameter \(\gamma\).

  • Thermal boundary layer thickness and heat flux at the surface increase upon increasing the temperature ratio parameter \(\theta_{w}\).

  • The effects of all the parameters on the non-alignment function \(h\) are qualitatively similar.

  • Temperature profiles correspond to the linear radiation case when temperature ratio parameter is sufficiently close to unity.

  • Stretching rates ratio parameter \(\gamma\) and heat source/sink parameter \(S\) are useful in enhancing the cooling rate of the stretching surface.

  • Cooling rate of the sheet is inversely proportional to the viscoelastic fluid parameter.

  • To our knowledge, the present work is the first attempt regarding the non-aligned stagnation-point flow of rate-type fluids. In future, possible extension of the present study for unsteady equations can be made. This would be helpful to understand the transition from unsteady flow to the steady-state flow.