1 Introduction

During the past few years, vast usage of new kinds of materials is growing in many engineering structures. One of these new materials is porous materials which have vast applications and are modeled for different usages such as biomedical applications [1,2,3] and energy absorption [4]. The thermal buckling of solid circular plate bounded with piezoelectric sensor–actuator patches with porous material properties varying along the thickness was studied by Joubaneh et al. [5]. Pei-Sheng [6] analyzed a failure model of simplified structures for isotropic three-dimensional reticulated porous materials under compressive loads. Chen et al. [7] performed examination on the elastic buckling and static bending of shear deformable FG porous beams based on the Timoshenko beam theory. The buckling behavior of a rectangular porous plate is studied by Magnucki et al. [8]. The mechanical behavior of isotropic porous beams is studied by Magnucki and Stasiewicz [9] under compressive force. The buckling and deflection of a circular porous plate under radial uniform compression and uniformly distributed load is considered by Magnucka-Blandzi [10]. The buckling analysis of circular plate made of porous material under thermal loads is performed by Jabbari et al. [11], and they also studied the same problem considering the layers of piezoelectric actuators [12] and also piezoelectric sensor–actuator patches [13]. The mechanical behavior of GASAR copper with cylindrical pores oriented in the direction of loading has been studied under uniaxial compressive loads [14]. Jabbari et al. [15] investigated on the thermal buckling of radially solid circular plate made of porous material with piezoelectric actuator layers. The transverse vibrations of a thin porous plate which is saturated by a fluid are studied by Leclaire et al. [16] based on the classical theory of homogeneous plates. The buckling of soft ferromagnetic FG circular plates made of porous material was studied by Jabbari et al. [17]. The buckling examination of isotropic three-dimensional reticulated porous metal foams and the failure analysis is performed by Liu [18]. Amirkhani et al. [19] studied the different pore geometries and their orientation with respect to the compressive loading direction on mechanical responses of scaffolds. Experimental study on the compressive behavior of porous titanium in the out-of-plane direction was studied by Li et al. [20]. The analysis on the buckling behavior of functionally graded piezoelectric plates with porosities is performed by Barati et al. [21].

The study of nanoporous structures is of great interest among researchers around the world. Using the theory of surface elasticity, Xia et al. [22] studied the mechanical properties of nanoporous materials. Yu et al. [23] studied the buckling of nanobeam using the size-dependent model, i.e., nonlocal thermoelasticity, and based on Euler–Bernoulli beam theory. Shen and Xiang [24] studied the postbuckling of nanocomposite cylindrical shells reinforced by single-walled carbon nanotubes (SWCNTs). Also, axial buckling of double-walled boron nitride nanotubes (DWBNNTs) under combined electro-thermo-mechanical loadings is investigated by Arani et al. [25]. Mohammadabadi et al. [26] studied the thermal effect on size-dependent buckling behavior of micro-composite laminated beams.

In addition to the vibrations, buckling of nanostructures is also important to study. Kiani [27] studied the elastic buckling of micro- and nanorods/tubes. Aydogdu [28] studied the bending, buckling and free vibration of nanobeams by a generalized nonlocal beam theory. Thai [29] studied the bending, buckling and vibration of nanobeams by nonlocal shear deformation beam theory. The critical force of axial buckling of a nanowire was studied by Wang and Feng [30] considering the effects of surface elasticity and residual surface tension. The nonlinear postbuckling load–deflection behavior of FG Timoshenko beam was studied by Paul and Das [31] under in-plane thermal loading. Ansari et al. [32] studied the postbuckling deflection of nanobeams considering the effect of surface stress. The size-dependent nonlinear vibration porous uniform and nonuniform micro-beams were studied by Shafiei et al. [33]. Moreover, there are a number of other papers considering the nonlinear behavior of micro- and nanobeams [34,35,36,37,38].

As you see, the absence of a deep study on the buckling and vibration of porous nanosize beams in the literature is sensible. So, we decided to study the buckling and nonlinear vibrations of a nanobeam with two types of porous materials based on Euler–Bernoulli beam theory and using the Eringen’s nonlocal elasticity theory. The boundary conditions are considered as clamped–clamped (CC) and simply supported–simply supported (SS). Using the GDQM and the iterative methods, the nonlinear governing equations are solved. The normalized and nondimensional frequencies and the critical buckling force are calculated for different values of nonlocal parameters, FG indexes, porosity volume fractions, etc.

2 Problem and formulation

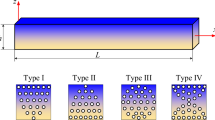
A functionally graded nanoscale porous Euler–Bernoulli beam is considered with length of ‘L,’ width ‘b’ and height ‘h’ which are located on x, y and z directions, respectively, as shown in Fig. 1.

Fig. 1
figure 1

Schematic of the FG nanobeam

Full size image

2.1 Functionally graded material

As the studied FG nanobeam is composed of metal and ceramic, the physical and mechanical properties of the nanobeam vary through the thickness (Fig. 1). The power law defines the variations of properties as follows:

$$V_{\text{c}} (z) = \left( {\frac{z}{h} + \frac{1}{2}} \right)^{n}$$
(1)
$$V_{\text{m}} (z) = 1 - V_{\text{c}} (z)$$
(2)

where V denotes the volume fraction, the subscripts ()c and ()m denote the ceramic and metal, respectively, and ‘n’ is the FG index which describes the volume fraction change of the materials composition (Fig. 1). h is the thickness of the beam, and z shows the position along the thickness of the beam. As Eqs. (1) and (2) define, the material of the bottom (z = − h/2) and the top surfaces (z = h/2) of the nanobeam is made of pure metal and pure ceramic, respectively. According to Eqs. (1) and (2), the physical and mechanical properties of the FG nanobeam can be defined as a function of ceramic and metal volume fraction as below:

$$F\left( z \right) = V_{\text{c}} \left( z \right)\left( {F_{\text{c}} - F_{\text{m}} } \right) + F_{\text{m}}$$
(3)

In Eq. (3), F(z) can be both the physical and mechanical properties of the nanobeam at a specific point (z). Also F1 and F2 are parameters of physical and mechanical properties of pure ceramic and pure metal, respectively.

2.2 Porous structures

Two different types of porosity distributions are shown in Fig. 2. According to Eqs. (1)–(3) and two types of porosity distributions [33], the physical and mechanical properties of the FG porous nanobeam such as mass density (ρ), Young’s modulus (E) and Poisson’s ratio (ν) can be defined as below.Porous Type 1:

$$\rho \left( z \right) = \rho_{\text{m}} + \left( {\rho_{\text{c}} - \rho_{\text{m}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} - \frac{\alpha }{2}\left( {\rho_{\text{c}} + \rho_{\text{m}} } \right)$$
(4a)
$$E\left( z \right) = E_{\text{m}} + \left( {E_{\text{c}} - E_{\text{m}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} - \frac{\alpha }{2}\left( {E_{\text{c}} + E_{\text{m}} } \right)$$
(4b)
$$\nu \left( z \right) = \nu_{\text{m}} + \left( {\nu_{\text{c}} - \nu_{\text{m}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} - \frac{\alpha }{2}\left( {\nu_{\text{c}} + \nu_{\text{m}} } \right)$$
(4c)

Porous Type 2:

$$\rho \left( z \right) = \rho_{\text{m}} + \left( {\rho_{\text{c}} - \rho_{\text{m}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} - \frac{\alpha }{2}\left( {\rho_{\text{c}} + \rho_{\text{m}} } \right)\left( {1 - 2\frac{\left| z \right|}{h}} \right)$$
(5a)
$$E\left( z \right) = E_{\text{m}} + \left( {E_{\text{c}} - E_{\text{m}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} - \frac{\alpha }{2}\left( {E_{\text{c}} + E_{\text{m}} } \right)\left( {1 - 2\frac{\left| z \right|}{h}} \right)$$
(5b)
$$\nu \left( z \right) = \nu_{\text{m}} + \left( {\nu_{\text{c}} - \nu_{\text{m}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} - \frac{\alpha }{2}\left( {\nu_{\text{c}} + \nu_{\text{m}} } \right)\left( {1 - 2\frac{\left| z \right|}{h}} \right)$$
(5c)

where α is the porosity volume fraction.

Fig. 2
figure 2

Cross-sectional area of FG porous nanobeam. a Even distribution of porosities (Type 1). b Uneven distribution of porosities (Type 2)

Full size image

2.3 Mathematical modeling

Euler–Bernoulli beam theory and the nonlocal Eringen’s theory are of many applications and have been used many times to study buckling and vibrations [39,40,41,42]. Thus, to prevent the unnecessary descriptions, the general nonlinear equation of vibration and buckling of FG Euler–Bernoulli nanobeam considering the boundary conditions is as follows:

$$\begin{aligned} & \delta u:\quad \frac{\partial }{{\partial x}}\left[ {A_{x} \frac{{\partial u}}{{\partial x}} + \frac{1}{2}A_{x} \left( {\frac{{\partial w\left( {x,t} \right)}}{{\partial x}}} \right)^{2} } \right] - \frac{\partial }{{\partial x}}\left[ {Bx\frac{{\partial ^{2} w}}{{\partial x^{2} }}} \right] \\ & \qquad = \frac{{\partial ^{2} }}{{\partial t^{2} }}\left[ {m_{0} u - m_{1} \frac{{\partial w}}{{\partial x}}} \right] - \left( {e_{0} a} \right)^{2} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left[ {m_{0} \frac{{\partial ^{2} u}}{{\partial x^{2} }} - m_{1} \frac{{\partial ^{3} w}}{{\partial x^{3} }}} \right] \\ \end{aligned}$$
(6a)
$$\begin{aligned} & \delta w:\quad - \frac{{\partial ^{2} }}{{\partial x^{2} }}\left[ {Cx\frac{{\partial ^{2} w_{~} }}{{\partial x^{2} }}} \right] + \frac{{\partial ^{2} }}{{\partial x^{2} }}\left[ {Bx\frac{{\partial u}}{{\partial x}}} \right] + \frac{\partial }{{\partial x}}\left[ {\left( {\bar{P} + \frac{1}{2}A_{x} \left( {\frac{{\partial w}}{{\partial x}}} \right)^{2} - B_{x} \frac{{\partial ^{2} w}}{{\partial x^{2} }}} \right)\frac{{\partial w}}{{\partial x}}} \right] \\ & \qquad \quad - \left( {e_{0} a} \right)^{2} \frac{{\partial ^{2} }}{{\partial x^{2} }}\left\{ {\frac{\partial }{{\partial x}}\left[ {\left( {\bar{P} + \frac{1}{2}A_{x} \left( {\frac{{\partial w}}{{\partial x}}} \right)^{2} - B_{x} \frac{{\partial ^{2} w}}{{\partial x^{2} }}} \right)\frac{{\partial w}}{{\partial x}}} \right]} \right\} \\ & \qquad = \frac{{\partial ^{2} }}{{\partial t^{2} }}\left[ {m_{0} w + m_{1} \frac{{\partial u}}{{\partial x}} - m_{2} \frac{{\partial ^{2} w}}{{\partial x^{2} }}} \right] - \left( {e_{0} a} \right)^{2} \frac{{\partial ^{2} }}{{\partial x^{2} }}\left[ {\frac{{\partial ^{2} }}{{\partial t^{2} }}\left( {m_{0} w + m_{1} \frac{{\partial u}}{{\partial x}} - m_{2} \frac{{\partial ^{2} w}}{{\partial x^{2} }}} \right)} \right] \\ \end{aligned}$$
(6b)

where a is the internal characteristic lengths, e0 indicates a material constant, and \(\bar{P}\) is the external axial load.

$$\left( {A_{x} ,B_{x} ,C_{x} } \right) = \int\limits_{ - h/2}^{h/2} {\int\limits_{ - b/2}^{b/2} {E\left( z \right)\left( {1,z,z^{2} } \right)\text{d}y{\text{d}}z} }$$
(7a)
$$\left( {m_{0} ,m_{1} ,m_{2} } \right) = \int\limits_{ - h/2}^{h/2} {\int\limits_{ - b/2}^{b/2} {\rho \left( z \right)\left( {1,z,z^{2} } \right){\text{d}}y{\text{d}}z} }$$
(7b)

The boundary conditions are as follows:

$$N = 0\quad {\text{or}}\quad u = 0\quad {\text{at}}\quad x = 0\quad {\text{and}}\quad x = L$$
(8a)
$$\frac{\partial M}{\partial x} + m_{2} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} = 0\quad {\text{or}}\quad w = 0\quad {\text{at}}\quad x = 0\quad {\text{and}}\quad x = L$$
(8b)
$$M = 0\quad {\text{or}}\quad \frac{\partial w}{\partial x} = 0\quad {\text{at}}\quad x = 0\quad {\text{and}}\quad x = L$$
(8c)

Based on nonlocal theory, N and M are defined as follows:

$$N = A_{x} \frac{\partial u}{\partial x} + \frac{1}{2}A_{x} \left( {\frac{{\partial w\left( {x,t} \right)}}{\partial x}} \right)^{2} + \left( {e_{0} a} \right)^{2} \frac{\partial }{\partial x}\left( {m_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }}} \right)$$
(9a)
$$M = - \,C_{x} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \left( {e_{0} a} \right)^{2} \left[ {m_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - m_{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right] - \left( {e_{0} a} \right)^{2} \frac{\partial }{\partial x}\left( {\bar{P}\frac{\partial w}{\partial x}} \right)$$
(9b)

3 Solution methodology

The generalized differential quadrature method (GDQM) has vastly been utilized to solve nonlinear equations and is proven to be accurate for this purpose [43, 44]. As the concepts of this method have been explained a lot in the literature [45,46,47,48,49,50,51,52,53,54], here we avoid repeating those explanations regarding GDQM.

In GDQM, the rth-order derivative of function \(f\left( {x_{i} } \right)\) is:

$$\left. {\frac{{\partial^{r} f\left( x \right)}}{{\partial x^{r} }}} \right|_{{x = x_{P} }} = \sum\limits_{j = 1}^{k} {C_{ij}^{(r)} f\left( {x_{i} } \right)}$$
(10)

where k is the number of grid points along x direction and \(C_{ij}\) is:

$$\begin{array}{*{20}l} {C_{ij}^{(1)} = \frac{{\bar{M}\left( {x_{i} } \right)}}{{\left( {x_{i} - x_{j} } \right)\bar{M}\left( {x_{j} } \right)}};} \hfill & {i,j = 1,2, \ldots ,n\quad {\text{and}}\quad i \ne j} \hfill \\ {C_{ij}^{(1)} = - \sum\limits_{j = 1,i \ne j}^{n} {C_{ij}^{(1)} } ;} \hfill & {i = j} \hfill \\ \end{array}$$
(11)

where \(\bar{M}\)(x) is defined as follows:

$$\bar{M}\left( {x_{i} } \right) = \prod\limits_{j = 1,j \ne i}^{k} {\left( {x_{i} - x_{j} } \right)}$$
(12)

The weighting coefficient C(r), along x direction, can be obtained as follows:

$$\begin{array}{*{20}l} {C_{ij}^{(r)} = r\left[ {C_{ij}^{(r - 1)} C_{ij}^{(1)} - \frac{{C_{ij}^{(r - 1)} }}{{\left( {x_{i} - x_{j} } \right)}}} \right];} \hfill & {i,j = 1,2, \ldots ,k,i \ne j\quad {\text{and}}\quad 2 \le r \le k - 1} \hfill \\ {C_{ii}^{(r)} = - \sum\limits_{j = 1,i \ne j}^{n} {C_{ij}^{(r)} } ;} \hfill & {i,j = 1,2, \ldots ,k\quad {\text{and}}\quad 1 \le r \le k - 1} \hfill \\ \end{array}$$
(13)

To obtain a better distribution for mesh points, Chebyshev–Gauss–Lobatto technique is applied as follows:

$$x_{i} = \frac{L}{2}\left( {1 - \cos \left( {\frac{{\left( {i - 1} \right)}}{{\left( {k - 1} \right)}}\pi } \right)} \right)\quad i = 1,2,3, \ldots ,k$$
(14)

The nonlinear motion equations of the FG porous nanobeam [Eqs. (6), (8)] are considered to be the combination of three matrixes. Thus, we can obtain the linear and nonlinear stiffness as

$$\left\{ {[K]_{\text{Linear}} + [K]_{\text{non - Linear}} - \omega^{2} [M]} \right\}\left\{ \lambda \right\} = 0$$
(15)

The nonlinear stiffness matrix is first neglected to solve the governing motion equation using the GDQM. So, by applying the weight coefficients [Eq. (13)] to the linear motion equations, we have:

$$\begin{aligned} & \delta u:\quad \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } \left[ {A_{x} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } U_{s} } \right] - \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } \left[ {Bx\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } W_{s} } \right] \\ & \qquad = \frac{{\partial ^{2} }}{{\partial t^{2} }}\left[ {m_{0} U_{s} - m_{1} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } W_{s} } \right] - \left( {e_{0} a} \right)^{2} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left[ {m_{0} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } U_{s} - m_{1} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(3)}} W_{s} } } \right] \\ \end{aligned}$$
(16a)
$$\begin{aligned} & \delta w:\quad \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } \left[ { - \,Cx\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } W_{s} } \right] + \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } \left[ {Bx\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } U_{s} } \right] + \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } \left( {\bar{P}\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} W_{s} } } \right) \\ & \qquad \quad - \left( {e_{0} a} \right)^{2} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } \left[ {\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } \left( {\bar{P}\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} W_{s} } } \right)} \right] \\ & \qquad = \frac{{\partial ^{2} }}{{\partial t^{2} }}\left[ \begin{gathered} m_{0} W_{s} + m_{1} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } U_{s} - m_{2} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} W_{s} } \hfill \\ - \left( {e_{0} a} \right)^{2} \frac{{\partial ^{2} }}{{\partial x^{2} }}\left( {m_{0} W_{s} + m_{1} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } U_{s} - m_{2} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } W_{s} } \right) \hfill \\ \end{gathered} \right] \\ \end{aligned}$$
(16b)

Then, applying the boundary conditions, Eq. (8), and assembling the related matrixes to the boundary conditions and governing equations, the linear fundamental frequency can be calculated as below:

$$\left[ {\begin{array}{*{20}c} {\left[ {K_{\text{dd}} } \right]} & {\left[ {K_{\text{db}} } \right]} \\ {\left[ {K_{\text{bd}} } \right]} & {\left[ {K_{\text{bb}} } \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\left\{ {\lambda_{\text{d}} } \right\}} \\ {\left\{ {\lambda_{\text{b}} } \right\}} \\ \end{array} } \right\} = \omega_{\text{Linear}}^{2} \left[ {\begin{array}{*{20}c} {\left[ {M_{\text{dd}} } \right]} & {\left[ {M_{\text{db}} } \right]} \\ {\left[ {M_{\text{bd}} } \right]} & {\left[ {M_{\text{bb}} } \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\left\{ {\lambda_{\text{d}} } \right\}} \\ {\left\{ {\lambda_{\text{b}} } \right\}} \\ \end{array} } \right\}$$
(17)

where b and d indexes represent the boundary and domain, respectively, and \(\lambda\) is the mode shape. To solve the nonlinear vibration equations, we need to know the linear mode shapes. U and W mode shapes can be obtained by Eq. (17). To obtain the nonlinear mode shapes, we first put the values of the calculated linear mode shapes in the nonlinear stiffness matrix, and then, using Eq. (6), and also coupling the linear and nonlinear stiffness matrixes with the mass matrix, we obtain the nonlinear frequency and mode shape. Then, to derive the convergent nonlinear results, the iteration method is employed to recalculate the results.

$$\begin{aligned} & \delta u:\quad \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } \left[ {A_{x} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } U_{s} + \frac{1}{2}A_{x} \left( {\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } W_{s} } \right)^{2} } \right] - \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } \left[ {Bx\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } W_{s} } \right] \\ & \qquad = \omega ^{2} _{{{\text{non - Linear}}}} \left( {m_{0} U_{s} - m_{1} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } W_{s} - \left( {e_{0} a} \right)^{2} \left[ {m_{0} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } U_{s} - m_{1} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(3)}} W_{s} } } \right]} \right) \\ \end{aligned}$$
(18a)
$$\begin{aligned} & \delta w:\quad \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } \left[ { - Cx\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } W_{s} } \right] + \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } \left[ {Bx\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } U_{s} } \right] \\ &\qquad \quad + \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } \left[ {\left( {\bar{P} + \frac{1}{2}A_{x} \left( {\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } W_{s} } \right)^{2} - B_{x} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } W_{s} } \right)\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } W_{s} } \right] \\ & \qquad \quad - \left( {e_{0} a} \right)^{2} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } \left\{ {\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } \left[ {\left( {\bar{P} + \frac{1}{2}A_{x} \left( {\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } W_{s} } \right)^{2} - B_{x} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } W_{s} } \right)\sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } W_{s} } \right]} \right\} \\ & \qquad = \omega ^{2} _{{{\text{non - Linear}}}} \left[ \begin{gathered} m_{0} W_{s} + m_{1} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } U_{s} - m_{2} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } W_{s} \hfill \\ - \left( {e_{0} a} \right)^{2} \frac{{\partial ^{2} }}{{\partial x^{2} }}\left( {m_{0} W_{s} + m_{1} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(1)}} } U_{s} - m_{2} \sum\limits_{{s = 1}}^{n} {C_{{rs}}^{{(2)}} } W_{s} } \right) \hfill \\ \end{gathered} \right] \\ \end{aligned}$$
(18b)

Now, by removing the time-dependent parameters, the dynamic equation is changed to the static equation and \(\bar{P}\) is the desired parameter. Then, using the similar solving procedure of eigenvalue problem which yielded for vibration frequency, we now obtain the critical buckling load.

$$\sum\limits_{s = 1}^{n} {C_{rs}^{(2)} } \left[ { - \,Cx\sum\limits_{s = 1}^{n} {C_{rs}^{(2)} } W_{s} } \right] + \sum\limits_{s = 1}^{n} {C_{rs}^{(2)} } \left[ {Bx\sum\limits_{s = 1}^{n} {C_{rs}^{(1)} } U_{s} } \right] = \bar{P}\left( {\left( {e_{0} a} \right)^{2} \sum\limits_{s = 1}^{n} {C_{rs}^{(4)} W_{s} } - \sum\limits_{s = 1}^{n} {C_{rs}^{(2)} } W_{s} } \right)$$
(19)

4 Numerical results

Here, the number of grid point is considered to be n = 29 which is sufficient to obtain the accurate results for the present analysis, and the mesh type is shown in Eq. (14). Metric dimension is used for the solving procedure, but the results are first made nondimensional and then normalized with respect to the linear and local result, by Eqs. (20) and (21). The nonlinear results are derived using iteration method. The numerical procedure is applied for the linear and nonlinear normalized and nondimensional frequencies and the buckling of the porous FG nanobeam to examine the effects of nonlinearity, porous volume fraction, nonlocal value, etc. To obtain the best results for the Euler–Bernoulli nanobeam, the ratio of length to height is set to be L/h = 40. The material of the nanobeam is considered as FG composed of metal and ceramic with varying composition through the thickness. In order to have better understanding of the results, nondimensional parameters are defined as follows:

$$\mu = \frac{{e_{0} a}}{L}$$
(20a)
$$\varPsi^{2} = \frac{{m_{0} }}{{Cx_{\text{ceramic}} }}L^{4} \omega^{2}$$
(20b)
$${\text{Amp}} = \frac{{q_{\hbox{max} } }}{{\tilde{r}}} = \sqrt {\frac{{h^{2} }}{12}}$$
(20c)
$$P_{\text{Cr}} = \bar{P} \times \frac{{L^{2} }}{{C_{x} }}$$
(20d)

where \(a\) is the internal characteristic length, and \(e_{0}\) defines a material constant. Also μ, Ψ, qmax, r, Amp and PCr are the nondimensional small-scale parameter, nondimensional frequency, vibration amplitude, gyration radius, nondimensional amplitude and critical buckling load, respectively [55]. Also normalize frequency is introduced as

$${\text{Normalized}}\;{\text{frequency}} = \frac{{{\text{Non - linear}}\;{\text{frequency}}\;{\text{of}}\;{\text{nano - beam}}}}{{{\text{Linear}}\;{\text{frequency}}\;{\text{of}}\;{\text{ceramic}}\;{\text{local}}\;{\text{beam}}}}$$
(21)

The mechanical properties of metal and ceramic which compose the FG nanobeam are presented in Table 1.

Table 1 The coefficients of Young’s modulus, mass density and Poisson’s ratio of ceramic (Al2O3) and metal (SUS304), [56]
Full size table

In order to prove the accuracy of the results, the first and second linear frequencies of nanobeams with CC and SS boundary conditions are compared with the results of Lu et al. [57] in Table 2. After that, the fundamental frequency and the critical buckling load of the porous nanobeam are depicted for different values of porosity volume fractions, FG index, nonlocal parameter, etc.

Table 2 Comparison of the first and second linear frequencies of SS and CC nanobeams with the results of Lu, Lee [57] for various nonlocal values
Full size table

Table 2 shows the validation of the results based on the first and the second linear frequencies of the nanobeam with CC and SS boundary conditions with the results of Lu et al. [57]. It can clearly be seen that the obtained linear frequencies are in perfect match with the results of Lu et al. [57] in different nonlocal values. Table 3 shows the good agreement of the results with the results of Malekzadeh and Shojaee [58], Shafiei et al. [55], Lestari and Hanagud [59] and Singh et al. [60] for clamped and simply supported nanobeams in different values of amplitude of nonlinearity.

Table 3 Validation with the normalized fundamental frequency of CC and SS nanobeams in different amplitudes
Full size table

Figures 3 and 4 show the nondimensional frequency versus the FG index (n) for different values of nonlocal parameters (μ) and porosity volume fractions (α), respectively, for Type 1 and Type 2 porous nanobeams under clamped–clamped (CC) boundary condition. It can be seen in these two figures that increasing the nonlocal parameter decreases the nondimensional frequency and increment of FG index increases the nondimensional frequency of both porous types. It is observed in Fig. 3 that the effect of the porosity volume fraction changes after n ≈ 1 (Type 1). As when n is lower than 1, increasing the porosity volume fraction increases the nondimensional frequency, but, after n ≈ 1, the nondimensional frequency decreases by increasing the porosity volume fraction. This is due to the change of material properties which can obviously be seen in Eq. (4). It is because when n < 1, increasing α increases the stiffness, but, when n is higher than 1, the stiffness decreases with the increment of porosity (α).

Fig. 3
figure 3

Nondimensional frequency versus FG index for clamped–clamped nanobeam porosity of Type 1

Full size image
Fig. 4
figure 4

Nondimensional frequency versus FG index for clamped–clamped nanobeam porosity of Type 2

Full size image

It is also obvious in Fig. 4 that the nondimensional frequency of Type 2 porous nanobeam increases with the porosity volume fraction in all values of FG index. Besides, a smooth convergence is seen in the values of the nondimensional frequency as the FG index increases. Comparison between Figs. 3 and 4 shows that the frequency of Type 2 porous nanobeam is lower than Type 1 when the FG index is low and porosity is high. But, in higher FG indexes, for example when n = 4, the differences of the frequencies of Type 1 and Type 2 are not so significant.

Figure 5 shows the normalized frequency of Type 1 porous nanobeam versus the nonlinear amplitude for different values of porous volume fraction and FG index for CC and SS boundary conditions. It is seen that increasing the amplitude increases the normalized frequency. Besides, it is seen that the dependency of the effect of the porous volume fraction on the value of the FG index occurs in both CC and SS boundary conditions. In addition, the frequency of the CC boundary condition is higher than that of SS boundary condition as the degree of freedom (DOF) of the CC boundary condition is lower.

Fig. 5
figure 5

Normalized frequency versus nonlinear amplitude for clamped nanobeam for porosity of Type 1 when \(\mu = 0.2\)

Full size image

Figure 6 shows the normalized frequency of Type 2 porous nanobeam versus the nonlinear amplitude when the nonlocal value is μ = 0.2. Similar to the previous figures, Fig. 6 shows that the normalized frequency decreases with the increment of the nonlocal value. It is also shown that as Type 2 porosity increases, the normalized frequency slightly decreases. This slight decrement of normalized frequency of Type 2 porous nanobeam which is due to the change of porosity is shown previously in Fig. 4.

Fig. 6
figure 6

Normalized frequency versus nonlinear amplitude for clamped nanobeam with \(n = 2\) and porosity of Type 2

Full size image

Figures 7 and 8, respectively, show the critical buckling load of Type 1 and 2 porous nanobeams versus the FG index for different values of porous volume fraction and nonlocal values for CC and SS boundary conditions. It is shown that increasing the FG index decreases the critical buckling load. However, this increment is mostly seen when FG index is lower than 1 and as FG index becomes higher, the effect of FG index on the critical buckling load decreases. Figures 7 and 8 also show that increasing the nonlocal value and porous volume fraction decreases the critical buckling load. In fact, increasing the nonlocal value decreases the stiffness of the nanobeam and decreases the critical buckling load. In addition, the critical buckling load of the CC boundary condition is higher than that of SS boundary condition as the DOF of the SS boundary condition is higher.

Fig. 7
figure 7

Nondimensional critical buckling load (PCr) of clamped–clamped Type 1 porous FG nanobeam versus FG index (n)

Full size image
Fig. 8
figure 8

Nondimensional critical buckling load (PCr) of simply supported—simply supported Type 1 porous FG nanobeam versus FG index (n)

Full size image

5 Conclusion

In this study, the nonlinear vibration behavior and buckling of porous FG nanobeam is studied. The nonlinear Von Kármán strains are considered to study the nonlinear behavior, and the boundary conditions are considered as clamped–clamped (CC) and simply supported–simply supported (SS). The nonlinear equations are derived based on Eringen’s theory, and GDQM is employed to calculate the results. The most important results of this work are:

  • The normalized frequency and the critical buckling load increase with the decrement of FG index and nonlocal value due to the decrement of the stiffness of the nanobeam.

  • The effect of the porosity on the normalized frequency depends on the value of the FG index and does not depend on the boundary condition.

  • The effect of Type 1 porosity on buckling force and normalized frequency is more than that of Type 2 porosity.

  • The effect of the porosity volume fraction on the normalized frequency depends on the FG index as when n is bigger than 1, the porosity increases the frequency, but when n is lower than 1, the frequency decreases by increasing the porosity volume fraction.