1 Introduction

In recent years, research into the mechanical behaviors of beam-type micro- and nano-structures has attracted considerable attention due to their several applications. A literature review on the studies performed on this issue shows that the majority of them are based on the continuum mechanics. The acceptability of continuum approaches can be attributed to their computational efficiency when they are compared with the atomistic approaches.

It has been proved that the mechanical behaviors of structures at small scales are size dependent [1–6], and continuum models used for the mechanical analyses of micro- and nano-structures must be size dependent in order to give accurate results. There are several size-dependent continuum theories by which the size effects can be incorporated into the continuum models. Among them, the surface stress [7, 8], couple stress [9–11] and nonlocal [12] theories can be mentioned. Up to now, numerous applications of these theories to different problems of small-scale structures have been reported (e.g., [13–24]).

In the middle of 1960s, Mindlin [25, 26] developed a size-dependent continuum theory called the strain gradient theory (SGT) in which the first and second derivatives of the strain tensor effective on the strain energy density were taken into account. In 2003, Lam et al. [27] made some modifications to this theory and proposed the modified strain gradient theory (MSGT). Based on MSGT, three length scale parameters corresponding to the dilatation gradient tensor, deviatoric gradient tensor and symmetric rotation gradient tensor are considered. One can find many papers in which MSGT has been used to capture the size effects on the mechanics of small-scale structures. For example, Ansari et al. [28] studied the size-dependent vibrations of curved micro-beams made of functionally graded materials (FGMs) based on MSGT. Akgöz and Civalek [29, 30] investigated the buckling of micro-beams using MSGT. Abbasi and Karami Mohammadi [31] developed a strain gradient model to study the resonant frequency and sensitivity of atomic force microscopy micro-cantilevers. Instability of electrostatic nano-bridges and nano-cantilevers was analyzed by Tadi Beni et al. [32] within the framework of MSGT. Zeighampour and Tadi Beni [33] developed a strain gradient Euler–Bernoulli beam model in order to investigate the free vibrations of nano-beams made of FGMs with radius varying along the length. Mohammadimehr et al. [34] studied the free vibrations of double-bonded piezoelectric Timoshenko micro-beams based on MSGT and surface stress elasticity theory.

Recently, studying the mechanical behaviors of viscoelastic micro- and nano-structures based on the size-dependent continuum theories has attracted the attention of some researchers. Herein, some of them are cited. Lei et al. [35] studied the free vibration of damped viscoelastic Euler–Bernoulli beams based on the nonlocal theory and Kelvin–Voigt model. In another work, Lei et al. [36] developed a Timoshenko beam model to analyze the damped vibrations of nonlocal Kelvin–Voigt viscoelastic beams. The dynamic stability problem of viscoelastic nano-beams subjected to compressive axial loading was addressed by Pavlović et al. [37]. The Kelvin–Voigt model in conjunction with the nonlocal theory was applied for modeling the nano-beams in that work. Cajic et al. [38] investigated the free damped transverse vibrations of nano-beams based on the nonlocal theory and the fractional derivative viscoelasticity. In the context of nonlocal theory and fractional calculus, Ansari et al. [39, 40] analyzed the linear and nonlinear vibrations of fractional viscoelastic nano-beams.

In the current work, the linear and nonlinear vibration characteristics of fractional viscoelastic micro-/nano-beams are studied within the framework of MSGT. The nonlinear fractional viscoelastic beam model is developed on the basis of the Timoshenko beam theory, von Kármán hypothesis and the Kelvin–Voigt model. Hamilton’s principle is utilized to obtain the governing equations and associated boundary conditions which are then solved in the linear and nonlinear regimes. The GDQ and FD methods are employed for solving the linear problem. Moreover, solving the nonlinear problem is done using the Galerkin and predictor–corrector methods. In the numerical results, the effects of different parameters including fractional-order, length scale parameter and viscoelasticity coefficient on the time response of viscoelastic beams under different boundary conditions are analyzed.

2 Derivation of governing equations

Based on MSGT [27], the strain energy in a deformed isotropic linear elastic material occupying region \(\Omega \) (with a volume element V) is given by

$$\begin{aligned} U=\frac{1}{2}\int _\Omega \left( {{\upsigma }_{{ij}} \varepsilon _{ij} +{{P}}_{i} \gamma _i +\tau _{ijk}^{\left( 1 \right) } \eta _{ijk}^{\left( 1 \right) } +m_{ij}^S \chi _{ij}^S } \right) \hbox {d}V \end{aligned}$$
(1)

where the deformation measures, i.e., the strain tensor, \(\varepsilon _{ij} \), the dilatation gradient tensor, \(\gamma _i \), the deviatoric stretch gradient tensor, \(\eta _{ijk}^{\left( 1 \right) } \), and the symmetric rotation gradient tensor, \(\chi _{ij}^S \), are defined as

$$\begin{aligned} \varepsilon _{ij}= & {} \frac{1}{2}\left( {u_{i,j} +u_{j,i}} \right) , \end{aligned}$$
(2)
$$\begin{aligned} \gamma _i= & {} \varepsilon _{mm,i}, \end{aligned}$$
(3)
$$\begin{aligned} \eta _{ijk}^{\left( 1 \right) }= & {} \frac{1}{3}\left( {\varepsilon _{jk,i} +\varepsilon _{ki,j} +\varepsilon _{ij,k} } \right) \nonumber \\&-\,\frac{1}{15}\left[ \delta _{ij} \left( {\varepsilon _{mm,k} +2\varepsilon _{mk,m} } \right) \right. \nonumber \\&+\,\delta _{jk} \left( {\varepsilon _{mm,i} +2\varepsilon _{mi,m} } \right) \nonumber \\&\left. +\,\delta _{ki} \left( {\varepsilon _{mm,j} +2\varepsilon _{mj,m}} \right) \right] \end{aligned}$$
(4)
$$\begin{aligned} \chi _{ij}^S= & {} \frac{1}{2}\left( {e_{ipq} \varepsilon _{qj,p} +e_{jpq} \varepsilon _{qi,p} } \right) \end{aligned}$$
(5)

in which \(u_i \) denotes the displacement vector, \(\varepsilon _{mm} \) denotes the dilatation strain, and \(\delta _{ij} \) and \(e_{ijk} \) denote the Kronecker delta and permutation tensor, respectively. Throughout this paper, the repeated indices (subscripts) signify summation from 1 to 3.

The stress measures consist of the classical stress, \(\sigma _{ij} \), and the higher-order stresses, \({P}_i \), \(\tau _{ijk}^{\left( 1 \right) } \), and \(m_{ij}^S \), which are the work-conjugate to the deformation measures, given by the following constitutive relations

$$\begin{aligned}&\sigma _{ij} =2\mu \left( {\varepsilon _{ij} +\frac{\nu }{1-2\nu }\varepsilon _{mm} \delta _{ij} } \right) , \end{aligned}$$
(6)
$$\begin{aligned}&{P}_i =2\mu l_0^2 \gamma _i, \end{aligned}$$
(7)
$$\begin{aligned}&\tau _{ijk}^{\left( 1 \right) } =2\mu l_1^2 \eta _{ijk}^{\left( 1 \right) }, \end{aligned}$$
(8)
$$\begin{aligned}&m_{ij}^S = 2\mu l_2^2 \chi _{ij}, \end{aligned}$$
(9)

In these relations, \(\mu \) and \(\nu \) are shear modules and Poisson’s ratio, respectively. Also, \(l_0, l_1 \) and \(l_2 \) are the additional and independent material length scale parameters associated with the dilatation gradients, and symmetric rotation gradients, respectively.

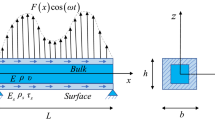
Consider a beam with length L, thickness h and width b. On the basis of the Timoshenko beam theory, the displacement field can be expressed as

$$\begin{aligned} u_1 =u\left( {x,t} \right) -z\psi \left( {x,t} \right) ,u_2 =0,u_3 =W\left( {x,t} \right) \end{aligned}$$
(10)

where u stands for the axial displacement of the centroid of sections and W is the lateral deflection of the beam. Using the von Kármán hypothesis, the strain components can be approximated as

$$\begin{aligned} \varepsilon _{11}= & {} \frac{\partial u_1 }{\partial x}+\frac{1}{2}\left( {\frac{\partial W}{\partial x}} \right) ^{2}=\frac{\partial u}{\partial x}+z\frac{\partial \psi }{\partial x}+\frac{1}{2}\left( {\frac{\partial W}{\partial x}} \right) ^{2},\nonumber \\ \gamma _{12}= & {} \frac{\partial W}{\partial x}+\psi \end{aligned}$$
(11)

Using Hamilton’s principle, the geometrically nonlinear governing equations of motion and boundary conditions of the beam with immovable supports are then derived as [41]

$$\begin{aligned}&{\overline{k_3}} \left( {\frac{\partial ^{2}W}{\partial x^{2}}+\frac{\partial \psi }{\partial x}} \right) +\left( {{\overline{k_6}} -{\overline{k_7}} } \right) \frac{\partial ^{4}W}{\partial x^{4}}\nonumber \\&\qquad +\left( {2{\overline{k_6}} +{\overline{k_7}} } \right) \frac{\partial ^{3}\psi }{\partial x^{3}}\left[ {\frac{{\overline{k_1}} }{2L}\int \limits _0^L \left( {\frac{\partial W}{\partial x}} \right) ^{2}\hbox {d}x} \right] \frac{\partial ^{2}W}{\partial x^{2}}\nonumber \\&\quad =\rho A\frac{\partial ^{2}W}{\partial t^{2}}-F\sin \left( {{\Omega }t} \right) \nonumber \\&{\overline{k_2}} \frac{\partial ^{2}\psi }{\partial x^{2}}-{\overline{k_3}} \left( {\frac{\partial W}{\partial x}+\psi } \right) -{\overline{k_4}} \frac{\partial ^{4}\psi }{\partial x^{4}}\nonumber \\&\qquad -\left( {{\overline{k_7}} -2{\overline{k_6}} } \right) \frac{\partial ^{3}W}{\partial x^{3}}+\left( {{\overline{k_7}} +4{\overline{k_6}} } \right) \frac{\partial ^{2}\psi }{\partial x^{2}}=\rho I\frac{\partial ^{2}\psi }{\partial t^{2}}\nonumber \\&\left( {\overline{k_2}} \frac{\partial \psi }{\partial x}-{\overline{k_4}} \frac{\partial ^{3}\psi }{\partial x^{3}}+\left( {{\overline{k_7}} -2{\overline{k_6}} } \right) \frac{\partial ^{2}W}{\partial x^{2}}\right. \nonumber \\&\qquad \left. +\left( {{\overline{k_7}} +4{\overline{k_6}} } \right) \frac{\partial \psi }{\partial x} \right) =0 \; or \;\delta \psi =0 \nonumber \\&{\overline{k_3}} \left( {\frac{\partial W}{\partial x}+\psi } \right) -\left( {{\overline{k_6}} +{\overline{k_7}} } \right) \frac{\partial ^{3}W}{\partial x^{3}}\nonumber \\&\qquad +\left( {2{\overline{k_6}} -{\overline{k_7}} } \right) \frac{\partial ^{2}\psi }{\partial x^{2}}=0\; or \; \delta W=0 \nonumber \\&{\overline{k_4}} \frac{\partial ^{2}\psi }{\partial x^{2}}=0 \; or \; \delta \left( {\frac{\partial \psi }{\partial x}} \right) =0\nonumber \\&\left( {{\overline{k_6}} +{\overline{k_7}} } \right) \frac{\partial ^{2}W}{\partial x^{2}}+\left( {{\overline{k_7}} -2{\overline{k_6}} } \right) \frac{\partial \psi }{\partial x}\nonumber \\&\quad =0 ~ { or} ~ \delta \left( {\frac{\partial W}{\partial x}} \right) =0 \end{aligned}$$
(12)

where \(F\sin \left( {{\Omega }t} \right) \) is related to the forced vibration problem, and

$$\begin{aligned} {\overline{k_1}}= & {} EA, \quad {\overline{k_2}} =EI+2\mu Al_0^2, \quad {\overline{k_3}} =k_s \mu A,\nonumber \\ {\overline{k_4}}= & {} \mu I\left( {2l_0^2 +\frac{4}{5}l_1^2 } \right) ,\quad {\overline{k_5}} =\mu A\left( {2l_0^2 +\frac{4}{5}l_1^2 } \right) ,\nonumber \\ {\overline{k_6}}= & {} \frac{8}{15}\mu Al_1^2, \quad {\overline{k_7}} =\frac{1}{4}\mu Al_2^2 \end{aligned}$$
(13)

Based on the fractional Kelvin–Voigt viscoelastic model, E and \(\mu \) are replaced with \(E\left( 1+\bar{{g}} \frac{\partial ^{\alpha }}{\partial {t}^{\alpha }} \right) \) and \(\mu \left( 1+\bar{{g}} \frac{\partial ^{\alpha }}{\partial {t}^{\alpha }} \right) \), where \(\bar{{g}} \) and \(\alpha \) indicate the viscoelasticity coefficient and fractional derivative order, respectively. Furthermore, the fractional derivative is defined as [42]

$$\begin{aligned} D_t^\alpha \left( w \right) =I^{1-\alpha }\left( \dot{w}\right)= & {} \frac{1}{\varGamma \left( 1-\alpha \right) }\int _0^t \frac{{w'\left( {t - \tau } \right) }}{{{\tau ^{\alpha }}}}\hbox {d}\tau \nonumber \\&+\, \frac{{w\left( 0 \right) }}{{\varGamma \left( {1 - \alpha } \right) {t^\alpha }}},\quad 0< \alpha < 1\nonumber \\ \end{aligned}$$
(14)

Accordingly, the governing equations of the fractional viscoelastic Timoshenko beam on the basis of the strain gradient theory and the Kelvin–Voigt linear viscoelastic model can be obtained as

$$\begin{aligned}&\left( {1+\bar{{g}} \frac{\partial ^{{\alpha }}}{\partial {t}^{{\alpha }}}} \right) \left\{ {\overline{k_3}} \left( {\frac{\partial ^{2}W}{\partial x^{2}}+\frac{\partial \psi }{\partial x}} \right) \right. \nonumber \\&\quad +\left( {{\overline{k_6}} -{\overline{k_7}}} \right) \frac{\partial ^{4}W}{\partial x^{4}}+\left( {2{\overline{k_6}}+{\overline{k_7}} } \right) \frac{\partial ^{3}\psi }{\partial x^{3}}\nonumber \\&\quad \left. +\left[ {\frac{{\overline{k_1}} }{2L} \int \limits _0^L \left( {\frac{\partial W}{\partial x}} \right) ^{2}\hbox {d}x} \right] \frac{\partial ^{2}W}{\partial x^{2}} \right\} \nonumber \\&\quad =\rho A\frac{\partial ^{2}W}{\partial t^{2}}-F\sin \left( {{\Omega }t} \right) \end{aligned}$$
(15a)
$$\begin{aligned}&\left( {1+\bar{{g}} \frac{\partial ^{{\alpha }}}{\partial {t}^{{\alpha }}}} \right) \left[ {\overline{k_2}} \frac{\partial ^{2}\psi }{\partial x^{2}}-{\overline{k_3}} \left( {\frac{\partial W}{\partial x}+\psi } \right) \right. \nonumber \\&\quad -\,{\overline{k_4}} \frac{\partial ^{4}\psi }{\partial x^{4}}-\left( {{\overline{k_7}} -2 {\overline{k_6 }}} \right) \frac{\partial ^{3}W}{\partial x^{3}}\nonumber \\&\quad \left. +\left( {{\overline{k_7}} +4{\overline{k_6}} } \right) \frac{\partial ^{2}\psi }{\partial x^{2}} \right] =\rho I\frac{\partial ^{2}\psi }{\partial t^{2}} \end{aligned}$$
(15b)

Introducing the following dimensionless parameters

$$\begin{aligned} w= & {} \frac{W}{L}, \zeta =\frac{x}{L}, O=L^{2}\sqrt{\frac{\rho A}{EI}}, \left\{ {\ell _0, \ell _1, \ell _2 } \right\} \nonumber \\= & {} \frac{\left\{ {l_0, l_1, l_2 } \right\} }{L}, \left\{ {\tau , {g}} \right\} =\frac{\left\{ {t, \bar{{g}} } \right\} }{O}, k_1 =\frac{AL^{2}}{I}, \nonumber \\ k_2= & {} \frac{\left( {EI+2\mu AL^{2}\ell _0^2 } \right) }{EI}, k_3 =\frac{k_s \mu AL^{2}}{EI},\nonumber \\ k_4= & {} \frac{\mu \left( {2\ell _0^2 +\frac{4}{5}\ell _1^2 } \right) }{EI}, \nonumber \\ k_5= & {} \frac{\mu A\left( {2\ell _0^2 +\frac{4}{5}\ell _1^2 } \right) L^{2}}{EI}, k_6 =\frac{8\mu AL^{2}\ell _1^2 }{15EI}, \nonumber \\ k_7= & {} \frac{\mu AL^{2}\ell _2^2 }{4EI},\nonumber \\ f= & {} \frac{FL^{3}}{EI}, \omega = {\Omega }\times O \end{aligned}$$
(16)

Equation (15) can be rewritten in the following dimensionless form

$$\begin{aligned}&\left( {1+{g}\frac{\partial ^{{\alpha }}}{\partial {\tau }^{{\alpha }}}} \right) \left[ k_3 \left( {\frac{\partial ^{2}w}{\partial \zeta ^{2}}+\frac{\partial \psi }{\partial \zeta }} \right) +\left( {k_6 -k_7 } \right) \frac{\partial ^{4}w}{\partial \zeta ^{4}}\right. \nonumber \\&\left. \qquad +\left( {2k_6 +k_7} \right) \frac{\partial ^{3}\psi }{\partial \zeta ^{3}}+\left[ {\frac{k_1 }{2}\int \limits _0^1 \left( {\frac{\partial w}{\partial \zeta }} \right) ^{2}\hbox {d}\zeta } \right] \frac{\partial ^{2}w}{\partial \zeta ^{2}} \right] \nonumber \\&\quad =\frac{\partial ^{2}W}{\partial \tau ^{2}}+f\sin \left( {\omega \tau } \right) \end{aligned}$$
(17a)
$$\begin{aligned}&\left( {1+{g}\frac{\partial ^{{\alpha }}}{\partial {\tau }^{{\alpha }}}} \right) \left[ k_2 \frac{\partial ^{2}\psi }{\partial x^{2}}-k_3 \left( {\frac{\partial W}{\partial x}+\psi } \right) \right. \nonumber \\&\qquad -\,k_4 \frac{\partial ^{4}\psi }{\partial x^{4}}-\left( {k_7 -2k_6 } \right) \frac{\partial ^{3}W}{\partial x^{3}}\nonumber \\&\qquad \left. +\left( {k_7 +4k_6 } \right) \frac{\partial ^{2}\psi }{\partial x^{2}} \right] =\frac{1}{k_1 }\frac{\partial ^{2}\psi }{\partial \tau ^{2}} \end{aligned}$$
(17b)

3 Solution approaches

3.1 Linear analysis

First, the linear vibration problem of the fractional viscoelastic beam is solved. To this end, the governing equations are discretized by the GDQ and FD methods in space and time domains.

Based on the GDQ method [43], the rth-order derivative of function \(f\left( x \right) \) including N grid points in the domain is approximated as

$$\begin{aligned} \left. {\frac{\partial ^{r}f\left( x \right) }{\partial x^{r}}} \right| _{x=x_i } =\sum _{j=1}^N \mathcal {W}_{ij}^{\left( r \right) } f\left( {x_j } \right) \end{aligned}$$
(18)

in which \(x_j \) signifies the coordinates of a discrete grid point in the variable domain, \(f\left( {x_j } \right) \) represents the value of function at the grid point \(x_j \), and \(\mathcal{W}_{ij}^{\left( r \right) } \) denotes the corresponding weighting coefficients which is approximated through the following formula

$$\begin{aligned} {\mathcal {W}}_{ij}^{\left( r \right) } =\left\{ {\begin{array}{l} \mathbf{I}_x,\quad \hbox {where}\; \mathbf{I}_x\; \hbox { is a }\; N\times N\; \hbox { identity matrix}, r=0 \\ \frac{\mathcal {P}\left( {x_i } \right) }{\left( {x_i -x_j } \right) \mathcal {P}\left( {x_j } \right) },\; \hbox { where } \; \mathcal {P}\left( {x_i } \right) =\mathop {\prod }_{j=1; j\ne i}^N \left( {x_i -x_j } \right) , i\ne j \;\hbox {and }\;i,j= 1,\ldots ,N \\ r\left[ {\mathcal{W}_{ij}^{\left( 1 \right) } \mathcal{W}_{ii}^{\left( {r-1} \right) } -\frac{\mathcal{W}_{ij}^{\left( {r-1} \right) } }{x_i -x_j }} \right] , i\ne j\; \hbox {and }\;i,j= 1,\ldots ,N\; \hbox {and}\; r=2,3,\ldots N \\ -\sum _{j=1; j\ne i}^N {\mathcal {W}}_{ij}^{\left( r \right) }, i=j \;\hbox {and }\;i,j= 1,\ldots ,N\; \hbox {and}\; r=1,2,3,\ldots N-1 \\ \end{array}} \right. \end{aligned}$$
(19)

By inserting the function values \(f\left( {x_j } \right) \) in a column vector as follows

$$\begin{aligned} \mathbf{F}=\left[ {f\left( {x_1 } \right) }\quad {f\left( {x_2 } \right) }\quad \cdots \quad {f\left( {x_N } \right) } \right] ^{\mathrm{T}} \end{aligned}$$
(20)

Equation (18) is rewritten as

$$\begin{aligned} \frac{\hbox {d}^{r}}{\hbox {d}x^{r}}{} \mathbf{F}=\mathbf{D}_x^{\left( r \right) } \mathbf{F} \end{aligned}$$
(21)

in which \(\mathbf{D}_x^{\left( r \right) } =\left[ {{\mathcal {W}}_{ij}^{\left( r \right) } } \right] \) is the operational matrix of differentiation, \(i,j=1,\ldots ,N \) and \( r=0,1,2,\ldots ,N-1\).

Now, the FD scheme is employed. The fractional-order derivative of a function at time t can be calculated according to the values of the function at times before t as [44]

$$\begin{aligned}&\frac{1}{{{{\Gamma }}\left( {1 - \alpha } \right) }} {\int }_0^{{t_{k + 1}}} \frac{{w'\left( {{t_{k + 1}} - \tau } \right) }}{{{\tau ^{~\alpha }}}}\hbox {d}\tau \nonumber \\&\quad = \frac{{{\tau ^\alpha }}}{{{{\Gamma }}\left( {2 - \alpha } \right) }}\sum _{j = 0}^k b_j^\alpha \left[ {w\left( {{t_{k + 1 - j}}} \right) - w\left( {{t_{k - j}}} \right) } \right] \nonumber \\&b_j^\alpha =\left( {j+1} \right) ^{1-\alpha }-j^{1-\alpha },\quad j=0,1,2,\ldots , n \end{aligned}$$
(22)

In this equation, \(0<\alpha <1\) is the order of fractional derivative, \(\tau \) is time step, and \(n+1\) is number of grid points.

In order to discretize the space domain, the grid points are generated via the shifted Chebyshev–Gauss–Lobatto equations as

$$\begin{aligned} \zeta _i =\frac{1}{2}\left( {1-\cos \frac{i-1}{n-1}\pi } \right) ,\quad i=1, 2, 3, \ldots , n \end{aligned}$$
(23)

In addition, the grid points in the time domain are located with invariant distances given by

$$\begin{aligned} \tau _j =j\frac{T}{m+1},\quad j=0, 2, 3, \ldots , m \end{aligned}$$
(24)

Now, introducing matrices \(\mathbf{W}\) and \({{\varvec{\uppsi }}}\) as

$$\begin{aligned} \mathbf{W}= & {} \left[ {{\begin{array}{cccc} {w_{10} }&{}\quad {w_{12} }&{}\quad \cdots &{}\quad {w_{1n} } \\ {w_{20} }&{}\quad \ddots &{}\quad \ddots &{}\quad {w_{2n} } \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ {w_{m0} }&{}\quad {w_{m2} }&{}\quad \cdots &{}\quad {w_{mn} } \\ \end{array} }} \right] , \quad \nonumber \\ {{\varvec{\uppsi }}}= & {} \left[ {{\begin{array}{cccc} {\theta _{10} }&{}\quad {\theta _{12} }&{}\quad \cdots &{}\quad {\theta _{1n} } \\ {\theta _{20} }&{}\quad \ddots &{}\quad \ddots &{}\quad {\theta _{2n} } \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ {\theta _{m0} }&{}\quad {\theta _{m2} }&{}\quad \cdots &{}\quad {\theta _{mn} } \\ \end{array} }} \right] , \nonumber \\ i= & {} 1 \ldots m, j=0 \ldots n \end{aligned}$$
(25)

in which \(w_{ij} =w\left( {x_i, t_j } \right) \) and using the GDQ and FD methods, one can arrive at

$$\begin{aligned}&\left[ k_3 \left( {\mathbf{D}_{\zeta }^2 \mathbf{W}\left( {\mathbf{I}_t^\mathrm{T} +g\mathbf{D}_{\tau }^{{\alpha }^{\mathrm{T}}}} \right) + \mathbf{D}_{\zeta }^1 {{\varvec{\uppsi }} }\left( {\mathbf{I}_t^\mathrm{T} +g\mathbf{D}_{\tau }^{{\alpha } ^{\mathrm{T}}}} \right) } \right) \right. \nonumber \\&\quad + \left( {k_6 -k_7 } \right) \mathbf{D}_{\zeta }^4 \mathbf{W}\left( {\mathbf{I}_t^\mathrm{T} +g\mathbf{D}_{\tau }^{{\alpha } ^{\mathrm{T}}}} \right) \nonumber \\&\quad \left. {+\left( {2k_6 +k_7 } \right) \mathbf{D}_{\zeta }^3 {{\varvec{\uppsi }} }\left( {\mathbf{I}_t^\mathrm{T} +g\mathbf{D}_{\tau }^{{\alpha }^{\mathrm{T}}}} \right) } \right] \nonumber \\&\quad +\,g\left( {\frac{1}{{\Gamma }\left( {1-\alpha } \right) {{\varvec{\tau }} }^{\alpha }}} \right) \nonumber \\&\quad \otimes \left( k_3 \mathbf{D}_{\zeta }^1 {{\varvec{\uppsi }} }_\mathbf{0} +k_3 \mathbf{D}_{\zeta }^2 \mathbf{W}_\mathbf{0} +\left( {k_6 -k_7 } \right) \mathbf{D}_{\zeta }^4 \mathbf{W}_\mathbf{0}\right. \nonumber \\&\quad \left. +\left( {2k_6 +k_7 } \right) \mathbf{D}_{\zeta }^3 {{\varvec{\uppsi }} }_\mathbf{0} \right) ^{T} \nonumber \\&\qquad = \mathbf{I}_\zeta \mathbf{WD}_{\tau }^{2^{\mathrm{T}}}+\sin \left( {\omega {\varvec{\tau }} } \right) \otimes {{\varvec{f}}}\left( \zeta \right) \end{aligned}$$
(26a)
$$\begin{aligned}&\left[ k_2 \mathbf{D}_{\zeta }^2 {{\varvec{\uppsi }} }\left( {\mathbf{I}_t^\mathrm{T} +g\mathbf{D}_{\tau }^{{\alpha } ^{\mathrm{T}}}} \right) -k_3 \left( \mathbf{D}_{\zeta }^1 \mathbf{W}\left( {\mathbf{I}_t^\mathrm{T} +g\mathbf{D}_{\tau }^{{\alpha }^{\mathrm{T}}}} \right) \right. \right. \nonumber \\&\left. +\,\mathbf{I}_\zeta {{\varvec{\uppsi }} }\left( {\mathbf{I}_t^\mathrm{T} +g\mathbf{D}_{\tau }^{{\alpha } ^{\mathrm{T}}}} \right) \right) -\,k_4 \mathbf{D}_{\zeta }^4 {{\varvec{\uppsi }} }\left( {\mathbf{I}_t^\mathrm{T} +g\mathbf{D}_{\tau }^{{\alpha }^{\mathrm{T}}}} \right) \nonumber \\&\qquad -\left( {k_7 -2k_6 } \right) \mathbf{D}_{\zeta }^3 \mathbf{W}\left( {\mathbf{I}_t^\mathrm{T} +g\mathbf{D}_{\tau }^{{\alpha }^{\mathrm{T}}}} \right) \nonumber \\&\qquad \left. {+\left( {k_7 +4k_6 } \right) \mathbf{D}_{\zeta }^2 {{\varvec{\uppsi }} }\left( {\mathbf{I}_t^\mathrm{T} +g\mathbf{D}_{\tau }^{{\alpha }^{\mathrm{T}}}} \right) } \right] \nonumber \\&\qquad +\,g\left( {\frac{1}{{\Gamma }\left( {1-\alpha } \right) {{\varvec{\tau }} }^{\alpha }}} \right) \nonumber \\&\qquad \otimes \left( k_2 \mathbf{D}_{\zeta }^2 {{\varvec{\uppsi }} }_\mathbf{0} -k_3 \mathbf{D}_{\zeta }^1 \mathbf{W}_\mathbf{0} -k_4 \mathbf{D}_{\zeta }^4 {{\varvec{\uppsi }} }_\mathbf{0} -k_3 \mathbf{I}_\zeta {{\varvec{\uppsi }}}_\mathbf{0}\right. \nonumber \\&\left. -\left( {k_7 -2k_6 } \right) \mathbf{D}_{\zeta }^3 \mathbf{W}_\mathbf{0} \right) ^{T} \nonumber \\&\qquad =\frac{1}{k_1 }{} \mathbf{I}_\zeta {{\varvec{\uppsi }} \mathbf{D}}_{\tau }^{2^{\mathrm{T}}} \end{aligned}$$
(26b)
$$\begin{aligned}&\left( {k_2 \mathbf{D}_{\zeta }^1 {{\varvec{\uppsi }} }-k_4 \mathbf{D}_{\zeta }^3 {{\varvec{\uppsi }} }+\left( {k_7 -2k_6 } \right) \mathbf{D}_{\zeta }^2 \mathbf{W}+\left( {k_7 +4k_6 } \right) \mathbf{D}_{\zeta }^1 {{\varvec{\uppsi }} }} \right) \nonumber \\&\left( {\mathbf{I}_t^\mathrm{T} +g\mathbf{D}_{\tau }^{{\alpha } ^{\mathrm{T}}}} \right) =0 \quad \hbox {or}\quad \delta \psi =0 \end{aligned}$$
(26c)
$$\begin{aligned}&\left( {k_3 \left( {\mathbf{D}_{\zeta }^1 \mathbf{W}+{{\varvec{\uppsi }} }} \right) -\left( {k_6 +k_7 } \right) \mathbf{D}_{\zeta }^3 \mathbf{W}+\left( {2k_6 -k_7 } \right) \mathbf{D}_{\zeta }^2 {{\varvec{\uppsi }} }} \right) \nonumber \\&\left( {\mathbf{I}_t^\mathrm{T} +g\mathbf{D}_{\tau }^{{\alpha } ^{\mathrm{T}}}} \right) =0 \quad \hbox {or}\quad \delta W=0 \end{aligned}$$
(26d)
$$\begin{aligned}&k_4 \mathbf{D}_{\zeta }^2 {{\varvec{\uppsi }} }\left( {\mathbf{I}_t^\mathrm{T} +g\mathbf{D}_{\tau }^{{\alpha }^{\mathrm{T}}}} \right) =0 \quad \hbox {or} \quad \delta \left( {\mathbf{D}_{\zeta }^1 {{\varvec{\uppsi }} }} \right) =0 \end{aligned}$$
(26e)
$$\begin{aligned}&\left( {\left( {k_6 +k_7 } \right) \mathbf{D}_{\zeta }^2 \mathbf{W}+\left( {k_7 -2k_6 } \right) \mathbf{D}_{\zeta }^1 {{\varvec{\uppsi }} }} \right) \left( {\mathbf{I}_t^\mathrm{T} +g\mathbf{D}_{\tau }^{{\alpha }^{\mathrm{T}}}} \right) =0 \;\nonumber \\&\quad \hbox {or} \quad \delta \left( {\mathbf{D}_{\zeta }^1 \mathbf{W}} \right) =0 \end{aligned}$$
(26f)

In these equations, \({{\varvec{\uppsi }} }_\mathbf{0} \) and \(\mathbf{W}_\mathbf{0} \) are the initial values of W and \(\psi \); \({{\varvec{\tau }} }\) is the vector of time; \(\otimes \) shows the Kronecker product; \(\mathbf{I}\) denotes the unit matrix; and \(\mathbf{D}_{t}^{\alpha } \) is the fractional derivative operator of order \(\alpha \).

For solving Eqs. (26a) and (26b), both initial displacement and initial velocity must be known. Herein, the mode shape corresponding to the linear vibration of elastic beam is used as the initial displacement, and the initial velocity is considered to be zero. Then, by applying the discretized boundary conditions to the governing equations, an algebraic set of equations is achieved from which the unknown matrices \(\mathbf{W}\) and \({{\varvec{\uppsi }} }\) can be determined.

3.2 Nonlinear analysis

In this subsection, the nonlinear problem is solved. To accomplish this aim, the Galerkin method is utilized first so as to convert the fractional integro-partial differential governing equations into fractional ordinary differential equations. In the next step, the obtained equations are arranged in an effective state-space form. Finally, the predictor–corrector method is used to solve the set of nonlinear fractional time-dependent equations and obtain the time response of fractional viscoelastic beam.

For the fractional viscoelastic beam under simply supported boundary conditions at two ends, the solution of Eq. (17) can be expressed as follows

$$\begin{aligned} w\left( {\zeta , \tau } \right)= & {} \sum _{n=1}^\infty \varphi _n \left( \tau \right) p_n\nonumber \\ {\psi }\left( {\zeta , \tau } \right)= & {} \sum _{n=1}^\infty \theta _n \left( \tau \right) {\Gamma }_{n} \end{aligned}$$
(27)

in which \(\varphi _n \left( \tau \right) \) indicates the time-dependent function; \(p_n = \sin \left( {n\pi \zeta } \right) \) and \({\Gamma }_{n} = \cos \left( {n\pi x} \right) \) are the mode functions corresponding to the simply supported fractional viscoelastic beam. The function of exciting force is considered as \(f=f_1 p_1 \left( \zeta \right) \).

Substitution of Eq. (27) into (17) and applying the Galerkin method for the resulting equation give the following fractional ordinary differential equations

$$\begin{aligned}&\left[ k_3 \left( \left\{ {\sum _{j=1}^N \int _0^1 p_i p_j^{{\prime }{\prime }} \hbox {d}\zeta } \right\} \left( {\varphi _j +\tau \varphi _j^{\left( \alpha \right) } } \right) \right. \right. \nonumber \\&\qquad \left. +\left\{ {\sum _{j=1}^N \int _0^1 p_i {\Gamma }_j^{\prime } \hbox {d}\zeta } \right\} \left( {\varTheta _j +{g}\varTheta _j^{\left( \alpha \right) } } \right) \right) \nonumber \\&\qquad +\left( {k_6 -k_7 } \right) \left\{ {\sum _{j=1}^N \int _0^1 p_i p_j^{IV} \hbox {d}\zeta } \right\} \left( {\varphi _j +\tau \varphi _j^{\left( \alpha \right) } } \right) \nonumber \\&\qquad +\left( {2k_6 +k_7 } \right) \left\{ {\sum _{j=1}^N \int _0^1 p_i {\Gamma }_j^{{\prime }{\prime }{\prime }} \hbox {d}\zeta } \right\} \left( {\varTheta _j +{g}\varTheta _j^{\left( \alpha \right) } } \right) \nonumber \\&\qquad +\left\{ \frac{k_1 }{2}\left\{ {\sum _{j=1}^N \sum _{k=1}^N \sum _{l=1}^N \int _0^1 p_i p_j^{{\prime }{\prime }} \hbox {d}\zeta \int _0^1 p_k^{\prime } p_l^{\prime } \hbox {d}\zeta } \right\} \right. \nonumber \\&\qquad \left. \left. \left( {\varphi _j \varphi _k \varphi _l +g\varphi _j \left( {\varphi _k \varphi _l } \right) ^{\left( \alpha \right) }} \right) \right\} \right] \nonumber \\&\quad =\left( {\sum _{j=1}^N \int _0^1 p_i p_j \hbox {d}\zeta } \right) \ddot{\varphi _j} +\left( {\sum _{j=1}^N \int _0^1 f_1 p_1 p_j \hbox {d}\zeta } \right) \nonumber \\&\sin \left( {\omega \tau } \right) \nonumber \\&\left[ {k_2 \left\{ {\sum _{j=1}^N \int _0^1 {\Gamma }_i {\Gamma }_j^{{\prime }{\prime }} \hbox {d}\zeta } \right\} \left( {\varTheta _j +{g}\varTheta _j^{\left( \alpha \right) } } \right) } \right. \nonumber \\&\qquad -\,k_3 \left( \left\{ {\sum _{j=1}^N \int _0^1 {\Gamma }_i p_j^{\prime } \hbox {d}\zeta } \right\} \left( {\varphi _j +\tau \varphi _j^{\left( \alpha \right) } } \right) \right. \nonumber \\&\qquad \left. +\left\{ {\sum _{j=1}^N \int _0^1 {\Gamma }_i {\Gamma }_j \hbox {d}\zeta } \right\} \left( {\varTheta _j +{g}\varTheta _j^{\left( \alpha \right) } } \right) \right) \nonumber \\&\qquad -\,k_4 \left\{ {\sum _{j=1}^N \int _0^1 {\Gamma }_i {\Gamma }_j^{IV} \hbox {d}\zeta } \right\} \left( {\varTheta _j +{g}\varTheta _j^{\left( \alpha \right) } } \right) \nonumber \\&\qquad -\left( {k_7 -2k_6 } \right) \left\{ {\sum _{j=1}^N \int _0^1 {\Gamma }_i p_j^{{\prime }{\prime }{\prime }} \hbox {d}\zeta } \right\} \left( {\varphi _j +{g}\varphi _j^{\left( \alpha \right) } } \right) \nonumber \\&\qquad \left. {+\left( {k_7 +4k_6 } \right) \left\{ {\sum _{j=1}^N \int _0^1 {\Gamma }_i {\Gamma }_j^{{\prime }{\prime }} \hbox {d}\zeta } \right\} \left( {\varTheta _j +{g}\varTheta _j^{\left( \alpha \right) } } \right) } \right] \nonumber \\&\quad =\frac{1}{k_1 }\left\{ {\sum _{j=1}^N \int _0^1 {\Gamma }_i {\Gamma }_j \hbox {d}\zeta } \right\} \ddot{\varTheta _j } \end{aligned}$$
(28)

Considering the following relations

$$\begin{aligned} {X_{i1}}= & {} {\varphi _i},\quad {X_{i2}} = {{\dot{\varphi } }_i},\quad {X_{i3}} = \varphi _i^{\left( \alpha \right) },\nonumber \\ {X_{im}}= & {} {\left( {{\varphi _i}{\varphi _{m - 3}}} \right) ^{\left( \alpha \right) }},\quad {X_{i5}} = {\theta _i},\nonumber \\ {X_{i6}}= & {} {{\dot{\theta } _i}},\quad {X_{i7}} = \theta _i^{\left( \alpha \right) } \end{aligned}$$
(29)

Equation (28) can be expressed in the following state-space form

$$\begin{aligned} \begin{aligned}&\frac{\partial X_{j1} }{\partial {t}} = X_{j2} \\&\frac{\partial X_{j2} }{\partial {t}} = \frac{\left[ {k_3 \left\{ {{\sum }_{j=1}^N {\int }_0^1 p_i p_j^{{\prime }{\prime }} \hbox {d}\zeta } \right\} \left( {k_6 -k_7 } \right) \left\{ {{\sum }_{j=1}^N {\int }_0^1 p_i p_j^{IV} \hbox {d}\zeta } \right\} } \right] \left( {X_{j1} +g\left( {X_{j3} +\frac{X_{j1_{0}} }{{\Gamma }\left( {1-\alpha } \right) t^{\alpha }}} \right) } \right) }{\left( {{\sum }_{j=1}^N {\int }_0^1 p_i p_j \hbox {d}\zeta } \right) }\\&\quad \quad \quad \quad +\frac{\frac{k_1 }{2}\left\{ {{\sum }_{j=1}^N {\sum }_{k=1}^N {\sum }_{l=1}^N {\int }_0^1 p_i p_j^{{\prime }{\prime }} \hbox {d}\zeta {\int }_0^1 p_k^{\prime } p_l^{\prime } \hbox {d}\zeta } \right\} \left\{ {X_{j1} X_{k1} X_{l1} +gX_{j1} \left( {X_{km} +\frac{X_{k1_{0}} X_{m1_{0}} }{{\Gamma }\left( {1-\alpha } \right) t^{\alpha }}} \right) } \right\} }{\left( {{\sum }_{j=1}^N {\int }_0^1 p_i p_j \hbox {d}\zeta } \right) } \\&\quad \quad \quad \quad +\frac{\left[ {\left( {2k_6 +k_7 } \right) +k_3 \left\{ {{\sum }_{j=1}^N {\int }_0^1 {\Gamma }_i {\Gamma }_j^{\prime } \hbox {d}\zeta } \right\} } \right] \left\{ {{\sum }_{j=1}^N {\int }_0^1 p_i {\Gamma }_j^{{\prime }{\prime }{\prime }} \hbox {d}\zeta } \right\} \left( {X_{j5} +{g}X_{j7} } \right) }{\left( {{\sum }_{j=1}^N {\int }_0^1 p_i p_j \hbox {d}\zeta } \right) } \\&\quad \quad \quad \quad +\frac{\left( {{\sum }_{j=1}^N {\int }_0^1 f_1 p_1 p_j \hbox {d}\zeta } \right) \sin \left( {X_8 } \right) }{\left( {{\sum }_{j=1}^N {\int }_0^1 p_i p_j \hbox {d}\zeta } \right) } \\&\frac{\partial ^{1-{\alpha }}X_{i3} }{\partial {t}^{1-\alpha }} = X_{i2} \\&\frac{\partial ^{1-\alpha }X_{im} }{\partial t^{1-\alpha }} = X_{i1} X_{\left( {m-3} \right) 2} +X_{\left( {m-3} \right) 1} X_{i2}\\&\frac{\partial X_{i5} }{\partial {t}} = X_{i6} \\&\frac{\partial X_{i6} }{\partial {t}} = \frac{\left[ {-k_4 \left\{ {{\sum }_{j=1}^N {\int }_0^1 {\Gamma }_i {\Gamma }_j^{IV} \hbox {d}\zeta } \right\} +\left( {k_7 +4k_6 +k_2 } \right) \left\{ {{\sum }_{j=1}^N {\int }_0^1 {\Gamma }_i {\Gamma }_j^{{\prime }{\prime }} \hbox {d}\zeta } \right\} -k_3 \left\{ {{\sum }_{j=1}^N {\int }_0^1 {\Gamma }_i {\Gamma }_j \hbox {d}\zeta } \right\} } \right] \left( {X_{j5} + {g}X_{j7} } \right) }{\frac{1}{k_1 }\left\{ {{\sum }_{j=1}^N {\int }_0^1 {\Gamma }_i {\Gamma }_j \hbox {d}\zeta } \right\} } \\&\quad \quad \quad \quad +\frac{\left[ {-k_3 \left\{ {{\sum }_{j=1}^N {\int }_0^1 {\Gamma }_i p_j^{\prime } \hbox {d}\zeta } \right\} -\left( {k_7 -2k_6 } \right) \left\{ {{\sum }_{j=1}^N {\int }_0^1 {\Gamma }_i p_j^{{\prime }{\prime }{\prime }} \hbox {d}\zeta } \right\} } \right] \left\{ {X_{j1} +g\left( {X_{j3} +\frac{X_{j1_{0}} }{{\Gamma }\left( {1-\alpha } \right) t^{\alpha }}} \right) } \right\} }{\frac{1}{k_1 }\left\{ {{\sum }_{j=1}^N {\int }_0^1 {\Gamma }_i {\Gamma }_j \hbox {d}\zeta } \right\} } \\&\frac{\partial ^{1-{\alpha }}X_{i7} }{\partial {t}^{1-\alpha }} = X_{i6} \\&\frac{\partial X_8 }{\partial {t}} = \omega \\ \end{aligned} \end{aligned}$$
(30)

The predictor–corrector method [45] is used to solve this set of nonlinear fractional ordinary equations in the time domain. Consider the fractional differential equation and corresponding initial conditions as

$$\begin{aligned} \left\{ {{\begin{array}{ll} D^{\alpha }x\left( t \right) =f\left( {t,x\left( t \right) } \right) , &{} 0\le t<T \\ x^{\left( k \right) }\left( 0 \right) =x_0^{\left( k \right) }, &{}k=0,1,2,\ldots ,n-1 \\ \end{array} }} \right. \end{aligned}$$
(31)

where \(n=\lceil \alpha \rceil \) shows the first integer which is not less than \(\alpha \) and \(\alpha >0\), but not necessarily \(\alpha \in N\). Moreover, \(x^{\left( k \right) }\) is the ordinary kth derivative of \(x\left( t \right) \).

Equation (31) can be rewritten as an equivalent Volterra integral equation and is defined by the following equation

$$\begin{aligned} x\left( t \right) =\sum _{k=0}^{n-1} \frac{x_0^{\left( k \right) } t^{k}}{k!}+\frac{1}{{\Gamma }\left( \alpha \right) }\int _0^t \left( {t-\tau } \right) ^{\alpha -1}f\left( {\tau , x\left( t \right) } \right) \hbox {d}\tau \nonumber \\ \end{aligned}$$
(32)

The integral form of fractional governing equation can be discretized in the time domain. To this end, the time domain grid points are written as

$$\begin{aligned} t_j =j\times t_s ; \quad t_s =\frac{T}{N}, \quad j=0,1,2,\ldots , N\in Z^{+} \end{aligned}$$
(33)

where N denotes the number of total grid points. For the discretized form of Eq. (32), one has

$$\begin{aligned}&x_h \left( {t_{n+1} } \right) = \sum _{k=0}^{\lceil \alpha \rceil -1} \frac{x_0^{\left( k \right) } t^{k}}{k!}\nonumber \\&\qquad +\frac{t_s^\alpha }{{\Gamma }\left( {\alpha +2} \right) }f\left( {t_{n+1}, x_h^p \left( {t_{n+1} } \right) } \right) \nonumber \\&\qquad +\,\frac{t_s ^{\alpha }}{{\Gamma }\left( {\alpha +2} \right) }\sum _{j=0}^n a_{j,n+1} f\left( {t_j, x_h \left( {t_j } \right) } \right) \nonumber \\&a_{j,n+1}=\left\{ \begin{array}{ll} n^{\alpha +1}-\left( {n-\alpha } \right) \left( {n+1} \right) ^{\alpha }, &{} j=0 \\ \left( {n-j+2} \right) ^{\alpha +1}+\left( {n-j} \right) ^{\alpha +1}-2\left( n-j+1 \right) ^{\alpha +1}, &{} 1\le j\le n \\ 1, &{} j=n+1 \\ \end{array} \right. \nonumber \\&x_h^p \left( {t_{n+1} } \right) = \sum _{k=0}^{\lceil \alpha \rceil -1} \frac{x_0^{\left( k \right) } t^{k}}{k!}\nonumber \\&\qquad +\frac{1}{{\Gamma }\left( \alpha \right) }\sum _{j=0}^n b_{j,n+1} f\left( {t_j, x_h \left( {t_j } \right) } \right) \nonumber \\&b_{j,n+1}= \frac{t_s ^{\alpha }}{\alpha }\left( {\left( {n-j+1} \right) ^{\alpha }-\left( {n-j} \right) ^{\alpha }} \right) , 1\le j\le n \end{aligned}$$
(34)

The aforementioned procedure is the well-known Adams–Bashforth–Moulton predictor–corrector scheme [46–48].

4 Results and discussion

In this section, selected numerical results are presented on the linear and nonlinear time responses of the fractional viscoelastic small-scale beams. C-C, C-SS and SS-SS end conditions are considered (simply supported and clamped ends are abbreviated to SS and C, respectively). It is assumed that \(E=427\,\hbox {GPa}\), \(\nu =0.17\) and \(\rho =3100\,\hbox {kg}/\hbox {m}^{3}\) [41].

Lam et al. [27] conducted experimental tests to evaluate the length scale parameter for an isotropic homogeneous micro-beam. They assumed that all the material length scale parameters are the same, i.e., \(l_0 =l_1 =l_2 =l\), and obtained \(l=17.6\;\upmu \hbox {m}\). However, to the authors’ knowledge, there are no available experimental data for the length scale parameters of viscoelastic micro-beams in the open literature. Hence, in order to quantitatively investigate the size effect on the behavior of viscoelastic small-scale beams, the values of length scale parameters are approximately assumed to be equal to \(l_0 =l_1 =l_2 =l=15\;\upmu \hbox {m}\) in the following examples. It should be noted that by choosing these parameters equal to zero, the governing equations based on the classical elasticity theory will be achieved. Also, by letting \(l_0 = l_1 =0\) and \(l_2 =l\), the governing equations based on modified couple stress theory are obtained.

Fig. 1
figure 1

Nonlinear time response of free vibration of the SS-SS fractional viscoelastic beam obtained by different numbers of terms used in the Galerkin method \(\left( {\mathbf {{g}=0.03}}, \frac{{{\varvec{h}}}}{{{\varvec{l}}}}=\mathbf{1}\right) \)

Full size image

In Fig. 1, the nonlinear time responses of free vibration of SS-SS beam based on different numbers of terms used in the Galerkin method [see Eq. (27)] are shown. It is observed that there is no considerable difference between the results corresponding to different numbers of terms employed in the Galerkin procedure. Therefore, one term will be used to generate the results provided.

Fig. 2
figure 2

Linear time response of free vibration of the SS-SS fractional viscoelastic beam obtained by different numbers of grid points \(\left( {\varvec{\alpha }} ={} \mathbf{0.5}, \mathbf{g}=\mathbf{0.03}, \frac{{{\varvec{h}}}}{{{\varvec{l}}}}={} \mathbf{1}\right) \)

Full size image

In addition, in Fig. 2, the convergence of results is checked in which the linear time response of free vibration of SS-SS beam is shown for different numbers of grid points. This figure indicates quite clearly the converging trend of the present numerical approach. Besides, one can find that 13 grid points are enough to obtain converged results.

Fig. 3
figure 3

Nonlinear time response of free vibration of the SS-SS fractional viscoelastic beam obtained based on different time steps \(\left( {\varvec{\alpha }} ={} \mathbf{0.5}, \mathbf{g}=\mathbf{0.03}, \frac{{{\varvec{h}}}}{{{\varvec{l}}}}={} \mathbf{1}\right) \)

Full size image

The influence of time step size is shown in Fig. 3. The calculations reveal that by choosing the time step larger than 0.001, the solution becomes unstable. But, for time steps smaller than 0.001, stable solutions are obtained. As shown in Fig. 3, there is no significant difference between the results by selecting different time steps smaller than 0.001, so the time step is taken to be 0.001.

Fig. 4
figure 4

Time response of free vibration of the SS-SS fractional viscoelastic beam obtained by the FD and predictor–corrector methods for different fractional orders \(\left( \mathbf{g}=\mathbf{0.03}, \frac{{{\varvec{h}}}}{{{\varvec{l}}}}=\mathbf{1}, \frac{{{\varvec{L}}}}{{{\varvec{h}}}}=\mathbf{10}, {{\varvec{b}}}={\varvec{2h}}\right) \)

Full size image

In Fig. 4, the time responses of the SS-SS beam obtained by the FD and predictor–corrector methods are shown for different fractional orders. It is observed that there is a good agreement between the results of two solution methods.

Fig. 5
figure 5

Comparison between the linear and nonlinear time responses of free vibration of SS-SS fractional viscoelastic beam with different initial displacements \(\left( \frac{{\varvec{h}}}{{\varvec{l}}}=\mathbf{1}, \frac{{{\varvec{L}}}}{{{\varvec{h}}}}=\mathbf{10}, {{\varvec{\alpha }} }=\mathbf{0.5}, {{\varvec{b}}}={\varvec{2h}}\right) \)

Full size image
Fig. 6
figure 6

Effect of fractional order on the nonlinear time response of free vibration of the fractional viscoelastic beam with SS-SS boundary conditions \(\left( \frac{h}{l}=1, \frac{L}{h}=10, {g}=0.03\right) \)

Full size image
Fig. 7
figure 7

Effect of fractional order on the linear time response of free vibration of the fractional viscoelastic beams with a C-C, b C-SS, c SS-SS boundary conditions \(\left( \frac{h}{l}=1,\frac{L}{h}=10, {g}=0.03\right) \)

Full size image
Fig. 8
figure 8

Effect of non-dimensional viscoelasticity coefficient on the nonlinear time response of free vibration of the fractional viscoelastic beam with SS-SS boundary conditions \(\left( {\varvec{\alpha }} =\mathbf{0.6}, \frac{{{\varvec{h}}}}{{{\varvec{l}}}}=\mathbf{1}, \frac{{{\varvec{L}}}}{{{\varvec{h}}}}=\mathbf{10}, {{\varvec{b}}}={\varvec{2h}}\right) \)

Full size image
Fig. 9
figure 9

Effect of non-dimensional viscoelasticity coefficient on the linear time response of free vibration of the fractional viscoelastic beams with a C-C, b C-SS, c SS-SS boundary conditions \(\left( {\varvec{\alpha }} =\mathbf{0.5}, \frac{{{\varvec{h}}}}{{{\varvec{l}}}}=\mathbf{1}, \frac{{{\varvec{L}}}}{{{\varvec{h}}}}=\mathbf{10}, {{\varvec{ b}}}={\varvec{2h}}\right) \)

Full size image
Fig. 10
figure 10

Effect of dimensionless length scale parameter on the nonlinear time response of free vibration of the fractional viscoelastic beam with SS-SS boundary conditions \(\left( {{\varvec{\alpha }} }=\mathbf{0.5}, \frac{{{\varvec{L}}}}{{{\varvec{h}}}}=\mathbf{10}, \mathbf{g}=\mathbf{0.03}\right) \)

Full size image
Fig. 11
figure 11

Effect of dimensionless length scale parameter on the linear time response of free vibration of the fractional viscoelastic beams with a C-C, b C-SS, c SS-SS boundary conditions \(\left( {{\varvec{\alpha }}}=\mathbf{0.5}, \mathbf{g}=\mathbf{0.03}, \frac{{{\varvec{L}}}}{{{\varvec{h}}}}=\mathbf{10}, {{\varvec{b}}}={\varvec{2h}}\right) \)

Full size image
Fig. 12
figure 12

Effect of fractional order on the nonlinear time response of forced vibration of fractional viscoelastic beams with SS-SS boundary conditions \(\big ({\varvec{\omega }} =\mathbf{10}, \mathbf{g}={\varvec{0.03}}, {{\varvec{f}}}_\mathbf{1} =\mathbf{1}, \frac{{{\varvec{h}}}}{{{\varvec{l}}}}=\mathbf{1}, \frac{{{\varvec{L}}}}{{{\varvec{h}}}}=\mathbf{10}\big )\)

Full size image
Fig. 13
figure 13

Effect of viscoelasticity parameter on the nonlinear time response of forced vibration of fractional viscoelastic beams with SS-SS boundary conditions \(\left( {\varvec{\omega }} =\mathbf{10}, {\varvec{\alpha }} ={\varvec{0.5}}, {{\varvec{f}}}_\mathbf{1} =\mathbf{1}, \frac{{{\varvec{h}}}}{{{\varvec{l}}}}=\mathbf{1}, \frac{{{\varvec{L}}}}{{{\varvec{h}}}}=\mathbf{10}\right) \)

Full size image

In Fig. 5, the linear time response of the SS-SS beam is compared with its nonlinear time responses for various initial displacement values. It is seen that as the initial displacement decreases, the nonlinear frequency tends to decrease and the effect of geometrical nonlinearity diminishes so that the linear and nonlinear curves tend to converge.

Figures 6 and 7 show the influence of fractional order on the time response of beams. Three values for the fractional order including 0.3, 0.6 and 0.9 are considered. One can find that the frequency of the system decreases with increasing \({\alpha }\). It is also seen that the decrease in maximum amplitude is intensified as this parameter gets larger. By elapsing time and the increase in damping due to increasing fractional order, the difference between the curves increases.

The effect of dimensionless viscoelasticity coefficient (g) on the vibrational behavior of beams is shown in Figs. 8 and 9. It is observed that increasing the viscoelasticity coefficient damps the vibrational behavior of the system. This damping is intensified by elapsing time. As it is expected, by elapsing time and the decrease in maximum amplitude, the frequency decreases more.

Figures 10 and 11 show the time response of beams for different dimensionless length scale parameters defined as h / l. In fact, the influence of small scale on the size-dependent behavior of the system can be studied in these figures. The results indicate that with decreasing dimensionless length scale parameter, the frequency of the system increases. Also, the maximum amplitude in each period decreases to a lesser extent as h / l decreases.

The nonlinear time responses of forced vibration of fractional viscoelastic beams are also illustrated in Figs. 12 and 13. From Fig. 12, one can find that changes in the maximum amplitude of vibration increase with decreasing fractional order. Also, increasing this parameter leads to the increase in period of vibration. The influence of viscoelasticity coefficient on the nonlinear time response of forced vibration is also shown in Fig. 13.

5 Conclusion

In the context of strain gradient theory, the size-dependent free and forced vibrations of fractional viscoelastic small-scale beams were studied in this article. The formulation was based on the Timoshenko beam theory, von Kármán geometrical nonlinear relations and the fractional Kelvin–Voigt viscoelastic model. After deriving the size-dependent governing equations, two solution approaches were employed to solve the linear and nonlinear vibration problems. In the linear solution, the GDQ and FD methods were employed in order to discretize the governing equations and boundary conditions. In the nonlinear solution approach, the Galerkin method was used to convert the fractional integro-partial differential governing equations into fractional ordinary differential equations that were then written in an effective state-space form. The predictor–corrector technique was also used to solve the set of nonlinear fractional time-dependent equations. The influences of fractional-order, viscoelasticity coefficient and length scale parameters on the linear and nonlinear time responses of the fractional viscoelastic small-scale beams were examined. It was observed that the frequency of the viscoelastic small-scale beams decreases as the fractional order increases. In addition, the damping of vibrations of system with increasing the viscoelasticity coefficient was shown. It was also revealed that the frequency of the system increases with decreasing thickness-to-length scale parameter ratio.