1 Introduction

The torsional vibration of drill-strings is one of the most destructive types of vibration present in drilling operations and if lateral and axial vibrations are small, a pure torsional model is able to represent the main features of the nonlinear drill-string dynamics [30]. The stick–slip phenomenon is considered the worst case in torsional vibration [1, 20, 42] and is commonly associated to the non-linear relationship between friction torque and the angular speed at the bit [17]. Given its origin, the stick–slip only occurs when the bit is in contact with the rock [1, 20, 42].

A variety of models have been developed to study the torsional vibration of drill-strings. In [2, 4, 7, 13, 39], the torsional vibration is modeled using a distributed parameter approach. On the other hand, the drill-string was modeled as a torsional pendulum in a lumped parameter approach in [14, 24, 29], with usually one or two degrees of freedom (DOF). Recently, the torsional pendulum model was used in [9, 18, 36, 43] and is the strategy adopted in this article.

The top rotational system is responsible for imposing the rotational speed of the drill-string and is sometimes modeled as a inertia with a control system [5, 23, 25] or, as in this paper, using the boundary condition of constant top rotational speed [17, 28, 29, 36, 42, 43].

The bit–rock interaction also plays an important role in every model in the literature. The uncoupled torsional vibration analysis usually use a friction model to include the bit–rock interaction into the model. Some authors use the dry friction model [17, 36, 43], while others include a decaying function in the slip phase [25, 37, 38]. The approach with the decaying function is observed in experimental results given in [5, 30]. Recently, Liu Hong et. al. [16] used the torsional pendulum modeling together with a decaying model for the torque on bit in order to estimate downhole conditions based on the measurements on the surface using Kalman estimators. A similar model is also used in [41] to design a robust output-feedback control to eliminate stick–slip oscillations.

In contrast to this approach, a different model was proposed by Detournay et. al. [10, 11] in which the bit–rock interaction is decomposed into cutting and frictional components. This approach is more common for the analysis of axial–torsional coupled vibration and was recently used in [3, 6, 9, 18]. Another model for the bit–rock interaction was recently proposed by Franca [12] for bits under rotary and percussive actions.

The bit–rock interaction is a source of many uncertainties in the drilling operation [6]. Hence, stochastic models have been developed to quantify these uncertainties such as the works by Spanos and Chevallier [35], Kotsonis and Spanos [21] and Ritto and colleagues [31,32,33,34]. The uncertainties were also taken into account in the dynamics of horizontal drill-strings in [8, 31]. The stochastic models are very important because they give us a lot of information that deterministic models are incapable of giving.

Concerning the drilling operation, it should be emphasized that the drill-string has to pass through different rocks to reach the petroleum reservoir, as illustrated in Fig. 1. The fact that rocks may present different mechanical characteristics as the drill-string moves downwards may be taken into account by means of an effective model associated to the bit-rock interaction. The functions adopted in this paper for rock transition were inspired by the measurements in [15, 26, 27]. To the authors’ best knowledge, such modeling has not been done yet.

The main contributions of this to work are (1) to approach the analysis of drill-string torsional dynamics when there is a passage from a soft to a harder rock layer, and (2) to assess the impact of uncertainties (in the bit–rock interaction model) on the drill-string dynamics. A simple 1-DOF lumped parameter model, based on [5, 25], is considered, and three different transition scenarios for the passage from a soft to a harder rock layer are proposed and analyzed.

In the first part of this paper the deterministic system is depicted, then a stochastic model is developed in order to assess the impact of uncertainties on the drill-string dynamics. In the second part, the numerical results are presented and analyzed and, finally, the concluding remarks are made in the last section.

2 Deterministic model

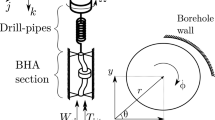
A drill-string consists basically of a Bottom Hole Assembly (BHA) and drill pipes that are attached to each other. The BHA is composed of the bit, stabilizers, and heavy pipes known as drill collars. Also, drilling mud is injected at the top of drill-string to clean, cool down and lubricate the bit, among other functions. The rotation is applied at the top of the drill-string by the top drive.

The mathematical model proposed in this paper is based on the work by Navarro-Lopez and Suarez [25] and is illustrated in Fig. 1. The drill-string is modeled as a torsional pendulum, and the bit–rock interaction is modeled as a friction torque at the bit.

This model has some simplification assumptions: (1) the borehole and drill-string are aligned in vertical position; (2) axial and lateral motions can be neglected; (3) the top rotational speed is constant; (4) a viscous damping model is considered to model the drilling mud friction, and any other friction (among pipes, connections etc).

Fig. 1
figure 1

Model sketch

Full size image

The drill pipes are represented as a torsional spring and they connect two inertias, representing the top rotary system and the BHA. The drilling mud is represented by the viscous friction at the bit. The bit–rock interaction is modeled by a friction torque. The equation of motion is then presented in Eq. 1.

$$\begin{aligned} J_\mathrm{b}\ddot{\theta _\mathrm{b}} +c(\dot{\theta _\mathrm{b}}-\Omega )+ k(\theta _\mathrm{b}-\Omega \mathrm{t})=- c_\mathrm{b}\dot{\theta _\mathrm{b}} - T_\mathrm{fb}\,, \end{aligned}$$
(1)

where \(\Omega\) is the constant speed imposed at the top; k and c are the stiffness and damping of the torsional spring, respectively; \(J_\mathrm{b}\) is the bottom inertia and is the sum of the BHA inertia with 1/3 of the drill pipes inertia [5, 25]; \(c_\mathrm{b}\) is the viscous parameter used to represent the mud and \(T_\mathrm{fb}\) if the torque on bit. The bit-rock interaction model considered here was first presented in [25] and is a combination of the switch model [22] and the dry friction model with a zero velocity band (Karnopp’s model) [19]. This model was chosen due to the fact that it can provide predictions in accordance with measured data [5]. Thus,

$$\begin{aligned} T_\mathrm{fb} = {\left\{ \begin{array}{ll} T_\mathrm{eb}(t,\dot{\theta _\mathrm{b}},\theta _\mathrm{b}), & \dot{\theta _\mathrm{b}}<D_\mathrm{v} \text { and } |T_\mathrm{eb}|<T_\mathrm{sb} \\ T_\mathrm{sb} \mathrm{sign}(T_\mathrm{eb}), & \dot{\theta _\mathrm{b}}<D_\mathrm{v} \text { and } |T_\mathrm{eb}|>T_\mathrm{sb}\\ T_\mathrm{b} \mathrm{sign}(\dot{\theta _\mathrm{b}}), & \dot{\theta _\mathrm{b}}>D_\mathrm{v}\\ \end{array}\right. }, \end{aligned}$$
(2)
$$\begin{aligned} T_\mathrm{b} = T_\mathrm{cb}+(T_\mathrm{sb}-T_\mathrm{cb})e^{-\gamma _\mathrm{b}\dot{\theta _\mathrm{b}}}\,, \end{aligned}$$
(3)
$$\begin{aligned} T_\mathrm{eb} (t,\dot{\theta _\mathrm{b}},\theta _\mathrm{b}) =c(\Omega -\dot{\theta _\mathrm{b}})+k(\Omega t - \theta _\mathrm{b}) - c_\mathrm{b}\dot{\theta _\mathrm{b}}\,, \end{aligned}$$
(4)
$$\begin{aligned} T_\mathrm{sb} = R_\mathrm{b} W_\mathrm{ob} \mu _\mathrm{sb}\,, \end{aligned}$$
(5)
$$\begin{aligned} T_\mathrm{cb} = R_\mathrm{b} W_\mathrm{ob} \mu _\mathrm{cb}\,, \end{aligned}$$
(6)

where \(T_\mathrm{eb}\) is the reaction torque in equilibrium that must overcome \(T_\mathrm{sb}\) to make the bit rotate; \(\mu _\mathrm{cb}\) and \(\mu _\mathrm{sb}\) are the Coulomb and static friction coefficients that contribute to \(T_\mathrm{cb}\) and \(T_\mathrm{sb}\) friction torques, respectively; \(T_\mathrm{b}\) is the friction torque when the bit is rotating; \(W_\mathrm{ob}\) is the weight on bit; \(R_\mathrm{b}\) is the bit radius; \(\gamma _\mathrm{b}\) is a positive constant used to model the transition between static and Coulomb friction torque by an exponential law and; \(\mathrm{sign}(x)\) is a function that returns 1 if x is positive and −1 if x is negative. The friction torque is plotted against bit rotational speed in Fig. 2 for the model parameters shown in Table 1.

Fig. 2
figure 2

Friction torque at the bit

Full size image

The first line of Eq. 2 represents the stick regime where the bit is stuck and the reaction force is not large enough to overcome the static friction torque. As the top rotary system continues to rotate, drill-string accumulates energy and increases the reaction torque until it reaches the static friction torque and the bit starts moving. Due to numerical problems, a zero velocity band is specified in a small enough neighborhood of \(\dot{\theta }_\mathrm{b} = 0\) which is characterized by the parameter \(D_\mathrm{v}\) as shown in Eq. 2. The second line of Eq. 2 specifies the stick–slip transition where the friction torque is equal to \(T_\mathrm{sb}\). The last line is about the slip regime and presents an exponential behavior between static and Coulomb friction torque.

The numerical values for the parameters used in this model are presented in Table 1.

Table 1 Parameters values
Full size table

Given that the friction torques \(T_\mathrm{sb}\) and \(T_\mathrm{cb}\) are essential for the bit-rock interaction model, and they mainly depend on the rock properties, they are chosen to model the passage from a soft to a harder rock layer during drilling operation.

In fact, the friction torques transition takes place as the drill-string moves downwards. Therefore, these changes can be modeled as a function of depth, as illustrated in Fig. 1. Nevertheless, for the sake of simplicity, this condition is modified, such that the friction torques are written as functions of time, i.e., \(T_\mathrm{cb}(t)\) and \(T_\mathrm{sb}(t)\). Three models are proposed to model the transition from a soft to a harder rock layer: step, linear and hyperbolic tangent (tan h). The step function is the sharpest one, followed by the linear and then the tanh function.

The friction torques transition in time is shown in Fig. 3. The static friction torque goes from \(T_\mathrm{sb1}=\) 6 N m to \(T_\mathrm{sb2}=8\) N m, and the Coulomb friction torque goes from \(T_\mathrm{cb1}=3\) N m to \(T_\mathrm{cb2}=5\) N m. These values were chosen arbitrarily due to the lack of an effective model that uses rock characteristics measured in field and the lack of field data in which both rock characteristics and dynamic data are measured. But, despite the arbitrarity of the choice, the models proposed here appears to be qualitatively good enough to be adjusted to fit rock strength experimental data as the ones presented in [15, 26, 27], for example. The initial time for the transition is set to \(t_1=30\) s to let the system enter the steady state, and transition is completed at \(t_2=70\) s, i.e., the transition takes 40 s. The final values for both friction torques are the ones given in Table 1.

Fig. 3
figure 3

Models for the transition between layers (a) static friction torque and (b) Coulomb friction torque

Full size image

3 Stochastic model

The stochastic model allows us to model uncertainties and evaluate their impact on the systems response. As stated before, the drilling operation is a process full of uncertainties, specially when it comes from the interaction of the drill-string with the rock. The magnitude of the static and Coulomb torques, as well as the time where the layer transitions occur, are modeled as random variables (boldface). As a consequence, the static and Coulomb torques become stochastic processes.

It is assumed that the supports of the variables are known and they satisfy the following conditions: (1) only positive values in a compact support are allowed for all variables; (2) coulomb friction torque (\(T_\mathrm{cb}\)) is always less than static friction torque (\(T_\mathrm{sb}\)) and; (3) the initial time of transition (\(t_1\)) is always less than the end time (\(t_2\)). The mean and variance are also known. The mean values were set as those in Sect. 2 and are equal to the mean of the support limits. The variance is such that the coefficient of variation is 5% and is less than the variance for a uniform distribution over the same support. This coefficient of variation is sufficient to let stick–slip oscillations to take place. The distribution chosen is the truncated Gaussian according to the maximum entropy principle [40]. The distribution parameters for each variable are found in Table 2.

Table 2 Parameters for the truncated gaussian distributions
Full size table

Due to the above modeling, the response of the system becomes random. Thus, the model (1)–(4) becomes:

$$\begin{aligned} J_\mathrm{b}{\ddot{{\boldsymbol{\theta}} _\mathrm{b}}} +c({\dot{{\boldsymbol{\theta}} _\mathrm{b}}}-\Omega )+ k({{\boldsymbol{\theta}} _\mathrm{b}}-\Omega t)=- c_\mathrm{b}{\dot{{\boldsymbol{\theta}} _\mathrm{b}}} - {{\bf{T}}_\mathrm{fb}}({\dot{{\boldsymbol{\theta}} _\mathrm{b}}})\,, \end{aligned}$$
(7)
$$\begin{aligned} {{\bf{T}}_\mathrm{fb}} = {\left\{ \begin{array}{ll} {{\bf{T}}_\mathrm{eb}} (t,{\dot{{\boldsymbol{\theta}} _\mathrm{b}},{\boldsymbol{\theta}} _\mathrm{b}}), & \quad\dot{{\boldsymbol{\theta}} _\mathrm{b}}<D_\mathrm{v} \text { and } |{\bf{T}}_\mathrm{eb}|<{\bf{T}}_\mathrm{sb} \\ {{\bf{T}}_\mathrm{sb}} \mathrm{sign}({{\bf{T}}_\mathrm{eb}}), & \quad \dot{{\boldsymbol{\theta}} _\mathrm{b}}<D_\mathrm{v} \text { and } |{\bf{T}}_\mathrm{eb}|>{\bf{T}}_\mathrm{sb}\\ {{\bf{T}}_\mathrm{b}}(t,{\dot{{\boldsymbol{\theta}} _\mathrm{b}}}) \mathrm{sign}({\dot{{\boldsymbol{\theta}} _\mathrm{b}}}), & \quad \dot{{\boldsymbol{\theta}} _\mathrm{b}}>D_\mathrm{v}\\ \end{array}\right. }, \end{aligned}$$
(8)
$$\begin{aligned} {{\bf{T}}_\mathrm{b}}(t,{\dot{{\boldsymbol{\theta}} _\mathrm{b}}}) = {{\bf{T}}_\mathrm{cb}(t)}+({{\bf{T}}_\mathrm{sb}(t)}-{{\bf{T}}_\mathrm{cb}(t)})e^{-\gamma _\mathrm{b}{\dot{{\boldsymbol{\theta}} _\mathrm{b}}}}, \end{aligned}$$
(9)
$$\begin{aligned} {{\bf{T}}_\mathrm{eb}} (t,{\dot{{\boldsymbol{\theta}} _\mathrm{b}},{\boldsymbol{\theta}} _\mathrm{b}}) =c(\Omega -{\dot{{\boldsymbol{\theta}} _\mathrm{b}}})+k(\Omega t - {{\boldsymbol{\theta}} _\mathrm{b}}) - c_\mathrm{b}{\dot{{\boldsymbol{\theta}} _\mathrm{b}}}, \end{aligned}$$
(10)

4 Numerical results

4.1 Deterministic response—no transition between layers

In this section the response of the system is analyzed without considering a transition between layers. This is an important step in order to understand some characteristics of the system under analysis.

Two bit speed responses are shown in Fig. 4. The response without stick–slip was computed with the parameters shown in Table 1, while the response with stick–slip was computed using half of the top rotational speed.

The response in Fig. 4 without stick–slip presents a zero velocity in the beginning (up to 5 s) due to the stick regime in the bit. As soon as the drill-string accumulates enough energy, the static friction torque is reached and the bit is released. After a transient period of time (about 15 s), the bit speed reaches the top rotational speed, as expected.

Otherwise, the response in Fig. 4 with stick–slip shows that the response reaches a limit cycle with high torsional oscillations. In the stick phase (bit speed equals to zero), the bit is stuck and the systems is accumulating energy. In the slip phase, the bit is released and it gains velocity.

Fig. 4
figure 4

Deterministic response of the system with and without stick–slip. Full line \(\Omega\) = 20 rad/s; dashed line \(\Omega\) = 10 rad/s

Full size image

Another interesting way to analyze the system response is by plotting the friction torque on the bit, which is shown in Fig. 5. The response without stick–slip presents an initial increasing of friction torque, due to the energy accumulation, until it reaches the static friction torque and then converges exponentially to the Coulomb friction torque. The exponential behavior happens very fast and cannot be noticed in Fig. 5a.

The stick–slip oscillations are characterized by the switch between static and Coulomb friction torques. A detailed analysis of the torque is shown in Fig. 5b. Before the bit sticks, the friction torque increases fast (first peak in Fig. 5b) because it passes through the static friction torque. It happens because of the exponential behavior of the chosen model. When the bit gets stuck, the drill-string starts accumulating energy again and the torque increases linearly, as shown in Fig. 5b.

Fig. 5
figure 5

Friction torque on the bit for a total simulation time and b between 21 and 28 s. Full line \(\Omega\) = 20 rad/s; dashed line \(\Omega\) = 10 rad/s

Full size image

4.2 Passage from a soft to a harder rock layer

Before solving the stochastic problem, the deterministic response is simulated considering the three proposed functions for the transition between two layers (step, linear and tanh). Figure 6 shows the bit rotational speed. Before the transition (\(t<30\) s), the system presents the same initial oscillations discussed in Sect. 4.1 for the three functions. It can be noticed that none of the transitions presented stick–slip oscillations. However, when a step function is considered, the bit sticks for a while and then is released again. As a consequence, it presents a higher oscillation in its transient. A detailed view is given in Fig. 6b and it shows that the bit does not stick immediately because of the system dynamics.

The system response for linear and tanh cases are very similar but with some peculiarities. In both cases, the bit does not stick but decelerates enough to accumulate energy in order to compensate the raise in friction torque. It can be seen in the zoomed view of Fig. 6a that, for the linear case, the bit reaches a new constant velocity value during the transition. It occurs because the bit does not stick and the particular solution for \(\theta _\mathrm{b}\) in Eq. 1 is also linear, which sums to homogeneous solution and adds a gap in angular velocity \(\dot{\theta _\mathrm{b}}\). There are some oscillations at the beginning and at the end of the transition due to system dynamics. On the other hand, in tanh case, there is no oscillation and the system response presents a behavior very similar to the tanh function itself because the deceleration increases and decreases in a progressive way, like the derivate of tangent function. Hence, the smoother the transition function is, the less oscillations occur in the bit rotational speed. This conclusion is in agreement with the investigation done by [23], where the concern was with how the driller applies the weight on bit.

The friction torque is shown in Fig. 7. For linear and tanh cases, the change in the friction torque on bit is the same as the function proposed for the change in Coulomb friction torque. This is due to the absence of bit sticking. In the case of the step function transition, a more detailed analysis should be done; see Fig. 7b. The friction torque on the bit raises immediately to \(T_\mathrm{cb2}\) at \(t=30\) s, then it raises again to the static torque value (exponential shape), and then decreases when the bit finally sticks (about 30.4 s). After that, the drill-string starts accumulating energy again until it overcome the static friction and the bit is released. Thus, the torque on bit reaches the new Coulomb friction torque.

Fig. 6
figure 6

Rotational speed of the bit with the change in bit-rock interaction parameters following: a step, linear and hyperbolic tangent functions in \(0<t<90\) and; b step function in \(29.9<t<30.5\)

Full size image
Fig. 7
figure 7

Friction torque on the bit with rock transition following: a step, linear and hyperbolic tangent functions in \(0<t<90\) and; b step function in \(29.9<t<30.5\)

Full size image

Now the stochastic results are analyzed. They were obtained using Monte Carlo Simulations, where the truncated samples from the truncated Normal random variables were obtained by the rejection method. It was performed 10,000 simulations in order to assure the convergence in mean square. The results are presented in Figs. 8 and 9 using a statistical envelope of 99%, which means that 99% of the results are between the two dashed lines (green and red), and the full black line is the mean value.

The stochastic results show that, for some Monte Carlo simulations, the system presented stick–slip oscillations before the beginning of transition between rock layers. The more severe case is a hard transition, represented by the step function. Figure 8a shows that many samples present stick–slip oscillations after the layer transition, which yields a very large statistical envelope. On the contrary, a smooth transition, represented by the linear and tanh functions, presented a statistical envelope very close to the mean value after the layer transition. This is because the stick–slip oscillations die out at the end of the transition because there is a reduction in \(T_\mathrm{sb}/T_\mathrm{cb}\) ratio. It can be seen in Fig. 8b for the linear case, which is very similar to tanh case. This means that sharp transitions between rock layers is very bad for the system performance, concerning torsional oscillations.

Fig. 8
figure 8

Envelope of 99% for the rotational speed of the bit when the change in bit-rock interaction parameters follow a a step function and b linear function

Full size image

The friction torque on the bit is shown in Fig. 9. In the step case, due to the occurrence of stick–slip oscillations, the envelope is much wider when compared to the other cases. In the linear and tanh cases, there are stick–slip oscillations in the beginning, as commented before, but, after the transition, the envelope ends up with only the uncertainties in the Coulomb friction. This behavior is shown in Fig. 9b only for linear case. The tanh case is similar, only the shape of the curves are smoother in the transition.

It should be noted that even though the envelope analysis did not show stick–slip oscillations in linear and tanh cases, it was observed that a few simulations presented this kind of behavior, but it was not enough to make a difference in the 99% envelope.

Fig. 9
figure 9

Envelope of 99% for the friction torque on bit when the change in bit-rock interaction parameters follow a a step function and b linear function

Full size image

Another way to analyze the presented stochastic results is proposed. If we fix the time at 100s and analyze the random bit speed at this instant time, it is possible to calculate the cumulative density function (CDF). The CDF for the step case is shown in Fig. 10 and is a combination of a discrete distribution concentrated at 0 and 20 rad/s and a continuous distribution with values from 0 to 80 rad/s. This is observed because of the jump type discontinuities in CDF. It also shows that most of simulations presented a rotational speed of 20 rad/s, indicating that there are no stick–slip oscillations. In the presence of stick–slip, different speeds appear at 100 s. The frequency of zero velocity values is higher because there are no variations in bit rotational speed when it is stuck and, in one stick–slip oscillation, the bit is stuck during almost half of the time. When the bit is slipping, there is a variation between zero and maximum velocities. The CDFs for linear and tanh cases are not shown because they were very similar to each other and only the discrete distribution at 20 rad/s appeared because there were very few responses with stick–slip oscillations.

Fig. 10
figure 10

Cumulative density function of bit rotational speed at \(t=100\) s when the change in bit-rock interaction parameters follow a step function

Full size image

5 Concluding remarks

This paper considered a simplified torsional dynamical model of one degree-of-freedom to describe drill-string dynamics. The rotational speed is prescribed at the top rotary system and the bit-interaction model is nonlinear. A stochastic model was also proposed to evaluate the impact of uncertainties in the system response.

To evaluate the passage from a soft to a harder rock layer, three transition functions were proposed: step, linear, tanh. Depending on the shape of this transition, the results are quite different. It was concluded that sharp transitions give worse results in terms of undesirable torsional oscillations. Uncertainties were considered in the bit–rock parameters. For the case considered, it was shown that the stick–slip oscillations vanished in the case of soft transitions, but it continued and increased for the sharp transition.

Further analysis should be performed in order to effective control the drill-string system to avoid stick–slip oscillations, and to analyze the probability of the system to become unstable.