Stochastic torsional stability of an oil drill-string

Abstract

The aim of this paper is to investigate the influence of uncertainties on the torsional vibration of drill-strings, in order to find out which uncertainty affects most significantly the torsional stability. The unstable torsional behavior is commonly associated to polycrystalline diamond compact bits, and manifests itself in the form of stick-slip oscillations. The stick-slip is a severe type of self-excited vibration characterized by large fluctuations in the rotation of the bit. It not only increases the bit wear, but also can cause drill-string failures. The analysis were done using a mathematical model of the drill-string based on classical torsion theory discretized by means of the finite element method. The bit-rock torque was included in the model as a nonlinear boundary condition at the bottom end of the drill-string. The values of the model parameters are typical values of a real drilling situation, which are subject to a high degree of uncertainty, what justifies a stochastic analysis. We have built probability distributions for the uncertain parameters and used Monte Carlo method to obtain the stochastic stability maps.

1 Introduction

1.1 Motivation

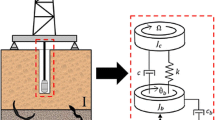
The drilling of petroleum wells is performed by a drilling rig. The details of the process of oil wells drilling can be found, for instance, in Halliburton [1]. In the rotary method, the drilling is accomplished through the bit rotation and the weight-on-bit, causing the fragmentation of the rock. Figure 1 sketches a rotary drilling rig and its main components. The drill-string is the component responsible for the transmission of rotation from the rotary table (or from the top drive) at the surface, to the bit, at the bottom of the well. It is composed basically by drill pipes, which are connected one to one from the surface until the bottom of the well, by drill collars, which are connected just below the drill pipes, and by stabilizers, which are distributed along the drill collars. A drill-string in operation is subject to torsional, lateral and axial vibrations [2], as depicted in the Fig. 2.

Fig. 1

Rotary drilling rig and its main components

Fig. 2

Common drill-string vibrations

The torsional vibration occurs mainly with polycrystalline diamond compact bits [3], commonly referred to as PDC bits. In some extreme cases of torsional vibration, the bit experiences a phenomenon called stick-slip, alternating stick phases with slip phases. During the stick phase, the bit becomes locked in the formation, with null rotation, while the rotary table continues to rotate. Thus, the drill-string is torsioned until the torque-on-bit reaches the maximum locking torque. When the torque-on-bit overcomes the maximum locking torque, the bit enters the slip phase. In the slip phase, the torsional elastic potential energy is suddenly released, causing a high rotational acceleration of the bit. The stick-slip is self-excited by the imposed rotation, and the whole cycle repeats itself. It not only increases the bit wear, but also can cause drill-string failures. It is worth to mention that the premature failure of the costly equipment usually employed in the oil drilling is totally undesirable, what makes the investigation of drill-string torsional vibration interesting for the oil industry.

1.2 Objective

The goal of this paper is to investigate the impact of parameter uncertainties in the system torsional stability. This will be done comparing the stochastic torsional stability maps of a drill-string for different degrees of uncertainty of the model parameters. The stability maps will be generated by means of computer simulations.

Stochastic models have been developed before, for different purposes, to quantify uncertainties in drill-string dynamics. See, for instance Spanos et al. [4], Kotsonis and Spanos [5], Ritto et al. [6,7,8,9], Ritto and Sampaio [10].

Pavone and Desplans [11] in 1994 had already recognized the stick-slip associated to drill-strings as a dynamic instability. The stability map of a dynamical system is a graphical representation of different types of behavior of a given solution of the system, as function of some input parameters. Each type of behavior is represented by a region in the stability map.

Fig. 3

Typical stability map of a drill-string

A typical stability map of a drill-string is depicted in the Fig. 3. In this case, the input parameters considered are $\Omega$ and $-(F_{Bit})_{z}$, where $\Omega$ is the imposed rotation and $(F_{Bit})_{z}$ is the weight-on-bit. We have put a minus sign in front of $(F_{Bit})_{z}$ in order to have positive values in the ordinate axis, since in our convention of axes direction, the z-axis points to the opposite direction of $(F_{Bit})_{z}$. All the regions colored in red are undesirable. The low rate of penetration region is a region in which the bit rate of penetration¹ is not economically viable. Here it is important to make a distinction, the minimum rate of penetration curve is a chosen constraint, and not a stability boundary. To ensure that the drill-string does not experience dangerous vibrations and the rate of penetration is economically viable, the driller should operate inside the optimum region, the blue area of the Fig. 3. There are also lateral vibrations constraints (forward and backward whirl), however, herein, we are concerned only with the stick-slip region given a certain minimum rate of penetration as constraint.

2 Deterministic model

We can find in the literature many different models to study the drill-string torsional dynamics, like the ones of Abbassian and Dunayevsky [13], Franca [14], Christoforou and Yigit [15], Germay et al. [16], Liu et al. [17], Ritto et al. [6], Percy [18] and Tucker and Wang [19] for instance. In some cases, the classical torsion theory is accurate enough to represent the drill-string torsional dynamics as shown in Ritto et al. [20], where field data of a $5 \phantom {\cdot } {\mathrm {km}}$ drill-string is presented. Thus we will use this theory to construct our mathematical model.

2.1 Continuum equation of motion

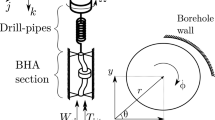
Our mechanical model of the drill-string is depicted in Fig. 4. It consists of a straight slender body, oriented so that its longitudinal dimension is vertical. The z-axis has vertical direction and points downwards. The origin O of the coordinate system is located at the surface. The x, y, z-axes constitute an orthogonal coordinate system and follow the right hand rule convention. The geometry of our idealized drill-string consists of a hollow circular cylinder with a piecewise constant cross section, characterized by the drill-pipe outer radius $R_{DPout}$, the drill-pipe inner radius $R_{DPin}$, the bottom-hole-assembly outer radius $R_{BHAout}$ and the bottom-hole-assembly inner radius $R_{BHAin}$. The values of the nominal parameters used in this article are shown in the Table 2.

Fig. 4

Idealized drill-string

Our unknown is the rotational displacement $\theta _{z}(z,t)$ of the cross sections around the z-axis, which, in our model, depends only on the longitudinal coordinate z and on the time t. We are primarily interested in calculating the rotational displacement of the bit, i.e. $\theta _{z}(L,t)$, where L is the drill-string total length. The equation of motion governing the torsional dynamics is the following [21]:

$$\begin{aligned} \rho (z) J(z)\frac{\partial ^{2}\theta _{z}(z,t)}{\partial t^{2}} - \frac{\partial }{\partial z} \left( G(z)J(z)\frac{\partial \theta _{z}(z,t)}{\partial z}\right) = m_{z}(z,t) \end{aligned}$$

(1)

where $\rho (z)$ is the density of the system, J(z) is the polar moment of inertia of the drill-string cross sections and G(z) is the shear modulus, both along the z-coordinate; $m_{z}(z,t)$ is the torsional torque per unit length. The two boundary conditions are as follows. We will assume that there is a control mechanism at the drive system so that the rotational speed at the top of the drill-string is held constant at $\Omega$. Thereby, the first boundary condition corresponds to an imposed rotational displacement $\theta _{z}(0,t) = \Omega t$. The cutting process, in its turn, causes a reaction torque-on-bit at the bottom of the drill-string, which will be modeled as a nonlinear boundary condition of the bit rotational speed ${d\theta _{Bit}}/{dt}$. So, the second boundary condition is a prescribed torque $M_{z}(L,t) = (M_{Bit})_{z}$.

Null initial conditions are considered, i.e., $\theta _{z}(z,0) = 0$ and $\frac{\partial \theta _{z}}{\partial t} (z,0) = 0$.

2.2 Discrete equation of motion

Our idealized drill-string has a piecewise constant cross section what makes it difficult to use analytical methods to solve the Eq. (1). Thus we will discretize it using the finite elements method (FEM). Thereby we obtain:

$$\begin{aligned} {\mathbf {M}}\ddot{\mathbf {u}} + {\mathbf {K}}{\mathbf {u}} = {\mathbf {f}}(\dot{\mathbf {u}}, t) \end{aligned}$$

(2)

where ${\mathbf {u}}$ is the rotational displacement vector, ${\mathbf {M}}$ is the mass matrix and ${\mathbf {K}}$ is the stiffness matrix² and ${\mathbf {f}}(\dot{{\mathbf {u}}}, t)$ is the external torque vector, which depends on the rotational velocity vector (by means of the imposed torque-on-bit boundary condition) and on the time (by means of the imposed rotational displacement boundary condition). The imposed rotational speed boundary condition is applied into the FEM formulation removing the degree of freedom of the first node, i.e. eliminating the first row and column from the global matrices; the column enters in the right hand side of the system as a torque vector ${\mathbf {f}}_{RT}(t) := -\Omega ({\mathbf {C}})_{...1} - \Omega t({\mathbf {K}})_{...1}$, where ${\mathbf {f}}_{RT}(t)$ is the rotary table torque, $({\mathbf {C}})_{...1}$ and $({\mathbf {K}})_{...1}$ are the first column of the damping matrix (defined in Sect. 2.5) and stiffness matrix, respectively, after eliminating the first row.

2.3 Bit-rock torque

The cutting process is a complicated phenomenon, which involves discontinuities and hysteresis.³ The torque-on-bit depends on the bit structure, rock properties, weight-on-bit (almost linear dependence) and on the bit rotation (nonlinear dependence). Fortunately, in some situations, the relation between the torque-on-bit and the bit rotation behaves like a friction law [23, 24]. For instance, field measurements show a velocity weakening effect [11]. The bit-rock interaction model used herein is a regularized one, which considers a steep straight line when the bit rotation is near to zero. Usually this strategy produces coherent results, as pointed by Tucker and Wang [19], Khulief et al. [25]. One can find in the literature other models that take into account explicitly stick and slip phases, such as in Leine et al. [26]. We will accommodate different bit shapes starting from heuristic considerations. To calculate $(M_{Bit})_{z}$, we have approximated the bit by a solid of revolution, depicted in the Fig. 5. The generating line is a function z(r), where r, $\varphi$, z are the cylindrical coordinates. The infinitesimal force $dF_{n}$ normal to the surface is given by $dF_{n} = (f_{Bit})_{z} \cdot (\cos \gamma )^{2} \, dS$, where $(f_{Bit})_{z}$ is the vertical load per unit horizontal area⁴, $\gamma$ is the slope angle of the tangent to z(r) at the considered position and dS is the infinitesimal area in which $dF_{n}$ is acting. From the geometry we have:

Fig. 5

Idealized bit

$$\begin{aligned} \begin{aligned} \cos \gamma&= \frac{1}{\sqrt{1+\left( \frac{dz}{dr}\right) ^{2}}}\\ dl&= \sqrt{1+\left( \frac{dz}{dr}\right) ^{2}}dr\\ dS&= r \, d\varphi \, dl \end{aligned} \end{aligned}$$

(4)

Using the Coulomb law of dry friction, we have $dF_{\varphi } = \mu \, dF_{n} \, {{{\mathrm{sgn}}}}({d\theta _{Bit}}/{dt})$, where $dF_{\varphi }$ is the infinitesimal force tangential to the surface, $\mu$ is a friction constant (equivalent to the kinetic coefficient of friction), ${{{\mathrm{sgn}}}}$ is the sign⁵ function and ${d\theta _{Bit}}/{dt}$ is the bit rotational velocity. Substituting the equation for $dF_{n}$ in the equation of the Coulomb law, using the geometric relations of the Eq. (4), and integrating over r and $\varphi$, we obtain the torque relative to the z-axis $(M_{Bit})_{z} = \bar{r}\mu \cdot (F_{Bit})_{z} \cdot {{\mathrm{sgn}}}({d\theta _{Bit}}/{dt})$, where $(F_{Bit})_{z}$ is the weight-on-bit and $\bar{r}$ is a function of the bit radius which depends on the bit geometry, defined by the following expression:

$$\begin{aligned} \bar{r} := \frac{2}{(R_{Bit})^{2}}\int _{0}^{R_{Bit}}\frac{r^{2}}{\sqrt{1 + \left( \frac{dz}{dr}\right) ^{2}}} \, dr \end{aligned}$$

(5)

where $R_{Bit}$ is the bit radius. For an ideal cylindrical bit, as the one considered herein, $\bar{r} \simeq 0.6667 R_{Bit}$. In order to avoid difficulties when differentiating $(M_{Bit})_{z}$, we have smoothed it, inspired by the bit-rock torque law of Khulief et al. [25]:

$$\begin{aligned} (M_{Bit})_{z} = \bar{r}\mu \cdot (F_{Bit})_{z} \cdot \left( \tanh \left( \alpha _{1}\frac{d\theta _{Bit}}{dt}\right) +\frac{\alpha _{2}\frac{d\theta _{Bit}}{dt}}{1+\alpha _{3}\left( \frac{d\theta _{Bit}}{dt}\right) ^{2}}\right) \end{aligned}$$

(6)

where $\alpha _{1}$, $\alpha _{2}$ and $\alpha _{3}$ are bit-rock interaction constants. The values of the bit-rock interaction constants used in this work were obtained by least squares fit from experimental data available in Ritto et al. [20] (see the Table 2). The graph of the function (6) is shown in the Fig. 6 for a cylindrical bit with $R_{Bit} = 0.2159 \phantom {\cdot } {\mathrm {m}}$ and different values of $-(F_{Bit})_{z}$.

Fig. 6

Model of the torque-on-bit

The nearly vertical stretches of the Fig. 6 are a consequence of the smoothing procedure of the discontinuity of the friction model. According to Brett [28] it is just this discontinuity, inherent of PDC bits which causes stick-slip. It is worth to mention that Lima et al. [29] concluded that the torsional stability of the drill-string is highly affected by how $(F_{Bit})_{z}$ is applied. In this work, we will consider that the drill-string is in static equilibrium before starting the rotational movement.

2.4 Mud polar moment

During the drilling operation, the well is flooded with mud. Although we did not model the mud flow, both its direct effect on the inertia of the system, and its indirect effect of viscous dissipation will be considered. Firstly note that:

$$\begin{aligned} \rho J\frac{\partial ^{2}\theta _{z}}{\partial t^{2}} = \frac{\partial }{\partial t}\left( \frac{dL}{dz}\right) \end{aligned}$$

(7)

where dL / dz is the total angular momentum of the system per unit length. The mud has rotational inertia, which contributes to the total angular momentum. This additional additional inertia should be accounted in the Eq. (1). We can do that in a simplified manner using the concept of apparent density:

$$\begin{aligned} \rho J\frac{\partial \theta _{z}}{\partial t} := \frac{dL}{dz} = \frac{dL_{DS}}{dz} + \frac{dL_{Mud}}{dz} \end{aligned}$$

(8)

where $\rho$ is the apparent density, J is the polar moment of inertia of the drill-string cross section, ${dL_{DS}}/{dz}$ is the angular momentum of the drill-string per unit length and ${dL_{Mud}}/{dz}$ is the angular momentum of the mud per unit length. Which in their turns are given by $\frac{dL_{DS}}{dz} = \rho _{DS}J\frac{\partial \theta _{z}}{\partial t}$ and $\frac{dL_{Mud}}{dz} = \rho _{Mud}J_{Mud}\frac{\partial \theta _{z}}{\partial t}$, where $\rho _{DS}$ is the drill-string density, $\rho _{Mud}$ is the mud density and $J_{Mud}$ is the mud polar moment of inertia, see Nogueira [30] for more details. Thereby, we obtain a correction for the density to be used in the Eq. (1):

$$\begin{aligned} \rho := \rho _{DS} + \left( \frac{J_{Mud}}{J}\right) \rho _{Mud} \end{aligned}$$

(9)

2.5 Damping

We will assume that the drill-string loses energy by viscous dissipation. Rather than considering a damping term directly in the Eq. (1), we will insert a damping matrix a posteriori in the global system of finite elements. In this work, we consider a proportional damping, i.e. we will assume that the damping matrix is diagonal in the modal coordinates. Consider the coordinate transformation ${\mathbf {u}} := {\mathbf {Q}}{\mathbf {q}}$, where ${\mathbf {Q}}$ is the modal matrix, ${\mathbf {q}}$ is called the modal coordinates vector. Substituting the coordinate transformation in the Eq. (2) and pre-multiplying the resulting equation by the transposed matrix ${\mathbf {Q}}^{\dag }$, we obtain:

$$\begin{aligned} {\mathbf {Q}}^{\dag }{\mathbf {M}}{\mathbf {Q}}\ddot{{\mathbf {q}}} + {\mathbf {Q}}^{\dag }{\mathbf {K}}{\mathbf {Q}}{\mathbf {q}} = {\mathbf {Q}}^{\dag }{\mathbf {f}}({\mathbf {Q}}\dot{\mathbf {{q}}}, t) \end{aligned}$$

(10)

The matrix ${\mathbf {Q}}$ has the property of simultaneously diagonalize ${\mathbf {M}}$ and ${\mathbf {K}}$ [31]. We can normalize ${\mathbf {Q}}$ such that ${\mathbf {Q}}^{\dag }{\mathbf {M}}{\mathbf {Q}} := \varvec{\delta }$ and ${\mathbf {Q}}^{\dag }{\mathbf {K}}{\mathbf {Q}} := \varvec{\omega }^{2}$, where $\varvec{\delta }$ is the identity matrix and $\varvec{\omega }^{2}$ is the square of the eigenvalues matrix.

The damping matrix can be inserted directly in the uncoupled system assuming that the damping matrix is diagonal:

$$\begin{aligned} \varvec{\delta }\ddot{{\mathbf {q}}} + {\mathbf {c}}{\dot{{\mathbf {q}}}} + \varvec{\omega }^{2}{\mathbf {q}} = {\mathbf {Q}}^{\dag }{\mathbf {f}}({{\mathbf {Q}}{\dot{\mathbf {q}}}}, t) \end{aligned}$$

(11)

The finite element damping matrix ${\mathbf {C}}$ can be obtained transforming ${\mathbf {c}}$ back to physical coordinates:

$$\begin{aligned} {\mathbf {C}} := {\mathbf {Q}}^{-\dag }{\mathbf {c}}{\mathbf {Q}}^{-1} \end{aligned}$$

(12)

where the superscript $-1$ denotes the inverse matrix. The matrix ${\mathbf {c}}$ can be evaluated in relation to the critical damping $\mathbf {c} := 2\varvec{\xi }\varvec{\omega }$, where $\varvec{\xi }$ is the damping ratio matrix. Finally, we get the following system of finite elements in physical coordinates:

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {u}} + \mathbf {C}\dot{\mathbf {u}} + \mathbf {K}\mathbf {u} = \mathbf {f}(\dot{\mathbf {u}}, t) \end{aligned}$$

(13)

2.6 Minimum rate of penetration

The minimum rate of penetration is a constraint we want to impose. To calculate the nominal rate of penetration, we will use an ad hoc equation derived by Depouhon [32] in 2007:

$$\begin{aligned} \frac{d(u_{Bit})_{z}}{dt} = \left( \frac{-(F_{Bit})_{z} - nR_{Bit}w\sigma _{c}}{2\pi R_{Bit}\alpha _{0}\sigma _{c}}\right) \frac{d\theta _{Bit}}{dt} \end{aligned}$$

(14)

where ${d(u_{Bit})_{z}}/{dt}$ is the rate of penetration, $(F_{Bit})_{z}$ is the weight-on-bit, n is the number of radial blades of the bit, $R_{Bit}$ is the bit radius, w is the width of the cutter wearflat⁶, $\sigma _{c}$ is the confined compressive strength of the rock, $\alpha _{0}$ is a dimensionless constant that depends on the inclination of the cutting force and ${d\theta _{Bit}}/{dt}$ is the bit rotational speed. The nominal rate of penetration is the penetration rate the bit would have if there was no vibration, that is, if the top rotation was fully transmitted to the bit. It can be calculated substituting directly ${d\theta _{Bit}}/{dt} = \Omega$ in the Eq. (14).

3 Stochastic model

In the present paper, we will use the probabilistic approach to take into account the uncertainties in the model parameters $\{\mu , \sigma _{C}, \varvec{\rho }_{Mud}, \varvec{\xi }\}$ i.e. these parameters will be modeled as random objects $\{X_{\mu }, X_{\sigma }, \mathbf {X}_{Mud}, \mathbf {X}_{\xi }\}$. The probability distributions for the uncertain parameters will be chosen with the available information using the maximum entropy principle [33, 34]. The results depend on the shape of the input probability distributions. Different input probabilistic models yield to different output probability distributions. If the shapes of the input distributions are similar, we would expect similar output statistics (i.e. mean, variance and higher moments). However, if one is interested in the tails of the output distributions, one should be more careful in selecting the appropriate distributions. Due to lack of information, all the random variables are considered independent from each other.

We solved numerically the stochastic system using the Monte Carlo method. In spite of not being the most computationally efficient method, it is sufficient when one is not interested in events with very low probabilities. If the interest is in reliability techniques, one can use other methods, such as Importance Sampling and Subset Simulation. When the bit-rock interaction, mud density and damping are random, we end up with the following stochastic system:

$$\begin{aligned} \mathcal {M}\ddot{\mathbf {U}} + \mathcal {C}\dot{\mathbf {U}} + \mathbf {K}\mathbf {U} = \mathcal {F}(\dot{\mathbf {U}}, t) \end{aligned}$$

(15)

where $\mathbf {U}$ is the random response, $\mathcal {M}$ is the random mass matrix [sc. depends on $\mathbf {X}_{Mud}$ by the Eq. (9)], $\mathcal {C}$ is the random damping matrix [(sc. depends on $\mathbf {X}_{\xi }$ by the Eq. (12)] and $\mathcal {F}(\dot{\mathbf {U}}, t)$ is the random torque vector [sc. depends on $X_{\mu }$ by the Eq. (6)]. In addition, the minimum rate of penetration is random [sc. depends on $X_{\sigma }$ by the Eq. (14)].

3.1 Friction constant, confined compressive strength

We will suppose that the information we have about the random variables $X_{\mu }$ and $X_{\sigma }$ is that each one of them belongs to an interval [a, b]. The probability distribution which maximizes the entropy with this constraint is the Uniform distribution [34]:

$$\begin{aligned} f_{X}(s) := \frac{1}{b-a} \end{aligned}$$

(16)

within the support [a, b] and equals to zero otherwise, where X represents $X_{\mu }$ or $X_{\sigma }$. The constants a, b are evaluated as follows:

$$\begin{aligned} {{\mathrm{\upmu }}}_{X} = {\frac{1}{2}}(a + b) \phantom {aaaa} {{\mathrm{\upsigma }}}_{X}^{2} = {\frac{1}{12}}(b - a)^{2} \end{aligned}$$

(17)

In the present paper, we have specified the mean ${{\mathrm{\upmu }}}_{X}$ and the coefficient of variation⁷ ${{\mathrm{cv}}}_{X}$, and then solved the relations (17) to find the constants a, b. The graph of the probability distribution of $X_{\mu }$ is shown in the Fig. 7 for different values of coefficient of variation.

Fig. 7

Probability distribution of $X_{\mu }$

3.2 Mud density

The mud carries with itself rock fragments and formation fluids which were contained in the reservoir rock [35]. The mud density $\mathbf {X}_{Mud}$ is actually the density of this mixture. Therefore we expect $\mathbf {X}_{Mud}$ to vary in time and along the longitudinal coordinate. However the time scale associated to the travel of the fragments up to the surface is much higher than the fundamental period of torsional vibration of the drill-string. Thus we will consider that $\mathbf {X}_{Mud}$ is a stochastic field which depends on the longitudinal coordinate z. The mud density at (a fixed) z is a random variable $X_{Mud}(z)$, which we assume belongs to a given interval [a, b]. And again the maximum entropy principle yields independent Uniform distributions for each $X_{Mud}(z)$.

3.3 Damping ratio

The damping ratio matrix can be expressed by $\varvec{\xi } := {{\mathrm{diag}}}(\xi _{1}, ..., \xi _{n})$, where $\xi _{i}$ is the damping ratio of the i-th vibration mode. Thus we will consider that $X_{\xi _{i}}$ is the random variable which corresponds to $\xi _{i}$. The available information we have about them is that $X_{\xi _{i}} > 0$ (viz. the undamped case does not exist in reality).

A common probabilistic distribution for positive random variables is the Lognormal distribution. This distribution might be achieved if one imposes two more constraints: the mean and the variance of its natural logarithm $\ln (X_{\xi _{i}})$. Hence, applying the maximum entropy principle these constraints yield the Lognormal distribution [36]:

$$\begin{aligned} f_{X_{\xi _{i}}}(s) := \frac{1}{s\,b\sqrt{2\pi }} \, \exp \left( -\frac{(\ln {s} - a)^{2}}{2b^{2}}\right) \end{aligned}$$

(18)

for positive s, where a is the scale constant and $b > 0$ is the shape constant. They are evaluated as follows:

$$\begin{aligned} {{\mathrm{\upmu }}}_{X_{\xi _{i}}} = \exp \left( a + \frac{b^{2}}{2}\right) \phantom {aaaa} {{\mathrm{\upsigma }}}_{X_{\xi _{i}}}^{2} = (\exp (b^{2}) - 1)\exp (2a + b^{2}) \end{aligned}$$

(19)

Again, we have specified the mean ${{\mathrm{\upmu }}}_{X_{\xi _{i}}}$ and the coefficient of variation ${{\mathrm{cv}}}_{X_{\xi _{i}}}$, and then solved the relations (19) to find the constants a, b, which are tabulated in the Table 1.

Table 1 Constants of the lognormal distribution

The graph of the probability distribution of $X_{\xi _{i}}$ is shown in the Fig. 8 for different values of coefficient of variation.

Fig. 8

Probability distribution of $X_{\xi _{i}}$

4 Stability analysis

In order to analyse the stability of the system (13), we should write it as a system of first order differential equations, and obtain the so called state space form of our problem:

$$\begin{aligned}\underbrace {{\left[ {\begin{array}{*{20}c} {{\mathbf{\dot{u}}}} \\ {{\mathbf{\ddot{u}}}} \\ \end{array} } \right]}}_{{{\mathbf{\dot{x}}}}} = \underbrace {{\left[ {\begin{array}{*{20}c} {\mathbf{0}} & \varvec{\delta } \\ { - {\mathbf{M}}^{{ - 1}} {\mathbf{K}}} & { - {\mathbf{M}}^{{ - 1}} {\mathbf{C}}} \\ \end{array} } \right]}}_{{\mathbf{A}}}\underbrace {{\left[ {\begin{array}{*{20}c} {{\mathbf{\dot{u}}}} \\ {{\mathbf{\ddot{u}}}} \\ \end{array} } \right]}}_{{\mathbf{x}}} + \underbrace {{\left[{\begin{array}{*{20}c} {\mathbf{0}} \\ {{\mathbf{M}}^{{ - 1}}{\mathbf{f}}} \\ \end{array} } \right]}}_{{\mathbf{B}}} \Rightarrow \left\{ {\begin{array}{*{20}l} {{\mathbf{\dot{x} =Ax}} + {\mathbf{B}}\left( {{\mathbf{x}},t} \right)} \\ {{\mathbf{x}}\;{\text{ = }}\;{\text{0 at }}t = 0} \\ \end{array} } \right.\end{aligned}$$

(20)

An equilibrium solution $\varvec{\Psi }$ is stable if, and only if the solution of the initial value problem $\varvec{\Phi }$ converges to $\varvec{\Psi }$. Otherwise, the equilibrium solution is semi-stable or unstable. In our case, we will evaluate the stability of the following equilibrium solution:

$$\begin{aligned} \varvec{\Psi } := \begin{bmatrix} \varvec{\Omega }t\\ \varvec{\Omega }\end{bmatrix} + \begin{bmatrix} \varvec{\theta }_{0}\\ {\mathbf {0}}\end{bmatrix} \end{aligned}$$

(21)

where $\varvec{\Omega }$ is a n dimensional vector whose entries are $\Omega$, $\varvec{\theta }_{0}$ is a n dimensional constant vector representing the static torsion deformation, which can be obtained forcing $\varvec{\Psi }$ to satisfy the system of differential equations in (20). $\varvec{\Psi }$ is the solution corresponding to every node rotating with the same rotational speed $\Omega$ of the top, that is without stick-slip. And it will be stable whenever the actual solution converges to it, that is when the stick-slip ceases in the long term.

The system is linearized around the equilibrium solution and a linear stability analysis is performed. Therefore an equilibrium solution $\varvec{\Psi }$ is stable if, and only if the real part of all eigenvalues of the jacobian matrix ${\mathbf {A} }+ \left. {\partial {\mathbf {B}}}/{\partial \mathbf {x}}\right| _{{\mathbf {x}} = \varvec{\Psi }}$ are less than zero. When the linear stability might be applied, it has the advantage of being relatively fast, because it does not require solving the dynamical system. So it is suitable for the application of brute force methods, such as the Monte Carlo method.

5 Results

5.1 Deterministic results

The results correspond to a drill-string with a cylindrical bit, considering the mud rotational inertia. The values of the variables are those of the Table 2. Figures 9 and 10 show the rotational speed of the drill-string as a function of time for two different pairs of $\Omega$ and $(F_{Bit})_{z}$. The first one is $\Omega = 15 \phantom {\cdot } \mathrm {rpm}$ and $(F_{Bit})_{z} = -200 \phantom {\cdot } \mathrm {kN}$. The second one is $\Omega = 50 \phantom {\cdot } \mathrm {rpm}$ and $(F_{Bit})_{z} = -50 \phantom {\cdot } \mathrm {kN}$. The dashed line is the rotational speed of the rotary table (RT) and the solid line is the rotational speed of the bit (Bit). The simulations were done with 20 finite elements, which is sufficient when considering only the torsional dynamics.

Fig. 9

Rotational velocity of the unstable response

Fig. 10

Rotational velocity of the stable response

The rotary table rotates always with the imposed (constant) rotation. Figure 9 represents the typical unstable response: the bit rotational speed does not converge to the imposed rotational speed. One can clearly notice the occurrence of oscillations, characterized by the bit halt and subsequent high speed up to several times the imposed rotation. Due to the regularization of the nonlinear bit-rock interaction, there is not a full stick phase, but just intervals with very low rotations. On the other hand, Fig. 10 represents the typical stable response, indicating the convergence of the bit rotational speed to the imposed rotational speed. It can be noticed the absence of the stick-slip cycles.

Before analyzing the stability maps, two dimensionless parameters are defined:

$$\begin{aligned} \pi _1 := \frac{-R_{Bit} \cdot (F_{Bit})_{z}}{k_1} \phantom {aaaaaa} \pi _2 := \frac{\Omega }{\omega _1} \end{aligned}$$

(22)

where $\pi _1$ is the ratio between the torque $-R_{Bit} \cdot (F_{Bit})_{z}$ and the torsional stiffness of the column $k_1$, and $\pi _2$ is the ratio between the imposed rotary table speed and the first natural frequency of the system. The stability maps of the next section are shown using these parameters, which makes the analysis much more general.

5.2 Stochastic results

Let us now show the stability maps and the stochastic results. We ran 1000 Monte Carlo simulations in a 300 by 300 grid. First we consider the uncertainties all together, with the following parameters: minimum penetration rate of $1.0 \times 10^{-3} \phantom {\cdot } \mathrm {m/s}$, ${{\mathrm{\upmu }}}_{X_{\mu }} = 0.310$, ${{\mathrm{cv}}}_{X_{\mu }} = 30\%$; ${{\mathrm{\upmu }}}_{X_{\sigma }} = 81.8 \phantom {\cdot } \mathrm {MPa}$, ${{\mathrm{cv}}}_{X_{\sigma }} = 20\%$; ${{\mathrm{\upmu }}}_{X_{Mud}} = 1440 \phantom {\cdot } \mathrm {kg/m^{3}}$, ${{\mathrm{cv}}}_{X_{Mud}} = 10\%$; ${{\mathrm{\upmu }}}_{X_{\xi }} = 0.30$, ${{\mathrm{cv}}}_{X_{\xi }} = 50\%$.

Figure 11 shows the stochastic torsional stability map, and Fig. 12 shows the stochastic minimum rate of penetration. The continuous black line represents the threshold of stability for the deterministic system. Above this line the system is unstable, and below this line the system is stable. This means that a combination of low imposed speed at the top and high weight-on-bit induces instability. On the other hand, we can scape from instability if the speed is increased and the weight-on-bit decreased. This stability map is typical for this system.

For the stochastic response, we consider different levels of probability of stability. The line with triangles (75%) represents a different threshold: below this line the probability of stability is 75%. If we want to improve the confidence, we might plot other lines. For instance, the 99% line means that below it the probability of stability is 99%. Note that if we improve the stability margin, the line shifts down, decreasing the stability region, which is coherent.

Fig. 11

Stochastic torsional stability map

Fig. 12

Stochastic minimum rate of penetration

There is a great difference between the deterministic curve and the $99\%$ probability of stability curve, i.e. uncertainties play an important role for the system analyzed. It is possible to construct a more complete stability map introducing colors to represent the probability of stability. Figure 13 superposes the stochastic torsional stability map and minimum rate of penetration map. To generate this map the probability of stability is computed for each point of the grid. The colors represent the probability ranges of the probability of stability.

Fig. 13

Stochastic complete stability map

The driller should aim the navy blue region when choosing the operational parameters (rotary table speed and weight-on-bit). The closer to the navy blue region, the higher is the probability of having a stable (optimum) behavior. Conversely, the closer to the scarlet red region, the higher the probability of having unstable behavior or low penetration rate. For instance, a point inside the cobalt blue area would have a probability between $90\%$ and $100\%$ of being stable. The small navy blue area on the right is the $100\%$ stability (optimum) probability region. In contrast, a point within the scarlet red area would have a probability between $0\%$ and $10\%$ of being optimum.

Now the effect of uncertainties are analyzed separately, one parameter at a time. To facilitate the interpretation of the results, the probability of stability of $90\%$ is set for all the next results. Figure 14 shows the $90\%$ stability threshold for several ${{\mathrm{cv}}}_{X_{\mu }}$, and Figs. 15 and 16 show the analogous results for ${{\mathrm{cv}}}_{X_{Mud}}$ and ${{\mathrm{cv}}}_{X_{\xi }}$, respectively. Figure 17 shows the $90\%$ stability threshold for minimum rate of penetration curves for several ${{\mathrm{cv}}}_{X_{\sigma }}$.

Fig. 14

Threshold of $90\%$ probability of torsional stability for several degrees of uncertainty in $\mu$

Fig. 15

Threshold of $90\%$ probability of torsional stability for several degrees of uncertainty in $\varvec{\rho }_{Mud}$

Fig. 16

Threshold of $90\%$ probability of torsional stability for several degrees of uncertainty in $\varvec{\xi }$

Fig. 17

Threshold of $90\%$ probability of minimum rate of penetration for several degrees of uncertainty in $\sigma _{C}$

At first glance, it can be noticed that the uncertainty in $\varvec{\rho }_{Mud}$ affected very little the torsional stability. This may be explained because we let $\rho _{Mud}$ vary along the drill-string, and when we increase the number of finite elements (sc. number of nodes), high values of $\rho _{Mud}$ in some nodes tend to be compensated by low values of $\rho _{Mud}$ in other nodes, so that the effect on the overall inertia of the system stays the same.

A very different situation is observed with the uncertainty in $\mu$ and $\varvec{\xi }$, both affecting significantly the torsional stability curve. The effect of the uncertainty in $\varvec{\xi }$ is even more pronounced than the corresponding of $\mu$. In the former case, the curves diverge much more when we increase the uncertainty. This result is in accordance with our previous intuition that the uncertainty in the damping is significative to the drill-string stability.

We can also notice that the uncertainty in $\sigma _{C}$ affects the minimum rate of penetration curve, displacing the curve upwards, reducing the optimal region.

6 Final remarks

6.1 Conclusion

A mathematical model of the torsional dynamics of an oil drill-string was developed using classical mechanical theories, and the torsional stability was analysed. The uncertainties related to the model parameters were taken into account to construct stochastic stability maps. It could be observed that the uncertainties play an important role in the results, diminishing the stability region.

In the stochastic stability map, the sharp boundaries delimitating the regions do not exist anymore, instead, we have transition regions with a non-null probability of being stable. It could be observed that when we take into account the uncertainties, we no longer have a well defined optimum region, instead, we have a region with flexible boundaries. In fact, the driller must choose which boundary he wants. The driller has no other alternative except assuming the risk of having an unstable behavior, because the optimum region becomes drastically reduced, for the parameters analyzed.

It was observed that the uncertainty in the damping is the most important for the stability analysis. This poses a problem because it is extremely difficult to measure the drill-string damping, but it is crucial for the mathematical model predictions.

6.2 Future works

In our stochastic modeling, we have considered only parametric uncertainties, it would be interesting to consider also model uncertainties, and how to perform the stability analysis in such case.

New models of the bit-rock interaction should be investigated. It would be interesting to consider a stochastic model for the bit-rock interaction, and how to perform the stability analysis in that case. We are currently following this path in LAVI (Laboratory of Acoustics and Vibrations of UFRJ). Our team is working on an experimental reduced scale drill-string instrumented to measure axial-torsional vibration, so that we can validate the models for bit-rock interaction. Also, we are developing different stochastic models for the bit-rock interaction.

The proposed model considers only the torsional degree of freedom of a drill-string. It would be interesting to improve it including bending and axial degrees of freedom. In this way, one could perform the stability analysis considering these new degrees of freedom, in order to reproduce the other instability regions of the Fig. 3.

Appendix A: data used in simulations

See Table 2.

Table 2 Values of the exact variables

The values of the material properties $\rho _{DS}$ and G are referred to ASTM-A36 structural steel. The values of the geological properties $\mu$ and $\sigma _{C}$ are referred to sandstone wet [37, 38], the values of the bit-rock interaction constants $\alpha _{1}$, $\alpha _{2}$ and $\alpha _{3}$ were obtained by least squares fit from field data [20].