1 Introduction

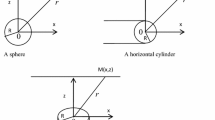
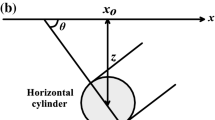
The geometrical parameters due to the causative source bodies are a commonly requested task in the interpretation of geophysical data. Many methods are derived to accomplish this task. For instance, a combined gravity or self-potential anomaly formula produced for simple geometrically shaped models can be signified through an analytical formula. This formula is a useful component to determine the depth, shape factor, polarization angle and amplitude factor connected to the physical effects of a buried structure. In this method, the gravity inversion aims to estimate the depth, amplitude and shape factors, while the self-potential inversion aims to estimate the same mentioned parameters and one or more parameters, which is called the angle of polarization for simple geometric shaped structures. These geometric shapes include a sphere, a horizontal cylinder, a semi-infinite vertical cylinder, and a dike. This method is reasonably suitable in some conditions, where some geological situations can have a distinct gravity or self-potential anomaly, which can be inverted as a single model. This suggests that quick and truthful quantitative elucidation approaches rely on simple geometric anomalies utilized for defining the inverse parameters of the subsurface model structures from observed gravity and self-potential data.

A number of fixed geometrical methods were introduced to decide the subsurface structure model parameters from gravity or self-potential data. They depend on graphical approaches, which apply characteristic points and distances (Nettleton 1976; Ram Babu and Atchuta Rao 1988; Essa 2007a), using matching curves (Murthy and Haricharan 1984) and using nomograms (Paul 1965; Bhattacharya and Roy 1981) all of them involving many approximations.

Several numerical methods have been established to construe gravity or self-potential data which includes Fourier transformation method (Sharma and Geldart 1968; Roy and Mohan 1984; Asfahani et al. 2001), Ratio methods (Bowin et al. 1986), Euler deconvolution (Thompson 1982; Reid et al. 1990; Roy et al. 2000), Werner deconvolution (Hartmann et al. 1971; Jain 1976), Mellin transformation (Mohan et al. 1986; Babu et al. 1991), Walsh transformation technique (Shaw et al. 1998; Al-Garni 2008), analytic signal method (Nandi et al. 1997; Sundarajan et al. 1998), linear and non-linear least-squares (Gupta 1983; Abdelrahman et al. 2003, 2008; El-Araby 2004; Essa et al. 2008), neural network application (Osman et al. 2007; Al-Garni 2010; Hajian et al. 2012), gradients (Aboud et al. 2004; Essa 2007b; Essa and Elhussein 2017; Roy 2019), and moving average method (Abdelrahman et al. 2006a, and 2009), 2D and 3D tomography and inversion (Biswas and Sharma 2017; Pham et al. 2018; Oksum et al. 2019; Vasiljević et al. 2019). The results of these approaches require a density data for the gravity elucidation and an existing intensity and a resistivity data for the self-potential explanation as a feature of the input, alongside a similar depth information gained from geologic as well as other geophysical information. Consequently, the subsequent model can fluctuate broadly relying upon these components if the gravity and self-potential inverse problem are ill-posed, unstable, and non-unique (Tarantola 2005; Mehanee and Essa 2015). Typical methods for acquiring steady solutions of an ill-posed inverse problem incorporate some regularization approaches (Tikhonov and Arsenin 1977; Ghanati et al. 2017). The three-dimensional gravity and self-potential result rely on a rigorous, estimation time, and priori information for inverting the model parameters. In addition, metaheuristic algorithms such as particle swarm algorithm (Essa and Munschy 2019; Essa 2020), anti-colony algorithm (Srivastava et al. 2014), simulated annealing (Biswas 2016a , b), and genetic algorithm (Montesinos et al. 2005; Di Maio et al. 2016) can be proposed to infer gravity and self-potential anomalies.

Moreover, Essa (2011) developed a semi-automatic approach to interpret gravity and self-potential data using a combined formula for both anomalies, which depends on knowing known the shape of the buried structures to estimate the depth and other model parameters.

The main objective and goal of the study is to develop a well-organized inversion method to overcome ill-posed and non-unique interpretation of gravity and self-potential data. The proposed nonlinear least-squares approach for gravity or self-potential inversion was established to estimate the depth (z) of the subsurface structures. The inverted problem of the depth was transformed into a nonlinear formula as z = f(z). This formula was deciphered for the depth by minimizing the objective function. By means of such assessed depth, a polarization angle and an amplitude factor emerged from the measured gravity or self-potential. The proposed approach relied on appraising the root mean square (μ-value) of the calculated buried model parameters for the causative bodies, which was utilized as a typical for detecting the optimal fit parameters of the subsurface model structure.

Finally, a nonlinear least-squares algorithm was applied to the synthetic examples with and without random noise. In addition, gravity and self-potential data set were used to investigate the sensitivity analysis of this method. This method was simultaneously tested on two real data sets, which revealed that the detected depths and other model parameters were in respectable covenant with the real ones.

1.1 The methodology

Essa (2010) proposed a combined gravity and/or self-potential for the simple shaped geological structures (spheres, cylinders, and sheets) as follows:

$${\text{g}}\left( {{\text{x}}_{{\text{i}}} ,{\text{ z}}} \right) = {\text{A}}\frac{{{\text{z}}^{{\text{j}}} }}{{\left( {{\text{x}}_{{\text{i}}}^{2} + {\text{z}}^{2} } \right)^{{\text{q}}} }},$$
(i)
$${\text{V}}\left( {{\text{x}}_{{\text{i}}} ,{\text{ z}}} \right) = {\text{A}}\frac{{{\text{x}}_{{\text{i}}} \left( {\cos {\uptheta }} \right) + {\text{z}}\left( {\sin {\uptheta }} \right)}}{{\left( {{\text{x}}_{{\text{i}}}^{2} + {\text{z}}^{2} } \right)^{{\text{q}}} }},$$
(ii)

to produce the following form:

$$P\left( {{\text{x}}_{{\text{i}}} ,{\text{ z}}} \right) = {\text{A}}\frac{{{\text{cx}}_{{\text{i}}} \left( {\cos {\uptheta }} \right)^{{\text{n}}} + {\text{z}}^{{\text{j}}} \left( {\sin {\uptheta }} \right)^{{\text{m}}} }}{{\left( {{\text{x}}_{{\text{i}}}^{2} + {\text{z}}^{2} } \right)^{{\text{q}}} }}{ },{\text{ i}} = 0,{ } \pm 1,{ } \pm 2,{ } \pm 3, \ldots ,{ } \pm {\text{k}}$$
(1)

where z is the depth of the body (unit), θ is the polarization angle (in case of self-potential data only), A is an amplitude factor depending on the physical features of the model (in gravity: mGal × unit2q − j but in self-potential mV × unit2q − j), xi is the horizontal coordinates (unit) and q is the shape factor of the model. Values of c, m, n, j, and q are specified in Table 1.

Table 1 Values of the parameters c, m, n, and j for various simple-geometric shapes in case of gravity and self-potential approaches (Essa, 2011)
Full size table

Equation (1) gives the next formula at the location of the anomaly origin, i.e. xi = 0 and P(xi, z) = P(0)

$$A = \frac{{P\left( 0 \right)z^{2q - j} }}{{\left( {\sin \theta } \right)^{m} }} ,$$
(2)

From Eq. (1), the next equations are attained at xi = ± N, N = 1, 2, 3,…, k

$$P\left( { + N} \right) = A\frac{{cN\left( {\cos \theta } \right)^{n} + z^{j} \left( {\sin \theta } \right)^{m} }}{{\left( {N^{2} + z^{2} } \right)^{q} }} ,\quad x_{i} = + N$$
(3)

and

$$P\left( { - N} \right) = A\frac{{ - cN\left( {\cos \theta } \right)^{n} + z^{j} \left( {\sin \theta } \right)^{m} }}{{\left( {N^{2} + z^{2} } \right)^{q} }} , \quad x_{i} = - N$$
(4)

From Eqs. (3) and (4), new two variables F and T are introduced as follows:

$$F = \frac{{P\left( { + N} \right) + P\left( { - N} \right)}}{2P\left( 0 \right)},$$
(5)

and

$$T = \frac{{P\left( { + N} \right) - P\left( { - N} \right)}}{2P\left( 0 \right)}.$$
(6)

From applying Eq. (5), the next form in shape (q) is deduced

$$q = \frac{lnF}{{ln\left( {\frac{{z^{2} }}{{N^{2} + z^{2} }}} \right)}}.$$
(7)

By using Eq. (3) and (4) and relieving in Eq. (6), we obtain the next form:

$$\frac{{\left( {\cos \theta } \right)^{n} }}{{\left( {\sin \theta } \right)^{m} }} = \frac{{T\left( {N^{2} + z^{2} } \right)^{q} }}{{cNz^{2q - j} }}.$$
(8)

In this way, we can rewrite Eq. (1) employing Eqs. (7) and (8) as follows

$$P\left( {x_{i} ,z} \right) = P\left( 0 \right)W\left( {x_{i} ,z} \right),$$
(9)

where

$$W\left( {x_{i} ,z} \right) = \frac{{2x_{i} T\left( {N^{2} + z^{2} } \right)^{{{\raise0.7ex\hbox{${lnF}$} \!\mathord{\left/ {\vphantom {{lnF} {ln\left( {\frac{{z^{2} }}{{N^{2} + z^{2} }}} \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${ln\left( {\frac{{z^{2} }}{{N^{2} + z^{2} }}} \right)}$}}}} + 2Nz^{{{\raise0.7ex\hbox{${lnF}$} \!\mathord{\left/ {\vphantom {{lnF} {ln\left( {\frac{{z^{2} }}{{N^{2} + z^{2} }}} \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${ln\left( {\frac{{z^{2} }}{{N^{2} + z^{2} }}} \right)}$}}}} }}{{2N\left( {x_{i}^{2} + z^{2} } \right)^{{{\raise0.7ex\hbox{${lnF}$} \!\mathord{\left/ {\vphantom {{lnF} {ln\left( {\frac{{z^{2} }}{{N^{2} + z^{2} }}} \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${ln\left( {\frac{{z^{2} }}{{N^{2} + z^{2} }}} \right)}$}}}} }} .$$

The unidentified depth in Eq. (9) can be gained applying the least-squares sense by minimizing the subsequent mathematical objective function in the real space. The form is:

$$z = arg\min \varphi \left( z \right) = \mathop \sum \limits_{i = 1}^{k} \left[ {\varphi \left( z \right)} \right]^{2} = \mathop \sum \limits_{i = 1}^{k} \left[ {P\left( {x_{i} } \right) - P\left( 0 \right)W\left( {x_{i} , z} \right)} \right]^{2} = minmum.$$
(10)

where P(xi) is the observed gravity or self-potential anomaly at xi, P(0) is the anomaly value at the origin (xi = 0), and k is the total number of collected data.

So, Eq. (10) can be solved using minimization, i.e., \(\frac{{\partial \mathop \sum \nolimits_{i = 1}^{k} \left[ {P\left( {x_{i} } \right) - P\left( 0 \right)W\left( {x_{i} , z} \right)} \right]^{2} }}{\partial z} = 0\), which leads to the next nonlinear formula in z:

$$f\left( z \right) = \mathop \sum \limits_{i = 1}^{k} \left[ {P\left( {x_{i} } \right) - P\left( 0 \right)W\left( {x_{i} , z} \right)} \right]W^{*} \left( {x_{i} ,z} \right) = 0,$$
(11)

where

$$W^{*} \left( {x_{i} ,z} \right) = \frac{{\partial W\left( {x_{i} , z} \right)}}{\partial z} .$$

Hence, Eq. (11) finally is

$$z_{f} = \frac{{\mathop \sum \nolimits_{i = 1}^{k} P\left( 0 \right)W^{*} \left( {x_{i} ,z_{i} } \right)}}{{P\left( 0 \right)\mathop \sum \nolimits_{i = 1}^{k} W\left( {x_{i} , z_{i} } \right)W^{*} \left( {x_{i} ,z_{i} } \right)}}$$
(12)

The depth (z) can be obtained by solving the nonlinear Eq. (12) applying a suitable iteration method (Mustoe and Barry 1998). The iteration form of Eq. (12) is:

$$z_{f} = f\left( {z_{i} } \right),$$
(13)

where zf and zi are the final and the initial depths, the iterative procedure finished at \(\left| {z_{f} - z_{i} } \right| \le E\), where E is a real number nearby zero. So, any initial guessing for the depth affected well because there is only one global minimum, i.e., no restrictions for the optimum range for the initial guess required.

Finally knowing the depth value, the shape factor (q), the angle of polarization (only in case of self-potential data) and the amplitude factor values are obtained from Eqs. (7), (8), and (2), respectively.

1.2 Determination of the best-fit parameters

The root mean square error (μ-value) has been utilized as a standard statistical metric to detect the model performance in the field of geosciences (Chai and Draxler 2014), i.e., the average model prediction error in the model parameters of interest.

Using the estimated model parameters from gravity or self-potential anomalies, we compute the μ-value in the following form:

$$\mu - value = \sqrt {\frac{{\mathop \sum \nolimits_{i = - k}^{ + k} \left[ {P\left( {x_{i} } \right) - P\left( {x_{i} ,z} \right)} \right]^{2} }}{2k + 1}} ,$$
(14)

where 2k + 1 is the number of collected points, and P(xi) and P(xi, z) are individually the observed and the computed forward model of gravity or self-potential anomalies. The model parameters, which give the minimum μ-values are the optimal fit parameters. In this way, we can detect the best-fit source parameters outcomes from all gravity or self-potential data.

Hence, we recommend a statement of origin to delineate data. In practice, since a field traverse has a subjective origin, the place of the model (xi = 0) in Eq. (1) must be delineated. In the gravity method, the maxima and/or the minima values of the profiles can be considered as the place of the origin of the body (xi = 0). While, the straight line connecting the maxima to the minima of the self-potential anomaly profile intersects the anomaly curve at the point xi = 0 (Stanley 1977). In addition, Abdelrahman et al. (2006b) acquainted a semi-automatic approach to describe the horizontal position of the structure applying a least-squares sense from a self-potential residual anomaly.

1.3 Synthetic examples

The benefits of the proposed method in this study were inspected through different synthetic cases, which include noise and anomalies produced by simple geometrically shapes (e.g., semi-infinite vertical, cylindrical, horizontal cylindrical, and spherical). The anomalies of the relevant models were generated using Eq. (1). In all cases studied, the synthetic anomalies were computed along with a profile extending 40 units with an interval of 1 unit.

1.4 First synthetic case (gravity anomalies)

Three gravity anomalies due to an infinitely extended semi-infinite vertical cylinder, horizontal cylinder, and sphere with source parameters: A = 500 mGal × unit, z = 3 unit and q = 0.5, A = 1500 mGal × unit, z = 5 unit and q = 1.0, and A = 2500 mGal × unit2, z = 7 unit and q = 1.5 were considered. The gravity anomalies of these three models are shown in Fig. 1. The generated gravity anomalies are inferred applying the procedures of the proposed approach, i.e., for each N value, the buried model parameters (z, q, A) was computed by utilizing Eqs. (12), (7), and (2), respectively. Besides, the fit between the observed and computed gravity anomaly was computed using the μ-value for each set of solutions through applying Eq. (14), whereas the evaluated gravity source parameters are presented in Tables 2, 3, and 4. The results in Tables 2, 3, and 4 demonstrate that the error (e) in all estimated parameters and the μ-value is equal to zero in case of free-noise anomalies used.

Table 2 Numerical results of the present method applied to synthetic example; the gravity anomaly profile over a semi-infinite vertical cylinder model (q = 0.5) with model parameters are z = 3 unit, A = 500 mGal × unit, and profile length = 40 unit without and with a 10% random noise
Full size table
Table 3 Numerical results of the present method applied to synthetic example; the gravity anomaly profile over a horizontal cylinder model (q = 1.0) with model parameters are z = 5 unit, A = 1500 mGal × unit, and profile length = 40 unit without and with a 10% random noise
Full size table
Table 4 Numerical results of the present method applied to synthetic example; the gravity anomaly profile over a sphere model (q = 1.5) with model parameters are z = 7 unit, A = 2500 mGal × unit2, and profile length = 40 unit, without and with a 10% random noise
Full size table

To check the stability of the suggested approach in the occurrence of noisy data, each gravity anomaly, P(xi), was tainted with a 10% random noise. The contaminated gravity anomalies were inferred by using the proposed method as mentioned above. The results are given in Tables 2, 3, and 4 for the same N value as follows:

First, Table 2 (in case of estimating parameters for the semi-infinite vertical cylinder) shows the estimated values for each model parameter (z, q, A), their percentage of error (e), and the μ-value. The minimum μ-value (5.80 mGal) happens at the N value equal 2 unit and the value of the depth (z) is 2.92 unit with 2.67% error, the shape (q) is 0.49 with 2% error, and the amplitude factor (A) equals 485.86 mGal × unit with 2.83% error.

Second, Table 3 for the horizontal cylinder model displays the values of all estimated parameters as z = 5.21 unit, q = 1.02, and A = 1575.18 mGal × unit, and the error in each parameter is 4.2%, 2%, and 5.01%, respectively. This result happens at the minimum μ-value (7.32 mGal) at N = 3 unit.

Finally, Table 4 clearly indicates that μ-value (0.68 mGal at N = 2 unit) is the minima value at which the values of depth (6.86 unit), the shape (1.51), and the amplitude factor (2542.49 mGal × unit2) and their errors are 2%, 0.67%, and 1.69%, respectively.

1.5 Second synthetic case (self-potential anomalies)

Using Eq. (1), three synthetic self-potential anomalies for a thin sheet, a horizontal cylinder, and a spherical model were created. The source parameters of these self-potential anomalies were: A = − 500 mV, z = 2 unit, θ = 30° and q = 0.5, A = − 2000 mV × unit, z = 4 unit, θ = 50° and q = 1.0, and A = − 3500 mV × unit2, z = 6 unit, θ = 70° and q = 1.5 (Fig. 2). The generated self-potential anomalies can be interpreted by using the proposed approach. For every N value, the model parameters (z, θ, q, and A) are computed by utilizing Eqs. (12), (8), (7), and (2), respectively. The μ-value is also computed applying Eq. (14) to measure the optimal fit between the observed and computed self-potential anomalies (Tables 5, 6, and 7).

Fig. 1
figure 1

The residual gravity anomalies of the buried structures representing by: a a semi-infinite vertical cylinder, b a horizontal cylinder and c a sphere as obtained from Eq. (1)

Full size image
Fig. 2
figure 2

The residual self-potential anomalies of the buried structures representing by: a a semi-infinite vertical cylinder, b a horizontal cylinder and c a sphere as obtained from Eq. (1)

Full size image
Table 5 Numerical results of the present method applied to synthetic example; the self-potential anomaly profile over a thin sheet model (q = 0.5) with model parameters are z = 2 unit, θ = 30°, A = -500 mV, and profile length = 40 unit without and with a 10% random noise
Full size table
Table 6 Numerical results of the present method applied to synthetic example; the self-potential anomaly profile over a horizontal cylinder model (q = 1.0) with model parameters are z = 4 unit, θ = 50°, A = -2000 mV × unit, and profile length = 40 unit, without and with a 10% random noise
Full size table
Table 7 Numerical results of the present method applied to synthetic example; the self-potential anomaly profile over a sphere model (q = 1.5) with model parameters are z = 6 unit, θ = 70°, A = -35,000 mV × unit2 and profile length = 40 unit, without and with a 10% random noise
Full size table

In case of using these anomalies without adding any noise, the results of the estimated parameters in Tables 5, 6, and 7 demonstrate that the error (e) in each parameter and the μ-value are equal to zero. While in case of adding a 10% random noise, the inversion process run and the optimal fit parameters are picked at the minimum μ-value as follows:

Table 5 shows that the minima μ-value is 10.78 mV occurring at N = 3 unit and at which the optimal fit parameters (z, θ, q, and A) are 2.08 unit, 28.98°, 0.52, − 496.75 mV with error of 4%, 3.40%, 3.37%, 0.65%, respectively. Table 6 further displays the results for the horizontal cylinder model self-potential inversion where the minima μ-value is 6.26 mV occurring at N = 10 unit and at which the optimal fit parameters (z, θ, q, and A) are 3.85 unit with 3.75% error, 50.98° with error of 1.96%, 0.98 with 2.47%, and − 1970.04 mV × unit with 1.50% error, respectively. Moreover, Table 7 presents the inverted parameter values (z, θ, q, and A) for a spherical model with values as 6.19 unit, 69.47°, 1.5, and − 3553.26 mV × unit2, with percentage of errors of 3.17%, 0.76%, 0%, and 1.52%, respectively, when this happens at N = 9 unit with the lowest μ-value (8.09 mV).

1.6 Third synthetic case (the effect of the location of origin)

To examine the effect of the location of origin; two synthetic data models with and without random errors were selected. The gravity model with the parameters: A = 600 mGal × unit, z = 8 unit, and q = 1.0, and a self-potential model with A = 600 mV × unit, z = 8 unit, θ = 30° and q = 1.0 investigated the effect of changing the value of location of origin by introducing an error of ± 0.5, ± 1.0, ± 1.5, and ± 2.5 unit to the location of origin in Eq. (1) (Fig. 3). Figure 3 shows the significance of choosing the location of origin in all the different model calculations vis-à-vis their μ-value errors.

Fig. 3
figure 3

The relation between offset and μ-value errors; a gravity model and b self-potential model

Full size image

In synthetic data without random errors, Fig. 3a, b show that the μ-value decreases to reach zero value at the correct solutions. But in synthetic data with a 10% random error, Fig. 3a, b show that the μ-value has a minimum value at the correct solutions. This kind of sensitivity analysis is important and necessary to test the effect of the location of origin as an important parameter in calculations.

1.7 Field examples

To clarify the benign application of new approaches established in the earlier sections, two residual field anomalies from Senegal and USA were sampled to interpret and inspect the stability and validity of the proposed method.

1.8 First real case: the Louga gravity anomaly

A residual gravity anomaly profile was collected from the west coast of Senegal (Nettleton, 1976). Figure 4 shows the appropriate residual gravity anomaly profile, 25 km long, and digitized at interims of 0.88 km. For every N value, the offered inverse method was utilized to the digitized anomaly profile to detect the model parameters z, q and A using Eqs. (12), (7) and (2), respectively (Table 8). Utilizing the estimated model parameters at various N values, the μ-value of the contrast among the observed and the calculated gravity anomalies (Fig. 4) was assessed. This Figure exhibits that the shape of the subsurface structure looks like a sphere (q = 1.55) at a depth of 9.09 km. The shape and the depth of the ore body attained through the current method are consistent very well with those achieved by Nettleton (1976) and Asfahani and Tlas (2011) (Table 9).

Fig. 4
figure 4

The measured gravity anomaly (open circles) over an area on the west coast of Senegal and the calculated response (solid circles) computed from the present inverse algorithm

Full size image
Table 8 Modeling results of the buried body of the Louga gravity anomaly, Senegal using the proposed method
Full size table
Table 9 Comparative results for the Louga gravity anomaly, Senegal
Full size table

Table 9 indicates that the gravity parameters obtained by the suggested approach are in acceptable concurrence with those reported in different studies. Overall, there is a realistic concurrence between all results, except the amplitude factor (A = 11,472.89 mGal × km2) value (Table 9). The difference in A value is due to a discrepancy in the units used for A, as these units rely upon the shape factor (q) of the body.

1.9 Second real case: the Malachite mine anomaly

Another self-potential profile was measured on the Malachite mine, Jefferson County, Colorado, USA collected by Heiland et al. (1945) (Fig. 5). These measurements were analyzed and described by Dobrin (1960). A sulphide ore body was found almost in vertical—cylindrical massive shaped with 11 m width and 13.7 m depth (drilling information; Heiland et al. 1945; Dobrin 1960). Moreover, the sulphide mine was an amphibolite belt constrained by a schist and gneiss. A quartz diorite sheet was sliced through schists with about vertical dip and with lenticular copper sulfides. The self-potential investigation helped in assessing the potential difference between equidistant points along with profile lines vertical to the extension of the ore body.

Fig. 5
figure 5

The measured self-potential anomaly (open circles) over the Malachite mine, Jefferson County, Colorado, USA and the calculated response (solid circles) computed from the present inverse algorithm

Full size image

This anomaly profile was digitized at an interim of 6.8 m. All digitized self-potential values were used to calculate the model parameters z, θ, q, and A applying Eqs. (12), (8), (7) and (2) for each N value, respectively (Table 10). The detected parameters were applied to decide the optimal fit of the geometric body (shape factor) by utilizing the μ-value standard. The model with a minimum μ-value (8.338 mV) was for a 3D semi-infinite vertical cylinder model. Its parameters were: z = 15.5 m, θ = 79.2°, q = 0.55, and A = − 240.4 mV (Fig. 5). The shape and the other model parameters recovered by our inversion method are in a good agreement with those attained by drilling information and with the outcomes available in other scientific literature such as Abdelrahman et al. (2004) and Tlas and Asfahani (2007) (Table 11).

Table 10 Modeling results of the buried body of the Malachite Mine self-potential anomaly, USA using the proposed method
Full size table
Table 11 Comparative results for the Malachite Mine self-potential anomaly, USA
Full size table

2 Conclusions

This study proposed nonlinear least-squares method to detect the depth of a subsurface structure and calculate the model parameters for simple-class geometrical shapes bodies: spherical, horizontally and vertically cylindrical, to interpret gravity and/or self-potential combined formula. The procedure of the offered method mainly relied upon deciphering a non-linear equation z = f(z) and the statistical μ-value criteria between observed and computed anomalies and determine a preferable structure for the gravity and/or self-potential anomaly. The efficiency and sensitivity of the proposed method were investigated through analyzing and interpreting synthetic theoretical examples. Furthermore, the advantage of using the proposed method over the earlier one is not need to priori information about the shape of the subsurface structure. The synthetic data revealed that the viability of the offered method was precise and firm. In addition, utilizing the proposed method to real data from Senegal and USA established that the acquired outcomes were reliable with the information from drilling and outcomes available in other works. Furthermore, the proposed method proved robust as it could be simply placed in a code. Besides, its convergence to the optimum model solutions was definite and rapid. Accordingly, this method is endorsed for routine exploration of field anomalies in an attempt to detect the geophysical parameters for the mentioned structures.