Regularized nonlinear inversion of magnetic anomalies of simple geometric models using Occam’s method: an application to the Morvarid iron-apatite deposit in Iran

Abstract

In this paper we tackle the problem of inverting geophysical magnetic data due to simple shape anomalies caused by thin sheet, cylinder and fault models using Occam’s inversion scheme. A significant aspect of using Occam’s inversion is the choice of the regularization parameter controlling the trade-off between the data fidelity and regularization term in the cost function of optimization problem, and consequently, reliable estimation of subsurface models. Two criteria L-curve and weighted generalized cross validation are considered in order to choose an optimum value of the regularization parameter. The proposed strategy was first evaluated on three theoretical synthetic models for each of the magnetic simple-shaped structures with different random errors, where a considerable agreement was obtained between the exactly known and estimated models. The validity of the technique was also applied to one real data set from Morvarid iron-apatite deposit, in Northwest Iran. The resulting inverted parameters using the proposed algorithm correspond reasonably closely with the known geology and nearby borehole information.

1 Introduction

Magnetic exploration is used to provide an indirect way to observe magnetic causative bodies such as magnetite-bearing minerals, titanium and molybdenum, mineralization such as heavy mineral sands and massive sulfides beneath the Earth’s surface by studying the anomalous magnetic field (Blakely 1995; Nabighian et al. 2005; Beiki and Pedersen 2012). Among the many approaches and techniques for quantitative interpretation of magnetic anomalies, some of the most popular include inversion processes in which the Earth’s geomagnetic measurements are transferred into a quantitative subsurface-property description such as the spatial location, the shape and magnetic susceptibility using an optimization problem in which an objective function comprising a measure of data misfit and a measure of model character is minimized. Many of inverse problems in geophysics are ill-posed means that the inverse problem is non-unique and unstable (i.e. any small perturbation of the input data can cause large perturbation of the estimated model) (Tikhonov and Arsenin 1977; Hansen 1998; Oldenburg and Li 2005). Therefore, to solve these problems we need special strategies known as regularization techniques (Abdelazeem 2013; Gheymasi and Gholami 2013; Ghanati et al. 2016). The inversion of magnetic data problem, which we aim to solve here, represents typical ill-posed problem. Although a unique solution may be found when a single causative body has a simple geometrical shape, the sensitivity of the problem to any additive noise, which leads to instable and invalid solutions, is still challenging (Salem et al. 2004). However, this drawback can be rectified through an increase of the over-determination ratio of the inverse problem (Dobróka et al. 2016).

Most literature reformulated such problems into a system of equations having better condition by adding different kinds of constraints to control the results as much as possible. For example, Menke (1984) suggested the generalized inverse technique through singular value decomposition in magnetic data interpretation. Raju (2003) applied Gauss–Newton solution and to avoid the singularity of the forward operator, a constant known as Marquardt’s parameter is added to the objective function. His strategy for the choice of the Marquardt’s parameter was based on the RMS error so that initially a large positive value of it is given as an input to the algorithm; if the RMS error is decreased the Marquardt’s parameter is reduced by dividing it by a constant factor (which is defined by the user). Asfahani and Tlas (2004) took advantage of an interpretative method based on the nonlinearly constrained least-squares minimization for interpreting magnetic anomalies due to faults and thin dike structures. Beiki and Pedersen (2012) developed a constrained inversion technique for estimating magnetic dike parameters. They used the Levenberg–Marquardt method together with the trust-region-reflective algorithm allowing for inequality constraints on the model parameters. A stochastic optimization approach called adaptive simulated annealing was proposed by Asfahani and Tlas (2007) applied to simple geometric magnetic anomalies. They concluded that, although the major preference of adaptive simulated annealing is to avoid becoming trapped at local minima of the objective function, it is computationally time-consuming as well as the convergence speed of the algorithm highly depends on the initial guess. However, running time of the simulated annealing algorithm can be significantly reduced using very fast simulated annealing (Sen and Stoffa 1995; Dobróka and Szabó 2011). Alimoradi et al. (2011) implemented the artificial neural network for determining the depth of dikes. Beside inversion techniques, a large number of semi-automatic methods have been developed for mapping the subsurface magnetic isolated targets. The most commonly and widely used of these are power spectrum (Bhattacharyya 1966; Spector and Grant 1970; Dondurur and Pamukçu 2003), Werner deconvolution (Werner 1955; Kilty 1983; Tsokas and Hansen 1996; Hansen 2002), source parameter imaging (Thurston and Smith 1997; Thurston et al. 1999, 2002; Phillips 2000), Euler deconvolution (Thompson 1982; Mushayandebvu et al. 2001; Beiki et al. 2011), statistical methods (Spector and Grant 1970; Treitel et al. 1971) and analytic signal (Nabighian 1972; Bastani and Pedersen 2001; Salem 2005; Yuan and Yu 2014) approaches.

The general objective of this study is to use the Occam’s inversion (Constable et al. 1987; Degroot-Hedlin and Constable 1990) to the recovery of magnetic anomalies of simple shape bodies caused by sheet, cylinder and fault structures. Furthermore, the performance of the L-curve and weighted generalized cross validation (W-GCV) techniques are compared and contrasted. There have been a few successful applications of the L-curve (Haber 1997; Johnstone and Gulrajani 2000, Farquharson and Oldenburg 2004; Stefan 2008; Vatankhah et al. 2014) and W-GCV (Chung et al. 2008; Viloche Bazan and Borges 2010; Abedi et al. 2013; Gholami and Sacchi 2012; Ghanati et al. 2015) criteria to choose an optimum value of the regularization parameter in non-linear problems in geophysics. In this paper, due to the nonlinearity of inverse modeling of the magnetic simple-shaped structures, a nonlinear least squares constrained minimization problem based on the Occam’s inversion is proposed. There is a crucial problem in using Occam’s inversion, which is the selection of the regularization parameter. We consider and characterize two methods (i.e., L-curve and W-GCV) in determining the optimal regularization parameter in solving the inversion problems corresponding to synthetic and real magnetic simple-shaped structures. The paper is organized as follows. In Sect. 2, the formulation of the total magnetic anomalies due to thin sheet, cylinder and fault is demonstrated. Next, in Sect. 3, we describe the estimation of the initial model corresponding to simple causative magnetic sources. Section 4 presents the theory of Occam’s inversion scheme as well as the L-curve and W-GCV functions to determine the regularization parameter. The performance of the described methods in synthetic and real examples is discussed in Sect. 5.

2 Theory

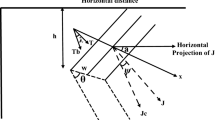
Simple geometrical shapes such as thin sheet, cylinder and fault models are widely used for the interpretation of magnetic field data (Nabighian 1972; Beiki et al. 2011). Figures 1a, c illustrate cross-sectional views of thin sheet, horizontal cylinder and fault models, respectively.

Fig. 1

Cross-section view of a two-dimensional, a thin sheet, b cylinder and c fault along with required parameters for forward modeling

2.1 Magnetic anomaly of a thin sheet

According to Stanley (1977) the magnetic anomalies of the total intensity which is influenced by a linear regional anomaly of slope $A$ with a base level $B$ over a thin sheet at any observed point M (Fig. 1a) along the x-axis may be written as follows:

$$ P\left( X \right) = F\frac{{\left( {X - \zeta } \right)\sin \varphi + Z\cos \varphi }}{{\left( {X - \zeta } \right)^{2} + Z^{2} }} + AX + B $$

(1)

where

$$ F = 2KT\beta \left( {1 - \cos^{2} I_{0} \cos^{2} \alpha } \right) $$

where F denotes amplitude coefficient, X (m) is distance of the observation M from the reference point R, O is origin of coordinates selected above the center of the anomaly, Z (m) is depth to top of the anomaly, $\zeta$ (m) is distance of the origin O from the reference point, $K$ (SI unit) is magnetic susceptibility contrast, $T$ (nT) is the earth’s magnetic field intensity, $\beta$ (m) is thickness of thin sheet, the inclination of the earth’s total magnetic field is $I_{0}$ (°), $\alpha$ (°) indicates strike azimuth of the body measured clockwise from magnetic north and index parameter $\varphi$ is defined as φ = 2I ^*₀   − δ −  90° −450° ≤ φ ≤ 90° where

$$ {\rm I}_{0}^{*} = \arctan \left( {\tan {\rm I}_{0} /\sin \alpha } \right) $$

In above expression, ${\text{\rm I}}_{0}^{*}$ is the effective inclination of the magnetic polarization in the vertical plane normal to the strike of the structure and $\delta$ is dip of the sheet varying from 0° to 180°.

2.2 Magnetic anomaly of a cylinder

The mathematical expression for the total magnetic anomaly together with the linear regional anomaly observed at a point M on the principle profile of an arbitrarily magnetized cylinder is presented by Prakas Rao et al. (1986), in the following way:

$$ P\left( X \right) = F\left( {\frac{{\left( {Z^{2} - \left( {X - \zeta } \right)^{2} } \right)\cos \varphi + 2\left( {X - \zeta } \right)Z\sin \varphi }}{{\left( {\left( {X - \zeta } \right)^{2} + Z^{2} } \right)^{2} }}} \right) + AX + B $$

(2)

where

$$ F = \frac{{2\pi r^{2} kT^{*} \sin I_{0} }}{{\sin I_{0}^{*} }} \quad \varphi = 2I_{0}^{*} - 180^{ \circ } \quad I_{0}^{*} = \arctan \left( {\tan I_{0} /\sin \alpha } \right)\quad T^{*} = T\left( {\frac{{\sin I_{0} }}{{\sin I_{0}^{*} }}} \right) $$

where $r$ is the radius of the cylinder and $T^{*}$ is the value of effective total intensity of magnetic polarization in the vertical plane normal to the strike of the body. The rest notations have the same meaning as that demonstrated in the previous expressions and are shown in Fig. 1b.

2.3 Magnetic anomaly of a fault

Stanley (1977) and Atchuta Rao et al. (1980) showed that the magnetic anomaly over a thin sheet is equivalent to the first horizontal derivative of the magnetic anomaly due to a fault. Thus integrating Eq. 1, we get the total magnetic anomaly for the fault structures as follows:

$$ P\left( X \right) = 0.5 F \sin \varphi \ln \left( {X^{2} - 2X\zeta + \zeta^{2} + Z^{2} } \right) + F\cos \varphi \tan^{ - 1} \left( {\frac{X - \zeta }{Z}} \right) + 0.5AX^{2} + BX $$

(3)

where

$$ F = 2KT\beta \left( {1 - \cos^{2} I_{0} \cos^{2} \alpha } \right) $$

The notations have the same meaning as that presented in the previous expressions and are illustrated in Fig. 1c. The object of inversion is to recover the unknown model parameters $F, \zeta , \varphi , Z, A,$ and $B$ from an observed data set.

3 Initial model estimation

In this paper, we follow the idea presented in Atchuta Rao et al. (1985) in order to estimate the initial solution prior to entering an optimization process. The initial solution with the thin sheet, cylinder and fault models can be obtained by rearranging the terms of Eqs. 1, 2 and 3, respectively. As a result, the initial model associated to the thin sheet anomaly by means of the discrete magnetic anomaly values $P\left( X \right)$ and the concerning distances $X$ may be rewritten as the polynomial below.

$$ P\left( X \right)X^{2} = P\left( X \right)X\varPsi_{1} + P\left( X \right)\varPsi_{2} + X^{3} \varPsi_{3} + X^{2} \varPsi_{4} + X\varPsi_{5} + \varPsi_{6} $$

(4)

After simplification

$$ \begin{aligned} & \varPsi_{1} = 2\zeta \\ & \varPsi_{2} = - \left( {Z^{2} + \zeta^{2} } \right) \\ & \varPsi_{3} = A \\ & \varPsi_{4} = \left( {B - 2A\zeta } \right) \\ & \varPsi_{5} = A\left( {Z^{2} + \zeta^{2} } \right) + F\sin \varphi - 2B\zeta \\ & \varPsi_{6} = B\left( {Z^{2} + \zeta^{2} } \right) + FZ\cos \varphi - F\zeta \sin \varphi \\ \end{aligned} $$

(5)

For cylinder model, by rearranging Eq. 2, we get

$$ P\left( X \right)X^{4} = P\left( X \right)X^{3} \varPsi_{1} + P\left( X \right)X^{2} \varPsi_{2} + P\left( X \right)X\varPsi_{3} + P\left( X \right)\varPsi_{4} + X^{2} \varPsi_{5} + X\varPsi_{6} + \varPsi_{7} + X^{3} \varPsi_{8} + X^{4} \varPsi_{9} + X^{5} \varPsi_{10} $$

(6)

After simplification

$$ \begin{aligned} & \varPsi_{1} = 4\zeta \\ & \varPsi_{2} = - \left( {2Z^{2} + 6\zeta^{2} } \right) \\ & \varPsi_{3} = 4\zeta \left( {\zeta^{2} + Z^{2} } \right) \\ & \varPsi_{4} = - \left( {\zeta^{2} + Z^{2} } \right)^{2} \\ & \varPsi_{5} = - 4A\zeta^{3} + 2BZ^{2} + 6B\zeta^{2} - D - 4A\zeta Z^{2} \\ & \varPsi_{6} = AZ^{4} - 4B\zeta^{3} + A\zeta^{4} + 2D\zeta + 2EZ - 4B\zeta Z^{2} + 2A\zeta^{2} Z^{2} \\ & \varPsi_{7} = 2B\zeta^{2} Z^{2} + B\zeta^{4} + BZ^{4} - 2E\zeta Z - D\zeta^{2} + DZ^{2} \\ & \varPsi_{8} = 6A\zeta^{2} - 4B\zeta + 2AZ^{2} \\ & \varPsi_{9} = - 4A\zeta + B \\ & \varPsi_{10} = A \\ \end{aligned} $$

(7)

where

$$ D = F \cos \varphi ,E = F \sin \varphi $$

Using matrix notation, Eqs. 4 and 6 can be expressed as follows:

$$ \varvec{P} = \varvec{C}{\varvec{\Psi}}\quad P \in {\mathbb{R}}^{\text{m}} , \quad C \in {\mathbb{R}}^{{{\text{m}} \times {\text{n}}}} \& {\varPsi } \in {\mathbb{R}}^{\text{n}} $$

(8)

Based on the above equation system, we deal with an over-determined system so that the coefficients ${\varPsi }_{1} , {\varPsi }_{2} , \ldots , {\varPsi }_{6}$ associated to thin sheet and coefficients ${\varPsi }_{1} , {\varPsi }_{2} , \ldots , {\varPsi }_{10}$ for cylinder are derived by Gaussian least squares method with the following normal equation.

$$ {\varvec{\Psi}} = \left[ {\varvec{C}^{T} \varvec{C}} \right]^{ - 1} \varvec{C}^{T} \varvec{P} $$

(9)

The initial solution corresponding to thin sheet and cylinder then obtained back from the coefficients ${\varPsi }_{1} , {\varPsi }_{2} , \ldots , {\varPsi }_{6}$ and ${\varPsi }_{1} , {\varPsi }_{2} , \ldots , {\varPsi }_{10}$ through Eq. 5 and 7, respectively. In Eq. 7, after estimating the values of $E$ and $D$, amplitude coefficient and index parameter for a cylinder model are defined as:

$$ \varphi = { \arctan }\left( {\frac{E}{D}} \right) $$

(10)

$$ F = \sqrt {D^{2} + E^{2} } $$

(11)

It should be noted that the parameter $\varphi$ obtained based on Eq. 8 varies between −90° and 90°. The value of $\varphi$ depends on the earth’s field inclination, profile azimuth and body dip. The proper quadrant of $\varphi$ is determined based on the maximum and minimum amplitudes and the corresponding maximum and minimum distances. The reader are referred to (Atchuta Rao et al. 1985; Raju 2003) for more details about determination of the correct value of the parameter $\varphi$. Our investigation showed that the initial solution obtained for a thin sheet model can be applied as an initial solution for a fault model.

4 Basic of inversion theory

4.1 Occam’s inversion

Occam’s inversion is a robust algorithm for nonlinear inversion introduced by Constable et al. (1987). Mathematically, Occam’s inversion is a generalized least squares inversion method under some specified model property constraint (Constable et al. 1987; DeGroot-Hedlin and Constable 1990). Thus make the inversion procedure more stable, of a narrower solution space and less model dependence (Aihua 2010). Occam’s method, in fact, uses the discrepancy principle and searches for the solution that minimizes a cost function as follows:

$$ \varphi \left( \varvec{m} \right) = \emptyset_{d} \left( \varvec{m} \right) + \lambda \emptyset_{m} \left( \varvec{m} \right) $$

(12)

where $\varvec{m}$ is the model parameter vector, $\emptyset_{d}$ is data misfit functional, $\emptyset_{m}$ denotes stabilizing functional and $\lambda$ is the regularization parameter which controls the trade-off between the data fidelity, $\emptyset_{d}$, and regularization term, $\emptyset_{m}$, in a minimization process.The data fidelity and regularization term are expressed as:

$$ \emptyset_{d} \left( \varvec{m} \right) = W_{d} \left[ {G\left( \varvec{m} \right) - \varvec{d}} \right]_{2}^{2} \quad \varvec{m} \in {\mathbb{R}}^{n} , \quad G \in {\mathbb{R}}^{m \times n} \;\& \; \varvec{d} \in {\mathbb{R}}^{m} $$

(13)

$$ \emptyset_{m} \left( \varvec{m} \right) = L\varvec{m}_{2}^{2} $$

(14)

where $G$ is the forward modeling operator which is nonlinear, $\varvec{d}$ is the observed data vector of length $m$, $W_{d}$ is an $m \times m$ data weighting matrix containing the reciprocal of variance for each datum (here we set $W_{d}$ to the identity matrix) and matrix $L$ indicates the regularization operator which is usually an approximation to $j{\text{th}}$-order difference operator. The choice of matrix $L$ depends on the prior assumptions about the model characteristics (Aster et al. 2013; Gheymasi and Gholami 2013). Operator matrix $L$ is defined as

$$ {\text{L}} = \left( {\begin{array}{*{20}c} { - 1} & { 1} & {\begin{array}{*{20}c} { \cdots } & { \cdots } & { 0} \\ \end{array} } \\ 0 & { - 1} & {\begin{array}{*{20}c} { 1} & { \cdots } & { 0} \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ { 0} \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { \vdots } \\ { \ldots } \\ \end{array} } & { \begin{array}{*{20}c} \vdots \\ { - 1} \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ 1 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right) \in {\mathbb{R}}^{{{\text{n}} - 1 \times {\text{n}}}} $$

(15)

In this research, the function $G\left( \varvec{m} \right)$ is nonlinear, thus, in order to use the Occam’s method, we should linearize this function.

Given a trial model $\varvec{m}^{k}$ ($k$ indicates the iteration number), using Taylor’s series expansion, we get

$$ G\left( {\varvec{m}^{k} + \delta \varvec{m}} \right) \approx G\left( {\varvec{m}^{k} } \right) + J\left( {\varvec{m}^{k} } \right)\delta \varvec{m} $$

(16)

where $J\left( \varvec{m} \right)$ is the linear differential operator obtained by truncating higher order terms of the Taylor’s series expansion (Roy 2008). Elements of $J\left( \varvec{m} \right)$ forms the Jacobian matrix in linearized inversion. Mathematically, this can be defined as

$$ J_{ij} \left( {\varvec{m}^{k} } \right) = \frac{{\partial G_{i} }}{{\partial \varvec{m}_{j} }}\quad i = 1, 2, 3, \ldots ,M\quad j = 1, 2, 3, \ldots , N $$

(17)

where $N$ is the number of model parameters and $M$ is the number of measured data, and a more detail of the Jacobian matrix corresponding to each of the simple geometric magnetic anomalies can be referred in “Appendix”.

Using Eq. 16, we get the objective function at the $\left( {k + 1} \right)th$ iteration as

$$ \varphi \left( {\varvec{m}^{k + 1} } \right) = \left\|W_{d} \left[ {J\left( {\varvec{m}^{k} } \right)\varvec{m}^{k+ 1} - \hat{d}\left( {\varvec{m}^{k} } \right)} \right]\right\|_{2}^{2} + \lambda^{2} \left\|L\left( {\varvec{m}^{k + 1} } \right)\right\|_{2}^{2} $$

(18)

where

$$ \hat{d}\left( {\varvec{m}^{k} } \right) = \varvec{d} - G\left( {\varvec{m}^{k} } \right) + J\left( {\varvec{m}^{k} } \right)\varvec{m}^{k} $$

(19)

Because $J\left( {\varvec{m}^{k} } \right)$ and $\hat{d}\left( {\varvec{m}^{k} } \right)$ are constant, Eq. 18 is in the form of a damped least squares problem which has the solution as follows

$$ \varvec{m}^{k + 1} = \varvec{m}^{k} + \delta \varvec{m} = \left( {J\left( {\varvec{m}^{k} } \right)^{T} W_{d}^{T} W_{d} J\left( {\varvec{m}^{k} } \right) + \lambda^{2} L^{T} L} \right)^{ - 1} J\left( {\varvec{m}^{k} } \right)^{T} W_{d}^{T} W_{d} \hat{d}\left( {\varvec{m}^{k} } \right) $$

(20)

It should be noted that, in Occam’s inversion the parameter of $\lambda$ is dynamically adjusted so that the solution will not pass the permitted misfit (Aster et al. 2013; Aihua 2010). Thus, by using an initial model we attain a model at each iteration and use this model as a starting model for the next until the misfit reaches to its desired value. In the next section, the choice of the regularization parameter through the L-curve and W-GCV techniques are presented.

4.2 Choosing the regularization parameter

4.2.1 L-curve

The L-curve criterion is a popular for choosing appropriate regularization parameters, when the data noise is not priori known (Hansen 2001). The L-curve is log–log parametric plot of the squared norm of the regularized solution, $\left\| {G\left( \varvec{m} \right) - \varvec{d}} \right\|_{2}^{2}$, and the squared norm of the regularized residual, $\left\| {L\varvec{m}} \right\|_{2}^{2}$, for a range of values of the regularization parameter (Agarwal 2003; Vogel 1996). After plotting the L-shaped curve, automatic selection of the L-corner is a major challenge, hence, several approaches have been developed to tackle this issue (Shahrak et al. 2013). Hansen (2001) proposed a method for picking the L-corner based on resorting to maximum curvature concept of the L-curve. The point of maximum curvature can be calculated by the formulation below.

$$ {\mathcal{K}}\left( \lambda \right) = 2\left( {\frac{{\phi_{d} \emptyset_{m} }}{{\partial \emptyset_{m} }}} \right)\left( {\frac{{\lambda^{2} \emptyset_{d} \partial \emptyset_{m} + 2\lambda \emptyset_{d} \emptyset_{m} + \lambda^{4} \emptyset_{m} \partial \emptyset_{m} }}{{\left( {\lambda^{2} \left( {\emptyset_{m} } \right)^{2} + \left( {\emptyset_{d} } \right)^{2} } \right)^{{\frac{3}{2}}} }}} \right) $$

(21)

where $\partial$ denotes the first derivative with respect to $\lambda$.

4.2.2 Weighted generalized cross validation (W-GCV)

Recently Chung et al. (2008) proposed weighted-GCV criterion for choosing the optimum values of the parameter regularization. The W-GCV function, applied to the regularized inverse problem, can be defined as

$$ {\mathcal{W}}\left( \lambda \right) = \frac{{\vartheta \left\| {G\left( {\varvec{m}_{\lambda } } \right) - \varvec{d}} \right\|_{2}^{2} }}{{trace\left( {I - \xi G\left( {G^{T} G + \lambda^{2} L^{T} L} \right)^{ - 1} G^{T} } \right)^{2} }} $$

(22)

In non-linear inverse problems the matrix $G$ is replaced by the Jacobian matrix, $J$. The most suitable parameter regularization, $\lambda$, can therefore be defined as the one that minimizes the W-GCV function (Wahba. 1990). It should be noted that the difference between the standard GCV and W-GCV is the additional weighting parameter. Choosing $\xi = 1$ results in the standard GCV function. Choosing $\xi > 1$ leads to smoother solutions, while $\xi < 1$ results in less smooth solutions (Chung et al. 2008). The optimum value of $\xi$ is experimentally determined (Chung et al. 2008; Chung and Nagy 2010) so that in our study, the value of $\xi$ is set 500. For a non-linear problem solved using an iterative approach, the W-GCV function can be applied to the linearized problem for a range of values of $\lambda$.

5 Numerical Results

5.1 Application to Synthetic data

In the following, functionality of the proposed inversion algorithm is demonstrated by presenting the results of performing synthetic magnetic anomaly inversion. Therefore, three synthetic examples corresponding to simple geometric models (thin sheet, cylinder and fault) with different added Gaussian noise are discussed.

5.1.1 Thin sheet Example

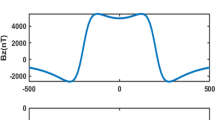
A theoretical synthetic magnetic anomaly due to a thin sheet model is studied using the following assumed parameters ${\upzeta } = 32\;{\text{m}};\,{\text{Z}} = 8;\,{\text{A}} = 0.25;\,{\text{B}} = 2$ and ${\text{K}} = 0.01\;{\text{SI}}$. The other parameters in calculating the anomaly are: δ = 60°; α = 0°; ${\text{\rm I}}_{0} = 15;\;{\upbeta } = 2\;{\text{m }}$ and ${\text{T}} = 45000$ nT. These parameters are applied to Eq. 1 in order to produce the concerning synthetic total magnetic anomaly. Then the generated anomaly is corrupted by 5 and 10% random errors. Figure 2 illustrates the synthetic magnetic anomaly profile contaminated with 5% Gaussian noise over the modeled thin sheet with a length of 64 m at a station interval of 1 m. Both generated random anomalies are thereafter subjected to interpretation of the proposed inversion algorithm, where the estimated parameters are illustrated in Table 1. Figure 3 depicts the L-curve based on the plot, in a log–log scale, of the regularized solution norm versus the residual norm for several values of ${\uplambda }$. The corner point can be considered as the point of maximum curvature (Hansen 2001). Figure 4 shows the optimum value of the L-curve in which the curvature obtained using Eq. 21 attains to maximum. In Fig. 5, we plot the W-GCV function (Eq. 22) with respect to a range of values of the regularization parameters, ${\uplambda }$, and the identified vertex (indicated by the asterisk) which denotes the optimal value of ${\uplambda }$. The calculated magnetic anomaly has been computed based on the evaluated parameters associated to the total magnetic anomaly with 5% additive noise and optimum value of ${\uplambda }$ as shown in Fig. 2. It should be pointed out that the calculated magnetic anomalies using the W-GCV and L-curve based methods are greatly close to each other.

Fig. 2

Synthetic total magnetic anomaly corrupted by 5% random error over a thin sheet structure with dip angle 60°, depth to the top 8 m, width 2 m and susceptibility contrast 0.01 SI (red), calculated anomaly using the W-GCV and L-curve based methods (blue), residual anomaly (green) and regional anomaly (black). (Color figure online)

Table 1 Numerical results of the synthetic magnetic anomaly due to the thin sheet with 5 and 10% Gaussian noise using the L-curve and W-GCV based techniques

Fig. 3

Regularization parameter estimation using L-curve for several values of $\lambda$

Fig. 4

Maximum curvature of L-curve implying the optimum value of the regularization parameter (red asterisk). (Color figure online)

Fig. 5

Regularization parameter estimation using W-GCV for several values of $\lambda$. The optimum value of the regularization parameter $\lambda$ is indicated by a red asterisk. (Color figure online)

To evaluate the quality of data fit at each iteration of the inversion process, root mean square error (RMSE) is defined as

$$ {\text{RMSE}} = \sqrt {\frac{{\emptyset_{\text{d}} }}{{\upchi }}} $$

(23)

where ${\upchi }$ denotes the number of observed data. We must take care to note that high RMSE is usually discussed as poor data fit and thus the inversion is not reliable. But Anscombe (1973) and Chatterjee and Firat (2007) proved that this supposition can be misleading in some cases. The RMS of data misfit for the synthetic thin sheet model shows that the inversion has converged at the sixth iteration (Fig. 6).

Fig. 6

RMS data misfit error versus iteration count for the first synthetic example (thin sheet). The inversion process converges in 6 iterations

5.1.2 Cylinder Example

Now the efficiency of the proposed inversion method is tested on a synthetic magnetic anomaly caused by a cylinder structure with radius equal to 10 m (with the same profile length and station interval defined in the first example). To generate the synthetic data, the assumed parameters in Table 2 are used in Eq. 2. Then the forward modeling responses are contaminated with 5 and 10% Gaussian noise. Table 2 shows the results of the second synthetic data set inversion based on the L-curve and W-GCV techniques so that the estimated parameters are in excellent concordance with the models from which the data were produced.

Table 2 Numerical results of the synthetic magnetic anomaly due to the cylinder with 5 and 10% Gaussian noise using the L-curve and W-GCV based techniques

5.1.3 Fault Example

As a final example, we generate synthetic data due to a fault model by forward modeling through Eq. 3 and the assumed parameters defined in Table 3 (with the same profile length and station interval defined in the first example). The other parameters in calculating the anomaly are: δ = 150°; α = 0°; ${\text{\rm I}}_{0} = 45;{\text{K}} = 0.01 {\text{SI }}$ and ${\text{T}} = 45000$ nT. Then 5 and 10% percent random noise is added to the forward modeling responses, respectively. Inversion results obtained using the proposed method along with automatic means of the regularization parameters selection are shown in Table 3.

Table 3 Numerical results of the synthetic magnetic anomaly due to the fault with 5 and 10% Gaussian noise using the L-curve and W-GCV based techniques

The results presented in Tables 1, 2 and 3 show a good and close agreement between exactly known and estimated model parameters, which consequently implies the reasonable competence of the proposed inversion algorithm and automatic techniques of the regularization parameter estimation. Furthermore, to appraise the quality of the inversion results the standard deviation of the estimated parameters of the magnetic anomalies derived from 10 independent runs of data creation is listed in Tables 1, 2 and 3.

5.2 Application to field data

After successful application of the present inversion algorithm in order to recover the magnetic anomaly parameters, in this section, the results of inverting one real data set using the proposed method are presented. The real data comes from Morvarid iron-apatite deposit, located in the Alborz volcano-plutonic belt, southeast Zanjan, in Northwest Iran. Figure 7 displays the Geographic location and schematic geological map along with mineralization of the prospecting area. In general, the exposed rocks, in the study area, are Eocene andesite, trachyandesite and basalt (both lava and pyroclastic). Oligo-Miocene quartz-syenite, quartz-monzonite, monzonite and monzogranite intrude the volcanic rocks. trace and rare earth element (REE) chemical composition of the intrusive rocks exhibit that they were emplaced in a volcanic arc setting. Mineralization is found mainly as vein, stockwork and hydrothermal breccias. The geometry of the faults controls the shape of the mineralization. Most of the veins are parallel. Paragenesis comprises magnetite, apatite, pyrite, chalcopyrite and secondary ones are hematite, malachite, azurite and goethite. The size of apatite crystals is variable of some millimeters to more than 20 cm. According to geology and microscopic study, main alteration types consist of argillic (illite, kaolinite and montmorillonite), sericitic, silicification, potassic, tourmalinization, epidotization, actinolitization and carbonate (Azizi et al. 2009; Mazhari et al. 2010). The magnetic survey was conducted over the study area, in which the intervals between profiles and stations are about 50 and 20 m, respectively. According to International Geomagnetic Reference Field (IGRF) model (IAGA 1985), the geomagnetic field is 47,400 nT, inclination = 54° and declination = 4.5°. The residual magnetic field anomaly is obtained by subtracting the IGRF from the measured total field (Fig. 8). Whereas the field data are corrupted by noise; hence, an upward-continuation filter is usually applied to remove anomalies due to artificial materials and to lower topographic effects on the magnetic anomaly (Telford et al. 1990; Williams 2008; Zeng et al 2007). Hence, the distance to continue up relative to the plane of observation was chosen equal to 10 m. In order to detect the features of the subsurface anomaly, we select a magnetic profile, oriented in the south-north direction, of 400 m along C–C′ so that the sampling interval is 10 m, and the location of the profile is marked by black line (Fig. 8). The magnetic anomaly was interpreted earlier by Fatehi et al. (2013) as due to a thin sheet body. A simplified geological section of the study area and location of the drilled borehole which gives an overview of the average lithology is presented in Fig. 9. From the borehole information, the lithology is characterized by about a 29.5 m surface layer (Gangue), followed by a high-grade iron layer of about 8 m thickness and a low-grade iron layer below. The field data inversion is implemented based on the strategy used in the synthetic data examples. Figure 10 illustrates the field data corresponding to the profile C–C′ (red circles) which is used for the inversion. To apply the proposed inversion technique, the optimum values of the regularization parameter were chosen equal to 5.1794 and 11.51E−02 based on the L-curve and W-GCV criteria, respectively. Figure 11 shows the L-curve plot along with the optimum value of the regularization parameter denoted by the red asterisk so that this amount corresponds to a point which the L-curve plot attains to the maximum curvature (Fig. 12), i.e. balancing the regularization term and fidelity data in the objective function of inverse problem. The optimum value of the regularization parameter derived from the W-GCV function is illustrated in Fig. 13. Finally, the model parameters obtained by the inversion of the field data using the L-curve and W-GCV based methods are presented in Table 4. The RMS of the data misfit, as a goodness-of-fit criterion during the inversion process, for the field example using the W-GCV and L-curve based methods is shown in Fig. 14. After 6 iterations the RMS stays nearly constant. The L-curve based inversion method has much slightly higher data RMS misfit error (90.2 nT) than the W-GCV based inversion method (89.02 nT). According to an excavated trench in nearby borehole, the depth of the magnetic thin sheet causing this anomaly is about 2 m, while this depth is estimated to be 2.6 m through the proposed inversion method. In general, the resulting magnetic parameters derived from the W-GCV and L-curve methods show that these ways to search the optimal regularization parameter lead to similar inversion results. It is well-know that any inverse problem is viewed as a combination of an estimation problem plus an appraisal problem (Snieder and Trampert 1999). One possible approach for the appraisal part is the covariance of the model parameters estimated by a linearized inversion (Menke 1984; Tarantola 1987). This is commonly used for models that comprise a small number of parameters. The main diagonal of the covariance matrix provides an estimate of how data uncertainties and errors in the assumptions about the model within the inversion process are mapped into parameter error. Based on the nonlinear inverse formulation implemented here, the model covariance matrix can be defined as:

$$ cov \left( m \right) = J^{\dag } \left( m \right)\left[ {cov d} \right] (J^{\dag } \left( m \right))^{T} $$

(24)

where the superscript $T$ denotes matrix transpose and $J^{\dag }$ is the generalized inverse of the Jacobian matrix so that $J^{\dag } = \left( {J\left( m \right)^{T} W_{d}^{T} W_{d} J\left( m \right) + \lambda^{2} L^{T} L} \right)^{ - 1} J\left( m \right)^{T}$. In addition, the estimation error of the $i$th model parameter is calculated using square root of covariance matrix (Eq. 24):

$$ \varepsilon \left( {m_{i} } \right) = sqrt\left( {cov\left( m \right)_{ii} } \right) $$

(25)

Fig. 7

geographic location of the study area (asterisk) in the simplified geological map of Iran (modified after Iranian National Geoscience Database) and schematic geological map of the study area (Morvarid iron-apatite deposit)

Fig. 8

Residual magnetic anomaly at Morvarid iron-apatite deposit and location of the borehole (open circle). Inversion is made along profile C–C′ crossing the borehole

Fig. 9

Simplified geological section of the study area and location of the drilled borehole which gives an overview of the average lithology (distances are in meter). It is characterized by about a 29.5 m surface layer (Gangue), followed by a high-grade iron layer of about 8 m thickness and a low-grade iron layer below. An excavated trench showing an outcrop of the anomaly

Fig. 10

Resampled data along the profile C–C′ shown in Fig. 8 (solid red circles) calculated anomaly using the W-GCV and L-curve based methods (blue), regional anomaly (black) and residual anomaly (green). (Color figure online)

Fig. 11

Regularization parameter estimation using L-curve for several values of $\lambda$ concerning the real data inversion

Fig. 12

Maximum curvature of L-curve implying the optimum value of the regularization parameter indicated by a red asterisk. (Color figure online)

Fig. 13

Regularization parameter estimation using the W-GCV for several values of $\lambda$ corresponding to the real data. The optimum value of the regularization parameter $\lambda$ is indicated by a red asterisk. (Color figure online)

Table 4 Results of inverse modeling and the diagonal elements of model resolution and the estimation error concerning Morvarid iron-apatite deposit using the W-GCV and L-curve based methods

Fig. 14

RMS data misfit error versus iteration count for the field data example, using the L-curve based inversion algorithm. Note that the L-curve based method has a slightly higher data RMS misfit error than the W-GCV based inversion method

The second tool we can use for assessment of a geophysical inverse model derived from a linear system is based on calculating the model resolution. Using the model resolution one can inquire how closely a particular estimate of the model parameters is to the true solution (Yao et al. 1999; Aster et al. 2013). The model resolution matrix is defined as:

$$ R \left( m \right) = J^{\dag } J^{T} $$

(26)

If the model resolution matrix is an identity matrix meaning that each model parameter is uniquely determined. If the model resolution matrix is not an identity matrix, then the estimates of the model parameters are really weighted averages of the true model parameters. Table 4 reports the diagonal elements of the model resolution matrix and the estimation error corresponding to each retrieved parameter.

6 Conclusions

We demonstrated the use of the Occam’s inversion technique in order to retrieve the magnetic parameters of simple geometric structures (thin sheet, cylinder and fault) including amplitude coefficient, location of the magnetic anomaly from the reference point, index parameter, depth to top of the anomaly as well as slope and base level of the linear regional anomaly, using two automatic ways of estimating the regularization parameter, the L-curve and W-GCV criteria. Despite both criteria act well, giving suitable values of the regularization parameter in the enormous majority of situations, both methods may experience some drawbacks; for example, in implementing the L-curve criterion, care must be taken in the numerical calculations of the L-curve’s curvature and in the W-GCV function, in order to obtain appropriate regularization parameters, the optimum choice of the value $\xi$ is a rather challenging task. In our experience, the implementation of the W-GCV function took more time in computation as compared to the L-curve criterion. The proposed method was very well validated through some simulated magnetic models with different Gaussian noise of 5 and 10%, where a very close correlation has been found between the exactly known and estimated parameters. The application of the present method on one real data set from Morvarid iron-apatite mine resulted in a reasonable agreement between the magnetic parameters of the observed anomaly and those obtained from drilling information. Furthermore, an estimate reliability of the model parameters was achieved by using the model resolution matrix and the model covariance matrix. This inversion approach can be evaluated using real magnetic inverse problem solution where much noise content in the data is expected.

Appendix: Calculation of the Jacobian matrix of sensitivities

• 1. Thin sheet and fault models

  $$ \begin{aligned} & \frac{\partial P\left( X \right)}{\partial F} = \frac{{\left( {X - \zeta } \right)\sin \varphi + Z\cos \varphi }}{{\left( {X - \zeta } \right)^{2} + Z^{2} }}, \\ & \frac{\partial P\left( X \right)}{\partial \zeta } = F\left\{ {\frac{{\left( {\left( {X - \zeta } \right)^{2} - Z^{2} } \right)\sin \varphi + 2Z\left( {X - \zeta } \right)\cos \varphi }}{{\left( {\left( {X - \zeta } \right)^{2} + Z^{2} } \right)^{2} }}} \right\} \\ & \frac{\partial P\left( X \right)}{\partial Z} = F\left\{ {\frac{{\left( {\left( {X - \zeta } \right)^{2} - Z^{2} } \right)\cos \varphi - 2Z\left( {X - D} \right)\sin \varphi }}{{\left( {\left( {X - \zeta } \right)^{2} + Z^{2} } \right)^{2} }}} \right\} \\ & \frac{\partial P\left( X \right)}{\partial \varphi } = F\left\{ {\frac{{\left( {X - \zeta } \right)\cos \varphi - Z\sin \varphi }}{{\left( {X - \zeta } \right)^{2} + Z^{2} }}} \right\} \\ & \frac{\partial P\left( X \right)}{\partial A} = X \\ & \frac{\partial P\left( X \right)}{\partial B} = 1 \\ \end{aligned} $$

  (24)

• 2. Cylinder model

  $$ \begin{aligned} & \frac{\partial P\left( X \right)}{\partial \zeta } = \left( {\frac{{ - D\left( {2X - 2\zeta } \right) + 2EZ}}{{\left( {\left( {X - \zeta } \right)^{2} + Z^{2} } \right)^{2} }} - \frac{{\left( {2D\left( {Z^{2} - \left( {X - \zeta } \right)^{2} } \right) + 4EZ\left( {X - \zeta } \right)} \right)\left( {2\zeta - 2X} \right)}}{{\left( {\left( {X - \zeta } \right)^{2} + Z^{2} } \right)^{3} }}} \right) \\ & \frac{\partial P\left( X \right)}{\partial Z} = \left( {\frac{{2DZ + 2E\left( {X - \xi } \right)}}{{\left( {\left( {X - \zeta } \right)^{2} + Z^{2} } \right)^{2} }} - \frac{{4Z\left( {D\left( {Z^{2} - \left( {X - \zeta } \right)^{2} } \right) + 2EZ\left( {X - \zeta } \right)} \right)}}{{\left( {\left( {X - \zeta } \right)^{2} + Z^{2} } \right)^{3} }}} \right) \\ & \frac{\partial P\left( X \right)}{\partial D} = \frac{{Z^{2} - \left( {X - \xi } \right)^{2} }}{{\left( {\left( {X - \zeta } \right)^{2} + Z^{2} } \right)^{2} }} \\ & \frac{\partial P\left( X \right)}{\partial E} = \frac{{2Z\left( {X - \zeta } \right)}}{{\left( {\left( {X - \zeta } \right)^{2} + Z^{2} } \right)^{2} }} \\ & \frac{\partial P\left( X \right)}{\partial A} = X \\ & \frac{\partial P\left( X \right)}{\partial B} = 1 \\ \end{aligned} $$

  (25)