A multistep collocation method for approximate solution of Volterra integro-differential equations of the third kind

Abstract

In this paper, we use the multistep collocation method for linear Volterra integro-differential equations of the third kind. First, the structure of multistep collocation method is described, then the convergence of the method and its order are investigated. The comparison of the proposed method with classical one-step collocation method shows that the order of convergence increases with the same computational cost. Some numerical examples are given in the last part of the article to illustrate the theoretical results.

1 Introduction

Many problems in mathematics, physics, biology and engineering involve integral equations and among them, some of the problems are in integro-differential equation form. For example, the problem of determining the shape of a simply supported sandwich beam leads up to a Volterra integro-differential equation (VIDE). Therefore, it is important to provide suitable numerical methods to solve such equations. In particular, great attention has been paid to collocation methods in some literature. For example, in Brunner (2004), the author has applied the collocation method to various classes of Volterra integral and differential equations. Seyed allaei et al have studied analytical properties of the third kind Volterra integral equation (VIE) in Seyed Allaei et al. (2015) and they have also applied the collocation method for solving this equation in Seyed Allaei et al. (2017). A spectral collocation method for a class of nonlinear Volterra Hammerstein integral equations of the third kind has been investigated in Laeli Dastjerdi and Shayanfard (2021). Also, a multistep collocation method for third kind VIEs has been studied in Shayanfard et al. (2019).

In this paper we consider first order linear Volterra integro-differential equation of the third kind:

$$\begin{aligned} t^\beta {y}'(t)=a_{1}(t)y(t)+g_{1}(t)+\int _{0}^{t}{k(t,x)y(x)dx},~~~y(0)=y_0,~~t\in I, \end{aligned}$$

(1)

in which, $\beta >0$, $a_{1}(t)=t^{\beta }a(t)$, $g_{1}(t)=t^{\beta }g(t)$, $k\in C(D)$ and $g(t),a(t)\in C(I)$, where $I=[0,T]$ and $D=\left\{ (t,x)\left| t\in I,\text { }0\le x\le t \right. \right\}$.

Numerical methods for (1) have also received attention. Recently a collocation method for (1) has been studied by Shayanfard et al. (2020). In Cardone and Conte (2013) the authors have analyzed the multistep collocation method for a class of VIDEs of the second kind. In the multistep collocation method the solution is approximated by a piecewise polynomial, which depends on solutions of r previous steps. The convergence order of this method is higher than classical one-step collocation methods with the same computational cost, see for example (Cardone and Conte 2013; Shayanfard et al. 2019). In this paper, we use the multistep collocation method for approximating solution of third kind Volterra integro-differential equation (1).

The paper is organized as follows:

In Sect. 2, the structure of the multistep collocation method is described, then it is applied to Eq. (1) and its corresponding equations are extracted. In Sect. 3, we have analyzed the convergence of the method by presenting and proving a theorem. Finally, to illustrate the theoretical results some numerical examples are considered in Sect. 4.

2 The multistep collocation method

We consider the first order linear Volterra integro-differential equation of the third kind:

$$\begin{aligned} t^\beta {y}'(t)=a_{1}(t)y(t)+g_{1}(t)+\int _{0}^{t}{k(t,x)y(x)dx},~~~y(0)=y_0,~~~t\in I, \end{aligned}$$

(2)

in which, $\beta >0$, $a_{1}(t)=t^{\beta }a(t)$, $g_{1}(t)=t^{\beta }g(t)$, $k\in C(D)$ and $g(t),a(t)\in C(I)$, where, $I=[0,T]$ and $D=\left\{ (t,x)\left| t\in I,\text { }0\le x\le t \right. \right\}$.

To assure to have a unique solution for Eq. (2), the following two theorems proved, respectively in Seyed Allaei et al. (2015) and Jiang and Ma (2013).

Theorem 2.1

Suppose that $q\ge 1$ is an integer number, $0<\beta <1$, $k(t,x)=x^{\beta +q-1}l(t,x)$ such that:

• (i) $\frac{\partial ^{j}k}{\partial t^j} \in C(D),~~~~~j=0,1,\ldots ,q$,

• (ii) $\frac{\partial ^{j}l}{\partial t^j} \in C(D),~~~~~j=0,1,\ldots ,q-1$,

• (iii) $H_{j+1}(t)=\frac{\partial ^{j}l}{\partial t^j}(t,t) \in C^{q-j-1}(I),~~~~~j=0,1,\ldots ,q-1$,

  then the operator

  $$\begin{aligned} (\Omega _{\beta }y)(t)=\int _{0}^{t}{t^{-\beta }k(t,x)y(x)dx},~~~~t\in I, \end{aligned}$$

  (3)

  is continuous from $C^{q-1}(I)$ to $C^{q}(I)$.

Theorem 2.2

If $a(t),g(t)\in C^{q-1}(I)$ and the assumptions of Theorem (2.1) hold, then Eq. (2) has a unique solution in $C^{q}(I)$.

Now, we express and construct the multistep collocation method of solving Eq. (2).

Consider $I_h=\left\{ t_n;~~0=t_0<t_1<\ldots <t_N=T\right\}$ as a partition for interval $I=[0,T]$, such that $h=\frac{T}{N}$, $t_n=nh$.

Also suppose that $0<c_1<c_2<\cdots <c_m\le 1$ are m collocation parameters and define the set of collocation points in the form

$$\begin{aligned} X_{h}=\left\{ t_{n,i}=t_{n}+c_{i}h;~~0\le n\le N-1,~~1\le i\le m\right\} . \end{aligned}$$

(4)

We approximate the solution y(t) of Eq. (2) with a function $P_{N}(t)$, which its restriction on the interval $\sigma _{n}= (t_n,t_{n+1}],$ is a polynomial of degree at most $m+r-1$ and its value on $\sigma _{n}$ depends on r previous approximations $y_{n-k}\simeq y(t_{n-k})$, $k=0,1,\ldots ,r-1$, which are computed in r previous steps. In other words,

$$\begin{aligned} {P_{N}(t_n+sh)}=\sum _{k=0}^{r-1}{\varphi _{k}(s)y_{n-k}}+h\sum _{j=1}^{m}{\psi _{j}(s)Y_{n,j}},~~s\in [0,1],~~n\ge r, \end{aligned}$$

(5)

in which, $Y_{n,j}={{P}'_{N}(t_{n,j})}$. It is worth pointing out that the starting values $y_1, y_2,\ldots , y_r$, which are needed in (5) may be approximated by an appropriate method such as classical one-step collocation method. Also, $\varphi _{k}(s)$ and $\psi _{j}(s)$ are polynomials of degree $m+r-1$ and are determined by interpolation conditions at the points $t_{n,j}$ and $t_{n-k}$, namely:

$$\begin{aligned} Y_{n,j}={{P}'_{N}(t_{n,j})},~~~j=1,\ldots ,m,~~~ y_{n-k}={P_{N}(t_{n-k})};~~~k=0,\ldots ,r-1. \end{aligned}$$

(6)

By replacing any specified set of collocation parameters $c_1,c_2,\ldots ,c_m$ in Eq. (5) and using (6), the Hermite–Birkhoff interpolation problem is obtained, that is:

$$\begin{aligned} \begin{aligned}&\varphi _{l}(-k)=\delta _{lk},~~~{\varphi }'_{l}(c_j)=0,\\&{\psi }' _{i}(c_{j})=\delta _{ij},~~~{\psi }_{i}(-k)=0, \end{aligned}~~~~~l,k=0,\ldots ,r-1, ~~i,j=1,\ldots ,m. \end{aligned}$$

(7)

Since Eq. (2) is valid for $P_{N}(t)$ at the collocation points $t_{n,j}$ and using (6), for $n=r-1,\ldots ,N-1,$ we have:

$$\begin{aligned} \left\{ \begin{aligned}&t_{n,i}^{\beta }{{Y}_{n,i}}={{a}_{1}}({{t}_{n,i}})\left( \sum \limits _{k=0}^{r-1}{{{\varphi }_{k}}({{c}_{i}}){{y}_{n-k}}+h\sum \limits _{j=1}^{m}{{{\psi }_{j}}({{c}_{i}}){{Y}_{n,j}}}}\right) +g_{1}(t_{n,i})+F_{n,i}+\zeta _{n,i} \\&{{y}_{n+1}}=\sum \limits _{k=0}^{r-1}{{{\varphi }_{k}}(1){{y}_{n-k}}}+h\sum \limits _{j=1}^{m}{{{\psi }_{j}}(1){{Y}_{n,j}}} \\ \end{aligned} \right. \end{aligned}$$

(8)

where

$$\begin{aligned} F_{n,i}=\int _{0}^{t_n}{k(t_{n,i},x){P_{N}}(x)dx},~~~~\zeta _{n,i}=\int _{t_n}^{t_{n,i}}{k(t_{n,i},x){P_{N}}(x)dx}. \end{aligned}$$

(9)

Now, using an appropriate change of variables and the definition of $P_{N}(t)$ in (5), we can write:

$$\begin{aligned} \begin{aligned} F_{n,i}&=h\sum \limits _{l=0}^{r-1}{\int \limits _{0}^{1}{ k(t_{n,i},t_l+sh){P_{N}(t_l+sh)}ds}}\\&\quad +\,h\sum \limits _{l=r}^{n-1}\sum \limits _{k=0}^{r-1}{\left( \int \limits _{0}^{1}{k(t_{n,i},t_l+sh)\ \varphi _k(s)ds}\right) y_{l-k}}\\&\quad +\,h^{2}\sum \limits _{l=r}^{n-1}\sum \limits _{j=1}^{m}{\left( \int \limits _{0}^{1}{k(t_{n,i},t_l+sh)\ \psi _{j}(s)ds}\right) Y_{l,j}},\\ \end{aligned}\nonumber \\ \end{aligned}$$

(10)

and

$$\begin{aligned} \begin{aligned} \zeta _{n,i}&=h\sum \limits _{k=0}^{r-1}{\left( \int \limits _{0}^{c_{i}}{ k(t_{n,i},t_n+sh)\varphi _{k}(s)ds}\right) }y_{n-k}\\&\quad +\,h^{2}\sum \limits _{j=1}^{m}{\left( \int \limits _{0}^{c_{i}}{k(t_{n,i},t_n+sh)\ \psi _{j}(s)ds}\right) Y_{n,j}}.\\ \end{aligned}\nonumber \\ \end{aligned}$$

(11)

Putting (10) and (11) in (8) leads to

$$\begin{aligned} \begin{aligned}&{t^{\beta }}_{n,i}Y_{n,i}-ha_{1}(t_{n,i})\sum \limits _{j=1}^{m}\psi _{j}(c_{i})Y_{n,j}-h^{2}\sum \limits _{j=1}^{m}{\left( \int \limits _{0}^{c_{i}}{k(t_{n,i},t_n+sh)\ \psi _{j}(s)ds}\right) Y_{n,j}}\\&\quad =a_{1}(t_{n,i})\sum \limits _{k=0}^{r-1}{\varphi _{k}(c_{i})y_{n-k}}+g_{1}(t_{n,i})+h\sum \limits _{l=0}^{r-1}{\int \limits _{0}^{1}{k(t_{n,i},t_{l}+sh){P_{N}(t_{l}+sh)}ds}}\\&\qquad +h\sum \limits _{l=r}^{n-1}\sum \limits _{k=0}^{r-1}{\left( \int \limits _{0}^{1}{k(t_{n,i},t_l+sh)\ \varphi _k(s)ds}\right) { y}_{l-k}}\\&\qquad +h^{2}\sum \limits _{l=r}^{n-1}\sum \limits _{j=1}^{m}{\left( \int \limits _{0}^{1}{k(t_{n,i},t_l+sh)\ \psi _{j}(s)ds}\right) Y_{l,j}}\\&\qquad +h\sum \limits _{k=0}^{r-1}\left( \int \limits _{0}^{c_{i}}{ k(t_{n,i},t_n+sh)\varphi _{k}(s)ds}\right) y_{n-k}.\\ \end{aligned}\nonumber \\ \end{aligned}$$

(12)

Now, we define the following vectors $Y^{(l)}\in {\mathbb {R}}^{r}$ and $U^{(l)}, G_{n}, D_{n}^{(l)} \in {\mathbb {R}}^{m}$ appropriately,

$$\begin{aligned}{} & {} Y^{(l)}=\left( y_{l},y_{l-1},\ldots ,y_{l-r+1}\right) ^{T},\qquad l=r,\ldots ,n, \end{aligned}$$

(13)

$$\begin{aligned}{} & {} U^{(l)}=\left( Y_{l,1},Y_{l,2},\ldots ,Y_{l,m}\right) ^{T},\qquad l=r,\ldots ,n, \end{aligned}$$

(14)

$$\begin{aligned}{} & {} G_{n}=\left( g_{1}(t_{n,1}),g_{1}(t_{n,2}),\ldots ,g_{1}(t_{n,m})\right) ^{T}, \end{aligned}$$

(15)

$$\begin{aligned}{} & {} D_{n}^{(l)}=\left[ \begin{matrix} \int \limits _{0}^{1}{k({{t}_{n,1}},{{t}_{l}}+sh){P_{N}}({{t}_{l}}+sh)ds} \\ \int \limits _{0}^{1}{k({{t}_{n,2}},{{t}_{l}}+sh){P_{N}}({{t}_{l}}+sh)ds} \\ \vdots \\ \int \limits _{0}^{1}{k({{t}_{n,m}},{{t}_{l}}+sh){P_{N}}({{t}_{l}}+sh)ds} \\ \end{matrix} \right] ,\qquad l=0,1,\ldots ,r-1,\ \end{aligned}$$

(16)

also the $(m \times m)$-matrices $(T^{\beta }_{n})$, A, $(A_{n})$, and $(m \times r)$-matrices $({\overline{B}}_{n}^{(l)})$, $({\widetilde{B}}_{n}^{(l)})$, C and $(C_{n})$ as follows:

$$\begin{aligned} T^{\beta }_{n}= & {} diag(t^\beta _{n,1},t^\beta _{n,2},\ldots ,t^\beta _{n,m}), \end{aligned}$$

(17)

$$\begin{aligned} {\overline{B}}_{n}^{(l)}= & {} {{\left[ \int \limits _{0}^{1}{k({{t}_{n,i}},{{t}_{l}}+sh){{\varphi }_{k}}(s)ds} \right] ,}_{i=1,\ldots ,m,~k=0,\ldots ,r-1}}~~l=r,\ldots ,n-1, \end{aligned}$$

(18)

$$\begin{aligned} {\overline{B}}_{n}^{(n)}= & {} {{\left[ \int \limits _{0}^{c_{i}}{k({{t}_{n,i}},{{t}_{n}}+sh){{\varphi }_{k}}(s)ds} \right] ,}_{i=1,\ldots ,m,~k=0,\ldots ,r-1}} \end{aligned}$$

(19)

$$\begin{aligned} {\widetilde{B}}_{n}^{(l)}= & {} {{\left[ \int \limits _{0}^{1}{k({{t}_{n,i}},{{t}_{l}}+sh){{\psi }_{j}}(s)ds} \right] ,}_{ i=1,\ldots ,m,~ j=1,\ldots ,m }}~~~~l=r,\ldots ,n-1, \end{aligned}$$

(20)

$$\begin{aligned} {\widetilde{B}}_{n}^{(n)}= & {} {\left[ \int \limits _{0}^{c_{i}}{k({{t}_{n,i}},{{t}_{n}}+sh){{\psi }_{j}}(s)ds} \right] ,}_{ i=1,\ldots ,m, j=1,\ldots ,m } \end{aligned}$$

(21)

$$\begin{aligned} A= & {} {{\left[ \psi _{j}(c_{i})\right] }_{i=1,\ldots ,m,j=1,\ldots ,m}}, \end{aligned}$$

(22)

$$\begin{aligned} A_{n}= & {} diag(a_{1}(t_{n,1}),a_{1}(t_{n,2}),\ldots ,a_{1}(t_{n,m}))A, \end{aligned}$$

(23)

$$\begin{aligned} C= & {} {\left[ \varphi _{k}(c_{i})\right] _{i=1,\ldots ,m,k=0,\ldots ,r-1}}, \end{aligned}$$

(24)

$$\begin{aligned} C_{n}= & {} diag\left( a_{1}(t_{n,1}),a_{1}(t_{n,2}),\ldots ,a_{1}(t_{n,m})\right) C. \end{aligned}$$

(25)

Using the above matrices, Eq. (8) can be rewritten in matrix form as follows:

$$\begin{aligned} \begin{aligned}&\left( T^{\beta }_{n}-h(A_{n}+h{\widetilde{B}}_{n}^{(n)})\right) U^{(n)}=C_{n}Y^{(n)}+G_{n}+h\sum \limits _{l=0}^{r-1}{D_{n}^{(l)}}\\&\quad +h\sum \limits _{l=r}^{n}{{\overline{B}}_{n}^{(l)}Y^{(l)}}+h^{2}\sum \limits _{l=r}^{n-1}{{\widetilde{B}}_{n}^{(l)}U^{(l)}}. \end{aligned}\nonumber \\ \end{aligned}$$

(26)

Solving (26) gives us the values of $Y_{n,j}$s. Note that the values of $y_{0},y_{1},\ldots ,y_{r-1}$ can be obtained by using one-step collocation methods. Also we can approximate the values of integrals arising in (26), by appropriate quadrature methods, see Cardone and Conte (2013).

To prove the method’s solvability, we have to prove that the matrices $\left( T^{\beta }_{n}-h(A_{n}+h{\widetilde{B}}_{n}^{(n)})\right)$ are nonsingular, which we see it in the following theorem.

Theorem 2.3

Consider Eq. (2) and suppose that $k\in C(D)$ and $0<\beta <1$. Then for any choice of collocation parameters $0<{{c}_{1}}<{{c}_{2}}<\cdots <{{c}_{m}}\le 1$ there exists an ${\bar{h}}>0$ such that all matrices $\left( T^{\beta }_{n}-h(A_{n}+h{\widetilde{B}}_{n}^{(n)})\right)$ are nonsingular for each $h\le {\bar{h}}$.

Proof

Similar to the proof of Theorem 3.1. in Shayanfard et al. (2020). $\square$

3 Convergence analysis

In this section, we analyze the convergence properties of multistep collocation method for Eq. (2).

Theorem 3.1

Consider Eq. (2) with $y(0)=y_{0}$. Suppose that the conditions of Theorem 2.1 hold and $a(t), g(t) \in C^{m+r}(I), k \in C^{m+r}(D)$. Let

$$\begin{aligned} {\widetilde{\Phi }}= \left[ \begin{matrix} {\varphi }_{0}(1)\quad \cdots \quad {{\varphi }_{r-2}}(1){{\varphi }_{r-1}}(1) \\ {{I}_{r-1}\qquad \quad {{{O}}_{r-1,1}}} \\ \end{matrix} \right] \end{aligned}$$

in which, $I_{r-1}$ is the identity matrix with dimension $r-1$ and $O_{r-1,1}$ is the $(r-1 \times 1)$ zero vector. If the starting errors, arising from approximation of $y_1, y_2,\ldots , y_r$ satisfy $|e(t)|=O(h^{m+r}),~~~t\in [t_0,t_{r}]$ and the spectral radius of the matrix ${\widetilde{\Phi }}$ is less than 1, then the global error of multistep collocation method satisfies ${\Vert } e{\Vert }_{\infty }=O(h^{m+r})$.

Proof

According to the assumptions of the current theorem and referring to Theorem 2.2, we conclude that Eq. (2) has a unique solution in $C^{m+r}[0,T]$.

Now, let y(t) and $P_{N}(t)$ be the exact and approximate solutions of (2), respectively. Thus the error $e(t)=y(t)-{P_{N}(t)}$ for $t \in X_{h}$ satisfy the following equation:

$$\begin{aligned} t^\beta {e}'(t)=a_{1}(t)e(t)+\int _{0}^{t}{k(t,x)e(x)dx},~~~~~t\in X_{h},. \end{aligned}$$

(27)

By Peano’s theorem (Brunner 2004) and similar to lemma 4.1 in Conte and Paternoster (2009), we can argue:

$$\begin{aligned} y(t_n+sh)=\sum _{k=0}^{r-1}{\varphi _{k}(s)y({t_{n-k}})}+h\sum _{j=1}^{m}{\psi _{j}(s){y}'(t_{n,j})}+h^{m+r}R_{m,r,n}(s),~~s\in [0,1], \end{aligned}$$

(28)

where $\varphi _{k}(s)$ and $\psi _{j}(s)$ are the same as in (7) and

$$\begin{aligned} R_{m,r,n}(s)= & {} \int _{-r+1}^{1}{k_{m,r}(s,\nu )y^{(m+r)}(t_{n}+\nu h) d\nu }, \end{aligned}$$

(29)

$$\begin{aligned} k_{m,r}(s,\nu )= & {} \frac{1}{(m+r+1)!}\left( (s-\nu )_{+}^{m+r-1}-\sum _{k=0}^{r-1}{\varphi _{k}(s)(-k-\nu )_{+}^{m+r-1}}\right) \nonumber \\{} & {} \qquad -\frac{h}{(m+r+1)!}\sum _{j=1}^{m}{\psi _{j}(s){({c}_{j}-\nu )_{+}^{m+r-1}}}. \end{aligned}$$

(30)

Thus by using Eq. (5), we have:

$$\begin{aligned} e(t_n+sh)=\sum _{k=0}^{r-1}{\varphi _{k}(s)e_{n-k}}+h\sum _{j=1}^{m}{\psi _{j}(s)\epsilon _{n,j}}+h^{m+r}R_{m,r,n}(s),~~s\in [0,1], \end{aligned}$$

(31)

in which, $e_{n-k}=e(t_{n-k})$ and $\epsilon _{n,j}=e'(t_{n,j})$ for $k=0,1,\ldots ,r-1$, $j=1,2,\ldots ,m$.

On the other hand, Eq. (2) is valid for both y(t) and $P_{N}(t)$ at the collocation points, so we can deduce:

$$\begin{aligned} \begin{aligned} t_{n,i}^{\beta }y'(t_{n,i})&= t_{n,i}^{\beta }a(t_{n,i})y(t_{n,i})+t_{n,i}^{\beta }g(t_{n,i})\\&\quad +\,h\sum _{l=0}^{n-1}{\int _{0}^{1}{k(t_{n,i},t_{l}+sh)y(t_{l}+sh)ds}}\\&\quad +\,h{\int _{0}^{c_i}}{k(t_{n,i},t_{n}+sh)y(t_n+sh)ds}\\ \end{aligned} \nonumber \\ \end{aligned}$$

(32)

and

$$\begin{aligned} \begin{aligned} t_{n,i}^{\beta }{{P}'_{N}(t_{n,i})}&= t_{n,i}^{\beta }a(t_{n,i}){P_{N}(t_{n,i})}+t_{n,i}^{\beta }g(t_{n,i})\\&\quad +\,h\sum _{l=0}^{n-1}{\int _{0}^{1}{k(t_{n,i},t_{l}+sh){P_{N}(t_{l}+sh)}ds}}\\&\quad +\,h{\int _{0}^{c_i}}{k(t_{n,i},t_{n}+sh){P_{N}(t_n+sh)}ds},~~~~~i=1,\ldots ,m,~~~n \ge r.\\ \end{aligned} \nonumber \\ \end{aligned}$$

(33)

By subtracting Eqs. (32) and (33), we have:

$$\begin{aligned} \begin{aligned} t_{n,i}^{\beta }e'(t_{n,i})&= t_{n,i}^{\beta }a(t_{n,i})e(t_{n,i})\\&\quad +h\sum _{l=0}^{n-1}{\int _{0}^{1}{k(t_{n,i},t_{l}+sh)e(t_{l}+sh)ds}}\\&\quad +h{\int _{0}^{c_i}}{k(t_{n,i},t_{n}+sh)e(t_n+sh)ds},~~~~i=1,\ldots ,m,~~~n \ge r.\\ \end{aligned} \end{aligned}$$

(34)

But by the assumptions of the current theorem for starting errors, we have:

$$\begin{aligned} e(t_l+sh)=h^{m+r}\gamma _l(s),~~~~~l=0,1,\ldots ,r-1, \end{aligned}$$

(35)

in which, $\Vert \gamma _l(s)\Vert _{\infty } \le M_{1}$ and $M_{1}>0$ is constant. Now, by inserting (35) and (31) in (34) the following equation is derived:

$$\begin{aligned} t_{n,i}^{\beta }\epsilon _{n,i}&=t_{n,i}^{\beta }a(t_{n,i})\left( \sum _{k=0}^{r-1}{\varphi _{k}(c_i)e_{n-k}}+h\sum _{j=1}^{m}{\psi _{j}(c_i)\epsilon _{n,j}}+h^{m+r}R_{m,r,n}(c_i)\right) \nonumber \\&\quad +\,h^{m+r+1}\sum _{l=0}^{r-1}{\int _{0}^{1}{k(t_{n,i},t_{l}+sh)\gamma _{l}(s)ds}}\nonumber \\&\quad +\,h\sum _{l=r}^{n-1}{\sum _{k=0}^{r-1}{\int _{0}^{1}{k(t_{n,i},t_l+sh)\varphi _{k}(s)e_{l-k}ds}}}\nonumber \\&\quad +\,h^{2}\sum _{l=r}^{n-1}{\sum _{j=1}^{m}{\int _{0}^{1}{k(t_{n,i},t_l+sh)\psi _{j}(s)\epsilon _{l,j}ds}}}\nonumber \\&\quad +\,h^{m+r+1}\sum _{l=r}^{n-1}{\int _{0}^{1}{k(t_{n,i},t_{l}+sh)R_{m,r,l}(s)ds}}\nonumber \\&\quad +\,h{\sum _{k=0}^{r-1}{\int _{0}^{c_i}{k(t_{n,i},t_n+sh)\varphi _{k}(s)e_{n-k}ds}}}\nonumber \\&\quad +\,h^{2}{\sum _{j=1}^{m}{\int _{0}^{c_i}{k(t_{n,i},t_n+sh)\psi _{j}(s)\epsilon _{n,j}ds}}}\nonumber \\&\quad +\,h^{m+r+1}{\int _{0}^{c_i}{k(t_{n,i},t_{n}+sh)R_{m,r,n}(s)ds}}. \end{aligned}$$

(36)

Now, we define the vectors ${\overline{\omega }}_{n}^{(l)} \in {\mathbb {R}}^m$ as:

$$\begin{aligned} {\overline{\omega }}_{n}^{(l)}=\left\{ \begin{aligned}&{\int _{0}^{1}{k(t_{n,i},t_{l}+sh)\gamma _l(s)ds}}, ~~~~~~~~ l=0,\ldots ,r-1, \\&{\int _{0}^{1}{k(t_{n,i},t_{l}+sh)R_{m,r,l}(s)ds}}, ~~~ l=r,\ldots ,n-1, \\&{\int _{0}^{c_i}{k(t_{n,i},t_{l}+sh)R_{m,r,l}(s)ds}},~~~ l=n. \end{aligned}\right. \end{aligned}$$

(37)

Then we can rewrite (36) as follows:

$$\begin{aligned} \begin{aligned}&\left( T^{\beta }_{n}-h(A_{n}+h{\widetilde{B}}_{n}^{(n)})\right) {\mathcal {E}}_n=C_{n}E_{n}+h\sum \limits _{l=r}^{n}{{\overline{B}}_{n}^{(l)}E_{l}}\\&\quad +h^{2}\sum \limits _{l=r}^{n-1}{{\widetilde{B}}_{n}^{(l)}{\mathcal {E}}_{l}+h^{m+r+1}\sum _{l=0}^{n}{\overline{\omega }}_{n}^{(l)}}+h^{m+r}\kappa _{n}, \end{aligned} \end{aligned}$$

(38)

in which, $E_{l}=\left( e_l,e_{l-1},\ldots ,e_{l-r+1}\right) ^{T}$ and ${\mathcal {E}}_{l}=\left( \epsilon _{l,1},\epsilon _{l,2},\ldots ,\epsilon _{l,m}\right) ^{T}$ for $l=r,\ldots ,n$ and

$$\begin{aligned} \kappa _{n}=diag\left[ a_{1}(t_{n,1}),\ldots ,a_{1}(t_{n,m})\right] \left[ \begin{matrix} R_{m,r,n}(c_{1}) \\ \vdots \\ R_{m,r,n}(c_{m}) \\ \end{matrix} \right] . \end{aligned}$$

(39)

Now, by choosing $s=1$ and $n=l-1$ in Eq. (31), we obtain the following system of linear equations:

$$\begin{aligned} E_l={\widetilde{\Phi }}E_{l-1}+h{\widetilde{\Psi }}\mathcal {E}_{l-1}+h^{m+r}{\widetilde{Q}}_{m,r,l-1},~~~~~l\ge r, \end{aligned}$$

(40)

where ${\widetilde{\Psi }}=\left[ \begin{aligned}&{{\psi }_{1}}(1)\text { }{{\psi }_{2}}(1)\text { }\ldots \text { }{{\psi }_{m}}(1) \\&\quad {{O}_{r-1,m}} \\ \end{aligned} \right]$ and ${\widetilde{Q}}_{m,r,j}=\left[ \begin{aligned}&R_{m,r,j}(1)\\&O_{r-1,1}\\ \end{aligned} \right]$.

By solving (40), we conclude:

$$\begin{aligned} E_l={\widetilde{\Phi }}^{l-r+1}E_{r-1}+\sum _{j=r-1}^{l-1}{{\widetilde{\Phi }}^{l-j+1}\left( {\widetilde{\Psi }}\mathcal {E}_{j}+h^{m+r}{\widetilde{Q}}_{m,r,j}\right) }, ~~l\ge r. \end{aligned}$$

(41)

Now, by replacing (41) in (38), we have:

$$\begin{aligned} \begin{aligned}&\left( T^{\beta }_{n}-h(A_{n}+h{\widetilde{B}}_{n}^{(n)})\right) {\mathcal {E}}_n=h^{m+r}\sum _{i=r-1}^{n-1}{{\widetilde{\Phi }}^{n-i-1}{\widetilde{Q}}_{m,r,i}}\\&\quad +h^{m+r+1}\sum _{l=r-1}^{n-1}\left( \sum _{i=l+1}^{n}{{\bar{B}}_{n}^{(i)}{\widetilde{\Phi }}^{i-l-1}}\right) {\widetilde{Q}}_{m,r,l}\\&\quad +h^{m+r+1}\sum _{l=1}^{r-2}\left( \sum _{i=l+r-1}^{n}{{\bar{B}}_{n}^{(i)}{\widetilde{\Phi }}^{i-l-1}}\right) {\widetilde{Q}}_{m,r,l}\\&\quad +\left( C_{n}{\widetilde{\Phi }}^{n-r+1}+h\sum _{l=r}^{n}{{\bar{B}}_{n}^{(l)}{\widetilde{\Phi }}^{l-r+1}} \right) E_{r-1}\\&\quad +\sum _{j=r-1}^{n-1}{{\widetilde{\Phi }}^{n-j-1}{\widetilde{\Psi }}{\mathcal {E}}_{j}}+h^2\sum _{l=r}^{n-1}{{\widetilde{B}}_{l}^{(l)}{\mathcal {E}}_l}\\&\quad +h\sum _{l=r}^{n}{{\bar{B}}_{n}^{(l)}\sum _{j=1}^{l-1}{{\widetilde{\Phi }}^{l-j-1}{\widetilde{\Psi }}{\mathcal {E}}_{j}}}\\&\quad +h^{m+r+1}\sum _{l=0}^{n}{{\bar{\omega }}_{n}^{(l)}}+h^{m+r}\kappa _{n}. \end{aligned}\nonumber \\ \end{aligned}$$

(42)

By using theorem 2.3 and referring to Brunner (2017), for $0<\beta <1$ and $h<{\overline{h}}$, there exists a constant $M_{2}$, such that:

$$\begin{aligned} {\Vert }T^{\beta }_{n}-h(A_{n}+h{\widetilde{B}}_{n}^{(n)}){\Vert }_{1}^{-1} \le M_{2}~, \end{aligned}$$

(43)

hence

$$\begin{aligned} \begin{aligned} {\Vert }{\mathcal {E}}_{n}{\Vert }_{1}&\le M_{2}{\Vert }C_{n}{\Vert }_{1}{\Vert }E_{n}{\Vert }_{1}+hM_{2}\sum _{l=r}^{n}{{\Vert }{\bar{B}}_{n}^{(l)}{\Vert }_{1}{\Vert }E_l{\Vert }_1}\\&\quad +\,h^{2}M_{2}\sum _{l=r}^{n-1}{{\Vert }{\widetilde{B}}_{n}^{(l)}{\Vert }_{1}{\Vert }{\mathcal {E}}_l{\Vert }_1}\\&\quad +\,h^{m+r+1}M_{2}\sum _{l=0}^{n}{{\Vert }{{\bar{\omega }}}_{n}^{(l)}{\Vert }_1}+M_2h^{m+r}{\Vert }\kappa _n{\Vert }_1.\\ \end{aligned}\nonumber \\ \end{aligned}$$

(44)

Now, by using (35) it is concluded that:

$$\begin{aligned} {\Vert }E_l{\Vert }_{1} \le rM_{1}h^{m+r}, \end{aligned}$$

(45)

also

$$\begin{aligned} {\Vert }{\widetilde{Q}}_{m,r,l}{\Vert }_1=|R_{m,r,l}(1)|\le D_{m,r}M_{m,r}, \end{aligned}$$

(46)

in which,

$$\begin{aligned} D_{m,r}=\underset{s\in [0,1]}{\mathop {\max }}\,\int \limits _{-r+1}^{1}{\left| {{k}_{m,r}}(s,\nu ) \right| d\nu },\quad M_{m,r}={\Vert }y^{(m+r)}{\Vert }_{\infty }. \end{aligned}$$

(47)

On the other hand, since $\rho ({\widetilde{\Phi }})<1$ then there is a constant $D_1$ independent of $k \in {\mathbb {N}}$, such that:

$$\begin{aligned} \sum _{l=0}^{k}{{\Vert }{\widetilde{\Phi }}^l{\Vert }_1}\le D_1,~~~~{\Vert }k_{n}{\Vert }\le \alpha _{1} D_{m,r}M_{m,r}, \end{aligned}$$

(48)

and

$$\begin{aligned} {\Vert }\omega _{n}^{(l)}{\Vert }_1 \le \alpha _{2} D_{m,r}k_{m,r},~~~~l=r,\ldots ,n, \end{aligned}$$

(49)

where, $\alpha _1$ and $\alpha _2$ are constants. From (42), we will have:

$$\begin{aligned} {\Vert }{\mathcal {E}}_{n}{\Vert }_1\le h^{m+r}(\lambda _{1})+\sum _{j=1}^{n-1}{\mu _{j}{\Vert }{\mathcal {E}}_j{\Vert }_1}, \end{aligned}$$

(50)

in which, $\lambda _1$ is a constant. Now, Gronwall’s inequality leads to:

$$\begin{aligned} {\Vert }{\mathcal {E}}_{n}{\Vert }_1\le h^{m+r}(\lambda _{1}) e^{\sum _{j=1}^{n-1}{\mu _{j}}}. \end{aligned}$$

(51)

Furthermore from Eq. (41), we deduce:

$$\begin{aligned} {\Vert }E_n{\Vert }_1 \le \lambda _2 h^{m+r}{\Vert }{\widetilde{\Psi }}{\Vert }_1 {D_1}^2 e^{\sum _{i=1}^{n-1}{\mu _i}}, \end{aligned}$$

(52)

in which,

$$\begin{aligned} \lambda _2=rD_1M_1+{\Vert }\widetilde{\Psi }{\Vert }_1D_1(l-r+1)\lambda _1e^{\sum _{i=1}^{n-1}{\mu _i}}+D_{m,r}M_{m,r}, \end{aligned}$$

(53)

and finally from Eq. (31)

$$\begin{aligned} |e(t_n+sh)| \le {\Vert }E_n{\Vert }_1\sum _{k=0}^{r-1}{|\varphi _k(s)|}+h{\Vert }{\mathcal {E}}_n{\Vert }_1 \sum _{j=1}^{m}{|\psi _j(s)|}+h^{m+r}D_{m,r}M_{m,r}. \end{aligned}$$

(54)

This inequality with (51) and (52) completes the proof. $\square$

4 Numerical experiments

In this section, we have carried out the multistep collocation method for some examples. We present two examples to numerically verify our results. The numerical order of convergence is defined by:

$$\begin{aligned} p={{\log }_{2}}\left( \tfrac{{{ {\Vert }{{e}_{{N}}} {\Vert }}_{\infty }}}{{{{\Vert } {{e}_{2N}} {\Vert }}_{\infty }}} \right) . \end{aligned}$$

and the errors are compared via ${{\Vert {{e}_{N}} \Vert }_{\infty }}=\sup _{1\le i\le N}\,\left| {{e}_{N}}({{t}_{i}}) \right|$.

Example 1

We consider the equation

$$\begin{aligned} t^{\frac{1}{2}}{y}'(t)=g_{1}(t)+\int _{0}^{t}{x^2y(x)dx},~~~~~t\in I,~~~y(0)=0, \end{aligned}$$

(55)

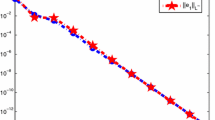
where, $g_{1}(t)=\frac{3}{2}t-\frac{2}{9}{t^{\frac{9}{2}}}$. The exact solution of this equation is $y(t)=\sqrt{t^3}$. Here, we have applied the 2-step collocation method with $m=1$ for different values of collocation parameter c. The results are shown in Table 1. Furthermore the absolute error on [0, 1], for choosing an arbitrary $c=\frac{1}{\sqrt{5}}$ and $N=16$ is shown in Fig. 1. Note that when $m=1$, the polynomials $\varphi _i,~i=0,1$ and $\psi _1$ are as follows:

$$\begin{aligned} \varphi _{0}(s)=\frac{1}{1+2c}(-s^2+2cs+1+2c), \quad \varphi _{1}(s)=\frac{1}{1+2c}(s^2-2cs), \quad \psi _{1}(s)=\frac{1}{1+2c}(s^2+s). \end{aligned}$$

Table 1 ${\Vert }e_N{\Vert }_\infty$ and p for Example 1 with $m=1$ and $r=2$

Table 2 ${\Vert }e_N{\Vert }_\infty$ and p for Example 2 with $m=2$ and $r=2$

Fig. 1

Absolute error for Example 1 with N $=$ 16 and $\textrm{c}=\frac{1}{\sqrt{5}}$

Fig. 2

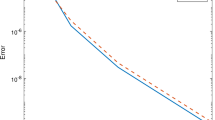
Absolute error for Example 2 with Gauss points And N $=$ 8

Example 2

We applied 2-step collocation method with $m=2$ for the Volterra integro-differential equation

$$\begin{aligned} t^{\frac{1}{2}}{y}'(t)=g_{1}(t)+\int _{0}^{t}{x(t-x)y(x)dx},~~~~~t\in I, \quad y(0)=0, \end{aligned}$$

(56)

where $g_1(t)=\frac{7}{3}{t}^{\frac{11}{6}}-\frac{9}{208}{t}^{\frac{16}{3}}$ and the exact solution is $y(t)={t}^{\frac{7}{3}}$. We have used Radau II 2-points $c_1=\frac{1}{3}$, $c_2=1$, Gauss points, $c_1=\frac{3-\sqrt{3}}{6}$, $c_2=\frac{3+\sqrt{3}}{6}$ and arbitrary points $c_1=\frac{3}{8}$, $c_2=\frac{7}{8}$ to approximate the solution of this equation. For each case the polynomials $\varphi _i, i=0,1$ and $\psi _j$, $j=1.2$ are different, for instance when we consider $c_1=\frac{3-\sqrt{3}}{6}$, $c_2=\frac{3+\sqrt{3}}{6}$, these polynomials are as follows:

$$\begin{aligned}{} & {} \varphi _0(s)=\frac{1}{6}\left( 2s^3-3s^2-s+6\right) ,~~~ \varphi _1(s)=-\frac{1}{6}\left( 2s^3-3s^2+s\right) ,\\{} & {} \psi _1(s)=-\frac{1}{12}\left( (4\sqrt{3}+2)s^3-3s^2-(4\sqrt{3}+5)s\right) ,\\{} & {} \psi _2(s)=\frac{1}{12}\left( (4\sqrt{3}-2)s^3+3s^2-(4\sqrt{3}-5)s\right) . \end{aligned}$$

The results are presented in Table 2. The absolute error for $N=8$, which we used Gauss points as collocation parameters is plotted in Fig. 2.

5 Conclusions

In this paper we applied a multistep collocation method to a linear Volterra integro-differential equation of the third kind with an initial value. Our observations show that under suitable conditions, this method has uniform order $m+r-1$, and increasing the number of collocation parameters and steps gives us better approximations of the solution. Also numerical experiments state that choosing specific values for collocation parameters leads to better results, But the values obtained for the order of convergence in the present examples are slightly less than the theoretical results, which can be caused by the approximation error of the integrals in the system, which we intend to investigate in future works.