1 Introduction

This work is concerned with numerical results for linear Volterra integral equations of the third kind of the form

$$\begin{aligned} {x^{\beta }}y(x)=f(x)+\int _{0}^{x}(x-t)^{-\alpha }k(x,t)y(t)\mathrm{d}t,~~~x\in I:=[0,T], \end{aligned}$$
(1)

where \(0\le \alpha <1\), \(0<\beta \le 1\), \(f(x)={x^{\beta }}g(x)\) with \(g(x)\in C(I)\), k is a real continuous function defined on \(D=\left\{ (x,t):0\le t\le x\le T \right\} \) and y(x) is an unknown function.

Volterra integral equations of the third kind have appeared in modeling numerous problems in various branches of science and engineering, such as heat transfer, population growth models and shock wave problems (Brunner 2017). Thus designing appropriate methods for solving these equations are of great importance.

The collocation methods are among the most suitable methods for solving integral equations. The idea of the collocation method is based on approximating the solution of an integral equation with a linear combination of an appropriate set of functions, which are usually piecewise polynomial functions belonging to a finite-dimensional space. Therefore, we obtain a system of equations that provides a suitable approximating polynomial for the solution. Single-step collocation methods for solving VIEs of the second kind are discussed in many researches (see Brunner 2004 and the references therein).

The existence, uniqueness and regularity of solutions of Eq. (1) have been studied in Allaei et al. (2015). Recently, single-step collocation methods for solving linear Volterra integral Eq. (1) have been explained by Seyed Allaei et al. in Allaei et al. (2017), and an analysis of the collocation methods for nonlinear Volterra integral equations of the third kind has been presented by Song et al. Song et al. (2019). The general multistep collocation methods for solving second-kind Volterra integral equations have been established in Conte and Paternoster (2009), and moreover the multistep Hermite collocation methods have been studied in Fazeli et al. (2012).

It follows from Seyed Allaei et al. Allaei et al. (2015) that under certain conditions on \(\alpha , \beta \) and k, the integral operator,

$$\begin{aligned} ({{V}_{k,\beta ,\alpha }}y)(x)=\int \limits _{0}^{x}{{{x}^{-\beta }}{{(x-t)}^{-\alpha }}k(x,t)y(t)\mathrm{d}t}, \end{aligned}$$
(2)

is compact and therefore the algebraic system arising from the collocation method is uniquely solvable for all sufficiently small mesh diameters. But in the noncompact cases, in general, the solvability of this system with uniform or graded mesh is not guaranteed and so in Allaei et al. (2017) the authors have applied the modified graded mesh to solve Eq. (1) with noncompact operator.

Our aim is to apply a multistep collocation method to approximate the solution of VIEs of the third kind when \({{V}_{k,\beta ,\alpha }}\) is compact.

In order to give an origin for VIEs of the third kind, we consider the first-kind VIEs

$$\begin{aligned} \int _{0}^{x}H(x,t)y(t)\mathrm{d}t=f(x), x\in [0,T]. \end{aligned}$$
(3)

Differentiating with respect to x, we obtain

$$\begin{aligned} H(x,x)y(x)+\int _{0}^{x}\frac{\partial H(x,t)}{\partial x}y(t)\mathrm{d}t=f'(x). \end{aligned}$$
(4)

If \(H(x,x)\ne 0\) for all \(x\in [0,T]\), then dividing (4) by H(x, x) we obtain the VIE of the second kind

$$\begin{aligned} y(x)=g(x)+\int _{0}^{x}k(x,t)y(t)\mathrm{d}t,~~~x\in [0,T], \end{aligned}$$
(5)

where \(g(x)=\frac{f'(x)}{H(x,x)}\) and \(k(x,t)=\frac{-H_{x}(x,t)}{H(x,x)}\). On the other hand, if H(x, x) vanishes on a non-empty proper subset of [0, T], then (4) is said to be a VIE of the third kind.

The rest of this paper is organized as follows.

In Sect. 2, first we present some preliminary theorems, and then the multistep collocation method is utilized for solving Volterra integral equations of the third kind (1). In Sect. 3, solvability of the method will be discussed. Section 4 is devoted to the convergence of the method, and finally in Sect. 5, the method will be evaluated with some examples.

2 Implementation of the method

In this section first, by noting some theorems we present some preliminary conditions, under which we can apply the multistep collocation method for (1) and then we describe the method and employ it for such equations.

Theorem 2.1

(Allaei et al. 2015) Suppose that in (1), \(\alpha =0\), \(0<\beta <1\) and \(k\in C(D)\). Then the integral operator \({{V}_{k,\beta ,0 }}\) is compact. Furthermore if for an integer \(m\ge 1\), \(g\in C^m(I)\) and the kernel k is of the form \(k(x,t)={t}^{\beta +m-1}h(x,t)\) which satisfies the following conditions:

  1. (i)

    \(\frac{{{\partial }^{j}}k}{\partial {{x}^{j}}}\in C(D)\) for \(j=0,1,...,m\),

  2. (ii)

    \(\frac{{{\partial }^{j}}h}{\partial {{x}^{j}}}\in C(D)\) for \(j=0,1,...,m-1\),

  3. (iii)

    \({{H}_{j+1}}(x)=\frac{{{\partial }^{j}}h}{\partial {{x}^{j}}}(x,x) \in C^{m-j-1}(I)\) for \(j=0,1,...,m-1\),

    then Eq. (1) has a unique solution in \(C^m(I)\).

Theorem 2.2

(Allaei et al. 2015) In Eq. (1), let \(0\le \alpha <1\) and \(\alpha +\beta =1\). Then for continuous kernel \(k\in C(D)\) with \(k(0,0)=0\), \({{V}_{k,\beta ,\alpha }}\) is a compact operator. Moreover if \(g(x)\in C^m(I)\) and \(k\in C^m(D),\) then (1) has a unique solution in \(C^m(I)\).

In the rest of the paper, we assume that the conditions of Theorems 2.1 or 2.2 are valid.

Now, we utilize a multistep collocation method for (1) with one of the cases given in the above theorems. To this end, first let \(h=\frac{T}{N}\) for some \(N\in {\mathbb {N}}\) and consider the uniform mesh

$$\begin{aligned} {{I}_{h}}=\left\{ {{x}_{i}}=ih;~~ i=0,1,\ldots ,N \right\} . \end{aligned}$$
(6)

Now, we approximate the solution of (1) in the space of all discontinuous piecewise polynomials with degrees at most \(m-1\)

$$\begin{aligned} S_{m-1}^{(-1)}({{I}_{h}})=\{u;\text { }u\left| _{{{\sigma }_{n}}}\in {{\pi }_{m-1}},\text { }0\le n\le N-1\} \right. , \end{aligned}$$

where \({{\sigma }_{n}}=({{x}_{n}},{{x}_{n+1}})\).

Suppose that the set of collocation points is given by

$$\begin{aligned} X_{h}=\left\{ {x}_{i}+c_{j}h:0<{{c}_{1}}<{{c}_{2}}<\cdots <{{c}_{m}}\le 1,~~ 0\le i \le N-1\right\} . \end{aligned}$$
(7)

Therefore, the approximate solution \({u}_{h}\) on \(({{x}_{n}},{{x}_{n+1}}]\) is defined by

$$\begin{aligned} {{u}_{h}}({{x}_{n}}+vh)=\sum _{k=0}^{r-1}{{{\phi }_{k}}(v){{y}_{n-k}}}+\sum \limits _{j=1}^{m}{{{\psi }_{j}}(v){{U}_{n,j}}}, ~~v\in (0,1],~~n=r,\ldots ,N-1, \end{aligned}$$
(8)

where \({{y}_{n-k}}={{u}_{h}}({{x}_{n-k}})\), \({{U}_{n,j}}={{u}_{h}}({{x}_{n,j}})\), \({{\phi }_{k}}(v)\) and \({{\psi }_{j}}(v)\) are polynomials of degree \(m+r-1\), which are determined by collocation conditions at the points \({{x}_{n-k}}\), \(k=0,1,\ldots ,r-1\) and \({{x}_{n,j}}\), \(j=1,2,\ldots ,m\).

Using the equalities \({{y}_{n-k}}={{u}_{h}}({{x}_{n-k}})\) and \({{U}_{n,j}}={{u}_{h}}({{x}_{n,j}})\) and substituting them in (8), we obtain the linear system (Conte and Paternoster 2009):

$$\begin{aligned} \left\{ \begin{aligned}&{{\phi }_{l}}(-k)={{\delta }_{lk}},\text { }{{\phi }_{l}}({{c}_{j}})=0\text { } \\&{{\psi }_{j}}(-k)=0,\text { }{{\psi }_{j}}({{c}_{i}})={{\delta }_{ij}} \\ \end{aligned} \right. ;~~~l,k=0,\ldots ,r-1\text { and }~i,j=1,\ldots ,m. \end{aligned}$$

Now with the idea of the collocation method, the function (8) must exactly satisfy (1) at the collocation points \({{x}_{n,j}}\), and so we have the following system of equations:

$$\begin{aligned} \left\{ \begin{aligned}&{{{x}^{\beta }_{n,j}}}{{U}_{n,j}}={{F}_{n,j}}+{{\Phi }_{n,j}}, \\&{{y}_{n+1}}=\sum \limits _{k=0}^{r-1}{{{\phi }_{k}}(1){{y}_{n-k}}}+\sum \limits _{j=1}^{m}{{{\psi }_{j}}(1){{U}_{n,j}}}, \\ \end{aligned} \right. \end{aligned}$$
(9)

in which

$$\begin{aligned} {{F}_{n,j}}= & {} f({{x}_{n,j}})+h\sum \limits _{d =0}^{n-1}{\int \limits _{0}^{1}{{{({{x}_{n,j}}-{{x}_{d }}-vh)}^{-\alpha }}k({{x}_{n,j}},{{x}_{d }}+vh){{u}_{ h }}({{x}_{d }}+vh)\mathrm{d}v}},\text { }\\ j= & {} 1,\ldots ,m, \end{aligned}$$

and

$$\begin{aligned} {{\Phi }_{n,j}}={{h}^{1-\alpha }}\int \limits _{0}^{{{c}_{j}}}{{{({{c}_{j}}-v)}^{-\alpha }}k({{x}_{n,j}},{{x}_{n}}+vh){{u}_{h}}({{x}_{n}}+vh)\mathrm{d}v},~~~~~~j=1,\ldots ,m. \end{aligned}$$

Inserting (8) into (9), we obtain

$$\begin{aligned} x_{n,j}^{\beta }{{U}_{n,j}}= & {} f({{x}_{n,j}})+{{h}^{1-\alpha }}\sum \limits _{d=0}^{r-1}{\int \limits _{0}^{1}{{{(n-d+{{c}_{j}}-v)}^{-\alpha }}k({{x}_{n,j}},{{x}_{d}}+vh){{u}_{h}}({{x}_{d}}+vh)\mathrm{d}v}} \nonumber \\&\quad +{{h}^{1-\alpha }}\sum \limits _{d=r}^{n-1}{\sum \limits _{k=0}^{r-1}{\left( \int \limits _{0}^{1}{{{(n-d+{{c}_{j}}-v)}^{-\alpha }}k({{x}_{n,j}},{{x}_{d}}+vh){{\phi }_{k}}(v)\mathrm{d}v} \right) {{y}_{d-k}}}}\nonumber \\&\quad +{{h}^{1-\alpha }}\sum \limits _{d=r}^{n-1}{\sum \limits _{l=1}^{m}{\left( \int \limits _{0}^{1}{{{(n-d+{{c}_{j}}-v)}^{-\alpha }}k({{x}_{n,j}},{{x}_{d}}+vh){{\psi }_{l}}(v)\mathrm{d}v} \right) {{U}_{d,l}}}} \nonumber \\&\quad +{{h}^{1-\alpha }}\text { }\sum \limits _{k=0}^{r-1}{\left( \int \limits _{0}^{{{c}_{j}}}{{{({{c}_{j}}-v)}^{-\alpha }}k({{x}_{n,j}},{{x}_{n}}+vh){{\phi }_{k}}(v)\mathrm{d}v} \right) {{y}_{n-k}}} \nonumber \\&\quad +{{h}^{1-\alpha }}\text { }\sum \limits _{l=1}^{m}{\left( \int \limits _{0}^{{{c}_{j}}}{{{({{c}_{j}}-v)}^{-\alpha }}k({{x}_{n,j}},{{x}_{n}}+vh){{\psi }_{l}}(v)\mathrm{d}v} \right) {{U}_{n,l}}}. \end{aligned}$$
(10)

Now, let

$$\begin{aligned} \begin{aligned}&{{Y}^{(d)}}={{\left( {{y}_{d}},{{y}_{d-1}},\ldots ,{{y}_{d-r+1}} \right) }^{T}}, ~~d=r,\ldots ,n,\\&{{U}^{(d)}}={{\left( {{U}_{d,1}},{{U}_{d,2}},\ldots ,{{U}_{d,m}} \right) }^{T}}, ~~d=r,\ldots ,n,\\&D_{n}^{(d)}=\left( \begin{aligned}&\int \limits _{0}^{1}{{{(n-d+{{c}_{1}}-v)}^{-\alpha }}k({{x}_{n,1}},{{x}_{d}}+vh){{u}_{h}}({{x}_{d}}+vh)\mathrm{d}v} \\&\int \limits _{0}^{1}{{{(n-d+{{c}_{2}}-v)}^{-\alpha }}k({{x}_{n,2}},{{x}_{d}}+vh){{u}_{h}}({{x}_{d}}+vh)\mathrm{d}v} \\&\vdots \\&\int \limits _{0}^{1}{{{(n-d+{{c}_{m}}-v)}^{-\alpha }}k({{x}_{n,m}},{{x}_{d}}+vh){{u}_{h}}({{x}_{d}}+vh)\mathrm{d}v} \\ \end{aligned} \right) , d=0,1,\ldots ,r-1,\\&{{T}^{\beta }_{n}}=diag\left( {x^{\beta }_{n,1}},{x^{\beta }_{n,2}},\ldots ,{x^{\beta }_{n,m}}\right) ,\\&{{F}_{n}}={{\left( f({{x}_{n,1}}),f({{x}_{n,2}}),\ldots ,f({{x}_{n,m}}) \right) }^{T}},\\ \end{aligned} \end{aligned}$$
(11)

and define the matrices \({\bar{B}}_{n}^{(d)}\in {{{\mathbb {R}}}^{m\times r}}\) and \({\tilde{B}}_{n}^{(d)}\in {{{\mathbb {R}}}^{m\times m}}\) by

$$\begin{aligned} \begin{aligned}&{{\left( {\bar{B}}_{n}^{(d)} \right) }_{i,k+1}}=\left\{ \begin{aligned}&\int \limits _{0}^{1}{{{(n-d+{{c}_{i}}-v)}^{-\alpha }}k({{x}_{n,i}},{{x}_{d}}+vh){{\phi }_{k}}(v)\mathrm{d}v};d=r,r+1,\ldots ,n-1 ,\\&\int \limits _{0}^{{{c}_{i}}}{{{({{c}_{i}}-v)}^{-\alpha }}k({{x}_{n,i}},{{x}_{n}}+vh){{\phi }_{k}}(v)\mathrm{d}v};d=n ,\\ \end{aligned} \right. \\ \end{aligned} \end{aligned}$$
(12)

for any \(1\le i\le m\), \(0\le k\le r-1\).

$$\begin{aligned} \begin{aligned}&{{\left( {\tilde{B}}_{n}^{(d)} \right) }_{i,j}}=\left\{ \begin{aligned}&\int \limits _{0}^{1}{{{(n-d+{{c}_{i}}-v)}^{-\alpha }}k({{x}_{n,i}},{{x}_{d}}+vh){{\psi }_{j}}(v)\mathrm{d}v};d=r,\ldots ,n-1 ,\\&\int \limits _{0}^{{{c}_{i}}}{{{({{c}_{i}}-v)}^{-\alpha }}k({{x}_{n,i}},{{x}_{n}}+vh){{\psi }_{j}}(v)\mathrm{d}v};d=n ,\\ \end{aligned} \right. \\ \end{aligned} \end{aligned}$$
(13)

for every \(1\le {i,j}\le m\).

Then (10) can be written in the matrix form

$$\begin{aligned} \begin{aligned}&(T_{n}^{\beta }-{{h}^{1-\alpha }}{\tilde{B}}_{n}^{(n)}){{U}^{(n)}}={{F}_{n}}+{{h}^{1-\alpha }}\sum \limits _{d=0}^{r-1}{D_{n}^{(d)}}+{{h}^{1-\alpha }}\sum \limits _{d=r}^{n-1}{{\tilde{B}}_{n}^{(d)}{{U}^{(d)}}}\\&\quad +{{h}^{1-\alpha }}\sum \limits _{d=r}^{n-1}{{\bar{B}}_{n}^{(d)}{{Y}^{(d)}}}+{{h}^{1-\alpha }}{\bar{B}}_{n}^{(n)}{{Y}^{(n)}}{.}\\ \end{aligned} \end{aligned}$$
(14)

By solving the above system of equations, \({{U}_{n,j}}\)’s and then \(u_h\) are determined. Of course, the starting values \({{y}_{1}},{{y}_{2}},\ldots ,{{y}_{_{r}}}\) can be obtained via a classical single-step method.

3 Solvability of the method

We will now prove the solvability of the linear system (14) caused by the multistep collocation method. To this end, we note that the corresponding operators are compact.

Theorem 3.1

Suppose that \(k\in C(D)\) and \(g\in C(I)\). Then for \(0\le \alpha <1\) and \(0<\beta <1\), or \(\beta =1\) with \(k(0,0)=0\), there exists an \({\bar{h}}>0\) such that for any \(0<h\le {\bar{h}}\) the matrix \(\left( {T^\beta _{n}}-{h}^{1-\alpha }{\tilde{B}}_{n}^{(n)} \right) \) is invertible for any n.

Proof

Since \(c_1> 0,\) the diagonal matrix \({{T}^{\beta }_{n}}\) is invertible. By the Neumann lemma (Atkinson 1989), it is enough to prove that there exists an \({\bar{h}}>0\) such that for any \(0<h\le {\bar{h}}\), \({{\left\| {{h}^{1-\alpha }}T_{n}^{-\beta }{\tilde{B}}_{n}^{(n)} \right\| }_{\infty }}<1\). But by the definitions of \({\tilde{B}}_{n}^{(n)}\) and \(T_{n}^{\beta }\), we have

$$\begin{aligned} {{\left( T_{n}^{-\beta }{\tilde{B}}_{n}^{(n)} \right) }_{i,j}}=x_{n,i}^{-\beta }\int \limits _{0}^{{{c}_{i}}}{{{({{c}_{i}}-v)}^{-\alpha }}k({{x}_{n,i}},{{x}_{n}}+vh){{\psi }_{j}}(v)\mathrm{d}v}, \end{aligned}$$
(15)

and therefore

$$\begin{aligned} \begin{aligned}&{{\left\| T_{n}^{-\beta }{\tilde{B}}_{n}^{(n)} \right\| }_{\infty }}=\underset{1\le i\le m}{\mathop {Max}}\,\sum \limits _{j=1}^{m}{\left| x_{n,i}^{-\beta }\int \limits _{0}^{{{c}_{i}}}{{{({{c}_{i}}-v)}^{-\alpha }}k({{x}_{n,i}},{{x}_{n}}+vh){{\psi }_{j}}(v)\mathrm{d}v} \right| } \\&\quad \le \underset{1\le i\le m}{\mathop {Max}}\, x_{n,i}^{-\beta }\int \limits _{0}^{{{c}_{i}}}{{{({{c}_{i}}-v)}^{-\alpha }}\left| k({{x}_{n,i}},{{x}_{n}}+vh) \right| \sum \limits _{j=1}^{m}{\left| {{\psi }_{j}}(v) \right| }\mathrm{d}v} \\&\quad \le x_{n,1}^{-\beta } \underset{{{x}_{n}}\le t\le x\le {{x}_{n+1}}}{\mathop {\sup }}\,\left| k(x,t) \right| {\gamma } \frac{c_{m}^{1-\alpha }}{1-\alpha }{,} \\ \end{aligned} \end{aligned}$$
(16)

where \({\gamma } =Max_{0\le v\le {{c}_{i}}}\,\sum \nolimits _{j=1}^{m}{\left| {{\psi }_{j}}(v) \right| }\).

Now, we consider the following two cases:

  1. (a)

    If \(\alpha +\beta \in (0,1)\) from (16), we have

    $$\begin{aligned} \begin{aligned} {{h}^{1-\alpha }}{{\left\| T_{n}^{-\beta }{\tilde{B}}_{n}^{(n)} \right\| }_{\infty }}&\le {{h}^{1-\alpha }}x_{n,1}^{-\beta }{{\left\| k \right\| }_{\infty }} \frac{{\gamma }c_{m}^{1-\alpha }}{1-\alpha } \\&<\frac{{{h}^{1-\alpha -\beta }}c_{m}^{1-\alpha }{{\left\| k \right\| }_{\infty }}{\gamma } }{(1-\alpha )c_{1}^{\beta }}. \\ \end{aligned} \end{aligned}$$
    (17)

    So by choosing \({\bar{h}}<{{\left( \frac{(1-\alpha )c_{m}^{\alpha -1}c_{1}^{\beta }}{2{{\left\| k \right\| }_{\infty }}{\gamma } } \right) }^{\frac{1}{1-\alpha -\beta }}}\), we obtain \({{h}^{1-\alpha }}{{\left\| T_{n}^{-\beta }{\tilde{B}}_{n}^{(n)} \right\| }_{\infty }}<\frac{1}{2}\).

  2. (b)

    If \(\alpha +\beta =1\) and \(k(0,0)=0\), then there exists a positive constant \(\varepsilon >0\) such that

\(\underset{0\le t\le x\le \varepsilon }{\mathop {\sup }}\,\left| k(x,t) \right| <\frac{c_{1}^{1-\alpha }c_{m}^{\alpha -1}(1-\alpha )}{2{\gamma } }\).

So for \(x_{n+1} \in (0,\varepsilon ]\) from (16), we have

$$\begin{aligned} \frac{{{h}^{1-\alpha }}}{x_{n,1}^{\beta }} \frac{{\gamma }c_{m}^{1-\alpha }}{1-\alpha }\underset{{{x}_{n}}\le t\le x\le {{x}_{n+1}}}{\mathop {\sup }}\,\left| k(x,t) \right| ={{\left( \frac{h}{x_{n,1}^{{}}} \right) }^{^{1-\alpha }}}\frac{{\gamma } c_{m}^{1-\alpha }}{1-\alpha }\underset{{{x}_{n}}\le t\le x\le {{x}_{n+1}}}{\mathop {\sup }}\,\left| k(x,t) \right| <\frac{1}{2}, \end{aligned}$$
(18)

for \(x_{n}\in [\frac{\varepsilon }{2},T]\),

$$\begin{aligned} {{\left( \frac{h}{x_{n,1}^{{}}} \right) }^{^{1-\alpha }}}\frac{{\gamma }c_{m}^{1-\alpha }}{1-\alpha }\underset{{{x}_{n}}\le t\le x\le {{x}_{n+1}}}{\mathop {\sup }}\,\left| k(x,t) \right| <{{\left( \frac{2h}{\varepsilon } \right) }^{1-\alpha }}\frac{{\gamma }c_{m}^{1-\alpha }}{1-\alpha } {{\left\| k \right\| }_{\infty }}, \end{aligned}$$
(19)

and by choosing \({\bar{h}}=\min \left\{ \frac{\varepsilon }{2},\frac{\varepsilon }{2{{c}_{m}}}{{\left( \frac{1-\alpha }{2{\gamma } {{\left\| k \right\| }_{\infty }}} \right) }^{\frac{1}{1-\alpha }}} \right\} \) the proof is completed. \(\square \)

4 Convergence analysis

In this section, we investigate the order of convergence of the multistep collocation solution to the exact solution.

Theorem 4.1

Suppose that one of the hypotheses of Theorems 2.1 or 2.2 are valid, \(k\in {{C}^{m+r}}(D)\), \(g\in {{C}^{m+r}}[0,T]\), and let \(e(x)=y(x)-{{u}_{h}}({x})\). If the starting error satisfies

$$\begin{aligned} {\left\| e \right\| }_{\infty ,[0,x_{r}]}=O(h^{m+r}), \end{aligned}$$
(20)

and the spectral radius of the matrix,

$$\begin{aligned} A=\left[ \begin{aligned}&{{\phi }_{0}}(1)\text { }\ldots \text { }{{\phi }_{r-2}}(1)\text { }{{\phi }_{r-1}}(1) \\&{{I}_{r-1}}~~~~~~~~~~~{{O}_{r-1,1}} \\ \end{aligned} \right] , \end{aligned}$$
(21)

is less than 1, then \({{\left\| \ e \right\| }_{\infty }}=O({{h}^{m+r}})\).

Proof

By the hypotheses of the theorem and referring (Allaei et al. 2015) we can conclude that Eq. (1) has a unique solution in \(C^{m+r}[0,T]\) and from Peano’s theorem (Brunner 2004), we conclude that for any \(v\in (0,1]\) we have

$$\begin{aligned} y({{x}_{n}}+vh)=\sum \limits _{k=0}^{r-1}{{{\phi }_{k}}(v)y({{x}_{n-k}})}+\sum \limits _{j=1}^{m}{{{\psi }_{j}}(v)y({{x}_{n,j}})}+{{h}^{m+r}}{{R}_{m,r,n}}(v), \end{aligned}$$
(22)

where \({{R}_{m,r,n}}(v)\) is given by

$$\begin{aligned} {{R}_{m,r,n}}(v)=\int \limits _{-r+1}^{1}{{{k}_{m,r}}(v,\tau ){{y}^{(m+r)}}({{x}_{n}}+\tau h)d\tau }, \end{aligned}$$

in which

$$\begin{aligned} {{k}_{m,r}}(v,\tau )= & {} \frac{1}{(m+r-1)!}[ (v-\tau )_{+}^{m+r-1}-\sum \limits _{k=0}^{r-1}{{{\phi }_{k}}(v)(-k-\tau )_{+}^{m+r-1}}\\&-\sum \limits _{j=1}^{m}{{{\psi }_{j}}(v)({{c}_{j}}-\tau )_{+}^{m+r-1}} ] \end{aligned}$$

is the Peano’s kernel, and

$$\begin{aligned} (v-\tau )_{+}^{p}=\left\{ \begin{aligned}&0~~~~~~~~~~;v<\tau , \\&{{(v-\tau )}^{p}}\text { ;}v\ge \tau . \\ \end{aligned} \right. \end{aligned}$$

Then from (8) and (22), it follows that

$$\begin{aligned} e({{x}_{n}}+vh)=\sum \limits _{k=0}^{r-1}{{{\phi }_{k}}(v){{e}_{n-k}}}+\sum \limits _{j=1}^{m}{{{\psi }_{j}}(v){{e}_{n,j}}}+{{h}^{m+r}}{{R}_{m,r,n}}(v)\text {, }n\ge r, \end{aligned}$$
(23)

where \({{e}_{n,j}}=e({{x}_{n,j}})\) and \({{e}_{n-k}}=e({{x}_{n-k}})\).

Now from (1), we have

$$\begin{aligned} \begin{aligned}&{{{x}^{\beta }_{n,j}}}y({{x}_{n,j}})=f({{x}_{n,j}})+h\sum \limits _{d=0}^{n-1}{\int \limits _{0}^{1}{{{({{x}_{n,j}}-{{x}_{d}}-vh)}^{-\alpha }}k({{x}_{n,i}},{{x}_{d}}+vh)y({{x}_{d}}+vh)\mathrm{d}v}}\text { } \\&\quad +h\int \limits _{0}^{{{c}_{j}}}{{{({{x}_{n,j}}-{{x}_{n}}-vh)}^{-\alpha }}k({{x}_{n,i}},{{x}_{n}}+vh)y({{x}_{n}}+vh)\mathrm{d}v}, \\ \end{aligned} \end{aligned}$$
(24)

and by using the first equation of (9), we have

$$\begin{aligned} \begin{aligned}&{{{x}^{\beta }_{n,j}}}{{u}_{h}}({{x}_{n,j}})=f({{x}_{n,j}})+{h}\sum \limits _{d=0}^{n-1}{\int \limits _{0}^{1}{{{({{x}_{n,j}}-{{x}_{d}}-vh)}^{-\alpha }}k({{x}_{n,j}},{{x}_{d}}+vh){{u}_{h}}({{x}_{d}}+vh)\mathrm{d}v}}\text { } \\&\quad +{{h}^{1-\alpha }}\int \limits _{0}^{{{c}_{j}}}{{{({{c}_{i}}-v)}^{-\alpha }}k({{x}_{n,j}},{{x}_{n}}+vh){{u}_{h}}({{x}_{n}}+vh)\mathrm{d}v}.\\ \end{aligned} \end{aligned}$$
(25)

By subtracting (25) from (24), we have

$$\begin{aligned} \begin{aligned}&{{{x}^{\beta }_{n,j}}}{{e}_{n,j}}={h}\sum \limits _{d=0}^{n-1}{\int _{0}^{1}{{{({{x}_{n,j}}-{{x}_{d}}-vh)}^{-\alpha }}k({{x}_{n,j}},{{x}_{d}}+vh)e({{x}_{d}}+vh)\mathrm{d}v}}\text {} \\&\quad +{{h}^{1-\alpha }}\int _{0}^{{{c}_{j}}}{{{({{c}_{j}}-v)}^{-\alpha }}k({{x}_{n,j}},{{x}_{n}}+vh)e({{x}_{n}}+vh)\mathrm{d}v}. \\ \end{aligned} \end{aligned}$$
(26)

But according to (20) for the starting error, we have

$$\begin{aligned} e({{x}_{d}}+vh)={{h}^{m+r}}{{\eta }_{d}}(v)\text {, }d=0,1,\ldots ,r-1, \end{aligned}$$
(27)

in which \({{\left\| {{\eta }_{d}} \right\| }_{\infty }}\le C\), where \(C>0\) is a constant.

By replacing from (27) and (23) in (26), we have

$$\begin{aligned}&{{{x}^{\beta }_{n,j}}}{{e}_{n,j}}={{h}^{m+r+1}}\sum \limits _{d=0}^{r-1}{\int \limits _{0}^{1}{{{({{x}_{n,j}}-{{x}_{d}}-vh)}^{-\alpha }}k({{x}_{n,j}},{{x}_{d}}+vh){{\eta }_{d}}(v)\mathrm{d}v}} \nonumber \\&\quad +{{h}}\sum \limits _{d=r}^{n-1}\int \limits _{0}^{1}{{({{x}_{n,j}}-{{x}_{d}}-vh)}^{-\alpha }}k({{x}_{n,j}},{{x}_{d}}+vh)\left( \sum \limits _{k=0}^{r-1}{{{\phi }_{k}}(v){{e}_{d-k}}}\right. \nonumber \\&\quad \left. +\sum \limits _{l=1}^{m}{{{\psi }_{l}}(v){{e}_{d,l}}}+{{h}^{m+r}}{{R}_{m,r,d}}(v)\right) \mathrm{d}v \nonumber \\&\quad +{{h}^{1-\alpha }}\int \limits _{0}^{{{c}_{i}}}{{{({{c}_{j}}-v)}^{-\alpha }}k({{x}_{n,j}},{{x}_{n}}+vh)\left( \sum \limits _{k=0}^{r-1}{{{\phi }_{k}}(v){{e}_{n-k}}}+\sum \limits _{l=1}^{m}{{{\psi }_{l}}(v){{e}_{n,l}}}+{{h}^{m+r}}{{R}_{m,r,n}}(v)\right) \mathrm{d}v}.\nonumber \\ \end{aligned}$$
(28)

Now suppose that the vectors \({\bar{\rho }}_{n}^{(d)}\in {{{\mathbb {R}}}^{m}}\) are defined by:

$$\begin{aligned} \begin{aligned}&{{\left( {\bar{\rho }}_{n}^{(d)} \right) }_{i}}=\left\{ \begin{aligned}&\int \limits _{0}^{1}{{{(n-d+{{c}_{i}}-v)}^{-\alpha }}k({{x}_{n,i}},{{x}_{d}}+vh){\eta _{d}}(v)\mathrm{d}v}~~~~~~~~~~;d=0,\ldots ,r-1 ,\\&\int \limits _{0}^{1}{{{(n-d+{{c}_{i}}-v)}^{-\alpha }}k({{x}_{n,i}},{{x}_{d}}+vh){{R}_{m,r,d}}(v)\mathrm{d}v}~~~~;d=r,\ldots ,n-1 ,\\&\int \limits _{0}^{{{c}_{^{i}}}}{{{({{c}_{i}}-v)}^{-\alpha }}k({{x}_{n,i}},{{x}_{n}}+vh){{R}_{m,r,n}}(v)\mathrm{d}v}~~~~~~~~~~~~~;d=n ,\\ \end{aligned} \right. \\ \end{aligned}\nonumber \\ \end{aligned}$$
(29)

for \( i=1,\ldots ,m\).

Then using (12), (13) and (29), we can rewrite (28) in the matrix form:

$$\begin{aligned} \begin{aligned}&{({{T}^{\beta }_{n}}-{{h}^{1-\alpha }}{\tilde{B}}_{n}^{(n)})E_{n}^{(2)}={{h}^{1-\alpha }}\sum \limits _{d=r}^{n-1}{{\tilde{B}}_{n}^{(d)}E_{d}^{(2)}}+{{h}^{1-\alpha }}\sum \limits _{d=r}^{n}{{\bar{B}}_{n}^{(d)}E_{d}^{(1)}}}\\&\quad +{{h}^{m+r+1-\alpha }}\sum \limits _{d=0}^{n}{{\bar{\rho }}_{n}^{(d)}},~~~n\ge r,\\ \end{aligned} \end{aligned}$$
(30)

where

\(E_{d}^{(1)}={{\left[ {{e}_{d}},{{e}_{d-1}},\ldots ,{{e}_{d-r+1}} \right] }^{T},}\) \(E_{d}^{(2)}={{\left[ {{e}_{d,1}},{{e}_{d,2}},\ldots ,{{e}_{d,m}} \right] }^{T}}\).

Since \(c_1> 0,\) the diagonal matrix \({{T}^{\beta }_{n}}\) is invertible for all \(n=0,1,\ldots ,N-1\), with \({{\left\| T_{n}^{-\beta } \right\| }_{\infty }}\le {{\left( {{c}_{1}}h \right) }^{-\beta }}\).

Now letting \(n=d-1\) and \(v=1\) in (23), we have

$$\begin{aligned} e({{x}_{d-1}}+h)=\sum \limits _{k=0}^{r-1}{{{\phi }_{k}}(1){{e}_{d-1-k}}}+\sum \limits _{j=1}^{m}{{{\psi }_{j}}(1){{e}_{d-1,j}}}+{{h}^{m+r}}{{R}_{m,r,d-1}}(1), \end{aligned}$$

and then the non-homogeneous linear difference system of equations

$$\begin{aligned} E_{d}^{(1)}=AE_{d-1}^{(1)}+SE_{d-1}^{(2)}+{{h}^{m+r}}{{\tilde{\varrho }}_{m,r,d-1}},~~~~~~d\ge r, \end{aligned}$$
(31)

is concluded, in which

$$\begin{aligned} {{{\tilde{\varrho }}}_{m,r,j}}=\left[ \begin{aligned}&{{R}_{m,r,j}}(1) \\&~ {{O}_{r-1,1}} \\ \end{aligned} \right] , \end{aligned}$$

and

$$\begin{aligned} S=\left[ \begin{aligned}&{{\psi }_{1}}(1)\text { }{{\psi }_{2}}(1)\text { }\ldots \text { }{{\psi }_{m}}(1)\text { } \\&~~~~~~~{{O}_{r-1,m}} \\ \end{aligned} \right] . \end{aligned}$$

By solving this system, we obtain

$$\begin{aligned} E_{d}^{(1)}={{A}^{d-r+1}}E_{r-1}^{(1)}+\sum \limits _{j=r-1}^{d-1}{{{A}^{d-j-1}}(SE_{j}^{(2)}+{{h}^{m+r}}{{{\tilde{\varrho }}}_{m,r,j}})}. \end{aligned}$$
(32)

In the next step by replacing (32) in (30), we obtain

$$\begin{aligned} \begin{aligned}&\left( I-{{h}^{1-\alpha }}{{{{\tilde{C}}}}_{n}^{(n)}} \right) E_{n}^{(2)}={{h}^{1-\alpha }}\sum \limits _{d=r}^{n-1}{{\tilde{C}}_{n}^{(d)}E_{d}^{(2)}}\\&\quad +{{h}^{1-\alpha }}\left( \sum \limits _{d=r}^{n}{{\bar{C}}_{n}^{(d)}{{A}^{d-r+1}}} \right) E_{r-1}^{(1)} \\&\quad +{{h}^{1-\alpha }}\sum \limits _{j=r}^{n-1}{\left( \sum \limits _{d=j+1}^{n}{{\bar{C}}_{n}^{(d)}{{A}^{d-j-1}}S} \right) E_{j}^{(2)}}\\&\quad +{{h}^{1-\alpha }}\left( \sum \limits _{d=r}^{n}{{\bar{C}}_{n}^{(d)}{{A}^{d-r}}S} \right) E_{r-1}^{(2)} \\&\quad +{{h}^{m+r-\alpha }}\sum \limits _{j=r-1}^{n-1}{\left( \sum \limits _{d=j+1}^{n}{{\bar{C}}_{n}^{(d)}{{A}^{d-j-1}}} \right) {{{{\tilde{\varrho }}}}_{m,r,j}}}\\&\quad +{{h}^{m+r+1-\alpha }}\sum \limits _{d=0}^{n}{T^{-\beta }_{n}{\bar{\rho }}_{n}^{(d)}}\text {, }~~~~~~n\ge r,\\ \end{aligned} \end{aligned}$$
(33)

where \({{\tilde{C}}}_{n}^{(d)}=T^{-\beta }_{n}{{\tilde{B}}}_{n}^{(d)}\), \({{\bar{C}}}_{n}^{(d)}=T^{-\beta }_{n}{{\bar{B}}}_{n}^{(d)}\), for \(d=r,\ldots ,n\).

Moreover, by using the assumption \(\rho (A)<1\), and doing some manipulations (Conte and Paternoster 2009), we have

$$\begin{aligned} {{\left\| E_{n}^{(2)} \right\| }_{1}}=O({h}^{m+r}), \end{aligned}$$
(34)

and

$$\begin{aligned} {{\left\| E_{n}^{(1)} \right\| }_{1}}=O({h}^{m+r}). \end{aligned}$$
(35)

Finally from (34), (35) and representation of the local error given in (23), there exists a positive constant \(D_0\) such that

$$\begin{aligned} \begin{aligned} \left\| y-u_{h}\right\| _{\infty }\le {{\Lambda }_{m,r}}({{\left\| E_{n}^{(1)} \right\| }_{1}}+{{\left\| E_{n}^{(2)} \right\| }_{1}})+{{h}^{m+r}}{{k}_{m,r}}{{M}_{m,r}} \le {D_0}{{h}^{m+r}},\\ \end{aligned} \end{aligned}$$
(36)

where \({{\Lambda }_{m,r}}=\max \left\{ {{\left\| {{\phi }_{k}} \right\| }_{\infty }},{{\left\| {{\psi }_{j}} \right\| }_{\infty }};k=0,...,r-1,j=1,...,m \right\} ,\) and \({{M}_{m,r}}={{\left\| {{y}^{(m+r)}} \right\| }_{\infty }}\), \({{k}_{m,r}}=\max _{v\in [0,1]}\int \limits _{-r+1}^{1}{\left| {{k}_{m,r}}(v,\tau ) \right| d\tau }.\)

\(\square \)

5 Numerical examples

In this section, we have carried out the multistep collocation method in the space \(S_{m-1}^{(-1)}({{I}_{h}})\) for solving some examples. We have considered two different cases of Eq. (1) with different values for \(\alpha \) and \(\beta \) explained in Theorems 2.1 and 2.2. Note that the errors are compared via \({{\left\| {{e}_{h}} \right\| }_{\infty }}= \sup \nolimits _{1\le i\le N} \,\left| {{e}_{h}}({{x}_{i}}) \right| \), and the numerical order of convergence which is defined by

$$\begin{aligned} p={{\log }_{2}}\left( \tfrac{{{\left\| {{e}_{{N}}} \right\| }_{\infty }}}{{{\left\| {{e}_{2N}} \right\| }_{\infty }}} \right) . \end{aligned}$$

Example 1

In this example, we consider the equation

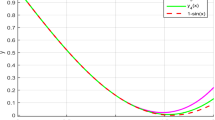
$$\begin{aligned} {{x}^{\frac{1}{2}}}y(x)=f(x)+\int \limits _{0}^{x}{{{(x-t)}^{\frac{-1}{2}}}{{t}^{2}}y(t)\mathrm{d}t},~~~x\in [0,1], \end{aligned}$$

in which, \(\alpha =\frac{1}{2}\), \(\beta =\frac{1}{2}\), \(k(x,t)={{t}^{2}}\) and \(f(x)=x^{2}-B(\frac{1}{2},\frac{9}{2})x^{4}\), where B(a, b) is the beta function. We apply a three-step collocation method to this equation with collocation parameters \({{c}_{1}}=\frac{3}{5}\), \({{c}_{2}}=\frac{9}{10}\), and with Radau II 2-points \({{c}_{1}}=\frac{1}{3}\), \({{c}_{2}}=1\) and Radau II 3-points \({{c}_{1}}=\frac{4-\sqrt{6}}{10}\),\({{c}_{2}}=\frac{4+\sqrt{6}}{10}\) and \({{c}_{3}}=1\). The exact solution is \(y(x)={{x}^{\frac{3}{2}}}\). The comparison between the exact solution and the multistep collocation solution with collocation parameters \({{c}_{1}}=\frac{3}{5}\) and \({{c}_{2}}=\frac{9}{10}\), for \(N=8\) are graphically shown in Fig. 1. The absolute errors and orders of convergence for this example are represented in Table 1, which are in agreement with the results in Theorem 4.1. An interesting result from Table 1 is that a superconvergence behavior can be obtained when Radau II points have been applied.

Fig. 1
figure 1

The exact solution and three-step collocation solution of Example 1 with \(N=8\)

Full size image
Table 1 \(||e||_\infty \) and order of convergence for Example 1 with different values of N with \(r=3\)
Full size table
Fig. 2
figure 2

The exact solution and three-step collocation solution of Example 2 with \(N=16\)

Full size image

Example 2

We consider the following Volterra integral equation of the third kind

$$\begin{aligned} xy(x)={{x}^{2}}(1-\frac{x}{3})+\int \limits _{0}^{x}{ty(t)\mathrm{d}t},~~~x\in [0,1], \end{aligned}$$
(37)

in which \(\alpha =0\), \(\beta =1\), \(k(x,t)=t\) and so \(k(0,0)=0\); thus by Theorem 2.2 the equation has a unique solution in \(C^{m+r}[0,1]\), which is given by \(y(x)=x\). We have applied a three-step collocation method on this equation with the Chebyshev nodes \({{c}_{1}}=\frac{1}{2}-\frac{1}{2\sqrt{2}}\) and \({{c}_{2}}=\frac{1}{2}+\frac{1}{2\sqrt{2}}\) (Stoer and Bulirsch 2002). The result for \(N=16\) is shown in Fig. 2.

6 Conclusions

In this paper, we have applied the multistep collocation method on some special cases of the Volterra integral equations of the third kind. It is observed that under some appropriate conditions on f(x) and k(x, t), and by increasing the numbers of collocation parameters and steps, an acceptable order of convergence, in comparison to the collocation method, can be achieved.