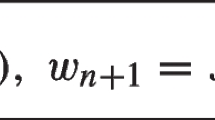An improved subgradient extragradient method with two different parameters for solving variational inequalities in reflexive Banach spaces

Abstract

In this paper, we combine the classical subgradient extragradient method with the Bregman projection method for solving variational inequality problems in reflexive Banach spaces. Specifically, we set two different parameters in the two-step projections, as opposed to consistent parameters in other results. In addition, the application of the inertial technique accelerates the iteration efficiency. Finally, we compare the proposed algorithm with other known results and find that our method effectively improves the convergence process.

1 Introduction

The main purpose of this paper is to study the variational inequality problem in Banach spaces. It is well known that the variational inequality problem consists in finding $p\in \mathcal {C}$ such that

$$\begin{aligned} \langle \mathscr {F}p,q-p\rangle \ge 0,\ \forall q\in \mathcal {C}, \end{aligned}$$

(1)

where $\mathscr {F}:\mathscr {B}\rightarrow \mathscr {B}^{*}$ is a nonlinear operator, $\langle t,s\rangle :\mathscr {B}^{*}\times \mathscr {B}\rightarrow \mathbb {R}$ is the duality pairing for $t\in \mathscr {B}^{*}$ and $s\in \mathscr {B}$, $\mathscr {B}$ is a real Banach space with the dual $\mathscr {B}^{*}$ and $\mathcal {C}$ is a nonempty closed convex subset of $\mathscr {B}$. Throughout the paper, to simplify the narrative, we denote the variational inequality problem and its solution set by VIP and $\mathcal {S}$ respectively.

The theory of variational inequalities can be traced back to the 1960s, when the problem first appeared in the Signorini problem proposed by Antonio Signorini, and then gradually obtained complete results in the research of Fichera, Stampacchia and Lions. With the continuous scientific and technological innovations, many researchers applied this theory to different fields such as mechanics, economics and mathematics. Particularly, in mathematics, the VIP is closely related to saddle-point, equilibrium and fixed-point problems, see for example, Yao et al. (2020), Ceng et al. (2014), Yao et al. (2011), Barbagallo and Di Vincenzo (2015), Lions (1977), Jitpeera and Kumam (2010) and the references therein.

In recent years, many different methods have been developed to solve VIP. One of the simplest of these methods is the projected gradient method (for short, PGM), which can be expressed as follows:

$$\begin{aligned} w_{i+1}=\mathscr {P}_\mathcal {C}(w_i-\tau \mathscr {A}w_i), \end{aligned}$$

(PGM)

where $\mathscr {P}_\mathcal {C}$ denotes the metric projection from Hilbert space $\mathscr {H}$ onto the feasible set $\mathcal {C}$, the operator $\mathscr {A}:\mathscr {H}\rightarrow \mathscr {H}$ is strongly monotone. Since the PGM is limited by strong assumptions, this will greatly affect its applicability. Therefore, Korpelevich (1976) proposed the extragradient method (for short, EGM) using the double-projection iteration, thereby weakening this condition and improving the applicability of the iterative method. The EGM is as follows:

$$\begin{aligned} \left\{ \begin{aligned}&t_i=\mathscr {P}_\mathcal {C}(w_i-\tau \mathscr {A}w_i),\\&w_{i+1}=\mathscr {P}_\mathcal {C}(w_i-\tau \mathscr {A}t_i), \end{aligned} \right. \end{aligned}$$

(EGM)

where $\mathscr {P}_\mathcal {C}: \mathscr {H}\rightarrow \mathcal {C}$ denotes the metric projection, $\mathscr {A}$ is monotone L-Lipschitz continuous operator and $\tau \in (0,\frac{1}{L})$. Under reasonable assumptions, Korpelevich obtained a weak convergence theorem for the sequence generated by EGM. Since then, the authors have combined various techniques to improve the convergence based on the EGM and have obtained further results, see for example, Jitpeera and Kumam (2010), Hieu et al. (2020), Xie et al. (2021), Dong et al. (2016), Tan et al. (2022) and the references therein.

However, although the EGM weakens the constraints based on the PGM, the projection onto the feasible set $\mathcal {C}$ must to be computed twice during each iteration of the loop. To reduce the computational effort, Censor et al. (2011) in a later study proposed the following subgradient extragradient method (for short, SEGM):

$$\begin{aligned} \left\{ \begin{aligned}&t_i=\mathscr {P}_\mathcal {C}(w_i-\tau \mathscr {A}w_i),\\&w_{i+1}=\mathscr {P}_{T_i}(w_i-\tau \mathscr {A}t_i), \end{aligned} \right. \end{aligned}$$

(SEGM)

where $\mathscr {P}_\mathcal {C}, \mathscr {A}$ and $\tau$ are the same as defined in EGM. In particular, they constructed a half-space $T_i:=\{x\in \mathscr {H}:\langle w_i-\tau \mathscr {A}w_i-t_i,x-t_i\rangle \le 0\}$ to replace the feasible set $\mathcal {C}$ in the second step of the projection process. By the definition of $T_i$, the projection is easy to calculate. The weak convergence theorem of SEGM in Hilbert spaces has been proved under some appropriate assumptions. At the same time, SEGM has also attracted the interest of many authors, see for instance, Jolaoso et al. (2021), Yao et al. (2022), Yang et al. (2020), Abubakar et al. (2022) and the references therein.

Noting that the above methods all yield the corresponding weak convergence theorems, it is natural to further consider the strong convergence. Kraikaew and Saejung (2014) combined the SEGM with the Halpern method and obtained the following algorithm:

$$\begin{aligned} \left\{ \begin{aligned}&t_i=\mathscr {P}_\mathcal {C}(w_i-\tau \mathscr {A}w_i),\\&s_i=\mathscr {P}_{T_i}(w_i-\tau \mathscr {A}t_i),\\&w_{i+1}=\alpha _{i}w_1+(1-\alpha _{i})s_i, \end{aligned} \right. \end{aligned}$$

(HSEGM)

where the metric projection $\mathscr {P}_\mathcal {C}$, the operator $\mathscr {A}$, the parameter $\tau$ and the half-space $T_i$ are defined in the same way as in the SEGM, $\{\alpha _{i}\}$ is a sequence in (0,1) satisfying $\lim _{i\rightarrow \infty }\alpha _i=0$ and $\sum _{i=1}^{\infty }\alpha _i=\infty$. By choosing appropriate values for the parameters, they obtained a strong convergence theorem for an iterative method for solving VIP in Hilbert space.

On the other hand, it is known that inertial technique can effectively accelerate the iterative process of algorithms. Therefore, authors added inertia term to the algorithm for solving VIP. For example, Thong and Hieu (2018) combined the inertial technique with the SEGM and thus obtained the following approach:

$$\begin{aligned} \left\{ \begin{aligned}&w_i=x_i+\alpha _i(x_i-x_{i-1}),\\&t_i=\mathscr {P}_\mathcal {C}(w_i-\tau \mathscr {A}w_i),\\&x_{i+1}=\mathscr {P}_{T_i}(w_i-\tau \mathscr {A}t_i), \end{aligned} \right. \end{aligned}$$

(ISEGM)

where $T_i:=\{x\in \mathscr {H}:\langle w_i-\tau \mathscr {A}w_i-t_i, x-t_i\rangle \le 0\}$, $\{\alpha _i\}$ is non-decreasing sequence and $0\le \alpha _{i}\le \alpha \le \sqrt{5}-2$, $\tau L\le \frac{\frac{1}{2}-2\alpha -\frac{1}{2}\alpha ^2-\delta }{\frac{1}{2}-\alpha +\frac{1}{2}\alpha ^2}$ for some $0<\delta <\frac{1}{2}-2\alpha -\frac{1}{2}\alpha ^2$. With a suitable choice of parameters, they proved that the sequence generated by the algorithm weakly converges to an element of the solution set $\mathcal {S}$ and that the operator $\mathscr {A}$ involved is monotone and L-Lipschitz continuous. Of course, the algorithm proposed by Thong and Hieu (2018) can be combined with the Halpern method, based on the ideas mentioned above, to obtain the corresponding strong convergence theorem.

Since Banach spaces have more general properties than Hilbert spaces, some authors have solved VIP in certain Banach spaces using tools based on existing results in Hilbert spaces. For example, Cai et al. (2018) combined the SEGM with the Halpern method and solved variational inequalities in 2-uniformly convex Banach spaces. The algorithm is iterated as follows:

$$\begin{aligned} \left\{ \begin{aligned}&t_i=\Pi _C(Jw_i-\tau \mathscr {A}w_i),\\&s_i=\Pi _{T_i}(Jw_i-\tau \mathscr {A}t_i),\\&w_{i+1}=J^{-1}(\alpha _{i}Jw_1+(1-\alpha _{i})Js_i), \end{aligned} \right. \end{aligned}$$

(BSEGM)

where $\Pi _\mathcal {C}:\mathscr {B}^{*}\rightarrow \mathcal {C}\subset \mathscr {B}$ is the generalized projection operator, $J:\mathscr {B}\rightarrow 2^{\mathscr {B}^{*}}$ is the normalized duality mapping and $\mathscr {B}$ is a real 2-uniformly convex Banach space with dual $\mathscr {B}^{*}$. The step size $\tau$ satisfies $0< \tau <\frac{1}{\mu L},$ where $\mu \ge 1$ is the 2-uniform convexity constant of $\mathscr {B}$ and L is the Lipschitz constant of $\mathscr {A}$. $\{\alpha _{i}\}$ is a sequence in (0,1) satisfying $\lim _{i\rightarrow \infty }\alpha _i=0$ and $\sum _{i=1}^{\infty }\alpha _i=\infty$. Cai et al. (2018) obtained a strong convergence theorem by choosing the appropriate parameters.

Furthermore, some authors have recently considered solving VIP in reflexive Banach spaces, see for instance, Jolaoso and Shehu (2022), Jolaoso et al. (2022), Oyewole et al. (2022), Reich et al. (2021), Abass et al. (2022) and the references therein. For example, Jolaoso and Shehu (2022) generalized the classical Tseng’s extragradient method proposed by Tseng (2000) to reflexive Banach spaces using Bregman projection, thus obtaining strong and weak convergence theorems under different conditions, respectively. In addition, Jolaoso et al. (2022) combined Popov’s method Popov (1980) with the SEGM to obtain that the sequence generated by the method converges to an element of $\mathcal {S}$ in reflexive Banach spaces by selecting appropriate parameters with the help of Bregman projection. In Reich et al. (2021), Reich et al. applied the inertial technique to the reflexive Banach space based on the hybrid and shrinking projection method and Tseng’s extragradient method and obtained a strong convergence theorem under reasonable assumptions. These results have a common feature in that they all achieve a generalization of the known results from Hilbert spaces to reflexive Banach spaces.

Motivated by the above works, in this paper, we propose a new inertial Bregman projection method for solving VIP in real reflexive Banach space. The modifications are as follows:

• Reich et al. (2021) successfully combined the inertial technique with the Tseng’s extragradient method and applied it to reflexive Banach spaces. Based on this, we found that adding inertial terms to the SEGM can also be achieved.

• In contrast to the above mentioned methods, we obtain a strong convergence theorem in reflexive Banach spaces by Halpern-type iteration and the concepts of Bregman distance and Bregman projection under suitable conditions. It is well known that strong convergence can be used to infer weak convergence, but the reverse is not necessarily true.

• We modify the step size parameter based on the SEGM. We set two different constant parameters to control the step size, which allows the algorithm to improve the convergence process of the iterative sequence without the restriction that the two parameters must be equal.

2 Preliminaries

This section collects several background material to facilitate the study that follows.

Let $f:\mathscr {B}\rightarrow \mathbb {R}$ be a proper convex and lower semicontinuous function. For simplicity, dom f denotes the domain of f, $\text {dom}\;f:=\{s\in \mathscr {B}:f(s)<\infty \}$. If $s\in$ int(dom f), then

• (i) the subdifferential of f at s is the convex set given by

  $$\begin{aligned} \partial f(s):=\{s^*\in \mathscr {B}^{*}:f(s)+\langle t-s,s^*\rangle \le f(t),\ \forall t\in \mathscr {B}\}. \end{aligned}$$

  (2)

• (ii) the Fenchel conjugate of f is the convex function $f^*:\mathscr {B}^{*}\rightarrow \mathbb {R}$ with

  $$\begin{aligned} f^*(s^*):=\sup \{\langle s,s^*\rangle -f(s):s\in \mathscr {B}\}. \end{aligned}$$

• (iii) the directional derivative of f at s is defined as

  $$\begin{aligned} f^{\circ }(s,t):=\lim _{n\rightarrow 0}\dfrac{f(s+nt)-f(s)}{n},\ \forall t\in \mathscr {B}. \end{aligned}$$

  (3)

• (iv) f is called G$\hat{a}$teaux differentiable at s, if the limit of (3) exists. At this time, the gradient of f at s is the linear function $\triangledown f(s)$ satisfying

  $$\begin{aligned} \langle \nabla f(s),t\rangle :=f^{\circ }(s,t),\ \forall t\in \mathscr {B}. \end{aligned}$$

• (v) f is said to Fréchet differentiable at s, if $n\rightarrow 0$ in (3) is attained uniformly for any $\Vert t\Vert =1$. f is called uniformly Fréchet differentiable on a subset $\mathcal {C}$, if $n\rightarrow 0$ in (3) is attained uniformly for any $\Vert t\Vert =1$ and $s\in \mathcal {C}\subset \mathscr {B}$.

The Banach space $\mathscr {B}$ is said to be reflexive, if $\mathscr {J}(\mathscr {B})=\mathscr {B}^{**}$, where $\mathscr {J}:\mathscr {B}\rightarrow \mathscr {B}^{**}$ is the standard embedding operator. Simultaneously, f is said to be Legendre if and only if it has the following forms:

• (P1) f is G$\hat{a}$teaux differentiable, dom$\nabla f$=int(dom f), int(dom f)$\ne \emptyset$,

• (P2) $f^*$ is G$\hat{a}$teaux differentiable, dom$\nabla f^*$=int(dom $f^*$), int(dom $f^*$)$\ne \emptyset$.

The reflexivity of $\mathscr {B}$ yields $(\partial f)^{-1}=\partial f^*$. And combining (P1) and (P2) shows that $\nabla f=(\nabla f^*)^{-1},\ \text {ran} \nabla f=\text {dom}\nabla f^*=\text {int(dom} f^*),\ \text {ran} \nabla f^*=\text {dom}\nabla f=\text {int(dom} f)$. Moreover, in the interior of their respective domains, f and $f^*$ are strictly convex and f is Legendre if and only if $f^*$ is Legendre.

Assume that f is G$\hat{a}$teaux differentiable, the Bregman distance associated to f is the function $\mathcal {D}_f:$dom$f\times$int(domf)$\rightarrow [0,+\infty )$ given by

$$\begin{aligned} \mathcal {D}_f(t,s):=f(t)-f(s)-\langle \triangledown f(s),t-s\rangle . \end{aligned}$$

One readily observes the following properties concerning to $\mathcal {D}_f$:

• (i) three point identity:

  $$\begin{aligned} \mathcal {D}_f(t,w)+\mathcal {D}_f(w,s)-\mathcal {D}_f(t,s)=\langle \triangledown f(w)-\triangledown f(s),w-t\rangle , \end{aligned}$$

• (ii) four point identity:

  $$\begin{aligned} \mathcal {D}_f(w,x)+\mathcal {D}_f(t,s)-\mathcal {D}_f(w,s)-\mathcal {D}_f(t,x)=\langle \triangledown f(s)-\triangledown f(x),w-t\rangle , \end{aligned}$$

  for any $s,t,w,x\in \mathscr {B}$.

We say that a G$\hat{a}$teaux differentiable function f belongs to $\beta$-strongly convex if

$$\begin{aligned} \langle \triangledown f(s)-\triangledown f(t),s-t\rangle \ge \beta \Vert s-t\Vert ^2,\ \forall s,t\in \text {dom}~f, \end{aligned}$$

namely,

$$\begin{aligned} f(t)\ge f(s)+\langle \triangledown f(s),t-s\rangle +\dfrac{\beta }{2}\Vert s-t\Vert ^2, \ \forall s,t\in \text {dom}~f. \end{aligned}$$

This gives that

$$\begin{aligned} \mathcal {D}_f(s,t)\ge \dfrac{\beta }{2}\Vert s-t\Vert ^2 \end{aligned}$$

(4)

for every $s\in$ dom f, $t\in$int(dom f).

The modulus of total convexity at $s\in$ int(dom f) denoted $v_f(s,\cdot ):[0,+\infty )\rightarrow [0,+\infty ]$ is given by

$$\begin{aligned} v_f(s,w):=\inf \{\mathcal {D}_f(t,s):t\in \text {dom} f,\Vert t-s\Vert =w\}. \end{aligned}$$

We say that f is totally convex at $u\in \text {int(dom}\ f)$, if $v_f(s,w)>0,\; \forall w>0$. Furthermore, the modulus of total convexity of f on nonempty subset $\mathcal {C}\subset \mathscr {B}$ is given by

$$\begin{aligned} v_f(\mathcal {C},w):=\inf \{v_f(s,w):s\in \mathcal {C}\cap \text {int(dom}\ f)\}. \end{aligned}$$

For given bounded subset $\mathcal {C}$ and $w>0$, the hypothesis of $v_f(\mathcal {C},w)>0$ yields that f is totally convex. Moreover, strongly convex function can derive totally convexity. Specially, when f is a Legendre function, we know that totally convexity is consistent with uniformly convexity of f. Besides, f belongs to strongly coercive if $\lim _{\Vert s\Vert \rightarrow \infty } \dfrac{f(s)}{\Vert s\Vert }=+\infty$.

Given a nonempty closed convex subset $\mathcal {C}\subset \mathscr {B}$, the operator $\mathscr {F}$ is

• (i) monotone on $\mathcal {C}$, if

  $$\begin{aligned} \langle \mathscr {F}s-\mathscr {F}t,s-t\rangle \ge 0,\ \forall \, s,t\in \mathcal {C}. \end{aligned}$$

• (ii) pseudomonotone on $\mathcal {C}$, if

  $$\begin{aligned} \langle \mathscr {F}s,t-s\rangle \ge 0 \Rightarrow \langle \mathscr {F}t,t-s\rangle \ge 0, \ \forall \, s,t\in \mathcal {C}. \end{aligned}$$

• (iii) L-Lipschitz continuous on $\mathcal {C}$, if there is an absolute constant L with

  $$\begin{aligned} \Vert \mathscr {F}s-\mathscr {F}t\Vert \le L\Vert s-t\Vert , \ \forall \, s,t\in \mathcal {C}. \end{aligned}$$

Assume that $B_r:=\{t\in \mathscr {B}:\Vert t\Vert <r,r>0\}$, $S_{\mathscr {B}}:=\{t\in \mathscr {B}:\Vert t\Vert =1\}$ and $\rho _r:[0,+\infty )\rightarrow [0,+\infty ]$ is the gauge of uniformly convexity of f,

$$\begin{aligned} \rho _r:=\inf _{x,y\in B_r, \Vert x-y\Vert =t, \alpha \in (0,1)} \dfrac{\alpha f(x)+(1-\alpha )f(y)-f(\alpha x+(1-\alpha )y)}{\alpha (1-\alpha )}. \end{aligned}$$

Then $f:\mathscr {B}\rightarrow \mathbb {R}$ is uniformly convex on bounded subsets of $\mathscr {B}$ if $\rho _r(t)>0,\ \forall r,t>0$. It is known that a strongly convex function is uniformly convex.

We will need several lemmas to obtain our main results.

Lemma 1

(Naraghirad and Yao 2013) If f is uniformly convex on bounded subsets of $\mathscr {B}$, then

$$\begin{aligned} f\left( \sum _{i=0}^{k}\alpha _i t_i\right) \le \sum _{i=0}^{k}\alpha _i f(t_i)-\alpha _i\alpha _j\rho _r(\Vert t_i-t_j\Vert ), \end{aligned}$$

for all $r>0$, $i,j\in \{0,1,2,\ldots ,k\},t_i\in B_r,\alpha _i \in (0,1)$ with $\sum _{i=0}^{k}\alpha _i=1$, where $\rho _r$ is the gauge of uniform convexity of f.

Lemma 2

(Butnariu and Iusem 2000) The function f is totally convex on bounded subsets of $\mathscr {B}$ if and only if, for $\{t_i\} \subset$ int(dom f) and $\{s_i\}\subset$ dom f, such that the first one is bounded,

$$\begin{aligned} \lim _{i\rightarrow \infty }\mathcal {D}_f(s_i,t_i)=0\Rightarrow \lim _{n\rightarrow \infty }\Vert s_i-t_i\Vert =0. \end{aligned}$$

Lemma 3

(Reich and Sabach 2009) If f is convex, bounded and uniformly Fréchet differentiable on bounded subsets of $\mathscr {B}$, then $\nabla f$ is uniformly continuous on bounded subsets of $\mathscr {B}$ from the strong topology of $\mathscr {B}$ to the strong topology of $\mathscr {B}^{*}$.

Lemma 4

(Zâlinescu 2002) If f is convex and bounded on bounded subsets of $\mathscr {B}$. Then the following are equivalent:

• 1. f is strongly coercive and uniformly convex on bounded subsets of $\mathscr {B}$.

• 2. dom $f^*=\mathscr {B}^{*}, f^*$ is bounded on bounded subsets and uniformly smooth on bounded subsets of $\mathscr {B}^{*}$.

• 3. dom $f^*=\mathscr {B}^{*}, f^*$ is Fréchet differentiable and $\nabla f^*$ is uniformly norm-to-norm continuous on bounded subsets of $\mathscr {B}^{*}$.

Lemma 5

(Butnariu and Iusem 2000) If f is strongly coercive, then

• 1. $\nabla f:\mathscr {B}\rightarrow \mathscr {B}^{*}$ is one-to-one, onto and norm-to-weak* continuous.

• 2. $\{t\in \mathscr {B}:\mathcal {D}_f(t,s)\le r\}$ is bounded for all $s\in \mathscr {B}$ and $r>0$.

• 3. dom$f^*=\mathscr {B}^{*}, f^*$ is G$\hat{a}$teaux differentiable and $\nabla f^*=(\nabla f)^{-1}$.

Lemma 6

(Martín-Márquez et al. 2013) Let f be G$\hat{a}$teaux differentiable on int(dom f) such that $\nabla f^*$ is bounded on bounded subsets of dom $f^*$. Let $t_0\in \mathscr {B}$ and $\{t_i\}\subset$ int$(\mathscr {B})$, if $\{\mathcal {D}_f(t_0,t_i)\}$ is bounded, then the sequence $\{t_i\}$ is bounded too.

Lemma 7

(Butnariu and Iusem 2000) Let $\mathcal {C}$ be a nonempty closed convex subset of a reflexive Banach space $\mathscr {B}$. A Bregman projection of $t\in \text {int(dom}\ f)$ onto $\mathcal {C}\subset \text {int(dom} \ f)$ is the unique vector $Proj_\mathcal {C}^f(t)\in \mathcal {C}$ which satisfies

$$\begin{aligned} \mathcal {D}_f(Proj_\mathcal {C}^f(t),t)=inf\{\mathcal {D}_f(s,t):s\in \mathcal {C}\}. \end{aligned}$$

Lemma 8

(Alber 1996; Censor and Lent 1981; Phelps 1993) Let $\mathcal {C}$ be a nonempty closed convex subset of a reflexive Banach space $\mathscr {B}$ and $t\in \mathscr {B}$. Let f be G$\hat{a}$teaux differentiable and totally convex function. Then

• 1. $p=Proj_\mathcal {C}^f(t) \Leftrightarrow \langle \nabla f(t)-\nabla f(p),s-p\rangle \le 0,\, \forall s\in \mathcal {C}.$

• 2. $\mathcal {D}_f(s,Proj_\mathcal {C}^f(t))+\mathcal {D}_f(Proj_\mathcal {C}^f(t),t)\le \mathcal {D}_f(s,t),\, \forall s\in \mathcal {C}.$

Define the bifunction $V_f:\mathscr {B}\times \mathscr {B}^{*}\rightarrow [0,+\infty )$ by

$$\begin{aligned} V_f(t,t^*):=f(t)-\langle t,t^*\rangle +f^*(t^*),\ \forall t\in \mathscr {B},t^*\in \mathscr {B}^*. \end{aligned}$$

Then

$$\begin{aligned} V_f(t,t^*)=\mathcal {D}_f(t,\nabla f^*(t^*)),\ \forall t\in \mathscr {B}, t^*\in \mathscr {B}^*, \end{aligned}$$

(5)

and

$$\begin{aligned} V_f(t,t^*)+\langle \nabla f^*(t^*)-t,s^*\rangle \le V_f(t,t^*+s^*),\, \forall t\in \mathscr {B}, t^*,s^*\in \mathscr {B}^*. \end{aligned}$$

(6)

In addition, if f is a proper lower semicontinuous function, then $f^*$ is a proper weak$^*$ lower semicontinuous and convex function. Hence, $V_f$ is convex in the second variable. And

$$\begin{aligned} \mathcal {D}_f(t,\nabla f^*(\sum _{i=1}^{N}s_i\nabla f(t_i)))\le \sum _{i=1}^{N}s_i \mathcal {D}_f(t,t_i) \end{aligned}$$

(7)

for all $x\in \mathscr {B}$, where $\{t_i\}_{i=1}^{N}\subset \mathscr {B}$ and $\{s_i\}_{i=1}^{N}\subset (0,1)$ with $\sum _{i=1}^{N}s_i=1$.

Lemma 9

(Maingé 2008) Let $\{w_i\}$ be a sequence of non-negative real number. If there is a subsequence $\{w_{i_j}\}$ of $\{w_i\}$ satisfies $w_{i_j}<w_{i_j+1}$ for all $j\in \mathbb {N}$, then there exists a non-decreasing sequence $\{m_k\}\subset \mathbb {N}$ such that $\lim _{k\rightarrow \infty }m_k=\infty$ and for all (sufficiently large) number $k\in \mathbb {N}$,

$$\begin{aligned} w_{m_k}\le w_{m_k+1},\quad w_k\le w_{m_k+1}. \end{aligned}$$

In fact, $m_k:=\max \{i\le k:w_i<w_{i+1}\}$.

Lemma 10

(Xu 2002) Let $\{a_i\}, \{b_i\}, \{c_i\}, \{\alpha _{i}\}$ and $\{\beta _i\}$ be sequences of non-negative real numbers such that $\{\alpha _{i}\}\subset (0,1), \sum _{i=1}^\infty \alpha _i=\infty , \lim \sup _{i\rightarrow \infty }b_{i}\le 0, \{\beta _i\}\subset [0,\frac{1}{2}], \sum _{i=1}^\infty c_i<\infty$, for $i\ge 1$,

$$\begin{aligned} a_{i+1}\le (1-\alpha _i-\beta _i)a_i+\beta _i a_{i-1}+\alpha _{i}b_i+c_i. \end{aligned}$$

Then $\lim _{i\rightarrow \infty }a_i=0$.

Lemma 11

(Mashreghi and Nasri 2010) If the mapping $h:[0,1]\rightarrow \mathscr {B}^*$ defined as $h(z)=\mathscr {F}(zs+(1-z)t)$ is continuous for all $s,t\in \mathcal {C}$, then $\mathscr {M}(\mathcal {C},\mathscr {F}):=\{s^*\in \mathcal {C}:\langle \mathscr {F}t,t-s^*\rangle , \forall t\in \mathcal {C}\}\subset \mathcal {S}$. Moreover, if $\mathscr {F}$ is pseudomonotone, then $\mathscr {M}(\mathcal {C},\mathscr {F})$ is closed, convex and $\mathscr {M}(\mathcal {C},\mathscr {F})=\mathcal {S}$.

3 Main results

In this section, we propose an inertial subgradient extragradient method with Bregman distance for solving pseudomonotone variational inequality problems in reflexive Banach spaces. First, we give the following assumptions:

(C1):

The feasible set $\mathcal {C}$ is a nonempty closed convex subset of real reflexive Banach space $\mathscr {B}$. The proper lower semicontinuous function $f:\mathscr {B}\rightarrow \mathbb {R}$ is strongly coercive Legendre which is bounded, uniformly Fréchet differentiable and $\beta$-strongly convex on bounded subsets of $\mathscr {B}$.

(C2):

The operator $\mathscr {F}:\mathscr {B}\rightarrow \mathscr {B}^*$ is pseudomonotone, L-Lipschitz continuous and satisfies the following condition:

$$\begin{aligned} \{q_i\}\subset \mathcal {C}, q_i\rightharpoonup q \Rightarrow \Vert \mathscr {F}q\Vert \le \liminf _{i\rightarrow \infty }\Vert \mathscr {F}q_i\Vert . \end{aligned}$$

(8)

The solution set $\mathcal {S}$ is nonempty.

(C3):

Let $\{\epsilon _i\}$ be a positive sequence such that $\lim _{i\rightarrow \infty }\frac{\displaystyle \epsilon _i}{\alpha _i} =0$, where $\{\alpha _i\}\subset (0,1),\,\lim _{i\rightarrow \infty }\alpha _i=0$ and $\sum _{i=1}^{\infty }\alpha _i=\infty$.

Now, we introduce the following algorithm.

Remark 1

: 1. Note that $\lim _{i\rightarrow \infty }\frac{\theta _i}{\alpha _i}\Vert w_i-w_{i-1}\Vert =0$. Indeed, for all i we have $\theta _i\le \frac{\displaystyle \epsilon _i}{\Vert w_i-w_{i-1}\Vert }$, it follows from (C3) that

$$\begin{aligned} \lim _{i\rightarrow \infty }\frac{\theta _i}{\alpha _i}\Vert w_i-w_{i-1}\Vert \le \lim _{i\rightarrow \infty } \frac{\displaystyle \epsilon _i}{\alpha _i} =0. \end{aligned}$$

2. If $t_i=x_i$, then $t_i\in \mathcal {S}$. Indeed, the definition of $\{t_i\}$ and Lemma 8(1) show that

$$\begin{aligned} \langle \nabla f(x_i)-\tau \mathscr {F}x_i-\nabla f(t_i),y-t_i\rangle \le 0,\ \forall y\in \mathcal {C}. \end{aligned}$$

Due to $t_i=x_i$, we get that

$$\begin{aligned} \tau \langle \mathscr {F}t_i,y-t_i\rangle \ge 0,\ \forall y\in \mathcal {C}. \end{aligned}$$

Since $\tau > 0$, then $t_i\in \mathcal {S}$. If $\mathscr {F}t_i=0$, it is easy to see that $t_i\in \mathcal {S}$.

Lemma 12

Assume that the conditions (C1–C3) hold. Let $\{t_i\},\{s_i\}$ and $\{x_i\}$ be the sequences produced by Algorithm 3. Then

$$\begin{aligned} \mathcal {D}_f(p,s_i)&\le \mathcal {D}_f(p,x_i)-\left( 1-\frac{\xi }{\tau }\right) \mathcal {D}_f(s_i,x_i)-\frac{\xi }{\tau }\left( 1-\dfrac{\tau L}{\beta }\right) \mathcal {D}_f(t_i,x_i)\\&\quad -\frac{\xi }{\tau }\left( 1-\dfrac{\tau L}{\beta }\right) \mathcal {D}_f(s_i,t_i) \end{aligned}$$

for every $p\in \mathcal {S}$.

Proof

Bearing in mind Lemma 8(1), the definition of $\{s_i\}$ yields that

$$\begin{aligned} \langle \nabla f(x_i)-\xi \mathscr {F}t_i-\nabla f(s_i), y-s_i\rangle \le 0,\ \forall y\in T_i. \end{aligned}$$

Due to $p\in \mathcal {S}\subset T_i$, we deduce that

$$\begin{aligned} \langle \nabla f(x_i)-\xi \mathscr {F}t_i-\nabla f(s_i), p-s_i\rangle \le 0, \end{aligned}$$

namely

$$\begin{aligned} \langle \nabla f(x_i)-\nabla f(s_i), p-s_i\rangle \le \xi \langle \mathscr {F}t_i, p-s_i\rangle . \end{aligned}$$

(9)

In light of the three point identity, we see that

$$\begin{aligned} \mathcal {D}_f(p,s_i)+\mathcal {D}_f(s_i,x_i)-\mathcal {D}_f(p,x_i)= \langle \nabla f(x_i)-\nabla f(s_i),p-s_i\rangle . \end{aligned}$$

(10)

Together (9) with (10),

$$\begin{aligned} \mathcal {D}_f(p,s_i)&\le \mathcal {D}_f(p,x_i)-\mathcal {D}_f(s_i,x_i)+\xi \langle \mathscr {F}t_i, p-s_i\rangle \nonumber \\&=\mathcal {D}_f(p,x_i)-\mathcal {D}_f(s_i,x_i)+\xi \langle \mathscr {F}t_i, p-t_i\rangle +\xi \langle \mathscr {F}t_i, t_i-s_i\rangle . \end{aligned}$$

(11)

Since $t_i\in \mathcal {C}$ and $p\in \mathcal {S}$, we have $\langle \mathscr {F}p,t_i-p\rangle \ge 0$. The pseudomonotonicity of $\mathscr {F}$ implies $\langle \mathscr {F}t_i,t_i-p\rangle \ge 0$. Thus (11) can be transformed into

$$\begin{aligned} \mathcal {D}_f(p,s_i)\le \mathcal {D}_f(p,x_i)-\mathcal {D}_f(s_i,x_i)+\xi \langle \mathscr {F}t_i, t_i-s_i\rangle . \end{aligned}$$

(12)

Next we estimate $\xi \langle \mathscr {F}t_i, t_i-s_i\rangle$. The three point identity shows that

$$\begin{aligned}&\mathcal {D}_f(s_i,x_i)-\tau \langle \mathscr {F}t_i, t_i-s_i\rangle \nonumber \\&\quad = \mathcal {D}_f(s_i,t_i)+\mathcal {D}_f(t_i,x_i)-\langle \nabla f(x_i)-\nabla f(t_i)-\tau \mathscr {F}t_i, s_i-t_i\rangle \nonumber \\&\quad =\mathcal {D}_f(s_i,t_i)+\mathcal {D}_f(t_i,x_i)-\langle \nabla f(x_i)-\tau \mathscr {F}x_i-\nabla f(t_i), s_i-t_i\rangle \nonumber \\&\qquad -\tau \langle \mathscr {F}x_i-\mathscr {F}t_i, s_i-t_i\rangle . \end{aligned}$$

(13)

Applying the definition of $T_i$ and $s_i\in T_i$, one readily observes

$$\begin{aligned} \langle \nabla f(x_i)-\tau \mathscr {F}x_i-\nabla f(t_i), s_i-t_i\rangle \le 0. \end{aligned}$$

(14)

It follows from (4) and (8) that

$$\begin{aligned} \tau \langle \mathscr {F}x_i-\mathscr {F}t_i,s_i-t_i\rangle&\le \tau \Vert \mathscr {F}x_i-\mathscr {F}t_i\Vert \Vert s_i-t_i\Vert \nonumber \\&\le \tau L\Vert x_i-t_i\Vert \Vert s_i-t_i\Vert \nonumber \\&\le \dfrac{\tau L }{2}\big (\Vert x_i-t_i\Vert ^2+\Vert s_i-t_i\Vert ^2\big )\nonumber \\&\le \dfrac{\tau L}{\beta }\big (\mathcal {D}_f(t_i,x_i)+\mathcal {D}_f(s_i,t_i)\big ). \end{aligned}$$

(15)

Combining (13), (14) and (15), then

$$\begin{aligned} \tau \langle \mathscr {F}t_i,t_i-s_i\rangle \le \mathcal {D}_f(s_i,x_i)-\left( 1-\dfrac{\tau L}{\beta }\right) \bigg (\mathcal {D}_f(t_i,x_i)+\mathcal {D}_f(s_i,t_i)\bigg ). \end{aligned}$$

(16)

Substituting (16) into (12), we obtain

$$\begin{aligned} \mathcal {D}_f(p,s_i)&\le \mathcal {D}_f(p,x_i)-\mathcal {D}_f(s_i,x_i)+\frac{\xi }{\tau } \mathcal {D}_f(s_i,x_i)\nonumber \\&\quad -\frac{\xi }{\tau }\left( 1-\dfrac{\tau L}{\beta }\right) \big (\mathcal {D}_f(t_i,x_i)+\mathcal {D}_f(s_i,t_i)\big )\nonumber \\&=\mathcal {D}_f(p,x_i)-\left( 1-\frac{\xi }{\tau }\right) \mathcal {D}_f(s_i,x_i)-\frac{\xi }{\tau }\left( 1-\dfrac{\tau L}{\beta }\right) \mathcal {D}_f(t_i,x_i)\nonumber \\&\quad -\frac{\xi }{\tau }\left( 1-\dfrac{\tau L}{\beta }\right) \mathcal {D}_f(s_i,t_i), \end{aligned}$$

(17)

which is the desired inequality. $\square$

Lemma 13

Suppose the conditions (C1–C3) hold. The sequence $\{w_i\}$ produced by Algorithm 3 is bounded.

Proof

As $\tau \in \left( 0,\frac{\beta }{L}\right)$ and $\xi \in (0,\tau ]$, we see that

$$\begin{aligned} 1-\frac{\xi }{\tau }\ge 0,\ \frac{\xi }{\tau }\left( 1-\dfrac{\tau L}{\beta }\right) >0. \end{aligned}$$

(18)

With (18) and Lemma 12 in hand, we get

$$\begin{aligned} \mathcal {D}_f(p,s_i)\le \mathcal {D}_f(p,x_i),\ \forall p\in \mathcal {S} . \end{aligned}$$

(19)

The definition of $\{w_i\}$ and (7) show that

$$\begin{aligned} \mathcal {D}_f(p,x_i)&= \mathcal {D}_f\Big (p,\nabla f^*\big (\nabla f(w_i)+\theta _i (\nabla f(w_{i-1})-\nabla f(w_{i})\big )\Big )\\&=\mathcal {D}_f\Big (p,\nabla f^*\big ((1-\theta _i) \nabla f(w_i)+\theta _i (\nabla f(w_{i-1})\big )\Big )\\&\le (1-\theta _i)\mathcal {D}_f(p,w_i)+\theta _i \mathcal {D}_f(p,w_{i-1}). \end{aligned}$$

Hence, with Lemma 1 in hand, the definition of $V_f$ and the property of $\rho _r^*$ yield that

$$\begin{aligned} \mathcal {D}_f(p,w_{i+1})&= \mathcal {D}_f\Big (p,\nabla f^*\big (\alpha _i \nabla f(w_1)+(1-\alpha _i) \nabla f(s_i)\big )\Big )\\&\le \alpha _i \mathcal {D}_f(p,w_1)+(1-\alpha _i)\mathcal {D}_f(p,s_i)\\&\le \alpha _i \mathcal {D}_f(p,w_1)+(1-\alpha _i)\mathcal {D}_f(p,x_i)\\&\le \alpha _i \mathcal {D}_f(p,w_1)+(1-\alpha _i)\left[ (1-\theta _i)\mathcal {D}_f(p,w_i)+\theta _i \mathcal {D}_f(p,w_{i-1})\right] \\&\le \alpha _i \mathcal {D}_f(p,w_1)+(1-\alpha _i)\max \left\{ \mathcal {D}_f(p,w_i), \mathcal {D}_f(p,w_{i-1})\right\} \\&\le \max \left\{ \mathcal {D}_f(p,w_1), \mathcal {D}_f(p,w_i), \mathcal {D}_f(p,w_{i-1})\right\} \end{aligned}$$

By induction, we conclude that

$$\begin{aligned} \mathcal {D}_f(p,w_{i+1})\le \max \left\{ \mathcal {D}_f(p,w_1),\mathcal {D}_f(p,w_0)\right\} . \end{aligned}$$

(20)

Consequently, the sequence $\{w_i\}$ is bounded by Lemma 6.$\square$

Lemma 14

Assume that the conditions (C1-C3) hold. Let $\{x_{i_k}\}$ be a subsequence of $\{x_i\}$ produced by Algorithm 3 such that $x_{i_k}\rightharpoonup q$ and $\lim _{k\rightarrow \infty }\Vert x_{i_k}-t_{i_k}\Vert =0$, then $q\in \mathcal {S}$.

Proof

Due to $t_{i_k}:=Proj_ \mathcal {C}^f\big (\nabla f^*(\nabla f(x_{i_k})-\tau \mathscr {F}x_{i_k})\big )$, it follows from Lemma 8(1) that

$$\begin{aligned} \langle \nabla f(x_{i_k})-\tau \mathscr {F}x_{i_k}-\nabla f(t_{i_k}),x-t_{i_k}\rangle \le 0, \ \forall x\in \mathcal {C}, \end{aligned}$$

that is

$$\begin{aligned} \frac{1}{\tau } \langle \nabla f(x_{i_k})-\nabla f(t_{i_k}),x-t_{i_k}\rangle \le \langle \mathscr {F}x_{i_k},x-t_{i_k}\rangle , \ \forall x\in \mathcal {C}. \end{aligned}$$

Hence,

$$\begin{aligned} \frac{1}{\tau } \langle \nabla f(x_{i_k})-\nabla f(t_{i_k}),x-t_{i_k}\rangle +\langle \mathscr {F}x_{i_k},t_{i_k}-x_{i_k}\rangle \le \langle \mathscr {F}x_{i_k},x-x_{i_k}\rangle , \ \forall x\in \mathcal {C}. \end{aligned}$$

(21)

Since $\lim \limits _{k\rightarrow \infty }\Vert x_{i_k}-t_{i_k}\Vert =0$, Lemma 3 yields that $\nabla f$ is uniformly continuous, then

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert \nabla f(x_{i_k})-\nabla f(t_{i_k})\Vert =0. \end{aligned}$$

Putting $k\rightarrow \infty$ in (21), $\tau > 0$ shows that

$$\begin{aligned} \liminf _{k\rightarrow \infty } \langle \mathscr {F}x_{i_k},x-x_{i_k}\rangle \ge 0, \ \forall x\in \mathcal {C}. \end{aligned}$$

(22)

We then conclude that

$$\begin{aligned} \langle \mathscr {F}t_{i_k},x-t_{i_k}\rangle&=\langle \mathscr {F}t_{i_k}-\mathscr {F}x_{i_k},x-x_{i_k}\rangle \nonumber \\&\quad +\langle \mathscr {F}x_{i_k},x-x_{i_k}\rangle +\langle \mathscr {F}t_{i_k},x_{i_k}-t_{i_k}\rangle . \end{aligned}$$

(23)

Due to $\lim \limits _{k\rightarrow \infty }\Vert x_{i_k}-t_{i_k}\Vert =0$ and the fact that $\mathscr {F}$ is Lipschitz continuous, we get

$$\begin{aligned} \liminf _{k\rightarrow \infty }\langle \mathscr {F}t_{i_k},x-t_{i_k}\rangle \ge 0. \end{aligned}$$

(24)

We now proceed to the proof of $q\in \mathcal {S}$. Given a sequence $\{\epsilon _k\}$ of positive numbers that decreases and tends to 0, for each k, it follows from (24) that there is the smallest positive integer $N_{k}$ such that

$$\begin{aligned} \langle \mathscr {F}t_{i_j},x-t_{i_j}\rangle +\epsilon _k\ge 0,\ \forall j\ge N_{k}, \end{aligned}$$

(25)

$\{\epsilon _k\}$ is decreasing implies that the sequence $\{N_{k}\}$ is increasing. Besides, for each k, there is a bounded sequence $\{v_{N_k}\}\subset \mathscr {B}$ such that $\epsilon _k = \langle \mathscr {F}t_{N_k},\epsilon _k v_{N_k}\rangle$. Thus, we have

$$\begin{aligned} \langle \mathscr {F}t_{N_k},x+\epsilon _k v_{N_k}-t_{N_k}\rangle \ge 0. \end{aligned}$$

The pseudomonotonicity of $\mathscr {F}$ shows that

$$\begin{aligned} \langle \mathscr {F}(x+\epsilon _k v_{N_k}),x+\epsilon _k v_{N_k}-t_{N_k}\rangle \ge 0, \end{aligned}$$

which implies that

$$\begin{aligned} \langle \mathscr {F}x,x-t_{N_k}\rangle \ge \langle \mathscr {F}x-\mathscr {F}(x+\epsilon _k v_{N_k}),x+\epsilon _k v_{N_k}-t_{N_k}\rangle -\langle \mathscr {F}x,\epsilon _k v_{N_k}\rangle . \end{aligned}$$

(26)

In light of $x_{i_k}\rightharpoonup q$ and $\lim \nolimits _{k\rightarrow \infty } \Vert x_{i_k}-t_{i_k} \Vert =0$, we have $t_{i_k}\rightharpoonup q\ (k\rightarrow \infty )$ and thus $q\in \mathcal {C}$. According to (8),

$$\begin{aligned} 0<\left\| \mathscr {F}q\right\| \le \liminf \limits _{k\rightarrow \infty }\left\| \mathscr {F}t_{i_k}\right\| , \end{aligned}$$

which implies that $\lim _{k\rightarrow \infty }\epsilon _k v_{N_k}=0$. Thus, letting $k\rightarrow \infty$ in (26), the Lipschitz continuity of $\mathscr {F}$ and the boundedness of $\{x_{N_k}\}$ and $\{ v_{N_k}\}$ show that

$$\begin{aligned} \liminf \limits _{k\rightarrow \infty }\langle \mathscr {F}x,x-t_{N_k}\rangle \ge 0. \end{aligned}$$

(27)

Hence, for all $x\in \mathcal {C}$,

$$\begin{aligned} \langle \mathscr {F}x,x-q\rangle =\lim \limits _{k\rightarrow \infty }\langle \mathscr {F}x,x-t_{N_k}\rangle =\liminf \limits _{k\rightarrow \infty }\langle \mathscr {F}x,x-t_{N_k}\rangle \ge 0. \end{aligned}$$

(28)

By Lemma 11, we see therefore that $q\in \mathcal {S}$. $\square$

Theorem 1

Assume that the conditions (C1–C3) hold. Then the sequence $\{w_i\}$ produced by Algorithm 3 strongly converges to $p=Proj_{\mathcal {S}}^f(w_1)$.

Proof

According to the definition of $\{w_i\}$, the formulas (5), (6) and (7) show that

$$\begin{aligned} \mathcal {D}_f(p,w_{i+1})&=\mathcal {D}_f\Big (p,\nabla f^*\big (\alpha _i \nabla f(w_1)+(1-\alpha _i) \nabla f(s_i)\big )\Big )\nonumber \\&=V_f\big (p,\alpha _i \nabla f(w_1)+(1-\alpha _i) \nabla f(s_i)\big )\nonumber \\&\le V_f\big (p,\alpha _i \nabla f(w_1)+(1-\alpha _i) \nabla f(s_i)-\alpha _i(\nabla f(w_1)-\nabla f(p))\big )\nonumber \\&\quad +\alpha _i\langle \nabla f(w_1)-\nabla f(p),w_{i+1}-p\rangle \nonumber \\&= V_f\big (p,\alpha _i \nabla f(p)+(1-\alpha _i) \nabla f(s_i)\big )+\alpha _i\langle \nabla f(w_1)-\nabla f(p),w_{i+1}-p\rangle \nonumber \\&\le \alpha _i \mathcal {D}_f(p,p)+(1-\alpha _i) \mathcal {D}_f(p,s_i)+\alpha _i\langle \nabla f(w_1)-\nabla f(p),w_{i+1}-p\rangle \nonumber \\&\le (1-\alpha _i)\mathcal {D}_f(p,x_i)+\alpha _i\langle \nabla f(w_1)-\nabla f(p),w_{i+1}-p\rangle \nonumber \\&\le (1-\alpha _i)\big [(1-\theta _i)\mathcal {D}_f(p,w_i)+\theta _i \mathcal {D}_f(p,w_{i-1})\big ]\nonumber \\&\quad +\alpha _i\langle \nabla f(w_1)-\nabla f(p),w_{i+1}-p\rangle \nonumber \\&=\big [1-\alpha _i-(1-\alpha _i)\theta _i\big ]\mathcal {D}_f(p,w_i)+(1-\alpha _i)\theta _i \mathcal {D}_f(p,w_{i-1})\nonumber \\&\quad +\alpha _i\langle \nabla f(w_1)-\nabla f(p),w_{i+1}-p\rangle . \end{aligned}$$

(29)

We now proceed to the proof of $w_i\rightarrow p$ in two cases:

Case 1: There exists $N\in \mathbb {N}$ such that $\{\mathcal {D}_f(p,w_i)\}_{n=N} ^\infty$ is nonincreasing. Thus $\{\mathcal {D}_f(p,w_i)\}$ is convergent and

$$\begin{aligned} \lim _{i\rightarrow \infty }\big (\mathcal {D}_f(p,w_i)-\mathcal {D}_f(p,w_{i+1})\big )=\lim _{i\rightarrow \infty }\big (\mathcal {D}_f(p,w_{i-1})-\mathcal {D}_f(p,w_{i})\big )=0. \end{aligned}$$

Moreover, it follows from Lemmas 12 and 13 that

$$\begin{aligned} \mathcal {D}_f(p,w_{i+1})&\le \alpha _i\mathcal {D}_f(p,w_1)+(1-\alpha _i)\mathcal {D}_f(p,s_i)\\&\le \alpha _i\mathcal {D}_f(p,w_1)+(1-\alpha _i)\big [\mathcal {D}_f(p,x_i)-(1-\frac{\xi }{\tau })\mathcal {D}_f(s_i,x_i)\\&\quad -\frac{\xi }{\tau }(1-\dfrac{\tau L}{\beta })\mathcal {D}_f(t_i,x_i) -\frac{\xi }{\tau }(1-\dfrac{\tau L}{\beta })\mathcal {D}_f(s_i,t_i)\big ]\\&\le \alpha _i\mathcal {D}_f(p,w_1)+(1-\alpha _i)\Big \{(1-\theta _i)\mathcal {D}_f(p,w_i)+\theta _i \mathcal {D}_f(p,w_{i-1})\\&\quad -(1-\frac{\xi }{\tau })\mathcal {D}_f(s_i,x_i) -\frac{\xi }{\tau }(1-\dfrac{\tau L}{\beta })\big [\mathcal {D}_f(t_i,x_i)+\mathcal {D}_f(s_i,t_i)\big ]\Big \}. \end{aligned}$$

Namely

$$\begin{aligned}&(1-\alpha _i)\frac{\xi }{\tau }\left( 1-\dfrac{\tau L}{\beta }\right) \big [\mathcal {D}_f(t_i,x_i)+\mathcal {D}_f(s_i,t_i)\big ]\nonumber \\&\quad \le \mathcal {D}_f(p,w_i)-\mathcal {D}_f(p,w_{i+1})+(1-\alpha _i)\theta _n[\mathcal {D}_f(p,w_{i-1})-\mathcal {D}_f(p,w_{i})]+\alpha _nM_1, \end{aligned}$$

(30)

for some $M_1>0$. Due to $\lim _{i\rightarrow \infty }\alpha _i=0$, combining (30) and (18), we can conclude that

$$\begin{aligned} \lim _{i\rightarrow \infty }\mathcal {D}_f(t_i,x_i)=\lim _{i\rightarrow \infty } \mathcal {D}_f(s_i,t_i)=0. \end{aligned}$$

(31)

Owing to Lemma 2, we have

$$\begin{aligned} \lim _{i\rightarrow \infty }\Vert t_i-x_i\Vert =\lim _{i\rightarrow \infty }\Vert s_i-t_i\Vert =0, \end{aligned}$$

(32)

which implies that

$$\begin{aligned} \lim _{i\rightarrow \infty }\Vert s_i-x_i\Vert \le \lim _{i\rightarrow \infty }\Vert s_i-t_i\Vert +\lim _{i\rightarrow \infty }\Vert t_i-x_i\Vert =0. \end{aligned}$$

(33)

At the same time, let $i\rightarrow \infty$, then

$$\begin{aligned} \Vert \nabla f(x_{i})-\nabla f(w_i)\Vert= & {} \alpha _i\frac{\theta _i}{\alpha _i}\Vert \nabla f(w_{i-1})-\nabla f(w_i)\Vert =\alpha _i\frac{\theta _i}{\alpha _i}\Vert w_{i-1}-w_i\Vert \rightarrow 0,\\ \Vert \nabla f(w_{i+1})-\nabla f(s_i)\Vert= & {} \alpha _i\Vert \nabla f(w_1)-\nabla f(s_i)\Vert \le \alpha _iM_2\rightarrow 0, \end{aligned}$$

for some $M_2>0$. From Lemma 4, the uniformly norm-to-norm continuity of $\nabla f^*$ implies that

$$\begin{aligned} \lim _{i\rightarrow \infty } \Vert x_{i}-w_i\Vert =\lim _{i\rightarrow \infty } \Vert w_{i+1}-s_i\Vert =0. \end{aligned}$$

(34)

Therefore, in light of (33) and (34),

$$\begin{aligned} \Vert w_{i+1}-w_i\Vert \le \Vert w_{i+1}-s_i\Vert +\Vert s_i-x_i\Vert +\Vert x_i-w_i\Vert \rightarrow 0\ (n\rightarrow \infty ). \end{aligned}$$

(35)

Since $\{w_i\}$ is bounded, there is a subsequence $\{w_{i_k}\}\subset \{w_i\}$ such that $w_{i_k}\rightharpoonup q$ and thus $x_{i_k}\rightharpoonup q$ as $k\rightarrow \infty$. Owing to Lemma 14, we can conclude that $q\in \mathcal {S}$. Combining with $p=Proj_{\mathcal {S}}^f(w_1)$, then

$$\begin{aligned} \limsup _{i\rightarrow \infty } \langle \nabla f(w_1)-\nabla f(p), w_{i}-p\rangle&=\lim _{k\rightarrow \infty } \langle \nabla f(w_1)-\nabla f(p),w_{i_k}-p\rangle \nonumber \\&=\lim _{k\rightarrow \infty } \langle \nabla f(w_1)-\nabla f(p),q-p\rangle \nonumber \\&\le 0, \end{aligned}$$

(36)

which means that

$$\begin{aligned} \limsup _{i\rightarrow \infty }\langle \nabla f(w_1)-\nabla f(p),w_{i+1}-p\rangle \le 0. \end{aligned}$$

(37)

Combining (29), (37) with Lemma 10, we see therefore that $\mathcal {D}_f(p,w_i)\rightarrow 0$ as $i\rightarrow \infty$, that is $w_i\rightarrow p$ as $i\rightarrow \infty$.

Case 2: There is a subsequence $\{\mathcal {D}_f(p,w_{i_j})\}\subset \{\mathcal {D}_f(p,w_{i})\}$ such that $\mathcal {D}_f(p,w_{i_j})<\mathcal {D}_f(p,w_{i_j+1})$ for all $j\in \mathbb {N}$. It follows from Lemma 9 that there exists a non-decreasing sequence $\{i_k\}\subset \mathbb {N}$ tending to infinity such that

$$\begin{aligned} \mathcal {D}_f(p,w_{i_k})\le \mathcal {D}_f(p,w_{i_k+1})\ \text {and} \ \mathcal {D}_f(p,w_{k})\le \mathcal {D}_f(p,w_{i_k+1}), \ \forall k\in \mathbb {N}. \end{aligned}$$

In Lemma 13 we obtain

$$\begin{aligned} \mathcal {D}_f(p,w_{{i}_k+1})\le \alpha _{i_k} \mathcal {D}_f(p,w_1)+(1-\alpha _{i_k})\mathcal {D}_f(p,w_{i_k}). \end{aligned}$$

Therefore, the fact $\lim _{i\rightarrow \infty }\alpha _i=0$ implies

$$\begin{aligned} \mathcal {D}_f(p,w_{{i}_k+1})-\mathcal {D}_f(p,w_{i_k})\rightarrow 0\ (k\rightarrow \infty ). \end{aligned}$$

Due to boundedness of $\{w_{i_k}\}$, there is a subsequence of $\{w_{i_k}\}$ still denoted by $\{w_{i_k}\}$ and $w_{i_k}\rightharpoonup q$. As stated in Case 1, we have

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert w_{i_k+1}-w_{i_k}\Vert =0, \quad \limsup _{k\rightarrow \infty } \langle \nabla f(w_1)-\nabla f(p), w_{{i_k}+1}-p\rangle \le 0. \end{aligned}$$

According to (29),

$$\begin{aligned} \mathcal {D}_f(p,w_{i_k+1})&\le (1-\alpha _{i_k})\mathcal {D}_f(p,w_{i_k})+\alpha _{i_k}\langle \nabla f(w_1)-\nabla f(p), w_{{i_k}+1}-p\rangle \\&\le (1-\alpha _{i_k})\mathcal {D}_f(p,w_{i_k+1})+\alpha _{i_k}\langle \nabla f(w_1)-\nabla f(p), w_{{i_k}+1}-p\rangle . \end{aligned}$$

The fact $\alpha _{i_k}>0$ shows that

$$\begin{aligned} \mathcal {D}_f(p,w_{k})\le \mathcal {D}_f(p,w_{i_k+1})\le \langle \nabla f(w_1)-\nabla f(p), w_{{i_k}+1}-p\rangle . \end{aligned}$$

Namely,

$$\begin{aligned} \limsup _{k\rightarrow \infty }\mathcal {D}_f(p,w_k)\le \limsup _{k\rightarrow \infty }\langle \nabla f(w_1)-\nabla f(p), w_{{i_k}+1}-p\rangle \le 0. \end{aligned}$$

Hence, $w_k\rightarrow p \ (k\rightarrow \infty )$, which is the desired result.$\square$

Next we apply the above result to Hilbert space. Let $f(s)=\frac{1}{2}\Vert s\Vert ^2$, we have $\mathcal {D}_f(s,t):=\dfrac{1}{2}\Vert s-t\Vert ^2,\ \forall s,t\in \mathcal {C}$, then

$$\begin{aligned} Proj_ \mathcal {C}^f\big (\nabla f^*(\nabla f(x_i)-\tau \mathscr {F}x_i)\big )=:\mathscr {P}_\mathcal {C}(x_i-\tau \mathscr {A}x_i), \end{aligned}$$

where $\mathcal {C}$ is nonempty closed convex subset of Hilbert space $\mathscr {H}$, $\mathscr {P}_\mathcal {C}$ is the metric projection of $\mathscr {H}$ onto $\mathcal {C}$. In this case, if $\theta _i=0$, we can obtain the following result.

Corollary 1

Assume that the feasible set $\mathcal {C}$ is a nonempty closed convex subset of a real Hilbert space $\mathscr {H}$, the solution set $\mathcal {S}$ is nonempty and the operator $\mathscr {A}:\mathscr {H} \rightarrow \mathscr {H}$ is pseudomonotone, L-Lipschitz continuous and satisfies $\{q_i\}\subset \mathcal {C}, q_i\rightharpoonup q \Rightarrow \Vert \mathscr {A}q\Vert \le \liminf _{i\rightarrow \infty }\Vert \mathscr {A}q_i\Vert$. Suppose $\tau \in (0,\frac{1}{L})$, $\xi \in (0,\tau ]$, $T_i:=\{x\in \mathscr {H}:\langle x_i-\tau \mathscr {A}x_i-t_i,x-t_i\rangle \le 0\}$, the sequence $\{\alpha _i\}\subset (0,1)$ satisfies $\lim _{i\rightarrow \infty }\alpha _i=0$ and $\sum _{i=1}^{\infty }\alpha _i=\infty$. Then the sequence $\{x_i\}$ produced by the following algorithm strongly converges to an element $p=\mathscr {P}_{\mathcal {S}}(x_1)$.

$$\begin{aligned} \left\{ \begin{aligned}&t_i=\mathscr {P}_\mathcal {C}(x_i-\tau \mathscr {A}x_i),\\&s_{i}=\mathscr {P}_{T_i}(x_i-\xi \mathscr {A}t_i),\\&x_{i+1}=\alpha _i x_1+(1-\alpha _{i})s_i. \end{aligned} \right. \end{aligned}$$

4 Numerical experiments

In this section, we perform two numerical examples to show the behaviors of Algorithm 3, and compare them with other algorithms. In both experiments the parameters are chosen as $\alpha _i=\frac{1}{i+1}$ and

$$\begin{aligned} \theta _i= {\left\{ \begin{array}{ll} \min \left\{ \frac{\displaystyle \epsilon _i}{\displaystyle \left\| w_i-w_{i-1}\right\| },\theta \right\} , &{}\text {if\ }w_i\ne w_{i-1},\\ \theta , &{}\text {otherwise},\\ \end{array}\right. } \end{aligned}$$

(38)

where $\epsilon _i=\frac{1}{(i+2)^{1.1}}$.

Example 1

Let $\mathscr {B}=L^{2}([0,1])$ endowed with norm $\Vert x\Vert _{\mathscr {B}}=(\int _{0}^{1}|x(t)|^{2}dt)^{\frac{1}{2}}$ and inner product $\langle x,y \rangle _{\mathscr {B}}=\int _{0}^{1}x(t)y(t)dt$ for all $x,y\in \mathscr {B}$. Consider $\mathcal {C}:=\{x \in \mathscr {B}:\Vert x\Vert \le 2\}$. Let $g: \mathcal {C}\rightarrow \mathbb {R}$ be defined by

$$\begin{aligned} g(s):=\frac{1}{1+\Vert s\Vert ^2}. \end{aligned}$$

Note that g is $L_g$-Lipchitz continuous with $L_g=\frac{16}{25}$ and $\frac{1}{5}\le g(s)\le 1,~~\forall s \in \mathcal {C}$. The Volterra integral operator $V:\mathscr {B}\rightarrow \mathscr {B}$ is given by

$$\begin{aligned} V(s)(t):=\int _0^t s(x)dx,~~\forall s \in L^2([0,1]), t \in [0,1]. \end{aligned}$$

Then V is bounded linear monotone operator. Define $\mathscr {F}:\mathcal {C}\rightarrow \mathscr {B}$ by

$$\begin{aligned} \mathscr {F}(s)(t):=g(s)V(s)(t),~~\forall s \in \mathcal {C}, t \in [0,1]. \end{aligned}$$

We see that $\mathscr {F}$ is not monotone on $\mathcal {C}$ but pseudomonotone and L-Lipschitz continuous with $L = 82/\pi$.

We compare our Algorithm 3 (shortly, OUR) with Algorithm 3.5 in Cai et al. (2018) (shortly, CGIS) and Algorithm 3 in Xie et al. (2023) (shortly, XCD). The parameters are set as follows:

Our Algorithm 3: $\tau =0.99/L, \xi =0.9/L, \theta =0.63$ and $\alpha _i=\frac{1}{i+1}$;

Algorithm 3 in Xie et al. (2023): $\mu =0.9,\, \tau _1=2$ and $\alpha _i=\frac{1}{i+1}$;

Algorithm 3.5 in Cai et al. (2018): $a=0.0001$, $\lambda _i=a + \frac{i(\frac{1}{L}-1)}{i+1}$ and $\alpha _i=\frac{1}{i+1}$.

Let $x_{0}=x_{1}=e^{2t}+\sin (3t)$, we observe from Fig. 1 that our Algorithm 3 is better than Algorithm 3.5 in Cai et al. (2018) and Algorithm 3 in Xie et al. (2023).

Fig. 1

The value of error versus the iteration numbers for Example 1

Example 2

Compare the performance of Algorithm 3 at different Bregman distances. Define the feasible set $\mathcal {C}$ by

$$\begin{aligned} \mathcal {C}=\left\{ x\in \mathbb {R}^m:x_{i}\ge 0, \sum _{i=1}^{m}x_{i}=1\right\} \end{aligned}$$

and define $f:\mathbb {R}^{m}\rightarrow \mathbb {R}$ by

$$\begin{aligned} (i) f(x)=\sum _{i=1}^{m} x_{i}\log (x_{i}), \quad (ii)f(x)=\frac{1}{2}\Vert x\Vert ^{2}. \end{aligned}$$

We see that f is strongly convex with $\beta =1$. Due to $\mathscr {B}=\mathbb {R}^{m}$, then $\nabla f^{*}(x)=(\nabla f)^{-1}(x)$. Therefore, for each f,

• (i) $\nabla f(x)=(1+\log (x_{1}),\ldots ,1+\log (x_{m}))^{T}$, $(\nabla f)^{-1}(x)=(\exp (x_{1}-1),\ldots ,$ $\exp (x_{m}-1))^{T}$,

• (ii) $\nabla f(x)=x$ and $(\nabla f)^{-1}(x)=x$.

The corresponding Bregman distances are given by

• (i) $\mathcal {D}_{f}(x,y)=\sum _{i=1}^{m}(x_{i}\log (\frac{x_{i}}{y_{i}})+y_{i}-x_{i})$ which is the Kullback–Leibler distance (shortly, KLD),

• (ii) $\mathcal {D}_{f}(x,y)=\frac{1}{2}\Vert x-y\Vert ^{2}$ which is the squared Euclidean distance (shortly, SED).

Next we define the operator $\mathscr {F}$ by $\mathscr {F}(x) = \max (x,0)$. Clearly, $\mathscr {F}$ is monotone and $\mathcal {S}={0}$. We compare the performance of Algorithm 3 using SED and KLD. The initial points are generated randomly for $m=20,50,80,120$, and $D_n=\Vert x_{n+1}-x_{n}\Vert <10^{-4}$ is used as stopping criterion. The computation results are shown in Fig. 2 and Table 1. It can be seen that the convergence of the algorithm is different for different Bregman distances. Different functions correspond to different Bregman distances. Therefore, we use the Bregman projection method to obtain better convergence behavior.

Example 3

Let the operator $\mathscr {F}(x): = M x + q$, where

$$\begin{aligned} M= BB^T+ G + D, \end{aligned}$$

and B is an $m\times m$ matrix, G is an $m\times m$ skew-symmetric matrix, D is an $m\times m$ diagonal matrix, whose diagonal entries are non-negative (so M is positive semidefinite), q is a vector in $\mathbb {R}^m$. The feasible set $\mathcal {C}\subset \mathbb {R}^m$ is a closed and convex subset defined by $\mathcal {C}: = \{x\in \mathbb {R}^m: Qx\le b\}$, where Q is an $k\times m$ matrix and b is a non-negative vector. It is clear that $\mathscr {F}$ is monotone and L-Lipschitz continuous with $L =\Vert M\Vert$. Let $q= 0$. Then, the solution set is $\{0\}$.

In this example, the initial values $x_0$ and $x_1$ are both set to $(1,1,\ldots ,1),k=20,m=10,\alpha _{i}=\frac{1}{i+1}$ and $\theta =0.5$. $\Vert x_{n+1}-x_n\Vert$ represents the error of the n-th step iteration. For the two key parameters $\tau$ and $\xi$ in Algorithm 3, we fix one parameter and change the remaining one. Finally, we get the following two cases, which are respectively shown in Figs. 3 and 4.

• 1. $\tau =0.99/L,\ 0.5/L,\ 0.01/L$ and $\xi =0.01/L$.

• 2. $\xi =0.01/L,\ 0.1/L,\ 0.2/L$ and $\tau =0.2/L$.

As shown in Figs. 3 and 4, each parameter will affect the convergence rate of our proposed algorithm, and the result of this effect is not monotonically increasing or decreasing with the parameter value. In particular, the values of $\tau$ and $\xi$ are often consistent in other known results, but our algorithm breaks this restriction. We can choose that $\tau$ and $\xi$ do not necessarily have to be the same, resulting in a better convergence behavior.

Fig. 2

Numerical behavior of all algorithms with different m in Example 2

Table 1 The number of termination iterations and execution time of our algorithm with different distances in Example 2

Fig. 3

The value of error versus the iteration numbers with different value on $\tau$ for Example 3 with $k=20,m=10,\xi =0.01/L$

Fig. 4

The value of error versus the iteration numbers for Example 3 with $k=20,m=10,\tau =0.2/L$

5 Conclusions

In this paper, we introduced an improved subgradient extragradient method with Bregman distance for solving pseudomonotone variational inequality problems. We generalized the classical subgradient extragradient method to reflexive Banach spaces and effectively added an inertia term to speed up the convergence process of the algorithm. In addition, we set two different step size parameters, which help us to choose more appropriate values and thus increase the convergence rate. Under reasonable assumptions, we proved that the sequence generated by the proposed algorithm strongly converges to a solution of variational inequality problems. Finally, we presented numerical experiments to verify that our algorithm is effective in improving the iteration efficiency.