1 Introduction

During the last decades, it is well known that the dynamic of neural networks has received considerable attention, because it is a key factor in applications. Due to the study of the last decades, research on real-value neural networks is mature, see Aouiti and Abed Assali (2019), Yang et al. (2013), Wu et al. (2012), Alimi et al. (2019), and Aouiti and Assali (2019). For example in Aouiti and Abed Assali (2019), the authors studied the stability of a class of delayed inertial neural networks via non-reduced-order method. In Yang et al. (2013), the synchronization for a class of coupled neural networks with mixed probabilistic time-varying delays and random coupling strengths was investigated by applying integral inequalities and Lyapunov functional method. In Wu et al. (2012), the existence and the global exponential stability for delayed impulsive cellular neural networks was studied by the Lyapunov functions and the Razumikhin technique. In Alimi et al. (2019), the finite-time and the fixed-time synchronization of inertial neural networks with proportional delays is discussed by using analytical techniques and Lyapunov functional.

On the other hand, the research of complex-valued neural networks and quaternion-valued neural networks has achieved significant success thanks to the perseverant efforts. Recently, various models of complex value and quaternion value neural networks are proposed and actively studied (see Hu and Wang 2012; Zhang et al. 2017; Aouiti et al. 2020; Zhang et al. 2013; Aouiti and Bessifi 2020; Tu et al. 2019a, b and the references cited therein). In addition, time delays, particularly time-varying delays are an essential characteristic of signal transmission between neurons, and the main cause of instability and oscillation. It is, therefore, necessary to study the stability of neural networks with time delays (Rakkiyappan et al. 2015; Xu et al. 2020; Xu and Aouiti 2020). Furthermore, due to the parallel pathways of a variety of axon sizes and lengths neural networks generally have a spatial nature, it is desired to model them by using distributed delays. Therefore, time-varying delays and distributed delays are an important parameter associated with neural networks (Aouiti et al. 2018; Achouri et al. 2020).

Clifford algebra was discovered by the British mathematician William K. Clifford (Clifford 1878). Clifford’s algebra is a generalization of real number, complex number and quaternion, which has significant and extensive application areas. It has been used in various domains including image and signal processing, neural computing, control problems, computer and robot vision, neural networks and other fields thanks to its powerful and practical framework for the solution and representation of a geometrical problem (Hitzer et al. 2013; Rivera-Rovelo and Bayro-Corrochano 2006; Kuroe 2011; Dorst et al. 2007; Li and Xiang 2019). As an example, in the world of neural networks, Pearson first suggested a Clifford value neural network in Pearson and Bisset (1992), which is represented by Clifford’s value differential equations. Later, Buchholz (2005) concluded that neural networks with Clifford value have greater advantages compared to neural networks with real value. In recent years, research on neural networks with Clifford value has become an active field research and received more attention. Because Clifford’s number multiplication does not satisfy the commutative law, therefore, it has brought great difficulties to the studies of neural networks with Clifford value. Consequently, the existing studies on the existence and the global exponential stability of the equilibrium point of neural networks with Clifford value are still very rare. Only a few publications have been published to date on the stability of the equilibrium point of Clifford-valued neural networks (Liu et al. 2016; Zhu and Sun 2016; Boonsatit et al. 2021; Rajchakit et al. 2021a, b, c, d, e). In Liu et al. (2016), the existence, the uniqueness and global asymptotic stability for the equilibrium for a class of Clifford-valued recurrent neural networks with time delays was investigated by applying differential inequality techniques and linear matrix inequality (LMI) technique. In Zhu and Sun (2016), authors investigated global exponential stability of Clifford-valued recurrent neural networks by Brouwer’s fixed point theorem and inequality technique. It should be noted that time-varying delays and distributed delays are not taken into account in Zhu and Sun (2016). On the other hand, time delays in Liu et al. (2016) are constant, which means that the outcomes therein are invalid to investigate Clifford-valued recurrent neural networks with time-varying delays and distributed delays. In Boonsatit et al. (2021), finite-/fixed-time synchronization for Clifford-valued recurrent neural networks with time-varying delays were studied by Lyapunov-Krasovskii functional and computational techniques. In Rajchakit et al. (2021a, 2021b), global exponential stability of Clifford-valued recurrent neural networks with time delays had been studied by using Lyapunov stability theory, linear matrix inequality techniques and analytical techniques. Global asymptotic stability and global exponential stability for delayed Clifford-valued neutral-type neural network models were investigated by employing the homeomorphism theory, linear matrix inequality and Lyapunov functional methods in Rajchakit et al. (2021e).

To the best of our knowledge, no major investigation on the global exponential stability for Clifford-valued recurrent neural networks involving time-varying delays and distributed delays (mixed time delays) have been carried out. Inspired by the above discussion and analysis, the main goal of this paper is to investigate the existence and the global exponential stability of the equilibrium point of Clifford-valued recurrent neural networks with mixed time delays. The existence of the equilibrium of the system is obtained using the fixed point theorem. In addition, by constructing appropriate delay differential inequality, some sufficient conditions for the global exponential stability of equilibrium are proved. Finally, an example is given to illustrate the effectiveness of the obtained results.

All the rest of the paper is organized into the following structure. In Sect. 2, some preliminaries are introduced that will be used later. Model descriptions is exhibited in Sect. 3. In Sect. 4, based on the Brouwer fixed point and inequality technique, we prove the existence of the equilibrium point and the stability of the addressed model. In Sect. 5, an example is given to show the effectiveness of the obtained results. In Sect. 6, conclusions is provided.

2 Notations and preliminaries

The following section introduces notations, definitions and preliminary facts that are used throughout this work (see Buchholz 2005).

For convenience, let \({\mathbb {R}}\) and \({\mathbb {A}}\) denote the real space and the real clifford space, respectively. Note by \({\overline{x}}\) the conjugate of the clifford number x. We define \({\mathbb {A}}\) is as the clifford which equipped with m generators algebra that has equipped over the real number \({\mathbb {R}}\). m the multiplicative generators \(e_1,e_2,\ldots ,e_m\) are named clifford generators that satisfy the relations

$$\begin{aligned} \left\{ \begin{array}{lr} e_{i} e_{j}+e_{j} e_{i}=0 &{} i \ne j \\ \\ e_{i}^{2}=-1 &{} i=1,2, \ldots , m. \end{array}\right. \end{aligned}$$

To keep it simple, if an element is the product of more than one Clifford generator, we write its clues together. As an example \(e_1e_2=e{12}\), \(e_{2}e_3=e_{23}\) and \(e_8e_6e_4e_2=e_{8642}\). So, A has its base in the following

$$\begin{aligned} \left\{ e_{A}=e_{h_{1} h_{2} \ldots h_{r}}, 1 \le h_{1}<h_{2}<\cdots <h_{r} \le m\right\} . \end{aligned}$$
(1)

Consequently, the real Clifford’s algebra consists of elements such as \(x=\sum \nolimits _{A}x^Ae_A\), in which \(x^A\in {\mathbb {R}}\) is a real number. If \(A=\emptyset \), therefore \(e_{\emptyset }\) can be described as \(e_0\) and \(x_0\) is the coefficient of the \(e_0\) component, i.e., \(x_0\) is real part of x, for more detail see Buchholz (2005). It can be concluded from these properties that

$$\begin{aligned} {\text {dim}}{\mathbb {A}}=\sum _{k=0}^{m}\left( \begin{array}{l} m \\ k \end{array}\right) =\sum _{k=0}^{m} \frac{m !}{k !(m-k) !}=2^{m}. \end{aligned}$$

Definition 1

(Buchholz 2005) For an arbitrary base vector, the conjugate is given:

$$\begin{aligned} {\bar{e}}_{A}=(-1)^{\frac{r(A)(r(A)+1)}{2}} e_{A}. \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{array}{c} e_{A} {\bar{e}}_{A}={\bar{e}}_{A} e_{A}=1, e_{A} {\bar{e}}_{B}=e_{B} {\bar{e}}_{A}(-1)^{\frac{p(p+1)}{2}}, \quad p=|r(B)-r(A)| \end{array} \end{aligned}$$

Definition 2

(Buchholz 2005) The inner product in the clifford domain is defined as:

$$\begin{aligned} (x, y):=[x {\bar{y}}]_{0}=\sum _{A} x^{A} y^{A}, \quad \forall x, y \in {\mathbb {A}}, \end{aligned}$$

in which \([\cdot ]_0\) indicates the coefficient of its \(e_0\)-component. The norm on \({\mathbb {A}}\) is correspondingly described as following

$$\begin{aligned} |x|_0=\sqrt{(x,x)}. \end{aligned}$$

Definition 3

(Buchholz 2005)

  1. 1.

    The derivative for \(x(t)=\sum \nolimits _{A}x^A(t)e_A\) is given as follows:

    $$\begin{aligned} {\dot{x}}(t)=\displaystyle \sum _{A}{\dot{x}}^A(t)e_A \end{aligned}$$
  2. 2.

    The integral for \(x(t)=\sum \nolimits _{A}x^A(t)e_A\) is given as follows:

    $$\begin{aligned} \displaystyle \int _{0}^{t}{\dot{x}}(s)ds=\displaystyle \int _{0}^{t}\displaystyle \sum _{A}{\dot{x}}^A(s)e_Ads=\left( \displaystyle \sum _{A}\displaystyle \int _{0}^{t}{\dot{x}}^A(s)ds\right) e_A. \end{aligned}$$

Proposition 1

(Buchholz 2005) Let \(x_1\), \(x_2\), \(x_3\), \(c\in {\mathbb {A}}\). Therefore,

  1. 1.

    \(x_1(x_2+x_3)=x_1x_2+x_1x_3\),

  2. 2.

    \((x_1+x_2)x_3=x_1x_3+x_2x_3\),

  3. 3.

    \(x_1x_2\ne x_2x_1\),

  4. 4.

    \(\lambda x_1=x_1\lambda \) if and only if for every \(\lambda \in {\mathbb {R}}\),

  5. 5.

    \(|x_1+x_2|_0\le |x_1|_0+|x_2|_0\),

  6. 6.

    \(|x_1x_2|_0\le |x_1|_0|x_2|_0\),

  7. 7.

    \(\displaystyle \int _{0}^{t}cx_1(s)ds=c\displaystyle \int _{0}^{t}x_1(s)ds\).

Lemma 1

(Zhu and Sun 2016) Let x(t), \(f(t)\in {\mathbb {A}}\), be two clifford-valued functions, where \(t>0\) and f(t) is a nonlinear function. In addition, let \(\varsigma \in {\mathbb {A}}\), \(\sigma \in {\mathbb {R}}\), if \({\dot{x}}+\sigma x(t)=f(t)\), therefore, \(x(t)=\varsigma e^{-\sigma t}+e^{-\sigma t}\displaystyle \int e^{\sigma t}f(t)dt\).

Lemma 2

(Minc 1988) Let \(M\ge 0\) be a square matrix. If \(\rho (A)<1\), therefore \((I_d-A)\ge 0\), where \(\rho (A)\) is the spectral radius of A and \(I_d\) indicates the identity matrix.

Lemma 3

(Minc 1988) If \(M=(m)_{n\times n}\) is M-matrix, therefore, the matrix MC(CM) is also M-matrix, in which \(C=diag(c_1,\ldots ,c_n)>0.\)

Lemma 4

(Shao 2009) Let \(M=(m)_{n\times n}\ge 0\) be a matrix, \(L=diag(l_1,\ldots ,l_n)0\) (\(l_i>,\;i=1,\ldots ,n\)) and \(C=diag(c_1,\ldots ,c_n)\) (\(c_i>,\;i=1,\ldots ,n\)). The matrix \(CL^{-1}-|M|\) is M-matrix if and only if \(\rho (C^{-1}|A|L)<1.\)

3 Setup of the problem

In this paper, we consider the following Clifford-valued recurrent neural network with mixed time delays:

$$\begin{aligned} \frac{dx_i(t)}{dt}= & {} -a_ix_i(t)+\displaystyle \sum _{j=1}^{n}b_{ij}f_j(x_j(t))+\displaystyle \sum _{j=1}^{n}c_{ij}f_j(x_j(t-\tau _j(t)))\nonumber \\{} & {} +\displaystyle \sum _{j=1}^{n}d_{ij}\int _{-\infty }^{t}K_{ij}(t-s)f_j(x_j(s))ds+I_i, \end{aligned}$$
(2)

where, \(i,j=1,2\ldots ,n\), n is the number of neuros, \(x_i(\cdot )\in {\mathbb {A}}\) denotes the state of neuro i, \(a_i>0\) is a real denotes the self-feedback connection weight, \(b_{ij}\), \(c_{ij}\), \(d_{ij}\in {\mathbb {A}}\) indicates the connection weights, \(f_j(\cdot )\in {\mathbb {A}}\) is the activation non-linear function, \(\tau _j(\cdot )\) is the transmission delays that verifies \(0\le \tau _j(t)\le \tau =\max _{1\le j\le n}\sup _{t\ge 0}\tau _j(t),\) \(K_{ij}(\cdot )\) is the kernel delay, \(I_i\in {\mathbb {A}}\) is external constant input.

The initial conditions of system (2) are

$$\begin{aligned} x_i(0)=\varphi (s),\; s\in (-\infty ,0]. \end{aligned}$$

For convenience, the equation (2) can be expressed in the vector form

$$\begin{aligned} {\dot{x}}(t)=-Ax(t)+Bf(x(t))+Cf(x(t-\tau (t)))+D\displaystyle \int _{-\infty }^{t}K(t-s)f(x(t))+I, \end{aligned}$$
(3)

where \(x=(x_1,\ldots ,x_n)^T\in {\mathbb {A}}^n\) is the state vector, \(A=diag(a_1,\ldots ,a_n)\in {\mathbb {R}}^{n\times n}\), \(B=(b_{ij})_{n\times n}\in {\mathbb {A}}^{n\times n}\), \(C=(c_{ij})_{n\times n}\in {\mathbb {A}}^{n\times n}\), \(D=(d_{ij})_{n\times n}\in {\mathbb {A}}^{n\times n}\), \(f(\cdot )=(f_1(\cdot ),\ldots ,f_n(\cdot ))^T\), \(I=(I_1,\ldots ,I_n)^T\), \(K(\cdot )=(k_{ij}(\cdot ))_{n\times n}\).

Remark 1

In this paper, the proposed system model is more general than the system model proposed in previous works (Zhu and Sun 2016; Rajchakit et al. 2021a). If the distributed time-varying delays is not considered, that is to make \(d_{ij}=0,\;\;i=j=1,2,\ldots ,n\), (2) becomes into the following system

$$\begin{aligned} \frac{dx_i(t)}{dt}=-a_ix_i(t)+\displaystyle \sum _{j=1}^{n}b_{ij}f_j(x_j(t))+\displaystyle \sum _{j=1}^{n}c_{ij}f_j(x_j(t-\tau _j(t)))+ I_i, \end{aligned}$$

which was studied in Rajchakit et al. (2021a), and if \(c_{ij}=d_{ij}=0,\;\;i=j=1,2,\ldots ,n\), (2) becomes into the following clifford-valued recurrent neural network without delays

$$\begin{aligned} \frac{dx_i(t)}{dt}= & {} -a_ix_i(t)+\displaystyle \sum _{j=1}^{n}b_{ij}f_j(x_j(t))+I_i, \end{aligned}$$

which was studied in Zhu and Sun (2016). Thus, it can be concluded that the model considered in this paper is more general than the ones in Zhu and Sun (2016) and Rajchakit et al. (2021a).

In this paper, the following hypotheses should be added:

\((H_1)\):

The activation functions \(f_j(x)\) satisfy the Lipschitz condition regarding to the n dimensional clifford vector. That is to say, there exist constants \(L^f_j>0\) such that \(|f_j(x)-f_j(y)|_0\le L^f_j|x-y|_0\) for all \(x,y\in {\mathbb {A}}\) and \(j=1,2,\ldots ,n\).

\((H_2)\):

The delay kernels \(K_{ij}(.):[0,+\infty )\rightarrow [0,+\infty )\), \(i,j=1,2,\ldots ,n\) satisfying

$$\begin{aligned} \displaystyle \int _{0}^{+\infty }K_{ij}(s)ds=1,\;\;\displaystyle \int _{0}^{+\infty }e^{\lambda s}K_{ij}(s)ds=k_{ij}<+\infty . \end{aligned}$$

where \(\lambda \) is positive number.

4 Main results

4.1 Existence and uniqueness of equilibrium point

We will study the existence and uniqueness of the equilibrium point of the model (2) in this subsection.

Theorem 1

Suppose that the system (3) satisfies (\(H_1\))–(\(H_2\)) and suppose that

$$\begin{aligned} \rho \left( A^{-1}(|B|_0+|C|_0+|D|_0)L^f\right) <1, \end{aligned}$$

then the system (3) has a unique equilibrium point \(x^*\in {\mathbb {A}}^n\), where \(A=diag(a_1,\ldots ,a_n)^T\), \(|B|_0=(|b_{ij}|_0)_{n\times n}\), \(|C|_0=(|c_{ij}|_0)_{n\times n}\), \(L^f=diag(L^f_1,\ldots ,L^f_n)^T\).

Proof

The equilibrium point \(x^*=(x^*_1,\ldots ,x^*_n)^T\) is obviously subjected to clifford algebra equation:

$$\begin{aligned} x_{i}=\frac{1}{a_{i}} \sum _{j=1}^{n} b_{i j} f_{j}\left( x_{j}\right) +\frac{1}{a_{i}} \sum _{j=1}^{n} c_{i j} f_{j}\left( x_{j}\right) +\frac{I_{i}}{a_{i}}, \quad (i=1,2, \ldots , n) \end{aligned}$$
(4)

Define

$$\begin{aligned} \varLambda _i(x)=(\varLambda _1(x),\ldots ,\varLambda _n(x))\in {\mathbb {A}}^n, \end{aligned}$$

where

$$\begin{aligned} \varLambda _i(x)=\frac{1}{a_{i}} \sum _{j=1}^{n} b_{i j} f_{j}\left( x_{j}\right) +\frac{1}{a_{i}} \sum _{j=1}^{n} c_{i j} f_{j}\left( x_{j}\right) +\frac{1}{a_{i}} \sum _{j=1}^{n} d_{i j} f_{j}\left( x_{j}\right) +\frac{I_{i}}{a_{i}}. \end{aligned}$$

Therefore,

$$\begin{aligned} |\varLambda _i(x)|_0\le & {} \frac{1}{a_{i}} \left| \sum _{j=1}^{n} b_{i j} f_{j}\left( x_{j}\right) \right| _0+\frac{1}{a_{i}} \left| \sum _{j=1}^{n} c_{i j} f_{j}\left( x_{j}\right) \right| _0+\frac{1}{a_{i}} \left| \sum _{j=1}^{n} d_{i j} f_{j}\left( x_{j}\right) \right| _0+\left| \frac{I_{i}}{a_{i}}\right| _0\nonumber \\\le & {} \frac{1}{a_{i}} \sum _{j=1}^{n}\left| b_{i j}\right| _0 \left| f_{j}\left( x_{j}\right) \right| _0+\frac{1}{a_{i}} \sum _{j=1}^{n} \left| c_{i j}\right| _0 \left| f_{j}\left( x_{j}\right) \right| _0\nonumber \\{} & {} +\,\frac{1}{a_{i}} \sum _{j=1}^{n} \left| d_{i j}\right| _0 \left| f_{j}\left( x_{j}\right) \right| _0 +\left| \frac{I_{i}}{a_{i}}\right| _0\nonumber \\\le & {} \frac{1}{a_{i}} \sum _{j=1}^{n}\left| b_{i j}\right| _0 \left| f_{j}\left( x_{j}\right) -f_j(0)+f_j(0)\right| _0\nonumber \\{} & {} +\,\frac{1}{a_{i}} \sum _{j=1}^{n} \left| c_{i j}\right| _0 \left| f_{j}\left( x_{j}\right) -f_j(0) +f_j(0)\right| _0\nonumber \\{} & {} +\,\frac{1}{a_{i}} \sum _{j=1}^{n} \left| d_{i j}\right| _0 \left| f_{j}\left( x_{j}\right) -f_j(0)+f_j(0)\right| _0+\left| \frac{I_{i}}{a_{i}}\right| _0\nonumber \\\le & {} \frac{1}{a_{i}} \sum _{j=1}^{n}\left| b_{i j}\right| _0 \left| f_{j}\left( x_{j}\right) -f_j(0)\right| _0+\frac{1}{a_{i}} \sum _{j=1}^{n}\left| b_{i j}\right| _0\left| f_j(0)\right| _0\nonumber \\{} & {} +\,\frac{1}{a_{i}} \sum _{j=1}^{n} \left| c_{i j}\right| _0 \left| f_{j}\left( x_{j}\right) -f_j(0)\right| _0\nonumber \\{} & {} +\,\frac{1}{a_{i}} \sum _{j=1}^{n} \left| c_{i j}\right| _0 \left| f_j(0)\right| _0+\frac{1}{a_{i}} \sum _{j=1}^{n} \left| d_{i j}\right| _0 \left| f_{j}\left( x_{j}\right) -f_j(0)\right| _0\nonumber \\{} & {} +\,\frac{1}{a_{i}} \sum _{j=1}^{n} \left| d_{i j}\right| _0 \left| f_j(0)\right| _0 +\left| \frac{I_{i}}{a_{i}}\right| _0\nonumber \\\le & {} \frac{1}{a_{i}} \sum _{j=1}^{n}\left| b_{i j}\right| _0 L^f_j\left| x_{j}\right| _0+\frac{1}{a_{i}} \sum _{j=1}^{n}\left| b_{i j}\right| _0\left| f_j(0)\right| _0+\frac{1}{a_{i}} \sum _{j=1}^{n} \left| c_{i j}\right| _0 L^f_j\left| x_{j}\right| _0\nonumber \\{} & {} +\,\frac{1}{a_{i}} \sum _{j=1}^{n} \left| c_{i j}\right| _0 \left| f_j(0)\right| _0\nonumber \\{} & {} +\,\frac{1}{a_{i}} \sum _{j=1}^{n} \left| d_{i j}\right| _0 L^f_j\left| x_{j}\right| _0+\frac{1}{a_{i}} \sum _{j=1}^{n} \left| d_{i j}\right| _0 \left| f_j(0)\right| _0+\left| \frac{I_{i}}{a_{i}}\right| _0\nonumber \\= & {} \frac{1}{a_{i}} \sum _{j=1}^{n}\left| b_{i j}\right| _0 L^f_j\left| x_{j}\right| _0+\frac{1}{a_{i}} \sum _{j=1}^{n} \left| c_{i j}\right| _0 L^f_j\left| x_{j}\right| _0+\frac{1}{a_{i}} \sum _{j=1}^{n} \left| d_{i j}\right| _0 L^f_j\left| x_{j}\right| _0+\gamma _i,\nonumber \\ \end{aligned}$$
(5)

where

$$\begin{aligned} \gamma _i= & {} \frac{1}{a_{i}} \displaystyle \sum _{j=1}^{n}\left| b_{i j}\right| _0\left| f_j(0)\right| _0+\frac{1}{a_{i}} \sum _{j=1}^{n} \left| c_{i j}\right| _0 \left| f_j(0)\right| _0+\frac{1}{a_{i}} \sum _{j=1}^{n} \left| d_{i j}\right| _0 \left| f_j(0)\right| _0\\{} & {} +\,\left| \frac{I_{i}}{a_{i}}\right| _0\ge 0,\;\;\text {for}\;i=1,\ldots ,n. \end{aligned}$$

Define

$$\begin{aligned} \varLambda (x)=(\varLambda _1(x),\ldots ,\varLambda _n(x))^T,\;|\varLambda (x)|_0=(|\varLambda _1(x)|_0,\ldots ,|\varLambda _n(x)|_0)^T\\ \gamma =(\gamma _1,\ldots ,\gamma _n)^T,\;x=(x_1,\ldots ,x_n)^T,\;|x|_0=(|x_1|_0,\ldots ,|x_n|_0)^T. \end{aligned}$$

Then the vector form is rewritten in the following form:

$$\begin{aligned} |\varLambda (x)|_0\le A^{-1}|B|_0L^f|x|_0+A^{-1}|C|_0L^f|x|_0+A^{-1}|D|_0L^f|x|_0+\gamma . \end{aligned}$$

Based on Lemma 3 and Lemma 4, since \(A^{-1}|B|_0L^f+A^{-1}|C|_0L^f+A^{-1}|D|_0L^f\) is non-negative matrix and \(\rho \left( A^{-1}|B|_0L^f+A^{-1}|C|_0L^f+A^{-1}|D|_0L^f\right) <1\), then \(I_d-\left( A^{-1}|B|_0L^f+A^{-1}|C|_0L^f+A^{-1}|D|_0L^f\right) \) is an M-matrix. Therefore, there exists vector \(\xi =(\xi _1,\ldots ,\xi _n)^T\) such that

$$\begin{aligned} \left( I_d-\left( A^{-1}|B|_0L^f+A^{-1}|C|_0L^f+A^{-1}|D|_0L^f\right) \right) \xi >\gamma . \end{aligned}$$

Hence, we have

$$\begin{aligned} |\varLambda (x)|_0\le & {} A^{-1}|B|_0L^f|x|_0+A^{-1}|C|_0L^f|x|_0+A^{-1}|D|_0L^f|x|_0+\gamma \\< & {} A^{-1}|B|_0L^f|x|_0+A^{-1}|C|_0L^f|x|_0+\bigg (I_d-\bigg (A^{-1}|B|_0L^f+A^{-1}|C|_0L^f\\{} & {} +\, A^{-1}|D|_0L^f\bigg )\bigg )\xi . \end{aligned}$$

Define \(\varOmega =\{x\in {\mathbb {A}}^n,\;|x|_0<\xi \}\), for any \(x\in {\mathbb {A}}^n\), we get \(|\varLambda (x)|_0\le \xi .\) Thus, the continuous operator \(\varLambda \) maps compact and convex set \(\varOmega \) into itself. Using Brouwer’s fixed point theorem, \(\varLambda \) has a fixed point \(x^*=(x^*_1,\ldots ,x^*_n)^T\) such as \(\varLambda (x^*)=x^*,\) which is the equilibrium point of system (3). Therefore, system (2) has one unique equilibrium point. \(\square \)

4.2 Global exponential stability

Some sufficient conditions to ensure the global exponential stability of the system (2) will be established in this subsection.

Theorem 2

Suppose that the spectral radius of the matrix \((A-\lambda I_d)^{-1}\big (|B|_0L^f+e^{\lambda \tau }|C|_0L^f+|J|_0L^f\big )\) is less than 1, that means \(\rho \bigg ((A-\lambda I_d)^{-1}\big (|B|_0L^f+e^{\lambda \tau }|C|_0L^f+|J|_0L^f\big )\bigg )<1\), in which \(|J|_0=(k_{ij}|d_{ij}|_0)_{n\times n}\) and \(\lambda >0\) is a small real constant, then the equilibrium point of system (3) is globally exponentially stable.

Proof

According to Lemma 1, the model (2) is transformed into the following equality:

$$\begin{aligned} w_i(t)= & {} w_i(0)e^{-a_it}+e^{-a_it}\displaystyle \sum _{j=1}^{n}b_{ij}\displaystyle \int _{0}^{t}e^{a_is}g_j(w_j(s))ds\nonumber \\{} & {} +\, e^{-a_it}\displaystyle \sum _{j=1}^{n}c_{ij}\displaystyle \int _{0}^{t}e^{a_is}g_j(w_j(s-\tau _j(s)))ds\end{aligned}$$
(6)
$$\begin{aligned}{} & {} +\, e^{-a_it}\displaystyle \sum _{j=1}^{n}d_{ij}\displaystyle \int _{0}^{t}e^{a_is}\int _{-\infty }^{t}K_{ij}(s-m)g_j(w_j(m))dmds, \end{aligned}$$
(7)

therefore

$$\begin{aligned} |w_i(t)|_0\le & {} |w_i(0)|_0e^{-a_it}+e^{-a_it}\displaystyle \sum _{j=1}^{n}|b_{ij}|_0\displaystyle \int _{0}^{t}e^{a_is}|g_j(w_j(s))|_0ds\nonumber \\{} & {} +\,e^{-a_it}\displaystyle \sum _{j=1}^{n}|c_{ij}|_0\displaystyle \int _{0}^{t}e^{a_is}|g_j(x_j(s-\tau _j(s)))|_0ds\end{aligned}$$
(8)
$$\begin{aligned}{} & {} +\,e^{-a_it}\displaystyle \sum _{j=1}^{n}|d_{ij}|_0\displaystyle \int _{0}^{t}e^{a_is}\int _{-\infty }^{t}K_{ij}(s-m)g_j(x_j(m))dmds\nonumber \\\le & {} |w_i(0)|_0e^{-a_it}+e^{-a_it}\displaystyle \sum _{j=1}^{n}|b_{ij}|_0L^f_j\displaystyle \int _{0}^{t}e^{a_is}|w_j(s)|_0ds\nonumber \\{} & {} +\,e^{-a_it}\displaystyle \sum _{j=1}^{n}|c_{ij}|_0L^f_j\displaystyle \int _{0}^{t}e^{a_is}|w_j(s-\tau _j(s))|_0ds\nonumber \\{} & {} +\,e^{-a_it}\displaystyle \sum _{j=1}^{n}|d_{ij}|_0L^f_j\displaystyle \int _{0}^{t}e^{a_is}\int _{-\infty }^{t}K_{ij}(s-m)w_j(m)dmds. \end{aligned}$$
(9)

Define

$$\begin{aligned} \theta _i(t)= & {} |w_i(0)|_0e^{-a_it}+e^{-a_it}\displaystyle \sum _{j=1}^{n}|b_{ij}|_0L^f_j\displaystyle \int _{0}^{t}e^{a_is}|w_j(s)|_0ds\nonumber \\{} & {} +\,e^{-a_it}\displaystyle \sum _{j=1}^{n}|c_{ij}|_0L^f_j\displaystyle \int _{0}^{t}e^{a_is}|w_j(s-\tau _j(s))|_0ds\nonumber \\{} & {} +\,e^{-a_it}\displaystyle \sum _{j=1}^{n}|d_{ij}|_0L^f_j\displaystyle \int _{0}^{t}e^{a_is}\int _{-\infty }^{t}K_{ij}(s-m)w_j(m)dmds. \end{aligned}$$

therefore, we get

$$\begin{aligned} |w_i(t)|_0\le & {} \theta _i(t) \end{aligned}$$

By calculating the derivative of \(\theta _i(\cdot )\), we obtain

$$\begin{aligned} {\dot{\theta }}_i(t)= & {} -a_i\theta _i(t)+\displaystyle \sum _{j=1}^{n}|b_{ij}|_0L^f_j|w_j(t)|_0dt\nonumber \\{} & {} +\,\displaystyle \sum _{j=1}^{n}|c_{ij}|_0L^f_j|w_j(t-\tau _j(t))|_0\nonumber \\{} & {} +\,\displaystyle \sum _{j=1}^{n}|d_{ij}|_0L^f_j\int _{-\infty }^{t}K_{ij}(t-m)w_j(m)dm. \end{aligned}$$

Let

$$\begin{aligned} q_i(t)= & {} e^{\lambda t}\theta _i(t),\;\;0<\lambda <\min \{a_1,a_2,\ldots ,a_n\}, \end{aligned}$$

then, we have

$$\begin{aligned} {\dot{q}}_i(t)\le & {} (\lambda -a_i)q_i(t)+e^{\lambda t}\displaystyle \sum _{j=1}^{n}|b_{ij}|_0L^f_j|w_j(t)|_0\nonumber \\{} & {} +\,e^{\lambda t}\displaystyle \sum _{j=1}^{n}|c_{ij}|_0L^f_j|w_j(t-\tau _j(t))|_0\nonumber \\{} & {} +\,e^{\lambda t}\displaystyle \sum _{j=1}^{n}|d_{ij}|_0L^f_j\int _{-\infty }^{t}K_{ij}(t-m)w_j(m)dm. \end{aligned}$$

Let \({\widetilde{q}}_j(t)=\displaystyle \max _{-\infty \le u\le t}q_j(u)\), we obtain

$$\begin{aligned} {\dot{q}}_i(t)\le & {} (\lambda -a_i)q_i(t)+\displaystyle \sum _{j=1}^{n}|b_{ij}|_0L^f_j{\widetilde{q}}_j(t)\nonumber \\{} & {} +\,\displaystyle \sum _{j=1}^{n}e^{\lambda \tau _{j}(t)}|c_{ij}|_0L^f_j{\widetilde{q}}_j(t)\nonumber \\{} & {} +\,\displaystyle \sum _{j=1}^{n}|d_{ij}|_0L^f_j{\widetilde{q}}_j(t)\int _{-\infty }^{t}e^{\lambda (t-m)}K_{ij}(t-m)dm. \end{aligned}$$

On the other hand,

$$\begin{aligned} {\dot{q}}_i(u)-(\lambda -a_i)q_i(u)\le & {} \displaystyle \sum _{j=1}^{n}|b_{ij}|_0L^f_j{\widetilde{q}}_j(u)+\displaystyle \sum _{j=1}^{n}e^{\lambda \tau _{j}(u)}|c_{ij}|_0L^f_j{\widetilde{q}}_j(u)\nonumber \\{} & {} +\,\displaystyle \sum _{j=1}^{n}|d_{ij}|_0L^f_j{\widetilde{q}}_j(u)k_{ij}. \end{aligned}$$

By integrating both sides from 0 to t, the following results are obtained

$$\begin{aligned} q_i(t)\le & {} q_i(0)e^{(\lambda -a_i)t}+\displaystyle \sum _{j=1}^{n}|b_{ij}|_0L^f_j{\widetilde{q}}_j(t)\displaystyle \int _{0}^{t}e^{(\lambda -a_i)(t-u)}du\\{} & {} +\,\displaystyle \sum _{j=1}^{n}e^{\lambda \tau _{j}(t)}|c_{ij}|_0L^f_j{\widetilde{q}}_j(t)\displaystyle \int _{0}^{t}e^{(\lambda -a_i)(t-u)}du\\{} & {} +\,\displaystyle \sum _{j=1}^{n}|d_{ij}|_0L^f_j{\widetilde{q}}_j(t)k_{ij}\displaystyle \int _{0}^{t}e^{(\lambda -a_i)(t-u)}du. \end{aligned}$$

In addition, note that

$$\begin{aligned} \displaystyle \int _{0}^{t}e^{(\lambda -a_i)(t-u)}du\le & {} \frac{1}{a_i-\lambda }, \end{aligned}$$

therefore

$$\begin{aligned} q_i(t)\le & {} q_i(0)+\frac{1}{a_i-\lambda }\displaystyle \sum _{j=1}^{n}|b_{ij}|_0L^f_j{\widetilde{q}}_j(t)+\frac{1}{a_i-\lambda }\displaystyle \sum _{j=1}^{n}e^{\lambda \tau _{j}(t)}|c_{ij}|_0L^f_j{\widetilde{q}}_j(t)\end{aligned}$$
(10)
$$\begin{aligned}{} & {} +\,\frac{1}{a_i-\lambda }\displaystyle \sum _{j=1}^{n}|d_{ij}|_0L^f_j{\widetilde{q}}_j(t)k_{ij}\end{aligned}$$
(11)
$$\begin{aligned}\le & {} q_i(0)+\frac{1}{a_i-\lambda }\displaystyle \sum _{j=1}^{n}L^f_j\bigg (|b_{ij}|_0+e^{\lambda \tau }|c_{ij}|_0+|d_{ij}|_0k_{ij}\bigg ){\widetilde{q}}_j(t) \end{aligned}$$
(12)

Define

$$\begin{aligned} Q(t)&=(q_1(t),\ldots ,q_n(t))^T,\\ {\widetilde{Q}}(t)&=({\widetilde{q}}_1(t),\ldots ,{\widetilde{q}}_n(t))^T,\\ q(0)&=(q_1(0),\ldots ,q_n(0))^T,\\ \varTheta (t)&=(\theta _1(t),\ldots ,\theta _n(t))^T,\\ w(t)&=(w_1(t),\ldots ,w_n)^T, \end{aligned}$$

then, Eq. (10) can be written as the following vector form:

$$\begin{aligned} Q(t)\le q(0)+(A-\lambda I_d)^{-1}\bigg (|B|_0L^f+e^{\lambda \tau }|C|_0L^f+|J|_0L^f\bigg ){\widetilde{Q}}(t). \end{aligned}$$

It follows that

$$\begin{aligned} {\widetilde{Q}}(t)\le q(0)+(A-\lambda I_d)^{-1}\bigg (|B|_0L^f+e^{\lambda \tau }|C|_0L^f+|J|_0L^f\bigg ){\widetilde{Q}}(t), \end{aligned}$$

then

$$\begin{aligned} \bigg [I_d-(A-\lambda I_d)^{-1}\bigg (|B|_0L^f+e^{\lambda \tau }|C|_0L^f+|J|_0L^f\bigg )\bigg ]{\widetilde{Q}}(t)\le q(0). \end{aligned}$$
(13)

Since \(\rho \bigg ((A-\lambda I_d)^{-1}\big (|B|_0L^f+e^{\lambda \tau }|C|_0L^f+|J|_0L^f\big )\bigg )\), \((A-\lambda I_d)^{-1}\big (|B|_0L^f+e^{\lambda \tau }|C|_0L^f+|J|_0L^f\big )\ge 0\), therefore, using Lemma 2, we obtain

$$\begin{aligned} \left( I_d-(A-\lambda I_d)^{-1}\bigg (|B|_0L^f+e^{\lambda \tau }|C|_0L^f+|J|_0L^f\bigg )\right) ^{-1}\ge 0, \end{aligned}$$

by using (13), we have

$$\begin{aligned} {\widetilde{Q}}(t)\le \left( I_d-(A-\lambda I_d)^{-1}\bigg (|B|_0L^f+e^{\lambda \tau }|C|_0L^f+|J|_0L^f\bigg )\right) ^{-1}|q(0)|_0. \end{aligned}$$
(14)

Because

$$\begin{aligned} e^{\lambda t}|w(t)|_0\le e^{\lambda t}\varTheta (t)=Q(t)\le {\widetilde{Q}}(t), \end{aligned}$$
(15)

from (14) and (15), we can obtain the following result:

$$\begin{aligned} |w(t)|_0\le & {} e^{-\lambda t}{\widetilde{Q}}(t)\\\le & {} \bigg (I_d-(A-\lambda I_d)^{-1}\big (|B|_0L^f+e^{\lambda \tau }|C|_0L^f+|J|_0L^f\big )\bigg )^{-1}|q(0)|_0e^{-\lambda t}. \end{aligned}$$

Hence, model (3) is globally exponentially stable. This completes the proof. \(\square \)

Remark 2

Recently, the authors in Zhu and Sun (2016) provided sufficient conditions for the existence and global exponential stability of Clifford-valued recurrent neural networks without delays. The authors in Liu et al. (2016) studied the existence and the stability of Clifford-valued neural networks with a constant delay. At present, our results in Theorem 1 and Theorem 2 complement the aforementioned work.

Remark 3

In recent years, it has been found that complex-valued and quaternion-valued neural networks have more advantages than real-valued neural networks in some practical applications. Consequently, there have been many papers on complex-valued and quaternion-valued neural networks (Hu and Wang 2012; Zhang et al. 2017; Aouiti et al. 2020; Zhang et al. 2013; Aouiti and Bessifi 2020; Tu et al. 2019a, b). The above result can be easily applied to real-valued, complex-valued and quaternion-valued recurrent neural networks. The Clifford-valued neural network model (2) includes real-valued \((m = 0)\), complex-valued \((m = 1)\) and quaternion-valued \((m = 2)\) neural network models as its special cases, which has important and extensive application fields.

Remark 4

In Boonsatit et al. (2021) and Rajchakit et al. (2021a), some authors have achieved the stability or synchronization of neural networks using the Lyapunov function method, and the decomposition method. In contrast to the method in the above papers, however, we obtain the global exponential stability of Clifford-valued neural networks by using the non-decomposition method, and the proof by inequality technique and matrix theory and its spectral theory. Hence, the aim of this paper is to investigate the global exponential stability of Clifford-valued neural networks.

Remark 5

Because of their practical importance and extensive applications in many fields, such as telecommunications and robotics, aerospace, signal filtering, parallel computing, data mining, several Clifford-valued neural networks have been studied with different methods in recent years, especially for stability, synchronization and pseudo almost automorphic problems. In Boonsatit et al. (2021), Rajchakit et al. (2021a), Rajchakit et al. (2021b), Rajchakit et al. (2021c), Rajchakit et al. (2021d), Rajchakit et al. (2021e) and Aouiti et al. (2021), the authors consider the stability problem for the delayed neural networks via the methods of Lyapunov function and Lyapunov-Krasovskii functional, Banach’s fixed point principle, as well as the matrix inequalities technique with a great deal of integral calculations. For example, Boonsatit et al. (2021) consider the finite-time and fixed-time synchronization for delayed Clifford-valued recurrent neural networks, where the finite/fixed-time synchronization criteria are established by Lyapunov-Krasovskii functional and computational techniques. Rajchakit et al. (2021a) investigate the global exponential stability in the Lagrange sense of the delayed Clifford-valued recurrent neural networks with Lyapunov stability theory, some analytical techniques and the linear matrix inequality (LMI) technique, based on which, the obtained conditions are given in terms of high-dimensional matrices. While in this paper, instead of using the methods above, the Brouwer’s fixed point theorem, the method of Clifford-valued variation parameter, inequality technique and matrix theory and its spectral theory are applied to investigate the considered Clifford-valued neural networks, which can help to avoid a large number of tedious calculations and high-dimensional matrices.

5 Numerical example

We consider the two-neuron Clifford-valued recurrent neural network with mixed time delays represented by:

$$\begin{aligned} \frac{dx_i(t)}{dt}= & {} -a_ix_i(t)+\displaystyle \sum _{j=1}^{2}b_{ij}f_j(x_j(t))+\displaystyle \sum _{j=1}^{2}c_{ij}f_j(x_j(t-\tau _j(t)))\nonumber \\{} & {} +\, \displaystyle \sum _{j=1}^{2}d_{ij}\int _{-\infty }^{t}K_{ij}(t-s)f_j(x_j(s))ds+I_i,\;\;i=1,2, \end{aligned}$$
(16)

where \(A=\left( \begin{array}{cc}10 &{} 0 \\ 0 &{} 20\end{array}\right) \),

\(B=\left( \begin{array}{cc} 2 &{} -1+e_{1}-e_{2}+e_{1} e_{2} \\ 1-e_{1}+e_{2}-e_{1} e_{2} &{} 3 \end{array}\right) \),

\(C=\left( \begin{array}{cc} 1-e_1-e_2 &{}\quad 1+2e_{1}+e_{1} e_{2} \\ 1-e_{1}+e_{2}&{}1+ e_1+e_2-e_{12} \end{array}\right) \),

\(D=\left( \begin{array}{cc} -2 &{}\quad -1-e_1 \\ 2-e_{1}+2e_{2}&{} \quad 2-2e_2 \end{array}\right) \),

\(I=\left( \begin{array}{c}\frac{3}{2} e_{1} \\ -\frac{1}{2}+\frac{3}{2} e_{2}+e_{1} e_{2}\end{array}\right) \),

and the activation functions is

$$\begin{aligned} f_{j}\left( u_{j}\right) =\frac{1-e^{-x_{j}^{0}}}{1+e^{-x_{j}^{0}}}+\frac{1}{1+e^{-x_{j}^{1}}} e_{1}+\frac{1-e^{-x_{j}^{2}}}{1+e^{-x_{j}^{2}}} e_{2}+\frac{1}{1+e^{-x_{j}^{12}}} e_{1} e_{2} \end{aligned}$$

where \(u_j=x^0_j+x^1_je_1+x^2_je_2+x^{12}_je_1e_2\in {\mathbb {A}}\), \(j=1,2.\)

We choose the time-varying delays \(\tau _1(t)=0.3+0.1\sin (t),\) \(\tau _2(t)=0.6+0.4\cos (t)\), \(\tau =1\), \(k_{ij}(t-s)=e^{-(t-s)},\) \(t\ge 0\), \(s\in (0,+\infty ].\)

We have in this example

$$\begin{aligned} L^f= & {} \left( \begin{array}{cc}\frac{1}{2} &{}\quad 0 \\ 0 &{}\quad \frac{1}{2}\end{array}\right) ,\\ |B|_0= & {} \left( \begin{array}{cc} 2 &{} \quad 2 \\ 2 &{}\quad 3 \end{array}\right) ,\\ |C|_0= & {} \left( \begin{array}{cc} \sqrt{3}&{} \sqrt{6} \\ \sqrt{3} &{} 2 \end{array}\right) ,\\ |D|_0= & {} \left( \begin{array}{cc} 2 &{} \sqrt{2} \\ 3 &{} 2\sqrt{2} \end{array}\right) , \end{aligned}$$

then,

$$\begin{aligned} A^{-1}|B|_0L^f+A^{-1}|C|_0L^f+A^{-1}|D|_0L^f=\left( \begin{array}{ccc} 0.2866 &{}\quad 0.2932 \\ 0.1683 &{}\quad 0.1957 \end{array}\right) \ge 0,\\ \rho \Bigg (A^{-1}|B|_0L^f+A^{-1}|C|_0L^f+A^{-1}|D|_0L^f\Bigg )=0.4679<1. \end{aligned}$$

So, the conditions of Theorem 1 hold and system (16) has at least an equilibrium point.

Now, we fix \(\lambda =0.1\), \(\tau =1\) then

$$\begin{aligned} |J|_0= & {} (k_{ij}|d_{ij}|_0)_{2\times 2}= \left( \begin{array}{ccc} \frac{2}{0.9} &{}\quad \frac{\sqrt{2}}{0.9}\\ \frac{3}{0.9} &{} \quad \frac{2\sqrt{2}}{0.9} \end{array}\right) , \end{aligned}$$

then

$$\begin{aligned} (A-\lambda I_d)^{-1}\big (|B|_0L^f+e^{\lambda \tau }|C|_0L^f+|J|_0L^f\big )=\left( \begin{array}{ccc} 0.3099 &{} 0.3171\\ 0.1821 &{} 0.2099 \end{array}\right) ,\\ \rho \Bigg ((A-\lambda I_d)^{-1}\big (|B|_0L^f+e^{\lambda \tau }|C|_0L^f+|J|_0L^f\big )\Bigg )=0.5053<1. \end{aligned}$$

Therefore, all the conditions of Theorem 2 hold, then the system (16) is globally exponentially stable.

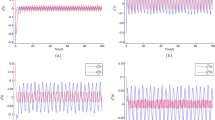
Using the Simulink toolbox in MATLAB, the fact is verified by the simulation in Figs. 1 and 2 with six different initial conditions which demonstrates the state trajectories of the system (16).

Fig. 1
figure 1

a The state trajectories of \(x_1^0(t)\) with 6 different initial conditions; b The state trajectories of \(x_1^1(t)\) with 6 different initial conditions; c The state trajectories of \(x_1^2(t)\) with 6 different initial conditions; d The state trajectories of \(x_1^{12}(t)\) with 6 different initial conditions

Full size image
Fig. 2
figure 2

a The state trajectories of \(x_2^0(t)\) with 6 different initial conditions; b The state trajectories of \(x_2^1(t)\) with 6 different initial conditions; c The state trajectories of \(x_2^2(t)\) with 6 different initial conditions; d The state trajectories of \(x_2^{12}(t)\) with 6 different initial conditions

Full size image

6 Conclusion

In this paper, the existence and the global exponential stability of the equilibrium point for a class of Clifford-valued recurrent neural networks with mixed time delays were proven using the Brouwer’s fixed point theorem, inequality technique, and the method of the Clifford-valued variation parameter. This is the first paper to study the global exponential stability for Clifford-valued neural networks with mixed time delays. The results of this article are essentially new, especially when our system degenerates into real, complex and quaternion value systems. Finally, the effectiveness of the results obtained is illustrated by an illustrative example.