1 Introduction

In the past years, many efforts have been spent in applications of neural networks to different fields along with the rising research interests of artificial neural networks. The various papers studying the real-valued neural networks are available on the Internet. Through the study of the past few decades, the research of the real-valued neural networks is mature, see [1–14]. Meanwhile, the research of complex-valued neural networks has achieved gratifying success under the perseverant efforts. Complex-valued RNNs have been an indispensable part in practical applications such as physical systems dealing with electromagnetic, ultrasonic, quantum waves, and light and show a remarkable advantage in various fields of engineering.

Several models of complex-valued neural networks have been established [15–21]. In [15], a delayed complex-valued recurrent neural network with two types of complex-valued activation functions was studied. Some sufficient conditions to ensure the existence and uniqueness equilibrium and the global asymptotic and exponential stability were obtained. In [17], a complex-valued recurrent neural network was studied by separating complex-valued neural networks into real and imaginary parts, and forming an equivalent real-valued system. Then sufficient conditions were provided to guarantee the existence, uniqueness and global asymptotic stability of the complex-valued equilibrium point. Moreover, quaternion-valued neural networks are proposed and actively studied [22, 23].

Clifford algebra (geometric algebra) was introduced by William K. Clifford (1845–1879). It has been applied to various fields such as neural computing, computer and robot vision, image and signal processing, control problems and other areas due to its practical and powerful framework for the representation and solution of geometrical problem, see [24–30] and references therein. Recently, as an extension of real value models, Clifford neural networks has become an active research field. Neural networks for function approximation require feature enhancement, rotation and dilatation operations. These operations are limited by the Euclidean metric in real-valued neural networks and can be carried out more efficiently in Clifford-valued neural networks due to the Clifford algebra coordinate-free framework which allows to process patterns between layers and make the metric possible only due to the promising projective split. A multilayered Clifford neural network model was fist proposed by Pearson in [31, 32]. Then, Buchholz derived that the Clifford multilayer neural networks perform superior to the usual real-valued neural networks in [33, 34]. In part II of[35], Sommer learned the Moebius transformations in Clifford algebra and pointed that Moebius transformations cannot be available to the usual real-valued neural networks. Clifford RNNs were first proposed by Y. Kuroe in [28] and [36]. In [28], three models of fully connected Clifford-valued Hopfield-type RNNs were proposed. Sufficient conditions for the existence of an energy function for two classes of Clifford-valued Hopfield-type RNNs were discussed. In [29], a novel self-organizing-type radial basis function (RBF) neural network was presented, and the neural computing field was extended to the geometric algebra. In [30], neural computation in Clifford-valued domain was studied.

Time delay is a main source of causing oscillation controllability and instability and has been recognized that is an inherent feature of signal transmission between neurons [5, 37, 38]. In this paper, we study the Clifford-valued recurrent neural networks with propagation delay rather than process delay (intrinsic delay such as autapse type) investigated in [39, 40]. In the past few decades, the stability of neural networks with time delays has been an attractive subject of research, see [1, 3, 6, 12, 15–18, 41] and so on. The stability criteria for delayed neural networks can be divided into two categories: delay-independent stability and delay-dependent stability. The later one is less conservative, especially when the delay is small [37].

Motivated the above discussions, we investigate the stability of Clifford-valued recurrent neural networks with time delays in this paper. To the best of our knowledge, there is no result on such topic. Compared with complex-valued and quaternion-valued neural networks, the main challenge is that the product of Clifford-valued elements with the involution is not a constant real number in general. Therefore, in this paper, we use the properties \(e_{A}\bar{e}_{A}=\bar{e}_{A}e_{A}=1\) to transform the complicated Clifford-valued RNNs into higher dimensional real-valued RNNs. Then, an asymptotic delay-independent stability condition and a delay-dependent exponential stability criterion of the considered Clifford-valued RNNs are derived. Moreover, we estimate the exponential convergence rates with the constant delay. The results can reduces to real-valued, complex-valued and quaternion-valued neural networks when \(m=0\), \(m=1\) and \(m=2\), respectively. Compared with the delay-independent results of [15–17] for complex-valued RNNs, our delay-dependent condition is less conservative when \(m=1\).

The paper is organized as follows. In Sect. 2, we introduce some notations used in the Clifford analysis, the model description and some definitions and lammas needed. Section 3 presents sufficient conditions to ensure the existence of the unique equilibrium, as well as the global asymptotic and exponential stability of the considered Clifford-valued RNNs. In Sect. 4, a numerical example is given to demonstrate the effectiveness of the proposed results.

2 Preliminaries

Throughout this paper, \(\mathbb {R}^{n}\), \(\mathscr {A}^{n}\), \(\mathbb {R}^{m\times n}\) and \(\mathscr {A}^{m\times n}\) represent, respectively, the n-dimensional real vector space, the n-dimensional real Clifford vector space, the set of all \(m\times n\) real matrices and the set of all \(m\times n\) real Clifford matrices. The superscript ‘T’ and ‘*’ denote, respectively, the matrix transposition and the matrix involution transposition. For a square real matrix B, \([B]^{s}\) is defined by \([B]^{s}=(B+B^{T})/2\). For simplicity, we denote \(x^{\tau }=x(t-\tau )\) and \(x_{k}^{\tau }=x_{k}(t-\tau ).\)

2.1 The Clifford algebra \(\mathscr {A}\)

\(\mathscr {A}\) equipped with m generators is defined as the Clifford algebra over the real number \(\mathbb {R}\) with m multiplicative generators \(e_{1},~e_{2},~\cdots ,~e_{m}\) called Clifford generators which satisfy the following relations

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} e_{i}e_{j}+ e_{j}e_{i}= 0 &{}i\ne j,\\ e_{i}^{2}= -1 &{}i= 1, 2, 3, \ldots , m. \end{array} \right. \end{aligned}$$

For simplicity, when one element is the product of multiple Clifford generators, we will write its subscripts together. For example \(e_{1}e_{2}=e_{12}\) and \(e_{6}e_{2}e_{4}e_{5}=e_{6245}\). Then \(\mathscr {A}\) has its basis as follows:

$$\begin{aligned} \begin{aligned} \{e_{A}=e_{h_{1}h_{2}\cdots h_{r}},~1\le h_{1}<h_{2}<\cdots <h_{r}\le m\}. \end{aligned} \end{aligned}$$
(1)

Therefore the real Clifford algebra consists of elements such as \(a=\sum \limits _Ax^{A}e_{A}\), where \(x^{A}\in \mathbb {R}\) is a real number. In particular, when \(A=\emptyset \), then \(e_{\emptyset }\) can be denoted as \(e_{0}\) and \(x^{0}\) is the coefficient of the \(e_{0}\)-component, see [42]. From these properties, it is concluded that

$$\begin{aligned} \dim \mathscr {A}=\sum _{k=0}^{m}{m\atopwithdelims ()k}=\sum _{k=o}^{m}\frac{m!}{k!(m-k)!}=2^{m}. \end{aligned}$$

Similar to the complex domain, the inversion for an arbitrary basic vector can be defined as follows:

$$\begin{aligned} \begin{aligned} (e_{h_{1}h_{2}\cdots h_{r}})^{\star }=(-1)^{r}e_{h_{1}h_{2}\cdots h_{r}} \end{aligned}, \end{aligned}$$

or

$$\begin{aligned} \begin{aligned} e_{A}^{\star }=(-1)^{n(A)}e_{A} \end{aligned}. \end{aligned}$$

where n(A) is r as \(e_{A}=e_{h_{1}h_{2}\cdots h_{r}}\).

Next, the main anti-automorphism in the Clifford algebra is called reversion or hermitian conjugation and given by

$$\begin{aligned} \begin{aligned} e_{A}^{\dag }=(-1)^{\frac{(n(A)-1)n(A)}{2}}e_{A} \end{aligned}. \end{aligned}$$

Now, we present the involution which is a combination of the reversion and the inversion introduced above. It is given as follows for a basic vector

$$\begin{aligned} \begin{aligned} \bar{e}_{A}=e_{A}^{\star \dag }=(-1)^{\frac{n(A)(n(A)+1)}{2}}e_{A} \end{aligned}. \end{aligned}$$

From the definition, it is directly deduced that \(e_{A}\bar{e}_{A}=\bar{e}_{A}e_{A}=1.\) Moreover, for any Clifford number \(x=\sum \limits _{A}x^{A}e_{A},\) its involution can be denoted by \(\bar{x}=\sum \limits _{A}x^{A}\bar{e}_{A}\). In addition to this, the involution also satisfies \(\overline{xy}=\bar{y}\bar{x},~\forall x,~y\in \mathscr {A}.\)

The inner product in Clifford domain is defined as follows

$$\begin{aligned} \begin{aligned} (\gamma ,\beta )_{0}:=2^{m}[\gamma \bar{\beta }]_{0} =2^{m}\sum \limits _{A}\gamma ^{A}\beta ^{A}~~~~ \forall ~\gamma ,~\beta \in \mathscr {A}, \end{aligned} \end{aligned}$$

where \([\gamma \bar{\beta }]_{0}\) denotes the coefficient of its \(e_{0}\)-component. The norm on \(\mathscr {A}\) is correspondingly defined as \(\mid \gamma \mid _{0}=\sqrt{(\gamma ,\gamma )_{0}}.\) Thus \(\mathscr {A}\) is a real Hilbert space and satisfies the Banach algebra with

$$\begin{aligned} \begin{aligned} \mid \gamma \beta \mid _{0}\le \mid \gamma \mid _{0} \mid \beta \mid _{0},~~~\forall ~\gamma ,~\beta \in \mathscr {A} \end{aligned}. \end{aligned}$$

Next we introduce a real functional on \(\mathscr {A}\), that is, \(\tau _{e_{A}}:\mathscr {A}\rightarrow \mathbb {R}\)

$$\begin{aligned} \begin{aligned} \langle \tau _{e_{A}},\gamma \rangle =2^{m}(-1)^{\frac{(n(A)+1)n(A)}{2}}\gamma ^{A} \end{aligned}. \end{aligned}$$

As a special case of \(A=\emptyset \), we have

$$\begin{aligned} \begin{aligned} \langle \tau _{e_{0}},\gamma \rangle =2^{m}[\gamma ]_{0} \end{aligned}. \end{aligned}$$

Therefore, it is concluded that \(\mid \gamma \mid _{0}^{2}= 2^{m}[\gamma \bar{\gamma }]_{0}= <\tau _{e_{0}},\gamma \bar{\gamma } >\).

Finally, the definition of the derivative for \(z(t)=\sum \limits _{A}z^{A}(t)e_{A}\) is given as:

$$\begin{aligned} \begin{aligned} \dot{z}(t)=\sum \limits _{A}\dot{z}^{A}(t)e_{A} \end{aligned}. \end{aligned}$$

where \(z^{A}(t)\) is a function with real value.

Due to \(e_{B}\bar{e}_{A}=(-1)^{\frac{n(A)(n(A)+1)}{2}}e_{B}e_{A}\), we can simplify and express \(e_{B}\bar{e}_{A}=e_{C}\) or \(e_{B}\bar{e}_{A}=-e_{C}\) with \(e_{C}\) being some basis of Clifford algebra in (1). For example, \(e_{12}\bar{e}_{23}=-e_{12}e_{23}=-e_{1}e_{2}e_{2}e_{3}=e_{1}e_{3}=e_{13}\). Hence it is possible to find a unique corresponding basis \(e_{C}\) for the given \(e_{B}\bar{e}_{A}\). Defining \(n(B\cdot \bar{A})\) satisfying that \(n(B\cdot \bar{A})=0\) when \(e_{B}\bar{e}_{A}=e_{C}\) and \(n(B\cdot \bar{A})=1\) when \(e_{B}\bar{e}_{A}=-e_{C}\), based on which \(e_{B}\bar{e}_{A}=(-1)^{n(B\cdot \bar{A})}e_{C}\). Moreover, for \(K=\sum \limits _{C}K^Ce_C\in \mathscr {A}\), we define \(K^{B\cdot \bar{A}}=(-1)^{n(B\cdot \bar{A})}K^{C}\) for \(e_{B}\bar{e}_{A}=(-1)^{n(B\cdot \bar{A})}e_{C}\). Therefore,

$$\begin{aligned} K^{B\cdot \bar{A}}e_{B}\bar{e}_{A}= & {} K^{B\cdot \bar{A}}(-1)^{n(B\cdot \bar{A})}e_{C}\\= & {} (-1)^{n(B\cdot \bar{A})}K^{C}(-1)^{n(B\cdot \bar{A})}e_{C}=K^{C}e_{C}. \end{aligned}$$

2.2 Model formulation and basic lemmas

Consider the following Clifford-valued RNNs with time delay

$$\begin{aligned} \left\{ \begin{array}{l} \dot{z}(t)=-Dz(t)+Kf(z(t))+Lg(z(t-\tau ))+u,\\ z(t)=\varphi (t),~~~t\in [-\tau , 0], \end{array}\right. \end{aligned}$$
(2)

where \(z=(z_{1}(t),~z_{2}(t),~\cdots ,~z_{n}(t))^{T}\in \mathscr {A}^{n}\) denotes the state vector, the self-feedback connection weight matrix D satisfies \(D=\mathrm{diag}(d_{1},d_{2},\cdots ,d_{n})\in \mathbb {R}^{n\times n}\) with \(d_{i}>0~(i=1,2,\cdots ,n),\) \(K=(k_{ij})_{n\times n}\in \mathscr {A}^{n\times n}\), \(L=(l_{ij})_{n\times n}\in \mathscr {A}^{n\times n}\) are the connection weight matrices without and with time delay. \(f(z(t))=(f_{1}(z_{1}(t)),~f_{2}(z_{2}(t)),~\cdots ,~f_{n}(z_{n}(t)))^{T}:\mathscr {A}^{n}\rightarrow \mathscr {A}^{n}\) is the vector-valued activation function. \(g(z(t-\tau ))=(g_{1}(z_{1}(t-\tau _{1})),~g_{2}(z_{2} (t-\tau _{2})),~\cdots ,~g_{n}(z_{n}(t-\tau _{n})))^{T}:\mathscr {A}^{n}\rightarrow \mathscr {A}^{n}\) is the vector-valued activation function with time delay, where elements of f(z(t)) and g(z(t)) are composed of Clifford-valued nonlinear functions. \(\tau _{i}~(i=1,2,\cdots ,n)\) and \( u=(u_{1},u_{2},\cdots ,u_{n})^{T}\in \mathscr {A}^{n}\) are constant time delays and the external input vector, respectively.

Now some basic definition and lemmas are presented which will be utilized in the following stability analysis.

Definition 1

Vector z is called an equilibrium point of the Clifford-valued RNNs (2) if it satisfies

$$\begin{aligned} \begin{aligned} -Dz(t)+Kf(z(t))+Lg(z(t))+u=0 \end{aligned}. \end{aligned}$$
(3)

Lemma 1

([15]) If \(H(x):\mathbb {R}^{2^{m}n}\rightarrow \mathbb {R}^{2^{m}n}\) is a continuous function and satisfies the following conditions:

  1. (1)

    H(x) is injective on \(\mathbb {R}^{2^{m}n};\)

  2. (2)

    \(\lim \limits _{\Vert x\Vert \rightarrow \infty }\Vert H(x)\Vert \rightarrow \infty \) as \(\Vert x\Vert \rightarrow \infty \), where \(||\cdot ||\) denotes the norm of \(\mathbb R^{2^{m}n};\)

    then H(x) is a homeomorphism of \(\mathbb {R}^{2^{m}n}\).

Lemma 2

([37]) For positive definite matrix \(P\in \mathbb {R}^{n\times n}\), positive real constant \(\varepsilon \) and \(a,b\in \mathbb {R}^{n}\), it holds that \(a^{T}b+b^{T}a\le \varepsilon a^{T}Pa+\varepsilon ^{-1}b^{T}P^{-1}b.\)

Lemma 3

(Schur Complement) Given constant matrices P, Q and R, where \(P^{T}=P\), \(Q^{T}=Q\), then

$$\begin{aligned} \begin{pmatrix} P&{}R\\ R^{T}&{}Q \end{pmatrix}>0 \end{aligned}$$

is equivalent to the following inequalities

$$\begin{aligned} Q>0,~~~~~~P-RQ^{-1}R^{T}>0. \end{aligned}$$

Assumption 1

Functions \(f_{i}(z),~g_{i}(z)~(i=1,2,\cdots ,n)\) satisfy the Lipschitz continuity condition regarding to the n-dimensional Clifford vector. That is, for each \(i=1,2,\cdots ,n,\) there exist positive constants \(\xi _{i},~\eta _{i}\) such that for any \(z, z'\in \mathscr {A}\),

$$\begin{aligned} \begin{aligned} \mid f_{i}(z)-f_{i}(z')\mid _{0}\le \xi _{i}\mid z-z'\mid _{0}\\ \mid g_{i}(z)-g_{i}(z')\mid _{0}\le \eta _{i}\mid z-z'\mid _{0} \end{aligned} \end{aligned}$$
(4)

where \(\xi _{i},~\eta _{i}~(i=1,2,\cdots ,n)\) are called Lipschitz constants.

3 Main Results

Firstly, we rewrite the Clifford-valued RNNs with the help of \(e_{A}\bar{e}_{A}=\bar{e}_{A}e_{A}=1\) and \(e_{B}\bar{e}_{A}e_{A}=e_{B}\). From the definition of \(K^C\), it is easy to find a unique \(K^C\) satisfying \(K^{C}e_{C}f^{A}e_{A}=(-1)^{n(B\cdot \bar{A})}K^{C}f^{A}e_{B}=K^{B\cdot \bar{A}}f^{A}e_{B}\), which implies the following system transformation. Decomposing (2) into \(\dot{z}=\sum \limits _{A}\dot{z}^{A}e_{A}\), it follows that

$$\begin{aligned} \dot{z}^{A}&=-Dz^{A}+\sum _{B}K^{A\cdot \bar{B}}f^{B}(z)\nonumber \\&\quad +\sum _{B}L^{A\cdot \bar{B}}g^{B}(z^{\tau })+u^{A}, \end{aligned}$$
(5)

where \( K^{A}=(k_{ij}^{A})_{n\times n}, ~L^{A}=(l_{ij}^{A})_{n\times n}, ~u^{A}=(u_{1}^{A},u_{2}^{A},\cdots ,u_{n}^{A})^{T},\) and \(f^{A}(z)=(f_{1}^{A}(z_{1}),f_{2}^{A}(z_{2}), \cdots ,f_{n}^{A}(z_{n}))^{T}, g^{A}(z^{\tau })=(g_{1}^{A}(z_{1}^{\tau }),g_{2}^{A}(z_{2}^{\tau }),\cdots ,g_{n}^{A}(z_{n}^{\tau }))^{T}\).

According to the basis of Clifford algebra, we are here to rewrite the Clifford-valued RNNs by novel real-valued ones.

Let

$$\begin{aligned}&w\!=\!\left( (z^{0})^{T},(z^{1})^{T},(z^{2})^{T},\cdots ,(z^{A})^{T},\right. \\&\left. \quad \quad \quad \cdots ,(z^{12\cdots m})^{T} \right) ^{T}\in \mathbb {R}^{2^{m}n},\\&\overline{f}(w)\!=\! \left( (f^{0}(z))^{T},(f^{1}(z))^{T},(f^{2}(z))^{T},\cdots ,(f^{A}(z))^{T},\right. \\&\left. \quad \quad \quad \quad \quad \cdots ,(f^{12\cdots m}(z))^{T}\right) ^{T},\\&\overline{g}(w^{\tau })\!=\!\left( (g^{0}(z^{\tau }))^{T},(g^{1}(z^{\tau }))^{T},(g^{2}(z^{\tau }))^{T},\right. \\&\left. \quad \quad \quad \quad \quad \cdots ,(g^{A}(z^{\tau }))^{T},\cdots ,(g^{12\cdots m}(z^{\tau }))^{T} \right) ^{T},\\&\overline{u}\!=\!\begin{pmatrix} (u^{0})^{T},(u^{1})^{T},(u^{2})^{T},\cdots ,(u^{A})^{T},\cdots ,(u^{12\cdots m})^{T} \end{pmatrix}^{T},\\ \end{aligned}$$
$$\begin{aligned}&\bar{D}=\begin{pmatrix} &{}D&{}0&{}\cdots &{}0\\ &{}0&{}D&{}\cdots &{}0\\ &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ &{}0&{}0&{}\cdots &{}D \end{pmatrix}_{2^{m}n\times 2^{m}n},\\&\bar{K}=\begin{pmatrix} &{}K^{0}&{}\cdots &{}K^{\bar{A}}&{}\cdots &{}K^{\overline{12\cdots m}}&{}\\ &{}K^{1}&{}\cdots &{}K^{1\cdot \bar{A}}&{}\cdots &{}K^{1\cdot \overline{12\cdots m}}&{}\\ &{}\vdots &{}\cdots &{}\vdots &{}\cdots &{}\vdots &{}\\ &{}K^{12\cdots m}&{}\cdots &{}K^{12\cdots m\cdot \bar{A}}&{}\cdots &{}K^{1\cdots m\cdot \overline{1\cdots m}} \end{pmatrix}_{2^{m}n\times 2^{m}n},\\&\bar{L}=\begin{pmatrix} &{}L^{0}&{}\cdots &{}L^{\bar{A}}&{}\cdots &{}L^{\overline{12\cdots m}}&{}\\ &{}L^{1}&{}\cdots &{}L^{1\cdot \bar{A}}&{}\cdots &{}L^{1\cdot \overline{12\cdots m}}&{}\\ &{}\vdots &{}\cdots &{}\vdots &{}\cdots &{}\vdots &{}\\ &{}L^{12\cdots m}&{}\cdots &{}L^{12\cdots m\cdot \bar{A}}&{}\cdots &{}L^{12\cdots m\cdot \overline{12\cdots m}} \end{pmatrix}_{2^{m}n\times 2^{m}n},\\&\bar{M}=\begin{pmatrix} &{}M^{T}M&{}0&{}\cdots &{}0\\ &{}0&{}M^{T}M&{}\cdots &{}0\\ &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ &{}0&{}0&{}\cdots &{}M^{T}M \end{pmatrix}_{2^{m}n\times 2^{m}n},\\&\bar{N}=\begin{pmatrix} &{}N^{T}N&{}0&{}\cdots &{}0\\ &{}0&{}N^{T}N&{}\cdots &{}0\\ &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ &{}0&{}0&{}\cdots &{}N^{T}N \end{pmatrix}_{2^{m}n\times 2^{m}n}, \end{aligned}$$

then it is deduced from (5) that

$$\begin{aligned} \left\{ \begin{array}{l} \dot{w}=-\bar{D}w+\bar{K}\bar{f}(w)+\bar{L}\bar{g}(w^{\tau })+\bar{u},\\ w(t)=\phi (t),~t\in [-\tau ,0]. \end{array} \right. \end{aligned}$$
(6)

Meanwhile, we can obtain the following inequalities : 

$$\begin{aligned}&\begin{aligned} \Vert \bar{f}(w)-\bar{f}(w')\Vert ^{2} \le (w-w')^{T}\bar{M}(w-w'), \end{aligned} \end{aligned}$$
(7)
$$\begin{aligned}&\begin{aligned} \Vert \bar{g}(w)-\bar{g}(w')\Vert ^{2} \le (w-w')^{T}\bar{N}(w-w'),~ \end{aligned} \end{aligned}$$
(8)

according to

$$\begin{aligned} \begin{aligned}&\langle \tau _{e_{0}},(f(z)-f(z'))^{*}(f(z)-f(z'))\rangle \\&\quad \le \langle \tau _{e_{0}},(z-z')^{*}M^{T}M(z-z')\rangle ,\\&\langle \tau _{e_{0}},(g(z)-g(z'))^{*}(g(z)-g(z'))\rangle \\&\quad \le \langle \tau _{e_{0}},(z-z')^{*}N^{T}N(z-z')\rangle \end{aligned} \end{aligned}$$

from Assumption 1, where

$$\begin{aligned}&M=\mathrm{diag}\{\xi _{1}, \xi _{2}, \cdots , \xi _{n}\},\nonumber \\&\quad N=\mathrm{diag}\{\eta _{1}, \eta _{2}, \cdots , \eta _{n}\}. \end{aligned}$$

Theorem 1

Under Assumption 1, a Clifford-valued RNNs (2) has an unique equilibrium point and it is globally asymptotically stable if there exist a positive \(P\in \mathbb {R}^{(2^{m}n)\times (2^{m}n)}\) and positive real constants \(\varepsilon _{1}, \varepsilon _{2}\) such that the following LMI holds:

$$\begin{aligned} \begin{pmatrix} &{}P\bar{D}+\bar{D}P-\varepsilon _{1} \bar{M}-\varepsilon _{2}\bar{N}&{}P\bar{K}&{}P\bar{L}&{}\\ &{}\bar{K}^{T}P&{}\quad \varepsilon _{1}I&{}\quad 0&{}\\ &{}\bar{L}^{T}P&{}\quad 0&{}\quad \varepsilon _{2}I&{}\\ \end{pmatrix}>0. \end{aligned}$$
(9)

Proof

It is obvious that the existence and uniqueness of the equilibrium point of the real-valued system (6) as well as its global asymptotic stability are equivalent to those of the Clifford-valued RNNs (2).

Define \(H(w)=-\bar{D}w+\bar{K}\bar{f}(w)+\bar{L}\bar{g}(w)+\bar{u}\) for convenience. First, we prove the injectiveness of the map H(w) under the given condition. Suppose that there exists w and \(w'~(w'\ne w)\) satisfying \(H(w')=H(w)\), then we get

$$\begin{aligned}&-\bar{D}(w-w')+\bar{K}(\bar{f}(w)-\bar{f}(w'))\nonumber \\&\quad +\bar{L}(\bar{g}(w)-\bar{g}(w'))=0. \end{aligned}$$
(10)

Left-multiplying both sides of the above equation by \(2(w-w')^{T}P\) gives that

$$\begin{aligned} \begin{aligned}&2(w-w')^{T}P\big (-\bar{D}(w-w')+\bar{K}(\bar{f}(w)\\&\quad -\bar{f}(w')) +\bar{L}(\bar{g}(w)-\bar{g}(w'))\big )=0, \end{aligned} \end{aligned}$$

that is to say

$$\begin{aligned}&(w-w')^{T}(-\bar{D}P-P\bar{D})(w-w')\nonumber \\&\quad +2(w-w')^{T}P\bar{K}(\bar{f}(w)-\bar{f}(w'))\nonumber \\&\quad +2(w-w')^{T}P\bar{L}(\bar{g}(w)-\bar{g}(w'))=0. \end{aligned}$$
(11)

Using Lemma 2 and (7)–(8), the left side of equality (11) can be transformed into the following form

$$\begin{aligned}&(w-w')^{T}(-\bar{D}P-P\bar{D})(w-w')\nonumber \\&\qquad +2(w-w')^{T}P\bar{K}(\bar{f}(w)-\bar{f}(w'))\nonumber \\&\qquad +2(w-w')^{T}P\bar{L}(\bar{g}(w)-\bar{g}(w'))\nonumber \\&\quad \le (w-w')^{T}(-\bar{D}P-P\bar{D})(w-w')\nonumber \\&\qquad +\varepsilon _{1}^{-1}(w-w')^{T}P\bar{K}\bar{K}^{T}P(w-w')\nonumber \\&\qquad +\varepsilon _{2}^{-1}(-w')^{T}P\bar{L}\bar{L}^{T}P(w-w')+\varepsilon _{1}(\bar{f}(w)\nonumber \\&\qquad -\bar{f}(w'))^{T}(\bar{f}(w)-\bar{f}(w'))+\varepsilon _{2}(\bar{g}(w)\nonumber \\&\qquad -\bar{g}(w'))^{T}(\bar{g}(w)-\bar{g}(w'))\nonumber \\&\quad \le (w-w')^{T}(-\bar{D}P-P\bar{D})(w-w')\nonumber \\&\qquad +\varepsilon _{1}^{-1}(w-w')^{T}P\bar{K}\bar{K}^{T}P(w-w')\nonumber \\&\qquad +\varepsilon _{2}^{-1}(w-w')^{T}P\bar{L}\bar{L}^{T}P(w-w')\nonumber \\&\qquad +\varepsilon _{1}(w-w')^{T}\bar{M}(w-w')\nonumber \\&\qquad +\varepsilon _{2}(w-w')^{T}\bar{N}(w-w')\nonumber \\&\quad =-(w-w')^{T}(\bar{D}P+P\bar{D}-\varepsilon _{1}^{-1}P\bar{K}\bar{K}^{T}P\nonumber \\&\qquad -\varepsilon _{2}^{-1}P\bar{L}\bar{L}^{T}P-\varepsilon _{1}\bar{M}-\varepsilon _{2}\bar{N})(w-w'). \end{aligned}$$
(12)

Due to Schur Complement and LMI condition (9), one derives

$$\begin{aligned} \begin{aligned}&\bar{D}P+P\bar{D}-\varepsilon _{1}^{-1}P\bar{K}\bar{K}^{T}P-\varepsilon _{2}^{-1}P\bar{L}\bar{L}^{T}P\\&\quad -\varepsilon _{1}\bar{M}-\varepsilon _{2}\bar{N}>0. \end{aligned} \end{aligned}$$
(13)

Therefore, \(H(w)-H(w')<0\), which is a contradiction to (11), and hence the map H(w) is injective.

Secondly, we will show that \(\lim \limits _{\Vert w\Vert \rightarrow \infty }\Vert H(w)\Vert \rightarrow \infty \) as \(\Vert w\Vert \rightarrow \infty \). It comes from (13) that

$$\begin{aligned} \begin{aligned}&-\bar{D}P-P\bar{D}+\varepsilon _{1}^{-1}P\bar{K}\bar{K}^{T}P+\varepsilon _{2}^{-1}P\bar{L}\bar{L}^{T}P\\&\quad +\varepsilon _{1}\bar{M}+\varepsilon _{2}\bar{N}<-\varepsilon I \end{aligned} \end{aligned}$$

holds for some sufficiently small \(\varepsilon >0\). Assume that \(w'=0\), we have

$$\begin{aligned} \begin{aligned}&2w^{T}P(H(w)-H(0))\\&\le w^{T}(-\bar{D}P-P\bar{D} +\varepsilon _{1}^{-1}P\bar{K}\bar{K}^{T}P +\varepsilon _{2}^{-1}P\bar{L}\bar{L}^{T}P\\&\quad +\varepsilon _{1}\bar{M}+\varepsilon _{2}\bar{N})w\\&\le -\varepsilon \Vert w\Vert ^{2}. \end{aligned} \end{aligned}$$

From the above inequality and Schwartz inequality, it is obtained that

$$\begin{aligned} \begin{aligned} \varepsilon \Vert w\Vert ^{2}\le 2\Vert w\Vert \Vert P\Vert (\Vert H(w)\Vert +\Vert H(0)\Vert ) \end{aligned}, \end{aligned}$$

which means

$$\begin{aligned} \begin{aligned} \frac{\varepsilon \Vert w\Vert }{2\Vert P\Vert }\le \Vert H(w)\Vert +\Vert H(0)\Vert \end{aligned}. \end{aligned}$$

Therefore, \(\lim \limits _{\Vert w\Vert \rightarrow \infty }\Vert H(w)\Vert \rightarrow \infty \) as \(\Vert w\Vert \rightarrow \infty \). According to Lemma 1, the map H(w) is homeomorphism on \(\mathbb {R}^{2^{m}n}\). Thus there exists an unique equilibrium point \(\hat{w}\) for (6).

In the following, we will prove the global asymptotic stablity of (6). First of all, we shift the equilibrium point of (6) into the origin by the transformation \(\tilde{w}=w-\hat{w}\), and rewrite (6) as

$$\begin{aligned} \begin{aligned} \dot{\tilde{w}}=-\bar{D}\tilde{w} +\bar{K}\tilde{f}(\tilde{w})+\bar{L}\tilde{g}(\tilde{w}^{\tau }), \end{aligned} \end{aligned}$$
(14)

where \(\tilde{f}(\tilde{w})=\bar{f}(\tilde{w}+\hat{w})-\bar{f}(\hat{w})\) and \(\tilde{g}(\tilde{w}^{\tau })=\bar{g}(\tilde{w}^{\tau }+\hat{w})-\bar{g}(\hat{w})\). It is clear that the system (6) is globally asymptotically stable if the system (14) is globally asymptotically stable for the origin. Construct the following Lyapunov-Krasovskii functional:

$$\begin{aligned} \begin{aligned} V(\tilde{w}(t))=\tilde{w}^{T}(t)P\tilde{w}(t) +\int _{t-\tau }^{t}\tilde{g}(\tilde{w}(s))^{T}\tilde{g}(\tilde{w}(s))\mathrm {d}s. \end{aligned} \end{aligned}$$

The time derivative of \(V(\tilde{w}(t))\) along the trajectories of system (14) is given by

$$\begin{aligned} \begin{aligned} \dot{V}(\tilde{w}(t))&=-\tilde{w}^{T}(P\bar{D}+\bar{D}P)\tilde{w} +2\tilde{w}^{T}P\bar{K}\tilde{f}(\tilde{w})\\&\qquad +2\tilde{w}^{T}P\bar{K}\tilde{g}(\tilde{w}^{\tau })+\tilde{g}(\tilde{w})^{T}\tilde{g}(\tilde{w})\\&\qquad -\tilde{g}(\tilde{w}^{\tau })^{T}\tilde{g}(\tilde{w}^{\tau })\\&\quad \le -\tilde{w}^{T}(P\bar{D}+\bar{D}P)\tilde{w}\\&\qquad +\varepsilon _{1}^{-1}\tilde{w}^{T}P\bar{K}\bar{K}^{T}P\tilde{w}+\varepsilon _{2}^{-1}\tilde{w}^{T}P\bar{L}\bar{L}^{T}P\tilde{w}\\&\qquad +\varepsilon _{1}\tilde{f}(\tilde{w})^{T}\tilde{f}(\tilde{w})+ \varepsilon _{2}\tilde{g}(\tilde{w})^{T}\tilde{g}(\tilde{w})\\&\quad \le -\tilde{w}^{T}(\bar{D}P+P\bar{D}-\varepsilon _{1}^{-1}P\bar{K}\bar{K}^{T}P\\&\qquad -\varepsilon _{2}^{-1}P\bar{L}\bar{L}^{T}P-\varepsilon _{1}\bar{M}-\varepsilon _{2}\bar{N})\tilde{w}. \end{aligned} \end{aligned}$$

Considering the inequality condition (9) and the Schur Complement, we can get \(\bar{D}P+P\bar{D}-\varepsilon _{1}^{-1}P\bar{K}\bar{K}^{T} P-\varepsilon _{2}^{-1}P\bar{L}\bar{L}^{T}P -\varepsilon _{1}\bar{M}-\varepsilon _{2}\bar{N}>0\), which means \(\dot{V}(\tilde{w}(t))<0\) when \(\tilde{w}(t)\ne 0\). Therefore, the Clifford-valued RNNs (2) are globally asymptotically stable.   \(\square \)

Remark 1

The obtained result can be easily applied to real-valued and complex-valued RNNs. When \(m=0\), the considered system reduces to the real-valued RNNs. For \(m=1\), it can be regarded a complex-valued RNNs. In [15], the nonsingular M-matrix was used on the stability analysis for complex-valued RNNs. Comparing Assumption 1 in this paper with Assumption 1 of [15], it is noticed that [15] needs some additional restrictions on the existence, continuity and boundedness conditions for the partial derivatives of the activation functions. While \(m=2\), we can derive the global asymptotic stability of quaternion-valued neural networks which has not been investigated either.

Corollary 1

Under Assumption 1, a Clifford-valued RNN (2) has an unique equilibrium point and it is globally exponentially stable if there exist a positive definite matrix P and a scalar \(k>0\) such that the following LMI holds:

$$\begin{aligned} \begin{pmatrix} &{}P\bar{D}+\bar{D}P-\bar{M}-\bar{N}-2kP&{}P\bar{K}&{}e^{k\tau }P\bar{L}&{}\\ &{}\bar{K}^{T}P&{}I&{}0&{}\\ &{}e^{k\tau }\bar{L}^{T}P&{}0&{}I&{}\\ \end{pmatrix}>0. \end{aligned}$$

Moreover

$$\begin{aligned} \begin{aligned} \Vert w-\hat{w}\Vert \le \sqrt{\frac{\lambda _{M}(P)}{\lambda _{m}(P)} +\frac{\lambda _{M}(\bar{N})}{\lambda _{m}(P)}\frac{1-e^{-2k\tau }}{2k}} \Vert \phi \Vert e^{-kt}. \end{aligned} \end{aligned}$$

Proof

The proof is similar to that of Theorem 1 and hence is omitted here. The main idea is sketched as follows.

As to the inequality (12), we could magnify it into the following form:

$$\begin{aligned} \begin{aligned} 0&\le -(w-w')^{T}(\bar{D}P+P\bar{D} -P\bar{K}\bar{K}^{T}P\\&\quad -P\bar{L}\bar{L}^{T}P-\bar{M}-\bar{N})(w-w')\\&\le -(w-w')^{T}(\bar{D}P+P\bar{D}-2kP -P\bar{K}\bar{K}^{T}P\\&\quad -e^{2k\tau }P\bar{L}\bar{L}^{T}P-\bar{M}-\bar{N})(w-w'). \end{aligned} \end{aligned}$$

On the other hand, the corresponding Lyapunov-Krasovskii functional is taken the following form:

$$\begin{aligned} \begin{aligned}&V(\tilde{w}(t))=e^{2kt}\tilde{w}^{T}(t)P\tilde{w}(t)\\&\quad +\int _{t-\tau }^{t}e^{2ks}\tilde{g}(\tilde{w}(s))^{T}\tilde{g} (\tilde{w}(s))\mathrm {d}s, \end{aligned} \end{aligned}$$

based on which the global exponential stability could be obtained. \(\square \)

Remark 2

In [15–17], a delay-independent global asymptotic stability of complex-valued RNNs is studied, while Corollary 1 gives a delay-dependent global exponential stability criterion which is less conservative. Moreover, the exponential convergence rates is estimated in the obtained results as well.

4 An Example

In this section, we will demonstrate Theorem 1 through the following example.

Consider a two-neuron Clifford-valued RNN described by

$$\begin{aligned} \left\{ \begin{array}{l} \dot{z}(t)=-Dz(t)+Kf(z(t))+Lg(z(t-\tau ))+u,\\ z(t)=\varphi (t),~~~t\in [-\tau , 0], \end{array}\right. \end{aligned}$$

where

$$\begin{aligned} D= & {} \begin{pmatrix} 60&{}\quad 0\\ 0&{}\quad 70 \end{pmatrix},~ L=\begin{pmatrix} -2&{}\quad 1+e_{12}-3e_{123}\\ 1-e_{12}+3e_{123}&{}\quad 2-2e_{13}-2e_{23} \end{pmatrix},\\ K= & {} \begin{pmatrix} -3-e_{2}-e_{3}+0.5e_{13}-e_{12}+0.5e_{23}&{}\quad -1-e_{1}+e_{123}\\ 1+e_{1}+3e_{13}-e_{123}+3e_{23}&{}\quad 3-2e_{2}-2e_{3}-2e_{12} \end{pmatrix} \end{aligned}$$

and the activation functions are

$$\begin{aligned} \begin{aligned} f_{j}(z_{j})&=\frac{1}{1+e^{-x_{j}^{0}}} -\frac{1}{2(1+e^{-x_{j}^{2}})}e_{2}\\&+\frac{2}{3(1+e^{-x_{j}^{12}})}e_{12} -\frac{2}{1+e^{-x_{j}^{123}}}e_{123}~~(j=1,2),\\ g_{j}(z_{j})&=\frac{1}{2(1+e^{-x_{j}^{3}})}e_{3} -\frac{1}{1+e^{-x_{j}^{13}}}e_{13}\\&-\frac{3}{4(1+e^{-x_{j}^{23}})}e_{23} +\frac{\sqrt{2}}{1+e^{-x_{j}^{123}}}e_{123}~~(j=1,2) \end{aligned} \end{aligned}$$

with \(z_{j}=\sum \limits _Ax_{j}^{A}e_{A}\in \mathscr {A}\) for \(j=1,~2\). We choose the constant delay parameters \(\tau =\{\tau _{1}, \tau _{2}\}=\{0.5, 1\}\) and the initial state \(\varphi _{1}(t)=2(2.5e_{0}-4.5e_{1}+4e_{2}-3e_{3}+1.5e_{12}-2e_{13}+6e_{23}-e_{123})\) for \(t \in [-\tau _{1},0]\), and \(\varphi _{2}(t)=2(-2.5e_{0}+1.5e_{1}-9e_{2}+3e_{3}-6e_{12}+5e_{13}-4e_{23}+8.5e_{123})\) for \(t \in [-\tau _{2},0]\). According to their definitions, we have

$$\begin{aligned}&K^{0}=\begin{pmatrix} -3&{}\quad -1\\ 1&{}\quad 3 \end{pmatrix}, K^{1}=\begin{pmatrix} 0&{}\quad -1\\ 1&{}\quad 0 \end{pmatrix},\\&K^{123}=\begin{pmatrix} 0&{}\quad 1\\ -1&{}\quad 0 \end{pmatrix},\quad K^{2}=K^{3}=K^{12}=\begin{pmatrix} -1&{}\quad 0\\ 0&{}\quad 2 \end{pmatrix}, \\&K^{13}=K^{23}=\begin{pmatrix} 0.5&{}\quad 0\\ 3&{}\quad 0 \end{pmatrix},\quad L^{123}=\begin{pmatrix} 0&{}\quad -3\\ 3&{}\quad 0 \end{pmatrix},\\&L^{0}=\begin{pmatrix} -2&{}\quad 1\\ 1&{}\quad 2 \end{pmatrix}, L^{12}=\begin{pmatrix} 0&{}\quad 1\\ -1&{}\quad 0 \end{pmatrix},\\&L^{1}=L^{2}=L^{3}=\begin{pmatrix} 0&{}\quad 0\\ 0&{}\quad 0 \end{pmatrix}, L^{13}=L^{23}=\begin{pmatrix} 0&{}\quad 0\\ 0&{}\quad 2 \end{pmatrix},\\&M=\begin{pmatrix} 4&{}\quad 0\\ 0&{}\quad 4 \end{pmatrix}, N=\begin{pmatrix} 2&{}\quad 0\\ 0&{}\quad 2 \end{pmatrix}. \end{aligned}$$

Based on the definition of \(\bar{K}\) and \(\bar{L}\), we can obtain

$$\begin{aligned} \bar{K}= & {} \begin{pmatrix} K^{0}&{}\quad -K^{1}&{}\quad -K^{2}&{}\quad -K^{3}&{}\quad -K^{12}&{}\quad -K^{13}&{}\quad -K^{23}&{}\quad K^{123}\\ K^{1}&{}\quad K^{0}&{}\quad -K^{12}&{}\quad -K^{13}&{}\quad K^{2}&{}\quad K^{3}&{}\quad -K^{123}&{}\quad -K^{23}\\ K^{2}&{}\quad K^{12}&{}\quad K^{0}&{}\quad -K^{23}&{}\quad -K^{1}&{}\quad K^{123}&{}\quad K^{3}&{}\quad K^{13}\\ K^{3}&{}\quad K^{13}&{}\quad K^{23}&{}\quad K^{0}&{}\quad -K^{123}&{}\quad -K^{1}&{}\quad -K^{2}&{}\quad -K^{12}\\ K^{12}&{}\quad -K^{2}&{}\quad K^{1}&{}\quad -K^{123}&{}\quad K^{0}&{}\quad -K^{23}&{}\quad -K^{13}&{}\quad -K^{3}\\ K^{13}&{}\quad -K^{3}&{}\quad K^{123}&{}\quad K^{1}&{}\quad K^{23}&{}\quad K^{0}&{}\quad -K^{12}&{}\quad K^{2}\\ K^{23}&{}\quad -K^{123}&{}\quad -K^{3}&{}\quad K^{2}&{}\quad -K^{13}&{}\quad K^{12}&{}\quad K^{0}&{}\quad -K^{1}\\ K^{123}&{}\quad K^{23}&{}\quad -K^{13}&{}\quad K^{12}&{}\quad K^{3}&{}\quad -K^{2}&{}\quad K^{1}&{}\quad K^{0}\\ \end{pmatrix},\\ \bar{L}= & {} \begin{pmatrix} L^{0}&{}\quad -L^{1}&{}\quad -L^{2}&{}\quad -L^{3}&{}\quad -L^{12}&{}\quad -L^{13}&{}\quad -L^{23}&{}\quad L^{123}\\ L^{1}&{}\quad L^{0}&{}\quad -L^{12}&{}\quad -L^{13}&{}\quad L^{2}&{}\quad L^{3}&{}\quad -L^{123}&{}\quad -L^{23}\\ L^{2}&{}\quad L^{12}&{}\quad L^{0}&{}\quad -L^{23}&{}\quad -L^{1}&{}\quad L^{123}&{}\quad L^{3}&{}\quad L^{13}\\ L^{3}&{}\quad L^{13}&{}\quad L^{23}&{}\quad L^{0}&{}\quad -L^{123}&{}\quad -L^{1}&{}\quad -L^{2}&{}\quad -L^{12}\\ L^{12}&{}\quad -L^{2}&{}\quad L^{1}&{}\quad -L^{123}&{}\quad L^{0}&{}\quad -L^{23}&{}\quad -L^{13}&{}\quad -L^{3}\\ L^{13}&{}\quad -L^{3}&{}\quad L^{123}&{}\quad L^{1}&{}\quad L^{23}&{}\quad L^{0}&{}\quad -L^{12}&{}\quad L^{2}\\ L^{23}&{}\quad -L^{123}&{}\quad -L^{3}&{}\quad L^{2}&{}\quad -L^{13}&{}\quad L^{12}&{}\quad L^{0}&{}\quad -L^{1}\\ L^{123}&{}\quad L^{23}&{}\quad -L^{13}&{}\quad L^{12}&{}\quad L^{3}&{}\quad -L^{2}&{}\quad L^{1}&{}\quad L^{0}\\ \end{pmatrix}. \end{aligned}$$

It can be checked that when \(\varepsilon _{1}=\varepsilon _{2}=1\), there exists a positive matrix \(P=(P_{1}~~P_{2}~~P_{3})\) satisfying (9) with

$$\begin{aligned} P_{1}= & {} \begin{pmatrix} 2.6449&{}\quad 0.2637&{}\quad 0.0324&{}\quad -0.2347&{}\quad 0.0081\\ 0.2637&{}\quad 1.7957&{}\quad 0.2008&{}\quad -0.0737&{}\quad -0.3096\\ 0.0324&{}\quad 0.2008&{}\quad 2.5660&{}\quad 0.2831&{}\quad -0.0648\\ -0.2347&{}\quad -0.0737&{}\quad 0.2831&{}\quad 1.6878&{}\quad -0.1734\\ 0.0081&{}\quad -0.3096&{}\quad -0.0648&{}\quad -0.1734&{}\quad 2.6993\\ 0.4114&{}\quad -0.0044&{}\quad 0.1340&{}\quad 0.0028&{}\quad 0.2670\\ 0.0336&{}\quad 0.1808&{}\quad -0.1059&{}\quad -0.3960&{}\quad -0.0042\\ -0.0790&{}\quad 0.0857&{}\quad 0.2766&{}\quad -0.0318&{}\quad 0.3636\\ -0.0464&{}\quad -0.2901&{}\quad 0.1109&{}\quad 0.4922&{}\quad -0.0531\\ 0.0236&{}\quad -0.4118&{}\quad 0.1046&{}\quad 0.1967&{}\quad -0.3622\\ 0.0195&{}\quad -0.3044&{}\quad -0.0935&{}\quad -0.1195&{}\quad 0.9302\\ 0.3721&{}\quad -0.0088&{}\quad 0.1086&{}\quad 0.0058&{}\quad 0.3870\\ -0.0281&{}\quad -0.2722&{}\quad -0.8552&{}\quad -0.4421&{}\quad 0.0806\\ 0.3521&{}\quad -0.0449&{}\quad -0.3785&{}\quad -0.3272&{}\quad 0.0603\\ 0.9137&{}\quad 0.4011&{}\quad 0.0215&{}\quad -0.3509&{}\quad 0.0129\\ 0.3935&{}\quad 0.3147&{}\quad 0.3533&{}\quad 0.0175&{}\quad -0.4025 \end{pmatrix},\\ P_{2}= & {} \begin{pmatrix} 0.4114&{}\quad 0.0336&{}\quad -0.0790&{}\quad -0.0464&{}\quad 0.0236\\ -0.0044&{}\quad 0.1808&{}\quad 0.0857&{}\quad -0.2901&{}\quad -0.4118\\ 0.1340&{}\quad -0.1059&{}\quad 0.2766&{}\quad 0.1109&{}\quad 0.1046\\ 0.0028&{}\quad -0.3960&{}\quad -0.0318&{}\quad 0.4922&{}\quad 0.1967\\ 0.2670&{}\quad -0.0042&{}\quad 0.3636&{}\quad -0.0531&{}\quad -0.3622\\ 1.6532&{}\quad -0.3396&{}\quad 0.0031&{}\quad 0.2306&{}\quad -0.0129\\ -0.3396&{}\quad 2.5373&{}\quad 0.2003&{}\quad -0.8288&{}\quad -0.1916\\ 0.0031&{}\quad 0.2003&{}\quad 1.6179&{}\quad -0.3554&{}\quad -0.2537\\ 0.2306&{}\quad -0.8288&{}\quad -0.3554&{}\quad 2.6583&{}\quad 0.2859\\ -0.0129&{}\quad -0.1916&{}\quad -0.2537&{}\quad 0.2859&{}\quad 1.7683\\ 0.3964&{}\quad -0.0744&{}\quad 0.1956&{}\quad 0.0709&{}\quad -0.2812\\ 0.3524&{}\quad -0.2240&{}\quad 0.0047&{}\quad 0.3427&{}\quad -0.0123\\ -0.1176&{}\quad 0.1492&{}\quad -0.2889&{}\quad -0.2581&{}\quad -0.2005\\ 0.0012&{}\quad 0.3688&{}\quad -0.0407&{}\quad -0.3178&{}\quad 0.1620\\ 0.3748&{}\quad 0.0276&{}\quad -0.1070&{}\quad -0.0448&{}\quad -0.0360\\ 0.0017&{}\quad 0.1087&{}\quad -0.0255&{}\quad -0.0581&{}\quad 0.1350 \end{pmatrix}, \end{aligned}$$
$$\begin{aligned} P_{3}= & {} \begin{pmatrix} 0.0195&{}\quad 0.3721&{}\quad -0.0281&{}\quad 0.3521&{}\quad 0.9137&{}\quad 0.3935\\ -0.3044&{}\quad -0.0088&{}\quad -0.2722&{}\quad -0.0449&{}\quad 0.4011&{}\quad 0.3147\\ -0.0935&{}\quad 0.1086&{}\quad -0.8552&{}\quad -0.3785&{}\quad 0.0215&{}\quad 0.3533\\ -0.1195&{}\quad 0.0058&{}\quad -0.4421&{}\quad -0.3272&{}\quad -0.3509&{}\quad 0.0175\\ 0.9302&{}\quad 0.3870&{}\quad 0.0806&{}\quad 0.0603&{}\quad 0.0129&{}\quad -0.4025\\ 0.3964&{}\quad 0.3524&{}\quad -0.1176&{}\quad 0.0012&{}\quad 0.3748&{}\quad 0.0017\\ -0.0744&{}\quad -0.2240&{}\quad 0.1492&{}\quad 0.3688&{}\quad 0.0276&{}\quad 0.1087\\ 0.1956&{}\quad 0.0047&{}\quad -0.2889&{}\quad -0.0407&{}\quad -0.1070&{}\quad -0.0255\\ 0.0709&{}\quad 0.3427&{}\quad -0.2581&{}\quad -0.3178&{}\quad -0.0448&{}\quad -0.0581\\ -0.2812&{}\quad -0.0123&{}\quad -0.2005&{}\quad 0.1620&{}\quad -0.0360&{}\quad 0.1350\\ 2.6244&{}\quad 0.2779&{}\quad 0.0947&{}\quad 0.0869&{}\quad 0.0198&{}\quad -0.4360\\ 0.2779&{}\quad 1.6529&{}\quad -0.1558&{}\quad 0.0023&{}\quad 0.4104&{}\quad 0.0032\\ 0.0947&{}\quad -0.1558&{}\quad 2.6219&{}\quad 0.2634&{}\quad -0.0153&{}\quad -0.2451\\ 0.0869&{}\quad 0.0023&{}\quad 0.2634&{}\quad 1.6662&{}\quad 0.2308&{}\quad 0.0133\\ 0.0198&{}\quad 0.4104&{}\quad -0.0153&{}\quad 0.2308&{}\quad 2.6484&{}\quad 0.2676\\ -0.4360&{}\quad 0.0032&{}\quad -0.2451&{}\quad 0.0133&{}\quad 0.2676&{}\quad 1.6624 \end{pmatrix}, \end{aligned}$$

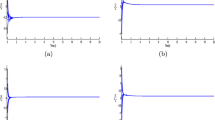
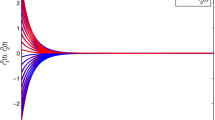
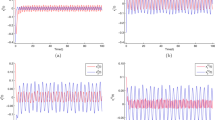
Therefore, the system is globally asymptotically stable from Theorem 1. The numerical simulations for trajectories are shown in Figs. 1 and 2. In the above two figures, each neuron has 8 lines corresponding to its components.

Fig. 1
figure 1

Trajectories of \(z_{1}\) in Example 1

Full size image
Fig. 2
figure 2

Trajectories of \(z_{2}\) in Example 1

Full size image

5 Conclusion

In this paper, we have proposed the Clifford-valued RNNs and explored the existence of the unique equilibrium and the stability of such systems. Some sufficient conditions ensuring the global asymptotic stability and the global exponential stability of the delayed Clifford-valued RNNs have been obtained in terms of LMIs. When the system reduces to a complex-valued (\(m=1\)) or real-valued neural network (\(m=0\)), the corresponding stability criterion could be obtained. At last, an example is given to show the effectiveness of the results given.