Boubaker polynomials and their applications for solving fractional two-dimensional nonlinear partial integro-differential Volterra integral equations

Abstract

The main aim of this paper is to expand an operational matrix method for solving two-dimensional nonlinear fractional partial integro-differential Volterra integral equation. First, we present and use the operational matrix of fractional integration of the Boubaker polynomials. Then, we prove the convergence analysis of the method. Finally, to explain the accuracy and efficiency of the proposed method, we provide some numerical examples and present the results in figures and tables.

1 Introduction

The spark of the integral equations started in 1823 along with the generalization of the tautochrone proposed by Abel, in which the solution of the problem was involved by the integral equation The latter equation is known as an integral equation of the first kind, In 1837, Liouville, a mathematician, realized in the course of solving a special second-order linear differential equation that the solution could be found by solving an integral equation completely different from previous ones. Therefore, he decided to call it the integral equation of the second kind.

According to the wide range of applications of the integral and integro-differential equations in different fields of sciences, many researchers used various numerical methods based on wavelets, polynomials and orthogonal functions for solving these equations. For more details, one can refer to Doha et al. (2011), Yi et al. (2013), Asgari and Ezzati (2017) and Schiavane et al. (2002). The fractional differential equations as well as integro-differential equations have been sprawled and traced in various scientific areas such as physics, engineering, chemistry, and biology (Safavi 2017; Nikan et al. 2021a, b; Fazli et al. 2015; Nikan and Avazzadeh 2021). As a result, various procedures for obtaining approximate solutions for these kind of equations have attracted many researchers. In recent years, several numerical methods have been devoted to solve fractional Volterra integral equation. The authors of Rahimkhani et al. (2017) applied Bernoulli wavelets operational matrix for solving fractional delay differential equations. Keshavarz et al. (2019) applied BWs method for solving nonlinear problems in calculus of variations. The authors of Rahimkhani et al. (2016) presented Bernoulli wavelets and their applications. In Rahimkhani and Ordokhani (2018), the authors solved partial differential equations using Bernoulli wavelets. Barikbin (2017) proposed a two-dimensional Bernoulli wavelets method for solving the fractional diffusion wave equation. To study the proposed numerical methods for solving some fractional differential equations, one can refer to Khajehnasiri and Safavi (2021), Ebadian and Khajehnasiri (2014), Heydari et al. (2014a), and Saadatmandi and Dehghan (2010).

Boubake (2007) developed Boubaker polynomials as a guide for solving heat transfer equations in one dimension. Various branches of science employ these sets of orthogonal functions today: cryogenics, biology, dynamical systems, economy, nonlinear systems, the approximation theory, thermodynamics, mechanics, hydrology, molecular dynamics, fundamental mathematics, biophysics, photovoltaic, complex analysis, matrix analysis, fundamental physics, applied mathematics, cryptography, and algebra Rabiei et al. (2017).

Boubaker polynomials have been successfully applied to solve several problems, but it has not been used to solve two-dimensional fractional partial Volterra integral equations. In addition, in approximating an arbitrary function, the advantages of Boubaker polynomials, over Boubaker polynomials, are given in Rabiei et al. (2018). Therefore, the numerical scheme developed in this paper uses Boubaker polynomials as basis functions, and our numerical results show that the method can efficiently solve this kind of problem. The benefit of this method is the low cost of setting up the equations without applying any projection method such as Galerkin and collocation.

Boubaker polynomials have recently been used to solve integral and differential fractions of fractional order by some researchers. The authors of Rabiei and Ordokhani (2018) employed the Boubaker hybrid function for solving fractional optimal control problems. In Rabiei et al. (2017), the fractional-order Boubaker function is used for solving delay fractional optimal control problems. In Davaeifar and Rashidinia (2016), the authors applied the Boubaker polynomials and collocation method to solve the systems of nonlinear Volterra–Fredholm integral equations. The authors of Rabiei and Ordokhani (2017) considered the Boubaker polynomials for solving pantograph delay differential equation.

It should be noted that the operational matrices of integration and differential play an important role in the development of numerical methods for solving integral and integro-differential equations, among which we can refer to the operational matrices in Yi and Huang (2014), Li a and Zhao (2010), Hesameddini and Shahbazi (2018), Jiaquan Xie (2017), Rawashdeh (2006), and Heydari et al. (2014b).

The two-dimensional fractional partial Volterra integral equations (2DFPVIEs) often occur in some advanced applications, for example, the footprints of such equations could be found in physics, especially in plasma. In addition, some investigations have been carried out by mathematicians (Xie et al. 2019; Xie and Yib 2019; Khajehnasiri et al. 2021; Najafalizadeh and Ezzati 2016; Safavi et al. 2021). In the present paper, we consider the following 2DFPVIEs:

$$\begin{aligned} D_{*\chi }^{\alpha }u(\chi ,\zeta )+ & {} D_{*\zeta }^{\beta }u(\chi ,\zeta )+ u(\chi ,\zeta )= g(\chi ,\zeta ) \nonumber \\+ & {} \frac{1}{\Gamma (\alpha )\Gamma (\beta )}\int _{0}^{\chi }\int _{0}^{\zeta }(\chi -\tau )^{(\alpha -1)}(\zeta -\eta )^{(\beta -1)}F(\chi ,\zeta ,\tau ,\eta ,u(\tau ,\eta ))\mathrm{d}\eta \mathrm{d}\tau ,\nonumber \\ \end{aligned}$$

(1)

with the initial conditions

$$\begin{aligned} \frac{\partial ^{i}}{\partial \chi ^{i}}u(0,\zeta )=\varrho _{i}(\zeta ),\quad i=0,1,\ldots , \rho -1,\quad \rho -1<\alpha \le \rho ,\quad \rho \in N, \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial ^{j}}{\partial \zeta ^{j}}u(\zeta ,0)=\delta _{j}(\zeta ),\quad j=0,1,\ldots , \gamma -1,\quad \gamma -1<\beta \le \gamma ,\quad \gamma \in N, \end{aligned}$$

(3)

where $D_\chi ^{\alpha }$ and $D_\zeta ^{\beta }$ are fractional differential operators with $\rho -1<\alpha \le \rho$, $\gamma -1< \beta \le \gamma$, $g \in L^{1} (R),$ is a known function defined on region $R:=[0,1]\times [0,1]$ and u is an unknown function that should be determined. We also suppose that the nonlinear function, F, would be as follows:

$$\begin{aligned} F(\chi ,\zeta ,\tau ,\eta ,u)=k_{}(\chi ,\zeta ,s,y)[u(\tau ,\eta )]^{P}, \end{aligned}$$

(4)

where p is a positive integer. Throughout our work, we initiated a new form of an operational matrix of fractional integration of Boubaker polynomials (BPs) to approximate the solution of 2DFPVIE. By the properties of the two-dimensional Boubaker polynomial (2DBPs) and utilizing operational matrices, Eqs. (1)–(3) were converted to an algebraic equation.

This paper is organized as follows: in Sect. 2, the basic concepts of fractional calculus are presented. Some necessary properties of the Boubaker polynomials and the operational matrix of integration, of 2DBPs are discussed in Sect. 3. In general, we describe the method in this section. Afterwards, the convergence analysis of the proposed method is analyzed by a theorem in Sect. 5. Section 6 shows the efficiency and accuracy of the proposed scheme by solving some numerical examples. Finally, Sect. 7 contains the concluding remarks.

2 Preliminaries

The fundamental characteristics and the fractional integral and derivative definitions are recalled in the following sections.

Definition 2.1

(Abbasa and Benchohra 2014) The Riemann–Liouville fractional integral of order $\alpha$ is defined as follows:

$$\begin{aligned} I_{\chi _{0}}^{\alpha } f(\chi )=\frac{1}{\Gamma (\alpha )} \int _{\chi _{0}}^{\chi } (\chi -\zeta )^{\alpha -1} f(\zeta )\mathrm{d}\zeta ,\quad \theta _{1}>0,\quad \chi >0. \end{aligned}$$

(5)

Definition 2.2

(Abbasa and Benchohra 2014) The Riemann–Liouville and Caputo fractional derivatives of order $\alpha$ is defined as follows:

$$\begin{aligned} D_{*\chi _{0}}^{\alpha }f(\chi )=\frac{\mathrm{d}^{n}}{\mathrm{{d}}\chi ^{n}}[I_{\chi _{0}}^{n-\alpha }f(\chi )], \end{aligned}$$

(6)

$$\begin{aligned} D_{*\chi _{0}}^{\alpha }f(\chi )=I_{\chi _{0}}^{n-\alpha }[\frac{\mathrm{d}^{n}}{\mathrm{{d}}\chi ^{n}}f(\chi )], \end{aligned}$$

(7)

such that $n-1\le \alpha <n$ and $n\in \mathcal {\mathbb {N}}$.

Clearly, we can write

$$\begin{aligned} D_{*\chi _{0}}^{\alpha }f(\chi )=\frac{1}{\Gamma (n-\alpha )}\frac{\mathrm{d}^{n}}{\mathrm{d}^{n}}\int _{\chi _{0}}^{\chi }(\chi -\zeta )^{n-\alpha -1}f(\zeta )\mathrm{d}\zeta ,\quad \chi >\chi _{0}. \end{aligned}$$

(8)

Lemma 2.3

(Mojahedfar and Marzabad 2017) If $n-1< \alpha \le n$, $n\in {\mathbb {N}}$, then $D_{*\chi }^{\alpha }I^{\alpha }u(\chi ,\zeta )=u(\chi ,\zeta )$, and

$$\begin{aligned} I^{\alpha }D_{*\chi }^{\alpha }{} u (\chi ,\zeta )=u (\chi ,\zeta )-\sum _{k=0}^{n-1}\frac{\partial ^{k}u(0^{+},\zeta )}{\partial \chi ^{k}}\frac{\chi ^{k}}{k!},\quad \chi >0. \end{aligned}$$

Lemma 2.4

(Mojahedfar and Marzabad 2017) If $n-1< \beta \le n$, $n\in {\mathbb {N}}$, then $D_{*\zeta }^{\beta }I^{\beta }u(\chi ,\zeta )=u(\chi ,\zeta )$, and:

$$\begin{aligned} I^{\beta }D_{*t}^{\beta }{} u (\chi ,\zeta )=u (\chi ,\zeta )-\sum _{k=0}^{n-1}\frac{\partial ^{k}u(\chi ,0^{+})}{\partial \zeta ^{k}}\frac{\zeta ^{k}}{k!},\quad \zeta >0. \end{aligned}$$

Definition 2.5

(Abbasa and Benchohra 2014) Let $\theta =(\alpha ,\beta )\in (0,\infty )\times (0,\infty ), D:=[0,a]\times [0,b], r=(0,0),$ and $u\in L^{1}(\Omega )$. The left-sided mixed Riemann–Liouville integral of order $(\alpha ,\beta )$ of u is defined by

$$\begin{aligned} (I_{\theta }^{(\alpha ,\beta )}u)(\chi ,\zeta )=\frac{1}{\Gamma (\alpha )\Gamma (\beta )}\int _{0}^{\chi }\int _{0}^{\zeta }(\chi -\tau )^{(\alpha -1)}(\zeta -\eta )^{(\beta -1)}u(\tau ,\eta )\mathrm{d}\eta \mathrm{d}\tau . \end{aligned}$$

(9)

In particular,

$1.\quad (I_{r}^{r}u)(\chi ,\zeta )=u(\chi ,\zeta ),$

$2.\quad (I_{r}^{\sigma }u)(\chi ,\zeta )=\int _{0}^{\chi }\int _{0}^{y}u(s,\zeta )\mathrm{{d}}\zeta \mathrm{{d}}s, (\chi ,\zeta )\in \Omega , \sigma =(1,1),$

$3.\quad (I_{r}^{\theta }u)(\chi ,0)=(I_{r}^{\theta })(0,\zeta )=0, \chi \in [0,a], y\in [0,b],$

$4.\quad I_{r}^{\theta }\chi ^{\lambda }\zeta ^{\omega }=\frac{\Gamma (1+\lambda )\times \Gamma (1+\omega )}{\Gamma (1+\lambda +\alpha )\times \Gamma (1+\omega +\beta )}\chi ^{\lambda +\alpha }\zeta ^{\omega +\beta },(\chi ,\zeta )\in \Omega , \lambda ,\omega \in (-1,\infty ).$

Definition 2.6

(Khajehnasiri et al. 2021) The Caputo time fractional derivative operative of order $\alpha >0$ is defined as

$$\begin{aligned} D_{*\zeta }^{\alpha }f(\chi ,\zeta )= & {} \frac{\partial ^{\alpha }f(\chi ,\zeta )}{\partial \zeta ^{\alpha }}\\= & {} \left\{ \begin{array}{cccc} \frac{1}{\Gamma (n-\alpha )}\int _{0}^{\zeta }\frac{\partial ^{\alpha }f(\chi ,\zeta )}{\partial s^{n}}(\zeta -s)^{n-\alpha -1}\mathrm{d}s, &{} n-1<\alpha <n\quad n\in N\bigcup \lbrace 0\rbrace \\ \frac{\partial ^{n}f(\chi ,\zeta )}{\partial \zeta ^{n}}, &{} n=\alpha . \end{array} \right. \end{aligned}$$

3 Boubaker polynomials

The BPs in the interval [0, 1] are defined as

$$\begin{aligned} B_{0}= & {} 1,\\ B_{n}(\chi )= & {} \sum _{p=0}^{\lfloor \frac{n}{2}\rfloor }(-1)^{p}\left( \begin{array}{ccccc} n-p\\ p \end{array}\right) \frac{n-4p}{m-p}\chi ^{n-2p},\quad n \geqslant 1, \end{aligned}$$

where $\lfloor . \rfloor$ is the floor function. The BPs have also a recursive relation:

$$\begin{aligned} B_{m}(\zeta )=\zeta B_{m-1}(\zeta )-B_{m-2}(\zeta ),\quad m>2. \end{aligned}$$

(10)

3.1 Approximation of the function

It is clear that

$$\begin{aligned} Y=\mathrm{span}\left\{ B_{0}(\zeta ), B_{1}(\zeta ),\ldots , B_{k}(\zeta )\right\} \end{aligned}$$

(11)

represents a closed as well as finite-dimensional subspace of the Hilbert space $H = L^{2}[0, 1].$ Therefore, for every $u\in H,$ we have a unique best approximation out of Y such as ${\tilde{u}}\in Y$ such that

$$\begin{aligned} \forall y\in Y, \quad \Vert u-{\tilde{u}}\Vert \le \Vert u-y\Vert . \end{aligned}$$

(12)

Therefore, for ${\tilde{u}}\in Y$, there is a unique set of coefficients $c_{0}, c_{1},\ldots ,c_{k}$ such that (Kreyszig 1978)

$$\begin{aligned} u(\zeta )\simeq {\tilde{u}}(\zeta )=\sum _{j=0}^{k}c_{j}B_{j}(\zeta )=C^{T}\Phi (\zeta ), \end{aligned}$$

(13)

where C and $\Phi (\zeta )$ are vectors as follows:

$$\begin{aligned} C=[c_{0},c_{1},\ldots , c_{k}]^{T}, \quad \Phi (\zeta )=[B_{0}(\zeta ), B_{1}(\zeta ), \ldots , B_{k}(\zeta )]^{T}. \end{aligned}$$

(14)

Suppose that

$$\begin{aligned} u_{j}=< u, B_{j}>=\int _{0}^{1}u(\zeta )B_{j}(\zeta )\mathrm{{d}}\zeta , \end{aligned}$$

(15)

in which $<\cdot ,\cdot>$ represents inner product, so we have

$$\begin{aligned} u_{j}\simeq \sum _{i=0}^{k}c_{i}\int _{0}^{1}B_{i}(\zeta )B_{j}(\zeta )\mathrm{{d}}\zeta =\sum _{i=0}^{m}c_{i}r_{ij},\quad j=0,1,\ldots , k, \end{aligned}$$

(16)

with

$$\begin{aligned} r_{ij}=\int _{0}^{1}B_{i}(\zeta )B_{j}(\zeta )\mathrm{{d}}\zeta \quad i,j=0,1,\ldots , k. \end{aligned}$$

(17)

Now, we can write

$$\begin{aligned} U =<u,\phi >= \begin{bmatrix} u_{0} \\ u_{1} \\ \vdots \\ u_{k}\\ \end{bmatrix},\quad R=[r_{ij}], \end{aligned}$$

(18)

where

$$\begin{aligned} u_{j}=C^{T}[r_{0j},r_{1j},\ldots , r_{kj}]^{T}. \end{aligned}$$

(19)

Therefore, we can conclude that $U^{T}=C^{T}R$, and C could be evaluated as

$$\begin{aligned} C=(R^{-1})^{T}<u,\phi >, \end{aligned}$$

(20)

where R represents an $(m+1) \times (m+1)$ matrix as

$$\begin{aligned} R=<\Phi (\zeta ), \Phi (\zeta )>=\int _{0}^{1}\Phi (\zeta )(\Phi (\zeta ))^{T}\mathrm{d}\zeta . \end{aligned}$$

(21)

A function $u(\chi ,\zeta )$ may be expanded in terms of two-dimensional Boubaker polynomials (2DBPs) as the following form:

$$\begin{aligned} u(\chi ,\zeta )\simeq \sum _{i=0}^{l}\sum _{j=0}^{k}c_{ij}B_{i,j}(\chi ,\zeta )=C^{T}\Phi (\chi ,\zeta ), \end{aligned}$$

(22)

where

$$\begin{aligned}&C=[c_{0,0},\ldots ,c_{0,k},\ldots ,c_{l,0}\ldots ,c_{l,k}]^{T},\quad B_{ij}(\chi ,\zeta )=B_{i}(\chi )B_{j}(\zeta ),\nonumber \\&\Phi (\chi ,\zeta )=[B_{0,0}(\chi ,\zeta ),\ldots , B_{0,k}(\chi ,\zeta ),\ldots , B_{l,0}(\chi ,\zeta ),\ldots , B_{l,k}(\chi ,\zeta )]^{T}\nonumber \\&\quad =\Phi (\chi )\otimes \Phi (\zeta ), \end{aligned}$$

(23)

and also, $\otimes$ is Kronecker product.

The BPs basis can be represented by

$$\begin{aligned} \Phi (\chi )=\Upsilon T_{m}(\chi ), \end{aligned}$$

(24)

where $\Upsilon =(\Lambda _{i,j})_{i,j=0}^{m}$ and $T_{m}(\chi )=[1,\chi ,\ldots ,\chi ^{m}]^{T}$ represents a matrix of order $(m+1)\times (m+1)$. Now, we concentrate on the following statements (Rabiei et al. 2017):

$$\begin{aligned} B_{n}(\chi )= & {} \sum _{p=0}^{\lfloor \frac{n}{2}\rfloor }(-1)^{p}\left( \begin{array}{ccccc} n-p\\ p \end{array}\right) \frac{n-4p}{m-p}\chi ^{n-2p},\quad n \geqslant 1, \end{aligned}$$

or

$$\begin{aligned} B_{n}(\chi )= & {} \sum _{j=n-2\lfloor \frac{n}{2}\rfloor }^{n}(-1)^{\frac{n-j}{2}}\left( \begin{array}{ccccc} \frac{n+j}{2}\\ \frac{n-j}{2} \end{array}\right) \frac{2j-n}{\frac{n+j}{2}}\chi ^{j}=\sum _{j=0}^{k}\Lambda _{i,j}\chi ^{j},\quad n \geqslant 1. \end{aligned}$$

Obviously, we can derive entries of the matrix $\Upsilon$ for all $n\ge 2$, $j=n-2\lfloor \frac{n}{2}\rfloor , \ldots , n,$ by the following rule:

$$\begin{aligned} \Lambda _{i,j}= & {} \left\{ \begin{array}{cccc} (-1)^{\frac{n-j}{2}} \left( \begin{array}{ccccc} \frac{n+j}{2}\\ \frac{n-j}{2} \end{array}\right) \frac{2j-n}{\frac{n+j}{2}}, &{} \mathrm{{if}}\; (n-j) \, \mathrm{{\,is \,even}}, \\ 0,\quad &{} \mathrm{{if}} \, (n-j) \,\mathrm{{is \,odd}}. \end{array} \right. \end{aligned}$$

According to the definition of $B_{0}(\zeta )$ and $B_{1}(\zeta )$, the previous formula for $i=1,$ and for $i=0$ are as follows:

$$\begin{aligned} \Lambda _{0,0}=1,\quad \Lambda _{0,j}=1,\quad j=1,\ldots , k. \end{aligned}$$

Now, we can present 2DBPs as follows:

$$\begin{aligned} B_{n,m}^{}(\chi ,\zeta )=\sum _{p=0}^{\lfloor \frac{n}{2}\rfloor }\sum _{q=0}^{\lfloor \frac{m}{2}\rfloor }(-1)^{p+q}\frac{n-4p}{n-p}\frac{m-4q}{m-q}\left( \begin{array}{ccccc} n-p\\ p \end{array}\right) \left( \begin{array}{ccccc} m-q\\ q \end{array}\right) \chi ^{(n-4p)}\zeta ^{(m-4q)}, \end{aligned}$$

where $m=0,1,\ldots ,M$, $n=0,1,\ldots ,N$, and $p=0,1,\ldots \lceil \frac{n}{2}\rceil$, $q=0,\ldots ,\lceil \frac{m}{2}\rceil$.

3.2 Operational matrix for fractional integration of 2DBPs

In this section, we describe the process of obtaining $P^{\alpha ,\beta },$ the operational matrix of fractional integration of 2DBPs, such that

$$\begin{aligned} I^{\alpha }I^{\beta }\Phi ^{}(\chi ,\zeta )=P^{\alpha ,\beta }\Phi ^{}(\chi ,\zeta ), \end{aligned}$$

(25)

where $\Phi (\chi ,\zeta )$ is defined in Eq. (23). By the help of definition of $B_{n,m}(\chi ,\zeta )$ and using the linearity of Riemann–Liouville fractional integration, one can derive that

$$\begin{aligned}&I^{\alpha }I^{\beta }B_{n,m}(\chi ,\zeta )\nonumber \\&\quad =\sum _{p=0}^{\lfloor \frac{n}{2}\rfloor }\sum _{q=0}^{\lfloor \frac{m}{2}\rfloor }(-1)^{p+q}\frac{n-4p}{n-p}\frac{m-4q}{m-q} \left( \begin{array}{ccccc} n-p\\ p \end{array}\right) \left( \begin{array}{ccccc} m-q\\ q \end{array}\right) I^{\alpha }I^{\beta }\chi ^{(n-4p)}\zeta ^{(m-4q)} \nonumber \\&=\sum _{p=0}^{\lfloor \frac{n}{2}\rfloor }b_{n,p}\chi ^{ n-2 p+\alpha }\sum _{q=0}^{\lfloor \frac{m}{2}\rfloor }b_{m,q}\zeta ^{ m-2q+\beta },\quad n,m\ge 2, \end{aligned}$$

(26)

where

$$\begin{aligned} b_{n,p}=(-1)^{p}\frac{(n-p-1)!(n-4p)}{p!\Gamma (n-2p+\alpha +1)}, \end{aligned}$$

(27)

$$\begin{aligned} b_{m,q}=(-1)^{q}\frac{(m-q-1)!(m-4q)}{q!\Gamma (m-2q+\beta +1)}. \end{aligned}$$

(28)

Now, we can expand $\chi ^{\alpha n-2\alpha p-v}$ and $\zeta ^{\beta m-2\beta q-w}$ in terms of BPs as

$$\begin{aligned} \chi ^{ n-2 p-\alpha }\simeq & {} \sum _{i=0}^{k}c_{pi}B_{i}^{}(\chi ), \end{aligned}$$

(29)

$$\begin{aligned} \zeta ^{m-2q-\beta }\simeq & {} \sum _{j=0}^{k}c_{qj}B_{j}^{}(\zeta ), \end{aligned}$$

(30)

where

$$\begin{aligned} c_{pi}=\frac{\langle \chi ^{ n-2 p+\alpha }, B_{i}(\zeta )\rangle }{\langle B_{i}(\zeta ), B_{i}(\zeta )\rangle },\quad c_{qj}=\frac{\langle t^{ m-2 q+\beta }, B_{j}(\zeta )\rangle }{\langle B_{j}(\zeta ), B_{j}(\zeta )\rangle }. \end{aligned}$$

(31)

By substituting Eqs. (29)–(31) in (26), we have

$$\begin{aligned} \begin{aligned}&I^{\alpha } B_{n}^{}(\chi ) \simeq \sum _{p=0}^{\lfloor \frac{n}{2}\rfloor }b_{n,p}\sum _{j=0}^{k}c_{p,j}B_{j}^{}(\chi )=\sum _{j=0}^{k}\left( \sum _{p=0}^{\lfloor \frac{n}{2}\rfloor }b_{n,p}c_{p,j}\right) B_{j}^{}(\chi )\\&I^{\beta } B_{m}^{}(\zeta ) \simeq \sum _{q=0}^{\lfloor \frac{m}{2}\rfloor }b_{m,q}\sum _{j=0}^{k}y_{q,j}B_{j}^{}(\zeta )=\sum _{j=0}^{k}\left( \sum _{q=0}^{\lfloor \frac{m}{2}\rfloor }b_{m,q}y_{q,j}\right) B_{j}^{}(\zeta ). \end{aligned} \end{aligned}$$

(32)

Now, by supposing

$$\begin{aligned} \theta _{n,j,p}=b_{n,p}c_{p,j},\quad \Omega _{m,i,q}=b_{m,q}y_{q,i}, \end{aligned}$$

(33)

we can write Eq. (32) in the following form:

$$\begin{aligned} I^{\alpha }B_{n}^{}(\chi )\simeq \left[ \sum _{p=0}^{\lfloor \frac{n}{2}\rfloor }\theta _{n,0,p}, \sum _{p=0}^{\lfloor \frac{n}{2}\rfloor }\theta _{n,1,p},\ldots , \sum _{p=0}^{\lfloor \frac{n}{2}\rfloor }\theta _{n,k,p}\right] \Phi ^{}(\chi ), \end{aligned}$$

(34)

$$\begin{aligned} I^{\beta }B_{m}^{}(\zeta )\simeq \left[ \sum _{q=0}^{\lfloor \frac{m}{2}\rfloor }\Omega _{m,0,q}, \sum _{q=0}^{\lfloor \frac{m}{2}\rfloor }\Omega _{m,1,q},\ldots , \sum _{q=0}^{\lfloor \frac{m}{2}\rfloor }\Omega _{m,k,q}\right] \Phi ^{}(\zeta ). \end{aligned}$$

(35)

For $n,m=0,1,$ we have

$$\begin{aligned} I^{\alpha }B_{0}(\chi )&=\frac{1}{\Gamma (\alpha +1)}\chi ^{\alpha },\quad I^{\alpha }B_{1}(\chi )=\frac{1}{\Gamma (\alpha +2)}\chi ^{\alpha +1},\\ I^{\beta }B_{0}(\zeta )&=\frac{1}{\Gamma (\beta +1)}\zeta ^{\alpha },\quad I^{\beta }B_{1}(\zeta )=\frac{1}{\Gamma (\beta +2)}\zeta ^{\beta +1}, \end{aligned}$$

so like the previous process $\chi ^{\alpha }$, $\chi ^{\alpha +1}$, $\zeta ^{\beta }$ and $\zeta ^{\beta +1}$ are expanded with respect to BPs as

$$\begin{aligned} \chi ^{\alpha }\simeq \sum _{j=0}^{k}v_{0,j}B_{j}(\chi ), \quad \chi ^{\alpha +1}\simeq \sum _{j=0}^{k}v_{1,j}B_{j}(\chi ) \end{aligned}$$

(36)

$$\begin{aligned} \zeta ^{\beta }\simeq \sum _{j=0}^{k}\omega _{0,j}B_{j}(\zeta ), \quad t^{\beta +1}\simeq \sum _{j=0}^{k}\omega _{1,j}B_{j}(\zeta ). \end{aligned}$$

(37)

Hence, by defining

$$\begin{aligned} P^{\alpha }= \begin{bmatrix} \frac{\upsilon _{0,0,0}}{\Gamma (\alpha +1)} &{} \frac{\upsilon _{0,1,0}}{\Gamma (\alpha +1)}&{}\ldots &{}\frac{\upsilon _{0,k,0}}{\Gamma (\alpha +1)} \\ \frac{\upsilon _{1,0,0}}{\Gamma (\alpha +1)} &{} \frac{\upsilon _{1,1,0}}{\Gamma (\alpha +1)}&{}\ldots &{}\frac{\upsilon _{1,k,0}}{\Gamma (\alpha +1)} \\ \sum _{p=0}^{1} \theta _{2,0,p}&{} \sum _{p=0}^{1} \theta _{2,1,p} &{}\ldots &{}\sum _{p=0}^{1} \theta _{2,k,p}\\ \vdots &{} \vdots &{} \vdots &{}\vdots \\ \sum _{p=0}^{\lfloor \frac{k}{2}\rfloor } \theta _{k,0,p}&{} \sum _{p=0}^{\lfloor \frac{k}{2}\rfloor } \theta _{k,1,p} &{}\ldots &{}\sum _{p=0}^{\lfloor \frac{k}{2}\rfloor } \theta _{k,k,p}\\ \end{bmatrix}, \end{aligned}$$

(38)

$$\begin{aligned} P^{\beta }= \begin{bmatrix} \frac{\omega _{0,0,0}}{\Gamma (\beta +1)} &{} \frac{\omega _{0,1,0}}{\Gamma (\beta +1)}&{}\ldots &{}\frac{\omega _{0,k,0}}{\Gamma (\beta +1)} \\ \frac{\omega _{1,0,0}}{\Gamma (\beta +1)} &{} \frac{\omega _{1,1,0}}{\Gamma (\beta +1)}&{}\ldots &{}\frac{\omega _{1,k,0}}{\Gamma (\beta +1)} \\ \sum _{q=0}^{1}\Omega _{2,0,q}&{} \sum _{q=0}^{1} \Omega _{2,1,q} &{}\ldots &{}\sum _{q=0}^{1} \Omega _{2,k,q}\\ \vdots &{} \vdots &{} \vdots &{}\vdots \\ \sum _{q=0}^{\lfloor \frac{k}{2}\rfloor } \Omega _{k,0,q}&{} \sum _{q=0}^{\lfloor \frac{k}{2}\rfloor }\Omega _{k,1,q} &{}\ldots &{}\sum _{q=0}^{\lfloor \frac{k}{2}\rfloor } \Omega _{k,k,q}\\ \end{bmatrix}, \end{aligned}$$

(39)

we conclude that

$$\begin{aligned} I^{\alpha }I^{\beta }\Phi (\chi ,\zeta )= & {} I^{\alpha }I^{\beta }\Phi (\chi )\otimes \Phi (\zeta )=I^{\alpha }\Phi (\chi )\otimes I^{\beta }\Phi (\zeta )=P^{\alpha }\Phi (\chi )\otimes P^{\beta }\Phi (\zeta )\nonumber \\= & {} (P^{\alpha }\otimes P^{\beta })\Phi (\chi ,\zeta ), \end{aligned}$$

(40)

hence,

$$\begin{aligned} P^{\alpha ,\beta }=P^{\alpha }\otimes P^{\beta }. \end{aligned}$$

(41)

Clearly, we have

$$\begin{aligned} I^{\alpha }\Phi (\chi ,\zeta )= & {} I^{\alpha }\Phi (\chi )\otimes \Phi (\zeta )\\= & {} I^{\alpha }\Phi (\chi )\otimes I \Phi (\zeta )\\= & {} P^{\alpha }\Phi (\chi )\otimes I \Phi (\zeta )\\= & {} (P^{\alpha }\otimes I)(\Phi (\chi )\otimes \Phi (\zeta ))=(P^{\alpha }\otimes I)\Phi (\chi ,\zeta ), \\ I^{\beta }\Phi (\chi ,\zeta )= & {} \Phi (\chi )\otimes I^{\beta }\Phi (\zeta )\\= & {} I\Phi (\chi )\otimes I^{\beta } \Phi (\zeta )\\= & {} I\Phi (\chi )\otimes P^{\beta } \Phi (\zeta )\\= & {} (I\otimes P^{\beta })(\Phi (\chi )\otimes \Phi (\zeta ))=(I\otimes P^{\beta })\Phi (\chi ,\zeta ), \end{aligned}$$

where I is the identity matrix. The product of two matrices of 2DBPs satisfies the following proposition:

$$\begin{aligned} \Phi (\chi ,\zeta )\Phi ^{T}(\chi ,\zeta )C\simeq {\tilde{C}}\Phi ^{}(\chi ,\zeta ), \end{aligned}$$

(42)

where ${\tilde{C}}$ is a matrix of order $(m+1)\cdot (n+1)\times (m+1)\cdot (n+1)$ and C is arbitrary vector (Rabiei et al. 2018).

3.3 Operational matrix of partial differential for 2DBPs

By applying the operator $D_{*}^{\beta }$ on the 2DBPs, $\Phi (\chi ,\zeta ),$ we have

$$\begin{aligned} D_{*}^{\beta }\Phi (\chi ,\zeta )= & {} D_{*}^{\beta }\Phi (\chi )\otimes \Phi (\zeta )\nonumber \\= & {} \Phi (\chi )\otimes D_{*}^{\beta } \Phi (\zeta )\nonumber \\= & {} I\Phi (\chi )\otimes D_{*\zeta }^{(\beta )}\Phi (\zeta )\nonumber \\= & {} (I\otimes D_{*\zeta }^{(\beta )}) (\Phi (\chi ) \otimes \Phi (\zeta ))\nonumber \\= & {} (I\otimes D_{*\zeta }^{(\beta )}) \Phi (\chi ,\zeta ), \end{aligned}$$

(43)

where $D_{*\zeta }^{(\beta )}$ is the operational matrix of differential for the $\Phi (\zeta )$. Therefore, $I\otimes D_{*\zeta }^{(\beta )}$ is defined as the operational matrix of partial differential for 2DBPs, $\Phi (\chi ,\zeta ),$ withe to variable t (Patel et al. 2018).

4 Applying the method

In this part, operational matrix of the 2DBPs is applied for solving Eq. (1). Let

$$\begin{aligned} D_{*}^{\alpha }{} u (\chi ,\zeta ) \simeq C^{T}\Phi (\chi ,\zeta ). \end{aligned}$$

(44)

Using Eq. (44) and Lemma (2.3), we have

$$\begin{aligned} u(\chi ,\zeta )=C^{T}(P^{\alpha }\otimes I)\Phi (\chi ,\zeta )+\sum _{k=0}^{n}\frac{\partial ^{k}u(0^{+},\zeta )}{\partial \chi ^{k}},\quad \chi >0. \end{aligned}$$

(45)

Therefore, by substituting the initial condition (2) as well as using 2DBPs to approximate the second term in the R.H.S of the above equation, we get

$$\begin{aligned} u(\chi ,\zeta )\simeq (C^{T}(P^{\alpha }\otimes I)+C_{p}^{T})\Phi (\chi ,\zeta ). \end{aligned}$$

(46)

Using Eq. (44), we can write

$$\begin{aligned} D_{*}^{\beta }u(\chi ,\zeta )\simeq & {} (C^{T}(P^{\alpha }\otimes I)+C_{p}^{T})D_{*}^{\beta }\Phi (\chi ,\zeta )\nonumber \\= & {} (C^{T}(P^{\alpha }\otimes I)+C_{p}^{T})D_{*}^{\beta }\Phi (\chi )\otimes \Phi (\zeta )\nonumber \\= & {} (C^{T}(P^{\alpha }\otimes I)+C_{p}^{T})\Phi (\chi )\otimes D_{*}^{\beta }\Phi (\zeta )\nonumber \\= & {} (C^{T}(P^{\alpha }\otimes I)+C_{p}^{T})I \Phi (\chi )\otimes D_{*t}^{(\beta )}\Phi (\zeta )\nonumber \\= & {} (C^{T}(P^{\alpha }\otimes I)+C_{p}^{T})(I\otimes D_{*\zeta }^{(\beta )}) \Phi (x)\otimes \Phi (\zeta )\nonumber \\= & {} (C^{T}(P^{\alpha }\otimes I)+C_{p}^{T})(I\otimes D_{*\zeta }^{(\beta )}) \Phi (\chi ,\zeta )=B^{(\beta )}\Phi (\chi ,\zeta ), \end{aligned}$$

(47)

where I is the identify matrix. In addition, from above equation, we conclude that

$$\begin{aligned} I^{\beta }D_{*}^{\beta }u(\chi ,\zeta )=B^{(\beta )}I^{\beta }\Phi (\chi ,\zeta ). \end{aligned}$$

(48)

Now, using Lemma (2.4) as well as condition (3), we have

$$\begin{aligned} u(\chi ,\zeta )-L_{P}^{T}\Phi (\chi ,\zeta )\simeq B^{(\beta )}I^{\beta } \Phi (\chi ,\zeta )=B^{(\beta )}(I^{\beta }\otimes P^{\beta }) \Phi (\chi ,\zeta ), \end{aligned}$$

(49)

where

$$\begin{aligned} \sum _{k=0}^{n-1}\frac{\partial ^{k}u(\chi ,0)}{\partial \zeta ^{k}}\frac{\zeta ^{k}}{k!}\simeq L_{p}^{T}\Phi (\chi ,\zeta ). \end{aligned}$$

(50)

Hence

$$\begin{aligned} D_{*}^{\beta }u(\chi ,\zeta )\simeq L_{p}^{T}+ B^{\beta }(I\otimes P^{\beta })D_{*}^{\beta }\Phi (\chi ,\zeta )=A^{(\beta )}\Phi (\chi ,\zeta ) \end{aligned}$$

(51)

$$\begin{aligned} A^{(\beta )}=L_{p}^{T}+B^{(\beta )}(I\otimes P^{\beta })(I\otimes D_{*\zeta }^{(\beta )}). \end{aligned}$$

(52)

To get the approximation of $[u(\tau ,\eta )]^{p}$, we have

$$\begin{aligned}{}[u(\tau ,\eta )]^{2}\simeq & {} (\Phi (\tau ,\eta )U)(\Phi ^{T}(\tau ,\eta )U)=(U^{T}\Phi (\tau ,\eta ))(\Phi ^{T}(\tau ,\eta )U)\\ {}= & {} U^{T}{\hat{U}}\Phi (\tau ,\eta )=\Phi ^{T}(\chi ,\zeta )e_{2}, \end{aligned}$$

where $e_{2}=(U^{T}{\hat{U}})^{T}$. In the same way, $[u(\tau ,\eta )]^{3}$ can be represented such as

$$\begin{aligned}{}[u(\tau ,\eta )]^{3}\simeq & {} (\Phi ^{T}(\tau ,\eta )U)(\Phi ^{T}(\tau ,\eta )e_{2})=(U^{T}\Phi (\tau ,\eta ))(\Phi ^{T}(\tau ,\eta )e_{2})\\ {}= & {} U^{T}{\hat{e}}_{2}\Phi (\tau ,\eta )=\Phi ^{T}(\tau ,\eta )e_{3}, \end{aligned}$$

where $e_{3}=(U^{T}{\hat{e}}_{2})^{T}$. Therefore, one can deduce that

$$\begin{aligned}{}[u(\tau ,\eta )]^{P}\simeq & {} (\Phi ^{T}(\tau ,\eta )U)(\Phi ^{T}(\tau ,\eta )e_{p-1})=(U^{T}\Phi (\tau ,\eta ))(\Phi ^{T}(\tau ,\eta )e_{p-1})\\ {}= & {} U^{T}{\hat{e}}_{p-1}\Phi (\tau ,\eta )=\Phi ^{T}(\tau ,\eta )e_{p}, \end{aligned}$$

where $e_{p}=(U^{T}{\hat{e}}_{p-1})^{T}$.

4.1 The method of solution

In this section, we present the proposed method based on the operational matrix to find the solution of Eq.(1) with the condition (2)–(3). To do this, we suppose

$$\begin{aligned}&u(\chi ,\zeta )=(C^{T}(P^{\alpha }\otimes I)+C_{p}^{T})^{T}\Phi (\chi ,\zeta )= \Phi ^{T}(\chi ,\zeta )(C^{T}(P^{\alpha }\otimes I)+C_{p}^{T})^{},\nonumber \\&G(\chi ,\zeta )=G^{T}\Phi (\chi ,\zeta )=G \Phi ^{T}(\chi ,\zeta ),\nonumber \\&[u(\tau ,\eta )]^{p_{}}= e_{p}^{T} \Phi (\tau ,\eta )=\Phi ^{T}(\tau ,\eta ) e_{p} ,\nonumber \\&\Phi (\chi ,\zeta )\Phi ^{T}(\chi ,\zeta )C={\tilde{C}} \Phi (\chi ,\zeta ),\nonumber \\&k_{}(\chi ,\zeta ,\tau ,\eta )=\Phi ^{T}(\chi ,\zeta )\cdot K_{}\cdot \Phi (\tau ,\eta ). \end{aligned}$$

(53)

Now, by substituting Eqs. (44) and (52) into Eq. (1), we get

$$\begin{aligned} C_{}^{T} \Phi _{}^{}(\chi ,\zeta )&+ A^{(\beta )^{T}} \Phi _{}^{}(\chi ,\zeta )+(C^{T}(P^{\alpha }\otimes I)+C_{p}^{T})^{T}\Phi (\chi ,\zeta )=G_{}^{T}\Phi _{}(\chi ,\zeta )\nonumber \\&+\frac{1}{\Gamma (\alpha )\Gamma (\beta )}\int _{0}^{\chi }\int _{0}^{\zeta }(\chi -\tau )^{(\alpha -1)}(\zeta -\eta )^{(\beta -1)}k_{}(\chi ,\zeta ,\tau ,\eta )[u_{}(\tau ,\eta )]^{p}\mathrm{d}\eta \mathrm{d}\tau .\nonumber \\ \end{aligned}$$

(54)

Substituting Eq. (53) into Eq. (54), we have

$$\begin{aligned}&C_{}^{T} \Phi _{}^{}(\chi ,\zeta )+ A^{(\beta )^{T}} \Phi _{}^{}(\chi ,\zeta )+(C^{T}(P^{\alpha }\otimes I)+C_{P}^{T})^{T}\Phi (\chi ,\zeta )=G_{}^{T}\Phi _{}(\chi ,\zeta )\\&\frac{1}{\Gamma (\alpha )\Gamma (\beta )}\int _{0}^{\chi }\int _{0}^{\zeta }(\chi -\tau )^{(\alpha -1)}(\zeta -\eta )^{(\beta -1)} \Phi _{}^{T}(\chi ,\zeta )K_{}\Phi _{}(\tau ,\eta )\Phi _{}^{T}(\tau ,\eta )e_{p}\mathrm{d}\eta \mathrm{d}\tau . \end{aligned}$$

Using the above equation, Eq. (53) can be rewritten as

$$\begin{aligned} C_{}^{T} \Phi _{}^{}(\chi ,\zeta )+ & {} A^{(\beta )^{T}} \Phi _{}^{}(\chi ,\zeta )+(C^{T}(P^{\alpha }\otimes I)+C_{p}^{T})^{T}\Phi (\chi ,\zeta )=G_{}^{T}\Phi _{}(\chi ,\zeta )\\&\Phi _{}^{T}(\chi ,\zeta )K_{}{\tilde{e}}_{p}\frac{1}{\Gamma (\alpha )\Gamma (\beta )}\int _{0}^{\chi }\int _{0}^{\zeta }(\chi -\tau )^{(\alpha -1)}(\zeta -\eta )^{(\beta -1)}\Phi _{}(\tau ,\eta )\mathrm{d}\eta \mathrm{d}\tau . \end{aligned}$$

Using (25), the integral part in the above equation can be written as

$$\begin{aligned} C_{}^{T} \Phi _{}^{}(\chi ,\zeta )+ & {} A^{(\beta )^{T}} \Phi (\chi ,\zeta )+(C^{T}(P^{\alpha })\otimes I)+C_{p}^{T})^{T}\Phi (\chi ,\zeta )=G_{}^{T}\Phi _{}(\chi ,\zeta )\\&\Phi _{}^{T}(\chi ,\zeta )K{\tilde{e}}_{p} P_{}^{\alpha ,\beta }\Phi _{}(\chi ,\zeta )=\left( \widetilde{K{\tilde{e}}_{p}P_{}^{\alpha ,\beta }} \right) ^{T}. \Phi _{}(\chi ,\zeta )+G_{}^{T}\Phi _{}(\chi ,\zeta ), \end{aligned}$$

or

$$\begin{aligned}&C_{}^{T} \Phi ^{}_{}(\chi ,\zeta )+A^{(\beta )^{T}} \Phi _{}^{}(\chi ,\zeta )+(C^{T}(P^{\alpha }\otimes I)+C_{p}^{T})^{T}\Phi (\chi ,\zeta )\\&\quad =\left( \widetilde{K{\tilde{e}}_{p}P_{}^{\alpha ,\beta }} \right) ^{T}. \Phi (\chi ,\zeta )+G_{}^{T}\Phi _{}(\chi ,\zeta ). \end{aligned}$$

Set

$$\begin{aligned} B_{}=\left( \widetilde{K{\tilde{e}}_{p}P_{}^{\alpha ,\beta }} \right) , \end{aligned}$$

so

$$\begin{aligned}&C_{}^{T} \Phi (\chi ,\zeta )+A^{(\beta )^{T}} \Phi _{}^{}(\chi ,\zeta )+(C^{T}(P^{\alpha }\otimes I)+C_{p}^{T})^{T}\Phi (\chi ,\zeta )\\&\quad =B_{}^{T}\Phi _{}(\chi ,\zeta )+G_{}^{T}\Phi _{}(\chi ,\zeta ). \end{aligned}$$

Therefore,

$$\begin{aligned} C_{}^{T}+A^{(\beta )^{T}} +(C^{T}(P^{\alpha }\otimes I)+C_{p}^{T})^{T}=B_{}^{T}+G_{}^{T}. \end{aligned}$$

(55)

The above equation is a system of algebraic equations. By solving the nonlinear system Eq. (55), the approximate solution of Eq. (1) is obtained.

5 Convergence analysis

The concept of convergence for numerical methods plays the key role for estimating the effectiveness of the methods. Therefore, in this section, we want to analyze the convergence of the proposed method based on the 2DBPs for solving 2DFPVIEs by expressing and proving a theorem. To do this, suppose that $\left( c([0,1)\times [0,1),\Vert \cdot \Vert \right)$ be the Banach space of all continuous function on $[0,1)\times [0,1)$ with norm

$$\begin{aligned} \Vert u(\chi ,\zeta )\Vert _{\infty }=\max \vert u(\chi ,\zeta )\vert , (\chi ,\zeta )\in [0,1)\times [0,1). \end{aligned}$$

(56)

Theorem 5.1

Assume that $u(\chi ,\zeta )$ and $u_{l,k}(\chi ,\zeta )$ are the exact solution and the approximate solution of Eq. (1) with initial condition (2)–(3), respectively. Moreover, let the following assumption are satisfied:

$$\begin{aligned}&\mathrm{{(1).}}\quad \Vert u(\chi ,\zeta )-u_{l,k}(\chi ,\zeta )\le L\parallel K(u(\chi ,\zeta ))-K(u_{l,k}(\chi ,\zeta ))\parallel ,\nonumber \\\end{aligned}$$

(57)

$$\begin{aligned}&\mathrm{{(2).}}\quad \Vert F(\chi ,\zeta ,\tau ,\eta ,u(\tau ,\eta ))-F(\chi ,\zeta ,\tau ,\eta ,u_{l,k}(\tau ,\eta ))\Vert \le M \parallel u(\tau ,\eta )-u_{l,k}(\tau ,\eta )\parallel ,\nonumber \\\end{aligned}$$

(58)

$$\begin{aligned}&\mathrm{{(3).}}\quad \frac{M}{\Gamma (\alpha +1)\Gamma (\beta +1)}<\frac{1}{L}, \end{aligned}$$

(59)

where $L,M>0$, $K(u(\chi ,\zeta ))=D_{*\chi }^{\alpha }(\chi ,\zeta )+D_{*\zeta }^{\beta }+u(\chi ,\zeta )$. Then, the solution of Eq. (1) with initial condition (2)–(3) using 2DBPs converges.

Proof

Clearly, we have

$$\begin{aligned} D_{\chi }^{\alpha }u(\chi ,\zeta )+ & {} D_{\zeta }^{\beta }u(\chi ,\zeta )+ u(\chi ,\zeta )= g(\chi ,\zeta )\nonumber \\+ & {} \frac{1}{\Gamma (\alpha )\Gamma (\beta )}\int _{0}^{\chi }\int _{0}^{\zeta }(\chi -\tau )^{(\alpha -1)}(\zeta -\eta )^{(\beta -1)}F(\chi ,\zeta ,\tau ,\eta ,u(\tau ,\eta ))\mathrm{d}\eta \mathrm{d}\tau , \nonumber \\\end{aligned}$$

(60)

$$\begin{aligned} D_{\chi }^{\alpha }u_{l,k}(\chi ,\zeta )+ & {} D_{\zeta }^{\beta }u_{l,k}(\chi ,\zeta )+ u_{l,k}(\chi ,\zeta )= g_{}(\chi ,\zeta ) \nonumber \\+ & {} \frac{1}{\Gamma (\alpha )\Gamma (\beta )}\int _{0}^{\chi }\int _{0}^{\zeta }(\chi -\tau )^{(\alpha -1)}(\zeta -\eta )^{(\beta -1)}F(\chi ,\zeta ,\tau ,\eta ,u_{l,k}(\tau ,\eta ))\mathrm{d}\eta \mathrm{d}\tau .\nonumber \\ \end{aligned}$$

(61)

By subtracting (61) from (60), we get

$$\begin{aligned}&\mid K(u(\chi ,\zeta ))-K(u_{l,k}(\chi ,\zeta ))\mid \\&\quad \le \frac{1}{\Gamma (\alpha )\Gamma (\beta )}\int _{0}^{\chi }\int _{0}^{\zeta }(\chi -\tau )^{(\alpha -1)}(\zeta -\eta )^{(\beta -1)}\\&\vert F(\chi ,\zeta ,\tau ,\eta ,u_{}(\tau ,\eta ))-F(\chi ,\zeta ,\tau ,\eta ,u_{l,k}(\tau ,\eta ))\vert \mathrm{d}\eta \mathrm{d}\tau ,\\&\quad \le \frac{1}{\Gamma (\alpha )\Gamma (\beta )}\int _{0}^{\chi }\int _{0}^{\zeta }(\chi -\tau )^{(\alpha -1)}(\zeta -\eta )^{(\beta -1)} \\&\Vert F(\chi ,\zeta ,\tau ,\eta ,u_{}(\tau ,\eta ))-F(\chi ,\zeta ,\tau ,\eta ,u_{l,k}(\tau ,\eta ))\Vert \mathrm{d}\tau \mathrm{d}\eta ,\\&\quad \le \frac{1}{\Gamma (\alpha )\Gamma (\beta )}M\Vert u(\chi ,\zeta )\\&\qquad -u_{l,k}(\chi ,\zeta )\Vert \int _{0}^{\chi }\int _{0}^{\zeta }(\chi -\tau )^{(\alpha -1)}(\zeta -\eta )^{(\beta -1)}\mathrm{d}\eta \mathrm{d}\tau ,\\&\quad =M\Vert u(\chi ,\zeta )-u_{l,k}(\chi ,\zeta )\Vert \left( I^{\alpha } (1) \right) \left( I^{\beta } (1) \right) \\&\quad =M\Vert u(\chi ,\zeta )-u_{l,k}(\chi ,\zeta )\Vert \frac{\Gamma (1)}{\Gamma (\alpha +1)} \chi ^{\alpha }\frac{\Gamma (1)}{\Gamma (\beta +1)}\zeta ^{\beta }\\&\quad \le \frac{M}{\Gamma (\alpha +1)\Gamma (\beta +1)}\Vert u(\chi ,\zeta )-u_{l,k}(\chi ,\zeta )\Vert . \end{aligned}$$

Now, we conclude that

$$\begin{aligned} \frac{1}{L}\Vert u(\chi ,\zeta )-u_{l,k}(\chi ,\zeta )\Vert\le & {} \Vert K(u(\chi ,\zeta )-K(u_{l,k}(\chi ,\zeta ) \Vert \nonumber \\\le & {} \frac{L}{\Gamma (\alpha +1)\Gamma (\alpha +1)}\Vert u(\chi ,\zeta )-u_{l,k}(\chi ,\zeta )\Vert . \end{aligned}$$

(62)

The above inequality implies that

$$\begin{aligned} \lim _{l,k\rightarrow \infty } \Vert u(\chi ,\zeta )-u_{l,k}(\chi ,\zeta )\Vert =0, \end{aligned}$$

(63)

which completes the proof. $\square$

6 Numerical examples

This section considers many instances to demonstrate the efficiency of the Boubaker polynomials operational matrix

Example 6.1

Consider the nonlinear two-dimensional fractional integro-differential equation

$$\begin{aligned} \frac{\partial ^{1/3} u_{}(\chi ,\zeta ) }{\partial \chi ^{1/3}}+\frac{\partial u_{}(\chi ,\zeta )}{\partial \zeta }-\int _{0}^{\chi }\int _{0}^{\zeta }\tau ^{2}\cos (\eta )(u_{}^{2}(\tau ,\eta )+\tau ^{2}\sin ^{2}(\eta ))\mathrm{d}\eta \mathrm{d}\tau =g_{}(\chi ,\zeta ), \end{aligned}$$

(64)

with

$$\begin{aligned} g_{}(\chi ,\zeta )=\frac{3}{2\Gamma (\frac{3}{2})}\sin (\zeta )\chi ^{\frac{2}{3}}-\chi \sin (\zeta )-\frac{1}{15}\chi ^{5}\sin (\zeta ) (\cos ^{2}(\zeta )-\sin ^{2} (\zeta )+2). \end{aligned}$$

(65)

Table 1 Absolute errors of the proposed method for Example (6.1)

Fig. 1

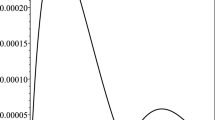
Numerical solutions (right) and analytical (left) of Example (6.1), $u_{}(\chi ,\zeta ),$ with $l,k=6$

Fig. 2

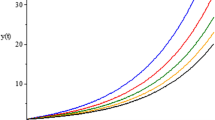
Numerical solutions (right) and analytical (left) of Example (6.2) $u_{}(\chi ,\zeta )$ with $l,k=6$

Fig. 3

Numerical solutions (right) and analytical (left) of Example (6.3), $u_{}(\chi ,\zeta ),$ with $l,k=7$

The exact solution of this equation is given by $u_{}(\chi ,\zeta )=\chi \cos (\zeta )$, for $\chi ,\zeta \in [0, 1]$ and with supplementary conditions

$$\begin{aligned} u_{}(0,\zeta )=0,\quad u(\chi ,0)=\chi . \end{aligned}$$

(66)

Numerical results are presented in Table 1 and Fig. 1.

Example 6.2

In the next example, the following 2DFPVIEs are considered:

$$\begin{aligned} \frac{\partial ^{2/3} u_{}(\chi ,\zeta ) }{\partial \chi ^{2/3}}+u_{}^{}(\chi ,\zeta )-\int _{0}^{\chi }\int _{0}^{\zeta }\eta ^{3}e^{-\eta }(u_{}(\tau ,\eta ))\mathrm{d}\eta \mathrm{d}\tau =g_{}(\chi ,\zeta ), \end{aligned}$$

(67)

Table 2 Absolute errors of the proposed method for Example (6.2)

Table 3 Absolute errors of the proposed method for Example (6.3)

Table 4 CPU time for different l, k

with

$$\begin{aligned} g_{}(\chi ,\zeta )=\frac{3}{2\pi }\left( e^{\zeta }\chi ^{\frac{1}{3}}\sqrt{3}\Gamma \left( \frac{2}{3}\right) \right) -2e^{-\zeta }+\zeta e^{-\zeta }+\chi ^{}(e^{\zeta })^{}-\frac{1}{8}\zeta ^{4}\chi ^{2}+\zeta ^{2}e^{-\zeta }-2e^{-\zeta }. \end{aligned}$$

(68)

The exact solution is given by $u_{}(\chi ,\zeta )=\chi e^{\zeta }$, for $\chi ,\zeta \in [0, 1]$ and with supplementary conditions $u_{}(0,\zeta )=0$. Numerical results are presented in Table 2 and Fig. 2.

Example 6.3

In the final example, the following 2DFPVIEs are considered:

$$\begin{aligned} \frac{\partial ^{1/2} u_{}(\chi ,\zeta ) }{\partial \chi ^{1/2}}+ & {} \frac{\partial u_{}^{\frac{3}{2}}(\chi ,\zeta )}{\partial \zeta ^{\frac{3}{2}}}+u_{}(\chi ,\zeta )-\int _{0}^{\chi }\int _{0}^{\zeta }(u_{}^{2}(\tau ,\eta ))\mathrm{d}\eta \mathrm{d}\tau =g_{}(\chi ,\zeta ), \end{aligned}$$

(69)

with

$$\begin{aligned} g_{}(\chi ,\zeta )= & {} \frac{2\sqrt{\chi }}{\sqrt{\pi }}+\frac{4\sqrt{\zeta }}{\sqrt{\pi }}+\chi +\zeta ^{2}+\frac{1}{5}\zeta \chi ^{5}+\frac{1}{3}\zeta ^{2}\chi ^{3}+\frac{1}{3}\zeta ^{3}\chi , \end{aligned}$$

for $\chi , \zeta \in [0, 1]$ and with supplementary conditions

$$\begin{aligned} u_{}(0,\zeta )=\zeta ^{2},\quad u_{}(\chi ,0)=\chi ,\quad \frac{\partial u_{}}{\partial \zeta }(\chi ,0)=0, \end{aligned}$$

(70)

which the exact solution is $u_{}(\chi ,\zeta )=\chi +\zeta ^{2}$. Some numerical results of this example are presented in Table 3 and Fig. 3.

7 Conclusion

In this article, we presented a new approach based on the 2DBPs for solving the two-dimensional nonlinear fractional partial integro-differential equation (Table 4). We derived the operational matrix of fractional integration of 2DBPs. By properties of 2DBPs and the use of operational matrices, we the considered Eq. (1) with the conditions (2)–(3) to a system of algebraic equations. The effectiveness and accuracy of the method were examined by some examples and the obtained results have shown remarkable performance of the proposed method. The obtained results show that the proposed method can be a suitable method for solving such problems.