Fractional shifted legendre tau method to solve linear and nonlinear variable-order fractional partial differential equations

Abstract

Here, we shed light on the fractional linear and nonlinear Klein–Gorden partial differential equations via Fractional Shifted Legendre Tau Method. With this objective, the operational matrices of fractional-order shifted Legendre functions (FSLFs) are derived and combined with the Tau method to convert the fractional-order differential equations to a system of solvable algebraic equations. The validity and the efficiency of the operational matrices are tested. Our findings yield an affirmative consequence, indicating applicability of the proposed method for nonlinear equations appearing in science and engineering.

Introduction

The fractional differential equations and the fractional calculus have been widely used in the modeling and simulation of the problems in science and engineering such as electrochemistry, elastoplastic, thermoelastic and viscoelasticity. [1,2,3,4]. The fractional derivatives are of significant interest in the development of methods [5,6,7,8,9,10,11] to solve the fractional partial differential equations (FPDEs) such as Klein–Gordon equation [12] appearing in many scientific applications, particularly, solid-state physics and nonlinear optics [13]. Besides, shallow water wave equations [14] can be modeled via this equation. In the recent years, some analytical and numerical methods have been proposed to find the approximation of Klein–Gordon FPDEs [12, 15, 16]. In [1], a spectral collocation method is proposed that applies Legendre polynomials to approximate the solutions. Spectral methods are classified as Pseudospectral, Collocation, Galerkin and Tau methods. The Tau method [17,18,19,20] has been extensively used in a wide range of problems arising in the mathematical modelings to find the solution of the differential equations. In this method, appropriate basis functions that are typically the eigenfunctions of a singular Sturm-Liouville problem are used for the projection of the residual functions. The auxiliary conditions operate as constraints on the expansion coefficients. Legendre functions are categorized in the class of orthogonal functions. Various studies have proven the efficiency of these polynomials in fractional differential equations. Rida and Yousef, [21] proposed the fractional extension of the classical Legendre polynomials that replace the integer-order derivative in Rodrigues formula [22] by fractional-order derivatives. The known complexity of these functions has limited their applicability in FDEs. Kazem [23] has proposed the orthogonal fractional-order Legendre functions based on the shifted Legendre polynomials to overcome the inherent complexity. The operational matrices of the fractional derivatives have been generated for some types of orthogonal polynomials including Chebyshev polynomials and Legendre polynomials, [24, 25]. In the literature, there have been reported also some analytical techniques to extract the exact solution of fractional differential equation, Lie symmetry analysis being among them [26,27,28,29].

In the current work, an in-depth study of the linear and nonlinear Klein–Gordon FPDEs with variable coefficients is accomplished. Fractional-order Legendre functions are used to find the numerical solutions of the FPDEs. It is worthy to note that this method does not make use of the discretization in time and space. In particular, the nonlinearity of the FPDEs can be controlled by fractional-order Legendre functions, a feature that makes our study unique.

The organization of the paper is as follows: First, we present some preliminaries from fractional calculus. In Sect. 3, we construct generalized fractional-order Legendre functions with an introduction to their properties. In the next section, the operational matrices of fractional derivative are obtained and we represent the numerical algorithms to solve the FPDEs with variable coefficients. Later, the provided algorithm is applied to the linear and the nonlinear Klein–Gordon FPDEs. Finally, the results are summarized and discussed in the last section.

Preliminaries

Some definitions of the fractional calculus are given in the following.

Definition 1

A real function f(t), $t>0$, is said to be in the space $C_\mu$, $\mu \in R$ if there exists a real number $p>\mu$, such that $f(t)=t^{p}f_{1}(t)$, where $f_{1}(t)\in C(0,\infty )$. Further, it is said to be in the space $C_{\mu }^{n}$ if and only if $f^{(n)}\in C_{\mu }$, $n\in {\mathbb {N}}$.

Definition 2

The Caputo fractional derivative operator, $D^{\alpha }$, of the order of $\alpha$, is defined by:

$$\begin{aligned}&(D^{\alpha }f)(x) \\&\quad = {\left\{ \begin{array}{ll} \frac{1}{\Gamma (m-\alpha )}\int _{0}^{x}\frac{f^{m}(\xi )}{(x-\xi )^{\alpha -m+1}}d\xi ,&\qquad (\alpha >0, m-1<\alpha <m),\\ \frac{d^{m}f(x)}{dx^{m}},&\qquad \alpha =m, \end{array}\right. } \end{aligned}$$

(1)

where $m\in {\mathbb {N}}$; $f: {\mathbb {R}}\longrightarrow {\mathbb {R}}$ and $x\rightarrow f(x)$ indicate a continuous (but not necessarily differentiable) function. Recall that for $\alpha \in {\mathbb {N}}$, the Caputo fractional differential operator coincides with the usual differential operator of integer order.

Here, we refer some basic properties of the Caputo fractional derivative.

For $f\in C_{\mu }$, $\mu \ge -1$, $\alpha \ge 0$, $\nu \ge -1$, ${\mathbb {N}}_{0}=\{0,1,2,\ldots \}$, and constant C one has:

$$\begin{aligned}&D^{\alpha }C=0,\quad \\&D^{\alpha }x^{\nu }= {\left\{ \begin{array}{ll} 0, & \quad \text{for} \quad \nu \in N_{0} \quad \text{and} qquad \nu < \lceil \alpha \rceil \\ \frac{\Gamma (\nu +1)}{\Gamma (\nu +1-\alpha )}x^{\nu -\alpha } ,& \quad \text{for} \quad \nu \in N_{0} \quad \text{and} \quad \nu \ge \lceil \alpha \rceil \end{array}\right. }\end{aligned}$$

(2)

$$\begin{aligned}&D^{\alpha }\left(\sum _{i=0}^{m}c_{i}f_{i}(x)\right)=\sum _{i=0}^{m}c_{i}D^{\alpha }f_{i}(x),\quad \text{where}~ \{c_i\}_{i=0}^{m}\quad \text{are real constants}. \end{aligned}$$

(3)

The ceiling function denotes the smallest integer greater than or equal to $\alpha$.

Definition 3

(Generalized Taylor’s formula). Suppose that $D^{i\alpha }f(x)\in {\mathcal {C}}(0,1]$ for $i=0,1,\ldots ,m-1$, then

$$\begin{aligned} f(x)=\sum _{i=0}^{m-1}\frac{x^{i\alpha }}{\Gamma (i\alpha )}D^{i\alpha }f(0^{+})+\frac{x^{m\alpha }}{\Gamma (m\alpha +1)}D^{m\alpha }f(\xi ) \end{aligned}$$

(4)

where $0<\xi \le x$, $\forall x\in (0,1]$, and one has

$$\begin{aligned} \mid f(x)-\sum _{i=0}^{m-1}\frac{t^{i\alpha }}{\Gamma (i\alpha +1)}D^{i\alpha }f(0^{+})\mid \le M_{\alpha }\frac{x^{m\alpha }}{\Gamma (m\alpha +1)}, \end{aligned}$$

(5)

where $M_{\alpha }\ge \mid D^{m\alpha }f(\xi )\mid$, note that the classical Taylor’s formula corresponds to the case of $\alpha =1$.

Fractional Legendre functions

The shifted Legendre polynomials

The Legendre polynomials, $P_{n}(z)$, that is defined on the interval of $(-1,1)$ with a weight function of $w(z)=1$ are given via the following recurrence formula

$$\begin{aligned}&P_{i+1}(z)=\frac{2i+1}{i+1}zP_{i}(z)-\frac{i}{i+1}P_{i-1}(z),\quad i=1,2,\ldots \\&P_{0}(z)=0,\quad P_{1}(z)=z. \end{aligned}$$

(6)

where $\int _{-1}^{1}P_{n}(z)P_{m}(z)dz=\frac{2}{2n+1}\delta _{nm}$, in which, $\delta _{mn}$ is Kronecker function. The transformation $z=2t-1$ transforms the existing interval to [0, 1] and the shifted Legendre polynomials, $P_{n}(2t-1)$, given by $L_{n}(t)$ are orthogonal with the weight function of $w_{s}(t)=1$ as

$$\begin{aligned} \int _{0}^{1}L_{n}(t)L_{m}(t)dt=\frac{1}{2n+1}\delta _{nm}, \end{aligned}$$

(7)

furthermore, they are derived as

$$\begin{aligned}L_{i+1}(t)&=\frac{(2i+1)(2t-1)}{i+1}L_{i}(t) \\&\quad -\frac{i}{i+1}L_{i-1}(t),\quad i=1,2,\ldots \end{aligned}$$

(8)

$$\begin{aligned}&L_{0}(t)=1,\quad L_{1}(t)=2t-1, \end{aligned}$$

(9)

with the analytical form of

$$\begin{aligned}&L_{n}(t)=\sum _{i=0}^{n}\gimel (n,i)~t^{i},\\&\gimel (n,i)=\frac{(-1)^{n+i}(n+i)!}{(n-i)!(i!)^{2}},\\&\quad ~\text{and}~L_{n}(0)=(-1)^{n},~L_{n}(1)=1. \end{aligned}$$

Fractional-order Legendre functions

Indeed, the transformation $t=x^{\alpha }$ ($\alpha >0$) is used on shifted Legendre polynomials to define the fractional-order Legendre functions. Herein, $FL_{i}^{\alpha }(x)$, indicates $L_{i}(x^{\alpha })$, in which, $i=1,2,\ldots$. Note that the defined fractional-order Legendre functions are a particular solution of the normalized eigenfunctions of the singular Sturm-Liouville equation [22].

$$\begin{aligned}&((x-x^{\alpha +1})FL_{i}^{'\alpha }(x))^{'}+\alpha ^{2}i(i+1)x^{\alpha -1}FL_{i}^{\alpha }(x) = 0,\\&\quad x\in (0,1). \end{aligned}$$

According to Eq. (8), one has

$$\begin{aligned}FL_{i+1}^{\alpha }(x)& =\frac{(2i+1)(2x^{\alpha }-1)}{i+1}FL_{i}^{\alpha }(x) \\&\quad -\frac{i}{i+1}FL_{i-1}^{\alpha }(x),\quad i=1,2,\ldots \end{aligned}$$

(10)

$$\begin{aligned}&FL_{0}^{\alpha }(x)=1,\quad FL_{1}^{\alpha }(x)=2x^{\alpha }-1, \end{aligned}$$

(11)

and the analytical form of $FL_{i}^{\alpha }(x)$ with the degree of $i\alpha$ is

$$\begin{aligned} FL_{i}^{\alpha }(x)=\sum _{s=0}^{i}b_{s,i}x^{s\alpha },\quad i=0,1,2,\ldots , \end{aligned}$$

(12)

where $b_{s,i}=\frac{(-1)^{i+s}(i+s)!}{(i-s)!(s!)^{2}}$, $FL_{i}^{\alpha }(0)=(-1)^{i}$, and $FL_{i}^{\alpha }(1)=1$. The fractional-order Legendre functions satisfy the following orthogonality property with the weight function $w(x)=x^{\alpha -1}$ on the interval (0, 1]

$$\begin{aligned} \int _{0}^{1}FL_{n}^{\alpha }(x)FL_{m}^{\alpha }(x)w(x)dx=\frac{1}{(2n+1)\alpha }\delta _{nm}. \end{aligned}$$

(13)

An arbitrary function f(x) that is square integrable in the interval of (0, 1] may be expressed in terms of the fractional-order Legendre functions as

$$\begin{aligned} f(x)=\sum _{i=0}^{\infty }a_{i}FL_{i}^{\alpha }(x), \end{aligned}$$

(14)

where the coefficients $a_i$ are given by

$$\begin{aligned} a_i= \alpha (2i+1)\int _{0}^{1}FL_{i}^{\alpha }(x)f(x)w(x)dx,\quad i=1,2,\ldots , \end{aligned}$$

(15)

In practice, only the first $m-$terms of the fractional-order Legendre function are considered. Therefore, one has

$$\begin{aligned} f(x)\simeq f_{m}(x)=\sum _{i=0}^{m-1}a_{i}FL_{i}^{\alpha }(x)=A^{T}\Phi _{\alpha }(x), \end{aligned}$$

(16)

where

$$\begin{aligned}&A=[a_0,a_1,\ldots ,a_m-1]^{T}, \end{aligned}$$

(17)

$$\begin{aligned}&\quad \Phi _{\alpha }(x)=[FL_{0}^{\alpha }(x),FL_{1}^{\alpha }(x),\ldots ,FL_{m-1}^{\alpha }(x)]^{T}. \end{aligned}$$

(18)

Theorem 1

Suppose $D^{i\alpha }f(x)\in {\mathcal {C}}(0,1]$ for $i=0,1,\ldots ,m-1$, $(2m+1)\alpha \ge 1$ and

$$\begin{aligned} {\mathbf {P}}^{\alpha }_{m}=span\{FL_{0}^{\alpha }(x),FL_{1}^{\alpha }(x),\ldots ,FL_{m-1}^{\alpha }(x)\}. \end{aligned}$$

If $f_m(x)=A^{T}\Phi (x)$ is the best approximation to f(x) from ${\mathbf {P}}^{\alpha }_{m}$, then the error bound is presented as follows:

$$\begin{aligned} \parallel f(x)-f_m(x)\parallel _{w}\le \frac{M_\alpha }{\Gamma (2m+1)}\sqrt{\frac{1}{(2m+1)\alpha }}, \end{aligned}$$

where $M_\alpha \ge \mid D^{m\alpha }f(x)\mid ,\quad x\in (0,1]$.

Proof

Consider the generalized Taylor formula

$$\begin{aligned} f(x)=\sum _{i=0}^{m-1}\frac{x^{i\alpha }}{\Gamma (i\alpha )}D^{i\alpha }f(0^{+})+\frac{x^{m\alpha }}{\Gamma (m\alpha +1)}D^{m\alpha }f(\xi ), \end{aligned}$$

(19)

where $0<\xi <x$, $x\in [0,1]$; using the Definition 3

$$\begin{aligned} \mid f(x)-\sum _{i=0}^{m-1}\frac{t^{i\alpha }}{\Gamma (i\alpha +1)}D^{i\alpha }f(0^{+})\mid \le M_{\alpha }\frac{x^{m\alpha }}{\Gamma (m\alpha +1)}, \end{aligned}$$

(20)

since $f_m(x)=A^{T}\Phi (x)$ is defined as the best approximation to f(x) from ${\mathbf {P}}_{m}^{\alpha }$, and $\sum _{i=0}^{m-1}\frac{t^{i\alpha }}{\Gamma (i\alpha +1)}D^{i\alpha }f(0^{+})\in {\mathbf {P}}_{m}^{\alpha }$, then

$$\begin{aligned}&\parallel f(x)-f_{m}(x)\parallel _{\omega }^{2}\le \parallel f(x)-\sum _{i=0}^{m-1}\frac{t^{i\alpha }}{\Gamma (i\alpha +1)}D^{i\alpha }f(0^{+})\parallel _{\omega } \\ &\quad\le\frac{M_\alpha ^{2}}{\Gamma (m\alpha +1)^2}\int _{0}^{1}x^{2m\alpha }x^{\alpha -1}dx, \\&\parallel f(x)-f_{m}(x)\parallel _{\omega }^{2}\le \frac{M_\alpha ^{2}}{\Gamma (m\alpha +1)^2}\int _{0}^{1}x^{(2m+1)\alpha -1}dx \\ &\quad = \frac{M_{\alpha }^{2}h^{\alpha }}{\Gamma (m\alpha +1)^{2}(2m+1)\alpha }, \end{aligned}$$

(21)

now, take the square roots to prove the theorem. Indeed, the convergence of the fractional-order Legendre functions to f(x) is described in the above theorem.

Definition 4

A function of two independent variable f(x, t) which is integrable in square $[0,1]\times [0,1]$ can be expanded as

$$\begin{aligned} f(x,t)=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }f_{ij}FL_{i}^{\alpha }(x)FL_{j}^{\beta }(t), \end{aligned}$$

(22)

where

$$\begin{aligned}&f_{ij}=(2i+1)(2j+1)\alpha \beta \int _{0}^{1} \\&\quad \int _{0}^{1}f(x,t)\omega (x,t)FL_{i}^{\alpha }(x)FL_{j}^{\beta }(t)dxdt, \\&\quad ~i,j=0,1,\ldots , \end{aligned}$$

(23)

Theorem 2

If the series $\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }f_{ij}FL_{i}^{\alpha }(x)FL_{j}^{\alpha }(t)$ converges uniformly to f(x, t) on $[0,1]\times [0,1]$, then one has

$$\begin{aligned}&f_{ij}\\ &\quad =(2i+1)(2j+1)\alpha \beta \int _{0}^{1} \int _{0}^{1}f(x,t)\omega (x,t)FL_{i}^{\alpha }(x)FL_{j}^{\beta }(t)dxdt. \end{aligned}$$

(24)

Proof

In Eq. (22), multiply both sides by $\omega (x,t)FL_{i}^{\alpha }(x)FL_{j}^{\beta }(t)$ (where n and m are fixed) and integrate with respect to x and t on $[0,1]\times [0,1]$ to have

$$\begin{aligned}&\int _{0}^{1}\int _{0}^{1}f(x,t)\omega (x,t)FL_{n}^{\alpha }(x)FL_{m}^{\beta }(t)dxdt \\&=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }f_{ij}\int _{0}^{1}\int _{0}^{1}\omega (x,t)FL_{i}^{\alpha }(x)FL_{j}^{\beta }(t) \\&\quad \times FL_{n}^{\alpha }(x)FL_{m}^{\beta }(t)dxdt \\&=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }f_{ij}\int _{0}^{1}w(x)FL_{i}^{\alpha }(x)FL_{n}^{\alpha }(x)dx \\&\quad \times \int _{0}^{1}w(t)FL_{j}^{\beta }(t)FL_{m}^{\beta }(t)dt\\&=f_{nm}\int _{0}^{1}\omega (x)[FL_{n}^{\alpha }(x)]^{2}dx\int _{0}^{1}\omega (t)[FL_{m}^{\beta }(t)]^{2}dt\\&=f_{nm}\frac{1}{(2n+1)\alpha }\frac{1}{(2m+1)\beta }, \end{aligned}$$

that gives rise to Eq. (23).

Theorem 3

If the series $\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }f_{ij}FL_{i}^{\alpha }(x)FL_{j}^{\beta }(t)$ converges uniformly to continuous function f(x, t) on $[0,1]\times [0,1]$, then it is a 2D expansion of fractional-order Legendre function of f(x, t).

Proof

(by contradiction) Suppose

$$\begin{aligned} f(x,t)=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }f_{ij}FL_{i}^{\alpha }(x)FL_{j}^{\beta }(t),\\ f(x,t)\sim \sum _{i=0}^{\infty }\sum _{j=0}^{\infty }g_{ij}FL_{i}^{\alpha }(x)FL_{j}^{\beta }(t), \end{aligned}$$

then there is at least one coefficient such that $f_{nm}\ne g_{nm}$. However,

$$\begin{aligned}&f_{nm}\\ & \quad =(2n+1)(2m+1)\alpha \beta \int _{0}^{1} \int _{0}^{1}f(x,t)\omega (x,t)FL_{n}^{\alpha }(x)FL_{m}^{\beta }(t)dxdt=g_{nm}. \end{aligned}$$

In practice, we seek the solution as the following, when the infinite series in Eq. (22) could be truncated to

$$\begin{aligned} f(x,t)\approx \sum _{i=0}^{m-1}\sum _{j=0}^{n-1}f_{ij}FL_{i}^{\alpha }(x)FL_{j}^{\beta }(t)=\Phi ^{T}_{\alpha }(x)F\Phi _{\beta }(t) \end{aligned}$$

(25)

where

$$\begin{aligned}&\Phi _{\alpha }(x)=[FL_{0}^{\alpha }(x),FL_{1}^{\alpha }(x),\ldots ,FL_{m-1}^{\alpha }(x)]^{T}, \\&\Phi _{\beta }(t)=[FL_{0}^{\beta }(t),FL_{1}^{\beta }(t),\ldots ,FL_{n-1}^{\beta }(t)]^{T}, \\&F=\{f_{ij}\}_{i,j=0}^{m-1,n-1}. \end{aligned}$$

(26)

Where the coefficients $f_{ij}$ are obtained by the Tau method. [30]

The fractional-order Legendre functions’s operational matrices of derivative and product

In the following, some properties of the fractional-order Legendre functions are discussed.

Lemma 1

The fractional-order Legendre functions’s Caputo fractional derivatives of order $\gamma >0$ are obtained as

$$\begin{aligned}&D^{\gamma }FL_{i}^{\alpha }(x)=\sum _{s=0}^{i}b^{'}_{s,i}\frac{\Gamma (s\alpha +1)}{\Gamma (s\alpha -\gamma +1)}x^{s\alpha -\gamma },\\&b^{'}_{s,i}=\\&\quad {\left\{ \begin{array}{ll} 0~,\qquad \qquad \qquad \quad ~ s\alpha \in {\mathbb {N}}_{0}~~\text{and}~~s\alpha <\gamma ,\\ b^{'}_{s,i}=b_{s,i}~,\qquad \qquad s\alpha \notin {\mathbb {N}}_{0}~~\text{and}~~s\alpha \ge [\gamma ]~~\text{or}~~s\alpha \in {\mathbb {N}}_{0}~~\text{and}~~s\alpha \ge \gamma \\ \end{array}\right. } \end{aligned}$$

Proof

Using Eqs. (2) and (12), one has

$$\begin{aligned} D^{\gamma }FL_{i}^{\alpha }(x)=\sum _{s=0}^{i}b_{s,i}D^{\gamma }x^{s\alpha } \end{aligned}$$

now by virtue of Eq. (3), the lemma is proved.

Lemma 2

Let $\gamma >0$, $\alpha \notin {\mathbb {N}}$, and $\alpha > \gamma /2$ then there exists

$$\begin{aligned}&\int _{0}^{1}D^{\gamma }FL_{i}^{\alpha }(x)FL_{j}^{\alpha }(x)\omega (x)dx \\&\quad =\sum _{s=0}^{i}\sum _{r=0}^{j}\frac{b^{'}_{s,i}b_{r,j}}{\alpha (s+r+1)-\gamma }\frac{\Gamma (s\alpha +1)}{\Gamma (s\alpha -\gamma +1)}, \end{aligned}$$

Proof

By means of the previous Lemma and (12)

$$\begin{aligned}&\int _{0}^{1}D^{\gamma }FL_{i}^{\alpha }(x)FL_{j}^{\alpha }(x)\omega (x)dx\\&\quad =\sum _{s=0}^{i}\sum _{r=0}^{j}\frac{b^{'}_{s,i}b_{r,j}\Gamma (s\alpha +1)}{\Gamma (s\alpha -\gamma +1)}\int _{0}^{1}x^{\alpha (s+r+1)-\gamma -1}dx, \end{aligned}$$

this integral exists for $\alpha > \gamma /2$, in which $\alpha \notin {\mathbb {N}}$. To prove the lemma, the above equation is integrated.

Remark 1

There exists the same results for $\alpha \in {\mathbb {N}}$ without assuming $\alpha >\gamma /2$.

Fractional differentiation matrices

The Caputo form of the fractional derivative of the order $\gamma >0$ of vector $\Phi _{\alpha }(x)$ may be approximated as

$$\begin{aligned} D^{\gamma }\Phi _{\alpha }(x)\simeq D^{(\gamma )}\Phi _{\alpha }(x), \end{aligned}$$

(27)

where $D^{(\gamma )}$ represents the operational matrix of fractional derivatives of fractional-order Legendre functions of order $\gamma >0$ of the vector $\Phi _{\alpha }(x)$. One can obtain the elements of this matrix using the following theorem.

Theorem 4

Suppose $\Phi _{\alpha }(x)$ denotes the vectors represented in Eq. (26), and $D^{(\gamma )}$ is the $m\times m$ operational matrix of Caputo fractional derivatives of order $\gamma >0$ and $\alpha >\gamma /2$, in which $\alpha \notin {\mathbb {N}}$, then the elements of $D^{(\gamma )}$ are given by

$$\begin{aligned}&D_{ij}^{(\gamma )}=\sum _{s=0}^{i}\sum _{r=0}^{j}\frac{b^{'}_{s,i}b_{r,j}}{\alpha (s+r+1)-\gamma }\frac{\Gamma (s\alpha +1)}{\Gamma (s\alpha -\gamma +1)}(2i+1)\alpha , \end{aligned}$$

(28)

$$\begin{aligned}&i,j=0,1,\ldots ,m-1, \end{aligned}$$

(29)

where

$$\begin{aligned}&b^{'}_{s,i}= {\left\{ \begin{array}{ll} 0~,\qquad \qquad \qquad \quad ~ s\alpha \in {\mathbb {N}}_{0}~~\text{and}~~s\alpha <\gamma ,\\ b^{'}_{s,i}=b_{s,i}~,\qquad \qquad s\alpha \notin {\mathbb {N}}_{0}~~\text{and}~~s\alpha \ge [\gamma ]~~\text{or}~~s\alpha \in {\mathbb {N}}_{0}~~\text{and}~~s\alpha \ge \gamma \\ \end{array}\right. } \end{aligned}$$

Proof

Using (27) and (13), one has

$$\begin{aligned} D^{\gamma }=\langle D^{\gamma }\Phi _{\alpha }(x),\Phi ^{T}_{\alpha }(x)\rangle {\mathfrak {D}}^{-1}, \end{aligned}$$

(30)

in which

$$\begin{aligned}&<D^{\gamma }\Phi _{\alpha }(x),\Phi ^{T}_{\alpha }(x)> = \big \{\int _{0}^{1}D^{\gamma }FL_{i}^{\alpha }(x)FL_{j}^{\alpha }(x)\omega (x)dx\big \}_{i,j=0}^{m-1}, \end{aligned}$$

(31)

$$\begin{aligned}&{\mathfrak {D}}^{-1}=diag\big \{(2i+1)\alpha \big \}_{i=0}^{m-1}, \end{aligned}$$

(32)

are substituted in Eq. (30) and by means of lemma 2 the theorem is proved. And in a similar way, one can obtain the Caputo fractional derivative of order $\gamma > 0$ with respect to variable t.

Remark 2

$\alpha \in {\mathbb {N}}$ renders the same operational matrix of derivatives.

Product matrix of the fractional-order Legendre functions

The product of two vectors that represent the fractional-order Legendre function is given by

$$\begin{aligned} \Phi _{\alpha }(x)\Phi _{\alpha }(x)^{T}A\simeq {\tilde{A}}\Phi _{\alpha }(x), \end{aligned}$$

(33)

in which ${\tilde{A}}$ is a $m\times m$ product matrix of vector A and the elements are obtained using the above equation and Eq. (13)

$$\begin{aligned} {\tilde{A}}_{ij}=\alpha (2j+1)\sum _{k=0}^{m-1}a_{k}g_{ijk},\quad i,j=0,1,\ldots ,m-1, \end{aligned}$$

(34)

where

$$\begin{aligned} g_{ijk}=\int _{0}^{1}FL_{i}^{\alpha }(x)FL_{j}^{\alpha }(x)FL_{k}^{\alpha }(x)\omega (x)dx, \end{aligned}$$

(35)

in order to get the elements of $g_{ijk}$, we have

$$\begin{aligned}&FL_{i}^{\alpha }(x)FL_{j}^{\alpha }(x) \\&\quad =\sum _{l=0}^{j}\frac{d_{j-l}d_{l}d_{i-l}}{d_{i+j-l}}\frac{2i+2j-4l+1}{2i+2j-2l+1}FL_{i+j-2l}^{\alpha }(x), \end{aligned}$$

(36)

where $j\le i$ and $d_l=(2l)!/2^l(l!)^2$. Multiply by $FL_{k}^{\alpha }(x)\omega (x)$ and then integrate from 0 to 1 by virtue of the orthogonality property in Eq. (13) to have

$$\begin{aligned}&g_{ijk}= {\left\{ \begin{array}{ll} \frac{d_{j-l}d_{l}d_{i-l}}{\alpha (2i+2j-2l+1)d_{i+j-l}}~,\qquad k=i+j-2l;~l=0,1,\ldots ,j,\\ 0~,\qquad \qquad \qquad \qquad ~~ k=i+j-2l;~l=0,1,\ldots ,j,\\ \end{array}\right. } \end{aligned}$$

(37)

which the introduced product matrix is similar to the product matrix of the shifted Legendre polynomials.

Remark 3

The product of the two fractional-order Legendre functions with the m term represented as $f(x)\simeq A^{T}\Phi _{\alpha }(x)$ and $g(x)\simeq B^{T}\Phi _{\alpha }(x)$ is obtained as

$$\begin{aligned} f(x)g(x)\simeq A^{T}\Phi _{\alpha }(x)\Phi _{\alpha }(x)^{T}B\simeq A^{T}{\tilde{B}}\Phi _{\alpha }(x). \end{aligned}$$

(38)

The following lemma is based on the above definition.

Lemma 3

The nonlinear operator ${\mathbf {N}}\big (f(x)\big )=f(x)^{k}$, where $f(x)\simeq A^{T}\Phi _{\alpha }(x)$ is approximated as

$$\begin{aligned} {\mathbf {N}}\big (f(x)\big )\simeq A^{T}{\tilde{A}}^{k-1}\Phi _{\alpha }(x). \end{aligned}$$

(39)

Proof

[23] From the above lemma $f(x)^{2}\simeq A^{T}{\tilde{A}}\Phi _{\alpha }(x)$ in which for $f(x)^{n}$ one has

$$\begin{aligned}& f(x)^{n}=f(x)^{2}f(x)^{n-2}\simeq A^{T}{\tilde{A}}\Phi _{\alpha }(x)f(x)f(x)^{n-3}\\ & \quad = A^{T}{\tilde{A}}\Phi _{\alpha }(x)\Phi _{\alpha }(x)^{T}A f(x)^{n-3} \\ &\quad \simeq A^{T}{\tilde{A}}^{2}\Phi _{\alpha }(x)f(x)^{n-3}\simeq \cdots \simeq A^{T}{\tilde{A}}^{n-1}\Phi _{\alpha }(x) \end{aligned}$$

Application of the fractional-order Legendre functions on linear and nonlinear Klein–Gordon equation

Consider the following FPDEs

$$\begin{aligned}&D^{\alpha }_{t}u(x,t)+D^{\beta }_{x}u(x,t)+N[u(x,t)]+L[u(x,t)]=g(x,t), \end{aligned}$$

(40)

$$\begin{aligned}&~~\qquad 0<x<1,\quad t>0,\quad \alpha ,\beta \in (1,2], \end{aligned}$$

(41)

where L and N are linear and nonlinear operators, respectively. $D^{\alpha }$ and $D^{\beta }$ are the Caputo fractional derivatives of the order $\alpha$ and $\beta$, respectively; g is a known analytic function.

For the cases in which $\beta$ is integer order and $\alpha$ represents fractional order, the unknown function u(x, t) is approximated as

$$\begin{aligned} u(x,t)\simeq U^{T}\Lambda (x,t)=U^{T}(\Phi (x)\otimes \Phi _{\alpha }(t)), \end{aligned}$$

(42)

where $\Lambda (x,t)$ is $nm\times 1$ matrix; $\Phi (x)$ and $\Phi _{\alpha }(t)$ are two $n\times 1$ and $m\times 1$ matrices, respectively. $U^T$ is $1\times nm$ unknown matrix. Also, we use this property of Kronecker product and the following lemmas in our study.

$$\begin{aligned} A_1B_1\otimes A_2B_2=(A_1\otimes A_2)(B_1\otimes B_2). \end{aligned}$$

(43)

Lemma 4

The derivative operator of the vector is given by

$$\begin{aligned} \frac{\partial }{\partial x}\Lambda (x,t)\simeq {\mathbf {D}}_{x}\Lambda (x,t), \end{aligned}$$

(44)

where

$$\begin{aligned} {\mathbf {D}}_x=D_x^{(1)}\otimes I_m. \end{aligned}$$

(45)

$D_x^{(1)}$ is the derivative of $\Phi (x)$ and $I_m$ is the identity matrix of order m.

Proof

$$\begin{aligned} \frac{\partial }{\partial x}\Lambda (x,t)=\Phi '(x)\otimes \Phi _{\alpha }(t). \end{aligned}$$

(46)

$\Phi '(x)=D^{(1)}_x\Phi (x)$ in which $D^{(1)}_x$ is the derivative matrix of vector $\Phi (x)$. By using Eq. (43), the proof of lemma is complete.

Remark 4

The Caputo fractional derivatives operator of order $\alpha >0$ of the vector $\Lambda (x,t)$ is expressed as

$$\begin{aligned} D_t^{\alpha }\Lambda (x,t)\simeq {\mathbf {D}}_t^{\alpha }\Lambda (x,t), \end{aligned}$$

(47)

${\mathbf {D}}_{t}^{\alpha }=I_n\otimes D_t^{(\alpha )}$ in which $D_t^{(\alpha )}$ is the Caputo fractional derivative matrix of vector $\Phi _\alpha (t)$.

Illustrative examples

Example 1

Consider fractional linear Klein–Gordon equation

$$\begin{aligned}&D^{\alpha }_{t}u(x,t)-D^{2}_{x}u(x,t)-u(x,t) \\&\quad =0,~~ 0<x<1,~ t>0,~\alpha \in (1,2] \end{aligned}$$

(48)

where the initial condition is $u(0,t)=1+\sin (x)$ and the exact solution to the problem is $u(x,t)=1+\sin (x)+\sum _{i=1}^{\infty }\frac{t^{i\alpha }}{\Gamma (i\alpha +1)}$.

Based on our method, the problem is reduced to

$$\begin{aligned} U^{T}[{\mathbf {D}}_{t}^{\alpha }\Lambda (x,t)-{\mathbf {D}}_x^{2}\Lambda (x,t)-\Lambda (x,t)]=0, \end{aligned}$$

(49)

which yields

$$\begin{aligned} U^{T}[{\mathbf {D}}_{t}^{\alpha }-{\mathbf {D}}_x^{2}-1]=0, \end{aligned}$$

(50)

and the initial condition $U^T\Lambda (x,0)=F^T\Phi (x)$ is satisfied. Using the Tau method and Kronecker property, one has

$$\begin{aligned}&U^T\big<\Phi (x)\otimes \Phi _{\alpha }(0),\Phi ^T(x)\big> \\&\quad =U^T\big <\Phi (x),\Phi ^T(x) \big >\otimes \Phi _{\alpha }(0)=U^T{\mathcal {B}}\otimes \Phi _{\alpha }(0)=F^T{\mathcal {B}}, \end{aligned}$$

multiply the above equation by ${\mathcal {B}}^{-1}$ to have

$$\begin{aligned} U^T\big [I_n\otimes \Phi _{\alpha }(0)\big ]=F^T. \end{aligned}$$

(51)

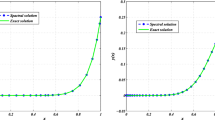
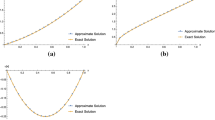
From Eqs. (50) and (51), we find the unknown coefficient vector U of the linear systems of matrix equation and then the approximate solution to u(x,t) is calculated. Here, $\Phi (x)$ and $\Phi _{\alpha }(t)$ are approximated using fractional-order Legendre polynomials with $n=6$ and $m=10$. Table 1 shows the absolute error when $\alpha =1$ at $t=1$ and different spatial points. Moreover, in Table 2, we present our approximate solutions for different values of $\alpha$ at various point. Our results reveal good agreement with the exact solution.

Table 1 The absolute error between the exact and approximation solution of $\alpha =1.1$ using $n=6$ and $m=10$ at $T=1$, and various spatial points

Table 2 Approximated solutions for different values of $\alpha$ in the example 1

Example 2

Consider the nonlinear fractional Klein–Gordon equation

$$\begin{aligned}&D^{2}_{t}u(x,t)-D^{\alpha }_{x}u(x,t)+u^{3}(x,t)=q(x,t), \end{aligned}$$

(52)

$$\begin{aligned}&~~\qquad 0<x<1,\quad t>0,\quad \alpha \in (1,2], \end{aligned}$$

(53)

subject to the initial conditions

$$\begin{aligned} u(x,0)=0,\qquad u_t(x,0)=0, \end{aligned}$$

(54)

where $q(x,t)=2x^{\alpha }-\Gamma (\alpha +1)t^2+x^{3\alpha }t^6$. The exact solution is $u(x,t)=x^{\alpha }t^2$.

Employ the described method and use Lemma 3

$$\begin{aligned}[U^T({\mathbf {D}}_t^2-{\mathbf {D}}_x^{\alpha })+{\tilde{N}}^T]\Lambda (x,t)=Q^T\Lambda (x,t), \end{aligned}$$

(55)

where ${\tilde{N}}=U^T{\tilde{U}}^2$ represents the nonlinear operator and $q(x,t)=Q^T\Lambda (x,t)$. The initial conditions satisfy the following equations

$$\begin{aligned}&U^T[I_n\otimes \Phi _{\alpha }(0)]=F^T,\qquad \qquad f(x)=F^T\Phi (x), \end{aligned}$$

(56)

$$\begin{aligned}&U^T[I_n\otimes D_t^{(\alpha )}\Phi _{\alpha }(0)]=M^T,\qquad m(x)=M^T\Phi (x), \end{aligned}$$

(57)

these conditions provide $2n-1$ equations of the linear subsection of the main matrix equation to be solved. We show this subsection as ${\mathfrak {L}}U=C_L$ in which ${\mathfrak {L}}$ and $C_L$ are $(2n-1)\times nm$ and $(2n-1)\times 1$ matrices, respectively. Moreover, Eq. (55) yields $nm-2n+1$ equations that represent the nonlinear algebraic system of the main matrix equation as ${\mathfrak {N}}U=C_N$; where ${\mathfrak {N}}$ and $C_N$ are $(nm-2n+1)\times nm$ and $(nm-2n+1)\times 1$ matrices, respectively.

To show the efficiency of our scheme, we define the norm of residual error as follows

$$\begin{aligned}&Res (x,t)=[U^T({\mathbf {D}}_t^2-{\mathbf {D}}_x^{\alpha })+U^T{\tilde{U}}^2]\Lambda (x,t)-Q^T\Lambda (x,t), \end{aligned}$$

(58)

$$\begin{aligned}&\Vert Res (x,t)\Vert ^2= \int _{0}^{1}\int _{0}^{1} Res ^{2}(x,t)dxdt. \end{aligned}$$

(59)

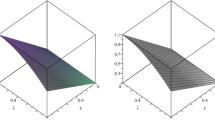
In Table 3, we show $\Vert Res(x,t)\Vert ^2$ for different values of $\alpha$ on $\Omega =[0,1]\times [0,1]$ interval using m and n equal to 3. From this Table, we see the fractional Legendre functions with only a few terms provides good agreement with the exact solution. Figure (1) represents the absolute error function for $\alpha =1.8$ at $t=0.25$ using m and n equal to 3. Our numerical results reveal good approximation of u(x, t), supporting the fractional Legendre functions.

Fig. 1

Absolute error function of example 2 for $\alpha =1.8$ at $t=0.25$ using $n=3$ and $m=3$

Table 3 $\Vert Res(x,t)\Vert ^2$ of the example 2 for various values of $\alpha$ on $\Omega =[0,1]\times [0,1]$ using $n=3$ and $m=3$

Conclusion

In this paper, fractional Legendre functions based on Legendre polynomials are defined. The corresponding operational matrix of fractional derivative is derived that is used to find the approximate solution of the linear and nonlinear fractional Klein–Gordon PDEs. Here, we show good accuracy is achieved with just a few terms of fractional-order Legendre function. The presented results illustrate the efficiency of the suggested method.