A transmission problem for the Timoshenko system with one local Kelvin–Voigt damping and non-smooth coefficient at the interface

Abstract

In this paper, we study the indirect stability of Timoshenko system with local or global Kelvin–Voigt damping, under fully Dirichlet or mixed boundary conditions. Unlike Zhao et al. (Acta Mathematica Sinica Engl Ser 21(3):655–666, 2004), Tian and Zhang (Mathematik und Physik 68(1), 2017), and Liu and Zhang (SIAM J Control Optim 56(6):3919–3947, 2018), in this paper, we consider the Timoshenko system with only one locally or globally distributed Kelvin–Voigt damping D [see System (1.1)]. Indeed, we prove that the energy of the system decays polynomially of type $t^{-1}$ and that this decay rate is in some sense optimal. The method is based on the frequency domain approach combining with multiplier method.

1 Introduction

In this paper, we study the indirect stability of a one-dimensional Timoshenko system with only one local or global Kelvin–Voigt damping. This system consists of two coupled hyperbolic equations:

$$\begin{aligned} \begin{array}{lll} \displaystyle {\rho _1 u_{tt}-k_1 \left( u_x+y\right) _x=0,} &{}\displaystyle {(x,t)\in \left( 0,L\right) \times \mathbb {R}_{+},}\\ \displaystyle { \rho _2y_{tt}-\left( k_2y_{x}+Dy_{xt}\right) _x+k_1\left( u_x+y\right) =0,} &{}\displaystyle {(x,t)\in \left( 0,L\right) \times \mathbb {R}_{+}.} \end{array} \end{aligned}$$

(1.1)

System (1.1) is subject to the following initial conditions:

$$\begin{aligned} \begin{array}{lll} u(x,0)=u_0(x),&{} u_t(x,0)=u_1(x),&{}x\in (0,L),\\ y(x,0)=y_0(x),&{} y_t(x,0)=y_1(x),&{}x\in (0,L), \end{array} \end{aligned}$$

(1.2)

in addition to the following boundary conditions:

$$\begin{aligned} u(0,t)=y(0,t)=u(L,t)=y(L,t)=0, \quad \displaystyle {t\in \mathbb {R}_+, } \end{aligned}$$

(1.3)

or

$$\begin{aligned} u(0,t)=y_x(0,t)=u(L,t)=y_x(L,t)=0, \quad \displaystyle {t\in \mathbb {R}_+. } \end{aligned}$$

(1.4)

Here, the coefficients $\rho _1,\ \rho _2,\ k_1$, and $k_2$ are strictly positive constant numbers. The function $D\in L^{\infty }(0,L)$, such that $D(x)\ge 0, \ \forall x\in [0, L]$. We assume that there exist $D_0>0$, $\alpha ,\ \beta \in \mathbb {R}$, $0\le \alpha < \beta \le L,$ such that:

$$\begin{aligned} D\in C\left( [\alpha ,\beta ]\right) \ \ \ \text {and}\ \ \ D(x)\ge D_0>0\ \ \ \forall \ x\in (\alpha , \beta ). \end{aligned}$$

(H)

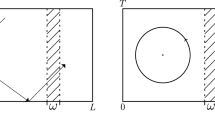
The hypothesis (H) means that the control D can be locally near the boundary (see Fig. 1a, b), or locally internal (see Fig. 2a), or globally (see Fig. 2b). Indeed, in the case when D is local damping (i.e., $\alpha \ne 0$ or $\beta \ne L$), we see that D is not necessary continuous over (0, L) (see Figs. 1a, b and 2a).

Fig. 1

The control is locally near the boundary

Fig. 2

The control is locally internal or globally

The Timoshenko system is usually considered in describing the transverse vibration of a beam and ignoring damping effects of any nature. Indeed, we have the following model, see in Timoshenko (1921):

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle {\rho \varphi _{tt}= \left( K\left( \varphi _x-\psi \right) \right) _x }\\ \displaystyle {I_{\rho } \psi _{tt}=\left( EI\psi _x\right) _{x}-K\left( \varphi _x-\psi \right) ,} \end{array} \right. \end{aligned}$$

where $\varphi$ is the transverse displacement of the beam and $\psi$ is the rotation angle of the filament of the beam. The coefficients $\rho ,\ I_\rho ,\ E,\ I,$ and K are, respectively, the density (the mass per unit length), the polar moment of inertia of a cross section, Young’s modulus of elasticity, the moment of inertia of a cross section, and the shear modulus, respectively.

The stabilization of the Timoshenko system with different kinds of damping has been studied in number of publications. For the internal stabilization, Raposo et al. (2005) showed that the Timoshenko system with two internal distributed dissipation is exponentially stable. Messaoudi and Mustafa (2008) extended the results to nonlinear feedback laws. Soufyane and Whebe (2003) showed that Timoshenko system with one internal distributed dissipation law is exponentially stable if and only if the wave propagation speeds are equal (i.e., $k_1/\rho _1=\rho _2/k_2$); otherwise, only the strong stability holds. Indeed, Muñoz Rivera and Racke (2008) they improved the results of Soufyane and Whebe (2003), where an exponential decay of the solution of the system has been established, allowing the coefficient of the feedback to be with an indefinite sign. Wehbe and Youssef (2009) proved that the Timoshenko system with one locally distributed viscous feedback is exponentially stable if and only if the wave propagation speeds are equal (i.e., $k_1/\rho _1=\rho _2/k_2$); otherwise, only the polynomial stability holds. Tebou in Tebou (2015) showed that the Timoshenko beam with same feedback control in both equations is exponentially stable. The stability of the Timoshenko system with thermoelastic dissipation has been studied in Sare and Racke (2009), Júnior et al. (2013), Fatori et al. (2014), and Hao and Wei (2018). The stability of Timoshenko system with memory type has been studied in Ammar-Khodja et al. (2003), Sare and Racke (2009), Guesmia and Messaoudi (2009), Messaoudi and Said-Houari (2009), and Abdallah et al. (2018). For the boundary stabilization of the Timoshenko beam, Kim and Renardy (1987) showed that the Timoshenko beam under two boundary controls is exponentially stable. Ammar-Khodja et al. (2007) studied the decay rate of the energy of the nonuniform Timoshenko beam with two boundary controls acting in the rotation-angle equation. In fact, under the equal speed wave propagation condition, they established exponential decay results up to an unknown finite-dimensional space of initial data. In addition, they showed that the equal speed wave propagation condition is necessary for the exponential stability. However, in the case of non-equal speed, no decay rate has been discussed. This result has been recently improved by Wehbe et al. in Bassam et al. (2015); i.e., the authors in Bassam et al. (2015) proved nonuniform stability and an optimal polynomial energy decay rate of the Timoshenko system with only one dissipation law on the boundary. In addition to the previously cited papers, we mention Akil et al. (2019) and Benaissa and Benazzouz (2017) for the stability of the Timoshenko system with fractional damping on the boundary. For the stabilization of the Timoshenko beam with nonlinear term, we mention Muñoz Rivera and Racke (2002), Alabau-Boussouira (2004), Araruna and Zuazua (2008), Messaoudi and Mustafa (2008), Cavalcanti et al. (2013), and Hao and Wei (2018).

Kelvin–Voigt material is a viscoelastic structure having properties of both elasticity and viscosity. There are a number of publications concerning the stabilization of wave equation with global or local Kelvin–Voigt damping. For the global case, the authors in Huang (1988) and Liu et al. (1998) proved the analyticity and the exponential stability of the semigroup. When the Kelvin–Voigt damping is localized on an interval of the string, the regularity and stability of the solution depend on the properties of the damping coefficient. Notably, the system is more effectively controlled by the local Kelvin–Voigt damping when the coefficient changes more smoothly near the interface (see Liu and Liu 1998; Renardy 2004; Zhang 2010; Liu and Zhang 2016; Liu et al. 2017).

Last but not least, in addition to the previously cited papers, the stability of the Timoshenko system with Kelvin–Voigt damping has been studied in few papers. Zhao et al. in Zhao et al. (2004) considered the Timoshenko system with local distributed Kelvin–Voigt damping:

$$\begin{aligned} \begin{array}{lll} \displaystyle {\rho _1 u_{tt}-\left[ k_1 \left( u_x+y\right) _x+D_1 (u_{xt}-y_t)\right] _x=0,} &{}\displaystyle {(x,t)\in \left( 0,L\right) \times \mathbb {R}_{+},}\\ \displaystyle { \rho _2y_{tt}-\left( k_2y_{x}+D_2y_{xt}\right) _x+k_1 \left( u_x+y\right) _x+D_1 (u_{xt}-y_t)=0,} &{}\displaystyle {(x,t)\in \left( 0,L\right) \times \mathbb {R}_{+}.} \end{array} \end{aligned}$$

(1.5)

They proved that the energy of the System (1.5) subject to Dirichlet–Neumann boundary conditions has an exponential decay rate when coefficient functions $D_1,\ D_2 \in C^{1,1}([0, L])$ and satisfy $D_1 \le c D_2 (c > 0).$ Tian and Zhang (2017) considered the Timoshenko System (1.5) under fully Dirichlet boundary conditions with locally or globally distributed Kelvin–Voigt damping when coefficient functions $D_1,\ D_2 \in C([0, L])$. First, when the Kelvin–Voigt damping is globally distributed, they showed that the Timoshenko System (1.5) under fully Dirichlet boundary conditions is analytic. Next, for their system with local Kelvin–Voigt damping, they analyzed the exponential and polynomial stability according to the properties of coefficient functions $D_1,\ D_2.$ Liu and Zhang (2018); on $(-1,1)\times \mathbb {R}_{+}$, they considered the Timoshenko System (1.5) under fully Dirichlet boundary conditions, such that $D_i \in L^\infty (-1,1)$, $D_i(x)=0$ for $\in x\in [-1,0],$ $D_i(x)>0$ is continuous for $x\in [0,1],$ for $i=1,2.$ Also, they assumed that there exist positive constants $k_1$, $k_2$ and nonnegative constants $\alpha _1,\ \alpha _2$, such that $\lim _{x\rightarrow 0^+}{D_i(x)}/{x^{\alpha _i}}=k_i$ for $i=1,2.$ They analyzed the exponential and polynomial stability according to the properties of coefficient functions $D_1,\ D_2.$ From the above, we conclude that the number of dampings and its localization play a crucial role in the stabilization of the system. Indeed and to say practically, more than one damping can be either impossible or expensive. Also, we cannot always specify the damping region. Due to the previous restrictions, we were motivated to study the stabilization of System (1.1) generally. Thus, in this paper, unlike Zhao et al. (2004), Tian and Zhang (2017) and Liu and Zhang (2018), we consider the Timoshenko system with only one locally (distributed in any subinterval of the domain) or globally distributed Kelvin–Voigt damping D [see System (1.1)]. Under hypothesis (H), we show that the energy of the Timoshenko System (1.1) subject to initial state (1.2) to either the boundary conditions (1.3) or (1.4) has a polynomial decay rate of type $t^{-1}$ and that this decay rate is in some sense optimal.

This paper is organized as follows: In Sect. 2, first, we show that the Timoshenko System (1.1) subject to initial state (1.2) to either the boundary conditions (1.3) or (1.4) can reformulate into an evolution equation and we deduce the well-posedness property of the problem by the semigroup approach. Second, using a criteria of Arendt and Batty (1988), we show that our system is strongly stable. In Sect. 3, we prove the polynomial energy decay rate of type $t^{-1}$ for the System (1.1)–(1.2) to either the boundary conditions (1.3) or (1.4). In Sect. 4, we prove that the energy decay rate of type $t^{-1}$ is in some sense optimal.

2 Well-posedness and strong stability

2.1 Well-posedness of the problem

In this part, under condition (H), using a semigroup approach, we establish well-posedness result for the Timoshenko System (1.1)–(1.2) to either the boundary conditions (1.3) or (1.4). The energy of solutions of the System (1.1) subject to initial state (1.2) to either the boundary conditions (1.3) or (1.4) is defined by:

$$\begin{aligned} E\left( t\right) = \frac{1}{2}\int _0^L\left( \rho _1\left| u_t\right| ^2+\rho _2\left| y_t\right| ^2 +k_1\left| u_x+y\right| ^2+k_2\left| y_x\right| ^2\right) \mathrm{{dx}}. \end{aligned}$$

Let $\left( u,y\right)$ be a regular solution for the System (1.1). Multiplying the first and the second equation of (1.1) by $u_t$ and $y_t,$ respectively, then using the boundary conditions (1.3) or (1.4), we get:

$$\begin{aligned} E'\left( t\right) =-\int _{0}^LD(x)\left| y_{xt}\right| ^2 \mathrm{{dx}}\le 0. \end{aligned}$$

Thus, System (1.1) subject to initial state (1.2) to either the boundary conditions (1.3) or (1.4) is dissipative in the sense that its energy is non-increasing with respect to the time t. Let us define the energy spaces $\mathcal {H}_1$ and $\mathcal {H}_2$ by:

$$\begin{aligned} \mathcal {H}_1=H_0^1\left( 0,L\right) \times L^2\left( 0,L\right) \times H_0^1\left( 0,L\right) \times L^2\left( 0,L\right) \end{aligned}$$

and

$$\begin{aligned} \mathcal {H}_2=H_0^1\left( 0,L\right) \times L^2\left( 0,L\right) \times H_*^1\left( 0,L\right) \times L^2\left( 0,L\right) , \end{aligned}$$

such that:

$$\begin{aligned} H_*^1(0,L)=\left\{ f\in H^1(0,L)\ |\ \int _0^Lf\mathrm{{dx}}=0\right\} . \end{aligned}$$

It is easy to check that the space $H_*^1$ is Hilbert spaces over $\mathbb {C}$ equipped with the norm:

$$\begin{aligned} \left\| u\right\| ^2_{H_*^1\left( 0,L\right) }=\left\| u_x\right\| ^2, \end{aligned}$$

where $\Vert \cdot \Vert$ denotes the usual norm of $L^2\left( 0,L\right)$. Both energy spaces $\mathcal {H}_1$ and $\mathcal {H}_2$ are equipped with the inner product defined by:

$$\begin{aligned} \left\langle U,\Phi \right\rangle _{\mathcal {H}_j}=\rho _1 \int _0^Lv\overline{\varphi }\, \mathrm{{dx}}+\rho _2 \int _0^Lz\overline{\theta }\, \mathrm{{dx}}+k_1\int _0^L\left( u_x+y\right) \overline{\left( \phi _x+\psi \right) }\, \mathrm{{dx}}+k_2\int _0^Ly_x\overline{\psi _x}\, \mathrm{{dx}} \end{aligned}$$

for all $U=\left( u,v,y,z\right)$ and $\Phi =\left( \phi ,\varphi ,\psi ,\theta \right)$ in $\mathcal {H}_j$,  $j=1,2$. We use $\Vert U\Vert _{\mathcal {H}_j}$ to denote the corresponding norms. We now define the following unbounded linear operators $\mathcal {A}_j$ in $\mathcal {H}_j$ by:

$$\begin{aligned} D\left( \mathcal {A}_1\right)= & {} \left\{ U=(u,v,y,z)\in \mathcal {H}_1\ |\ v,\ z \in H^1_0(0,L),\ u\in H^2\left( 0,L\right) ,\right. \\&\left. \left( k_2y_{x}+Dz_{x}\right) _x\in L^2\left( 0,L\right) \right\} ,\\ D\left( \mathcal {A}_2\right)= & {} \bigg \{U=(u,v,y,z)\in \mathcal {H}_2\ |\ v \in H^1_0(0,L),\ z\in H^1_*(0,L),\ u\in H^2\left( 0,L\right) ,\\&\left( k_2y_{x}+Dz_{x}\right) _x\in L^2\left( 0,L\right) , \ y_x(0)=y_x(L)=0\bigg \} \end{aligned}$$

and for $j=1,2:$

$$\begin{aligned}&\mathcal {A}_jU=\left( v,\frac{k_1}{\rho _1}(u_x+y)_x,z,\frac{1}{\rho _2}\left( k_2y_{x} +Dz_x\right) _x-\frac{k_1}{\rho _2}(u_x+y)\right) ,\\&\quad \forall \ U=\left( u,v,y,z\right) \in D\left( \mathcal {A}_j\right) . \end{aligned}$$

If $U=\left( u,u_t,y,y_t\right)$ is the state of System (1.1)–(1.2) to either the boundary conditions (1.3) or (1.4), then the Timoshenko system is transformed into a first order evolution equation on the Hilbert space $\mathcal {H}_j$:

$$\begin{aligned} \left\{ \begin{array}{c} U_t(x,t)=\mathcal {A}_jU(x,t),\\ U\left( x,0\right) =U_0(x), \end{array} \right. \end{aligned}$$

(2.1)

where:

$$\begin{aligned} U_0\left( x\right) =\left( u_0(x),u_1(x),y_0(x),y_1(x)\right) . \end{aligned}$$

Proposition 2.1

Under hypothesis (H), for $j=1,2,$ the unbounded linear operator $\mathcal {A}_j$ is m-dissipative in the energy space $\mathcal {H}_j$.

Proof

Let $j=1,2$, for $U=(u,v,y,z)\in D\left( \mathcal {A}_j\right)$, one has:

$$\begin{aligned} \Re \left\langle \mathcal {A}_jU,U\right\rangle _{\mathcal {H}_j}= -\int _{0}^LD(x)\left| z_{x}\right| ^2 \mathrm{{dx}}\le 0, \end{aligned}$$

which implies that $\mathcal {A}_j$ is dissipative under hypothesis (H). Here, $\Re$ is used to denote the real part of a complex number. We next prove the maximality of $\mathcal {A}_j$. For $F=(f_1,f_2,f_3,f_4)\in \mathcal {H}_j$, we prove the existence of $U=(u,v,y,z)\in D(\mathcal {A}_j)$, unique solution of the equation:

$$\begin{aligned} -\mathcal {A}_jU=F. \end{aligned}$$

Equivalently, one must consider the system given by:

$$\begin{aligned}&-v=f_1, \end{aligned}$$

(2.2)

$$\begin{aligned}&-{k_1}(u_x+y)_x={\rho _1}f_2, \end{aligned}$$

(2.3)

$$\begin{aligned}&-z=f_3, \end{aligned}$$

(2.4)

$$\begin{aligned}&-\left( {k_2}y_{x}+Dz_x\right) _x+{k_1}(u_x+y)={\rho _2}f_4, \end{aligned}$$

(2.5)

with the boundary conditions:

$$\begin{aligned} u(0)=u(L)=v(0)=v(L)=0\ \ \ \text {and}\ \ \ \left\{ \begin{array}{ll} y(0)=y(L)=z(0)=z(L)=0,\quad \text {for }j=1,\\ y_x(0)=y_x(L)=0,\qquad \qquad \qquad \,\,\, \text {for }j=2. \end{array}\right. \end{aligned}$$

(2.6)

Using the fact that $F\in \mathcal {H}_j,$ we get that $(v,z)\in \mathcal {V}_j(0,L)$, where $\mathcal {V}_1(0,L)=H_0^1(0,L)\times H_0^1(0,L)$ and $\mathcal {V}_2(0,L)=H_0^1(0,L)\times H_*^1(0,L)$. Now, let $(\varphi ,\psi )\in \mathcal {V}_j(0,L)$, multiplying Eqs. (2.3) and (2.5) by $\overline{\varphi }$ and $\overline{\psi }$, respectively, integrating in (0, L), taking the sum, then using Eq. (2.4) and the boundary condition (2.6), we get:

$$\begin{aligned}&\int _0^L \left( k_1 \left( u_x+y \right) \overline{\left( \varphi _x+\psi \right) }+k_2y_x\overline{\psi _{x}}\right) \mathrm{{dx}}=\int _0^L\left( \rho _1 f_1 \bar{\varphi }+\rho _2f_4\bar{ \psi }+D\left( f_3\right) _x\overline{\psi _x}\right) \mathrm{{dx}},\nonumber \\&\quad \forall \ (\varphi ,\psi )\in \mathcal {V}_j(0,L). \end{aligned}$$

(2.7)

The left-hand side of (2.7) is a bilinear continuous coercive form on $\mathcal {V}_j(0,L)\times \mathcal {V}_j(0,L)$, and the right-hand side of (2.7) is a linear continuous form on $\mathcal {V}_j(0,L)$. Then, using Lax–Milligram theorem [see in Pazy (1983)], we deduce that there exists $(u,y)\in \mathcal {V}_j(0,L)$ unique solution of the variational Problem (2.7). Thus, using (2.2), (2.4), and classical regularity arguments, we conclude that $-\mathcal {A}_jU=F$ admits a unique solution $U\in D\left( \mathcal {A}_j\right)$ and consequently $0\in \rho (\mathcal {A}_j)$, where $\rho \left( \mathcal {A}_j\right)$ denotes the resolvent set of $\mathcal {A}_j$. Then, $\mathcal {A}_j$ is closed and consequently $\rho \left( \mathcal {A}_j\right)$ is open set of $\mathbb {C}$ [see Theorem 6.7 in Kato (1995)]. Hence, we easily get $\lambda \in \rho \left( \mathcal {A}_j\right)$ for sufficiently small $\lambda >0$. This, together with the dissipativeness of $\mathcal {A}_j$, implies that $D\left( \mathcal {A}_j\right)$ is dense in $\mathcal {H}_j$ and that $\mathcal {A}_j$ is m-dissipative in $\mathcal {H}_j$ [see Theorems 4.5, 4.6 in Pazy (1983)]. Thus, the proof is complete. $\square$

Thanks to Lumer–Phillips theorem [see Liu and Zheng 1999; Pazy 1983], we deduce that $\mathcal {A}_j$ generates a $C_0$-semigroup of contraction $e^{t\mathcal {A}_j}$ in $\mathcal {H}_j$, and therefore, Problem (2.1) is well posed. Then, we have the following result.

Theorem 2.2

Under hypothesis (H), for $j=1,2,$ for any $U_0\in \mathcal {H}_j$, the Problem (2.1) admits a unique weak solution $U(x,t)=e^{t\mathcal {A}_j}U_0(x)$, such that $U\in C\left( \mathbb {R}_{+};\mathcal {H}_j\right) .$ Moreover, if $U_0\in D\left( \mathcal {A}_j\right) ,$ then $U\in C\left( \mathbb {R}_{+};D\left( \mathcal {A}_j\right) \right) \cap C^1\left( \mathbb {R}_{+};\mathcal {H}_j\right) .$ $\square$

Before starting the main results of this work, we introduce here the notions of stability that we encounter in this work.

Definition 2.3

Let $A:D(A)\subset H\rightarrow H$ generate a C$_0-$semigroup of contractions $\left( e^{t A}\right) _{t\ge 0}$ on H. The $C_0$-semigroup $\left( e^{t A}\right) _{t\ge 0}$ is said to be:

• 1. strongly stable if:

  $$\begin{aligned} \lim _{t\rightarrow +\infty } \Vert e^{t A}x_0\Vert _{H}=0, \quad \forall \ x_0\in H; \end{aligned}$$

• 2. exponentially (or uniformly) stable if there exist two positive constants M and $\epsilon$ such that

  $$\begin{aligned} \Vert e^{t A}x_0\Vert _{H} \le Me^{-\epsilon t}\Vert x_0\Vert _{H}, \quad \forall \ t>0, \ \forall \ x_0\in {H}; \end{aligned}$$

• 3. polynomially stable if there exists two positive constants C and $\alpha$, such that:

  $$\begin{aligned} \Vert e^{t A}x_0\Vert _{H}\le C t^{-\alpha }\Vert A x_0\Vert _{H}, \quad \forall \ t>0, \ \forall \ x_0\in D\left( A\right) . \end{aligned}$$

  In that case, one says that solutions of (2.1) decay at a rate $t^{-\alpha }$. The $C_0$-semigroup $\left( e^{t A}\right) _{t\ge 0}$ is said to be polynomially stable with optimal decay rate $t^{-\alpha }$ (with $\alpha >0$) if it is polynomially stable with decay rate $t^{-\alpha }$ and, for any $\varepsilon >0$ small enough, there exists solutions of (2.1) which do not decay at a rate $t^{-(\alpha +\varepsilon )}$. $\square$

We now look for necessary conditions to show the strong stability of the $C_0$-semigroup $\left( e^{t A}\right) _{t\ge 0}$. We will rely on the following result obtained by Arendt and Batty in Arendt and Batty (1988).

Theorem 2.4

(Arendt and Batty (1988)) Assume that A is the generator of a C$_0-$semigroup of contractions $\left( e^{tA}\right) _{t\ge 0}$ on a Hilbert space H. If A has no pure imaginary eigenvalues and $\sigma \left( A\right) \cap i\mathbb {R}$ is countable, where $\sigma \left( A\right)$ denotes the spectrum of A, then the $C_0$-semigroup $\left( e^{tA}\right) _{t\ge 0}$ is strongly stable. $\square$

Our subsequent findings on polynomial stability will rely on the following result from Borichev and Tomilov (2010), Liu and Rao (2005), Batty and Duyckaerts (2008), which gives necessary and sufficient conditions for a semigroup to be polynomially stable. For this aim, we recall the following standard result [see Borichev and Tomilov 2010; Liu and Rao 2005; Batty and Duyckaerts 2008 for part (i) and Huang (1985); Prüss (1984) for part (ii)].

Theorem 2.5

Let $A:D(A)\subset H\rightarrow H$ generate a C$_0-$semigroup of contractions $\left( e^{t A}\right) _{t\ge 0}$ on H. Assume that $i\lambda \in \rho (A),\ \forall \ \lambda \in \mathbb {R}$. Then, the $C_0$-semigroup $\left( e^{t A}\right) _{t\ge 0}$ is:

• (i) Polynomially stable of order $\frac{1}{\ell }\, (\ell >0)$ if and only if:

  $$\begin{aligned} \lim \sup _{\lambda \in \mathbb {R},\ |\lambda |\rightarrow \infty } |\lambda |^{-\ell }\left\| \left( i\lambda I-A\right) ^{-1}\right\| _{\mathcal {L}\left( H\right) }<+\infty . \end{aligned}$$

• (ii) Exponentially stable if and only if:

  $$\begin{aligned} \lim \sup _{\lambda \in \mathbb {R},\ |\lambda |\rightarrow \infty }\left\| \left( i\lambda I-A\right) ^{-1}\right\| _{\mathcal {L}\left( H\right) }<+\infty . \end{aligned}$$

  $\square$

2.2 Strong stability

In this part, we use general criteria of Arendt-B-atty in Arendt and Batty (1988) [see Theorem 2.4] to show the strong stability of the $C_0$-semigroup $e^{t\mathcal {A}_j}$ associated to the Timoshenko System (2.1). Our main result is the following theorem.

Theorem 2.6

Assume that (H) is true. Then, for $j=1,2,$ the $C_0-$semigroup $e^{t\mathcal {A}_j}$ is strongly stable in $\mathcal {H}_j$; i.e., for all $U_0\in \mathcal {H}_j$, the solution of (2.1) satisfies:

$$\begin{aligned} \lim _{t\rightarrow +\infty }\left\| e^{t\mathcal {A}_j} U_0\right\| _{\mathcal {H}_j}=0. \end{aligned}$$

The argument for Theorem 2.6 relies on the subsequent lemmas.

Lemma 2.7

Under hypothesis (H), for $j=1,2,$ one has:

$$\begin{aligned} \ker \left( i\lambda I-{\mathcal {A}_j}\right) =\{0\},\ \ \forall \lambda \in \mathbb {R}. \end{aligned}$$

Proof

For $j=1,2$, from Proposition 2.1, we deduce that $0\in \rho \left( \mathcal {A}_j\right)$. We still need to show the result for $\lambda \in \mathbb {R^*}$. Suppose that there exists a real number $\lambda \ne 0$ and $U=\left( u,v,y,z\right) \in D\left( \mathcal {A}_j\right)$, such that:

$$\begin{aligned} {\mathcal {A}_j} U=i\lambda U. \end{aligned}$$

Equivalently, we have:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {v} =\displaystyle {i\lambda u},\\ \displaystyle {{k_1}(u_x+y)_x}=\displaystyle {i{\rho _1}\lambda v},\\ \displaystyle {z}=\displaystyle {i\lambda y},\\ \displaystyle {\left( {k_2} y_{x}+Dz_x\right) _x-{k_1}(u_x+y)}=\displaystyle {i{\rho _2}\lambda z}. \end{array} \right. \end{aligned}$$

(2.8)

First, a straightforward computation gives:

$$\begin{aligned} 0=\Re \left\langle i\lambda U,U\right\rangle _{{\mathcal {H}}_j}=\Re \left\langle {\mathcal {A}_j} U,U\right\rangle _{{\mathcal {H}_j}}=-\int _{0}^LD(x)\left| z_{x}\right| ^2 \mathrm{{dx}}; \end{aligned}$$

using hypothesis (H), we deduce that:

$$\begin{aligned} Dz_x=0 \quad \text { {in} }\ (0,L) \ \ \ \text {and}\ \ \ z_x=0 \quad \text { {in} }\ (\alpha ,\beta ). \end{aligned}$$

(2.9)

Inserting (2.9) in (2.8), we get:

$$\begin{aligned}&u=y_x=0,\quad \text {in }\ (\alpha ,\beta ), \end{aligned}$$

(2.10)

$$\begin{aligned}&{k_1} u_{xx}+{\rho _1}\lambda ^2 u+{k_1} y_x=0,\quad \text {in }\ (0,L), \end{aligned}$$

(2.11)

$$\begin{aligned}&-k_1 u_x +{k_2} y_{xx}+\left( {\rho _2}\lambda ^2-{k_1}\right) y=0,\ \text {in }\ (0,L), \end{aligned}$$

(2.12)

with the following boundary conditions:

$$\begin{aligned}&u(0)=u(L)=y(0)=y(L)=0, \text { if }\ j=1\ \ \ \text {or} \nonumber \\&\quad u(0)=u(L)=y_x(0)=y_x(L)=0, \text { if }j=2. \end{aligned}$$

(2.13)

In fact, System (2.11)–(2.13) admit a unique solution $(u,y)\in C^2((0,L))$. From (2.10) and by the uniqueness of solutions, we get:

$$\begin{aligned} u=y_x=0,\quad \text {{in} }\ (0,L). \end{aligned}$$

(2.14)

• 1. If $j=1$, from (2.14) and the fact that $y(0)=0,$ we get $u=y=0$ in (0, L),  and hence, $U=0$. In this case, the proof is complete.

• 2. If $j=2$, from (2.14) and the fact that $y\in H^1_*(0,L)\, (i.e.,\ \int _0^L y \mathrm{{dx}}=0),$ we get $u=y=0$ in (0, L);  therefore, $U=0$. Thus, the proof is complete.

$\square$

Lemma 2.8

Under hypothesis (H), for $j=1,2,$ for all $\lambda \in \mathbb {R}$, then $i\lambda I-\mathcal {A}_j$ is surjective.

Proof

Let $F=(f_1,f_2,f_3,f_4) \in \mathcal {H}_j$, and we look for $U=(u,v,y,z) \in D(\mathcal {A}_j)$ solution of:

$$\begin{aligned} (i\lambda U-\mathcal {A}_j)U=F. \end{aligned}$$

Equivalently, we have:

$$\begin{aligned}&v=i\lambda u-f_1, \end{aligned}$$

(2.15)

$$\begin{aligned}&z=i\lambda y-f_3, \end{aligned}$$

(2.16)

$$\begin{aligned}&\lambda ^2 u+\frac{k_1}{\rho _1}(u_x+y)_x=F_1, \end{aligned}$$

(2.17)

$$\begin{aligned}&\lambda ^2 y+{\rho _2}^{-1}\left[ \left( {k_2}+i\lambda D\right) y_{x}\right] _x-\frac{k_1}{\rho _2}(u_x+y)=F_2, \end{aligned}$$

(2.18)

with the boundary conditions:

$$\begin{aligned} u(0)=u(L)=v(0)=v(L)=0\ \ \ \text {and}\ \ \ \left\{ \begin{array}{ll} y(0)=y(L)=z(0)=z(L)=0,\quad \text {for }j=1,\\ y_x(0)=y_x(L)=0,\qquad \qquad \qquad \,\,\, \text {for }j=2, \end{array}\right. \end{aligned}$$

(2.19)

such that:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle {F_1=-f_2-i\lambda f_1\in L^2(0,L)} ,\\ \displaystyle {F_2=-f_4-i\lambda f_3+{\rho _2}^{-1}\left( D\left( f_3\right) _x\right) _{x}\in H^{-1}(0,L)}. \end{array} \right. \end{aligned}$$

We define the operator $\mathcal {L}_j$ by:

$$\begin{aligned}&\mathcal {L}_j\mathcal {U}=\left( -\frac{k_1}{\rho _1}(u_x+y)_{x}, - \rho _2^{-1}\left[ \left( {k_2}+i\lambda D\right) y_{x}\right] _x+\frac{k_1}{\rho _2}(u_x+y) \right) ,\\&\quad \forall \ \mathcal {U}=(u,y)\in \mathcal {V}_j(0,L), \end{aligned}$$

where:

$$\begin{aligned} \mathcal {V}_1(0,L)=H_0^1(0,L)\times H_0^1(0,L)\ \ \ \text {and}\ \ \ \mathcal {V}_2(0,L)=H_0^1(0,L)\times H_*^1(0,L). \end{aligned}$$

Using Lax–Milgram theorem, it is easy to show that $\mathcal {L}_j$ is an isomorphism from $\mathcal {V}_j(0,L)$ onto $(H^{-1}\left( 0,L\right) )^2$. Let $\mathcal {U}=\left( u,y\right)$ and $F=\left( -F_1,-F_2\right)$, and then, we transform System (2.17)–(2.18) into the following form:

$$\begin{aligned} \mathcal {U}-\lambda ^2\mathcal {L}^{-1}_j\mathcal {U}=\mathcal {L}^{-1}F. \end{aligned}$$

(2.20)

Using the compactness embeddings from $L^2(0,L)$ into $H^{-1}(0,L)$ and from $H^1_0(0,L)$ into $L^{2}(0,L)$, and from $H^1_L(0,L)$ into $L^{2}(0,L)$, we deduce that the operator $\mathcal {L}_j^{-1}$ is compact from $L^2(0,L)\times L^2(0,L)$ into $L^2(0,L)\times L^2(0,L)$. Consequently, by Fredholm alternative, proving the existence of $\mathcal {U}$ solution of (2.20) reduces to proving $\ker \left( I-\lambda ^2\mathcal {L}^{-1}_j\right) =0$. Indeed, if $\left( \varphi ,\psi \right) \in \ker (I-\lambda ^2\mathcal {L}_j^{-1})$, then we have $\lambda ^2 \left( \varphi ,\psi \right) - \mathcal {L}_j \left( \varphi ,\psi \right) =0$. It follows that:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\lambda ^2 \varphi +\frac{k_1}{\rho _1}(\varphi _x+\psi )_x =0,}\\ \displaystyle {\lambda ^2 \psi +{\rho _2}^{-1}\left[ \left( {k_2}+i\lambda D\right) \psi _{x}\right] _x-\frac{k_1}{\rho _2}(\varphi _x+\psi )=0,} \end{array} \right. \end{aligned}$$

(2.21)

with the following boundary conditions:

$$\begin{aligned}&\varphi (0)=\varphi (L)=\psi (0)=\psi (L)=0, \text { if }j=1\ \ \ \text {or} \nonumber \\&\quad \varphi (0)=\varphi (L)=\psi _x(0)=\psi _x(L)=0, \text { if }j=2. \end{aligned}$$

(2.22)

It is now easy to see that if $(\varphi ,\psi )$ is a solution of System (2.21)–(2.22), then the vector V defined by:

$$\begin{aligned} V= \left( \varphi ,i\lambda \varphi ,\psi ,i\lambda \psi \right) \end{aligned}$$

belongs to $D(\mathcal {A}_j)$ and $i\lambda V-\mathcal {A}_jV=0.$ Therefore, ${V}\in \ker \left( i\lambda I-{\mathcal {A}_j}\right)$. Using Lemma 2.7, we get $V=0$, and so:

$$\begin{aligned} \ker (I-\lambda ^2\mathcal {L}^{-1}_j)=\{0\}. \end{aligned}$$

Thanks to Fredholm alternative, Eq. (2.20) admits a unique solution $(u,v) \in \mathcal {V}_j(0,L)$. Thus, using (2.15), (2.17) and a classical regularity arguments, we conclude that $\left( \ i\lambda -\mathcal {A}_j\right) U=F$ admits a unique solution $U\in D\left( \mathcal {A}_j\right)$. Thus, the proof is complete. $\square$

We are now in a position to conclude the proof of Theorem 2.6.

Proof of Theorem 2.6

Using Lemma 2.7, we directly deduce that ${\mathcal {A}}_j$ ha non pure imaginary eigenvalues. According to Lemmas 2.7, 2.8 and with the help of the closed graph theorem of Banach, we deduce that $\sigma ({\mathcal {A}}_j)\cap i\mathbb {R}=\{\emptyset \}$. Thus, we get the conclusion by applying Theorem 2.4 of Arendt and Batty. $\square$

3 Polynomial stability

In this section, we use the frequency domain approach method to show the polynomial stability of $\left( e^{t\mathcal {A}_j}\right) _{t\ge 0}$ associated with the Timoshenko System (2.1). We prove the following theorem.

Theorem 3.1

Under hypothesis (H), for $j=1,2,$ there exists $C>0$, such that for every $U_0\in D\left( \mathcal {A}_j\right)$, we have:

$$\begin{aligned} E\left( t\right) \le \frac{C}{t}\left\| U_0\right\| ^2_{D\left( \mathcal {A}_j\right) },\quad \ t>0. \end{aligned}$$

(3.1)

Since $\ i\mathbb {R}\subseteq \rho \left( \mathcal {A}_j\right) ,$ then for the proof of Theorem 3.1, according to Theorem 2.5, we need to prove that:

$$\begin{aligned} \sup _{\lambda \in \mathbb {R}}\left\| \left( i\lambda I-\mathcal {A}_j\right) ^{-1}\right\| _{\mathcal {L}\left( \mathcal {H}_j\right) } =O\left( \lambda ^{2}\right) . \end{aligned}$$

(3.2)

We will argue by contradiction. Therefore, suppose that there exists $\left\{ (\lambda _n,U_n=(u_n,v_n,y_n,\right. \left. z_n))\right\} _{n\ge 1}\subset \mathbb {R}\times D\left( \mathcal {A}_j\right)$, with $\lambda _n>1$ and:

$$\begin{aligned} \lambda _n\rightarrow +\infty ,\ \ \Vert U_n\Vert _{\mathcal {H}_j}=1, \end{aligned}$$

(3.3)

such that:

$$\begin{aligned} \lambda _n^{2}\left( \ i\lambda _n U_n-\mathcal {A}_jU_n\right) =\left( f_{1,n},f_{2,n},f_{3,n},f_{4,n}\right) \rightarrow 0\ \text { in } \mathcal {H}_j. \end{aligned}$$

(3.4)

Equivalently, we have:

$$\begin{aligned}&i{\lambda _n}u_n- {v_n}=\lambda _n^{-2}f_{1,n}\rightarrow 0\text { in } H^1_0(0,L), \end{aligned}$$

(3.5)

$$\begin{aligned}&i \lambda _n v_n-\frac{k_1}{\rho _1 }((u_n)_x+y_n)_x =\lambda _n^{-2}f_{2,n}\rightarrow 0\text { in } L^2(0,L), \end{aligned}$$

(3.6)

$$\begin{aligned}&i \lambda _ny_n-{z_n}=\lambda _n^{-2}f_{3,n}\rightarrow 0\text { in } \mathcal {W}_j(0,L) , \end{aligned}$$

(3.7)

$$\begin{aligned}&i{\lambda _n} z_n- \frac{k_2}{\rho _2}\left( (y_n)_{x}+\frac{D}{k_2}(z_n)_x\right) _x+\frac{k_1}{\rho _2 }((u_n)_x+y_n)=\lambda _n^{-2}f_{4,n}\rightarrow 0\text { in } L^2(0,L), \end{aligned}$$

(3.8)

where:

$$\begin{aligned} \mathcal {W}_j(0,L)=\left\{ \begin{array}{ll} \displaystyle {H^1_0(0,L),\quad \text {if }j=1}, \\ \displaystyle {H^1_*(0,L) ,\quad \text {if }j=2}.\end{array}\right. \end{aligned}$$

In the following, we will check the condition (3.2) by finding a contradiction with (3.3) such as $\left\| U_n\right\| _{\mathcal {H}_j} =o(1).$ For clarity, we divide the proof into several lemmas. From now on, for simplicity, we drop the index n.

Lemma 3.2

Under hypothesis (H), for $j=1,2,$ the solution $U=(u,v,y,z)\in D(\mathcal {A}_j)$ of System (3.5)–(3.8) satisfies the following asymptotic behavior estimates:

$$\begin{aligned}&\int _{0}^LD(x)\left| z_{x}\right| ^2 \mathrm{{dx}}=o\left( \lambda ^{-2}\right) , \ \int _{\alpha }^\beta \left| z_x\right| ^2 \mathrm{{dx}}=o\left( \lambda ^{-2}\right) , \end{aligned}$$

(3.9)

$$\begin{aligned}&\int _{\alpha }^\beta \left| y_{x}\right| ^2 \mathrm{{dx}}=o\left( \lambda ^{-4}\right) . \end{aligned}$$

(3.10)

Proof

First, taking the inner product of (3.4) with U in $\mathcal {H}_j$, then using the fact that U is uniformly bounded in $\mathcal {H}_j$, we get:

$$\begin{aligned} \int _{0}^L D(x)\left| z_{x}\right| ^2 \mathrm{{dx}}= & {} -\lambda ^{-2}\Re \left( \left\langle \lambda ^{2}\mathcal {A}_jU,U\right\rangle _{\mathcal {H}_j}\right) \\= & {} \lambda ^{-2}\Re \left( \left\langle \lambda ^{2}\left( i\lambda U-\mathcal {A}_jU\right) ,U\right\rangle _{\mathcal {H}_j}\right) =o\left( \lambda ^{-2}\right) ; \end{aligned}$$

hence, we get the first asymptotic estimate of (3.9). Next, using hypothesis (H) and the first asymptotic estimate of (3.9), we get the second asymptotic estimate of (3.9). Finally, from (3.4), (3.7), and (3.9), we get the asymptotic estimate of (3.10). Thus, the proof is complete. $\square$

Let $g \in C^1\left( [\alpha ,\beta ]\right)$, such that:

$$\begin{aligned} g(\beta )=-g(\alpha ) = 1,\quad \max \limits _ {x \in [\alpha , \beta ]} |g(x)|= c_g\quad \text {and}\quad \max \limits _ {x \in [\alpha , \beta ]} |g'(x)| = c_{g'}, \end{aligned}$$

where $c_g$ and $c_{g'}$ are strictly positive constant numbers.

Remark 3.3

It is easy to see the existence of g(x). For example, we can take $g(x)=\cos \left( \frac{ (\beta -x)\pi }{\beta -\alpha }\right)$ to get $g(\beta )=-g(\alpha )=1$, $g\in C^1([\alpha ,\beta ])$, $|g(x)| \le 1$ and $|g'(x)|\le \frac{\pi }{\beta -\alpha }$. Also, we can take:

$$\begin{aligned} g(x)={x}^{2}- \left( \beta + \alpha -2\, \left( \beta -\alpha \right) ^{-1} \right) x+\alpha \,\beta -\left( \beta +\alpha \right) \left( \beta -\alpha \right) ^{-1}. \end{aligned}$$

$\square$

Lemma 3.4

Under hypothesis (H), for $j=1,2,$ the solution $U=(u,v,y,z)\in D(\mathcal {A}_j)$ of System (3.5)–(3.8) satisfies the following asymptotic behavior estimates:

$$\begin{aligned}&|z(\beta )|^2+|z(\alpha )|^2 \le \left( \frac{\rho _2\lambda ^{\frac{1}{2}}}{2k_2}+2 \, c_{g'} \right) \int _\alpha ^\beta |z|^2 \, \mathrm{{dx}}+o\left( \lambda ^{-\frac{5}{2}}\right) , \end{aligned}$$

(3.11)

$$\begin{aligned}&\left| \left( {y}_x+\frac{D(x)}{k_2}{z}_x\right) (\alpha )\right| ^2+ \left| \left( {y}_x+\frac{D(x)}{k_2}{z}_x\right) (\beta )\right| ^2\le \frac{\rho _2 \lambda ^{\frac{3}{2}}}{2k_2} \int _\alpha ^\beta |z|^2 \mathrm{{dx}} +o\left( \lambda ^{-1}\right) .\nonumber \\ \end{aligned}$$

(3.12)

Proof

The proof is divided into two steps.

Step 1. In this step, we prove the asymptotic behavior estimate of (3.11). For this aim, first, from (3.7), we have:

$$\begin{aligned} z_x = i \lambda y_x- \lambda ^{-2}\, (f_3)_x \quad \text {in} \quad L^2(\alpha ,\beta ). \end{aligned}$$

(3.13)

Multiplying (3.13) by $2\, g \overline{z}$ and integrating over $(\alpha ,\beta ),$ and then taking the real part, we get:

$$\begin{aligned} \int _\alpha ^\beta g(x)\, (|z|^2)_x \, \mathrm{{dx}} = \Re \left\{ 2i \lambda \int _\alpha ^\beta g(x)\, y_x\overline{z}\mathrm{{dx}}\right\} - \Re \left\{ 2\lambda ^{-2}\,\int _\alpha ^\beta g(x)\, (f_3)_x\overline{z} \mathrm{{dx}}\right\} ; \end{aligned}$$

using by parts integration in the left-hand side of above equation, we get:

$$\begin{aligned} \left[ g(x)\, |z|^2\right] ^{\beta }_{\alpha } =\int _\alpha ^\beta g'(x)\, |z|^2 \, \mathrm{{dx}}+ \Re \left\{ 2i \lambda \int _\alpha ^\beta g(x)\, y_x\overline{z}\mathrm{{dx}}\right\} - \Re \left\{ 2\lambda ^{-2}\,\int _\alpha ^\beta g(x)\, (f_3)_x\overline{z} \mathrm{{dx}}\right\} . \end{aligned}$$

Consequently, we have:

$$\begin{aligned} |z(\beta )|^2+|z(\alpha )|^2 \le c_{g'}\int _\alpha ^\beta |z|^2 \, \mathrm{{dx}}+ 2 \lambda \, c_g \int _\alpha ^\beta |y_x|\left| {z}\right| \mathrm{{dx}}+2\lambda ^{-2} \, c_g\,\int _\alpha ^\beta \left| (f_3)_x\right| \left| {z}\right| \, \mathrm{{dx}}. \end{aligned}$$

(3.14)

On the other hand, we have:

$$\begin{aligned} 2 \lambda \, c_g |y_x| |z|\le \frac{\rho _2\lambda ^{\frac{1}{2}}|z|^2}{2k_2}+\frac{2k_2\lambda ^{\frac{3}{2}} \, c_g^2}{\rho _2}|y_x|^2\ \ \ \text {and} \ \ \ 2 \lambda ^{-2} |(f_3)_x| |z|\le c_{g'} \, |z|^2+\frac{c_g ^ 2 \, \lambda ^{-4} }{c_{g'}}|(f_3)_x|^2. \end{aligned}$$

Inserting the above equation in (3.14), then using (3.10) and the fact that $(f_3)_x\rightarrow 0$ in $L^2(\alpha ,\beta )$, we get:

$$\begin{aligned} |z(\beta )|^2+|z(\alpha )|^2 \le \left( \frac{\rho _2\lambda ^{\frac{1}{2}}}{2k_2}+2 \, c_{g'} \right) \int _\alpha ^\beta |z|^2 \, \mathrm{{dx}}+o\left( \lambda ^{-\frac{5}{2}}\right) ; \end{aligned}$$

hence, we get (3.11).

Step 2. In this step, we prove the following asymptotic behavior estimate of (3.12). For this aim, first, multiplying (3.8) by $-\frac{2\rho _2}{k_2}\, g \left( \overline{y}_x+\frac{D(x)}{k_2} \overline{z}_x\right)$ and integrating over $(\alpha ,\beta ),$ and then taking the real part, we get:

$$\begin{aligned}&\int _\alpha ^\beta g(x)\left( \left| {y}_x+\frac{D(x)}{k_2}{z}_x\right| ^2\right) _x\, \mathrm{{dx}} =\frac{2\rho _2 \lambda }{k_2}\Re \left\{ i \int _\alpha ^\beta g(x) z\left( \overline{y}_x+\frac{D(x)}{k_2} \overline{z}_x\right) \, \mathrm{{dx}}\right\} \\&\quad +\frac{2k_1}{k_2 }\Re \left\{ \int _\alpha ^\beta g(x) \left( u_x+y\right) \left( \overline{y}_x+\frac{D(x)}{k_2} \overline{z}_x\right) \mathrm{{dx}}\right\} \\&\quad -\frac{2\rho _2 \lambda ^{-2}}{k_2}\,\Re \left\{ \int _\alpha ^\beta g(x) f_4\left( \overline{y}_x+\frac{D(x)}{k_2} \overline{z}_x\right) \mathrm{{dx}}\right\} ; \end{aligned}$$

using by parts integration in the left-hand side of above equation, we get:

$$\begin{aligned}&\left[ g(x)\left| {y}_x+\frac{D(x)}{k_2}{z}_x\right| ^2\right] _\alpha ^\beta =\int _\alpha ^\beta g'(x)\left| {y}_x+\frac{D(x)}{k_2}{z}_x\right| ^2\, \mathrm{{dx}} \\&\quad +\frac{2\rho _2 \lambda }{k_2}\Re \left\{ i \int _\alpha ^\beta g(x) z\left( \overline{y}_x+\frac{D(x)}{k_2} \overline{z}_x\right) \, \mathrm{{dx}}\right\} \\&\quad +\frac{2k_1}{k_2 }\Re \left\{ \int _\alpha ^\beta g(x) \left( u_x+y\right) \left( \overline{y}_x+\frac{D(x)}{k_2} \overline{z}_x\right) \mathrm{{dx}}\right\} \\&\quad -\frac{2\rho _2 \lambda ^{-2}}{k_2}\,\Re \left\{ \int _\alpha ^\beta g(x) f_4\left( \overline{y}_x+\frac{D(x)}{k_2} \overline{z}_x\right) \mathrm{{dx}}\right\} . \end{aligned}$$

Consequently, we have:

$$\begin{aligned}&\left| \left( {y}_x+\frac{D(x)}{k_2}{z}_x\right) (\alpha )\right| ^2+ \left| \left( {y}_x+\frac{D(x)}{k_2}{z}_x\right) (\beta )\right| ^2 \le \frac{2\rho _2\, c_g \lambda }{k_2} \int _\alpha ^\beta \left| z\right| \left| {y}_x+\frac{D(x)}{k_2} {z}_x\right| \, \mathrm{{dx}} \\&c_{g'}\int _\alpha ^\beta \left| {y}_x+\frac{D(x)}{k_2}{z}_x\right| ^2\, \mathrm{{dx}} +\frac{2k_1\, c_g}{k_2 } \int _\alpha ^\beta \left| u_x+y\right| \left| {y}_x+\frac{D(x)}{k_2} {z}_x\right| \mathrm{{dx}}\\&\quad +\frac{2\rho _2\, c_g \lambda ^{-2}}{k_2}\int _\alpha ^\beta \left| f_4\right| \left| {y}_x+\frac{D(x)}{k_2} {z}_x\right| \mathrm{{dx}}. \end{aligned}$$

Now, using Cauchy–Schwarz inequality, and Eqs. (3.9)–(3.10), the fact that $f_4\rightarrow 0$ in $L^2(\alpha ,\beta )$, and the fact that $u_x+y$ is uniformly bounded in $L^2(\alpha ,\beta )$ in the right-hand side of above equation, we get:

$$\begin{aligned}&\left| \left( {y}_x+\frac{D(x)}{k_2}{z}_x\right) (\alpha )\right| ^2+ \left| \left( {y}_x+\frac{D(x)}{k_2}{z}_x\right) (\beta )\right| ^2\nonumber \\&\quad \le \frac{2\rho _2\, c_g \lambda }{k_2} \int _\alpha ^\beta \left| z\right| \left| {y}_x+\frac{D(x)}{k_2} {z}_x\right| \, \mathrm{{dx}} +o\left( \lambda ^{-1}\right) . \end{aligned}$$

(3.15)

On the other hand, we have:

$$\begin{aligned} \frac{2\rho _2\, c_g \lambda }{k_2} \, |z|\left| {y}_x+\frac{D(x)}{k_2} {z}_x\right| \le \frac{\rho _2\lambda ^{\frac{3}{2}}}{2k_2}|z|^2+\frac{2\rho _2\lambda ^{\frac{1}{2}}\, c_g^2}{k_2} \left| {y}_x+\frac{D(x)}{k_2} {z}_x\right| ^2. \end{aligned}$$

Inserting the above equation in (3.15), and then using Eqs. (3.9)–(3.10), we get:

$$\begin{aligned} \left| \left( {y}_x+\frac{D(x)}{k_2}{z}_x\right) (\alpha )\right| ^2+ \left| \left( {y}_x+\frac{D(x)}{k_2}{z}_x\right) (\beta )\right| ^2\le \frac{\rho _2 \lambda ^{\frac{3}{2}}}{2k_2} \int _\alpha ^\beta |z|^2 \mathrm{{dx}} +o\left( \lambda ^{-1}\right) ; \end{aligned}$$

hence, we get (3.12). Thus, the proof is complete. $\square$

Lemma 3.5

Under hypothesis (H), for $j=1,2,$ the solution $U=(u,v,y,z)\in D(\mathcal {A}_j)$ of System (3.5)–(3.8) satisfies the following asymptotic behavior estimates:

$$\begin{aligned}&|u_x(\alpha )+y(\alpha )|^2=O\left( 1\right) ,\ |u_x(\beta )+y(\beta )|^2=O\left( 1\right) . \end{aligned}$$

(3.16)

$$\begin{aligned}&|u(\alpha )|^2=O\left( \lambda ^{-2}\right) ,\ |u(\beta )|^2=O\left( \lambda ^{-2}\right) , \end{aligned}$$

(3.17)

$$\begin{aligned}&|v(\alpha )|^2=O\left( 1\right) ,\ |v(\beta )|^2=O\left( 1\right) . \end{aligned}$$

(3.18)

Proof

Multiplying Eq. (3.6) by $-\frac{2\rho _1}{k_1}g\left( \overline{u}_{x}+\overline{y}\right)$ and integrating over $(\alpha ,\beta ),$ and then taking the real part and using the fact that $u_x+y$ is uniformly bounded in $L^2(\alpha ,\beta )$, $f_2\rightarrow 0$ in $L^2(\alpha ,\beta )$, we get:

$$\begin{aligned}&\int _{\alpha }^{\beta }g(x)\left( \left| u_x+y\right| ^2\right) _x\, \mathrm{{dx}}-\frac{2 \rho _1\lambda }{k_1} \Re \left\{ i\int _{\alpha }^{\beta } g(x)\overline{u}_{x}\, v\, \mathrm{{dx}} \right\} \nonumber \\&\quad =\frac{2 \rho _1\lambda }{k_1} \Re \left\{ i\int _{\alpha }^{\beta } g(x) \overline{y}\, v\, \mathrm{{dx}} \right\} +o\left( \lambda ^{-2}\right) . \end{aligned}$$

(3.19)

Now, we divided the proof into two steps.

Step 1. In this step, we prove the asymptotic behavior estimates of (3.16)–(3.17). First, from (3.5), we have:

$$\begin{aligned} -i\lambda \, v=\lambda ^2 u+ i\lambda ^{-1}f_{1}. \end{aligned}$$

Inserting the above equation in the second term in left of (3.19), and then using the fact that $u_x$ is uniformly bounded in $L^2(\alpha ,\beta )$ and $f_1\rightarrow 0$ in $L^2(\alpha ,\beta )$, we get:

$$\begin{aligned}&\int _{\alpha }^{\beta }g(x)\left( \left| u_x+y\right| ^2\right) _x\, \mathrm{{dx}}+\frac{ \rho _1 \lambda ^2}{k_1} \int _{\alpha }^{\beta } g(x) \left( \left| u\right| ^2\right) _x \mathrm{{dx}} \\&\quad =-\frac{2 \rho _1 \lambda ^2}{k_1} \Re \left\{ \int _{\alpha }^{\beta } g(x)\, u\, \overline{y} \mathrm{{dx}} \right\} +o\left( \lambda ^{-1}\right) . \end{aligned}$$

Using by parts integration and the fact that $g(\beta )=-g(\alpha ) = 1$ in the above equation, we get:

$$\begin{aligned}&\left| u_x(\beta )+y(\beta )\right| ^2+\frac{ \rho _1 \lambda ^2}{k_1} \left| u(\beta )\right| ^2 +\left| u_x(\alpha )+y(\alpha )\right| ^2+\frac{ \rho _1 \lambda ^2}{k_1} \left| u(\alpha )\right| ^2\\&\quad =\int _{\alpha }^{\beta }g'(x)\left| u_x+y\right| ^2 \mathrm{{dx}}\\&\qquad +\frac{ \rho _1 \lambda ^2}{k_1} \int _{\alpha }^{\beta } g'(x) \left| u\right| ^2 \mathrm{{dx}} -\frac{2 \rho _1 \lambda ^2}{k_1} \Re \left\{ \int _{\alpha }^{\beta } g(x)\, u\, \overline{y} \mathrm{{dx}} \right\} +o\left( \lambda ^{-1}\right) ; \end{aligned}$$

consequently:

$$\begin{aligned}&\left| u_x(\beta )+y(\beta )\right| ^2+\frac{ \rho _1 \lambda ^2}{k_1} \left| u(\beta )\right| ^2 +\left| u_x(\alpha )+y(\alpha )\right| ^2\\&\quad +\frac{ \rho _1 \lambda ^2}{k_1} \left| u(\alpha )\right| ^2 \le c_{g'} \int _{\alpha }^{\beta }\left| u_x+y\right| ^2 \mathrm{{dx}}\\&\quad +\frac{ \rho _1\, c_{g'} \lambda ^2}{k_1} \int _{\alpha }^{\beta } \left| u\right| ^2 \mathrm{{dx}} +\frac{2 \rho _1\, c_g \lambda ^2}{k_1} \int _{\alpha }^{\beta } \left| u\right| \left| {y}\right| \mathrm{{dx}} +o\left( \lambda ^{-1}\right) . \end{aligned}$$

Next, since $\lambda \, u,\ \lambda \, y$ and $u_x+y$ are uniformly bounded, then from the above equation, we get (3.16) and (3.17).

Step 2. In this step, we prove the asymptotic behavior estimates of (3.18). First, from (3.5), we have:

$$\begin{aligned} -i\lambda \overline{u}_x= \overline{v}_x-\lambda ^{-2}(\overline{f}_{1})_x. \end{aligned}$$

Inserting the above equation in the second term in left of (3.19), and then using the fact that v is uniformly bounded in $L^2(\alpha ,\beta )$ and $(f_1)_x\rightarrow 0$ in $L^2(\alpha ,\beta )$, we get:

$$\begin{aligned}&\int _{\alpha }^{\beta }g(x)\left( \left| u_x+y\right| ^2\right) _x\, \mathrm{{dx}}+\frac{ \rho _1 }{k_1} \int _{\alpha }^{\beta } g(x) \left( \left| v\right| ^2\right) _x \mathrm{{dx}} \\&\quad =-\frac{2 \rho _1 \lambda ^2}{k_1} \Re \left\{ \int _{\alpha }^{\beta } g(x)\, u\, \overline{y} \mathrm{{dx}} \right\} +o\left( \lambda ^{-1}\right) . \end{aligned}$$

Similar to step 1, using by parts integration and the fact that $g(\beta )=-g(\alpha ) = 1$ in the above equation, and then using the fact that $v,\ \lambda \, u,\ \lambda \, y$ and $u_x+y$ are uniformly bounded in $L^2(\alpha ,\beta )$, we get (3.18). Thus, the proof is complete. $\square$

Lemma 3.6

Under hypothesis (H), for $j=1,2,$ and for $\lambda$ large enough, the solution $U=(u,v,y,z)\in D(\mathcal {A}_j)$ of System (3.5)–(3.8) satisfies the following asymptotic behavior estimates:

$$\begin{aligned}&\int _\alpha ^\beta |z|^2 \, \mathrm{{dx}}= o\left( \lambda ^{-\frac{5}{2}}\right) ,\qquad \int _\alpha ^\beta |y|^2 \, \mathrm{{dx}}= o\left( \lambda ^{-\frac{9}{2}}\right) , \end{aligned}$$

(3.20)

$$\begin{aligned}&\left| \left( {y}_x+\frac{D(x)}{k_2}{z}_x\right) (\alpha )\right| ^2=o\left( \lambda ^{-1}\right) ,\qquad \left| \left( {y}_x+\frac{D(x)}{k_2}{z}_x\right) (\beta )\right| ^2=o\left( \lambda ^{-1}\right) . \end{aligned}$$

(3.21)

Proof

The proof is divided into two steps.

Step 1. In this step, we prove the following asymptotic behavior estimate:

$$\begin{aligned} \left| \frac{i k_1}{\rho _2 \lambda } \int _\alpha ^\beta \left( u_x+y\right) \overline{z} \, \mathrm{{dx}}\right| \le \left( \frac{1}{4}+\frac{k_2 c_{g'}}{\rho _2\lambda ^{\frac{1}{2}}} +\frac{ k_1}{\rho _2 \lambda ^2 }\right) \int _\alpha ^\beta |z|^2 \, \mathrm{{dx}}+o\left( \lambda ^{-3}\right) . \end{aligned}$$

(3.22)

For this aim, first, we have:

$$\begin{aligned} \left| \frac{i k_1}{\rho _2 \lambda } \int _\alpha ^\beta \left( u_x+y\right) \overline{z} \, \mathrm{{dx}}\right| \le \left| \frac{i k_1}{\rho _2 \lambda } \int _\alpha ^\beta y\overline{z} \, \mathrm{{dx}}\right| +\left| \frac{i k_1}{\rho _2 \lambda } \int _\alpha ^\beta u_x\overline{z} \, \mathrm{{dx}}\right| . \end{aligned}$$

(3.23)

Now, from (3.7) and using the fact that $f_3\rightarrow 0$ in $L^2(\alpha ,\beta )$ and z is uniformly bounded in $L^2(\alpha ,\beta )$, we get:

$$\begin{aligned} \left| \frac{i k_1}{\rho _2 \lambda } \int _\alpha ^\beta y\overline{z} \, \mathrm{{dx}}\right| \le \frac{ k_1}{\rho _2 \lambda ^2 }\int _\alpha ^\beta |{z}|^2 \mathrm{{dx}}+o\left( \lambda ^{-4}\right) . \end{aligned}$$

(3.24)

Next, by using by parts integration, we get:

$$\begin{aligned} \left| \frac{i k_1}{\rho _2 \lambda } \int _\alpha ^\beta u_x\overline{z} \, \mathrm{{dx}}\right| =\left| -\frac{i k_1}{\rho _2 \lambda }\int _\alpha ^\beta u \overline{z}_x \, \mathrm{{dx}}+\frac{i k_1}{\rho _2 \lambda } u(\beta ) \overline{z}(\beta )-\frac{i k_1}{\rho _2 \lambda } u(\alpha ) \overline{z}(\alpha )\right| ; \end{aligned}$$

consequently:

$$\begin{aligned} \left| \frac{i k_1}{\rho _2 \lambda } \int _\alpha ^\beta u_x\overline{z} \, \mathrm{{dx}}\right| \le \frac{ k_1}{\rho _2 \lambda }\int _\alpha ^\beta \left| u \right| \left| {z}_x\right| \mathrm{{dx}}+\frac{k_1}{\rho _2 \lambda }\left( \left| u(\beta )\right| \left| {z}(\beta )\right| +\left| u(\alpha )\right| \left| {z}(\alpha )\right| \right) . \end{aligned}$$

(3.25)

On the other hand, we have:

$$\begin{aligned}&\frac{k_1}{\rho _2 \lambda }\left( \left| u(\beta )\right| \left| {z}(\beta )\right| +\left| u(\alpha )\right| \left| {z}(\alpha )\right| \right) \le \frac{k_1^2}{2k_2\rho _2\lambda ^{\frac{3}{2}}}\left( \left| u(\alpha )\right| ^2+\left| u(\beta )\right| ^2 \right) \\&\quad +\frac{k_2}{2\rho _2\lambda ^{\frac{1}{2}}}\left( \left| z(\alpha )\right| ^2+\left| z(\beta )\right| ^2 \right) . \end{aligned}$$

Inserting (3.11) and (3.17) in the above equation, we get:

$$\begin{aligned} \frac{k_1}{\rho _2 \lambda }\left( \left| u(\beta )\right| \left| {z}(\beta )\right| +\left| u(\alpha )\right| \left| {z}(\alpha )\right| \right) \le \left( \frac{1}{4}+\frac{k_2 c_{g'}}{\rho _2\lambda ^{\frac{1}{2}}} \right) \int _\alpha ^\beta |z|^2 \, \mathrm{{dx}}+o\left( \lambda ^{-3}\right) . \end{aligned}$$

Substituting the above equation in (3.25), and then using (3.9) and the fact that $\lambda u$ is bounded in $L^2(\alpha ,\beta )$, we get:

$$\begin{aligned} \left| \frac{i k_1}{\rho _2 \lambda } \int _\alpha ^\beta u_x\overline{z} \, \mathrm{{dx}}\right| \le \left( \frac{1}{4}+\frac{k_2 c_{g'}}{\rho _2\lambda ^{\frac{1}{2}}} \right) \int _\alpha ^\beta |z|^2 \, \mathrm{{dx}}+o\left( \lambda ^{-3}\right) . \end{aligned}$$

Finally, inserting the above equation and Eq. (3.24) in (3.23), we get (3.22).

Step 2. In this step, we prove the asymptotic behavior estimates of (3.20)–(3.21). For this aim, first, multiplying (3.8) by $-i \lambda ^{-1}\rho _2^{-1} \overline{z}$ and integrating over $(\alpha ,\beta ),$ and then taking the real part, we get:

$$\begin{aligned} \int _\alpha ^\beta | z|^2\, \mathrm{{dx}}= & {} -\frac{k_2 }{\rho _2\lambda } \Re \left\{ i \int _\alpha ^\beta \left( y_{x}+\frac{D}{k_2}z_x\right) _x\,\overline{z} \, \mathrm{{dx}}\right\} \\&+\frac{ k_1}{\rho _2 \lambda }\Re \left\{ i \int _\alpha ^\beta \left( u_x+y\right) \overline{z} \, \mathrm{{dx}}\right\} - \lambda ^{-3}\Re \left\{ i \int _\alpha ^\beta f_4\overline{z} \, \mathrm{{dx}}\right\} ; \end{aligned}$$

consequently:

$$\begin{aligned} \int _\alpha ^\beta | z|^2\, \mathrm{{dx}}\le & {} \frac{ k_2}{\rho _2\lambda }\left| \int _\alpha ^\beta \left( y_{x}+\frac{D}{k_2}z_x\right) _x\,\overline{z} \, \mathrm{{dx}}\right| \nonumber \\&+\left| \frac{i k_1}{\rho _2\lambda }\int _\alpha ^\beta \left( u_x+y\right) \overline{z} \, \mathrm{{dx}}\right| + \lambda ^{-3}\int _\alpha ^\beta \left| f_4\right| \left| z \right| \mathrm{{dx}}. \end{aligned}$$

(3.26)

From the fact that z is uniformly bounded in $L^2(\alpha ,\beta )$ and $f_5\rightarrow 0$ in $L^2(\alpha ,\beta )$, we get:

$$\begin{aligned} \lambda ^{-3}\int _\alpha ^\beta \left| f_4\right| \left| z \right| \mathrm{{dx}}=o\left( \lambda ^{-3}\right) . \end{aligned}$$

(3.27)

Inserting (3.22) and (3.27) in (3.26), we get:

$$\begin{aligned} \int _\alpha ^\beta | z|^2\, \mathrm{{dx}}\le & {} \frac{ k_2}{\rho _2\lambda }\left| \int _\alpha ^\beta \left( y_{x}+\frac{D}{k_2}z_x\right) _x\,\overline{z} \, \mathrm{{dx}}\right| \nonumber \\&+\left( \frac{1}{4}+\frac{k_2 c_{g'}}{\rho _2\lambda ^{\frac{1}{2}}} +\frac{ k_1}{\rho _2 \lambda ^2 }\right) \int _\alpha ^\beta |z|^2 \, \mathrm{{dx}}+o\left( \lambda ^{-3}\right) . \end{aligned}$$

(3.28)

Now, using by parts integration and (3.9)–(3.10), we get:

$$\begin{aligned}&\left| \int _\alpha ^\beta \left( y_{x}+\frac{D}{k_2}z_x\right) _x\,\overline{z} \, \mathrm{{dx}}\right| =\left| \left[ \left( y_{x}+\frac{D}{k_2}z_x\right) \,\overline{z} \right] ^\beta _\alpha -\int _\alpha ^\beta \left( y_{x}+\frac{D}{k_2}z_x\right) \overline{z}_x \, \mathrm{{dx}}\right| \nonumber \\&\quad \le \left| \left( y_{x}+\frac{D}{k_2}z_x\right) (\beta )\right| \left| {z}(\beta )\right| +\left| \left( y_{x}+\frac{D}{k_2}z_x\right) (\alpha )\right| \left| {z}(\alpha )\right| +\int _\alpha ^\beta \left| y_{x}+\frac{D}{k_2}z_x\right| \left| {z}_x\right| \, \mathrm{{dx}} \nonumber \\&\quad \le \left| \left( y_{x}+\frac{D}{k_2}z_x\right) (\beta )\right| \left| {z}(\beta )\right| +\left| \left( y_{x}+\frac{D}{k_2}z_x\right) (\alpha )\right| \left| {z}(\alpha )\right| +o\left( \lambda ^{-2}\right) . \end{aligned}$$

(3.29)

Inserting (3.29) in (3.28), we get:

$$\begin{aligned} \begin{array}{ll} \displaystyle { \left( \frac{3}{4}-\frac{k_2 c_{g'}}{\rho _2\lambda ^{\frac{1}{2}}} -\frac{ k_1}{\rho _2 \lambda ^2 }\right) \int _\alpha ^\beta | z|^2\, \mathrm{{dx}} }\\ \displaystyle { \le \frac{k_2 }{\rho _2\lambda }\left( \left| \left( y_{x}+\frac{D}{k_2}z_x\right) (\beta )\right| \left| {z}(\beta )\right| + \left| \left( y_{x}+\frac{D}{k_2}z_x\right) (\alpha )\right| \left| {z}(\alpha )\right| \right) +o\left( \lambda ^{-3}\right) . } \end{array} \end{aligned}$$

(3.30)

Now, for $\zeta =\beta$ or $\zeta =\alpha$, we have:

$$\begin{aligned} \frac{ k_2}{ \rho _2\lambda } \left| \left( y_{x}+\frac{D}{k_2}z_x\right) (\zeta )\right| \left| {z}(\zeta )\right| \le \frac{ k_2\, \lambda ^{-\frac{1}{2}}}{2\rho _2}|z(\zeta )|^2+\frac{ k_2\, \lambda ^{-\frac{3}{2}}}{2\rho _2}\left| \left( y_{x}+\frac{D}{k_2}z_x\right) (\zeta ) \right| ^2. \end{aligned}$$

Inserting the above equation in (3.30), we get:

$$\begin{aligned}&\left( \frac{3}{4}-\frac{k_2 c_{g'}}{\rho _2\lambda ^{\frac{1}{2}}} -\frac{ k_1}{\rho _2 \lambda ^2 }\right) \int _\alpha ^\beta | z|^2\, \mathrm{{dx}}\\&\quad \le \frac{ k_2\, \lambda ^{-\frac{3}{2}}}{2\rho _2}\left( \left| \left( y_{x}+\frac{D}{k_2}z_x\right) (\alpha ) \right| ^2+\left| \left( y_{x}+\frac{D}{k_2}z_x\right) (\beta ) \right| ^2\right) \\&\qquad +\frac{ k_2\, \lambda ^{-\frac{1}{2}}}{2\rho _2}\left( |z(\alpha )|^2+|z(\beta )|^2\right) +o\left( \lambda ^{-3}\right) . \end{aligned}$$

Substituting Eqs. (3.11) and (3.12) in the above inequality, we obtain:

$$\begin{aligned} \left( \frac{3}{4}-\frac{k_2 c_{g'}}{\rho _2\lambda ^{\frac{1}{2}}} -\frac{ k_1}{\rho _2 \lambda ^2 }\right) \int _\alpha ^\beta | z|^2\, \mathrm{{dx}} \le \left( \frac{1}{2}+\frac{k_2\, c_{g'}}{\rho _2 \lambda ^{\frac{1}{2}} }\right) \int _\alpha ^\beta |z|^2 \, \mathrm{{dx}}+o\left( \lambda ^{-\frac{5}{2}}\right) ; \end{aligned}$$

consequently:

$$\begin{aligned} \left( \frac{1}{4}-\frac{2k_2 c_{g'}}{\rho _2\lambda ^{\frac{1}{2}}} -\frac{ k_1}{\rho _2 \lambda ^2 }\right) \int _\alpha ^\beta |z|^2 \, \mathrm{{dx}}\le o\left( \lambda ^{-\frac{5}{2}}\right) , \end{aligned}$$

since $\lambda \rightarrow +\infty$, for $\lambda$ large enough, we get:

$$\begin{aligned} 0 < \left( \frac{1}{4}-\frac{2k_2 c_{g'}}{\rho _2\lambda ^{\frac{1}{2}}} -\frac{ k_1}{\rho _2 \lambda ^2 }\right) \int _\alpha ^\beta |z|^2 \, \mathrm{{dx}}\le o\left( \lambda ^{-\frac{5}{2}}\right) ; \end{aligned}$$

hence, we get the first asymptotic estimate of (3.20). Then, inserting the first asymptotic estimate of (3.20) in (3.7), we get the second asymptotic estimate of (3.20). Finally, inserting (3.20) in (3.12), we get (3.21). Thus, the proof is complete. $\square$

Lemma 3.7

Under hypothesis (H), for $j=1,2,$ and for $\lambda$ large enough, the solution $U=(u,v,y,z)\in D(\mathcal {A}_j)$ of System (3.5)–(3.8) satisfies the following asymptotic behavior estimates:

$$\begin{aligned} \int _\alpha ^\beta |u_x|^2 \, \mathrm{{dx}}= o\left( 1\right) \ \ \ \text {and} \ \ \ \int _\alpha ^\beta |v|^2 \, \mathrm{{dx}}= o\left( 1\right) . \end{aligned}$$

(3.31)

Proof

The proof is divided into two steps.

Step 1. In this step, we prove the first asymptotic behavior estimate of (3.31). First, multiplying Eq. (3.8) by $\frac{\rho _2}{k_1}\left( \overline{u}_x+\overline{y}\right)$ and integrating over $(\alpha ,\beta )$, we get:

$$\begin{aligned}&\int _{\alpha }^\beta \left| u_x+y\right| ^2\mathrm{{dx}}- \frac{k_2}{k_1}\int _{\alpha }^\beta \left( y_{x}+\frac{D}{k_2}z_x\right) _x\left( \overline{u}_x +\overline{y}\right) \mathrm{{dx}}\\&\quad =-\frac{i\rho _2\lambda }{k_1} \int _{\alpha }^\beta z\left( \overline{u}_x+\overline{y}\right) \mathrm{{dx}}+\frac{\rho _2}{k_1\lambda ^{2}}\int _{\alpha }^\beta f_{4}\left( \overline{u}_x+\overline{y}\right) \mathrm{{dx}}; \end{aligned}$$

using by parts integration in the second term in the left-hand side of above equation, we get:

$$\begin{aligned} \begin{array}{ll} \displaystyle { \int _{\alpha }^\beta \left| u_x+y\right| ^2\mathrm{{dx}}+ \frac{k_2}{k_1}\int _{\alpha }^\beta \left( y_{x}+\frac{D}{k_2}z_x\right) \left( \overline{u}_x+ \overline{y}\right) _x\mathrm{{dx}} =\frac{k_2}{k_1}\left[ \left( y_{x}+\frac{D}{k_2}z_x\right) \left( \overline{u}_x+\overline{y} \right) \right] _{\alpha }^\beta }\\ \displaystyle { -\frac{i\rho _2\lambda }{k_1} \int _{\alpha }^\beta z\left( \overline{u}_x+\overline{y}\right) \mathrm{{dx}} +\frac{\rho _2}{k_1\lambda ^{2}}\int _{\alpha }^\beta f_{4}\left( \overline{u}_x +\overline{y}\right) \mathrm{{dx}}}. \end{array} \end{aligned}$$

(3.32)

Next, multiplying Eq. (3.6) by $\frac{\rho _1k_2}{k_1^2} \left( \overline{y}_x+\frac{D}{k_2}\overline{z}_x\right)$ and integrating over $(\alpha ,\beta )$, and then using the fact that $f_2\rightarrow 0$ in $L^2(0,L)$ and Eqs. (3.9)–(3.10), we get:

$$\begin{aligned}&-\frac{k_2}{k_1 }\int _{\alpha }^\beta \left( \overline{y}_x+\frac{D}{k_2}\overline{z}_x\right) \left( u_x+y\right) _x\mathrm{{dx}} =-\frac{i\rho _1k_2\, \lambda }{k_1^2} \int _{\alpha }^\beta v \left( \overline{y}_x+\frac{D}{k_2}\overline{z}_x\right) \mathrm{{dx}}\\&\quad +\frac{\rho _1k_2}{k_1^2\lambda ^{2}}\int _{\alpha }^\beta f_{2}\left( \overline{y}_x+\frac{D}{k_2}\overline{z}_x\right) \mathrm{{dx}}; \end{aligned}$$

consequently:

$$\begin{aligned}&-\frac{k_2}{k_1 }\int _{\alpha }^\beta \left( {y}_x+\frac{D}{k_2}{z}_x\right) \left( \overline{u}_x+\overline{y}\right) _x\mathrm{{dx}} =\frac{i\rho _1k_2\, \lambda }{k_1^2} \int _{\alpha }^\beta \overline{v} \left( {y}_x+\frac{D}{k_2}{z}_x\right) \mathrm{{dx}}\nonumber \\&\quad +\frac{\rho _1k_2}{k_1^2 \lambda ^{2}}\int _{\alpha }^\beta \overline{f}_{2}\left( {y}_x+\frac{D}{k_2}{z}_x\right) \mathrm{{dx}}. \end{aligned}$$

(3.33)

Adding (3.32) and (3.33), we obtain:

$$\begin{aligned}&\int _{\alpha }^\beta \left| u_x+y\right| ^2\mathrm{{dx}} =-\frac{i\rho _2\lambda }{k_1} \int _{\alpha }^\beta z\left( \overline{u}_x+\overline{y}\right) \mathrm{{dx}}+\frac{k_2}{k_1}\left[ \left( y_{x} +\frac{D}{k_2}z_x\right) \left( \overline{u}_x+\overline{y}\right) \right] _{\alpha }^\beta \\&\quad +\frac{i\rho _1k_2\, \lambda }{k_1^2} \int _{\alpha }^\beta \overline{v} \left( {y}_x+\frac{D}{k_2}{z}_x\right) \mathrm{{dx}}+\frac{\rho _2}{k_1\lambda ^{2}}\int _{\alpha }^\beta f_{4}\left( \overline{u}_x+\overline{y}\right) \mathrm{{dx}}\\&\quad +\frac{\rho _1k_2}{k_1^2 \lambda ^{2}}\int _{\alpha }^\beta \overline{f}_{2}\left( {y}_x+\frac{D}{k_2}{z}_x\right) \mathrm{{dx}}; \end{aligned}$$

therefore:

$$\begin{aligned}&\int _{\alpha }^\beta \left| u_x+y\right| ^2\mathrm{{dx}} \le \frac{\rho _2\lambda }{k_1} \int _{\alpha }^\beta \left| z\right| \left| {u}_x+{y}\right| \mathrm{{dx}}+\frac{k_2}{k_1} \left| \left( y_{x}+\frac{D}{k_2}z_x\right) (\beta )\right| \left| {u}_x(\beta )+ {y}(\beta )\right| \nonumber \\&\quad +\frac{k_2}{k_1} \left| \left( y_{x}+\frac{D}{k_2}z_x\right) (\alpha )\right| \left| {u}_x(\alpha )+{y}(\alpha )\right| +\frac{\rho _1k_2\, \lambda }{k_1^2} \int _{\alpha }^\beta \left| {v}\right| \left| {y}_x+\frac{D}{k_2}{z}_x\right| \mathrm{{dx}}\nonumber \\&\quad +\frac{\rho _2}{k_1\lambda ^{2}}\int _{\alpha }^\beta \left| f_{4}\right| \left| {u}_x+{y}\right| \mathrm{{dx}}+\frac{\rho _1k_2}{k_1^2 \lambda ^{2}}\int _{\alpha }^\beta \left| {f}_{2}\right| \left| {y}_x+\frac{D}{k_2}{z}_x\right| \mathrm{{dx}} . \end{aligned}$$

(3.34)

From (3.4), (3.9), (3.10), (3.16), (3.20), (3.21), and the fact that $v,\ u_x+y$ are uniformly bounded in $L^2(\alpha ,\beta )$, we obtain:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\left| \left( y_{x}+\frac{D}{k_2}z_x\right) (\beta )\right| \left| {u}_x(\beta ) +{y}(\beta )\right| =o\left( \lambda ^{-\frac{1}{2}}\right) },\\ \displaystyle {\left| \left( y_{x}+\frac{D}{k_2}z_x\right) (\alpha )\right| \left| {u}_x(\alpha ) +{y}(\alpha )\right| =o\left( \lambda ^{-\frac{1}{2}}\right) },\\ \displaystyle {\lambda \int _{\alpha }^\beta \left| z\right| \left| {u}_x+{y}\right| \mathrm{{dx}}=o\left( \lambda ^{-\frac{1}{4}}\right) ,\ \lambda \int _{\alpha }^\beta \left| {v}\right| \left| {y}_x+\frac{D}{k_2}{z}_x\right| \mathrm{{dx}}=o(1)},\\ \displaystyle {\lambda ^{-2}\int _{\alpha }^\beta \left| f_{4}\right| \left| {u}_x+{y}\right| \mathrm{{dx}}=o\left( \lambda ^{-2}\right) ,\ \lambda ^{-2}\int _{\alpha }^\beta \left| {f}_{2}\right| \left| {y}_x+\frac{D}{k_2}{z}_x\right| \mathrm{{dx}}=o\left( \lambda ^{-3}\right) }. \end{array} \right. \end{aligned}$$

Inserting the above equation in (3.34), we get:

$$\begin{aligned} \int _{\alpha }^\beta \left| u_x+y\right| ^2\mathrm{{dx}}=o(1). \end{aligned}$$

From the above equation and (3.20), we get the first asymptotic estimate of (3.31).

Step 2. In this step, we prove the second asymptotic behavior estimate of (3.31). Multiplying (3.6) by $-i\lambda ^{-1} \overline{v}$ and integrating over $(\alpha ,\beta ),$ and then taking the real part, we get:

$$\begin{aligned} \int _\alpha ^\beta \left| v\right| ^2\mathrm{{dx}}=-\frac{ k_1 }{\rho _1\lambda }\Re \left\{ i\int _\alpha ^\beta (u_x+y)_x\overline{v}\, \mathrm{{dx}}\right\} -\lambda ^{-3}\Re \left\{ i\int _\alpha ^\beta f_{2}\overline{v}\, \mathrm{{dx}}\right\} ; \end{aligned}$$

using by parts integration in the second term in the right-hand side of above equation, we get:

$$\begin{aligned} \int _\alpha ^\beta \left| v\right| ^2\mathrm{{dx}}= & {} \frac{ k_1 }{\rho _1\lambda }\Re \left\{ i\int _\alpha ^\beta \left( u_x+y\right) {\overline{v}_x}\mathrm{{dx}}\right\} \\&-\frac{k_1}{\rho _1 {\lambda } }\Re \left\{ i \left[ (u_x+y)\overline{v}\right] _\alpha ^\beta \right\} -\lambda ^{-3}\Re \left\{ i\int _\alpha ^\beta f_{2}\overline{v}\, \mathrm{{dx}}\right\} . \end{aligned}$$

Consequently, we obtain:

$$\begin{aligned} \int _\alpha ^\beta \left| v\right| ^2\mathrm{{dx}}\le & {} \frac{ k_1 }{\rho _1\lambda }\int _\alpha ^\beta \left| u_x+y\right| \left| {v}_x\right| \mathrm{{dx}}\\&+\frac{k_1}{\rho _1 {\lambda } }\left( |u_x(\beta )+y(\beta )||{v}(\beta )|+|u_x(\alpha )+y(\alpha )|{v}(\alpha )|\right) \\&+\lambda ^{-3}\int _\alpha ^\beta \left| f_{2}\right| \left| {v}\right| \mathrm{{dx}}. \end{aligned}$$

Finally, from (3.16), (3.18), (3.20), the first asymptotic behavior estimate of (3.31), the fact that $\lambda ^{-1} v_x,\ v$ are uniformly bounded in $L^2(\alpha ,\beta )$, and the fact that $f_2\rightarrow 0$ in $L^2(\alpha ,\beta )$, we get the second asymptotic behavior estimate of (3.20). Thus, the proof is complete. $\square$

Lemma 3.8

Under hypothesis (H), for $j=1,2,$ the solution $U=(u,v,y,z)\in D(\mathcal {A}_j)$ of System (3.5)–(3.8) satisfies the following asymptotic behavior estimate:

$$\begin{aligned} \Vert U\Vert _{\mathcal {H}_j}=o\left( 1\right) ,\quad \text {over } \left( 0,L\right) . \end{aligned}$$

Proof

First, under hypothesis (H), for $j=1,2,$ and for $\lambda$ large enough, from Lemmas 3.5, 3.6 and 3.7, we deduce that:

$$\begin{aligned} \Vert U\Vert _{\mathcal {H}_j}=o\left( 1\right) ,\quad \text {over } \left( \alpha ,\beta \right) . \end{aligned}$$

(3.35)

Now, let $\phi \in H^1_0\left( 0,L\right)$ be a given function. We proceed the proof in two steps.

Step 1. Multiplying Eq. (3.6) by $2{\rho _1 } \phi \overline{u}_x$ and integrating over (0, L),  and then using the fact that $u_x$ is bounded in $L^2(0,L)$, $f_2\rightarrow 0$ in $L^2(0,L)$, and $\phi (0)=\phi (L)=0$ to get:

$$\begin{aligned} \Re \left\{ {2i\rho _1 } \lambda \int _0^L \phi v\overline{u}_x \mathrm{{dx}}\right\} + k_1\int _0^L \phi ' |u_x|^2\mathrm{{dx}} -\Re \left\{ 2k_1\int _0^L \phi \overline{u}_x y_x \mathrm{{dx}}\right\} =o(\lambda ^{-2}) . \end{aligned}$$

(3.36)

From (3.5), we have:

$$\begin{aligned} i{\lambda }\overline{u}_x= -\overline{v}_x-\lambda ^{-2}(\overline{f}_{1})_x. \end{aligned}$$

Inserting the above equation in (3.36), then using the fact that $(f_1)_x\rightarrow 0$ in $L^2(0,L)$, and the fact that v is bounded in $L^2(0,L)$, we get:

$$\begin{aligned} {\rho _1 } \int _0^L \phi '|v|^2 \mathrm{{dx}}+k_1 \int _0^L \phi ' |u_x|^2\mathrm{{dx}} -\Re \left\{ 2k_1\int _0^L \phi \overline{u}_x y_x \mathrm{{dx}}\right\} =o(\lambda ^{-2}) . \end{aligned}$$

(3.37)

Similarly, multiplying Eq. (3.8) by $2\rho _2 \phi \left( \overline{y}_x+\frac{D}{k_1} \overline{z}_x\right)$ and integrating over (0, L),  and then using by parts integration and $\phi (0)=\phi (L)=0$ to get:

$$\begin{aligned}&\Re \left\{ {2i\rho _2} {\lambda }\int _0^L \phi z \overline{y}_x \mathrm{{dx}}\right\} + k_2\int _0^L \phi ' \left| y_x+\frac{D}{k_2}z_x\right| ^2 \mathrm{{dx}}+\Re \left\{ 2k_1 \int _0^L \phi \overline{y}_x u_x\mathrm{{dx}}\right\} \nonumber \\&\quad =-\lambda ^{-1}\Re \left\{ 2k_1\int _0^L \phi \lambda y \overline{y}_x \mathrm{{dx}} \right\} -\Re \left\{ \frac{2i\rho _2 }{k_1} {\lambda }\int _0^L D(x) \phi z \overline{z}_x \mathrm{{dx}}\right\} \nonumber \\&\qquad -\Re \left\{ 2 \int _0^L D(x) \phi \overline{z}_x u_x\mathrm{{dx}}\right\} \nonumber \\&\qquad -\Re \left\{ 2\int _0^L D(x) \phi \overline{z}_x y\mathrm{{dx}} \right\} +\Re \left\{ {2\rho _2 } \lambda ^{-2}\int _0^L \phi f_4\overline{y}_x\mathrm{{dx}}\right\} \nonumber \\&\qquad +\Re \left\{ \frac{2\rho _2 }{k_1} \lambda ^{-2}\int _0^LD(x) \phi f_4\overline{z}_x\mathrm{{dx}}\right\} . \end{aligned}$$

(3.38)

For all bounded $h\in L^2(0,L)$, using Cauchy–Schwarz inequality, the first estimation of (3.9), and the fact that $D\in L^{\infty }(0,L)$, we obtain:

$$\begin{aligned}&\Re \left\{ \int _0^L D(x) h \overline{z}_x \mathrm{{dx}}\right\} \nonumber \\&\quad \le \left( \sup _{x\in (0,L)}D^{1/2}(x)\right) \left( \int _0^L D(x) |{z}_x|^2 \mathrm{{dx}}\right) ^{1/2} \left( \int _0^L |h|^2 \mathrm{{dx}}\right) ^{1/2}=o(\lambda ^{-1}). \end{aligned}$$

(3.39)

From (3.38) and using (3.39), the fact that $z,\ \lambda y,\ y_x$ are bounded in $L^2(0,L)$, the fact that $f_4\rightarrow 0$ in $L^2(0,L)$, we get:

$$\begin{aligned} \Re \left\{ 2i\rho _2 {\lambda }\int _0^L \phi z \overline{y}_x \mathrm{{dx}}\right\} + k_2\int _0^L \phi ' \left| y_x+\frac{D}{k_2}z_x\right| ^2 \mathrm{{dx}}+\Re \left\{ 2k_1 \int _0^L \phi \overline{y}_x u_x\mathrm{{dx}}\right\} =o(1). \end{aligned}$$

(3.40)

On the other hand, from (3.7), we have:

$$\begin{aligned} i{\lambda }\overline{y}_x= -\overline{z}_x-\lambda ^{-2}(\overline{f}_{3})_x. \end{aligned}$$

Inserting the above equation in (3.40), then using the fact that $(f_3)_x\rightarrow 0$ in $L^2(0,L)$, and the fact that z is bounded in $L^2(0,L)$, we get:

$$\begin{aligned} \rho _2\int _0^L \phi ' |z|^2\mathrm{{dx}}+k_2\int _0^L \phi ' \left| y_x+\frac{D}{k_2}z_x\right| ^2 \mathrm{{dx}}+\Re \left\{ 2k_1 \int _0^L \phi \overline{y}_x u_x\mathrm{{dx}}\right\} =o(1). \end{aligned}$$

(3.41)

Adding (3.37) and (3.41), we get:

$$\begin{aligned} \int _0^L \phi '\left( \rho _1 |v|^2+\rho _2 |z|^2+k_1 |u_x|^2+k_2 \left| y_x+\frac{D}{k_2}z_x\right| ^2 \right) \mathrm{{dx}}=o(1). \end{aligned}$$

(3.42)

Step 2. Let $\epsilon >0$, such that $\alpha +\epsilon <\beta$ and define the cut-off function $\varsigma _1 \text { in } C^1\left( \left[ 0,L\right] \right)$ by:

$$\begin{aligned} 0\le \varsigma _1 \le 1,\ \varsigma _1=1 \text { on } \left[ 0,\alpha \right] \text { and } \varsigma _1=0 \text { on } \left[ \alpha +\epsilon ,L\right] . \end{aligned}$$

Take $\phi =x \varsigma _1$ in (3.42), and then use the fact that $\left\| U\right\| _{\mathcal {H}_j}=o\left( 1\right)$ on $\left( \alpha ,\beta \right)$ (i.e., (3.35)), the fact that $\alpha<\alpha +\epsilon <\beta$, and (3.9)–(3.10), we get:

$$\begin{aligned} \int _0^\alpha \left( \rho _1 |v|^2+\rho _2 |z|^2+k_1 |u_x|^2+k_2 \left| y_x+\frac{D}{k_2}z_x\right| ^2 \right) \mathrm{{dx}}=o(1). \end{aligned}$$

(3.43)

Moreover, using Cauchy–Schwarz inequality, the first estimation of (3.9), the fact that $D\in L^{\infty }(0,L)$, and (3.43), we get:

$$\begin{aligned} \begin{array}{rl} \displaystyle {\int _0^\alpha |y_x|^2\mathrm{{dx}}}&{}\le \displaystyle { 2\int _0^\alpha \left| y_x+\frac{D}{k_2}z_x\right| ^2\mathrm{{dx}}+\frac{2}{k_2^2}\int _0^\alpha D(x)^2\left| z_x\right| ^2\mathrm{{dx}}},\\ &{}\le \displaystyle {2\int _0^\alpha \left| y_x+\frac{D}{k_2}z_x\right| ^2\mathrm{{dx}}+\frac{2 \left( \sup _{x\in (0,\alpha )}D(x)\right) }{k_2^2}\int _0^\alpha D(x)\left| z_x\right| ^2\mathrm{{dx}}},\\ &{}=\displaystyle {o(1)}. \end{array} \end{aligned}$$

(3.44)

Using (3.43) and (3.44), we get:

$$\begin{aligned} \left\| U\right\| _{\mathcal {H}_j}=o\left( 1\right) \text { on }(0,\alpha ). \end{aligned}$$

Similarly, by symmetry, we can prove that: $\left\| U\right\| _{\mathcal {H}_j}=o\left( 1\right) \text { on }(\beta ,L)$ and therefore:

$$\begin{aligned} \left\| U\right\| _{\mathcal {H}_j}=o\left( 1\right) \text { on }(0,L). \end{aligned}$$

Thus, the proof is complete.$\square$

Proof of Theorem 3.1

Under hypothesis (H), for $j=1,2,$ from Lemma 3.8, we have $\Vert U\Vert _{\mathcal {H}_j}=o\left( 1\right) ,$ over (0, L), which contradicts (3.3). This implies that:

$$\begin{aligned} \displaystyle {\sup _{\lambda \in \mathbb {R}}\left\| \left( i\lambda Id-\mathcal {A}_j\right) ^{-1}\right\| _{\mathcal {L}\left( \mathcal {H}_j\right) }=O\left( \lambda ^{2}\right) }. \end{aligned}$$

The result follows from Theorem 2.5 part (i). $\square$

Remark 3.9

From Lemmas 3.5, 3.6 and 3.7, we deduce that $\Vert U\Vert _{\mathcal {H}_j}=o\left( 1\right) ,$ over $\left( \alpha ,\beta \right) .$ After that in Lemma 3.8, we have chosen a particular function $\phi \in H^1_0\left( 0,L\right)$, to get $\Vert U\Vert _{\mathcal {H}_j}=o\left( 1\right) ,$ on $\left( 0,L\right) .$ We note that while proving theses lemmas, we have not used the boundary conditions of u and y. Therefore, we conclude that our study is at the same time valid for fully Dirichlet and mixed boundary conditions. $\square$

It is very important to ask the question about the optimality of (3.1). In the next section, we will prove that the decay rate (3.1) is optimal in some cases.

4 Upper bound estimation of the polynomial decay rate

In this section, our goal is to show that energy of the Timoshenko System (1.1)–(1.2) with Dirichlet–Neumann boundary conditions (1.4) has the optimal polynomial decay rate of type $t^{-1}$.

4.1 Optimal polynomial decay rate of $\mathcal {A}_2$ with global Kelvin–Voigt damping

In this part, we show that the energy of the Timoshenko System (1.1)–(1.2) with global Kelvin–Voigt damping, and with Dirichlet–Neumann boundary conditions (1.4) has the optimal polynomial decay rate of type $t^{-1}$. For this aim, assume that:

$$\begin{aligned} D(x)=D_0>0,\ \forall x\in (0,L), \end{aligned}$$

(H1)

where $D_0$ is a strictly positive constant number. We prove the following theorem.

Theorem 4.1

Under hypothesis (H1), for all initial data $U_0\in D\left( \mathcal {A}_2\right)$ and for all $t>0,$ the energy decay rate in (3.1) is optimal, i.e., for $\epsilon >0\left( \text {small enough}\right)$, we cannot expect the energy decay rate $t^{-\frac{2}{{2-\epsilon }}}$.

Proof

Following to Borichev and Tomilov (2010) [see Theorem 2.4 part (i)], it suffices to show the existence of sequences $\left( \lambda _n\right) _n\subset \mathbb {R}$ with $\lambda _n\rightarrow +\infty$, $\left( U_n\right) _n\subset D\left( \mathcal {A}_2\right)$, and $\left( F_n\right) _n\subset \mathcal {H}_2$, such that $\left( i\lambda _n I-\mathcal {A}_2\right) U_n=F_n$ is bounded in $\mathcal {H}_2$ and $\lambda _n^{-2+\epsilon }\Vert U_n\Vert _{\mathcal {H}_2}\rightarrow +\infty$. Set:

$$\begin{aligned}&F_n =\left( 0,\sin \left( \frac{n\pi x}{L}\right) ,0,0\right) ,\ U_n=\left( A_n\sin \left( \frac{n\pi x}{L}\right) ,i\lambda _n A_n\sin \left( \frac{n\pi x}{L}\right) ,\right. \\&\quad \left. B_n\cos \left( \frac{n\pi x}{L}\right) ,i\lambda _n B_n\cos \left( \frac{n\pi x}{L}\right) \right) \end{aligned}$$

and

$$\begin{aligned} \lambda _n=\frac{n\pi }{L}\sqrt{\frac{k_1}{\rho _1}} ,\quad A_n=-\frac{in\pi D_0}{k_1\, L}\sqrt{\frac{\rho _1}{k_1}}+\frac{k_2}{k_1}\left( \frac{\rho _2}{k_2}-\frac{\rho _1}{k_1}\right) -\frac{\rho _1 L^2}{k_1 \pi ^2 n^2},\quad B_n=\frac{\rho _1 L}{k_1 n\pi }. \end{aligned}$$

(4.1)

Clearly that $U_n\in D\left( \mathcal {A}_2\right) ,$ and $F_n$ is bounded in $\mathcal {H}_2$. Let us show that:

$$\begin{aligned} \left( i\lambda _n I-\mathcal {A}_2\right) U_n=F_n. \end{aligned}$$

Detailing $\left( i\lambda _n I-\mathcal {A}_2\right) U_n$, we get:

$$\begin{aligned} \left( i\lambda _n I-\mathcal {A}_2\right) U_n=\left( 0,C_{1,n}\sin \left( \frac{n\pi x}{L}\right) ,0,C_{2,n} \cos \left( \frac{n\pi x}{L}\right) \right) , \end{aligned}$$

where:

$$\begin{aligned} C_{1,n}= & {} \left( \frac{k_1}{\rho _1} \left( \frac{n\pi }{L}\right) ^2-\lambda ^2_n \right) A_n+\frac{k_1 n\pi }{\rho _1 L}B_n,\ C_{2,n}=\frac{n\pi k_1}{\rho _2 L} A_n\nonumber \\&+\left( -\lambda ^2_n+\frac{k_1}{\rho _2}+\frac{{k_2}+i \lambda _n D_0 }{\rho _2} \left( \frac{n\pi }{L}\right) ^2\right) B_n. \end{aligned}$$

(4.2)

Inserting (4.1) in (4.2), we get:

$$\begin{aligned} C_{1,n}=1\ \ \ \text {and}\ \ \ C_{2,n}=0; \end{aligned}$$

hence, we obtain:

$$\begin{aligned} \left( i\lambda _n I-\mathcal {A}_2\right) U_n=\left( 0,\sin \left( \frac{n\pi x}{L}\right) ,0,0\right) =F_n. \end{aligned}$$

Now, we have:

$$\begin{aligned} \left\| U_n\right\| ^2_{\mathcal {H}_2}\ge \rho _1\int ^L_0\left| i\lambda _n A_n\sin \left( \frac{n\pi x}{L}\right) \right| ^2\mathrm{{dx}}=\frac{\rho _1\, L\, \lambda _n^2 }{2}\left| A_n\right| ^2\sim \lambda ^4_n. \end{aligned}$$

Therefore, for $\epsilon >0\left( \text {small enough}\right)$, we have:

$$\begin{aligned} \lambda _n^{-2+\epsilon }\left\| U_n\right\| _{\mathcal {H}_2}\sim \lambda _n^\epsilon \rightarrow +\infty . \end{aligned}$$

Finally, following to Borichev and Tomilov (2010) [see Theorem 2.4 part (i)], we cannot expect the energy decay rate $t^{-\frac{2}{{2-\epsilon }}}$. $\square$

Note that Theorem 4.1 also implies that our system is non-uniformly stable.

Remark 4.2

In fact, when the Kelvin–Voigt damping is global (i.e., under hypothesis (H1)), if mixed Dirichlet–Neumann boundary conditions (1.4) are considered in System (1.1)–(1.2) instead of fully Dirichlet boundary conditions (1.3), then the decay rate (3.1) is optimal [see Theorem 4.1]. Indeed, the idea is to find a sequence of $\left( \lambda _n\right) _n\subset \mathbb {R}$ with $\lambda _n\rightarrow +\infty$ and a sequence of vectors $\left( U_n\right) _n\subset D\left( \mathcal {A}_2\right)$, such that $\left( i\lambda _n I-\mathcal {A}_2\right) U_n$ is bounded in $\mathcal {H}_2$ and $\lambda _n^{-2+\epsilon }\Vert U_n\Vert _{\mathcal {H}_2}\rightarrow +\infty$ for $\epsilon >0\left( \text {small enough}\right)$. In the case of Dirichlet–Neumann boundary condition, this approach worked well because of the fact that all eigenmodes are separable, i.e., the system operator can be decomposed to a block-diagonal form according to the frequency when the state variables are expanded into Fourier series. However, in the case of fully Dirichlet boundary conditions, this approach has no success in the literature to our knowledge, and the problem is still open. $\square$

4.2 Optimal polynomial decay rate of $\mathcal {A}_2$ with local Kelvin–Voigt damping

In this part, under the equal speed wave propagation condition (i.e., $\frac{\rho _1}{k_1}=\frac{\rho _2}{k_2}$), we use the classical method developed by Littman and Markus in Littman and Markus (1988) [see also Curtain and Zwart (1995)], to show that the Timoshenko System (1.1)–(1.2) with local Kelvin–Voigt damping, and with Dirichlet–Neumann boundary conditions (1.4) is not exponentially stable. Also, we will prove the optimality of estimation (3.1). For this aim, assume that:

$$\begin{aligned} \frac{\rho _1}{k_1}=\frac{\rho _2}{k_2}\ \ \text {and}\ \ \ D(x)=\left\{ \begin{array}{ll} 0,&{} 0<x\le \alpha ,\\ D_0&{} \alpha <x\le L, \end{array}\right. \end{aligned}$$

where $D_0\in \mathbb {R}^+_{*}$ and $\alpha \in (0,L)$. For simplicity and without loss of generality, in this part, we take $\frac{\rho _1}{k_1}=1$, $D_0=k_2$, $L=1$, and $\alpha =\frac{1}{2}$, and hence, the above hypothesis becomes:

$$\begin{aligned} \frac{\rho _1}{k_1}=\frac{\rho _2}{k_2}=1\ \ \text {and}\ \ \ D(x)=\left\{ \begin{array}{ll} 0,&{} 0<x\le \frac{1}{2},\\ k_2&{} \frac{1}{2}<x\le 1. \end{array}\right. \end{aligned}$$

(H2)

Our first result in this part is the following theorem.

Theorem 4.3

Under hypothesis (H2). The semigroup generated by the operator $\mathcal {A}_2$ is not exponentially stable in the energy space $\mathcal {H}_2.$

For the proof of Theorem 4.3, we recall the following definitions: the growth bound $\omega _0\left( \mathcal {A}_2\right)$ and the spectral bound $s\left( \mathcal {A}_2\right)$ of $\mathcal {A}_2$ are defined, respectively, as:

$$\begin{aligned} \omega _0(\mathcal {A}_2)=\lim _{t\rightarrow \infty }\frac{\log \left\| e^{t\mathcal {A}_2}\right\| _{\mathcal {L}(\mathcal {H}_2)}}{t}\ \ \ \text {and}\ \ \ s\left( \mathcal {A}_2\right) =\sup \left\{ \Re \left( \lambda \right) :\ \lambda \in \sigma \left( \mathcal {A}_2\right) \right\} . \end{aligned}$$

From the Hille–Yoside theorem [see also Theorem 2.1.6 and Lemma 2.1.11 in Curtain and Zwart (1995)], one has that:

$$\begin{aligned} s\left( \mathcal {A}_2\right) \le \omega _0\left( \mathcal {A}_2\right) . \end{aligned}$$

By the previous results, one clearly has that $s\left( \mathcal {A}_2\right) \le 0$ and the theorem would follow if equality holds in the previous inequality. It therefore amounts to show the existence of a sequence of eigenvalues of $\mathcal {A}_2$ whose real parts tend to zero.

Since $\mathcal {A}_2$ is dissipative, we fix $\alpha _0>0$ small enough and we study the asymptotic behavior of the eigenvalues $\lambda$ of $\mathcal {A}_2$ in the strip:

$$\begin{aligned} S=\left\{ \lambda \in \mathbb {C}:-\alpha _0\le \Re (\lambda )\le 0\right\} . \end{aligned}$$

First, we determine the characteristic equation satisfied by the eigenvalues of $\mathcal {A}_2$. For this aim, let $\lambda \in \mathbb {C}^*$ be an eigenvalue of $\mathcal {A}_2$ and let ${U=\left( u,\lambda u,y,\lambda y\right) \in D(\mathcal {A}_2)}$ be an associated eigenvector. Then, the eigenvalue problem is given by:

$$\begin{aligned} \lambda ^2u-u_{xx}-y_x=0,&x\in (0,1), \end{aligned}$$

(4.3)

$$\begin{aligned} c^2u_x+ \left( \lambda ^2+c^2\right) y-\left( 1+\frac{D}{k_2}\lambda \right) y_{xx}=0,&x\in (0,1), \end{aligned}$$

(4.4)

with the boundary conditions:

$$\begin{aligned} u(0)=y_x(0)=u(1)=y_x(1)=0, \end{aligned}$$

(4.5)

where $c=\sqrt{k_1 k_2^{-1}}$. We define:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {u^-(x):=u(x)}, \ \displaystyle {y^-(x):=y(x)},\quad \displaystyle {x\in (0,1/2)}, \\ \displaystyle {u^+(x):=u(x)},\ \displaystyle {y^+(x):=y(x)},\quad \displaystyle {x\in [1/2,1)}. \end{array} \right. \end{aligned}$$

Thus, System (4.3)–(4.5) become:

$$\begin{aligned} \lambda ^2u^--u^-_{xx}-y^-_x=0,&x\in (0,1/2), \end{aligned}$$

(4.6)

$$\begin{aligned} c^2u^-_x+ \left( \lambda ^2+c^2\right) y^--y^-_{xx}=0,&x\in (0,1/2), \end{aligned}$$

(4.7)

$$\begin{aligned} \lambda ^2u^+-u^+_{xx}-y^+_x=0,&x\in [1/2,1), \end{aligned}$$

(4.8)

$$\begin{aligned} c^2u^+_x+ \left( \lambda ^2+c^2\right) y^+-\left( 1+\lambda \right) y^+_{xx}=0,&x\in [1/2,1), \end{aligned}$$

(4.9)

with the boundary conditions:

$$\begin{aligned}&u^-(0)=y^-_x(0)=0, \end{aligned}$$

(4.10)

$$\begin{aligned}&u^+(1)=y^+_x(1)=0, \end{aligned}$$

(4.11)

and the continuity conditions:

$$\begin{aligned} u^-(1/2)= & {} u^+(1/2),\quad u_x^-(1/2)= u^+_{x}(1/2),\quad y^-(1/2)=y^+(1/2),\nonumber \\ y^-_x(1/2)= & {} \left( 1+\lambda \right) y^+_x(1/2). \end{aligned}$$

(4.12)

To proceed, we set the following notation. Here and below, in the case where z is a non zero non-real number, we define (and denote) by $\sqrt{z}$ the square root of z, i.e., the unique complex number with positive real part whose square is equal to z. Our aim is to study the asymptotic behavior of the large eigenvalues $\lambda$ of ${\mathcal {A}_2}$ in S. By taking $\lambda$ large enough, the general solution of System (4.6)–(4.7) with boundary condition (4.10) is given by:

$$\begin{aligned}\left\{ \begin{array}{ll} \displaystyle { u^-(x)=\alpha _1 \sinh (r_1 x)+\alpha _2\sinh (r_2 x),}\\ \displaystyle { y^-(x)=\alpha _1\frac{\lambda ^2-r_1^2}{r_1} \cosh (r_1 x)+\alpha _2\frac{\lambda ^2-r_2^2}{r_2}\cosh (r_2 x),} \end{array}\right. \end{aligned}$$

and the general solution of Eqs. (4.8)–(4.9) with boundary condition (4.11) is given by:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle { u^+(x)=\beta _1 \sinh (s_1 (1-x))+\beta _2\sinh (s_2 (1-x)),} \\ \displaystyle { y^+(x)=-\beta _1\frac{\lambda ^2-s_1^2}{s_1} \cosh (s_1 (1-x))-\beta _2\frac{\lambda ^2-s_2^2}{s_2}\cosh (s_2 (1-x)),} \end{array}\right. \end{aligned}$$

where $\alpha _1,\ \alpha _2,\ \beta _1,\ \beta _2\in \mathbb {C}$:

$$\begin{aligned} r_1=\lambda \sqrt{1+\frac{i c}{\lambda }},\qquad r_2=\lambda \sqrt{1-\frac{i c}{\lambda }} \end{aligned}$$

(4.13)

and

$$\begin{aligned} s_1=\sqrt{\frac{\lambda + \frac{\lambda ^2}{2}\left( 1 +\sqrt{1 -\frac{4c^2}{ \lambda ^3}-\frac{4 c^2}{ \lambda ^4}}\right) }{ 1+\frac{1}{\lambda } }}, \qquad s_2=\sqrt{\frac{\lambda + \frac{\lambda ^2}{2}\left( 1 -\sqrt{1 -\frac{4c^2}{ \lambda ^3}-\frac{4 c^2}{ \lambda ^4}}\right) }{ 1+\frac{1}{\lambda } }}. \end{aligned}$$

(4.14)

The boundary conditions in (4.12) can be expressed by:

$$\begin{aligned} M\left( \alpha _1,\alpha _2, \beta _1, \beta _2 \right) ^\top =0, \end{aligned}$$

such that:

$$\begin{aligned} M=\begin{pmatrix} \sinh \left( \frac{r_1}{2} \right) &{}\sinh \left( \frac{r_2}{2} \right) &{}-\sinh \left( \frac{s_1}{2} \right) &{}-\sinh \left( \frac{s_2}{2} \right) \\ \frac{r_1}{i \, c\, \lambda ^2}\cosh \left( \frac{r_1}{2} \right) &{}\frac{r_2}{i \, c\, \lambda ^2}\cosh \left( \frac{r_2}{2} \right) &{}\frac{s_1}{i \, c\, \lambda ^2}\cosh \left( \frac{s_1}{2} \right) &{}\frac{s_2}{i \, c\, \lambda ^2}\cosh \left( \frac{s_2}{2} \right) \\ r_1^2\sinh \left( \frac{r_1}{2} \right) &{}r_2^2\sinh \left( \frac{r_2}{2} \right) &{}\left( \lambda ^3-(\lambda +1) s_1^2\right) \sinh \left( \frac{s_1}{2} \right) &{}\left( \lambda ^3-(\lambda +1) s_2^2\right) \sinh \left( \frac{s_2}{2} \right) \\ r_1^{-1}\cosh \left( \frac{r_1}{2} \right) &{}r_2^{-1}\cosh \left( \frac{r_2}{2} \right) &{}s_1^{-1}\cosh \left( \frac{s_1}{2} \right) &{}s_2^{-1}\cosh \left( \frac{s_2}{2} \right) \end{pmatrix}. \end{aligned}$$

Denoting the determinant of a matrix M by det(M), consequently, System (4.6)–(4.12) admits a non trivial solution if and only if $\displaystyle {det\left( M\right) }=0$. Using Gaussian elimination, $\displaystyle {det\left( M\right) }=0$ is equivalent to $\displaystyle {det\left( \tilde{M}\right) }=0$, where $\tilde{M}$ is given by:

$$\begin{aligned} \tilde{M}=\begin{pmatrix} \sinh \left( \frac{r_1}{2} \right) &{}\sinh \left( \frac{r_2}{2} \right) &{}-\sinh \left( \frac{s_1}{2} \right) &{}-1-e^{-s_2} \\ \frac{r_1}{i \, c\, \lambda ^2}\cosh \left( \frac{r_1}{2} \right) &{}\frac{r_2}{i \, c\, \lambda ^2}\cosh \left( \frac{r_2}{2} \right) &{}\frac{s_1}{i \, c\, \lambda ^2}\cosh \left( \frac{s_1}{2} \right) &{}\frac{s_2}{i \, c\, \lambda ^2}\left( 1+ e^{-s_2}\right) \\ r_1^2\sinh \left( \frac{r_1}{2} \right) &{}r_2^2\sinh \left( \frac{r_2}{2} \right) &{}\left( \lambda ^3-(\lambda +1) s_1^2\right) \sinh \left( \frac{s_1}{2} \right) &{}\left( \lambda ^3-(\lambda +1) s_2^2\right) \left( 1- e^{-s_2}\right) \\ r_1^{-1}\cosh \left( \frac{r_1}{2} \right) &{}r_2^{-1}\cosh \left( \frac{r_2}{2} \right) &{}s_1^{-1}\cosh \left( \frac{s_1}{2} \right) &{}s_2^{-1}\left( 1+ e^{-s_2}\right) \end{pmatrix} . \end{aligned}$$

One gets that:

$$\begin{aligned}&det\left( \tilde{M}\right) =g_1 \cosh \left( \frac{r_1}{2} \right) \cosh \left( \frac{r_2}{2} \right) \sinh \left( \frac{s_1}{2} \right) +g_2 \sinh \left( \frac{r_1}{2} \right) \cosh \left( \frac{r_2}{2} \right) \cosh \left( \frac{s_1}{2} \right) \nonumber \\&\quad +g_3 \cosh \left( \frac{r_1}{2} \right) \sinh \left( \frac{r_2}{2} \right) \cosh \left( \frac{s_1}{2} \right) +g_4\sinh \left( \frac{r_1}{2} \right) \sinh \left( \frac{r_2}{2} \right) \cosh \left( \frac{s_1}{2} \right) \nonumber \\&\quad +g_5 \cosh \left( \frac{r_1}{2} \right) \sinh \left( \frac{r_2}{2} \right) \sinh \left( \frac{s_1}{2} \right) +g_6 \sinh \left( \frac{r_1}{2} \right) \cosh \left( \frac{r_2}{2} \right) \sinh \left( \frac{s_1}{2} \right) \nonumber \\&\quad \bigg (-g_1 \cosh \left( \frac{r_1}{2} \right) \cosh \left( \frac{r_2}{2} \right) \sinh \left( \frac{s_1}{2} \right) -g_2 \sinh \left( \frac{r_1}{2} \right) \cosh \left( \frac{r_2}{2} \right) \cosh \left( \frac{s_1}{2} \right) \nonumber \\&\quad -g_3 \cosh \left( \frac{r_1}{2} \right) \sinh \left( \frac{r_2}{2} \right) \cosh \left( \frac{s_1}{2} \right) +g_4\sinh \left( \frac{r_1}{2} \right) \sinh \left( \frac{r_2}{2} \right) \cosh \left( \frac{s_1}{2} \right) \nonumber \\&\quad +g_5 \cosh \left( \frac{r_1}{2} \right) \sinh \left( \frac{r_2}{2} \right) \sinh \left( \frac{s_1}{2} \right) +g_6 \sinh \left( \frac{r_1}{2} \right) \cosh \left( \frac{r_2}{2} \right) \sinh \left( \frac{s_1}{2} \right) \bigg ) e^{-s_2}, \end{aligned}$$

(4.15)

such that:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle {g_1=\frac{\left( \lambda +1\right) \left( r_1^2-r_2^2\right) \left( s_1^2-s_2^2\right) }{i\, c\, r_1 r_2 \lambda ^2},\quad g_2=\frac{\left( r_2^2-s_1^2\right) \left( \left( \lambda +1\right) s_2^2-\lambda ^3-r_1^2\right) }{i\, c\, s_1 r_2 \lambda ^2}},\\ \displaystyle {g_3=-\frac{\left( r_1^2-s_1^2\right) \left( \left( \lambda +1\right) s_2^2-\lambda ^3-r_2^2\right) }{i\, c\, r_1 s_1 \lambda ^2}},\quad \displaystyle {g_4=\frac{\left( r_1^2-r_2^2\right) \left( s_1^2-s_2^2\right) }{i\, c\, s_1 s_2 \lambda ^2}},\\ \displaystyle {g_5=\frac{\left( r_1^2-s_2^2\right) \left( \left( \lambda +1\right) s_1^2-\lambda ^3-r_2^2\right) }{i\, c\, s_2 r_1 \lambda ^2}},\quad \displaystyle {g_6=-\frac{\left( r_2^2-s_2^2\right) \left( \left( \lambda +1\right) s_1^2-\lambda ^3-r_1^2\right) }{i\, c\, r_2 s_2 \lambda ^2}}. \end{array}\right. \end{aligned}$$

(4.16)

Proposition 4.4

Under hypothesis (H2), there exist $n_0\in \mathbb {N}$ sufficiently large and two sequences $\left( \lambda _{1,n}\right) _{ |n|\ge n_0}$ and $\left( \lambda _{2,n}\right) _{ |n|\ge n_0}$ of simple roots of $\det (\tilde{M})$ (that are also simple eigenvalues of $\mathcal {A}_2$) satisfying the following asymptotic behavior:

Case 1. If there exist no integers $\kappa \in \mathbb {N}$, such that $c= 2\kappa \pi$ (i.e., $\sin \left( \frac{c}{4}\right) \ne 0$ and $\cos \left( \frac{c}{4}\right) \ne 0$), then:

$$\begin{aligned} \lambda _{1,n}= & {} 2i n\pi -\frac{2\left( 1-i{{\,\mathrm{sign}\,}}(n)\right) \sin \left( \frac{c}{4}\right) ^2}{\left( 3 +\cos \left( \frac{c}{2}\right) \right) \sqrt{\pi |n|}}+O\left( n^{-1}\right) , \end{aligned}$$

(4.17)

$$\begin{aligned} \lambda _{2,n}= & {} 2i n\pi +\pi i+i\arccos \left( \cos \left( \frac{c}{4}\right) \right) -\frac{(1-i{{\,\mathrm{sign}\,}}(n)) \cos \left( \frac{c}{4}\right) ^2}{\left( 1+\cos \left( \frac{c}{4}\right) ^2\right) \sqrt{\pi |n|}}+O\left( n^{-1}\right) . \end{aligned}$$

(4.18)

Case 2. If there exists $\kappa _0\in \mathbb {N}$, such that $c=2\left( 2\kappa _0+1\right) \pi$, (i.e., $\cos \left( \frac{c}{4}\right) = 0$), then:

$$\begin{aligned} \lambda _{1,n}= & {} 2i n\pi -\frac{1-i{{\,\mathrm{sign}\,}}(n)}{ \sqrt{\pi |n|}}+O\left( n^{-1}\right) , \end{aligned}$$

(4.19)

$$\begin{aligned} \lambda _{2,n}= & {} 2i n\pi +\frac{3\pi i}{2}+\frac{i \, c^2}{32\pi n}-\frac{\left( 8+i (3\pi -2)\right) \, c^2}{128\pi ^2 n^2}+O\left( |n|^{-5/2}\right) . \end{aligned}$$

(4.20)

Case 3. If there exists $\kappa _1\in \mathbb {N}$, such that $c=4\kappa _1 \pi$, (i.e., $\sin \left( \frac{c}{4}\right) = 0$), then:

$$\begin{aligned} \lambda _{1,n}= & {} 2i n\pi +\frac{i \, c^2}{32\pi n}-\frac{c^2}{16\pi ^2 n^2}+O\left( |n|^{-5/2}\right) , \end{aligned}$$

(4.21)

$$\begin{aligned} \lambda _{2,n}= & {} 2i n\pi +\pi i+\frac{i \, c^2}{32\pi n}-\frac{\left( 4+i\pi \right) \, c^2}{64\pi ^2 n^2}+O\left( |n|^{-5/2}\right) . \end{aligned}$$

(4.22)

Here, ${{\,\mathrm{sign}\,}}$ is used to denote the sign function or signum function.

The argument for Proposition 4.4 relies on the subsequent lemmas.

Lemma 4.5

Under hypothesis (H2), let $\lambda$ be a large eigenvalue of $\mathcal {A}_2$, and then, $\lambda$ is large root of the following asymptotic equation:

$$\begin{aligned} F(\lambda ):=f_0(\lambda ) +\frac{f_1(\lambda )}{\lambda ^{1/2}}+\frac{ f_2(\lambda )}{8\lambda }+\frac{f_3(\lambda )}{8\lambda ^{3/2}}+\frac{ f_4(\lambda )}{128\lambda ^{2}}+\frac{f_5(\lambda )}{128\lambda ^{5/2}}+O\left( \lambda ^{-3}\right) =0, \end{aligned}$$

(4.23)

where:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {f_0(\lambda ) =\sinh \left( \frac{3\lambda }{2}\right) +\sinh \left( \frac{\lambda }{2}\right) \cos \left( \frac{c}{2}\right) }, \\ \displaystyle {f_1(\lambda ) =\cosh \left( \frac{3\lambda }{2}\right) -\cosh \left( \frac{\lambda }{2}\right) \cos \left( \frac{c}{2}\right) }, \\ \displaystyle {f_2(\lambda ) =c^2\, \cosh \left( \frac{3\lambda }{2}\right) -4c\, \cosh \left( \frac{\lambda }{2}\right) \sin \left( \frac{c}{2}\right) }, \\ \displaystyle {f_3(\lambda ) =c^2\sinh \left( \frac{3\lambda }{2}\right) -4\cosh \left( \frac{3\lambda }{2}\right) +12c\,\sinh \left( \frac{\lambda }{2}\right) \sin \left( \frac{c}{2}\right) +4\cosh \left( \frac{\lambda }{2}\right) \cos \left( \frac{c}{2}\right) }, \\ \displaystyle {f_4(\lambda ) =c^2\left( c^2-56\right) \sinh \left( \frac{3\lambda }{2}\right) -32c^2\,\cosh \left( \frac{3\lambda }{2}\right) }\\ \displaystyle {\quad +8c^2\left( c\sin \left( \frac{c}{2}\right) -8\cos \left( \frac{c}{2}\right) +1\right) \sinh \left( \frac{\lambda }{2}\right) }\\ \displaystyle {\quad -32c\, \left( 8\sin \left( \frac{c}{2}\right) +c \cos \left( \frac{c}{2}\right) \right) \cos \left( \frac{c}{2}\right) },\\ \displaystyle {f_5(\lambda ) =-40c^2\sinh \left( \frac{3\lambda }{2}\right) +\left( c^4-88c^2+48\right) \cosh \left( \frac{3\lambda }{2}\right) }\\ \displaystyle {\quad +32c\left( 5\sin \left( \frac{c}{2}\right) +c\cos \left( \frac{c}{2}\right) \right) \sinh \left( \frac{\lambda }{2}\right) }\\ \displaystyle {\quad -\left( 8 c^3\sin \left( \frac{c}{2}\right) -16(4c^2-3) \cos \left( \frac{c}{2}\right) -24c^2\right) \cos \left( \frac{c}{2}\right) }. \end{array} \right. \end{aligned}$$

(4.24)

Proof

Let $\lambda$ be a large eigenvalue of $\mathcal {A}_2$, and then, $\lambda$ is root of $det\left( \tilde{M}\right)$. In this lemma, we furnish an asymptotic development of the function $det\left( \tilde{M}\right)$ for large $\lambda$. First, using the asymptotic expansion in (4.13) and (4.14), we get:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {r_1=\lambda +\frac{i\, c}{2}+\frac{c^2}{8\lambda }-\frac{i\, c^3}{16\lambda ^2}+O\left( \lambda ^{-3}\right) ,\ r_2=\lambda -\frac{i\, c}{2}+\frac{c^2}{8\lambda }+\frac{i\, c^3}{16\lambda ^2}+O\left( \lambda ^{-3}\right) ,}\\ \displaystyle { s_1=\lambda -\frac{c^2}{2\lambda ^2} +O\left( \lambda ^{-5}\right) ,\ s_2=\lambda ^{1/2}-\frac{1}{2\lambda ^{1/2}}+\frac{4 c^2+3}{8\lambda ^{3/2}}+O\left( \lambda ^{-5/2}\right) .} \end{array} \right. \end{aligned}$$

(4.25)

Inserting (4.25) in (4.16), we get:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle {g_1=2-\frac{c^2}{\lambda ^2}+O\left( \lambda ^{-3}\right) ,\quad g_2=1+\frac{i\, c}{2\lambda }-\frac{(3c-16i)\, c}{8\lambda ^2}+O\left( \lambda ^{-3}\right) }, \\ \displaystyle {g_3=1-\frac{i\, c}{2\lambda }-\frac{(3c+16i)\, c}{8\lambda ^2}+O\left( \lambda ^{-3}\right) ,}\quad \displaystyle {g_4= 2\lambda ^{1/2}-\frac{1}{\lambda ^{3/2}}-\frac{4c^2-3}{4\lambda ^{5/2}} +O\left( \lambda ^{-7/2}\right) }, \\ \displaystyle {g_5=\lambda ^{1/2}-\frac{1-3i\, c}{2\lambda ^{3/2}} -\frac{7c^2-3-10i\, c}{8\lambda ^{5/2}}+O\left( \lambda ^{-7/2}\right) },\quad \\ \displaystyle {g_6=\lambda ^{1/2}-\frac{1+3i\, c}{2\lambda ^{3/2}} -\frac{7c^2-3+10i\, c}{8\lambda ^{5/2}}+O\left( \lambda ^{-7/2}\right) }. \end{array}\right. \end{aligned}$$

(4.26)

Substituting (4.26) in (4.15), and then using the fact that real part of $\lambda$ is bounded in S, we get:

$$\begin{aligned} \begin{array}{lll} \displaystyle {det\left( \tilde{M}\right) }= \displaystyle {\sinh \left( L_1\right) +\sinh \left( L_2\right) \cosh \left( L_3\right) } +\displaystyle {\frac{\cosh \left( L_1\right) -\cosh \left( L_2\right) \cosh \left( L_3\right) }{\lambda ^{1/2}}}\\ \quad +\displaystyle {\frac{i\, c\, \cosh \left( L_2\right) \sinh \left( L_3\right) }{2\lambda } } -\displaystyle {\frac{\cosh \left( L_1\right) -\cosh \left( L_2\right) \cosh \left( L_3\right) +3i\, c\, \sinh \left( L_2\right) \sinh \left( L_3\right) }{2\lambda ^{3/2}}} \\ \quad -\displaystyle {\frac{7c^2\, \sinh \left( L_1\right) +8c^2\,\sinh \left( L_2\right) \cosh \left( L_3\right) -32i\, c\, \cosh \left( L_2\right) \sinh \left( L_3\right) -c^2\sinh \left( L_4\right) }{16\lambda ^{3/2}}} \\ \quad \displaystyle {-\frac{(11c^2-6) \cosh \left( L_1\right) -(8c^2-6)\,\cosh \left( L_2\right) \cosh \left( L_3\right) +20i\, c\, \sinh \left( L_2\right) \sinh \left( L_3\right) -3c^2\,\cosh \left( L_4\right) }{16\lambda ^{5/2}}} \\ \quad \displaystyle {+\left( \sinh \left( L_1\right) +\sinh \left( L_2\right) \cosh \left( L_3\right) +O\left( \lambda ^{-1/2}\right) \right) e^{-s_2}+O\left( \lambda ^{-3}\right) }, \end{array} \end{aligned}$$

(4.27)

where:

$$\begin{aligned} L_1=\frac{r_1+r_2+s_1}{2},\quad L_2=\frac{s_1}{2},\quad L_3=\frac{r_1-r_2}{2},\quad L_4=\frac{r_1+r_2-s_1}{2} . \end{aligned}$$

Next, from (4.25) and using the fact that real part of $\lambda$ is bounded S, we get:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle { \sinh \left( L_1 \right) =\sinh \left( \frac{3\lambda }{2}\right) +\frac{c^2\,\cosh \left( \frac{3\lambda }{2} \right) }{8\lambda } +\frac{c^2\,\left( c^2\,\sinh \left( \frac{3\lambda }{2}\right) -32\cosh \left( \frac{3\lambda }{2} \right) \right) }{128\lambda ^2}+O\left( \lambda ^{-3}\right) ,}\\ \displaystyle {\cosh \left( L_1 \right) =\cosh \left( \frac{3\lambda }{2}\right) +\frac{c^2\,\sinh \left( \frac{3\lambda }{2}\right) }{8\lambda } +\frac{c^2\,\left( c^2\,\cosh \left( \frac{3\lambda }{2}\right) -32\sinh \left( \frac{3\lambda }{2}\right) \right) }{128\lambda ^2} +O\left( \lambda ^{-3}\right) ,}\\ \displaystyle {\sinh \left( L_2\right) =\sinh \left( \frac{\lambda }{2}\right) -\frac{c^2\, \cosh \left( \frac{\lambda }{2}\right) }{4\lambda ^2}+O\left( \lambda ^{-4}\right) ,}\\ \displaystyle {\cosh \left( L_2 \right) =\cosh \left( \frac{\lambda }{2}\right) -\frac{c^2\, \sinh \left( \frac{\lambda }{2}\right) }{4\lambda ^2}+O\left( \lambda ^{-4}\right) ,}\\ \displaystyle {\sinh \left( L_3 \right) =i\sin \left( \frac{c}{2}\right) -\frac{i\, c^3\,\cos \left( \frac{c}{2}\right) }{16\lambda ^2}+O\left( \lambda ^{-3}\right) ,}\\ \displaystyle {\cosh \left( L_3 \right) =\cos \left( \frac{c}{2}\right) +\frac{c^3\,\cos \left( \frac{c}{2}\right) }{16\lambda ^2}+O\left( \lambda ^{-3}\right) ,}\\ \displaystyle {\sinh \left( L_4 \right) =\sinh \left( \frac{\lambda }{2}\right) +O\left( \lambda ^{-1}\right) ,}\quad \displaystyle {\cosh \left( L_4 \right) =\cosh \left( \frac{\lambda }{2}\right) +O\left( \lambda ^{-1}\right) .} \end{array}\right. \end{aligned}$$

(4.28)

On the other hand, from (4.25) and (4.28), we obtain:

$$\begin{aligned}&\left( \sinh \left( L_1\right) +\sinh \left( L_2\right) \cosh \left( L_3\right) +O\left( \lambda ^{-1/2}\right) \right) e^{-s_2}\nonumber \\&\quad =-\left( \sinh \left( \frac{3\lambda }{2}\right) +\sinh \left( \frac{\lambda }{2}\right) \cos \left( \frac{c}{2}\right) \right) e^{-\sqrt{\lambda }}. \end{aligned}$$

(4.29)

Since the real part of $\sqrt{\lambda }$ is positive, we obtain:

$$\begin{aligned} \lim _{|\lambda |\rightarrow \infty }\frac{e^{-\sqrt{\lambda }}}{\lambda ^{3}}=0; \end{aligned}$$

hence:

$$\begin{aligned} e^{-\sqrt{\lambda }}=o\left( \lambda ^{-3}\right) . \end{aligned}$$

(4.30)

Therefore, from (4.29), (4.30), and using the fact that real part of $\lambda$ is bounded S, we get:

$$\begin{aligned} \left( \sinh \left( L_1\right) +\sinh \left( L_2\right) \cosh \left( L_3\right) +O\left( \lambda ^{-1/2}\right) \right) e^{-s_2}=o\left( \lambda ^{-3}\right) . \end{aligned}$$

(4.31)

Finally, inserting (4.28) and (4.31) in (4.27), we get $\lambda$ is large root of F, where F defined in (4.23). Thus, the proof is complete. $\square$

Lemma 4.6

Under hypothesis (H2), there exist $n_0\in \mathbb {N}$ sufficiently large and two sequences $\left( \lambda _{1,n}\right) _{ |n|\ge n_0}$ and $\left( \lambda _{2,n}\right) _{ |n|\ge n_0}$ of simple roots of F (that are also simple eigenvalues of $\mathcal {A}_2$) satisfying the following asymptotic behavior:

$$\begin{aligned} \lambda _{1,n}=2i\pi n+i\pi +\epsilon _{1,n},\quad \text {such that }\lim _{|n|\rightarrow +\infty }\epsilon _{1,n}=0 \end{aligned}$$

(4.32)

and

$$\begin{aligned} \lambda _{2,n}=2 n\pi i+i\pi +i\, \arccos \left( \cos ^2\left( \frac{c}{4}\right) \right) +\epsilon _{2,n},\quad \text {such that }\lim _{|n|\rightarrow +\infty }\epsilon _{2,n}=0. \end{aligned}$$

(4.33)

Proof

First, we look at the roots of $f_0$. From (4.24), we deduce that $f_0$ can be written as:

$$\begin{aligned} f_0(\lambda )=2\sinh \left( \frac{\lambda }{2}\right) \left( \cosh \left( \lambda \right) +\cos ^2\left( \frac{c}{4}\right) \right) . \end{aligned}$$

(4.34)

The roots of $f_0$ are given by:

$$\begin{aligned}\left\{ \begin{array}{ll} \displaystyle { \mu _{1,n}=2 n\pi i,}&{} n\in \mathbb {Z},\\ \displaystyle { \mu _{2,n}=2 n\pi i+i\pi +i\, \arccos \left( \cos ^2\left( \frac{c}{4}\right) \right) ,}&{} n\in \mathbb {Z}. \end{array}\right. \end{aligned}$$

Now, with the help of Rouché’s theorem, we will show that the roots of F are close to $f_0$. Let us start with the first family $\mu _{1,n}$. Let $B_n=B\left( 2n\pi i, r_n\right)$ be the ball of centrum $2n\pi i$ and radius $r_n=\frac{1}{|n|^{\frac{1}{4}}}$ and $\lambda \in \partial B_n$; i.e., $\lambda =2n\pi i+r_n e^{i\theta },\ \theta \in [0,2\pi )$. Then:

$$\begin{aligned} \sinh \left( \frac{\lambda }{2}\right)= & {} \left( -1\right) ^n\sinh \left( \frac{r_n e^{i\theta }}{2}\right) =\frac{ \left( -1\right) ^n\, r_n e^{i\theta } }{2}+O(r_n^2),\ \cosh (\lambda )\nonumber \\= & {} \cosh \left( r_n e^{i\theta }\right) =1+O(r_n^2). \end{aligned}$$

(4.35)

Inserting (4.35) in (4.34), we get:

$$\begin{aligned} f_0(\lambda )= \left( -1\right) ^n\, r_n e^{i\theta }\left( 1+\cos ^2\left( \frac{c}{4}\right) \right) +O(r_n^3). \end{aligned}$$

It follows that there exists a positive constant C, such that:

$$\begin{aligned} \forall \ \lambda \in \partial B_n, \quad \left| f_0\left( \lambda \right) \right| \ge C\, r_n=\frac{C}{|n|^{\frac{1}{4}}}. \end{aligned}$$

On the other hand, from (4.23), we deduce that:

$$\begin{aligned} \left| F(\lambda )-f_0(\lambda )\right| =O\left( \frac{1}{\sqrt{\lambda }}\right) =O\left( \frac{1}{\sqrt{|n|}}\right) . \end{aligned}$$

It follows that, for |n| large enough:

$$\begin{aligned} \forall \ \lambda \in \partial B_n, \quad \left| F(\lambda )-f_0\left( \lambda \right) \right| <\left| f_0(\lambda )\right| . \end{aligned}$$

Hence, with the help of Rouché’s theorem, there exists $n_0\in \mathbb {N}^*$ large enough, such that $\forall \ |n|\ge n_0\ \ \left( n\in \mathbb {Z}^*\right) ,$ the first branch of roots of F, denoted by $\lambda _{1,n}$ are close to $\mu _{1,n}$, hence we get (4.32). The same procedure yields (4.33). Thus, the proof is complete. $\square$

Remark 4.7

From Lemma 4.6, we deduce that the real part of the eigenvalues of $\mathcal {A}_2$ tends to zero, and this is enough to get Theorem 4.3. However, we look forward to knowing the real part of $\lambda _{1,n}$ and $\lambda _{2,n}$. Since in the final of this section, we will use the real part of $\lambda _{1,n}$ and $\lambda _{2,n}$ for the optimality of polynomial stability. $\square$

We are now in a position to conclude the proof of Proposition 4.4.

Proof of Proposition 4.4

The proof is divided into two steps.

Step 1. Calculation of $\epsilon _{1,n}$. From (4.32), we have:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\cosh \left( \frac{3\lambda _{1,n}}{2}\right) =(-1)^n\, \cosh \left( \frac{3\epsilon _{1,n}}{2}\right) ,\ \sinh \left( \frac{3\lambda _{1,n}}{2}\right) =(-1)^n\, \sinh \left( \frac{3\epsilon _{1,n}}{2}\right) ,} \\ \displaystyle {\cosh \left( \frac{\lambda _{1,n}}{2}\right) =(-1)^n\, \cosh \left( \frac{\epsilon _{1,n}}{2}\right) ,\ \sinh \left( \frac{\lambda _{1,n}}{2}\right) =(-1)^n\, \sinh \left( \frac{\epsilon _{1,n}}{2}\right) ,} \end{array}\right. \end{aligned}$$

(4.36)

and

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\frac{1}{\lambda _{1,n}}= -\frac{i}{2\pi n}+O\left( \epsilon _{1,n}\, n^{-2}\right) +O\left( n^{-3}\right) ,\ \frac{1}{\lambda ^2_{1,n}}= -\frac{1}{4\pi ^2 n^2}+O\left( n^{-3}\right) }, \\ \displaystyle {\frac{1}{\sqrt{\lambda _{1,n}}}=\frac{1-i{{\,\mathrm{sign}\,}}(n)}{2\sqrt{\pi |n|}} +O\left( \epsilon _{1,n}\, |n|^{-3/2}\right) +O\left( |n|^{-5/2}\right) }, \\ \displaystyle {\frac{1}{\sqrt{\lambda ^3_{1,n}}}=\frac{-1-i{{\,\mathrm{sign}\,}}(n)}{4\sqrt{\pi ^3 |n|^3}}+O\left( |n|^{-5/2}\right) ,\ \frac{1}{\sqrt{\lambda ^5_{1,n}}}=O\left( |n|^{-5/2}\right) }. \end{array}\right. \end{aligned}$$

(4.37)

On the other hand, since $\lim _{|n|\rightarrow +\infty }\epsilon _{1,n}=0$, we have the asymptotic expansion:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\cosh \left( \frac{3\epsilon _{1,n}}{2}\right) =1+\frac{9\epsilon _{1,n}^2}{8}+O(\epsilon _{1,n}^4)},\ \displaystyle {\sinh \left( \frac{3\epsilon _{1,n}}{2}\right) =\frac{3\epsilon _{1,n}}{2}+O(\epsilon _{1,n}^3) },\\ \displaystyle {\cosh \left( \frac{\epsilon _{1,n}}{2}\right) =1+\frac{\epsilon _{1,n}^2}{8}+O(\epsilon _{1,n}^4)},\ \displaystyle {\sinh \left( \frac{\epsilon _{1,n}}{2}\right) =\frac{\epsilon _{1,n}}{2}+O(\epsilon _{1,n}^3) }. \end{array} \right. \end{aligned}$$

(4.38)

Inserting (4.38) in (4.36), we get:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\cosh \left( \frac{3\lambda _{1,n}}{2}\right) =(-1)^n+\frac{9(-1)^n\, \epsilon _{1,n}}{8}+O(\epsilon _{1,n}^4),}\\ \displaystyle {\sinh \left( \frac{3\lambda _{1,n}}{2}\right) =\frac{3(-1)^n\, \epsilon _{1,n}}{2}+O(\epsilon _{1,n}^3) ,} \\ \displaystyle {\cosh \left( \frac{\lambda _{1,n}}{2}\right) =(-1)^n+\frac{(-1)^n\, \epsilon _{1,n}}{8}+O(\epsilon _{1,n}^4),}\\ \displaystyle {\sinh \left( \frac{\lambda _{1,n}}{2}\right) =\frac{(-1)^n\, \epsilon _{1,n}}{2}+O(\epsilon _{1,n}^3) .} \end{array}\right. \end{aligned}$$

(4.39)

Substituting (4.37) and (4.39) in (4.23), we get:

$$\begin{aligned} \begin{array}{ll} \displaystyle {\frac{\epsilon _{1,n }}{2}\left( 3+\cos \left( \frac{c}{2}\right) \right) +\frac{\left( 1-i{{\,\mathrm{sign}\,}}(n)\right) \left( 1-\cos \left( \frac{c}{2}\right) \right) }{2\sqrt{\pi \, |n|}}+\frac{i\, c\left( 4\sin \left( \frac{c}{2}\right) -c\right) }{16\pi n}} \\ \quad \displaystyle {+\frac{\left( 1+i{{\,\mathrm{sign}\,}}(n)\right) \left( 1-\cos \left( \frac{c}{2}\right) \right) }{8\sqrt{\pi ^3\, |n|^3}} +\frac{8 c \sin \left( \frac{c}{2}\right) +\left( 1+\cos \left( \frac{c}{2}\right) \right) c^2}{16\pi ^2n^2} }\\ \quad \displaystyle { +O\left( |n|^{-5/2}\right) +O\left( \epsilon _{1,n }\, |n|^{-3/2}\right) +O\left( \epsilon _{1,n }^2\, |n|^{-1/2}\right) +O\left( \epsilon _{1,n }^3\right) =0}. \end{array} \end{aligned}$$

(4.40)

We distinguish two cases:

Case 1. If $\sin \left( \frac{c}{4}\right) \ne 0,$ then:

$$\begin{aligned} 1-\cos \left( \frac{c}{2}\right) =2\sin ^2\left( \frac{c}{4}\right) \ne 0; \end{aligned}$$

therefore, from (4.40), we get:

$$\begin{aligned} \frac{\epsilon _{1,n}}{2}\left( 3+ \cos \left( \frac{c}{2}\right) \right) + \frac{\sin ^2\left( \frac{c}{4}\right) \left( 1-i {{\,\mathrm{sign}\,}}\left( n\right) \right) }{\sqrt{|n|\pi }}+O\left( \epsilon _{1,n}^3\right) +O\left( |n|^{-1/2}\,\epsilon _{1,n}^2\right) +O\left( n^{-1}\right) =0; \end{aligned}$$

hence, we get:

$$\begin{aligned} \epsilon _{1,n}=- \frac{2\sin ^2\left( \frac{c}{4}\right) \left( 1-i {{\,\mathrm{sign}\,}}\left( n\right) \right) }{\left( 3+ \cos \left( \frac{c}{2}\right) \right) \sqrt{|n|\pi }}+O\left( n^{-1}\right) . \end{aligned}$$

(4.41)

Inserting (4.41) in (4.32), we get (4.17) and (4.19).

Case 2. If $\sin \left( \frac{c}{4}\right) =0,$ then:

$$\begin{aligned} 1-\cos \left( \frac{c}{2}\right) =2\sin ^2\left( \frac{c}{4}\right) =0\ \ \ \text {and}\ \ \ \sin \left( \frac{c}{2}\right) =2\sin \left( \frac{c}{4}\right) \cos \left( \frac{c}{4}\right) =0. \end{aligned}$$

Consequently, from (4.40), we get:

$$\begin{aligned} 2{\epsilon _{1,n }}-\frac{i\, c^2}{16\pi n} +\frac{c^2}{8\pi ^2n^2} +O\left( |n|^{-5/2}\right) +O\left( \epsilon _{1,n }\, |n|^{-3/2}\right) +O\left( \epsilon _{1,n }^2\, |n|^{-1/2}\right) +O\left( \epsilon _{1,n }^3\right) =0. \end{aligned}$$

(4.42)

Solving Eq. (4.42), we get:

$$\begin{aligned} \epsilon _{1,n}=\frac{i\, c^2}{32\pi n}-\frac{c^2}{16\pi ^2 n^2}+O\left( |n|^{-5/2}\right) . \end{aligned}$$

(4.43)

Inserting (4.43) in (4.32), we get (4.21).

Step 2. Calculation of $\epsilon _{2,n}$. We distinguish three cases:

Case 1. If $\sin \left( \frac{c}{4}\right) \ne 0$ and $\cos \left( \frac{c}{4}\right) \ne 0$, then $0<\cos ^2\left( \frac{c}{4}\right) < 1.$ Therefore:

$$\begin{aligned} \zeta :=\arccos \left( \cos ^2\left( \frac{c}{4}\right) \right) \in \left( 0,\frac{\pi }{2}\right) . \end{aligned}$$

From (4.33), we have:

$$\begin{aligned} \frac{1}{\sqrt{\lambda _{2,n}}}=\frac{1-i{{\,\mathrm{sign}\,}}(n)}{2\sqrt{\pi |n|}}+O\left( |n|^{-3/2}\right) \ \ \ \text {and} \ \ \ \frac{1}{{\lambda _{2,n}}}=O(n^{-1}). \end{aligned}$$

(4.44)

Inserting (4.33) and (4.44) in (4.23), we get:

$$\begin{aligned} \begin{array}{ll} \displaystyle { 2\sinh \left( \frac{\lambda _{2,n}}{2}\right) \left( \cosh \left( \lambda _{2,n}\right) +\cos ^2\left( \frac{c}{4}\right) \right) }\\ \quad \displaystyle {+\frac{\cosh \left( \frac{\lambda _{2,n}}{2}\right) \left( \cosh \left( \lambda _{2,n}\right) -\cos ^2\left( \frac{c}{4}\right) \right) \left( 1-i{{\,\mathrm{sign}\,}}(n)\right) }{\sqrt{\pi |n|}}+O(n^{-1})=0.} \end{array} \end{aligned}$$

(4.45)

From (4.33), we obtain:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\cosh (\lambda _{2,n}) =-\cos ^2\left( \frac{c}{4}\right) \cosh \left( \epsilon _{2,n}\right) -i\sin \left( \zeta \right) \sinh \left( \epsilon _{2,n}\right) ,}\\ \displaystyle {\cosh \left( \frac{\lambda _{2,n}}{2}\right) =(-1)^n\, \left( -\sin \left( \frac{\zeta }{2}\right) \cosh \left( \frac{\epsilon _{2,n}}{2}\right) +i\, \cos \left( \frac{\zeta }{2}\right) \sinh \left( \frac{\epsilon _{2,n}}{2}\right) \right) ,} \\ \displaystyle {\sinh \left( \frac{\lambda _{2,n}}{2}\right) =(-1)^n\, \left( -\sin \left( \frac{\zeta }{2}\right) \sinh \left( \frac{\epsilon _{2,n}}{2}\right) +i\, \cos \left( \frac{\zeta }{2}\right) \cosh \left( \frac{\epsilon _{2,n}}{2}\right) \right) .} \end{array}\right. \end{aligned}$$

(4.46)

Since $\zeta =\arccos \left( \cos ^2\left( \frac{c}{4}\right) \right) \in \left( 0,\frac{\pi }{2}\right)$, we have:

$$\begin{aligned} \sin \left( \zeta \right) =\left| \sin \left( \frac{c}{4}\right) \right| \sqrt{1+\cos ^2\left( \frac{c}{4}\right) },\ \cos \left( \frac{\zeta }{2} \right) =\frac{\sqrt{1+\cos ^2\left( \frac{c}{4}\right) }}{\sqrt{2}} ,\ \sin \left( \frac{\zeta }{2} \right) =\frac{\left| \sin \left( \frac{c}{4}\right) \right| }{\sqrt{2}}. \end{aligned}$$

(4.47)

On the other hand, since $\lim _{|n|\rightarrow +\infty }\epsilon _{2,n}=0$, we have the asymptotic expansion:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle { \cosh \left( \epsilon _{2,n}\right) =1+O(\epsilon _{2,n}^2),\ \sinh \left( \epsilon _{2,n}\right) =\epsilon _{2,n}+O(\epsilon _{2,n}^3),} \\ \displaystyle { \cosh \left( \frac{\epsilon _{2,n}}{2}\right) =1+O(\epsilon _{2,n}^2),\ \sinh \left( \frac{\epsilon _{2,n}}{2}\right) =\frac{\epsilon _{2,n}}{2}+O(\epsilon _{2,n}^3).} \end{array}\right. \end{aligned}$$

(4.48)

Inserting (4.47) and (4.48) in (4.46), we get:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\cosh (\lambda _{2,n}) =-\cos ^2\left( \frac{c}{4}\right) -i\, \epsilon _{2,n} \,\left| \sin \left( \frac{c}{4}\right) \right| \sqrt{1+\cos ^2\left( \frac{c}{4}\right) }+O(\epsilon _{2,n}^2),}\\ \displaystyle {\cosh \left( \frac{\lambda _{2,n}}{2}\right) =\frac{(-1)^n}{\sqrt{2}}\, \left( \frac{i\, \epsilon _{2,n}\, \sqrt{1+\cos ^2\left( \frac{c}{4}\right) }}{2}-\left| \sin \left( \frac{c}{4}\right) \right| \right) +O(\epsilon _{2,n}^2),} \\ \displaystyle {\sinh \left( \frac{\lambda _{2,n}}{2}\right) =-\frac{(-1)^n}{2\sqrt{2}}\, \left( \left| \sin \left( \frac{c}{4}\right) \right| \, \epsilon _{2,n}-2i\, \sqrt{1+\cos ^2\left( \frac{c}{4}\right) }\right) +O(\epsilon _{2,n}^2).}\\ \end{array}\right. \end{aligned}$$

(4.49)

Inserting (4.49) in (4.45), we get:

$$\begin{aligned}\begin{array}{ll} \displaystyle { \sqrt{2}\, (-1)^n \, \left| \sin \left( \frac{c}{4}\right) \right| \, \left( 1+\cos ^2\left( \frac{c}{4}\right) \right) \, \left( \epsilon _{2,n}+\frac{ \cos ^2\left( \frac{c}{4}\right) \left( 1-i{{\,\mathrm{sign}\,}}(n)\right) }{ \left( 1+\cos ^2\left( \frac{c}{4}\right) \right) \, \sqrt{\pi |n|}} \right) }\\ \quad \displaystyle {+O(n^{-1})+O(\epsilon _{2,n}^2)+O\left( |n|^{-1/2}\,\epsilon _{2,n}\right) =0.} \end{array} \end{aligned}$$

Consequently, since in this case, $\cos \left( \frac{c}{4}\right) \ne 0$, then we get:

$$\begin{aligned} \epsilon _{2,n}=-\frac{ \cos ^2\left( \frac{c}{4}\right) \left( 1-i{{\,\mathrm{sign}\,}}(n)\right) }{ \left( 1+\cos ^2\left( \frac{c}{4}\right) \right) \, \sqrt{\pi |n|}}+O(n^{-1}). \end{aligned}$$

(4.50)

Substituting (4.50) in (4.40), we get (4.18).

Case 2. If $\cos \left( \frac{c}{4}\right) = 0$, then:

$$\begin{aligned} \cos \left( \frac{c}{2}\right) =-1\ \ \ \text {and}\ \ \ \sin \left( \frac{c}{2}\right) =0. \end{aligned}$$

(4.51)

In this case, $\lambda _{2,n}$ becomes:

$$\begin{aligned} \lambda _{2,n}=2i n\pi +\frac{3\pi \, i}{2}+\epsilon _{2,n}. \end{aligned}$$

(4.52)

Therefore, we have:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\cosh \left( \frac{3\lambda _{2,n}}{2}\right) =\frac{(-1)^n}{\sqrt{2}}\, \left( \cosh \left( \frac{3\epsilon _{2,n}}{2}\right) +i\sinh \left( \frac{3\epsilon _{2,n}}{2}\right) \right) ,} \\ \displaystyle { \sinh \left( \frac{3\lambda _{2,n}}{2}\right) =\frac{(-1)^n}{\sqrt{2}}\, \left( i\cosh \left( \frac{3\epsilon _{2,n}}{2}\right) +\sinh \left( \frac{3\epsilon _{2,n}}{2}\right) \right) ,} \\ \displaystyle {\cosh \left( \frac{\lambda _{2,n}}{2}\right) =\frac{(-1)^n}{\sqrt{2}}\, \left( -\cosh \left( \frac{\epsilon _{2,n}}{2}\right) +i\sinh \left( \frac{\epsilon _{2,n}}{2}\right) \right) ,} \\ \displaystyle { \sinh \left( \frac{\lambda _{2,n}}{2}\right) =\frac{(-1)^n}{\sqrt{2}}\, \left( i\cosh \left( \frac{\epsilon _{2,n}}{2}\right) -\sinh \left( \frac{\epsilon _{2,n}}{2}\right) \right) .} \end{array}\right. \end{aligned}$$

(4.53)

On the other hand, since $\lim _{|n|\rightarrow +\infty }\epsilon _{2,n}=0$, we have the asymptotic expansion:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\cosh \left( \frac{3\epsilon _{2,n}}{2}\right) =1+\frac{9\epsilon _{2,n}^2}{8}+O(\epsilon _{2,n}^4)},\ \displaystyle {\sinh \left( \frac{3\epsilon _{2,n}}{2}\right) =\frac{3\epsilon _{2,n}}{2}+O(\epsilon _{2,n}^3) },\\ \displaystyle {\cosh \left( \frac{\epsilon _{2,n}}{2}\right) =1+\frac{\epsilon _{2,n}^2}{8}+O(\epsilon _{2,n}^4)},\ \displaystyle {\sinh \left( \frac{\epsilon _{2,n}}{2}\right) =\frac{\epsilon _{2,n}}{2}+O(\epsilon _{2,n}^3) }. \end{array} \right. \end{aligned}$$

(4.54)

Inserting (4.54) in (4.53), we get:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\cosh \left( \frac{3\lambda _{2,n}}{2}\right) =\frac{(-1)^n}{\sqrt{2}}\, \left( 1+ \frac{3i\, \epsilon _{2,n}}{2}+\frac{9\epsilon _{2,n}^2}{8}+O(\epsilon _{2,n}^3)\right) ,} \\ \displaystyle { \sinh \left( \frac{3\lambda _{2,n}}{2}\right) =\frac{(-1)^n}{\sqrt{2}}\, \left( i+ \frac{3\, \epsilon _{2,n}}{2}+\frac{9i\, \epsilon _{2,n}^2}{8}+O(\epsilon _{2,n}^3)\right) ,} \\ \displaystyle {\cosh \left( \frac{\lambda _{2,n}}{2}\right) =\frac{(-1)^n}{\sqrt{2}}\, \left( -1+ \frac{i\, \epsilon _{2,n}}{2}-\frac{\epsilon _{2,n}^2}{8}+O(\epsilon _{2,n}^3)\right) ,} \\ \displaystyle { \sinh \left( \frac{\lambda _{2,n}}{2}\right) =\frac{(-1)^n}{\sqrt{2}}\, \left( i- \frac{ \epsilon _{2,n}}{2}+\frac{i\, \epsilon _{2,n}^2}{8}+O(\epsilon _{2,n}^3)\right) .} \end{array}\right. \end{aligned}$$

(4.55)

Moreover, from (4.52), we get:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\frac{1}{\lambda _{2,n}}= -\frac{i}{2\pi n}+\frac{3 i \pi }{8\pi ^2 n^2}+O\left( \epsilon _{2,n}\, n^{-2}\right) +O\left( n^{-3}\right) ,\ \frac{1}{\lambda ^2_{2,n}}= -\frac{1}{4\pi ^2 n^2}+O\left( n^{-3}\right) }, \\ \displaystyle {\frac{1}{\sqrt{\lambda _{2,n}}}=\frac{1-i{{\,\mathrm{sign}\,}}(n)}{2\sqrt{\pi |n|}} +\frac{3\, (-{{\,\mathrm{sign}\,}}(n)+i)}{16\sqrt{\pi |n|^3}} +O\left( \epsilon _{2,n}\, |n|^{-3/2}\right) +O\left( |n|^{-5/2}\right) }, \\ \displaystyle {\frac{1}{\sqrt{\lambda ^3_{2,n}}}=\frac{-1-i{{\,\mathrm{sign}\,}}(n)}{4\sqrt{\pi ^3 |n|^3}}+O\left( |n|^{-5/2}\right) ,\ \frac{1}{\sqrt{\lambda ^5_{2,n}}}=O\left( |n|^{-5/2}\right) }. \end{array}\right. \end{aligned}$$

(4.56)

Inserting (4.51), (4.55), and (4.56) in (4.23), we get:

$$\begin{aligned} \begin{array}{ll} \displaystyle {\frac{i\, \epsilon _{2,n}^2}{2}+\left( 1+\frac{{{\,\mathrm{sign}\,}}(n)+i}{2\sqrt{\pi \, |n|}}+\frac{3 c^2}{64\pi n}\right) \, \epsilon _{2,n}-\frac{i\, c^2}{32\pi n}+\frac{({{\,\mathrm{sign}\,}}(n)-i)\, c^2}{64\sqrt{\pi ^3|n|^3}}}\\ \quad \displaystyle {+\frac{\left( 64-i\left( c^2-24\pi +16\right) \right) \, c^2}{1024 \pi ^2 n^2}}\\ \quad \displaystyle { +O\left( |n|^{-5/2}\right) +O\left( \epsilon _{2,n }\, |n|^{-3/2}\right) +O\left( \epsilon _{2,n }^2\, |n|^{-1/2}\right) +O\left( \epsilon _{2,n }^3\right) =0}. \end{array} \end{aligned}$$

(4.57)

From (4.57), we get:

$$\begin{aligned} \epsilon _{2,n}-\frac{i\, c^2}{32\pi n}+O\left( \epsilon _{2,n }\, |n|^{-1/2}\right) +O\left( \epsilon _{2,n }^2\right) =0; \end{aligned}$$

hence:

$$\begin{aligned} \epsilon _{2,n}=\frac{i\, c^2}{32\pi n}+\frac{\xi _{n}}{n}, \quad \text {such that }\lim _{|n|\rightarrow +\infty }\xi _{n}=0. \end{aligned}$$

(4.58)

Inserting (4.58) in (4.57), we get:

$$\begin{aligned} \frac{\xi _{n}}{n}+\frac{\left( 8+i\, (3\pi -2)\right) \, c^2 }{128\pi ^2 n^2}+O\left( \xi _n\, |n|^{-3/2}\right) +O\left( |n|^{-5/2}\right) =0; \end{aligned}$$

therefore:

$$\begin{aligned} \xi _{n}=-\frac{\left( 8+i\, (3\pi -2)\right) \, c^2 }{128\pi ^2 n}+O(n^{-3/2}). \end{aligned}$$

(4.59)

Inserting (4.58) in (4.59), we get:

$$\begin{aligned} \epsilon _{2,n}=\frac{i\, c^2}{32\pi n}-\frac{\left( 8+i\, (3\pi -2)\right) \, c^2 }{128\pi ^2 n^2}+O(n^{-5/2}). \end{aligned}$$

(4.60)

Finally, inserting (4.60) in (4.52), we get (4.20).

Case 3. If $\sin \left( \frac{c}{4}\right) = 0$, then:

$$\begin{aligned} \cos \left( \frac{c}{2}\right) =1\ \ \ \text {and}\ \ \ \sin \left( \frac{c}{2}\right) =0. \end{aligned}$$

(4.61)

In this case, $\lambda _{2,n}$ becomes:

$$\begin{aligned} \lambda _{2,n}=2i n\pi +i\,\pi +\epsilon _{2,n}. \end{aligned}$$

(4.62)

Similar to case 2, from (4.62) and using the fact that $\lim _{|n|\rightarrow +\infty }\epsilon _{2,n}=0$, we have the asymptotic expansion:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\cosh \left( \frac{3\lambda _{2,n}}{2}\right) =-\frac{3i\, (-1)^n\, \epsilon _{2,n}}{2}+O\left( \epsilon _{2,n}^3\right) ,}\\ \displaystyle { \sinh \left( \frac{3\lambda _{2,n}}{2}\right) =-i\, (-1)^n\, \left( 1+\frac{9 \epsilon _{2,n}^2}{8}\right) +O(\epsilon _{2,n}^4),}\\ \displaystyle {\cosh \left( \frac{3\lambda _{2,n}}{2}\right) =\frac{i\, (-1)^n\, \epsilon _{2,n}}{2}+O\left( \epsilon _{2,n}^3\right) ,}\\ \displaystyle { \sinh \left( \frac{3\lambda _{2,n}}{2}\right) =i\, (-1)^n\, \left( 1+\frac{ \epsilon _{2,n}^2}{8}\right) +O(\epsilon _{2,n}^4).} \end{array}\right. \end{aligned}$$

(4.63)

Moreover, from (4.62), we get:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\frac{1}{\lambda _{2,n}}= -\frac{i}{2\pi n}+\frac{ i\, \pi }{4\pi ^2 n^2}+O\left( \epsilon _{2,n}\, n^{-2}\right) +O\left( n^{-3}\right) ,\ \frac{1}{\lambda ^2_{2,n}}= -\frac{1}{4\pi ^2 n^2}+O\left( n^{-3}\right) ,} \\ \displaystyle {\frac{1}{\sqrt{\lambda _{2,n}}}=\frac{1-i{{\,\mathrm{sign}\,}}(n)}{2\sqrt{\pi |n|}} +\frac{ (1+i\,{{\,\mathrm{sign}\,}}(n))\, \epsilon _{2,n}+ (-{{\,\mathrm{sign}\,}}(n)+i)\,\pi }{8\sqrt{\pi |n|^3}}} \\ \quad \displaystyle {+\frac{3\, (1-i{{\,\mathrm{sign}\,}}(n))}{64\sqrt{\pi |n|^5}}+O\left( \epsilon _{2,n}\, |n|^{-5/2}\right) +O\left( |n|^{-7/2}\right) }, \\ \displaystyle {\frac{1}{\sqrt{\lambda ^3_{2,n}}}=\frac{-1-i{{\,\mathrm{sign}\,}}(n)}{4\sqrt{\pi ^3 |n|^3}}+\frac{3\, ({{\,\mathrm{sign}\,}}(n)+i)}{16\sqrt{\pi ^3 |n|^5}}+O\left( \epsilon _{2,n}\, |n|^{-5/2}\right) +O\left( |n|^{-7/2}\right) }, \\ \displaystyle {\frac{1}{\sqrt{\lambda ^5_{2,n}}}=\frac{-1+i{{\,\mathrm{sign}\,}}(n)}{8\sqrt{\pi ^5 |n|^5}}+O\left( |n|^{-7/2}\right) ,\ \ \frac{1}{\lambda _{2,n}^3}=O\left( n^{-3}\right) }. \end{array}\right. \end{aligned}$$

(4.64)

Inserting (4.61), (4.63), and (4.64) in (4.23), we get:

$$\begin{aligned} \begin{array}{ll} \displaystyle {-i\, \epsilon _{2,n}^2+\left( -\frac{ {{\,\mathrm{sign}\,}}(n)+i}{\sqrt{\pi |n|}}-\frac{3 c^2}{32\pi n}+\frac{{{\,\mathrm{sign}\,}}(n)-i+(1+i{{\,\mathrm{sign}\,}}(n))\, \pi }{4\sqrt{\pi ^3|n|^3}}\right) \, \epsilon _{2,n}}\\ \quad \displaystyle {-\frac{({{\,\mathrm{sign}\,}}(n)-i)\, c^2}{32\sqrt{\pi ^3|n|^3}}} \\ \quad \displaystyle {+\frac{i\, c^4}{512\pi ^2 n^2}-\frac{3\left( 3 ({{\,\mathrm{sign}\,}}(n)+i)-(1-i {{\,\mathrm{sign}\,}}(n))\, \pi \right) \, c^2}{128\sqrt{\pi ^5|n|^5}}} \\ \quad \displaystyle { +O\left( n^{-3}\right) +O\left( \epsilon _{2,n }\, n^{-2}\right) +O\left( \epsilon _{2,n }^2\, n^{-1}\right) +O\left( \epsilon _{2,n }^3\right) =0}. \end{array} \end{aligned}$$

(4.65)

Similar to case 2, solving Eq. (4.65), we get:

$$\begin{aligned} \epsilon _{2,n}=\frac{i \, c^2}{32\pi n}-\frac{\left( 4+i\pi \right) \, c^2}{64\pi ^2 n^2}+O\left( |n|^{-5/2}\right) . \end{aligned}$$

(4.66)

Finally, inserting (4.66) in (4.62), we get (4.22). Thus, the proof is complete.

Proof of Theorem 4.3

From Proposition 4.4, the operator $\mathcal {A}_2$ has two branches of eigenvalues with eigenvalues admitting real parts tending to zero. Hence, the energy corresponding to the first and second branch of eigenvalues has no exponential decaying. Therefore, the total energy of the Timoshenko System (1.1)–(1.2) with local Kelvin–Voigt damping, and with Dirichlet–Neumann boundary conditions (1.4), has no exponential decaying in the equal speed case. $\square$

Our second result in this part is following theorem.

Theorem 4.8

Under hypothesis (H2), for all initial data $U_0\in D\left( \mathcal {A}_2\right)$ and for all $t>0,$ if there exists $\kappa \in \mathbb {N}$, such that $c:=\sqrt{\frac{k_1}{k_2}}=2\kappa \pi$, then the energy decay rate in (3.1) is optimal; i.e., for $\epsilon >0\left( \text {small enough}\right)$, we cannot expect the energy decay rate $t^{-\frac{2}{{2-\epsilon }}}$.

For the proof of Theorem 4.8, we first recall Theorem 3.4.1 stated in Nadine (2016).

Theorem 4.9

Let $A:D(A)\subset H\rightarrow H$ generate a C$_0-$semigroup of contractions $\left( e^{t A}\right) _{t\ge 0}$ on H. Assume that $i\mathbb {R}\in \rho (A)$. Let $\left( \lambda _{k,n}\right) _{1\le k\le k_0,\ n\ge 1}$ denote the kth branch of eigenvalues of A and $\left( e_{k,n}\right) _{1\le k\le k_0,\ n\ge 1}$ the system of normalized associated eigenvectors. Assume that for each $1\le k\le k_0$, there exist a positive sequence $\mu _{k,n}\rightarrow \infty$ as $n\rightarrow \infty$ and two positive constant $\alpha _k>0, \beta _k>0$, such that:

$$\begin{aligned} \Re (\lambda _{k,n})\sim - \frac{\beta _k}{\mu _{k,n}^{\alpha _k}} \ \ \ \text {and}\ \ \ \Im (\lambda _{k,n})\sim \mu _{k,n}\ \ \ \text {as } n\rightarrow \infty . \end{aligned}$$

(4.67)

Here, $\Im$ is used to denote the imaginary part of a complex number. Furthermore, assume that for $u_0\in D(A)$, there exists constant $M>0$ independent of $u_0$, such that:

$$\begin{aligned} \left\| e^{t A}u_0\right\| _{H}^2\le \frac{M}{t^{\frac{2}{\ell _k}}}\left\| u_0\right\| _{D(A)}^2,\ \ \ell _k=\max _{1\le k\le k_0} \alpha _k,\ \ \forall \ t>0. \end{aligned}$$

(4.68)

Then, the decay rate (4.68) is optimal in the sense that for any $\epsilon >0$, we cannot expect the energy decay rate $t^{-\frac{2}{\ell _k-\epsilon }}.$ $\square$

Proof of Theorem 4.8

If condition (H2) holds, first following Theorem 3.1, for all initial data $U_0\in D\left( \mathcal {A}_2\right)$ and for all $t>0,$ we get (4.68) with $\ell _k=2$. Furthermore, from Proposition 4.4 (case 2 and case 3), we remark that:

Case 1. If there exists $\kappa _0\in \mathbb {N}$, such that $c=2\left( 2\kappa _0+1\right) \pi$, we have:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\Re \left( \lambda _{1,n}\right) \sim -\frac{1}{\pi ^{1/2} |n|^{1/2}}, \ \ \ \Im \left( \lambda _{1,n}\right) \sim 2 n\pi },\\ \displaystyle {\Re \left( \lambda _{2,n}\right) \sim -\frac{ c^2}{16\pi ^2 n^2}, \ \ \ \Im \left( \lambda _{2,n}\right) \sim \left( 2 n+\frac{3}{2}\right) \pi }, \end{array} \right. \end{aligned}$$

then (4.67) holds with $\alpha _1=\frac{1}{2}$ and $\alpha _2=2$. Therefore, $\ell _{k}=2=\max (\alpha _1,\alpha _2).$ Then, applying Theorem 4.9, we get that the energy decay rate in (3.1) is optimal.

Case 2. If there exists $\kappa _1\in \mathbb {N}$, such that $c=4\kappa _1 \pi$, we have:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\Re \left( \lambda _{1,n}\right) \sim -\frac{c^2}{16\pi ^2 n^2}, \ \ \ \Im \left( \lambda _{1,n}\right) \sim 2 n\pi },\\ \displaystyle {\Re \left( \lambda _{2,n}\right) \sim -\frac{ c^2}{16\pi ^2 n^2}, \ \ \ \Im \left( \lambda _{2,n}\right) \sim \left( 2 n+1\right) \pi }, \end{array} \right. \end{aligned}$$

then (4.67) holds with $\alpha _1=2$ and $\alpha _2=2$. Therefore, $\ell _{k}=2=\max (\alpha _1,\alpha _2).$ Then, applying Theorem 4.9, we get that the energy decay rate in (3.1) is optimal. $\square$

Remark 4.10

It would be very interesting to study the optimal decay rate for the Timoshenko System (1.1)–(1.2) with Dirichlet–Neumann boundary conditions (1.4) when $\frac{\rho _1}{k_1}\ne \frac{\rho _2}{k_2}$ or with fully Dirichlet boundary conditions (1.3). However, in these cases, we can no longer calculate explicitly the eigenvalues as in Proposition 4.4. $\square$