Asymptotic numerical method for third-order singularly perturbed convection diffusion delay differential equations

Abstract

In this paper, an asymptotic numerical method based on a fitted finite difference scheme and the fourth-order Runge–Kutta method with piecewise cubic Hermite interpolation on Shishkin mesh is suggested to solve singularly perturbed boundary value problems for third-order ordinary differential equations of convection diffusion type with a delay. An error estimate is derived using the supremum norm and it is of almost first-order convergence. A nonlinear problem is also solved using the Newton’s quasi linearization technique and the present asymptotic numerical method. Numerical results are provided to illustrate the theoretical results.

1 Introduction

Delay differential equations (DDEs) are differential equations in which the unknown function not only evaluated at present but also evaluated at some past values of the independent variable. DDEs arise in many fields of science and technology such as, mathematical physics, control theory, neural network, medicine, biology, population dynamics model, etc. In the recent past years, the problem of finding numerical solutions for higher order singularly perturbed problems without delay are paid more attention, to cite a few (Cañada et al. 2006; Murray 2002; Kuang 1993).

Nowadays, there has been growing interest for solving higher order singularly perturbed delay differential equation, where the highest order derivative is multiplied by small positive parameter $\varepsilon$$(0<\varepsilon \ll 1)$ which contains at least one delay term, called singularly perturbed delay differential equation (SPDDE). This type of differential equation plays a vital role in mathematical modeling of various practical phenomena, such as variational problem in control theory Glizer (2003), predator-prey model Gourley and Kuang (2004), description of human pupil-light reflex Longtin and Milton (1988). It is well-known fact that the solution of the singularly perturbed differential equations with or without delay, generally exhibits boundary layer(s) and interior layer(s). Classical numerical methods for solving such type of problems are known to be inadequate, due to the presence of boundary layer(s) and interior layer(s) when the perturbation parameter tends to zero. It is quite important to adapt the non-classical numerical method called $\varepsilon$-uniform numerical method, in which the error bound is independent of the perturbation parameter $\varepsilon .$

In the literature, quite a good number of articles have been reported for singularly perturbed higher order ordinary differential equations of convection diffusion and reaction diffusion type without delay. In Chen and Wang (2016) presented numerical methods based on rational spectral collocation in barycentric form with $\sinh$ transformation. The authors of (Valanarasu and Ramanujam 2007a, b), respectively, applied asymptotic numerical methods for third-order ordinary differential equations of convection and reaction diffusion type problem with discontinuous source term. Whereas Christy Roja and Tamilselvan (2016, 2018) have constructed overlapping Schwarz method for third-order reaction and convection diffusion problem and proved that the method is almost second order convergence. Few authors in the literature have applied some numerical methods for singularly perturbed fourth-order differential equations. To mention a few: Cen et al. (2017) applied higher a order hybrid finite difference scheme on Shishkin mesh for fourth-order singularly perturbed problems (SPPs) and proved that the scheme is almost fourth order. Lodhi and Mishra (2016) applied quintic B-spline method for the system of differential equations and proved that the method is second-order convergence. Chandru and Shanthi (2016) suggested fitted finite difference method on a piecewise uniform Shishkin mesh for convection diffusion turning point problem.

Recently, the authors in Mahendran and Subburayan 2018; Subburayan and Mahendran 2018 applied fitted finite difference methods combined with linear interpolation techniques for third order delay differential equations. As mentioned in the abstract, an asymptotic numerical method combined with fourth-order Runge–Kutta method on Shishkin mesh is suggested to solve the following problem (2)–(3).

The rest of the paper is organized as follows: Sect. 2 presents the statement and the equivalent form of the problem with sufficiently differentiable coefficient functions. The stability results are stated in Sect. 3. Some results pertaining to the given problem (2)–(3) and its auxiliary problem are given in Sect. 4. Section 5 deals with fourth-order Runge–Kutta method with piecewise cubic Hermite interpolation on Shishkin mesh for reduced problem and fitted finite difference scheme for auxiliary problem. Section 6 deals with nonlinear problem. Numerical examples are illustrated in Sect. 7 to validate the theoretical results. The paper is concluded with concluding remarks.

The following notations are used in the rest of the article:

• $\varepsilon$ is small parameter such that $0<\varepsilon \ll 1$.

• The set (0, 2) is denoted as $\varOmega$ and its closure is ${\bar{\varOmega }}.$ Further $\varOmega ^{*}=\varOmega ^{-}\cup \varOmega ^{+},$ where $\varOmega ^{-}=(0,1)$ and $\varOmega ^{+}=(1,2).$

• ${\bar{\varOmega }}^{N}$ denotes the set of mesh points $\{x_{0},\ x_{1},\ \ldots ,x_{N}\}.$

• The norm $\parallel \star \parallel$ denotes the supremum norm $\parallel \psi \parallel _{\omega }=\sup _{x\in \omega }|\psi (x)|.$

• The sets $Y,\ Y^{*},\ Y_{1},\ Y_{1}^{*},\ Y_{2},$ and $Y_{2}^{*}$, respectively, defined as $Y=C^{1}({\overline{\varOmega }})\cap C^{2}(\varOmega )\cap C^{3}(\varOmega ),$$Y^{*}=C^{1}({\overline{\varOmega }})\cap C^{2}(\varOmega )\cap C^{3}(\varOmega ^{*}),$$Y_{1}=C^{0}({\overline{\varOmega }})\cap C^{1}(0, 2]$, $Y_{1}^{*}=C^{0}({\overline{\varOmega }})\cap C^{1}(\varOmega ^{*}\cup \{2\})$, $Y_{2}=C^{0}({\overline{\varOmega }})\cap C^{2}(\varOmega )$, and $Y^{*}_{2}=C^{0}({\overline{\varOmega }})\cap C^{1}(\varOmega )\cap C^{2}(\varOmega ^{*})$.

2 The continuous problem

The works of Valanarasu (2006), Shanthi and Ramanujam (2002) and Valarmathi and Ramanujam (2002) motivate us to consider the following third order SPDDE:

Find $u\in Y$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} -\varepsilon u^{\prime \prime \prime }(x)+a(x)u^{\prime \prime }(x)+b(x)u^{\prime }(x)+c(x)u(x)+d(x)u^{\prime }(x-1)=f(x), \quad x\in \varOmega ,\\ u(x)=\phi (x), x\in [-1,0], u^{\prime }(2)=\ell ,\ \phi \in C^{1}[-1,0], \end{array}\right. } \end{aligned}$$

(1)

where $a(x)\ge \alpha _{1}>\alpha +2>3,$$b(x)\ge \beta _{0}\ge 0$, $\gamma _{0}\le c(x)\le \gamma \le 0,$$\eta _{0}\le d(x)\le 0$, $2\alpha +24\gamma _{0}+5\eta _{0}>0$ and $a,\ b,\ c,\ d,\ f$ are sufficiently differentiable on ${\bar{\varOmega }}.$

The above BVP (1) can be written into the following equivalent problem:

Find $\overline{u}=(u_{1},u_{2}),$$u_{1}\in Y_{1}$, $u_{2} \in Y_{2}$ such that

$$\begin{aligned}&P_{1} \overline{u}(x)= u_{1}^{\prime }(x)-u_{2}(x)=0,\ x\in (0,2], \end{aligned}$$

(2)

$$\begin{aligned}&P_{2}\overline{u}(x)= {\left\{ \begin{array}{ll} -\varepsilon u_{2}^{\prime \prime }(x)+a(x)u_{2}^{\prime }(x)+b(x)u_{2}(x)+c(x)u_{1}(x)\\ \quad \quad =f(x)-d(x)\phi ^{\prime }(x-1), x\in \varOmega ^{-},\\ -\varepsilon u_{2}^{\prime \prime }(x)+a(x)u_{2}^{\prime }(x)+b(x)u_{2}(x)+c(x)u_{1}(x)\\ \quad \quad +d(x)u_{2}(x-1)=f(x), x\in \varOmega ^{+}, \end{array}\right. } \end{aligned}$$

(3)

$u_{1}(0)=\phi (0),$$u_{2}(0)=\phi ^{\prime }(0),$$u_{2}(1-)=u_{2}(1+),$$u_{2}^{\prime }(1-)=u_{2}^{\prime }(1+),$$u_{2}(2)=\ell ,$ where $u_{2}(1-)$ and $u_{2}(1+)$ represent left and right limits of $u_{2}$ at $x=1,$ respectively.

3 Stability results

This section presents the maximum principle and stability result for the above problem (2)–(3).

Theorem 1

(Maximum Principle) Suppose that $\overline{w}=(w_{1},\ w_{2}),$$w_{1}\in C^{1}(\varOmega ), w_{2}\in C^{0}(\bar{\varOmega })\cap C^{2}(\varOmega ^{*})$ satisfies $w_{1}(0)\ge 0$ and $w_{2}(0)\ge 0,\ w_{2}(2)\ge 0,$$P_{1}\overline{w}(x)\ge 0,$$\forall x\in \varOmega \cup \{2\} ,$$P_{2}\overline{w}(x)\ge 0,$$\forall x\in \varOmega ^{*}$ and $w_{2}^{\prime }(1+)-w_{2}^{\prime }(1-)=[w_{2}^{\prime }](1)\le 0$. Then $w_{i}(x)\ge 0, \ \forall x\in \overline{\varOmega },\ i=1,2.$

Proof

Refer [Mahendran and Subburayan (2018), Theorem 3.1]

An immediate consequence of the above theorem is the following stability result.

Corollary 1

For any ${\bar{u}}=(u_{1},u_{2}),$$u_{1}\in Y_{1},$$u_{2}\in Y_{2}$, and for $i=1,2$ we have

$$\begin{aligned} |u_{i}(x)|\le C \max \Big \{|u_{1}(0)|,|u_{2}(0)|,|u_{2}(2)|,\sup _{\varsigma _{1} \in \varOmega \cup \{2\}}|P_{1}\overline{u}(\varsigma _{1})|, \sup _{\varsigma _{2} \in \varOmega ^{*}} |P_{2}\overline{u}(\varsigma _{2})|\Big \}, \forall x\in {\overline{\varOmega }}. \end{aligned}$$

Proof

Refer [Mahendran and Subburayan (2018), Corollary 3.2]

Note: Using the above result, one can prove that, the solution of the above problem (2)–(3) is unique, if it exists.

4 Analytical results

In this section, we present some analytical results for the solution of the problem (2)–(3).

Consider the reduced problem, find ${\bar{u}}_{0}=(u_{01},u_{02})$, $u_{01}$, $u_{02}$$\in Y_{1}$ such that

$$\begin{aligned}&u^{\prime }_{01}(x)-u_{02}(x)=0,\ x \in (0,2], \end{aligned}$$

(4)

$$\begin{aligned}&a(x)u^{\prime }_{02}(x)+b(x)u_{02}(x)+c(x)u_{01}(x)+d(x)u_{02}(x-1)=f(x),\ x\in (0,2], \end{aligned}$$

(5)

    $u_{01}(0)=\phi (0)$, $u_{02}(x)=\phi ^{\prime }(x),\ x\in [-1,0].$

Assume that $|u^{\prime \prime }_{02}(x)|\le C,\ x\in \varOmega ^{*}.$ The following theorem gives the estimate of $|u_{k}-u_{0k}|$ for $k=1 ,\ 2.$

Theorem 2

Let ${\bar{u}}$ be the solution of the problem (2)–(3) and ${\bar{u}}_{0}$ be its reduced problem solution defined by (4)–(5). Then $|u_{k}(x)-u_{0k}(x)|\le C_{1}\{{\varepsilon +\varepsilon ^{2-k} \exp (\frac{-\alpha (2-x)}{\varepsilon })}\},$$x\in {\bar{\varOmega }}$, $k=1 ,\ 2.$

Proof

Refer [Mahendran and Subburayan (2018), Theorem 4.2].

4.1 Auxiliary problem

We now define an auxiliary problem as follows: Find ${\bar{u}}^{*}=(u^{*}_{1}, u^{*}_{2})$, $u^{*}_{1}\in Y_{1}, u^{*}_{2}\in Y_{2}$ such that

$$\begin{aligned} P_{1}^{*}{{\bar{u}}^{*}(x)}&:=u^{*{\prime }}_{1}(x)-u^{*}_{2}(x)=0,\ x\in (0, 2], \end{aligned}$$

(6)

$$\begin{aligned} P^{*}_{2}{\bar{u}}^{*}(x)&:=-\varepsilon u^{*{\prime \prime }}_{2}(x)+a(x)u^{*{\prime }}_{2}(x)+b(x)u^{*}_{2}(x)+c(x)u^{*}_{1}(x)=f^{*}(x),\ x\in \varOmega , \end{aligned}$$

(7)

where $f^{*}(x)={\left\{ \begin{array}{ll} f(x)-d(x)\phi ^{\prime }(x-1),\ x\in (0, 1),\\ f(x)-d(x)u_{02}(x-1),\ x\in [1, 2). \end{array}\right. }$

Theorem 3

(Maximum Principle) Suppose that $\overline{w}=(w_{1},\ w_{2}),$$w_{1}\in C^{1}(\varOmega ), w_{2}\in C^{0}({\bar{\varOmega }})\cap C^{2}(\varOmega ^{*})$ satisfies $w_{1}(0)\ge 0$ and $w_{2}(0)\ge 0,\ w_{2}(2)\ge 0,$$P^{*}_{1}\overline{w}(x)\ge 0,$$\forall x\in \varOmega \cup \{2\} ,$$P^{*}_{2}\overline{w}(x)\ge 0,$$\forall x\in \varOmega ^{*}$ and $w_{2}^{\prime }(1+)-w_{2}^{\prime }(1-)=[w_{2}^{\prime }](1)\le 0$. Then $w_{i}(x)\ge 0, \ \forall x\in {\overline{\varOmega }},\ i=1,2.$

Proof

Refer [Valanarasu and Ramanujam (2007a), Theorem 2.2].

Theorem 4

Let ${\bar{u}}$ and ${\bar{u}}^{*}$ be the solutions of the problem (2)–(3) and (6)–(7), respectively. Then $|u_{k}(x)-u^{*}_{k}(x)|\le C\varepsilon ,\ x\in {\bar{\varOmega }},$$k=1,\ 2.$

Proof

Consider the barrier function ${\bar{\phi }}^{\pm }(x)=(\phi _{1}^{\pm }, \phi _{2}^{\pm })$, where

$$\begin{aligned} \phi _{k}^{\pm }(x)=C_{1}\varepsilon s_{k}(x)\pm (u_{k}(x)-u^{*}_{k}(x)),\ x\in {\bar{\varOmega }}, k=1, 2. \end{aligned}$$

Now,

$$\begin{aligned} P^{*}_{1}{\bar{\phi }}^{\pm }(x)&=\phi ^{\pm {\prime }}_{1}(x)-\phi ^{\pm }_{2}(x)=C_{1}\varepsilon (1-\frac{1}{8}-\frac{x}{2})\pm [P^{*}_{1}{\bar{u}}(x) -P^{*}_{1}{\bar{u}}^{*}(x)] \ge 0,\ x\in (0, 2]. \end{aligned}$$

Let $x\in \varOmega ^{-},$ then

$$\begin{aligned} P^{*}_{2}{\bar{\phi }}^{\pm }(x)&=-\varepsilon \phi ^{\pm {\prime \prime }}_{2}(x)+a(x)\phi ^{\pm {\prime }}_{2}(x)+b(x)\phi ^{\pm }_{2}(x)+c(x)\phi ^{\pm }_{1}(x)\\&=C_{1}\varepsilon \left[ \frac{a(x)}{2}+b(x)(\frac{1}{8}+\frac{x}{2})+c(x)(1+x) \right] \pm [P^{*}_{2}{\bar{u}}(x) - P^{*}_{2}{\bar{u}}^{*}(x)]\\&\ge C_{1} \varepsilon \left[ \frac{4\alpha _{1}+\beta _{0}+16\gamma _{0}}{8}\right] \pm 0\ge 0. \end{aligned}$$

Similarly one can prove that $P^{*}_{2}{\bar{\phi }}^{\pm }(x)\ge 0,\ x\in \varOmega ^{+}.$ Let $x=1,$ then

$$\begin{aligned}{}[\phi ^{\pm {\prime }}_{2}](1)&=\phi ^{\pm {\prime }}_{2}(1+)- \phi ^{\pm {\prime }}_{2}(1-) = C_{1}\varepsilon \left( \frac{-1}{4}\right) \pm 0\ \le 0. \end{aligned}$$

Then, by Theorem 3, we have $\phi _{k}^{\pm }(x)\ge 0, \forall x\in {\bar{\varOmega }}, \ k=1, 2.$ That is, $|u_{k}(x)-u^{*}_{k}(x)|\le C\varepsilon , \forall x\in {\bar{\varOmega }}.$

5 The discrete problem

In this section, the fourth-order Runge–Kutta method with piecewise cubic Hermite interpolation on Shishkin mesh is presented for the reduced problem (4)–(5). Further a fitted finite difference scheme for the auxiliary problem for (6)–(7) is also presented.

5.1 Piecewise uniform mesh

The BVP (2)–(3) and the auxiliary problem (6)–(7) exhibit a strong boundary layer at $x=2$ and weak interior layer at $x=1.$ Furthermore, $x=1$ is a primary discontinuous point [Bellen and Zennaro (2003), Section 2.1.1] for the reduced problem (4)–(5). Therefore, we divide the interval into four subintervals, namely $[0, 1-\tau ],$$[1-\tau , 1],$$[1, 2-\tau ],$$[2-\tau , 2].$ where $\tau =\min \{0.5, \frac{2\varepsilon \ln N}{\alpha }\}.$ Let $h=4N^{-1}\tau$ and $H=4 N^{-1}(1-\tau ).$ The mesh ${\bar{\varOmega }}^{N}=\{x_{0},x_{1},\ldots ,x_{N}\}$ is defined by $x_{0}=0.0$, $x_{i}=x_{0}+iH, \ i=1,\ldots ,\frac{N}{4},$    $x_{i+\frac{N}{4}}=x_{\frac{N}{4}}+ih,\ i=1,\ldots ,\frac{N}{4},$$x_{i+\frac{N}{2}}=x_{\frac{N}{2}}+iH, i=1,\ldots ,\frac{N}{4},$    $x_{i+\frac{3N}{4}}=x_{\frac{3N}{4}}+ih,\ i=1,\ldots ,\frac{N}{4}.$

5.2 Runge–Kutta method with piecewise cubic Hermite interpolation

The fourth-order Runge–Kutta method with piecewise cubic Hermite interpolation [Bellen and Zennaro (2003), Chapter 6] on Shishkin mesh ${\bar{\varOmega }}^{N}$ is applied to obtain numerical solution for (4)–(5). In fact, the numerical solution is given by

$$\begin{aligned} {\bar{U}}_{0}(x_{i})=(U_{01}(x_{i}), U_{02}(x_{i})), \quad i=0, \dots , N, \end{aligned}$$

(8)

where

$$\begin{aligned} U_{01}(x_{0})= & {} \phi (x_{0}),\quad U_{02}(x_{0})=\phi ^{\prime } (x_{0}), \end{aligned}$$

(9)

$$\begin{aligned} U_{0j}(x_{i})= & {} U_{0j}(x_{i})+\frac{1}{6}[K_{j1}+2K_{j2}+2K_{j3}+K_{j4}],\ i=1, \ldots , N, \ j=1,2, \end{aligned}$$

(10)

$$\begin{aligned} K_{11}= & {} h_{i}[U_{02}(x_{i})],\\ K_{21}= & {} \frac{h_{i}}{a({x_{i}})} [f(x_{i})-b(x_{i})U_{02}(x_{i})-c(x_{i})U_{01}(x_{i})-d(x_{i})U_{02}^{I}(x_{i})],\\ K_{12}= & {} h_{i} \left[ U_{02}(x_{i})+\frac{K_{21}}{2} \right] ,\\ K_{22}= & {} \frac{h_{i}}{a \left( {x_{i}+\frac{h_{i}}{2}}\right) }\left[ f \left( x_{i}+\frac{h_{i}}{2}\right) -b\left( x_{i}+\frac{h_{i}}{2}\right) \left( U_{02}(x_{i})+\frac{K_{21}}{2}\right) \right. \\&\left. -c \left( x_{i}+\frac{h_{i}}{2}\right) \left( U_{01}(x_{i})+\frac{K_{11}}{2} \right) -d \left( x_{i}+\frac{h_{i}}{2}\right) U_{02}^{I} \left( x_{i}+\frac{h_{i}}{2}\right) \right] ,\\ K_{13}= & {} h_{i} \left[ U_{02} \left( x_{i}+\frac{h_{i}}{2} \right) +\frac{K_{22}}{2} \right] ,\\ K_{23}= & {} \frac{h_{i}}{a \left( {x_{i}+\frac{h_{i}}{2}}\right) } \left[ f \left( x_{i}+\frac{h_{i}}{2}\right) -b \left( x_{i}+\frac{h_{i}}{2} \right) \left( U_{02}(x_{i})+\frac{K_{22}}{2}\right) \right. \\&\left. -c \left( x_{i}+\frac{h_{i}}{2} \right) \left( U_{01}(x_{i})+\frac{K_{12}}{2}\right) -d \left( x_{i}+\frac{h_{i}}{2}\right) U_{02}^{I} \left( x_{i}+\frac{h_{i}}{2}\right) \right] ,\\ K_{14}= & {} h_{i} [U_{02}(x_{i}+h_{i})+K_{23}],\\ K_{24}= & {} \frac{h_{i}}{a({x_{i}}+h_{i})}[f(x_{i}+h_{i})-b(x_{i}+h_{i})(U_{02}(x_{i})+k_{23})\\&-c(x_{i}+h_{i})(U_{01}(x_{i}+K_{13})-d(x_{i}+h_{i})U_{02}^{I}(x_{i}+h_{i})],\\ h_{i}= & {} x_{i}-x_{i-1},\ i=\ 1,2,\ldots ,N.\\ U_{02}^{I}(x)= & {} {\left\{ \begin{array}{ll} \phi ^{\prime } (x-1), x\in [x_{i}, x_{i+1}], i=\ 0,\ldots , \frac{N}{2}-1,\\ U_{02}(x_{j})A_{j}(x-1)+U_{02}(x_{j+1})A_{j+1}(x-1)+B_{j}(x-1){\tilde{f}} (x_{j})\\ +B_{j+1}(x-1){\tilde{f}}(x_{j+1}),\ x\in [x_{i}, x_{i+1}], i=\frac{N}{2},\ldots , N-1, j=i-\frac{N}{2}, \end{array}\right. }\\ A_{j}(x)= & {} \left[ 1-\frac{2(x-x_{j})}{x_{j}-x_{j+1}} \right] \frac{(x-x_{j+1})^{2}}{(x_{j}-x_{j+1})^{2}},\quad A_{j+1}(x)= \left[ 1-\frac{2(x-x_{j+1})}{x_{j+1}-x_{j}}\right] \frac{(x-x_{j})^{2}}{(x_{j+1}-x_{j})^{2}},\\ B_{j}(x)= & {} \frac{(x-x_{j})(x-x_{j+1})^{2}}{(x_{j}-x_{j+1})^{2}},\ B_{j+1}(x)=\frac{(x-x_{j+1})(x-x_{j})^{2}}{(x_{j+1}-x_{j})^{2}},\\ {\tilde{f}}(x_{j})= & {} \frac{1}{a(x_{j})}[f(x_{j})-b(x_{j})U_{02}(x_{j})-c(x_{j})U_{01}(x_{j})-d(x_{j}) \phi ^{\prime } (x_{j}-1)]. \end{aligned}$$

The following theorem gives the error estimate for the above method (9)–(10).

Theorem 5

Let ${\bar{u}}_{0}(x)$ be the solution of the problem (4)–(5). Further , let ${\bar{U}}_{0}(x_{i})=(U_{01}(x_{i}), U_{02}(x_{i}))$ be its numerical solution defined by (8). Then, ${\parallel {\bar{u}}_{0}-{\bar{U}}_{0}\parallel }_{{\bar{\varOmega }}^{N}}\le C \hbar ^{4},$ where $\hbar = \max \{h_{i}\}^{N}_{i=1}.$

Proof

Refer [Bellen and Zennaro (2003), Theorem 6.2.1].

5.3 Fitted finite difference scheme for the auxiliary problem (6)–(7)

On the mesh ${\bar{\varOmega }}^{N},$ we define the following finite difference scheme.

If the exact solution of the reduced problem (4)–(5) is known, then one can use the following scheme:

$$\begin{aligned} P^{*N}_{1}{\bar{U}}^{*}(x_{i})= & {} D^{-}U^{*}_{1}(x_{i})-U^{*}_{2}(x_{i})=0, x\in (0,2]\cap {\bar{\varOmega }}^{N},\nonumber \\ P^{*N}_{2}{\bar{U}}^{*}(x_{i})= & {} -\varepsilon \delta ^{2} U^{*}_{2}(x_{i})+a(x_{i})D^{-}U^{*}_{2}(x_{i})+b(x_{i})U^{*}_{2}(x_{i}) \end{aligned}$$

(11)

$$\begin{aligned}&+ \, c(x_{i})U^{*}_{1}(x_{i}) =F^{*}(x_{i}),\ x_{i}\in {\bar{\varOmega }}^{N}{\setminus }\{x_{0},x_{\frac{N}{2}},x_{N}\}, \nonumber \\ U^{*}_{1}(x_{0})= & {} u^{*}_{1}(0), \ U^{*}_{2}(x_{0})=u^{*}_{2}(0),\ D^{-}U^{*}_{2}(x_{\frac{N}{2}})=\ D^{+}U^{*}_{2}(x_{\frac{N}{2}}),U^{*}_{2}(x_{N})=u^{*}_{2}(2),\nonumber \\ \end{aligned}$$

(12)

where

$$\begin{aligned} \delta ^{2}U^{*}_{2}(x_{i})= & {} \frac{2}{x_{i+1}-x_{i-1}}[D^{+}U^{*}_{2}(x_{i})-D^{-}U^{*}_{2}(x_{i})]\nonumber \\ D^{-}U^{*}_{2}(x_{i})= & {} \frac{U^{*}_{2}(x_{i})-U^{*}_{2}(x_{i-1})}{x_{i}-x_{i-1}},\quad \ D^{+}U^{*}_{2}(x_{i})=\frac{U^{*}_{2}(x_{i+1})-U^{*}_{2}(x_{i})}{x_{i+1}-x_{i}}\nonumber \\ F^{*}(x_{i})= & {} {\left\{ \begin{array}{ll} f(x_{i})-d(x_{i})\phi ^{\prime } (x_{i}-1),\ x_{i}\in \varOmega ^{-}\cap {\bar{\varOmega }}^{N}\\ f(x_{i})- d(x_{i})u_{02}(x_{i}-1),\ x_{i}\in \varOmega ^{+}\cap {\bar{\varOmega }}^{N}. \end{array}\right. } \end{aligned}$$

(13)

If the numerical solution of the reduced problem is known, then one can use the following scheme:

$$\begin{aligned} P^{*N}_{1}{\tilde{\bar{U}}}^{*}(x_{i})= & {} D^{-}{\tilde{U}}^{*}_{1}(x_{i})-{\tilde{U}}^{*}_{2}(x_{i})=0, x\in (0,2]\cap {\bar{\varOmega }}^{N},\nonumber \\ P^{*N}_{2}{\tilde{\bar{U}}}^{*}(x_{i})= & {} -\varepsilon \delta ^{2} {\tilde{U}}^{*}_{2}(x_{i})+a(x_{i})D^{-}{\tilde{U}}^{*}_{2}(x_{i})+b(x_{i}){\tilde{U}}^{*}_{2}(x_{i}) \end{aligned}$$

(14)

$$\begin{aligned}&+c(x_{i})\tilde{U}^{*}_{1}(x_{i}) =\tilde{F}^{*}(x_{i}),\ x_{i}\in {\bar{\varOmega }}^{N}{\setminus }\{x_{0},x_{\frac{N}{2}},x_{N}\}, \nonumber \\ {\tilde{U}}^{*}_{1}(x_{0})= & {} u^{*}_{1}(0), \ {\tilde{U}}^{*}_{2}(x_{0})=u^{*}_{2}(0),\ D^{-}{\tilde{U}}^{*}_{2}(x_{\frac{N}{2}})=\ D^{+}{\tilde{U}}^{*}_{2}(x_{\frac{N}{2}}),{\tilde{U}}^{*}_{2}(x_{N})=u^{*}_{2}(2),\nonumber \\ \end{aligned}$$

(15)

where

$$\begin{aligned} \tilde{F^{*}}(x_{i})= {\left\{ \begin{array}{ll} f(x_{i})-d(x_{i})\phi ^{\prime } (x_{i}-1),\ x_{i}\in \varOmega ^{-}\cap {\bar{\varOmega }}^{N},\\ f(x_{i})- d(x_{i})U_{02}(x_{i-\frac{N}{2}}),\ x_{i}\in \varOmega ^{+}\cap {\bar{\varOmega }}^{N}. \end{array}\right. } \end{aligned}$$

(16)

5.4 Discrete stability results

Theorem 6

(Discrete Maximum Principle) Let ${\bar{W}}(x_{i})=(W_{1}(x_{i}),W_{2}(x_{i}))$ be a mesh function satisfying $W_{1}(x_{0})\ge 0,$$W_{2}(x_{0})\ge 0,$$W_{2}(x_{N})\ge 0,$$P_{1}^{*N}{\bar{W}}(x_{i})\ge 0, \ x_{i}\in (0, 2]\cap {\bar{\varOmega }}^{N},$$P_{2}^{*N}{\bar{W}}(x_{i})\ge 0,\ x_{i}\in \varOmega ^{*}\cap {\bar{\varOmega }}^{N}$ and $[D]W_{2}(x_{N/2})\le 0$. Then, $W_{1}(x_{i})\ge 0$ and $W_{2}(x_{i})\ge 0$, $x_{i}\in {\overline{\varOmega }}^{N}$.

Proof

Refer [Mahendran and Subburayan (2018), Theorem 5.1].

A consequence of the above theorem is the following stability result.

Theorem 7

Let ${\bar{U}}^{*}(x_{i})$ be a numerical solution of (6)–(7) defined by either (11)–(13) or (14)–(16). Then

$$\begin{aligned} |U^{*}_{k}(x_{i})|&\le C \max \Big \{|U^{*}_{1}(x_{0})|,|U^{*}_{2}(x_{0})|,|U^{*}_{2}(x_{N})|,\sup _{x_{j} \in (0, 2]\cap {\bar{\varOmega }}^{N}}|P^{*N}_{1}\overline{U}^{*}(x_{j})|,\\&\quad \sup _{x_{j}\in \varOmega ^{*}\cap {\bar{\varOmega }}^{N}} |P^{*N}_{2}\overline{U}^{*}(x_{j})|\Big \}, \forall x_{i}\in {\overline{\varOmega }}^{N},\ k=1,2. \end{aligned}$$

5.5 Error estimates

Theorem 8

Let ${\bar{u}}^{*}$ be the solution of the auxiliary problem (6)–(7) and let $\bar{U}^{*}(x_{i})$ be its numerical solution defined by (11)–(13). If $\varepsilon \le C N^{-1},$ then

$|u^{*}_{k}(x_{i})-U^{*}_{k}(x_{i})| \le CN^{-1}\ln N ,$ $x_{i}\in {\bar{\varOmega }}^{N},$ $k=1,2.$

Proof

Refer [Valanarasu and Ramanujam (2007a), Theorem 5.2].

Theorem 9

Let ${\bar{U}}^{*}(x_{i})$ and ${\tilde{\bar{U}}}^{*}(x_{i})$ be two mesh functions defined by (11)–(13) and (14)–(16), respectively. Then $\Vert {\bar{U}}^{*}-{\tilde{\bar{U}}}^{*}\Vert _{{\bar{\varOmega }}^{N}} \le C \hbar ^{4},$ where $\hbar = \max \{h_{i}\}^{N}_{i=1}.$

Proof

Let ${\bar{Z}}(x_{i})= {\bar{U}}^{*}(x_{i})-{\tilde{\bar{U}}}^{*}(x_{i}).$ Then $\Vert {\bar{Z}}(x_{0})\Vert =0,$$\Vert {\bar{Z}}(x_{N})\Vert =0,$

$$\begin{aligned} P_{1}^{*N}{\bar{Z}}(x_{i})&=0,\ x_{i}\in (0, 2]\cap {\bar{\varOmega }}^{N},\\ P_{2}^{*N}{\bar{Z}}(x_{i})&= F^{*}(x_{i})-\tilde{F}^{*}(x_{i})\\&= F^{*}(x_{i})-F^{*}(x_{i})-{\left\{ \begin{array}{ll}0,\ x_{i}\in \varOmega ^{-}\cap {\bar{\varOmega }}^{N},\\ d(x_{i})[u_{02}(x_{i}-1)-U_{02}(x_{i}-1)], \ x_{i}\in \varOmega ^{+}\cap {\bar{\varOmega }}^{N}. \end{array}\right. } \end{aligned}$$

Then by the Theorems 5 and 7, we have the desired result.

Theorem 10

Let ${\tilde{\bar{U}}}^{*}(x_{i})$ be a numerical solution of (6)–(7) defined by (14)–(16). Then $|u^{*}_{k}(x_{i})-{\tilde{U}}^{*}_{k}(x_{i})| \le CN^{-1} \ln N ,$$x_{i}\in {\bar{\varOmega }}^{N},$$k= 1,2.$

Proof

Note that,

$$\begin{aligned} |u_{k}^{*}(x_{i})-{\tilde{U}}_{k}^{*}(x_{i})|&\le |u_{k}^{*}(x_{i})-U_{k}^{*}(x_{i})|+|U_{k}^{*}(x_{i})-{\tilde{U}}_{k}^{*}(x_{i})|,\ x_{i}\in {\bar{\varOmega }}^{N},\ \\&\le C N^{-1}\ln N+C\hbar ^{4}\le C N^{-1}\ln N,\ k=1,2, \end{aligned}$$

where $\hbar = \max \{h_{i}\}^{N}_{i=1}.$

Theorem 11

Let ${\bar{u}}$ be the solution of (2)–(3) and ${\bar{U}}^{*}$ be its numerical solution defined by (11)–(13). If $\varepsilon \le CN^{-1},$ then $|u_{k}(x_{i})-U^{*}_{k}(x_{i})| \le CN^{-1} \ln N ,$$x_{i}\in {\bar{\varOmega }}^{N},$$k= 1,2.$

Proof

Let $x_{i}\in {\bar{\varOmega }}.$ Then,

$$\begin{aligned} |u_{k}(x_{i})-U_{k}^{*}(x_{i})|&=|u_{k}(x_{i})- u_{k}^{*}(x_{i})+u_{k}^{*}(x_{i})-U_{k}^{*}(x_{i})|\\&\le |u_{k}(x_{i})- u_{k}^{*}(x_{i})|+|u_{k}^{*}(x_{i})-U_{k}^{*}(x_{i})|\\&\le C \varepsilon +C N^{-1}\ln N \le C N^{-1} \ln N,\ k=1,2. \end{aligned}$$

Which concludes the proof.

Similar to the above theorem, one can prove the following.

Theorem 12

Let ${\bar{u}}$ be the solution of (2)–(3) and ${\tilde{\bar{U}}}^{*}$ be its numerical solution defined by (14)–(16). If $\varepsilon \le CN^{-1},$ then $|u_{k}(x_{i})-{\tilde{U}}^{*}_{k}(x_{i})| \le CN^{-1} \ln N ,$$x_{i}\in {\bar{\varOmega }}^{N},$$k= 1,2.$

6 Nonlinear problem

Consider the nonlinear BVP

$$\begin{aligned}&-\varepsilon u^{\prime \prime \prime }(x)+a(x)u^{\prime \prime }(x)-F(x,u(x),u^{\prime } (x),{\tilde{u}}^{\prime } (x))=0, \quad x\in \varOmega ,\end{aligned}$$

(17)

$$\begin{aligned}&u(x)=\phi (x),\ u^{\prime } (x)=\phi ^{\prime } (x),\ x\in [-1,0],\ u^{\prime } (2)=\ell \end{aligned}$$

(18)

where ${\tilde{u}}^{\prime } (x)=u^{\prime } (x-1),$ with

$$\begin{aligned} F_{u^{\prime }}(x,u,u^{\prime },{\tilde{u}}^{\prime })\le -\beta \le 0,\ F_{u}(x,u,u^{\prime },{\tilde{u}}^{\prime })\ge -\gamma \ge 0,\ F_{{\tilde{u}}^{\prime }}(x,u,u^{\prime },{\tilde{u}}^{\prime })\ge -\eta \ge 0. \end{aligned}$$

Assume that the reduced problem

$$\begin{aligned}&a(x)u_{0}^{\prime \prime }(x)-F (x, u_{0}(x), u_{0}^{\prime }(x) ,{\tilde{u}}_{0}^{\prime }(x) ) = 0, \end{aligned}$$

(19)

$$\begin{aligned}&u_{0}(x) = \phi (x),\ x\in [-1,0],\ u_{0}^{\prime }(x) = \phi ^{\prime }(x),\ x\in [-1,0],\ \end{aligned}$$

(20)

has a solution. Here, the Newton’s method of Linearization discussed in (Valanarasu 2006; Doolan et al. 1980 is applied to linearize the problem. This method yields the sequence $\{u^{[k+1]}\}_{k=0}^{\infty }$ of successive approximations with a proper choice of initial guess. For each fixed non-negative integer k, ${\bar{u}}^{[k+1]}(x)=(u_{1}^{[k+1]},u_{2}^{[k+1]})$ is the solution of the following linear problem:

$$\begin{aligned} P_{1}^{[k]}{\bar{u}}^{[k+1]}= & {} u_{1}^{\prime [k+1]}(x)-u_{2}^{[k+1]}(x)=0,\ x\in (0,2],\nonumber \\ P_{2}^{[k]}{\bar{u}}^{[k+1]}= & {} -\varepsilon u_{2}^{{\prime \prime }[k+1]}(x)+a(x)u_{2}^{ \prime [k+1]}(x)+b^{k}(x)u_{2}^{[k+1]}(x) \end{aligned}$$

(21)

$$\begin{aligned}&+c^{k}(x)u_{1}^{[k+1]}(x)+d^{k}(x){\tilde{u}}_{2}^{[k+1]}(x)=G^{k}(x),\ x\in \varOmega , \end{aligned}$$

(22)

where

$$\begin{aligned} b^{k}(x)&=-F_{u_{2}}(x,u_{1}^{[k]},u_{2}^{[k]},{\tilde{u}}_{2}^{[k]}),\ c^{k}(x)=-F_{u_{1}}(x,u_{1}^{[k]},u_{2}^{[k]},{\tilde{u}}_{2}^{[k]}),\\ d^{k}(x)&=-F_{{\tilde{u}}_{2}}(x,u_{1}^{[k]},u_{2}^{[k]},{\tilde{u}}_{2}^{[k]}),\\ G^{k}(x)&=F(x,u_{1}^{[k]},u_{2}^{[k]},{\tilde{u}}_{2}^{[k]})-b^{k}(x)u_{2}^{[k]}-c^{k}(x)u_{1}^{[k]}-d^{k}(x){\tilde{u}}_{2}^{[k]}. \end{aligned}$$

For convenience, respectively, we denote $F(x,u_{1}(x),u_{2}(x),{\tilde{u}}_{2}(x)),$$F(x,u^{[k]}_{1}(x),u^{[k]}_{2}(x),{\tilde{u}}^{[k]}_{2}(x)),$$F_{u_{1}}(x,u^{[k]}_{1}(x),u^{[k]}_{2}(x),{\tilde{u}}^{[k]}_{2}(x)),$$F_{u_{2}}(x,u^{[k]}_{1}(x),u^{[k]}_{2}(x),{\tilde{u}}^{[k]}_{2}(x))$ and $F^{k}_{{\tilde{u}}_{2}}(x,u^{[k]}_{1}(x),u^{[k]}_{2}(x),{\tilde{u}}^{[k]}_{2}(x))$ by F,  $F^{k},$$F^{k}_{u_{1}},$$F^{k}_{u_{2}}$ and $F^{k}_{{\tilde{u}}_{2}}.$ To prove the convergence of the successive iteration, the following theorem is established.

Theorem 13

Suppose $\mid F_{u_{1}u_{1}}\mid ,$$\mid F_{u_{2}u_{2}}\mid ,$$\mid F_{u_{1}u_{2}}\mid ,$$\mid F_{u_{2}{\tilde{u}}_{2}}\mid ,$$\mid F_{{\tilde{u}}_{2}{u}_{1}}\mid$ and $\mid F_{{\tilde{u}}_{2}{\tilde{u}}_{2}}\mid$ are bounded above by $M<1.$ Let $\{{\bar{u}}^{[k]}\}_{0}^{\infty }$ be the Newton sequence defined by (21)–(22). Then, for all $x \in {\bar{\varOmega }},$ we have

$$\begin{aligned} \parallel {\bar{u}}^{[k+1]}-{\bar{u}}\parallel \le M \parallel {\bar{u}}^{[k]}-{\bar{u}}\parallel ^{2} \end{aligned}$$

Proof

It is easy to see that

$$\begin{aligned} P^{k}_{1} ({\bar{u}}^{[k+1]}-{\bar{u}})&=0 \end{aligned}$$

and

$$\begin{aligned}&P^{k}_{2}({\bar{u}}^{[k+1]}-{\bar{u}})=F^{k}-u^{[k]}_{1}F^{k}_{u_{1}}-u^{[k]}_{2}F^{k}_{u_{2}}-{\tilde{u}}^{[k]}_{2}F^{k}_{{\tilde{u}}_{2}}-(F-u_{1}F^{k}_{u_{1}}-u_{2}F^{k}_{u_{2}}-{{\tilde{u}}}_{2}F^{k}_{{\tilde{u}}_{2}})\\&\quad =F^{k}-F+(u_{1}-u^{[k]}_{1})F^{k}_{u_{1}}+(u_{2}-u^{[k]}_{2})F^{k}_{u_{2}}+({\tilde{u}}_{2}-{\tilde{u}}^{[k]}_{2}){F}^{k}_{{\tilde{u}}_{2}}\\&\quad =F^{k}-\Big \{(F^{k}+(u_{1}-u^{[k]}_{1})F^{k}_{u_{1}}+(u_{2}-u^{[k]}_{2})F^{k}_{u_{2}}+({\tilde{u}}_{2}-{\tilde{u}}^{[k]}_{2}){F}^{k}_{{\tilde{u}}_{2}})\\&\qquad + \, \frac{1}{2}\Big [((u_{1}-u^{[k]}_{1})^{2}F_{u_{1}u_{1}}({\bar{\theta }})+(u_{2}-u^{[k]}_{2})^{2}F_{u_{2}u_{2}}({\bar{\theta }})+({\tilde{u}}_{2}-{\tilde{u}}^{[k]}_{2})^{2}F_{{\tilde{u}}_{2}{\tilde{u}}_{2}}({\bar{\theta }}))\\&\qquad + \, 2(u_{1}-u^{[k]}_{1})(u_{2}-u^{[k]}_{2})F_{u_{1}u_{2}}({\bar{\theta }})+2(u_{2}-u^{[k]}_{2})({\tilde{u}}_{2}-{\tilde{u}}^{[k]}_{2})F_{{u}_{2}{\tilde{u}}_{2}}({\bar{\theta }})\\&\qquad +2({\tilde{u}}_{2}-{\tilde{u}}^{[k]}_{2})(u_{1}-u^{[k]}_{1})F_{{\tilde{u}}_{2}{u}_{1}}({\bar{\theta }})\Big ]\Big \}\\&\qquad + \, (u_{1}-u^{[k]}_{1})F^{k}_{u_{1}}+(u_{2}-u^{[k]}_{2})F^{k}_{u_{2}}+({\tilde{u}}_{2}-{\tilde{u}}^{[k]}_{2}){F}^{k}_{{\tilde{u}}_{2}} \end{aligned}$$

where ${\bar{\theta }}=(x,\theta , \theta ^{\prime }, \tilde{\theta }^{\prime })$ is such that $(x, u_{1}, u_{2}, {\tilde{u}}_{2})>{\bar{\theta }}>(x, u^{[k]}_{1}, u^{[k]}_{2}, {\tilde{u}}^{[k]}_{2})$.

$$\begin{aligned}&P^{k}_{2}({\bar{u}}^{[k+1]}-{\bar{u}})=-\frac{1}{2}\Big \{(u_{1}-u^{[k]}_{1})^{2}F_{u_{1}u_{1}}({\bar{\theta }})+(u_{2}-u^{[k]}_{2})^{2}F_{u_{2}u_{2}}({\bar{\theta }})+({\tilde{u}}_{2}-{\tilde{u}}^{[k]}_{2})^{2}F_{{\tilde{u}}_{2}{\tilde{u}}_{2}}({\bar{\theta }})\\&\quad +2(u_{1}-u^{[k]}_{1})(u_{2}-u^{[k]}_{2})F_{u_{1}u_{2}}({\bar{\theta }})\\&\quad +2(u_{2}-u^{[k]}_{2})({\tilde{u}}_{2}-{\tilde{u}}^{[k]}_{2})F_{{u}_{2}{\tilde{u}}_{2}}({\bar{\theta }})+2({\tilde{u}}_{2}-{\tilde{u}}^{[k]}_{2})(u_{1}-u^{[k]}_{1})F_{{\tilde{u}}_{2}{u}_{1}}({\bar{\theta }}) \Big \}. \end{aligned}$$

Then, we have

$$\begin{aligned}&\mid P^{k}_{2}({\bar{u}}^{[k+1]}-{\bar{u}})\mid \le M \Big \{ \mid u^{[k]}_{1}-u_{1}\mid ^{2}+\mid u^{[k]}_{2}-u_{2}\mid ^{2}+\mid {\tilde{u}}^{[k]}_{2}-{\tilde{u}}_{2}\mid ^{2}\\&\qquad +\mid u^{[k]}_{1}-u_{1}\mid \mid u^{[k]}_{2}-u_{2}\mid +\mid u^{[k]}_{2}-u_{2}\mid \mid {\tilde{u}}^{[k]}_{2}-{\tilde{u}}_{2}\mid \\&\qquad +\mid {\tilde{u}}^{[k]}_{2}-{\tilde{u}}_{2}\mid \mid u^{[k]}_{1}-u_{1}\mid \Big \}\\&\quad \le M \parallel {\bar{u}}^{[k]}-{\bar{u}} \parallel ^{2}. \end{aligned}$$

Then by the Corollary 1, we have the desired result.

To observe the asymptotic behavior of the solution of the linearized singularly perturbed third-order delay differential equations, we consider the following constant coefficient problem:

$$\begin{aligned}&-\varepsilon u^{\prime \prime \prime }(x)+4u^{\prime \prime }(x)-u^{\prime }(x-1)=0,\ x\in \varOmega , \end{aligned}$$

(23)

$$\begin{aligned}&u(x)=x,\ x\in [-1,0],\ u^{\prime }(x)=1,\ x\in [-1,0],\ u^{\prime }(2)=2. \end{aligned}$$

(24)

The reduced problem solution of the above problem (23)–(24) is

$$\begin{aligned} u_{0}(x)&= x+\frac{x^{2}}{8}, \ x\in [0,1], \end{aligned}$$

(25)

$$\begin{aligned} u_{0}(x)&=x+\frac{x^{2}}{8}+\frac{(x-1)^{3}}{96},\ x\in [1,2]. \end{aligned}$$

(26)

Furthermore, the solution of the problem (23)–(24) is

$$\begin{aligned} u(x)= & {} \left[ 1-\frac{4C^{*}}{\varepsilon }\right] x+C^{*}\left[ \exp \left( \frac{4x}{\varepsilon }\right) -1\right] +\frac{x^{2}}{8},\ x \in [0, 1],\\ u(x)= & {} D\left[ x-\frac{\varepsilon }{4}\exp \left( \frac{-4}{\varepsilon }(2-x)\right) \right] +E+\varepsilon \exp \left( \frac{-4}{\varepsilon }(2-x)\right) \left[ \frac{47}{128}-\frac{\varepsilon }{128}\right] \\&+ \, \frac{L_{1}}{2}\left[ \varepsilon \exp \left( \frac{-4}{\varepsilon }\right) +\varepsilon +\frac{\varepsilon ^{2}}{8}-x^{2}\exp \left( \frac{-4}{\varepsilon }\right) -\frac{x \varepsilon }{2}\exp \left( \frac{-4}{\varepsilon }(2-x)\right) \right] \\&+ \, \frac{x^{2}}{8}+\frac{\varepsilon x^{2}}{128}+\frac{(x-1)^{3}}{96},\ x\in [1,2] \end{aligned}$$

where $C^{*}= \varepsilon \exp \left( \frac{-4}{\varepsilon }\right) L_{1}$

$$\begin{aligned}&L_{1}=\frac{\frac{3\varepsilon }{256}\exp \left( \frac{-4}{\varepsilon }\right) -\frac{15}{128} \exp \left( \frac{-4}{\varepsilon }\right) +\frac{\varepsilon ^{2}}{1024}\exp \left( \frac{-4}{\varepsilon }\right) +\frac{\varepsilon ^{3}}{1024}}{\frac{5}{4}\exp \left( \frac{-8}{\varepsilon } \right) -1+\frac{1}{4}\exp \left( \frac{-4}{\varepsilon } \right) -\frac{\varepsilon }{8}\exp \left( \frac{-4}{\varepsilon } \right) +\frac{\varepsilon }{8}\exp \left( \frac{-8}{\varepsilon }\right) }\\ D&\quad =\frac{1+\frac{\varepsilon }{64}+\frac{\varepsilon ^{2}}{256}+\frac{-4}{\varepsilon }\left[ -1+\frac{31\varepsilon }{64}-\frac{\varepsilon ^{2}}{128}\right] -\exp \left( \frac{-8}{\varepsilon }\right) \left[ \frac{205}{128}+\frac{43}{256}\varepsilon +\frac{\varepsilon ^{2}}{512}\right] }{1+\exp \left( \frac{-4}{\varepsilon }\right) \left[ \frac{\varepsilon }{8}-\frac{1}{4}\right] -\exp \left( \frac{-8}{\varepsilon }\right) \left[ \frac{\varepsilon }{8}+\frac{5}{4}\right] }\\ E&\quad =\left[ 1-\frac{49}{128}\varepsilon \exp \left( \frac{-4}{\varepsilon }\right) -\frac{\varepsilon ^{2}}{128}\exp \left( \frac{-4}{\varepsilon }\right) \right] -L_{1}\left[ \frac{\varepsilon }{2}\exp \left( \frac{-8}{\varepsilon }\right) +\frac{5}{4}\varepsilon \exp \left( \frac{-4}{\varepsilon }\right) \right. \\&\qquad \left. -\varepsilon +\frac{\varepsilon ^{2}}{16}\exp \left( \frac{-4}{\varepsilon }\right) \right] -\frac{7}{2}\exp \left( \frac{-4}{\varepsilon }\right) L_{1}- D\left[ 1-\frac{\varepsilon }{4}\exp \left( \frac{-4}{\varepsilon }\right) \right] . \end{aligned}$$

It is observed that,

$$\begin{aligned} u(x)&\sim u_{0}(x)+O(\varepsilon )\exp \left( \frac{-4(1-x)}{\varepsilon }\right) +O(\varepsilon ),\ x\in [0,1] \ \text {and}\\ u(x)&\sim u_{0}(x)+O(\varepsilon )\exp \left( \frac{-4(2-x)}{\varepsilon }\right) +O(\varepsilon ),\ x\in [1,2]. \end{aligned}$$

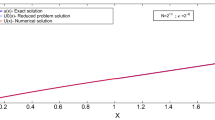
In the above model problem (23)–(24), we considered third-order convection diffusion problem with constant coefficients and the solution exhibits interior layer at $x=1$ and boundary layer at $x=2.$ Figure 1 presents the exact solution and reduced problem solution to (23)–(24) for fixed $\varepsilon =2^{-5}$ and $N=2^{7}$.

Fig. 1

The exact solution and reduced problem solution of the problem (23)–(24)

From the above observation, one can see that the reduced problem solution is a reasonable good approximate solution to the original problem when $\varepsilon$ is small. Therefore, choose the initial guess as the reduced problem solution, that is, ${\bar{u}}^{[0]}=(u_{1}^{[0]},u_{2}^{[0]})$ and $u_{1}^{[0]}=u_{0},$$u_{2}^{[0]}=u_{0}^{\prime }.$

From the Theorem 2, we have $|u_{k}(x)-u_{0k}(x)|\le C \varepsilon ,\ x \in [0, 1],\ k=1, 2.$ Therefore, the above problem (21)-(22) has the following auxiliary problem.

$$\begin{aligned} P_{1}^{*[k]}{\bar{u}}^{*[k+1]}= & {} u_{1}^{*[k+1]^{\prime }}(x)-u_{2}^{*[k+1]}(x)=0, x\in (0, 2]\nonumber \\ P_{2}^{*[k]}{\bar{u}}^{*[k+1]}= & {} -\varepsilon u_{2}^{*[k+1]^{\prime \prime }}(x)+a(x)u_{2}^{*[k+1]^{\prime }}(x)+b^{k}(x)u_{2}^{*[k+1]}(x) \end{aligned}$$

(27)

$$\begin{aligned}&+ \, c^{k}(x)u_{1}^{*[k+1]}(x)=G^{*k}(x),\ x\in \varOmega , \end{aligned}$$

(28)

where

$$\begin{aligned} b^{k}(x)&=-F_{u_{2}}(x,u_{1}^{*[k]},u_{2}^{*[k]},{\tilde{u}}_{2}^{*[k]}),\ c^{k}(x)=-F_{u_{1}}(x,u_{1}^{*[k]},u_{2}^{*[k]},{\tilde{u}}_{2}^{*[k]}),\\ d^{k}(x)&=-F_{{\tilde{u}}_{2}}(x,u_{1}^{*[k]},u_{2}^{*[k]},{\tilde{u}}_{2}^{*[k]}),\\ G^{*k}(x)&=F(x,u_{1}^{*[k]},u_{2}^{*[k]},{\tilde{u}}_{2}^{*[k]}) -b^{k}(x)u_{2}^{*[k]}-c^{k}(x)u_{1}^{*[k]} -d^{k}(x)[{\tilde{u}}_{02}^{*[k]}-{\tilde{u}}_{02}^{*[k+1]}]. \end{aligned}$$

Table 1 Numerical results for the Example 1

7 Numerical illustrations

In this section, we present three examples to illustrate the numerical methods presented in this paper and also to estimate the error and the experiment rate of convergence of the computed solution, we use the double mesh principle for the following test problems. For this, we put $D_{\varepsilon }^{M}=\max _{0\le i\le M} \mid U_{i}^{M}-U_{2i}^{2M}\mid ,$ where $U_{i}^{M}$ and ${U_{2i}^{2M}}$ are the $i^{th}$ components of the numerical solutions on meshes of M and 2M points, respectively. We compute the uniform error and rate of convergence as $D^{M}=\max _{\varepsilon } D_{\varepsilon }^{M}\ \text {and}\quad p^{M}=\log _{2}\Big (\frac{D^{M}}{D^{2M}} \Big ).$ For the following examples the numerical results are presented for the values of perturbation parameter $\varepsilon \in \{2^{-4},\ 2^{-5},\ \ldots ,\ 2^{-23}\}$.

Example 1

Consider the BVP

$$\begin{aligned} {\left\{ \begin{array}{ll} -\varepsilon u^{\prime \prime \prime }(x)+a(x)u^{\prime \prime }(x)+b(x)u^{\prime }(x)+c(x)u(x)+d(x)u^{\prime }(x-1)=f(x),\ x\in \varOmega ,\\ u(x)=\phi (x), x\in [-1,0], u^{\prime }(2)=\ell , \phi (x)\in C^{1}([-1,0]), \end{array}\right. } \end{aligned}$$

where $a(x)=16,$$b(x)=0,$$c(x)=-1,$$d(x)=-1,$$f_{1}=0,$$f_{2}=0;$$\phi _{1}=1+x,$$\phi _{2}= 1$. Table 1 presents the values of $D_{k}^{M}$ and $p_{k}^{M},\ k=1,2$ corresponding to the solution components $U_{1},$$U_{2}$.

Table 2 For fixed $N=32$ and $\varepsilon =2^{-6}$, the iterations of $u_{1}$ of the Example 2

Table 3 For fixed $N=32$ and $\varepsilon =2^{-6}$, the iterations of $u_{2}$ of the Example 2

Fig. 2

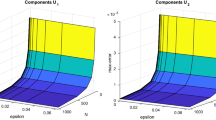
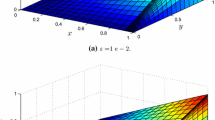
Iterative solutions of $u_{1}$ of the Example 2

Fig. 3

Iterative solutions of $u_{2}$ of the Example 2

Example 2

$$\begin{aligned} {\left\{ \begin{array}{ll} -\varepsilon u^{\prime \prime \prime }(x)+2u^{\prime \prime }(x)=[u^{\prime }(x-1)]^2,\ x\in \varOmega ,\\ u(x)=1,\ x\in [-1,0],\ u^{\prime }(x)=0,\ x\in [-1,0],\ u^{\prime }(2)=0. \end{array}\right. } \end{aligned}$$

Tables 2 and 3 present the iterative numerical solutions (Figs. 2, 3) for $u_{1}$ and $u_{2}$ for the fixed value of $N=32$ and $\varepsilon =2^{-6}$ and the Table 4 presents the values of $D_{k}^{M}$ and $p_{k}^{M},\ k=1,2$ corresponding to the solution components $U_{1},$$U_{2}$.

8 Concluding remarks

Third-order singularly perturbed delay differential equations of convection diffusion type are considered in this article. It is estimated that, $|u_{k}(x)-u_{0k}(x)|\le C \varepsilon ,\ x\in [0,1].$ Using this result, we obtained the auxiliary problem for the given problem. A fitted finite difference method is applied for the auxiliary problem. Furthermore, it is proved that, the present method is of almost first order convergence. In Subburayan and Mahendran (2018), the authors have applied fitted finite difference scheme with piecewise linear interpolation for the given differential equation, whereas in this article, the interpolation function is applied to calculate the reduced problem solution. The present method can be easily extended to nonlinear problems. Numerical examples are given to illustrate the theoretical results see Tables 1, 2, 3 and 4.

Table 4 Numerical results for the Example 2