Parameter-uniform numerical method for singularly perturbed 2D delay parabolic convection–diffusion problems on Shishkin mesh

Abstract

In this article, we study the numerical solution of a singularly perturbed 2D delay parabolic convection–diffusion problem. First, we discretize the domain with a uniform mesh in the temporal direction and a special mesh in the spatial directions. The numerical scheme used to discretize the continuous problem, consists of the implicit-Euler scheme for the time derivative and the classical upwind scheme for the spatial derivatives. Stability analysis is carried out, and parameter-uniform error estimates are derived. The proposed scheme is of almost first-order (up to a logarithmic factor) in space and first-order in time. Numerical examples are carried out to verify the theoretical results.

1 Introduction

The boundary layer phenomena has considerable importance in the area of fluid flow problems. From mathematical perspective, such kind of problem is called the singular perturbation problem (SPP) and the solution of such problem exhibits boundary layers due to the small parameter $\varepsilon$ multiplied with the diffusion term. The Navier-Stokes equation with a high Reynolds number is one of the most striking examples of SPPs.

In this article, we are focused on the delay differential equation (DDE) which is singularly perturbed in nature. DDE plays a crucial role in the area of biosciences and engineering. For instance, prey-predator model, ecological system, chemostat model and control theory. To understand the application of singularly perturbed delay parabolic differential equation (SPDPDE) in a better way, one can see the example given in [14], which models a furnace used to process metal sheet. In that model, the delay occurs due to the finite speed of the controller. The so-called Britton model [2] in population dynamics is another example of delay problem, which is given by

$$\begin{aligned} u_t=\varepsilon \varDelta u +u(1-g*u) \end{aligned}$$

with

$$\begin{aligned} g*u=\int _{t-\tau }^t \int _\varOmega g(x-y,t-s) u(y,s) dyds. \end{aligned}$$

Here, u(x, t) is a population density, which evolves through random migration (modeled by the diffusion term) and reproduction (modeled by the nonlinear reaction term). The latter part contains a convolution operator with a kernel g(x, t), which models the distributed age-structure dependence of the evolution and its dependence on the population levels in the neighborhood.

Various techniques are available in the literature for solving SPDPDEs. Some researchers ignore the ‘delay’ effect, but in [8], Kuang emphasized about the importance of the delay term. The use of Taylor series approximation for the delay term is also not an effective way, because the solution of the approximated singularly perturbed partial differential equation (SPPDE) may behave quite differently from the original solution.

In the past few decades, several numerical treatments were proposed for SPPDEs. For instance, one can see [10, 11], where the theory and numerical method for 2D singularly perturbed elliptic problems have been analyzed. In [11], the authors considered a convection–diffusion type problem, where they have given an asymptotic analysis. Same type of problem has been considered in [10], but their the authors used a hybrid finite difference scheme to solve such problem. Time dependent problems have also been analyzed in many papers (see [3, 4], for instance, and references therein). In [4], the authors considered a convection–diffusion problem and they solved their model problem by a fractional step method, whereas in [3], the authors used the classical implicit method to solve their model problem.

However, the theory and the numerical solution of a SPDPDEs are still in initial stage. To obtain the uniformly convergent numerical solution for the SPDPDEs of reaction-diffusion type, the classical finite difference schemes are applied on the Shishkin mesh by Ansari et al. [1] and on layer-adapted equidistribution mesh by Gowrisankar and Natesan [6]. To obtain the numerical solution of SPDPDEs of convection–diffusion type, Gowrisankar and Natesan [7] applied the classical upwind finite difference scheme on the Shishkin mesh, and in [5], the authors devised a hybrid scheme to increase the order of convergence. These existing literatures (involving delay term) are mainly focused on 1D case.

In this paper, we consider the following singularly perturbed 2D delay parabolic convection–diffusion initial-boundary-value problem (IBVP) with Dirichlet boundary conditions on the boundaries. Let $\mathfrak {G}=\mathfrak {D}\times \varLambda _t$, $\mathfrak {D}=(0,1)^2$, $\varLambda _t=(0,T]$ and $\varUpsilon =\partial \mathfrak {D} \cup \varUpsilon _b$, where $\varUpsilon _b=\overline{\mathfrak {D}}\times [-\tau ,0]$.

$$\begin{aligned} \left\{ \begin{array}{ll} u_t + \mathcal {L}_\varepsilon u(x,y,t)=-c(x,y)u(x,y,t-\tau ) + f(x,y,t),&{}\quad (x,y,t) \in \mathfrak {G},\\ u(x,y,t)=\varphi _b(x,y,t),&{}\quad (x,y,t)\in \varUpsilon _b,\\ u(x,y,t)= 0,&{}\quad (x,y,t)\in \partial \mathfrak {D}\times \overline{\varLambda }_t, \end{array}\right. \end{aligned}$$

(1)

where

$$\begin{aligned} \mathcal {L}_\varepsilon u=-\varepsilon \varDelta u + \mathbf {a}(x,y).\nabla u + b(x,y)u, \end{aligned}$$

$0<\varepsilon \ll 1$ is the singular perturbation parameter and $\tau >0$ is the delay parameter. We assume that the coefficients $\mathbf {a}=(a_1,a_2),\,b\,\text{ and }\,c$ are sufficiently smooth and bounded functions along with the conditions $a_1(x,y)\ge \alpha _x>0,\,a_2(x,y)\ge \alpha _y>0,\,b(x,y)\ge 0$ and c(x, y) is nonzero on $\mathfrak {\overline{D}}$.

The delay parabolic IBVP (1) admits a unique solution u(x, y, t), under sufficient smoothness and necessary compatibility conditions (given in Sect. 2), imposed on the functions $f\,\text{ and }\,\varphi _b$. The solution u(x, y, t) exhibits a regular boundary layer of width $O(\varepsilon )$ along the sides $x=1$ and $y=1$, and a corner layer at $(x,y)=(1,1)$ [12].

The main aim of this article is to devise an $\varepsilon$-uniform numerical scheme to solve the delay parabolic PDE (1). Because of the presence of boundary layers in the spatial directions, we discretize the spatial domain by the piecewise-uniform Shishkin mesh and the temporal domain by the uniform mesh. Then, to obtain the discrete problem, we apply the implicit-Euler scheme for the time derivative and the classical upwind scheme for the spatial derivatives. Numerical stability of the proposed scheme is studied. The proposed method is of almost first-order accurate in spatial variables and first-order accurate in temporal variable. Numerical experiments are carried out to show the accuracy and efficiency of the proposed method.

The rest of the paper is structured as follows: In Sect. 2, a-priori bounds on the derivatives of the analytical solution of Eq. (1) via decomposition have been discussed. Section 3 describes the piecewise-uniform Shishkin mesh and the upwind scheme. The main result of $\varepsilon$-uniform convergence has been given in Sect. 4. In Sect. 5, extensive numerical experiments are carried out to verify the theoretical result and to demonstrate the accuracy of the method. Finally, the paper ends with Sect. 6, that summarizes the main conclusions.

C has been used as a generic positive constant which is independent of $\varepsilon$, the mesh points and the mesh sizes throughout the paper. Standard supremum norm has been denoted by $\left\| \cdot \right\| _{\infty }$ and is defined by

$$\begin{aligned} \left\| g\right\| _{\infty }=\sup _{(x,y,t)\in \mathfrak {G}}\left| g(x,y,t)\right| , \end{aligned}$$

for a function g defined on some domain $\mathfrak {G}$.

2 Bounds on the solution decomposition

The analytical aspects of the solution of Eq. (1) is discussed in this section. These properties will be required for the proof of $\varepsilon$-uniform error estimate. In order to analyze the solution of Eq. (1), we need the definition stated below.

Definition 1

Let $\mu \in (0,1)$. A function $\chi : \mathfrak {G}\rightarrow \mathbb {R}$ is said to be uniformly Hölder continuous with exponent $\mu$ in $\mathfrak {G}$, if the quantity

$$\begin{aligned} {[\chi ]_{\mu , \mathfrak {G}}=\displaystyle {\sup _{(x,y,t),\,(x',y',t')\in \mathfrak {G}}}\dfrac{\left| \chi (x,y,t)-\chi (x',y',t')\right| }{\left[ \text{ dist }((x,y,t),\,(x',y',t'))\right] ^{\mu }}}, \end{aligned}$$

is finite, where $\text{ dist }((x,y,t),\,(x',y',t'))=\left( (x-x')^2+(y-y')^2+|t-t'|\right) ^{1/2}$.

The space consisting of Hölder continuous functions is called Hölder continuous space, and it is denoted by .

For the existence and uniqueness of the solution of Eq. (1), we assume that the data are Hölder continuous and also satisfy the compatibility conditions [9] at the corner points

$$\begin{aligned} f(0,0,t)=f(0,1,t)=f(1,0,t)=f(1,1,t)=0,\quad t\in \overline{\varLambda }_t, \end{aligned}$$

and at the initial time level:

$$\begin{aligned} \begin{array}{ll} \varphi _b(x,y,0)=0,&{}\quad \text{ in }\quad \partial \mathfrak {D},\\ \mathcal {L}_\varepsilon \varphi _b(x,y,0)=-c(x,y)\varphi _b(x,y,-\tau )+f(x,y,0),&{}\quad \text{ in }\quad \partial \mathfrak {D}. \end{array} \end{aligned}$$

In order to have , we assume that data of the problem are sufficiently smooth and satisfy stronger compatibility conditions. The additional sufficient higher-order compatibility conditions for Eq. (1) can be obtained by differentiating Eq. (1) with respect to t, i.e., we get

$$\begin{aligned} \dfrac{\partial ^2 u}{\partial t^2}-\mathcal {L}_\varepsilon (\mathcal {L}_\varepsilon u)=\dfrac{\partial F}{\partial t}-\mathcal {L}_\varepsilon F, \end{aligned}$$

where $F=f-cu(x,y,t-\tau )$. Now, by employing the boundary condition given in Eq. (1), we obtain the second-order compatibility condition

$$\begin{aligned} \mathcal {L}_\varepsilon \left( \mathcal {L}_\varepsilon \varphi _b(x,y,0)\right) =\mathcal {L}_\varepsilon F(x,y,0)-\dfrac{\partial F}{\partial t}(x,y,0),\quad \text{ in }\quad \partial \mathfrak {D}. \end{aligned}$$

For the convergence analysis, we decompose the solution of problem Eq. (1) as $u=G+E$, where G and E are the smooth and singular components, respectively, which are defined as solutions of the following problems, i.e., E is the solution of

$$\begin{aligned} \left\{ \begin{array}{ll} E_t + \mathcal {L}_\varepsilon E(x,y,t)=-c(x,y)E(x,y,t-\tau ),&{}\quad (x,y,t) \in \mathfrak {G},\\ E(x,y,t)=0,&{}\quad (x,y,t)\in \varUpsilon _b,\\ E(x,y,t)= -G(x,y,t),&{}\quad (x,y,t)\in \partial \mathfrak {D}\times \overline{\varLambda }_t, \end{array}\right. \end{aligned}$$

and G is the restriction of $G^{*}$ to $\mathfrak {G}$, where $G^{*}$ is the solution of

$c^{*},\,f^{*}$ are smooth extensions of $c,\,f$ to $\mathfrak {G}^{*}$, the domain $\mathfrak {D}^{*}$ is a smooth extension of $\mathfrak {D}$, $\varphi _b^{*}$ is smooth extension of $\varphi _b$ to $\varUpsilon _b^{*}$, $\varphi ^{*}$ is a smooth and compatible function and $\mathcal {L}^{*}_\varepsilon$ corresponds to the current extensions of the data.

Since, we have assumed $a_1(x,y)\ge \alpha _x>0,\,a_2(x,y)\ge \alpha _y>0$, the singular component E can be decomposed into the sum $E=E_1+E_2+E_{12}$, where, $E_1$ and $E_2$ are the singular components associated with the sides $x=1$ and $y=1$, respectively, and $E_{12}$ is a corner layer function associated with the corner (1, 1).

We assume that $E_1$ (similarly $E_2$) is the restriction of $E_1^{**}$ to $\mathfrak {G}$, where $E_1^{**}$ is the solution of

The domain $\mathfrak {D}^{**}$ is the smooth extension of $\mathfrak {D}$ near the vertex (1, 1). Toward the boundary side $x=1$, $\partial \mathfrak {D}_1^{**}$ is an extension beyond the vertex (1, 1) and $\partial \mathfrak {D}_2^{**}=\partial \mathfrak {D}^{**} \backslash \partial \mathfrak {D}_1^{**}$. $G^{**}$ is a smooth and compatible extension of G to $\partial \mathfrak {D}_1^{**}$.

Finally, $E_{12}$ is defined as the solution of the problem

$$\begin{aligned} \left\{ \begin{array}{ll} (E_{12})_t + \mathcal {L}_\varepsilon E_{12}(x,y,t)=-c(x,y)E_{12}(x,y,t-\tau ),&{}\quad (x,y,t) \in \mathfrak {G},\\ E_{12}(x,y,t)=0,&{} \quad (x,y,t)\in \varUpsilon _b,\\ E_{12}(x,y,t)= -(G+E_1+E_2),&{}\quad (x,y,t)\in \partial \mathfrak {D}\times \overline{\varLambda }_t. \end{array}\right. \end{aligned}$$

The following theorem gives the bounds on $G,\,E_1,\,E_2\,\text{ and }\,E_{12}$, and its partial derivatives which play a vital role in the error analysis in Sect. 4. Before stating the theorem, with out loss of generality, we assume that $\varphi _b(x,y,t) = 0,\,\, (x,y,t)\in \varUpsilon _b$.

Theorem 1

For all non-negative integers $k_1,\,k_2,\,k_t$ satisfying $k_s+2k_t\le 4$, $k_s=k_1+k_2,\,$ the components of u satisfy the following bounds for all $(x,y,t)\in \mathfrak {G}$.

$$\begin{aligned} \begin{array}{l} \left| \dfrac{\partial ^{k_s+k_t}G}{\partial x^{k_1}\partial y^{k_2} \partial t^{k_t}}\right| \le C,\\ \left| \dfrac{\partial ^{k_s+k_t}E_1}{\partial x^{k_1}\partial y^{k_2} \partial t^{k_t}}\right| \le C \varepsilon ^{-k_1}\exp (-\alpha _x(1-x)/\varepsilon ),\\ \left| \dfrac{\partial ^{k_s+k_t}E_2}{\partial x^{k_1}\partial y^{k_2} \partial t^{k_t}}\right| \le C \varepsilon ^{-k_2}\exp (-\alpha _y(1-y)/\varepsilon ),\\ \left| \dfrac{\partial ^{k_s+k_t}E_{12}}{\partial x^{k_1}\partial y^{k_2} \partial t^{k_t}}\right| \le C \varepsilon ^{-k_s}\min \left\{ \exp (-\alpha _x(1-x)/\varepsilon ),\exp \left( -\alpha _y(1-y)/\varepsilon \right) \right\} . \end{array} \end{aligned}$$

Proof

In the first time level, i.e., when $t\in (0,\tau ]$, the DPDE (1) can be written as

$$\begin{aligned} \left\{ \begin{array}{ll} u_t + \mathcal {L}_\varepsilon u(x,y,t)=-c(x,y)u(x,y,t-\tau ) + f(x,y,t),&{}\quad (x,y,t) \in \mathfrak {D}\times (0,\tau ),\\ u(x,y,t)=0,&{}\quad (x,y,t)\in \varUpsilon _b,\\ u(x,y,t)= 0,&{}\quad (x,y,t)\in \partial \mathfrak {D}\times [0,\tau ]. \end{array}\right. \end{aligned}$$

(2)

Now, by using the initial condition, the above equation can be reduced to

$$\begin{aligned} u_t + \mathcal {L}_\varepsilon u(x,y,t)=f(x,y,t),\quad (x,y,t) \in \mathfrak {D}\times (0,\tau ). \end{aligned}$$

(3)

Following the result given in [3], we decompose the solution of Eq. (3) as $u=G+E_1+E_2+E_{12}$, which will satisfy the required bounds, when $(x,y,t)\in \mathfrak {D}\times (0,\tau )$.$\square$

Then, we proceed to the next time level, i.e., $t\in (\tau ,2\tau ]$. In that case, Eq. (1) can be written as

$$\begin{aligned} \left\{ \begin{array}{ll} u_t + \mathcal {L}_\varepsilon u(x,y,t)=-c(x,y)u(x,y,t-\tau ) + f(x,y,t),&{} \quad (x,y,t) \in \mathfrak {D}\times (\tau ,2\tau ),\\ u(x,y,t)={u_\tau }(x,y,t),&{} \quad (x,y,t)\in \mathfrak {D}\times [0,\tau ],\\ u(x,y,t)= 0,&{}\quad (x,y,t)\in \partial \mathfrak {D}\times [\tau ,2\tau ], \end{array}\right. \end{aligned}$$

(4)

where $u_\tau$ is the solution of Eq. (2).

One can verify that, the above equation satisfies the required compatibility conditions and the right hand side term of Eq. (4) has sufficient smoothness. Therefore, by using the result given in [4, Appendix A] and [13], we can obtain the required bounds for $G,\,E_1,\,E_2\, \text{ and }\,E_{12}$, when $t\in [\tau ,2\tau ]$.

By proceeding in an analogous way, one can obtain the required bounds for $t\ge 2\tau$.

$\square$

3 Domain discretization

We consider the rectangular mesh $\overline{\mathfrak {D}}^N$ which is defined to be tensor product of the 1D Shishkin meshes, i.e., $\overline{\mathfrak {D}}^N=\overline{\varOmega }_x^N\times \overline{\varOmega }_y^N$. As the layers are along the sides $x=1$ and $y=1$, we define the mesh on $\overline{\varOmega }_x^N$ by dividing the domain [0, 1] into two sub-domains $[0,1-\rho _x]$ and $(1-\rho _x,1]$ and each sub-domain will have N / 2 uniform mesh-intervals, i.e., $\overline{\varOmega }_x^N=\{0=x_0,x_1,\ldots ,x_{N/2}=1-\rho _x,\ldots ,x_N=1\}$. Similarly, we define $\overline{\varOmega }_y^N=\{0=y_0,y_1,\ldots ,y_{N/2}=1-\rho _y,\ldots ,y_N=1\}$. The transition points $1-\rho _l,\,l=x,\,y$, which separate the coarse and fine portions of the mesh, are obtained by taking

$$\begin{aligned} \rho _l = \min \left\{ \dfrac{1}{2},\rho _{l,0}\varepsilon \ln N\right\} ,\quad l=x,\,y, \end{aligned}$$

where $\rho _{l,0}\ge 1/{\alpha _l}$. In the analysis, we shall assume that $\rho _l=\rho _{l,0}\varepsilon \ln N$. Note that if $\rho _l=1/2$, then mesh is uniform and in such cases the method can be analyzed in the classical way.

We denote the mesh-sizes in both the spatial directions by

$$\begin{aligned}&h_{x,i}=x_i-x_{i-1},\quad i=1,\ldots ,N, \quad \widehat{h}_{x,i}=h_{x,i}+h_{x,i+1},\quad i=1,\ldots ,N-1,\\&h_{y,j}=y_j-y_{j-1},\quad j=1,\ldots ,N,\quad \widehat{h}_{y,j}=h_{y,j}+h_{y,j+1},\quad j=1,\ldots ,N-1, \end{aligned}$$

and let $H_l=2(1-\rho _l)/N$ and $h_l=2\rho _l/N$, $l=x,\,y,$ be the mesh-sizes in $[0,1-\rho _l]$ and $[1-\rho _l,1]$ respectively. Then it is easy to see that

$$\begin{aligned} N^{-1}\le H_l\le 2N^{-1},\quad h_l=2\rho _{l,0}\varepsilon N^{-1}\ln N,\quad l=x,\,y. \end{aligned}$$

On the time domain $\overline{\varLambda }_t$, we introduce the equidistant meshes with uniform time step $\varDelta t$ such that

$$\begin{aligned} \varLambda _t^M=\left\{ t_n=n\varDelta t, n=0,\ldots ,M, \varDelta t= T/M\right\} , \end{aligned}$$

where M is the number of mesh-points in the t-direction on the interval [0, T] and $\varDelta t$ satisfies the constraint $p\varDelta t= \tau$, where p is a positive integer, $t_n=n\varDelta t,\,n \ge -p.$

We define the discrete domain by $\mathfrak {G}^{N,M}=\overline{\mathfrak {G}}^{N,M}\cap \mathfrak {G}$ where $\overline{\mathfrak {G}}^{N,M}= \overline{{\varOmega }}_x^N \times \overline{{\varOmega }}_y^N\times \varLambda _t^M,$ and $\varUpsilon _b^N=\overline{{\varOmega }}_x^N \times \overline{{\varOmega }}_y^N\times \varLambda _t^p$, where $\varLambda _t^p$ denotes the set of $p+1$ uniform mesh-points in $[-\tau ,0]$ and ${\varOmega }_x^N=\overline{\varOmega }_{x}^N\cap \varOmega _{x}$, ${\varOmega }_y^N=\overline{\varOmega }_{y}^N\cap \varOmega _{y}$. The boundary points of $\overline{\mathfrak {G}}^{N,M}$ are $\varUpsilon ^N=\{\overline{\mathfrak {G}}^{N,M}\cap \varUpsilon \}\cup \varUpsilon _b^N$. We further discretize ${\overline{\mathfrak {G}}_s}^{N,M}=\mathfrak {D}^N \times \varLambda _{s,t}^p$, where $\varLambda _{s,t}^p$ denotes the set of $p+1$ uniform mesh-points in $[(s-1)\tau ,s \tau ]$, for $s=1,2,\ldots ,k.$ From the above discretization we can observe that $\overline{\mathfrak {G}}^{N,M}=\bigcup _{s=1}^k {\overline{\mathfrak {G}}_s}^{N,M}$.

3.1 Numerical scheme

Before describing the scheme, for a given mesh function $q(x_i,y,t_n)=q_{x_i,y}^n,\,y\in \varOmega _y^N$, define the forward difference operator $\delta _x^+$, the backward difference operator $\delta _x^-$ (for first-order spatial derivative) and the central difference operator $\delta _{x}^{2}$ (for second-order spatial derivative) in spatial x-direction by

$$\begin{aligned}&\delta _{x}^{+}q_{x_i,y}^{n}=\dfrac{q_{x_{i+1},y}^{n}-q_{x_{i},y}^{n}}{h_{x,i+1}},\qquad \delta _{x}^{-}q_{x_i,y}^{n}=\dfrac{q_{x_i,y}^{n}-q_{x_{i-1},y}^{n}}{h_{x,i}}\\&\quad \text{ and }\quad \delta _{x}^{2} q_{x_i,y}^{n}=\dfrac{2\left( \delta _{x}^{+}q_{x_i,y}^{n} - \delta _{x}^{-}q_{x_i,y}^{n}\right) }{\widehat{h}_{x,i}}, \end{aligned}$$

respectively.

Similarly, for a given mesh function $q(x,y_j,t_n)=q_{x,y_j}^n,\,x\in \varOmega _x^N$, we define the difference operators $\delta _{y}^{+},\,\delta _{y}^{-}$ and $\delta _{y}^{2}$. The backward difference operator $\delta _{t}^{-}$ is defined by

$$\begin{aligned} \delta _{t}^{-}q_{x_i,y_j}^{n}=\dfrac{q_{x_i,y_j}^{n}-q_{x_{i},y_j}^{n-1}}{\varDelta t} \end{aligned}$$

to approximate the first-order derivative in temporal direction.

We replace the time derivative by the implicit-Euler scheme and the spatial derivatives by the upwind scheme in Eq. (1), and obtain the following discrete problem:

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \left( \delta _t^{-}+\mathcal {L}_{\varepsilon }^N\right) U_{i,j}^{n+1}=-c_{i,j}U_{i,j}^{n+1-p} + f_{i,j}^{n+1},&{}\text{ on }\quad \mathfrak {G}^{N,M},\\ U_{i,j}^{-s}=\varphi _b\left( x_i,y_j,-t_{s}\right) ,&{} i,j=0,\ldots ,N,\; \text{ and }\quad s=0,\ldots ,\,p,\\ U_{i,j}^{n+1}= 0,&{} i=0,N \,\text{ or }\quad j=0,N,\; \text{ and }\quad n=0,\ldots ,M-1, \end{array}\right. \end{aligned}$$

(5)

where

$$\begin{aligned} \mathcal {L}_{\varepsilon }^N U_{i,j}^{n+1}= - \varepsilon \left( \delta _x^2+\delta _y^2\right) U_{i,j}^{n+1}+a_{1;i,j}\delta _x^-U_{i,j}^{n+1} + a_{2;i,j}\delta _y^-U_{i,j}^{n+1}+b_{i,j}U_{i,j}^{n+1}. \end{aligned}$$

After rearranging the terms in Eq. (5), we obtain the following system of equations:

$$\begin{aligned} \left\{ \begin{array}{ll} r_{i,j-}U_{i,j-1}^{n+1}+r_{i-,j}U_{i-1,j}^{n+1} &{}+ r_{i,j}U_{i,j}^{n+1}+r_{i+,j}U_{i+1,j}^{n+1}+r_{i,j+}U_{i,j+1}^{n+1}= g_{i,j}^{n+1},\\ &{}\quad \text{ for }\quad i,j=1,\ldots ,N-1,\; \text{ and }\quad n=0,\ldots ,M-1,\\ U_{i,j}^{-s}=\varphi _b\left( x_i,y_j,-t_{s}\right) ,&{} \quad i,j=0,\ldots ,N,\; \text{ and }\quad s=0,\ldots ,\,p,\\ U_{i,j}^{n+1}= 0, &{} \quad i=0,N\quad \text{ or }\quad j=0,N,\; \text{ and }\quad n=0,\ldots ,M-1, \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} \left\{ \begin{array}{ll} r_{i-,j}=\left( -\dfrac{2\varepsilon }{\widehat{h}_{x,i} h_{x,i}}-\dfrac{a_{1;i,j}}{h_{x,i}}\right) ,&{} r_{i+,j}=\left( -\dfrac{2\varepsilon }{\widehat{h}_{x,i} h_{x,i+1}}\right) ,\\ r_{i,j-}=\left( -\dfrac{2\varepsilon }{\widehat{h}_{y,j} h_{y,j}}-\dfrac{a_{2;i,j}}{h_{y,j}}\right) ,&{} r_{i,j+}=\left( -\dfrac{2\varepsilon }{\widehat{h}_{y,j} h_{y,j+1}}\right) ,\\ r_{i,j}=\dfrac{1}{\varDelta t}-r_{i-,j}-r_{i+,j}-r_{i,j-}-r_{i,j+}+b_{i,j},&{} g_{i,j}^{n+1}=\dfrac{U_{i,j}^n}{\varDelta t}-c_{i,j}U_{i,j}^{n-p+1}+f_{i,j}^{n+1}. \end{array} \right. \end{aligned}$$

The following discrete maximum principle on $\mathfrak {G}^{N,M}$ provides the $\varepsilon$-uniform stability of the difference operator $(\delta _t^{-}+\mathcal {L}_{\varepsilon }^N)$ (see [3]).

Lemma 1

(Discrete maximum principle) Suppose that the discrete function $\varPsi _{i,j}^n$ satisfies $\varPsi _{i,j}^n\ge 0$ on $\varUpsilon ^N$. Then $(\delta _t^{-} + \mathcal {L}_{\varepsilon }^N)\varPsi _{i,j}^n\ge 0$ on $\mathfrak {G}^{N,M}$ implies that $\varPsi _{i,j}^n\ge 0$ at each point of $\overline{\mathfrak {G}}^{N,M}$.

Proof

Assume that there exist a point $(x_i^*,y_j^*,t_n^*)\in \overline{\mathfrak {G}}^{N,M}$, such that

$$\begin{aligned} \varPsi \left( x_i^*,y_j^*,t_n^*\right) =\displaystyle {\min _{\left( x_i,y_j,t_n\right) \in \overline{\mathfrak {G}}^{N,M}}}\varPsi \left( x_i,y_j,t_n\right) < 0. \end{aligned}$$

Clearly $(x_i^*,y_j^*,t_n^*)\notin \varUpsilon ^N$, which implies $(x_i^*,y_j^*,t_n^*)\in \mathfrak {G}^{N,M}$.

Therefore, $\varPsi (x_i^*,y_j^*,t_n^*)-\varPsi (x_i^*,y_j^*,t_{n-1}^*)< 0$, $\varPsi (x_i^*,y_j^*,t_n^*)-\varPsi (x_{i-1}^*,y_j^*,t_n^*)< 0$, $\varPsi (x_i^*,y_j^*,t_n^*)-\varPsi (x_i^*,y_{j-1}^*,t_n^*)< 0$, $\varPsi (x_{i+1}^*,y_j^*,t_n^*)-\varPsi (x_i^*,y_j^*,t_n^*)> 0$ and $\varPsi (x_i^*,y_{j+1}^*,t_n^*)-\varPsi (x_i^*,y_j^*,t_n^*)> 0$.

Now, by applying the operator $(\delta _t^{-} + \mathcal {L}_{\varepsilon }^N)$ on $\varPsi (x_i^*,y_j^*,t_n^*)$, along with the above inequalities, we get

$$\begin{aligned} \left( \delta _t^{-} + \mathcal {L}_{\varepsilon }^N\right) \varPsi \left( x_i^*,y_j^*,t_n^*\right) < 0, \end{aligned}$$

which is a contradiction as $(\delta _t^{-} + \mathcal {L}_{\varepsilon }^N)\varPsi (x_i,y_j,t_n)\ge 0$, for all $(x_i,y_j,t_n)\in \mathfrak {G}^{N,M}$. Hence $\varPsi (x_i,y_j,t_n)\ge 0$, for all $(x_i,y_j,t_n)\in \overline{\mathfrak {G}}^{N,M}$.$\square$

4 Error analysis

Here, we provide the main theorem for the $\varepsilon$-uniform convergence of the numerical solution in the discrete maximum norm.

Theorem 2

Let u and U be the solutions of the continuous problem (1) and the discrete problem (5), respectively. Then, we have the following error bound

$$\begin{aligned} \left\| u(x_i,y_j,t_n)-U_{i,j}^n\right\| _{\infty }\le C\left( N^{-1}\ln N + \varDelta t\right) ,\quad \left( x_i,y_j,t_n\right) \in \mathfrak {G}^{N,M}. \end{aligned}$$

Proof

We can notice that on the first interval $[0,\tau ]$, i.e., where the time discretization parameter n varies from $0\, \text{ to } \,p$, the initial conditions of the continuous problem (1) and the discrete problem (5) will be same. So, the analysis can be carried out in the same way as one can do for a problem with out delay. Hence, by using the convergence result of [3], we can obtain

$$\begin{aligned} \left\| u(x_i,y_j,t_n)-U_{i,j}^n\right\| _{\infty }\le C(N^{-1}\ln N + \varDelta t),\quad \left( x_i,y_j,t_n\right) \in \mathfrak {G}_1^{N,M}. \end{aligned}$$

(6)

For the second interval $(\tau ,2\tau ]$, the approach of [3] is not applicable because, the value of the delay term involves in the right hand side of Eq. (5) will be the numerical solution obtained in previous time interval $[0,\tau ]$. So, we will provide the detailed proof to get the error over the interval $(\tau ,2\tau ]$.

On the domain $\mathfrak {G}_2=\mathfrak {D}\times (\tau ,2\tau )$, we consider the following singularly perturbed delay parabolic PDE:

(7)

where $u_\tau$ is the exact solution on $\mathfrak {G}_1$.

We discretize Eq. (7) by means of the implicit-Euler scheme for the time derivative and the upwind scheme for the spatial derivatives to determine the numerical solution U of Eq. (7) at $\mathfrak {G}_2^{N,M}$. Hence the discretization takes the form,

$$\begin{aligned} \left\{ \begin{array}{ll} \delta _t^-U_{i,j}^n - \varepsilon \left( \delta _x^2+\delta _y^2\right) U_{i,j}^n+a_{1;i,j}\delta _x^-U_{i,j}^n+a_{2;i,j} &{} \delta _y^-U_{i,j}^n+b_{i,j}U_{i,j}^n\\ \quad =-\,c_{i,j}U_{i,j}^{n-p} + f_{i,j}^n,&{}\quad \text{ on }\quad \mathfrak {G}_2^{N,M},\\ U(x_i,y_j,t_n)=U_1(x_i,y_j,t_n),&{}\quad (x_i,y_j,t_n)\in \overline{\mathfrak {G}}_1^{N,M},\\ U(x_i,y_j,t_n)= 0,&{}\quad i=0,N\quad \text{ or }\quad j=0,N,\\ &{}\quad \text{ and }\quad t_n\in \varLambda _{2,t}^p, \end{array}\right. \end{aligned}$$

(8)

where $U_1(\cdot ,\cdot ,\cdot )$ is the numerical solution calculated on $\mathfrak {G}_1^{N,M}$.

Now, we split the solution of Eq. (7) as $u=G+E_1+E_2+E_{12}$, where the initial conditions in $\mathfrak {G}_1$ are $G=u_\tau (x,y,t),\,E_1=0,\,E_2=0\,\text{ and }\,E_{12}=0$. Following the continuous problem, we decompose the solution of the discrete problem (8), as

$$\begin{aligned} U_{i,j}^n=G_{i,j}^n+{E_1}_{i,j}^n+{E_2}_{i,j}^n+{E_{12}}_{i,j}^n, \end{aligned}$$

where $G_{i,j}^n$ is the solution of

$$\begin{aligned} \left\{ \begin{array}{ll} \delta _t^-G_{i,j}^n - \varepsilon \left( \delta _x^2+\delta _y^2\right) G_{i,j}^n+a_{1;i,j}\delta _x^-G_{i,j}^n&{}+\,a_{2;i,j} \delta _y^-G_{i,j}^n+b_{i,j}G_{i,j}^n\\ \quad =-c_{i,j}G_{i,j}^{n-p} + f_{i,j}^n,&{}\quad \text{ on }\quad \mathfrak {G}_2^{N,M},\\ G_{i,j}^n=U_1(x_i,y_j,t_n),&{}\quad \text{ on }\quad \overline{\mathfrak {G}}_1^{N,M},\\ G_{i,j}^n=G(x_i,y_j,t_n),&{}\quad i=0,N\quad \text{ or }\quad j=0,N,\\ &{}\quad \text{ and }\quad t_n\in \varLambda _{2,t}^p, \end{array}\right. \end{aligned}$$

(9)

and ${E_\ell }_{i,j}^n$, $\ell =1,\,2,\,12$, satisfy

$$\begin{aligned} \left\{ \begin{array}{ll} \delta _t^-{E_\ell }_{i,j}^n - \varepsilon \left( \delta _x^2+\delta _y^2\right) {E_\ell }_{i,j}^n+a_{1;i,j}\delta _x^-{E_\ell }_{i,j}^n&{}+\,a_{2;i,j} \delta _y^-{E_\ell }_{i,j}^n+b_{i,j}{E_\ell }_{i,j}^n\\ \quad =-c_{i,j}{E_\ell }_{i,j}^{n-p},&{}\quad \text{ on }\quad \mathfrak {G}_2^{N,M},\\ {E_\ell }_{i,j}^n={E_\ell }(x_i,y_j,t_n),&{} \quad \text{ on }\quad \overline{\mathfrak {G}}_1^{N,M},\\ {E_\ell }_{i,j}^n={E_\ell }(x_i,y_j,t_n),&{} \quad i=0,N\quad \text{ or }\quad j=0,N,\\ &{}\quad \text{ and }\quad t_n\in \varLambda _{2,t}^p. \end{array}\right. \end{aligned}$$

(10)

The error can be splitted as

$$\begin{aligned}&\left\| u(x_i,y_j,t_n)-U_{i,j}^n\right\| _{\infty } \le \left\| G(x_i,y_j,t_n)-G_{i,j}^n\right\| _{\infty }+\left\| {E_1}(x_i,y_j,t_n)-{E_1}_{i,j}^n\right\| _{\infty } \nonumber \\&\quad + \left\| {E_2}(x_i,y_j,t_n)-{E_2}_{i,j}^n\right\| _{\infty } + \left\| {E_{12}}(x_i,y_j,t_n)-{E_{12}}_{i,j}^n\right\| _{\infty }. \end{aligned}$$

(11)

We will find the error separately for each term in the above equation.

Error analysis for the smooth component of the solution: Employing the initial condition for the smooth part of the solution and the error estimate given in Eq. (6) along with the Taylor’s expansions, we obtain the truncation error for Eq. (9), as

$$\begin{aligned}&\left\| \left( \delta _{t}^{-}+\mathcal {L}_{\varepsilon }^N\right) \left( G\left( x_i,y_j,t_n\right) -G_{i,j}^n\right) \right\| _{\infty }\\&\quad \le \left[ C\left( N^{-1}\ln N+\varDelta t\right) +\varDelta t \left\| \dfrac{\partial ^2 G}{\partial t^2}\right\| _{\infty }\right. \\&\qquad +\dfrac{\varepsilon }{3}\left( h_{x,i}+h_{x,i+1}\right) \left\| \dfrac{\partial ^3G}{\partial x^3}\right\| _{\infty }+a_{1;i,j}\dfrac{h_{x,i}}{2}\left\| \dfrac{\partial ^2 G}{\partial x^2}\right\| _{\infty }\\&\qquad \left. +\dfrac{\varepsilon }{3}\left( h_{y,j}+h_{y,j+1}\right) \left\| \dfrac{\partial ^3G}{\partial y^3}\right\| _{\infty }+a_{2;i,j}\dfrac{h_{y,j}}{2}\left\| \dfrac{\partial ^2 G}{\partial y^2}\right\| _{\infty }\right] .\end{aligned}$$

Now $h_{x,i}\le 2N^{-1},\,h_{y,j}\le 2N^{-1}$ and by using the bounds of the derivatives of G given in Theorem 1, we obtain

$$\begin{aligned} \left\| \left( \delta _{t}^{-}+\mathcal {L}_{\varepsilon }^N\right) \left( G\left( x_i,y_j,t_n\right) -G_{i,j}^n\right) \right\| _{\infty }\le C\left( N^{-1}\ln N+\varDelta t\right) , \end{aligned}$$

for $1\le i,j\le N-1$. Now, by choosing appropriate barrier function and applying the discrete maximum principle (Lemma 1), we can get

$$\begin{aligned} \left\| \left( G\left( x_i,y_j,t_n\right) -G_{i,j}^n\right) \right\| _\infty \le C\left( N^{-1}\ln N+\varDelta t\right) . \end{aligned}$$

(12)

Next we shall estimate the error associated to the layer component $E_1$ by separately providing the proofs in two spatial subregions depending on the location of mesh-point $x_i$.

Error analysis for the boundary layer components of the solution: First, we consider the outer region in the x-direction, i.e., $x\in [0,1-\rho _x]$. By following the proof of bound for $E_1$ in fixed time level $t_n$ from [10], we get

$$\begin{aligned} \left| {E_1}\left( x_i,y_j,t_n\right) -{E_1}_{i,j}^n\right| \le C N^{-1}, \end{aligned}$$

(13)

for $0\le i \le N/2$ and $0\le j\le N$.

Next, we find the estimate $|{E_1}(x_i,y_j,t_n)-{E_1}_{i,j}^n|$ for $N/2<i<N$ and $0<j<N$, by means of consistency and barrier function argument. The truncation error for Eq. (10), can be written as

$$\begin{aligned} \left( \delta _{t}^{-}+\mathcal {L}_{\varepsilon }^N\right) \left( {E_1}\left( x_i,y_j,t_n\right) -{E_1}_{i,j}^n \right)&=c_{i,j} \left( E_1\left( x_i,y_j,t_{n-p}\right) - {{E_1}_{i,j}}^{n-p}\right) \\&\quad + \left( \left( \dfrac{\partial }{\partial t} + \mathcal {L}_\varepsilon \right) - \left( \delta _t^-+\mathcal {L}_{\varepsilon }^N\right) \right) E_1. \end{aligned}$$

Now, by using the initial condition of Eq. (10) in the above equation, we get

$$\begin{aligned} \left( \delta _{t}^{-}+\mathcal {L}_{\varepsilon }^N\right) \left( {E_1}\left( x_i,y_j,t_n\right) -{E_1}_{i,j}^n \right) =\left( \left( \dfrac{\partial }{\partial t} + \mathcal {L}_\varepsilon \right) - \left( \delta _t^-+\mathcal {L}_{\varepsilon }^N\right) \right) E_1. \end{aligned}$$

Therefore, the Taylor’s expansions yield

$$\begin{aligned}&\left\| (\delta _{t}^{-}+\mathcal {L}_{\varepsilon }^N) \left( {E_1}(x_i,y_j,t_n)-{E_1}_{i,j}^n \right) \right\| _{\infty }\\&\quad \ \le \left[ \dfrac{\varepsilon }{3}(h_{x,i}+h_{x,i+1})\left\| \dfrac{\partial ^3E_1}{\partial x^3}\right\| _{\infty }\right. +\dfrac{\varepsilon }{3}(h_{y,j}+h_{y,j+1})\left\| \dfrac{\partial ^3E_1}{\partial y^3}\right\| _{\infty }\nonumber \\&\quad \ \quad +\dfrac{h_{x,i}}{2}a_{1;i,j}\left\| \dfrac{\partial ^2E_1}{\partial x^2}\right\| _{\infty }+\dfrac{h_{y,j}}{2}a_{2;i,j}\left\| \dfrac{\partial ^2E_1}{\partial y^2}\right\| _{\infty } \left. +\varDelta t \left\| \dfrac{\partial ^2E_1}{\partial t^2}\right\| _{\infty }\right] . \end{aligned}$$

Since $h_{x,i}=2\rho _{x,0}\varepsilon N^{-1}\ln N$, for $N/2<i<N$, along with the bounds of the derivatives of $E_1$ given in Theorem 1, the truncation error becomes

$$\begin{aligned}&\left\| \left( \delta _{t}^{-}+\mathcal {L}_{\varepsilon }^N\right) \left( {E_1}(x_i,y_j,t_n)-{E_1}_{i,j}^n \right) \right\| _{\infty }\\&\quad \le C\left[ \dfrac{\varepsilon ^{-1}}{\alpha _x}N^{-1}\ln N \exp \left( \dfrac{-\alpha _x(1-x_i)}{\varepsilon }\right) \right. \\&\quad \quad \left. +\dfrac{\varepsilon }{3}(h_{y,j}+h_{y,j+1})\exp \left( \dfrac{-\alpha _x(1-x_i)}{\varepsilon }\right) \right. \\&\quad \quad +\dfrac{h_{y,j}}{2}a_{2;i,j}\exp \left( \dfrac{-\alpha _x(1-x_i)}{\varepsilon }\right) \left. +\varDelta t \exp \left( \dfrac{-\alpha _x(1-x_i)}{\varepsilon }\right) \right] , \end{aligned}$$

after simplification, we obtain that

$$\begin{aligned} \left\| \left( \delta _{t}^{-}+\mathcal {L}_{\varepsilon }^N\right) \left( {E_1}(x_i,y_j,t_n)-{E_1}_{i,j}^n \right) \right\| _{\infty }\le & {} C\left[ \dfrac{\varepsilon ^{-1}}{\alpha _x}N^{-1}\ln N \exp \left( \dfrac{-\alpha _x(1-x_i)}{\varepsilon }\right) \right. \\&\left. +\varDelta t \exp \left( \dfrac{-\alpha _x(1-x_i)}{\varepsilon }\right) \right] . \end{aligned}$$

Let us choose $\phi _{i,j}^n=C\left( N^{-1}\ln N \left[ \displaystyle {\prod \nolimits _{k=i+1}^N} \left( 1+\dfrac{\alpha _x h_{x,k}}{\varepsilon }\right) ^{-1}\right] +\varDelta t\right)$ as a barrier function, and by applying the discrete maximum principle (Lemma 1), we get

$$\begin{aligned} \left\| \left( {E_1}\left( x_i,y_j,t_n\right) -{E_1}_{i,j}^n \right) \right\| _{\infty }\le C\left( N^{-1}\ln N+\varDelta t\right) . \end{aligned}$$

(14)

We can get the bound for the other boundary layer part $E_2$ in an analogous way. Therefore, for $0\le i,j\le N$, we can have

$$\begin{aligned} \left\| \left( {E_2}(x_i,y_j,t_n)-{E_2}_{i,j}^n \right) \right\| _{\infty }\le C\left( N^{-1}\ln N+\varDelta t\right) . \end{aligned}$$

(15)

Error analysis for the corner layer component of the solution: By following the proof of bound for $E_{12}$ in fixed time level $t_n$ from [10], we get

$$\begin{aligned} \left| {E_{12}}\left( x_i,y_j,t_n\right) -{E_{12}}_{i,j}^n\right| \le C N^{-1}, \end{aligned}$$

(16)

for $0\le i+j \le 3N/2$.

Next, we will use the Taylor series approach to estimate the truncation error for $i+j>3N/2$. The local truncation error for the difference Eq. (10) of the corner layer part $E_{12}$ can be written as

$$\begin{aligned} \left( \delta _{t}^{-}+\mathcal {L}_{\varepsilon }^N\right) \left( {E_{12}}\left( x_i,y_j,t_n\right) -{E_{12}}_{i,j}^n \right)= & {} c_{i,j} \left( E_{12}(x_i,y_j,t_{n-p})- {{E_{12}}_{i,j}}^{n-p}\right) \\&+ \left( \left( \dfrac{\partial }{\partial t} + \mathcal {L}_\varepsilon \right) - \left( \delta _t^-+\mathcal {L}_{\varepsilon }^N\right) \right) E_{12}. \end{aligned}$$

By employing the initial condition in the above equation, we get

$$\begin{aligned} \left( \delta _{t}^{-}+\mathcal {L}_{\varepsilon }^N\right) \left( {E_{12}}\left( x_i,y_j,t_n\right) -{E_{12}}_{i,j}^n \right) =\left( \left( \dfrac{\partial }{\partial t} + \mathcal {L}_\varepsilon \right) - \left( \delta _t^-+\mathcal {L}_{\varepsilon }^N\right) \right) E_{12}. \end{aligned}$$

Next, by using the Taylor’s expansions, we obtain

$$\begin{aligned}&\left\| (\delta _{t}^{-}+\mathcal {L}_{\varepsilon }^N) \left( {E_{12}}(x_i,y_j,t_n)-{E_{12}}_{i,j}^n \right) \right\| _{\infty }\\&\quad \le \left[ \dfrac{\varepsilon }{3}(h_{x,i}+h_{x,i+1})\left\| \dfrac{\partial ^3E_{12}}{\partial x^3}\right\| _{\infty }\right. \left. +\dfrac{\varepsilon }{3}(h_{y,j}+h_{y,j+1})\left\| \dfrac{\partial ^3E_{12}}{\partial y^3}\right\| _{\infty }\right. \nonumber \\&\quad \quad +\dfrac{h_{x,i}}{2}a_{1;i,j}\left\| \dfrac{\partial ^2E_{12}}{\partial x^2}\right\| _{\infty } \left. +\dfrac{h_{y,j}}{2}a_{2;i,j}\left\| \dfrac{\partial ^2E_{12}}{\partial y^2}\right\| _{\infty }+\varDelta t \left\| \dfrac{\partial ^2E_{12}}{\partial t^2}\right\| _{\infty }\right] . \end{aligned}$$

Since $h_{x,i}=2\rho _{x,0}\varepsilon N^{-1}\ln N$ and $h_{y,j}=2\rho _{y,0}\varepsilon N^{-1}\ln N$, for $i+j>3N/2$ along with the bounds of the derivatives of $E_{12}$, we get the truncation error as

$$\begin{aligned}&\left\| \left( \delta _{t}^{-}+\mathcal {L}_{\varepsilon }^N\right) \left( {E_{12}}\left( x_i,y_j,t_n\right) -{E_{12}}_{i,j}^n \right) \right\| _{\infty } \\&\quad \le C\left[ \dfrac{\varepsilon ^{-1}}{\alpha _x}N^{-1}\ln N \min \left\{ \exp \left( \dfrac{-\alpha _x(1-x_i)}{\varepsilon }\right) ,\exp \left( \dfrac{-\alpha _y(1-y_i)}{\varepsilon }\right) \right\} \right. \\&\qquad +\dfrac{\varepsilon ^{-1}}{\alpha _y}N^{-1}\ln N \min \left\{ \exp \left( \dfrac{-\alpha _x(1-x_i)}{\varepsilon }\right) ,\exp \left( \dfrac{-\alpha _y(1-y_i)}{\varepsilon }\right) \right\} \\&\qquad \left. +\varDelta t \min \left\{ \exp \left( \dfrac{-\alpha _x(1-x_i)}{\varepsilon }\right) ,\exp \left( \dfrac{-\alpha _y(1-y_i)}{\varepsilon }\right) \right\} \right] . \end{aligned}$$

Now, by choosing a barrier function

$$\begin{aligned} \phi _{i,j}^n= & {} C\Bigg (\varDelta t+N^{-1}\ln N \left[ \displaystyle \prod _{k=i+1}^N \left( 1+\dfrac{\alpha _x {h_{x,k}}}{\varepsilon }\right) ^{-1}\right] \\&\left. +N^{-1}\ln N \left[ \displaystyle \prod _{k=j+1}^N \left( 1+\dfrac{\alpha _y {h_{y,k}}}{\varepsilon }\right) ^{-1}\right] \right) \end{aligned}$$

and by using the discrete maximum principle (Lemma 1), we get

$$\begin{aligned} \left\| \left( {E_{12}}(x_i,y_j,t_n)-{E_{12}}_{i,j}^n \right) \right\| _{\infty }\le C(N^{-1}\ln N+\varDelta t). \end{aligned}$$

(17)

Finally, by combining all the bounds from Eqs. (12)–(17), then employing on Eq. (11), we can get the required bound on $\mathfrak {G}_2^{N,M}$.

For $t\ge 2\tau$, we can obtain the desired error bound in a similar way as done above.$\square$

5 Numerical results

To verify the error estimate obtained in Theorem 2, here we carry out some numerical experiments for the following 2D test problems by choosing $T=2$ and $\rho _{l,0}=2.2,\,l=x,\,y$. In the tables, we begin with $N = 8$, $\varDelta t = 0.2$ and $p=1/\varDelta t$ and we multiply N by two and divide $\varDelta t$ by two.

Example 1

Consider the following singularly perturbed 2D delay parabolic IBVP with constant coefficients:

$$\begin{aligned} \left\{ \begin{array}{ll} u_t -\varepsilon \varDelta u +u_x +u_y=u(x,y,t-1) + f(x,y,t),&{}\quad (x,y,t) \in \mathfrak {D}\times (0,2],\\ u(x,y,t)=\varphi _b(x,y,t),&{}\quad (x,y,t)\in \overline{\mathfrak {D}}\times [-1,0],\\ u(x,y,t)= 0,&{}\quad (x,y,t)\in \partial \mathfrak {D}\times [0,2]. \end{array}\right. \end{aligned}$$

The source function f(x, y, t) and the initial data $\varphi _b(x,y,t)$ are such that the exact solution of the above problem is

$$\begin{aligned} u(x,y,t)= & {} (1-\exp (-t))\left( m_1+m_2x+\exp (-(1-x)/\varepsilon )\right) \\&\times \left( m_1+m_2y+\exp \left( -(1-y)/\varepsilon \right) \right) , \end{aligned}$$

where $m_1=-\exp (-1/\varepsilon ),\,m_2=-1-m_1$.

Table 1 Maximum pointwise errors and the corresponding order of convergence for Example 1

Table 2 Maximum pointwise errors and the corresponding order of convergence for Example 2

For each $\varepsilon$ the maximum pointwise error is calculated by

$$\begin{aligned} e_{\varepsilon }^{N, \varDelta t}= \max _{(x_i,y_j,t_n)\in \mathfrak {G}^{N,M}}\left| u(x_i,y_j,t_n)-U(x_i,y_j,t_n)\right| , \end{aligned}$$

where $u(x_i,y_j,t_n)\,\text{ and }\,U(x_i,y_j,t_n)$ denote the exact solution and the numerical solution obtained in $\mathfrak {G}^{N,M}$ with N mesh-intervals in the spatial directions and M mesh-intervals in the temporal direction, such that $\varDelta t= T/M$ is the uniform mesh-size. In addition, the corresponding order of convergence for each $\varepsilon$ is determined by

$$\begin{aligned} p_{\varepsilon }^{N,\varDelta t}=\log _{2}\left( \dfrac{e_{\varepsilon }^{N,\varDelta t}}{e_{\varepsilon }^{2N,\varDelta t/2}}\right) . \end{aligned}$$

Now, for each N and $\varDelta t$, we define the $\varepsilon$-uniform maximum pointwise error by

$$\begin{aligned} e^{N,\varDelta t}=\displaystyle {\max _\varepsilon e_\varepsilon ^{N,\varDelta t}}, \end{aligned}$$

and the corresponding $\varepsilon$-uniform order of convergence by

$$\begin{aligned} p^{N,\varDelta t}=\log _{2}\left( \dfrac{e^{N,\varDelta t}}{e^{2N,\varDelta t/2}}\right) . \end{aligned}$$

Next, we consider an example with variable convection coefficients.

Example 2

Consider the following singularly perturbed 2D delay parabolic IBVP:

$$\begin{aligned} \left\{ \begin{array}{ll} u_t -\varepsilon \varDelta u +(1+x(1-x))u_x +(1+y(1-y))u_y&{}\\ \quad =u(x,y,t-1) + f(x,y,t),&{}\quad (x,y,t) \in \mathfrak {D}\times (0,2],\\ u(x,y,t)=\varphi _b(x,y,t),&{} \quad (x,y,t)\in \overline{\mathfrak {D}}\times [-1,0],\\ u(x,y,t)= 0,&{} \quad (x,y,t)\in \partial \mathfrak {D}\times [0,2]. \end{array}\right. \end{aligned}$$

Here also, we choose the source function f(x, y, t) and the initial data $\varphi _b(x,y,t)$ in such a way, so that they fit with the same exact solution as mentioned in the Example 1.

Fig. 1

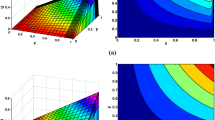
Surface plots of the numerical solutions U at $t=2$ and $N=32$ for Example 1. a$\varepsilon =1e-2$. b$\varepsilon =1e-4$

Fig. 2

Visualization of the order of convergence through loglog plot for Example 1

Fig. 3

Visualization of the order of convergence through loglog plot Example 2

The calculated maximum pointwise errors and the corresponding order of convergence for Examples 1 and 2 are presented in Tables 1 and 2, respectively, for various values of $\varepsilon$ and N. In both the tables, we can observe that for a fixed $\varepsilon$, the maximum pointwise errors decrease monotonically as N increases, which confirm that the implicit upwind scheme (5) is $\varepsilon$-uniform convergent. It also reflects the fact that the classical upwind scheme applied on this class of problem results almost first-order convergence. To visualize the appearance of the boundary layer and its behavior for different $\varepsilon$, we have given the surface plots for $\varepsilon =10^{-2},\,10^{-4}$ and $N=32$ in Fig. 1, for Example 1.

In order to reveal the numerical order of convergence, we have plotted the maximum pointwise errors (in loglog scale) in Figs. 2 and 3, for Examples 1 and 2, respectively, which again confirm the almost first-order convergence of the scheme.

6 Conclusions

In this paper, we have analyzed an efficient numerical scheme for the singularly perturbed 2D delay parabolic convection–diffusion problem of the form (1), using the uniform mesh for the temporal domain and a special piecewise-uniform Shishkin mesh for the spatial domains. For the discretization of the continuous problem, we have used the implicit-Euler scheme and the classical upwind scheme to the temporal and spatial derivatives, respectively. For the proposed scheme, the stability and error analysis have been carried out, which shows that the method converges uniformly with first-order (up to a logarithmic factor) in space and first-order in time. Along with the analysis, we have presented some numerical examples to verify the theoretical findings.