Single-valued neutrosophic context analysis at distinct multi-granulation

Abstract

In the current era, most of the researchers addressed an issue while dealing with uncertainty and indeterminacy that exists in fuzzy attributes. It becomes more complex when indeterminacy exists independently when compared to acceptation and rejection part. Due to which, some of the researchers tried to develop a three-way fuzzy concept lattice using neutrosophic set for characterization of uncertainty based on its acceptation, rejection, and uncertain parts, independently. In this process, a problem was addressed while processing the neutrosophic context based on user-required subset of attributes. It takes more time to extract interesting pattern from a given neutrosophic context having a large number of attributes. One of the solutions is to decompose the neutrosophic context via a defined multi-granulation for the truth, falsity and indeterminacy, membership values. To accomplish this task, a method is proposed in this paper using the computing paradigm of granular computing and applied lattice theory with an example.

1 Introduction

The development of neutrosophic set¹ given a mathematical way to characterize the indeterminacy in data with fuzzy attributes more independently rather than its acceptation and rejection part as discussed in Singh (2018e). This notable advantage of neutrosophic set theory (Smarandache 1999) molds the data analytics researchers in various applications as discussed (Broumi et al. 2018a, b). In this direction, one of the mathematical models called three-way fuzzy concept lattice (Singh 2017) using the neutrosophic set is introduced for data processing tasks by Singh (2018a) based on user-required subsets of attributes. However, this method is useful for the users who are experts and able to decide particular subset of attributes for solving the particular problem. Otherwise, it becomes difficult in case of non-expert user who want to investigate the pattern using each subset. In this case, the proposed method takes exponential time and become irrelevant for larger context. It is one of the hot spots of researchers while introducing a new mathematical model need to focused on its scalability also. Hence the current paper focused on neutrosophic set-based granular decomposition of context and its concept lattice building for multi-decision process.

Table 1 Overview of potential findings on neutrosophic set for data analytics

Table 1 represents the comparative study for some of the recent literature on neutrosophic context and its lattice theory for knowledge processing tasks. It can be observed that the neutrosophic concept lattice (Mittal et al. 2017; Singh 2017) provides a new mathematical model for handling the truth, falsity and indeterminacy in the fuzzy attributes, independently. Some other researchers tried to developed partial ordering in three-way decision space as discussed by Qi et al. (2014) and Hu (2016) for dealing with fuzzy attributes. Other researchers focused on characterizing the acceptation, rejection and uncertain part of the fuzzy attributes which are dependent on each other as elaborated by Yao (2016, 2018) and Pedrycz (1998). Its concepts used to work somehow like intuitionistic fuzzy topological space (Lupianez 2008) or vague space (Singh 2018d). Peng and Dai (2018) discussed the recent research trends in neutrosophic set theory for better understanding. In this process, a problem arises while dealing with independent three-way decision space as discussed by Li et al. (2013, 2015, 2016). One of the best suitable examples is attendance marking of any student in the class contains indeterminacy which arises due to following unavoidable reasons:

• The student is on leave without any information.

• The student is on duty for departmental work.

• The student had an accident due to which did not attend the class.

• The student is not interested to join the class.

• The student left the university and did not inform any official.

• The student is on sick leave.

• The student playing sports, attending conference, FDP, or some other leave specially granted by the university.

• The student is powerful and knows that he/she will get attendance by influence.

• The professor fears the student due to his caste, religion, money or other influencing parameters in context of country like India.

• The attendance data manipulated by academic for the particular students or faculty.

The above-mentioned uncertainty in real-life data sets creates several issues in multi-decision process. One of the major issues that arises with the professor while marking attendance (i.e., present or absent) of a student. Same time the difficulty arises with university team to stop biasness among students are provide an adequate attendance system. The reason is sometimes the student attendance was marked present unknowingly. Sometimes it may be marked absent unknowingly. It is totally vague or uncertain information for the faculty which creates major issues with his honesty, dignity as well as his/her reputation. The problem arises with academic team to equally distribute the leave among the students to believe them in the systems. The characterization of genuine leave, not-genuine leave or uncertain leave based on faculty and student-wise is a difficult task. It is just because the current attendance system is unable to measure the indeterminacy in the attendance system beyond the present and absent system. Due to that some of the genuine students as well as faculties suffered. To resolve this issue the current paper tried to represent the attendance of students using the neutrosophic set rather than binary system. It is an indeed requirement when the leave of powerful students or wrong student is granted which may affect the university reputation among the students as well as career of some good students. To resolve these real-life issues, current paper introduces neutrosophic set-based representation of attendance and its pattern analysis. Let X is total number of classes then the presence of student can be characterized by truth-membership function ($T_{X} (N)$), the absence of student as false membership function ($F_{X} (N)$), whereas the faculty do not know any thing about his/her presence or absent then it can be considered as an indeterminacy function ($I_{X} (N)$). It can be observed that the neutrosophic set (Smarandache 1999, 2018) tries to approximate the linguistics by a defined fuzzy membership values in the given three-way fuzzy space more precisely when compared to fuzzy sets (Zadeh 1975). The problem arises with faculty to represent this neutrosophic relation in the context and find some pattern for knowledge processing tasks: sometimes trying to navigate it for different attendance system to measure the facts about student presence in the faculty classes beyond 70 percent or below 70 percent, etc. To approximate this issue, two methods are introduced in this paper: the first method tries to discover some neutrosophic set-based pattern and the second method focuses on its precise navigation on attendance system at different granulation defined for truth, falsity and indeterminacy membership values. The analysis derived from the proposed method is also compared with recently available approaches in neutrosophic concept lattice on various parameters.

The rest part of the paper is organized as follows: Sect. 2 provides preliminaries about neutrosophic set based context analysis. Section 3 provides the proposed method for analysis of single-valued neutrosophic contexts using applied lattice theory and multi-granulation. Section 4 illustrates the proposed method with an example. Section 5 includes discussion followed by conclusions and references.

2 Preliminaries

2.1 Neutrosophic set-based three-way fuzzy context

Definition 1

(Formal fuzzy context) (Burusco and Fuentes-Gonzalez 1994): a formal fuzzy context is a triplet $\mathbf{K } = (\textit{X}, \textit{Y}, {\tilde{R}}$), where X is a set of objects, Y is a set of attributes and ${\tilde{R}}$ is an L-relation between X and Y, ${\tilde{R}}$: X$\times$Y$\rightarrow \textit{L}$. Each relation ${\tilde{R}}(\textit{x},\textit{y})\in L$ represents the membership value at which the object $x\in \textit{X}$ has the attribute $y\in \textit{Y}$ in [0, 1]where L is a support set of some complete residuated lattice L.

Definition 2

(Three-way fuzzy context) (Singh 2017): a three-polar fuzzy context can be represented as K = (X, Y, ${\tilde{R}}$) where X represents set of objects, Y represents set of three-polar attributes and ${\tilde{R}}$ represents three-polar relationship characterized by truth ($T_{{\tilde{R}}}(x,y)$), indeterminacy ($I_{{\tilde{R}}}(x,y)$) and false ($F_{{\tilde{R}}}(x,y)$) membership value at which the object $x\in \textit{X}$ has the attribute $y\in \textit{Y}$ in three-polar space [0,1]$^3$ where ($T_{{\tilde{R}}}(x,y)$), ($I_{{\tilde{R}}}(x,y)$) and ($F_{{\tilde{R}}}(x,y)$) are real standard or non-standard subsets of $]0^{-} ,1^{+}[$. It means ${\tilde{R}}= \{ ((x,y), T_{{\tilde{R}}}(x,y), I_{{\tilde{R}}}(x,y), F_{{\tilde{R}}}(x,y): \forall x \in X, y \in Y \}$ where $0^{-} \le T_{{\tilde{R}}}(x,y) + I_{{\tilde{R}}}(x,y)+ F_{{\tilde{R}}}(x,y) \le 3^{+}$. It should be noted that $0^{-}= 0-\epsilon$, where 0 represents its standard part and $\epsilon$ represents its non-standard part. Similarly, $1^{+}= 1+\epsilon$ ($3^{+}= 3+\epsilon$) where 1 (or 3) represents standard part and $\epsilon$ represents its non-standard part. Hence, the real standard format (0, 1) or [0, 1] can be also used to represent the relationship among objects and attributes set using neutrosophic set.

Example 1

Let us suppose, a professor wants to measure the regularity of his/her student based on his/her attendance. It is well known that the current attendance system allows the professor to write present or absent of a student in the given class. It unable to represent uncertain attendance arises via sick leave, medical leave, sports leave, random leave, accidental leave, bunk of class or leaving the university at the given time. All of these irregularities can be characterized via acceptation, rejection and uncertain part of a defined single-valued neutrosophic set. A student present in the class 70 percent whereas 20 percent absent then there may exists 10 percent or more indeterminacy. It can be represented using the neutrosophic values (0.7, 0.2, 0.1).

Definition 3

(Residuated lattice) (Pollandt 1998): it is a basic structure of truth degrees L = $(L,\wedge ,\vee ,\otimes ,\rightarrow ,0,1)$ where 0 and 1 represent least and greatest elements, respectively. L is a complete residuated lattice iff:

• (1) $(L,\wedge ,\vee ,0,1)$ is a complete lattice.

• (2) $(L,\otimes ,1)$ is commutative monoid.

• (3) $\otimes$ and $\rightarrow$ are adjoint operators (called as multiplication and residuum, respectively), that is $a \otimes b \le c$ iff $a\le b\rightarrow c, \forall a,b,c\in \textit{L}$. The operators $\otimes$ and $\rightarrow$ are defined distinctly by Lukasiewicz, Go$\ddot{}$del, and Goguen t-norms and their residua. In this paper, Go$\ddot{}$del t-norms and their residua is used as given below:

Gödel:

• $a \otimes b$ = min (a, b),

• $a \rightarrow b$ = 1 if $a \le b$, otherwise b.

The L-set can be extended to finite set $\left\{ 0, \frac{2}{n}, \frac{3}{n}, \ldots , \frac{n-1}{n}, 1\right\}$ where $n \in N^{+}$ to represent the acceptation part. Similarly, it can be defined for rejection $n \in N^{-}$ as well as uncertain parts, independently as shown in Singh (2017, 2018a, b, c). Recently, the properties of skew residuated lattice is also studied to measure this type of context precisely (Zhi et al. 2018).

Definition 4

(Formal fuzzy concepts): for any L-set A$\in L^{X}$ of objects, and B$\in L^{Y}$ of attributes we can define L-set A$^{\uparrow }\in L^{Y}$ of attributes and L-set B$^{\downarrow }\in L^{X}$ of objects as follows (Burusco and Fuentes-Gonzalez 1994):

• (1) A$^{\uparrow } (y)=\wedge _{x\in {\textit{X}}}( \textit{A}(x) \rightarrow {\tilde{R}}(\textit{x},\textit{y}))$,

• (2) B$^{\downarrow } (x)=\wedge _{y\in {\textit{Y}}}( \textit{B}(y) \rightarrow {\tilde{R}}(\textit{x},\textit{y}))$.

A$^{\uparrow } (x)$ is interpreted as the L-set of attribute y $\in \textit{Y}$ shared by all objects from A. Similarly, B$^{\downarrow } (x)$ is interpreted as the L-set of all objects x$\in \textit{X}$ having the attributes from B in common. The fuzzy formal concept is a pair of (A, B)$\in L^{X}\times L^{Y}$ satisfy $\textit{A}^{\uparrow }=\textit{B}$ and $\textit{B}^{\downarrow }=\textit{A}$, where fuzzy set of objects A called as extent and fuzzy set of attributes B called as intent. Sometimes the author may focus on crisply generated concepts when the expert knows that attributes is not variable. In this paper, it is well known that faculty used to take all classes which is static only student attendance varies.

Definition 5

(Three-polar neutrosophic concepts) Singh (2017): the pair (A, B) is called as three-polar formal concept iff $\textit{B}^{\downarrow }$ =$(\textit{A}, [T_A, I_A, F_A )$ and $\textit{A}^{\uparrow }$=$(B,[T_B, I_B, F_B])$. The $\downarrow$ is applied on three-polar set of attributes as follows:

$$\begin{aligned} \textit{A}^{\uparrow } (y))= & {} ((\wedge T_{x\in {\textit{X}}}( \textit{A}(T_x) \rightarrow {\tilde{R}}(T_{\textit{x},\textit{y}}))), (\vee I_{x\in {\textit{X}}}( \textit{A}(I_x) \rightarrow {\tilde{R}}(I_{\textit{x},\textit{y}}))), (\vee F_{x\in {\textit{X}}}( \textit{A}(F_x) \rightarrow {\tilde{R}}(F_{\textit{x},\textit{y}})))),\\ \textit{B}^{\uparrow } (x))= & {} ((\wedge T_{y\in {\textit{Y}}}( \textit{B}(T_y) \rightarrow {\tilde{R}}(T_{\textit{y},\textit{Y}}))), (\vee I_{y\in {\textit{Y}}}( \textit{B}(I_y) \rightarrow {\tilde{R}}(I_{\textit{y},\textit{Y}}))), (\vee F_{y\in {\textit{Y}}}( \textit{B}(F_y) \rightarrow {\tilde{R}}(F_{\textit{y},\textit{y}})))), \end{aligned}$$

It provides the following objects and attributes set as per properties of neutrosophic set:

$$\begin{aligned} \textit{A}= & {} \left\{ x_{i}, (T_{A}(x_{i}), I_{A}(x_{i}), F_{A}(x_{i})) \in [0,1]^3: \forall x_{i} \in X\right\} .\\ \textit{B}= & {} \left\{ y_{j}, (T_{B}(y_{j}), I_{B}(y_{j}), F_{B}(y_{j})) \in [0,1]^3: \forall y_{j} \in Y\right\} . \end{aligned}$$

It represents pair of neutrosophic set having a object and attributes set (A, B) as a pattern. In which, the objects set includes maximal membership with respect to integrating the information from the given neutrosophic attributes set and vice versa. In case the obtained pair of neutrosophic set forms the concept then none of extra attribute (or object) set can be investigated which will make the obtained membership bigger than previous one.

Definition 6

(Partial ordering of fuzzy concepts) (Burusco and Fuentes-Gonzalez 1994): a formal fuzzy concept is a maximal rectangle of a given fuzzy context K filled with membership value between [0, 1], which is an ordered pair of two sets (A, B), where A$\subseteq$ X called as fuzzy extent, and B$\subseteq$ Y is called as fuzzy intent. The set of formal fuzzy concepts(C), generated from a given formal fuzzy context K, defines the partial ordering principle, i.e., $(\textit{A}_{1},\textit{B}_{1})\le (\textit{A}_{2},\textit{B}_{2})\Longleftrightarrow \textit{A}_{1}\subseteq \textit{A}_{2}(\Longleftrightarrow \textit{B}_{2}\subseteq \textit{B}_{1})$ for every fuzzy formal concept.

Definition 7

(Partial ordering among three-way fuzzy concepts) (Hu 2016): let $C_{1}$ and $C_{2}$ be two three-polar concepts generated from context K using the properties of neutrosophic set. Then $C_{1}\subseteq C_{2}$ iff $T_{C_{1}}(x) \le T_{C_{2}}(x)$, $I_{C_{1}}(x) \ge I_{C_{2}}(x)$, $F_{C_{1}}(x) \ge F_{C_{2}}(x)$ for any $x \in X$. ($C, \wedge , \vee$) is bounded lattice. Also the structure ($C, \wedge , \vee , (1,0,0), (0, 1, 1), \lnot$) follow the De Morgan’s law.

Definition 8

(Complete lattice) (Wile 1982) (Ganter and Wille 1999): in the complete lattice there exist an infimum and a supremum for some formal concepts as given follows:

• $\wedge _{j\in J}(A_{j}, B_{j}) = (\bigcap _{j\in J} A_{j}, (\bigcup _{j\in J}B_{j})^{\downarrow \uparrow })$,

• $\vee _{j\in J} (A_{j}, B_{j}) = ((\bigcup _{j \in J} A_{j})^{\uparrow \downarrow },\bigcap _{j\in J} B_{j})$.

Definition 9

(Single-valued neutrosophic graph) (Kandasamy and Smarandache 2014; Broumi et al. 2016): let $G=$ (V, E) is a neutrosophic graph in which the vertices (V) can be characterized by a truth-membership function $T_{v}(v_{i})$, a indeterminacy-membership function $I_{v}(v_{i})$ and a falsity-membership function $F_{v} (v_{i})$ where $\left\{ (T_{v}(v_{i}), I_{v}(v_{i}), F_{v}(v_{i})) \in [0,1]^3\right\}$ for all $v_{i} \in V$. Similarly the edges (E) can be defined as a neutrosophic set:

$\left\{ (T_{E}(V \times V), I_{E}(V \times V), F_{E}(V \times V)) \in [0,1]^3\right\}$ for all $V \times V \in E$ such that:

$$\begin{aligned} T_{E}(v_{i}v_{j})\le & {} \text {min} [T_{E}(v_{i}, T_{E}(v_{j})],\\ I_{E}(v_{i}v_{j})\ge & {} \text {max} [I_{E}(v_{i}, I_{E}(v_{j})],\\ F_{E}(v_{i}v_{j})\ge & {} \text {max} [F_{E}(v_{i}, F_{E}(v_{j})].\\ \end{aligned}$$

The single-valued neutrosophic graph is complete iff:

$$\begin{aligned} T_{E}(v_{i}v_{j})= & {} \text {min} [T_{E}(v_{i}), T_{E}(v_{j})],\\ I_{E}(v_{i}v_{j})= & {} \text {max} [I_{E}(v_{i}), I_{E}(v_{j})],\\ F_{E}(v_{i}v_{j})= & {} \text {max} [F_{E}(v_{i}), F_{E}(v_{j})].\\ \end{aligned}$$

It is noted that $\left\{ (T_{E}(v_{i}v_{j}), I_{E}(v_{i}v_{j}), F_{E}(v_{i}v_{j}))\right\} = (0, 0, 0) \forall (v_{i}, v_{i}) \in (V \times V {\setminus } E$).

The above-mentioned definitions and examples approve that the neutrosophic concepts can be generated to measure the pattern of student attendance using the properties of abstract algebra. In this case the faculty used to take all classes which is defined from the university only the attendance of students varies. Some time the student is present, absent or leave. This three type of decision space can be represented using single-valued neutrosophic relation for approximation of uncertainty about their attendance. Bao et al. (2018) and Yang et al. (2016, 2017) introduced recently some new operators to achieve the same. In this case, the problem arises when the expert or Professor wants to find the most suitable student and its next neighbor for multi-decision tasks. To achieve this goal, Lindig (2002) introduced a method based on the Next Neighbor for building the concept lattice and its easier algorithm to build the lattice too (Aswani Kumar and Singh 2014). The neutrosophic lattice can be studied in Kandasamy and Smarandache (2014) whereas the neutrosophic implications can be studied in Broumi and Smarandache (2014). These studies motivated to open the new pinnacle of neutrosophic context and its processing using the properties of Next Neighbor and granular computing. The calculus of granular computing provides multiple ways to deal with any given fuzzy context (Aswani Kumar and Singh 2014) for precise analysis of hidden pattern (Singh and Gani 2015) in the given data sets. Hence, the current paper tried to introduce this methodology for dealing with neutrosophic context.

3 Proposed method

This section proposed two methods to analyze the single-valued neutrosophic context using the algebra of Galois connection and multi-granulation.

3.1 The proposed method for generating neutrosophic concepts based on their Next Neighbors

In this section a method is proposed to generate the neutrosophic set-based concepts based on their Next Neighbors as follows:

• Step (1) Let us consider, a single-valued neutrosophic context $\mathbf{K } = (\textit{X}, \textit{Y}, {\tilde{R}})$ where X represents set of objects, Y represents set of attributes and ${\tilde{R}}$ represents single-valued neutrosophic relationship among them in three-polar space [0, 1]$^3$.

• Step (2) The hidden pattern in the given single-valued neutrosophic context can be found using the application of Galois connection on the given objects set as follows:

  $$\begin{aligned} \left\{ x_{i}, (T_{A(x_{i})}, I_{A(x_{i})}, F_{A(x_{i})}) \right\} ^{\uparrow }. \end{aligned}$$

  It provides the maximal set of single-valued neutrosophic set of attributes which covers the objects set maximally.

• Step (3) The single-valued neutrosophic membership value for the obtained objects set can be computed as follows:

  $$\begin{aligned} T_{A_{s_i}}(x_{i})= & {} \text {min}_{j \in T_{B_{s_j}}}(\mu ^{{\tilde{R}}}_{T}(x_i,y_j)).\\ I_{A_{s_i}}(x_{i})= & {} \text {max}_{j \in I_{B_{s_j}}}(\mu ^{{\tilde{R}}}_{I}(x_i,y_j)).\\ F_{A_{s_i}}(x_{i})= & {} \text {max}_{j \in F_{B_{s_j}}}(\mu ^{{\tilde{R}}}_{T}(x_i,y_j)). \end{aligned}$$

• Step (4) The maximal covering objects while integrating the information from above obtained set can be discovered as follows:

  $$\begin{aligned} \left\{ y_{j}, (T_{B(y_{j})}, I_{B(y_{j})}, F_{B(y_{j})}) \right\} ^{\downarrow }. \end{aligned}$$

• Step (5) The single-valued neutrosophic membership value for the obtained attribute set can be computed as follows:

  $$\begin{aligned} T_{B_{s_j}}(y_{j})= & {} \text {min}_{i \in T_{A_{s_i}}}(\mu ^{{\tilde{R}}}_{T}(x_i,y_j)).\\ I_{B_{s_j}}(y_{j})= & {} \text {max}_{i \in I_{A_{s_i}}}(\mu ^{{\tilde{R}}}_{I}(x_i,y_j)).\\ F_{B_{s_j}}(y_{j})= & {} \text {max}_{i \in F_{A_{s_i}}}(\mu ^{{\tilde{R}}}_{T}(x_i,y_j)). \end{aligned}$$

• Step (6) The generated pattern of object and attribute set ($A_{s_i}$, $B_{s_j}$) is called as neutrosophic concept.

• Step (7) The Lower Neighbor of the first concept can be generated via appending the uncovered attributes with its maximal acceptance (1, 0, 0), i.e., :$y_k$=$Y-y_{j}$ where $j\le m$ and $k \le m|$.

• Step (8) The concepts for the obtained Lower Neighbor can be investigated using the Galois connection as shown in Step 2 and 6.

• Step (9) The Lower Neighbor having maximal membership value for the truth, minimal for indeterminacy and minimal for falsity can be as its Next Neighbors. These steps repeated for each Next Neighbors till all the attributes are covered.

• Step (10) Neutrosophic concept lattice can be build using their discovered Next Neighbors. The code is shown in Table 2.

Table 2 Proposed algorithm for generating the neutrosophic concepts using their Next Neighbor

Complexity: Let us suppose, there are n number of objects and m number of attributes exists in the given neutrosophic context as shown in Table 2. The proposed method discover Lower Neighbors for the given attributes (i.e., m) which may take O$(m^2)$ time complexity. Thereafter, it connects with Galois connection for investigating the corresponding object and attributes set which may take O$(m^{3} *n)$ time complexity for each Lower Neighbors (C), respectively. In this way, the proposed method take maximum O$(|C|.n.m^{3})$ time complexity where, C is Lower Neighbor.

3.2 A granular-based method for decomposing the neutrosophic context

This section introduces a method is proposed to zoom in and zoom out the this single-valued neutrosophic context based on defined granulation for the truth, falsity, and indeterminacy-membership values, independently. Recently, this property of granular computing is applied in unipolar fuzzy context (Singh and Aswani Kumar 2012; Singh and Gani 2015) as well as three-way fuzzy contexts (Singh 2018a, b, d). This paper focuses on decomposition of single-valued neutrosophic contexts and its transformation into a binary context via a defined granulation for the truth, false and indeterminacy values as given below:

• Step 1 Let us suppose, a single-valued neutrosophic context K = (X, Y, ${\tilde{R}}$) where, $|X|=n$, $|Y|=m$ and, ${\tilde{R}}$ represents the neutrosophic relationship among them.

• Step 2 Decide the level of granulation for the truth, i.e., $\alpha$, indeterminacy, i.e., $\alpha$, and falsity, i.e., $\gamma$ values.

• Step 3 The neutrosophic context can be decomposition for this granulation into binary context when true membership values is greater than chosen threshold, indeterminacy-membership values less than the chosen granulation, falsity-membership values less than the chosen granulation.

• Step 4 The mathematical representation of proposed method is as follows : If $\{T_{{\tilde{R}}(x,y)}| \mu _{T_{{\tilde{R}}(x,y)}} \ge \alpha \}$ and If $\{I_{{\tilde{R}}(x,y)}| \mu _{I_{{\tilde{R}}(x,y)}} \le \beta \}$, and If $\{F_{{\tilde{R}}(x,y)}| \mu _{F_{{\tilde{R}}(x,y)}} \le \gamma \}$ then represent 1 otherwise 0.

• Step 5 The decomposed single-valued neutrosophic contexts K$_{\alpha , \beta , \gamma }$ and satisfies following properties:

  • K= $\bigcup _{\alpha _i, \beta _i, \gamma _i}$.

  • K$_{\alpha _{1}, \beta _{1}, \gamma _{1}}$ $\subseteq$ K$_{\alpha _{2}, \beta _{2}, \gamma _{2}}$ when $\alpha _{1}$ $\ge$ $\alpha _{2}$, $\beta _{1}$ $\le$ $\beta _{2}$, $\gamma _{1}$ $\le$ $\gamma _{2}$.

• Step 6 In this way the given neutrosophic contexts can be zoom in and zoom out using different threshold values.

• Step 7 Write the obtained binary context and build the concept lattice.

• Step 8 The pseudo-code is written in form of an algorithm as shown in Table 3.

Table 3 Proposed algorithm for decomposition of a neutrosophic context

Complexity: Table 3 shows that the pseudo-code for the decomposition of a neutrosophic context having n number of objects and m number of attributes. The proposed method decomposed the context based on user defined granulation for neutrosophic relationship, i.e., $(\alpha , \beta , \gamma )$. In this way the granulation need to check for each entries for the given membership values three times, i.e., O($m^{3}$) or O($n^{3}$).

4 Illustration

In this section, both of the proposed methods are illustrated to analyze the student attendance pattern.

4.1 Single-valued neutrosophic concepts generation

Recently, three-way fuzzy concept lattice is introduced by Singh (2017) for analysis of hidden pattern in the given neutrosophic context based on user-required subset of neutrosophic attributes (Singh 2018a, b, c, d). However the author addressed that, the subset-based method is useful when user is expert and able to decide the particular subset for discovery of pattern. It becomes irrelevant in case user is non-expert and unable to decide the subset. In this case user may require all single-valued neutrosophic concepts for multi-decision process. Same time it become exponential while dealing with large number of single-valued neutrosophic attributes. To resolve this issue, the current paper proposed a method in Sect. 3.1 using the mathematics of Next Neighbor algorithm. To illustrate the proposed method a real-life example is given below:

Example 2

Let us suppose, the academic team of a university wants to analyze the pattern among attendance of students $(x_1, x_2, x_3)$ using their attendance in the class of following faculties $(y_1, y_2, y_3)$.

• Let us suppose, a student $x_1$ is 65 percent present in the class of faculty $y_1$. It can be characterized by truth-membership values.

• The same student $x_1$ is 25 percent absent in the class of faculty ($y_1$). It can be characterized by falsity-membership values.

• The faculty $y_1$ is 10 percent unaware about present and absent of the student $x_1$ attendance in the class. It can be characterized by indeterminacy-values.

The above information about the student attendance can be written using a single-valued neutrosophic set (0.65, 0.25, 0.1). It can be written on the entry of $x_1,y_1$ shown in Table 4 to form the single-valued neutrosophic matrix. Similarly, other entries of single-valued neutrosophic matrix shown in Table 4 can be written. Subsequently, the attendance of students for other faculties ($y_2$ $y_3$) can be written using the neutrosophic context shown in Table 5.

The problem is to investigate the pattern in the attendance of students and its next successors for analysis of genuine or un-genuine leave. Same time finding the faculty which classes the students attend maximally and which faculty less. To resolve this issue, the hidden single-valued neutrosophic pattern can be generated using the proposed algorithm shown in Sect. 3.1 as given below:

Table 4 The attendance representation of students ($x_1, x_2, x_3$) in class of faculty $y_1$ using the neutrosophic set

Table 5 The single-valued neutrosophic set-based representation of students attendance

• Step (1) Let us consider, the single-valued neutrosophic context as shown in Table 5.

• Step (2) Apply the Galois connection on the given object set for its maximal acceptance as given below $\frac{(1, 0, 0)}{x_1}$+$\frac{(1, 0, 0)}{x_2}$+$\frac{(1, 0, 0)}{x_3}$ using the $\uparrow$ of Galois connection. It provides the pattern for maximal attendance of each studnets in the given faculties, i.e., $y_1, y_2, y_3$.

• Step (3) It provides following single-valued neutrosophic attributes, i.e., attendance of students in the given faculties and their classes:

  $$\begin{aligned} \frac{(0.65, 0.25, 0.1)}{y_1}+\frac{(0.73, 0.25, 0.0)}{y_2}+\frac{(0.65, 0.25, 0.1)}{y_3}. \end{aligned}$$

• Step (4) In similar manner try to connect the attendance and its closeness with the real student attendance using $\downarrow$:

  $$\begin{aligned} \frac{(0.65, 0.25, 0.1)}{y_1}+\frac{(0.73, 0.25, 0.0)}{y_2}+\frac{(0.65, 0.25, 0.1)}{y_3}^\downarrow . \end{aligned}$$

• Step (5) It provides the maximal covering attendance of students while integrating the faculties classes as given below:

  $$\begin{aligned} \frac{(0.74, 0.25, 0.0)}{x_1}+\frac{(0.74, 0.10, 0.0)}{x_2}+\frac{(0.73, 0.2, 0.0)}{x_3} \end{aligned}$$

• Step (6) In this way, it provides following single-valued neutrosophic concept:

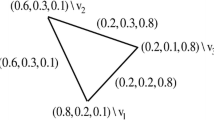
1. Extent:

$$\begin{aligned} \frac{(0.74, 0.25, 0.0)}{x_1}+\frac{(0.74, 0.10, 0.0)}{x_2}+\frac{(0.73, 0.2, 0.0)}{x_3}. \end{aligned}$$

Intent:

$$\begin{aligned} \frac{(0.65, 0.25, 0.1)}{y_1}+\frac{(0.73, 0.25, 0.0)}{y_2}+\frac{(0.65, 0.25, 0.1)}{y_3}. \end{aligned}$$

Information: It represents that each of the students attend the classes of faculty ($y_2$) maximally, i.e., 73 percent when compared to any other faculty. Each of these students are equally absent, i.e., 25 percent on classes of each faculties. Same time each of the faculty equally, i.e., 10 percent unknown about their absentee. It provides an information that faculty ($y_2$) is may be teaching good/making the class more interactive or strictly follow the rules of university. Due to which, each of the students attend his/her class maximally whereas other classes they may used to come college but did not attend the classes.

Step (7) Now append the attribute $y_1$, $y_2$ and $y_3$ one by one to analyze the real pattern of students attendance when each of the faculties have completed all the class in the given semester.

It is well known that each faculty used to take all the class in the given semester defined for completion of the course. Hence, in this case the truth value will be 1.0, false membership values will be 0 and indeterminacy is 0. It provides following neutrosophic concepts by adding $y_1$:

2. Extent:

$$\begin{aligned} \frac{(0.65, 0.25, 0.1)}{x_1}+\frac{(0.72, 0.1, 0.1)}{x_2}+\frac{(0.69, 0.21, 0.1)}{x_3} \end{aligned}$$

Intent:

$$\begin{aligned} \frac{(1.0, 0.0, 0.0)}{y_1}+\frac{(0.73, 0.25, 0.0)}{y_2}+\frac{(0.65, 0.25, 0.1)}{y_3} \end{aligned}$$

Information: It represents that the student $x_2$ attends maximum 72 percent classes of faculty $y_1$.

Step (8) Similarly, other Next Neighbor concepts can be generated by appending $y_2, y_3$:

3. Extent:

$$\begin{aligned} \frac{(0.74, 0.25, 0.0)}{x_1}+\frac{(0.73, 0.1, 0.0)}{x_2}+\frac{(0.73, 0.2, 0.0)}{x_3} \end{aligned}$$

Intent:

$$\begin{aligned} \frac{(0.65, 0.25, 0.1)}{y_1}+\frac{(1.0, 0.0, 0.0)}{y_2}+\frac{(0.65, 0.25, 0.1)}{y_3} \end{aligned}$$

Information: It represents that the student $x_2$ attends maximum 73 percent classes of faculty $y_2$.

4. Extent:

$$\begin{aligned} \frac{(0.65, 0.25, 0.1)}{x_1}+\frac{(0.74, 0.1, 0.0)}{x_2}+\frac{(0.7, 0.2, 0.1)}{x_3} \end{aligned}$$

Intent:

$$\begin{aligned} \frac{(0.65, 0.25, 0.1)}{y_1}+\frac{(0.73, 0.25, 0.0)}{y_2}+\frac{(1.0, 0.0, 0.0)}{y_3} \end{aligned}$$

Information: It represents that the student $x_2$ attends maximum 74 percent classes of faculty $y_3$.

Step (9). In a similar way all concepts can be discovered via appending uncovered attributes:

5. Extent:

$$\begin{aligned} \frac{(0.65, 0.25, 0.1)}{x_1}+\frac{(0.72, 0.1, 0.0)}{x_2}+\frac{(0.69, 0.21, 0.1)}{x_3} \end{aligned}$$

Intent:

$$\begin{aligned} \frac{(1.0, 0.0, 0.0)}{y_1}+\frac{(1.0, 0.0, 0.0)}{y_2}+\frac{(0.65, 0.25, 0.1)}{y_3} \end{aligned}$$

6. Extent:

$$\begin{aligned} \frac{(0.65, 0.25, 0.1)}{x_1}+\frac{(0.72, 0.1, 0.1)}{x_2}+\frac{(0.69, 0.21, 0.1)}{x_3} \end{aligned}$$

Intent:

$$\begin{aligned} \frac{(1.0, 0.0, 0.0)}{y_1}+\frac{(0.73, 0.25, 0.0)}{y_2}+\frac{(1.00, 0.0, 0.0)}{y_3} \end{aligned}$$

7. Extent:

$$\begin{aligned} \frac{(0.65, 0.25, 0.1)}{x_1}+\frac{(0.73, 0.1, 0.0)}{x_2}+\frac{(0.7, 0.2, 0.1)}{x_3} \end{aligned}$$

Intent:

$$\begin{aligned} \frac{(0.65, 0.25, 0.1)}{y_1}+\frac{(1.0, 0.0, 0.0)}{y_2}+\frac{(1.0, 0.0, 0.0)}{y_3} \end{aligned}$$

8. Extent:

$$\begin{aligned} \frac{(0.65, 0.25, 0.1)}{x_1}+\frac{(0.72, 0.1, 0.1)}{x_2}+\frac{(0.69, 0.21, 0.1)}{x_3} \end{aligned}$$

Intent:

$$\begin{aligned} \frac{(1.0, 0.0, 0.0)}{y_1}+\frac{(1.0, 0.0, 0.0)}{y_2}+\frac{(1.0, 0.0, 0.0)}{y_3} \end{aligned}$$

Information: It represents that the student $x_2$ attends maximum 72 percent classes of each faculty whereas the student $x_3$ as second.

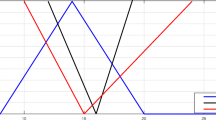
Step (10) The neutrosophic concept lattice can be build using their generated Next Neighbors as shown in Fig. 1.

Fig. 1

A concept lattice generated at (0.7, 0, 0)-granulation as shown in Table 7

This provides an information that the student $x_2$ attends maximum classes of each faculties whereas the student $x_3$ as second. It means the student $x_2$ leaves the classes due to genuine reasons and deserves to get indeterminacy in the attendance, i.e., OD, sick leave, medical leave or other grants.

Similarly, each of the students attend maximum class of faculty $y_2$ due to his/her good teaching, making the class more interactive or strictly follow the rules of university. Hence, the absentee of this faculty are genuine. They should be given leaves to stop them from being debarred from examination as shown in Table 6.

In case the grant leave or other liabilities is given to student $x_1$ or students of faculty $y_1$ then management can easily find their is flaw in the decision. In this way, the proposed method will be useful to analyze the manipulation of attendance due to influence of student and faculty in the system. It will be helpful in minimizing the wrong message about the university management policies towards studying/upcoming students, their parents as well as faculties.

Table 6 The information extracted from Fig. 1

Table 7 The decomposition of context shown in Table 5 at granulation (0.7, 0, 0)

5 The decomposition of neutrosophic context at different granulation

The previous section shows that neutrosophic set-based neutrosophic attendance system needs to be implemented in the education system. It is indeed a requirement to provide a peaceful unbiased environment to the students and faculties. In this case, a problem arises that management do not want all the pattern. They have lack of time and need some results based on their decided parameters for the present absent and uncertainty in the attendance of student. As for example, the university team wants to know the students which has more than 70 percent attendance to grant their leave or other liabilities. Same time the management wants to know which particular faculty students have been given more sick leave, OD, medical leave or grace. In this case, the level of granulation for truth-membership values is given 0.7, absent 0 and uncertain 0, i.e., (0.7, 0, 0). This level can be applied on neutrosophic context shown in Fig. 1. It provides the decomposed context shown in Fig. 2. The concept lattice generated from this context is shown in Fig. 1. It represents that the student $x_2$ attends maximum classes of each faculty, whereas all students attend maximum classes of faculty $y_2$. In this case the leave of student $x_2$ and subject of faculty $y_2$ should be given for each students to stop them being debarred. This corresponds to the neutrosophic concept lattice shown in Fig. 2. However this method provides numerals way to zoom in and zoom out the given contexts for precise analysis of pattern.

Fig. 2

A neutrosophic set-based concept lattice generated from Table 5

The result of both of the methods concordant with subset-based method introduced by Singh (2017) as well as distance method shown in Singh (2018a). However, to achieve this goal the proposed method takes less time complexity. It will be useful for processing any single-valued neutrosophic contexts at user defined multi-granulation (Fig. 3).

Fig. 3

A graphical analysis of the proposed method

6 Discussion

There are less papers that discussed about single-valued neutrosophic concept lattice. The author tried to search some of the potential research papers on this topic in the Scopus data base for comparative analysis of current paper.

The author found some of the papers using the keyword “‘Neutrosophic Concept Lattice”’ in the Scopus indexing as shown in Table 8. The Scopus shows that three-way fuzzy concept lattice using the neutrosophic set is first paper which introduced the idea of neutrosophic concept lattice (Singh 2017). It is published in “International Journal of Machine Learning and Cybernetics, Springer” in Year 2017. Same time this paper is one of the highly cited among all the papers of neutrosophic concept lattice as per Scopus till now. It means the paper provides one of innovative ideas and founding idea in field of neutrosophic concept lattice as discussed in Peng and Dai (2018). Subsequently, others methods are introduced for neutrosophic concept lattice using different metric as shown in Table 8. Some of the closely related methods from them are compared with the proposed methods in Table 9 on various parameters.

Table 8 The papers available on neutrosophic concept lattice in SCOPUS

Table 9 The comparison of the proposed method with recently introduced relevant methods

Table 9 represents the comparative analysis of the proposed method while considering the other methods. It represents that the proposed method is distinct from all of the approaches due to its concept lattice building and navigation at multi-granulation. One of the best examples is given of the proposed method for manipulation of academic attendance analysis. In future, the author will focus on other extensions of neutrosophic set (Singh 2018c; Smarandache 2018) for multi-decision process.

7 Conclusions

The current paper aimed at analysis of hidden pattern in single-valued neutrosophic context using metric of Galois connection and multi-granulation for multi-decision process. One of the real-life examples for the proposed methods are also shown related to academic attendance system. It is shown that the proposed method takes less time complexity when compared to the subset-based methods (Singh 2017, 2018a). However, the multi-granulation provides an alternative way to deal with single-valued neutrosophic context when compared to other available approaches (Singh 2017, 2018a, b).

In the near future, the author will try to focus on introducing some other techniques to deal with neutrosophic context and its randomness measurement.