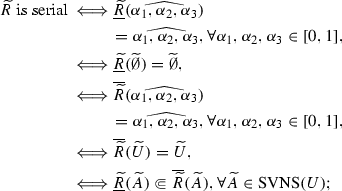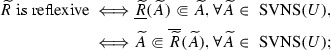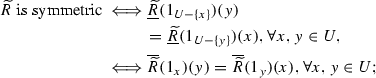A hybrid model of single valued neutrosophic sets and rough sets: single valued neutrosophic rough set model

Abstract

Smarandache initiated neutrosophic sets (NSs) as a tool for handling undetermined information. Wang et al. proposed single valued neutrosophic sets (SVNSs) that is an especial NSs and can be used expediently to deal with real-world problems. In this paper, we propose single valued neutrosophic rough sets by combining single valued neutrosophic sets and rough sets. We study the hybrid model by constructive and axiomatic approaches. Firstly, by using the constructive approach, we propose the lower/upper single valued neutrosophic approximation operators and illustrate the connections between special single valued neutrosophic relations (SVNRs) and the lower/upper single valued neutrosophic approximation operators. Then, by using the axiomatic approach, we discuss the operator-oriented axiomatic characterizations of single valued neutrosophic rough sets. We obtain that different axiom sets of the lower/upper single valued neutrosophic set-theoretic operators guarantee the existence of different classes of SVNRs which produce the same operators. Finally, we introduce single valued neutrosophic rough sets on two-universes and an algorithm of decision making based on single valued neutrosophic rough sets on two-universes, and use an illustrative example to demonstrate the application of the proposed model.

1 Introduction

Although there are many theories of dealing with imprecise information and knowledge, such as fuzzy set theory, intuitionistic fuzzy set theory and rough set theory, they can only solve a part of uncertain problems in real-world. To this end, Smarandache (1998, 1999) initiated neutrosophic set theory by fusing the non-standard analysis and a tri-component set. A NS consists of three membership functions (truth-membership function, indeterminacy membership function and falsity-membership function), where every function value is a real standard or non-standard subset of the nonstandard unit interval $]0^{-}, 1^{+}[$. NSs has achieved good applications in image processing and cluster analysis (Guo and Cheng 2009; Guo and Sengur 2015). By applying the neutrosophic idea to logics, Riverain (Rivieccio 2008) proposed neutrosophic logics which is a generalization of fuzzy logics and studied some basic properties. By combining neutrosophic set theory and rough set theory (Pawlak 1982), Broumi and Smarandache (2014) and Salama and Broumi (2014) initiated a new hybrid mathematical structure called rough neutrosophic sets, handling incomplete and indeterminate information, and studied some operations and their properties.

Wang et al. (2010) proposed SVNSs by simplifying NSs. SVNSs can also be looked as an extension of intuitionistic fuzzy sets (Atanassov 1986), in which three membership functions are unrelated and their function values belong to the unit closed interval. SVNSs results in a new hot research issue. Ye (2013, (2014a) proposed decision making based on correlation coefficients and weighted correlation coefficient of SVNSs, and illustrated the application of proposed methods. Majumdar and Samant (2014) studied distance, similarity and entropy of SVNSs from a theoretical aspect. Şahin and Küçük (2015) proposed a subsethood measure of SVNSs based on distance and showed its effectiveness by an example. Peng et al. (2014) gave some novel operations of SVNSs and proposed a ranking approach which can be used to solve decision-making problems based on outranking relation of simplified neutrosophic numbers. Yang et al. (2016) proposed SVNRs and studied some kinds of kernels and closures of SVNRs.

Pawlak (1982) initiated rough set theory which has proved to be an efficient theory in dealing with imperfect information. For the study of rough sets, the constructive approach and algebraic approach are two important methods (Yao 2015). Many kinds of rough set models were constructed by using the constructive approach including arbitrary binary relation-based rough sets (Yao 1998a, b), covering-based rough sets (Bonikowski et al. 1998; Zhu and Wang 2007), fuzzy rough sets and rough fuzzy sets (Dubois and Prade 1990). Pei and Wu et al. studied generalized fuzzy rough sets from different point of views (Pei 2005; Wu et al. 2003; Yeung et al. 2005). Cornelis et al. (2003) first proposed intuitionistic fuzzy rough sets and obtained some important results. Intuitionistic fuzzy rough sets has been addressed by many researchers (Yang et al. 2012; Zhou and Wu 2008; Yang et al. 2012). Zhang et al. gave a general framework of intuitionistic fuzzy rough set theory (Zhang et al. 2012). By use of the axiomatic approach, rough set approximation operators can be characterized by a pair of dual abstract operators with a set of axioms. Yao (1998a) systematically illustrated axiomatic characterizations of crisp rough sets. Mi and Zhang (2004) studied axiomatic characterizations of fuzzy rough sets. Wu et al. (2016) studied constructions and axiomatic characterizations of (S, T)-fuzzy rough sets based on a triangular conorm S and a triangular norm T. Zhou and Hu (2016) applied axiomatic approaches to rough set models on a complete completely distributive lattice. Zhang (2013) applied interval type-2 fuzzy sets to rough set and studied the constructions and axiomatic characterizations interval type-2 fuzzy sets. Yang et al. (2014) proposed hesitant fuzzy rough sets and studied the model’s axiomatic characterizations by combining hesitant fuzzy sets and rough sets. As a continuation of Yang et al. (2014),  Zhang et al. (2016) further gave the construction and axiomatic characterizations of interval-valued hesitant fuzzy rough sets, and illustrated the application of the model.

SVNSs and rough sets are two different tools of dealing with inaccuracy information. To exploit simultaneously the advantages of SVNSs and rough sets, it is necessary to establish a hybrid model of SVNSs and rough sets. For this purpose, Broumi and Smarandache proposed single valued neutrosophic information systems based on rough set theory. They studied rough approximation of every single valued neutrosophic set in the single valued neutrosophic information system and investigated the knowledge reduction and extension of the single valued neutrosophic information system. Along this line, in the present paper, we shall propose single valued neutrosophic rough sets by fusing SVNSs and rough sets, and explore a general framework of the study of single valued neutrosophic rough sets. Concretely, we shall study the hybrid model by using constructive and axiomatic approaches.

The rest of this paper is organized as follows. In the next section, we provide the basic notions and operations of Pawlak rough sets, NSs and SVNSs. Based on a SVNR, Sect. 3 proposes the notion of single valued neutrosophic rough sets by use of the constructive approach. Properties of lower/upper approximation operators are studied. The connections between special SVNRs and single valued neutrosophic lower/upper approximation operators are explored. In Sect. 4, we investigate the axiomatic characterizations of single valued neutrosophic rough sets. In other words, it is obtained that single valued neutrosophic approximation lower/upper operators can be defined by axioms. In Sect. 5, single valued neutrosophic rough sets on two-universes is introduced, and an example is used to illustrate the usefulness of given rough set model. The last section summarizes the conclusions and gives an outlook for future research.

2 Preliminaries

In this section, we give basic notions and operations on Pawlak rough sets, NSs and SVNSs.

2.1 Pawlak rough sets

Definition 2.1

(Pawlak 1982, 1991). Let U be a non-empty finite universe and R be an equivalence relation in U. (U, R) is called a Pawlak approximation space. $\forall X\subseteq U$, the lower and upper approximations of X, denoted by $\underline{R}(X)$ and $\overline{R}(X)$, are defined as follows, respectively:

$$\begin{aligned} \underline{R}(X)= & {} \{x\in U\mid [x]_{R}\subseteq X\},\\ \overline{R}(X)= & {} \{x\in U\mid [x]_{R}\cap X\ne \emptyset \}, \end{aligned}$$

where $[x]_{R}=\{y\in U\mid (x,y)\in R\}$. $\underline{R}$ and $\overline{R}$ are called as lower and upper approximation operators, respectively. The pair $(\underline{R}(X), \overline{R}(X))$ is called a Pawlak rough set.

2.2 Neutrosophic sets and single valued neutrosophic sets

Definition 2.2

(Smarandache 1998). Let U be a space of points (objects), with a generic element in U denoted by x. A NS $\widetilde{A}$ in U is characterized by three membership functions, a truth-membership function $T_{\widetilde{A}}$, an indeterminacy membership function $I_{\widetilde{A}}$ and a falsity-membership function $F_{\widetilde{A}}$, where $\forall x\in U$, $T_{\widetilde{A}}(x)$, $I_{\widetilde{A}}(x)$ and $F_{\widetilde{A}}(x)$ are real standard or non-standard subsets of $]0^{-},1^{+}[$.

There is no restriction on the sum of $T_{\widetilde{A}}(x)$, $I_{\widetilde{A}}(x)$ and $F_{\widetilde{A}}(x)$, thus $0^{-}\le$ sup $T_{\widetilde{A}}(x)+$ sup $I_{\widetilde{A}}(x)+$ sup $F_{\widetilde{A}}(x)\le 3^{+}$.

Definition 2.3

(Smarandache 1998). Let $\widetilde{A}$ and $\widetilde{B}$ be two NSs in U. If $\forall x\in U$, inf $T_{\widetilde{A}}(x)\le$ inf $T_{\widetilde{B}}(x)$, sup $T_{\widetilde{A}}(x)\le$ sup $T_{\widetilde{B}}(x)$, inf $I_{\widetilde{A}}(x)\ge$ inf $I_{\widetilde{B}}(x)$, sup $I_{\widetilde{A}}(x) \ge$ sup $I_{\widetilde{B}}(x)$, inf $F_{\widetilde{A}}(x)\ge$ inf $F_{\widetilde{B}}(x)$ and sup $F_{\widetilde{A}}(x)\ge$ sup $F_{\widetilde{B}}(x)$, then we called $\widetilde{A}$ is contained in $\widetilde{B}$, denoted by $\widetilde{A}\Subset \widetilde{B}$.

To apply NSs conveniently, Wang et al. proposed SVNSs as follows.

Definition 2.4

(Wang et al. 2010). Let U be a space of points (objects), with a generic element in U denoted by x. A SVNS $\widetilde{A}$ in U is characterized by three membership functions, a truth-membership function $T_{\widetilde{A}}$, an indeterminacy membership function $I_{\widetilde{A}}$ and a falsity-membership function $F_{\widetilde{A}}$, where $\forall x\in U$, $T_{\widetilde{A}}(x),I_{\widetilde{A}}(x),F_{\widetilde{A}}(x)\in [0,1]$.

There is no restriction on the sum of $T_{\widetilde{A}}(x)$, $I_{\widetilde{A}}(x)$, and $F_{\widetilde{A}}(x)$, thus $0\le T_{\widetilde{A}}(x)+I_{\widetilde{A}}(x)+F_{\widetilde{A}}(x)\le 3$.

The SVNS $\widetilde{A}$ can be denoted by $\widetilde{A}=\{\langle x,T_{\widetilde{A}}(x), I_{\widetilde{A}}(x),F_{\widetilde{A}}(x)\rangle \mid x\in U\}$ or $\widetilde{A}=(T_{\widetilde{A}},I_{\widetilde{A}},F_{\widetilde{A}})$. $\forall x\in U$, $\widetilde{A}(x)=(T_{\widetilde{A}}(x),I_{\widetilde{A}}(x), F_{\widetilde{A}}(x))$, and $(T_{\widetilde{A}}(x),I_{\widetilde{A}}(x), F_{\widetilde{A}}(x))$ is called a single valued neutrosophic number.

In this paper, SVNS(U) will denote the family of all SVNSs in U. Let $\widetilde{A}$ be a SVNS in U. If $\forall x\in U$, $T_{\widetilde{A}}(x)=0$ and $I_{\widetilde{A}}(x)=F_{\widetilde{A}}(x)=1$, then $\widetilde{A}$ is called an empty SVNS, denoted by $\widetilde{\emptyset }$. If $\forall x\in U$, $T_{\widetilde{A}}(x)=1$, and $I_{\widetilde{A}}(x)=F_{\widetilde{A}}(x)=0$, then $\widetilde{A}$ is called a full SVNS, denoted by $\widetilde{U}$. $\forall \alpha _{1},\alpha _{2},\alpha _{3}\in [0,1]$, $\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}$ denotes a constant SVNS satisfying, $T_{\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}}(x)=\alpha _{1}, I_{\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}}(x)=\alpha _{2}, F_{\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}}(x)=\alpha _{3}$.

For any $y\in U$, a single valued neutrosophic singleton set $1_{y}$ and its complement $1_{U-\{y\}}$ are defined as: $\forall x\in U$,

$$\begin{aligned}&T_{1_{y}}(x)=\left\{ \begin{array}{ll} 1, &{} x=y\\ 0,&{} x\ne y \end{array}\right. , \ \ I_{1_{y}}(x)=F_{1_{y}}(x)=\left\{ \begin{array}{ll} 0,&{} x=y\\ 1, &{} x\ne y \end{array}\right. ;\\&T_{1_{U-\{y\}}}(x)=\left\{ \begin{array}{ll} 0, &{} x=y\\ 1, &{} x\ne y \end{array}\right. , \\&I_{1_{U-\{y\}}}(x)=F_{1_{U-\{y\}}}(x)=\left\{ \begin{array}{ll} 1, &{} x=y\\ 0, &{} x\ne y \end{array}\right. . \end{aligned}$$

Definition 2.5

(Ye 2014b). Let $\widetilde{A}$ and $\widetilde{B}$ be two SVNSs in U. If for any $x\in U$, $T_{\widetilde{A}}(x)\le T_{\widetilde{B}}(x)$, $I_{\widetilde{A}}(x)\ge I_{\widetilde{B}}(x)$ and $F_{\widetilde{A}}(x)\ge F_{\widetilde{B}}(x)$, then we called $\widetilde{A}$ is contained in $\widetilde{B}$, i.e., $\widetilde{A}\Subset \widetilde{B}$. If $\widetilde{A}\Subset \widetilde{B}$ and $\widetilde{B}\Subset \widetilde{A}$, then we called $\widetilde{A}$ is equal to $\widetilde{B}$, denoted by $\widetilde{A}=\widetilde{B}$.

It is easy to see that Definition 2.5 is consistent to Definition 2.3, and Definition 2.5 can be regarded as a special case of Definition 2.3.

Definition 2.6

(Wang et al. 2010). Let $\widetilde{A}$ be a SVNS in U. The complement of $\widetilde{A}$ is denoted by $\widetilde{A}^{c}$, where $\forall x\in U$, $T_{\widetilde{A}^{c}}(x)=F_{\widetilde{A}}(x)$, $I_{\widetilde{A}^{c}}(x)= 1-I_{\widetilde{A}}(x)$, and $F_{\widetilde{A}^{c}}(x)=T_{\widetilde{A}}(x)$.

Definition 2.7

(Yang et al. 2016). Let $\widetilde{A}$ and $\widetilde{B}$ be two SVNSs in U.

• (1) The union of $\widetilde{A}$ and $\widetilde{B}$ is a SVNS $\widetilde{C}$, denoted by $\widetilde{C}=\widetilde{A}\Cup \widetilde{B}$, where $\forall x\in U$,

  $T_{\widetilde{C}}(x)=T_{\widetilde{A}}(x)\vee T_{\widetilde{B}}(x)$, $I_{\widetilde{C}}(x)=I_{\widetilde{A}}(x)\wedge I_{\widetilde{B}}(x)$ and $F_{\widetilde{C}}(x)=F_{\widetilde{A}}(x)\wedge F_{\widetilde{B}}(x)$;

• (2) The intersection of $\widetilde{A}$ and $\widetilde{B}$ is a SVNS $\widetilde{D}$, denoted by $\widetilde{D}=\widetilde{A}\Cap \widetilde{B}$, where $\forall x\in U$,

  $T_{\widetilde{D}}(x)=T_{\widetilde{A}}(x)\wedge T_{\widetilde{B}}(x)$, $I_{\widetilde{D}}(x)=I_{\widetilde{A}}(x)\vee I_{\widetilde{B}}(x)$, and $F_{\widetilde{D}}(x)=F_{\widetilde{A}}(x)\vee F_{\widetilde{B}}(x)$, where “$\vee$” and “$\wedge$” denote maximum and minimum, respectively.

Proposition 2.1

(Yang et al. 2016). Let $\widetilde{A}$ and $\widetilde{B}$ be two SVNSs in U. The following results hold:

• (1) $\widetilde{A}\Subset \widetilde{A}\Cup \widetilde{B}$ and $\widetilde{B}\Subset \widetilde{A}\Cup \widetilde{B}$;

• (2) $\widetilde{A}\Cap \widetilde{B}\Subset \widetilde{A}$ and $\widetilde{A}\Cap \widetilde{B}\Subset \widetilde{B}$;

• (3) $(\widetilde{A}^{c})^{c}=\widetilde{A}$;

• (4) $(\widetilde{A}\Cup \widetilde{B})^{c}=\widetilde{A}^{c}\Cap \widetilde{B}^{c}$;

• (5) $(\widetilde{A}\Cap \widetilde{B})^{c}=\widetilde{A}^{c}\Cup \widetilde{B}^{c}$.

Table 1 SVNR $\widetilde{R}$

Table 2 Complement $\widetilde{R}^{c}$ of $\widetilde{R}$

3 The constructive approach of single valued neutrosophic rough sets

3.1 The notion of single valued neutrosophic rough sets

In this section, we will introduce notions of single valued neutrosophic approximations and single valued neutrosophic rough sets. To begin with, we recall some notions of single valued neutrosophic relations (Yang et al. 2016).

A SVNS $\widetilde{R}$ in $U\times U$ is called a single valued neutrosophic relation (SVNR) in U, denoted by $\widetilde{R}=\{\langle (x,y),T_{\widetilde{R}}(x,y),I_{\widetilde{R}}(x,y), F_{\widetilde{R}}(x,y)\rangle \mid (x,y)\in U\times U\}$, where $T_{\widetilde{R}}: U\times U\longrightarrow [0,1]$, $I_{\widetilde{R}}: U\times U\longrightarrow [0,1]$, and $F_{\widetilde{R}}: U\times U\longrightarrow [0,1]$ denote the truth-membership function, indeterminacy membership function, and falsity-membership function of $\widetilde{R}$, respectively.

Let $\widetilde{R}$ be a SVNR in U, the complement $\widetilde{R}^{c}$ of $\widetilde{R}$ is defined as,

$$\begin{aligned} \widetilde{R}^{c}= & {} \{\langle (x,y),T_{\widetilde{R}^{c}}(x,y),I_{\widetilde{R}^{c}}(x,y),F_{\widetilde{R}^{c}} (x,y)\rangle \mid (x,y)\\&\in U\times U\}, \end{aligned}$$

where $\forall (x,y)\in U\times U$, $T_{\widetilde{R}^{c}}(x,y)=F_{\widetilde{R}}(x,y)$, $I_{\widetilde{R}^{c}}(x,y)=1-I_{\widetilde{R}}(x,y)$ and $F_{\widetilde{R}^{c}}(x,y)=T_{\widetilde{R}}(x,y)$.

Example 3.1

Let $U=\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\}$. A SVNR $\widetilde{R}$ in U is given in Table 1. We can get $\widetilde{R}^{c}$ which is given in Table 2.

Let $\widetilde{R}$ be a SVNR in U. If $\forall x\in U$, $T_{\widetilde{R}}(x,x)=1$ and $I_{\widetilde{R}}(x,x)=F_{\widetilde{R}}(x,x)=0$, then $\widetilde{R}$ is called a reflexive SVNR. If $\forall x,y\in U$, $T_{\widetilde{R}}(x,y)=T_{\widetilde{R}}(y,x)$, $I_{\widetilde{R}}(x,y)=I_{\widetilde{R}}(y,x)$ and $F_{\widetilde{R}}(x,y)=F_{\widetilde{R}}(y,x)$, then $\widetilde{R}$ is called a symmetric SVNR. If $\forall x\in U$, $\bigvee _{y\in U}T_{\widetilde{R}}(x,y)=1$ and $\bigwedge _{y\in U} I_{\widetilde{R}}(x,y)=\bigwedge _{y\in U}F_{\widetilde{R}}(x,y)=0$, then $\widetilde{R}$ is called a serial SVNR. If $\forall x,y,z\in U$, $\bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge T_{\widetilde{R}}(y,z))\le T_{\widetilde{R}}(x,z)$, $\bigwedge _{y\in U}(I_{\widetilde{R}}(x,y)\vee I_{\widetilde{R}}(y,z))\ge I_{\widetilde{R}}(x,z)$ and $\bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee F_{\widetilde{R}}(y,z))\ge F_{\widetilde{R}}(x,z)$, then $\widetilde{R}$ is called a transitive SVNR, where “$\vee$” and “$\wedge$” denote maximum and minimum, respectively.

Similarly to the union and intersection of SVNSs, we can define the union $\widetilde{R_{1}}\Cup \widetilde{R_{2}}$ and intersection $\widetilde{R_{1}}\Cap \widetilde{R_{2}}$ of two SVNRs $\widetilde{R_{1}}$ and $\widetilde{R_{1}}$. It is easy to verify that the union and intersection of SVNRs satisfy commutative law, associative law and distributive law.

Definition 3.1

Let $\widetilde{R}$ be a SVNR in U, the tuple $(U, \widetilde{R})$ is called a single valued neutrosophic approximation space. $\forall \widetilde{A}\in$ SVNS(U), the lower and upper approximations of $\widetilde{A}$ with respect to $(U, \widetilde{R})$, denoted by $\underline{\widetilde{R}}(\widetilde{A})$ and $\overline{\widetilde{R}}(\widetilde{A})$, are two SVNSs whose membership functions are defined as: $\forall x\in U$,

$$\begin{aligned} T_{\underline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee T_{\widetilde{A}}(y)),\\ I_{\underline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge I_{\widetilde{A}}(y)),\\ F_{\underline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge F_{\widetilde{A}}(y));\\ T_{\overline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge T_{\widetilde{A}}(y)),\\ I_{\overline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigwedge _{y\in U}(I_{\widetilde{R}}(x,y)\vee I_{\widetilde{A}}(y)),\\ F_{\overline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee F_{\widetilde{A}}(y)). \end{aligned}$$

The pair $(\underline{\widetilde{R}}(\widetilde{A}),\overline{\widetilde{R}}(\widetilde{A}))$ is called the single valued neutrosophic rough set of $\widetilde{A}$ with respect to $(U,\widetilde{R})$. $\underline{\widetilde{R}}$ and $\overline{\widetilde{R}}$ are referred to as the single valued neutrosophic lower and upper approximation operators, respectively.

Example 3.2

Let $U=\{x_{1},x_{2},x_{3}\}$, $\widetilde{R}\in$ SVNS$(U\times U)$ is given in Table 3. $\widetilde{A}=\{\langle x_{1},(0.2,0.8,0.1)\rangle , \langle x_{2}, (1,0.3,1)\rangle ,\langle x_{3},(0.5,0.3,0)\rangle \}$ is a SVNS in U.

Table 3 SVNR $\widetilde{R}$

According to Definition 3.1, we have

$$\begin{aligned} T_{\underline{\widetilde{R}}(\widetilde{A})}(x_{1})= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x_{1},y)\vee T_{\widetilde{A}}(y))=0.5,\\ I_{\underline{\widetilde{R}}(\widetilde{A})}(x_{1})= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x_{1},y))\wedge I_{\widetilde{A}}(y))=0.8,\\ F_{\underline{\widetilde{R}}(\widetilde{A})}(x_{1})= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x_{1},y)\wedge F_{\widetilde{A}}(y))=0.2;\\ T_{\overline{\widetilde{R}}(\widetilde{A})}(x_{1})= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x_{1},y)\wedge T_{\widetilde{A}}(y))=0.5,\\ I_{\overline{\widetilde{R}}(\widetilde{A})}(x_{1})= & {} \bigwedge _{y\in U}(I_{\widetilde{R}}(x_{1},y)\vee I_{\widetilde{A}}(y))=0.3,\\ F_{\overline{\widetilde{R}}(\widetilde{A})}(x_{1})= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x_{1},y)\vee F_{\widetilde{A}}(y))=0.5. \end{aligned}$$

Hence, $\underline{\widetilde{R}}(\widetilde{A})(x_{1})=(0.5,0.8,0.2)$ and $\overline{\widetilde{R}}(\widetilde{A})(x_{1})=(0.5,0.3,0.5)$.

Similarly, we can obtain

$$\begin{aligned} \underline{\widetilde{R}}(\widetilde{A})(x_{2})= & {} (0.3,0.8,0.5), \overline{\widetilde{R}}(\widetilde{A}) (x_{2})=(0.5,0.4,0),\\ \underline{\widetilde{R}}(\widetilde{A})(x_{3})= & {} (0.2,0.3,0.4), \overline{\widetilde{R}}(\widetilde{A})(x_{3})=(0.5,0.3,0). \end{aligned}$$

3.2 The properties of single valued neutrosophic rough sets

Next, we discuss the properties of single valued neutrosophic rough sets.

Theorem 3.1

Let $(U, \widetilde{R})$ be a single valued neutrosophic approximation space. The single valued neutrosophic lower and upper approximation operators defined in Definition 3.1 have the following properties: $\forall \widetilde{A},\widetilde{B}\in$ SVNS(U), $\forall \alpha _{1},\alpha _{2},\alpha _{3}\in [0,1]$,

• (1) $\underline{\widetilde{R}}(\widetilde{U})=\widetilde{U}$, $\overline{\widetilde{R}}(\widetilde{\emptyset })=\widetilde{\emptyset }$;

• (2) If $\widetilde{A}\Subset \widetilde{B}$, then $\underline{\widetilde{R}}(\widetilde{A})\Subset \underline{\widetilde{R}}(\widetilde{B})$ and $\overline{\widetilde{R}}(\widetilde{A})\Subset \overline{\widetilde{R}}(\widetilde{B})$;

• (3) $\underline{\widetilde{R}}(\widetilde{A}\Cap \widetilde{B})=\underline{\widetilde{R}}(\widetilde{A})\Cap \underline{\widetilde{R}}(\widetilde{B})$, $\overline{\widetilde{R}}(\widetilde{A}\Cup \widetilde{B})=\overline{\widetilde{R}}(\widetilde{A})\Cup \overline{\widetilde{R}}(\widetilde{B})$;

• (4) $\underline{\widetilde{R}}(\widetilde{A}\Cup \widetilde{B})\Supset \underline{\widetilde{R}}(\widetilde{A})\Cup \underline{\widetilde{R}}(\widetilde{B})$, $\overline{\widetilde{R}}(\widetilde{A}\Cap \widetilde{B})\Subset \overline{\widetilde{R}}(\widetilde{A})\Cap \overline{\widetilde{R}}(\widetilde{B})$;

• (5) $\underline{\widetilde{R}}(\widetilde{A}^{c})= (\overline{\widetilde{R}}(\widetilde{A}))^{c}$, $\overline{\widetilde{R}}(\widetilde{A}^{c})= (\underline{\widetilde{R}}(\widetilde{A}))^{c};$

• (6) $\underline{\widetilde{R}}(A\Cup \widehat{\alpha _{1},\alpha _{2},\alpha _{3}})=\underline{\widetilde{R}}(\widetilde{A})\Cup \widehat{\alpha _{1},\alpha _{2},\alpha _{3}}$, $\overline{\widetilde{R}}(A\Cap \widehat{\alpha _{1},\alpha _{2},\alpha _{3}})=\overline{\widetilde{R}} (\widetilde{A})\Cap \widehat{\alpha _{1},\alpha _{2},\alpha _{3}}$;

• (7) $\underline{\widetilde{R}}(\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}) =\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}\Longleftrightarrow \underline{\widetilde{R}}(\widetilde{\emptyset })=\widetilde{\emptyset }$,

  $\overline{\widetilde{R}}(\widehat{\alpha _{1},\alpha _{2},\alpha _{3}})= \widehat{\alpha _{1},\alpha _{2},\alpha _{3}}\Longleftrightarrow \overline{\widetilde{R}}(\widetilde{U})=\widetilde{U}$.

Proof

(2) and (4) are following immediately from Definition 3.1. We only show (1), (3) and (5)–(7).

(1) By Definition 3.1, $\forall x\in U$,

$$\begin{aligned} T_{\underline{\widetilde{R}}(\widetilde{U})}(x)= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee T_{\widetilde{U}}(y))=\bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee 1)=1,\\ I_{\underline{\widetilde{R}}(\widetilde{U})}(x)= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge I_{\widetilde{U}}(y))\\= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge 0)=0,\\ F_{\underline{\widetilde{R}}(\widetilde{U})}(x)= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge F_{\widetilde{U}}(y))=\bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge 0)=0. \end{aligned}$$

Therefore, $\underline{\widetilde{R}}(\widetilde{U})=\widetilde{U}$.

By Definition 3.1,

$$\begin{aligned} T_{\overline{\widetilde{R}}(\widetilde{\emptyset })}(x)= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge T_{\widetilde{\emptyset }}(y))=\bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge 0)=0,\\ I_{\overline{\widetilde{R}}(\widetilde{\emptyset })}(x)= & {} \bigwedge _{y\in U}(I_{\widetilde{R}}(x,y)\vee I_{\widetilde{\emptyset }}(y))=\bigwedge _{y\in U}(I_{\widetilde{R}}(x,y)\vee 1)=1,\\ F_{\overline{\widetilde{R}}(\widetilde{\emptyset })}(x)= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee F_{\widetilde{\emptyset }}(y))=\bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee 1)=1. \end{aligned}$$

Thus, $\overline{\widetilde{R}}(\widetilde{\emptyset })=\widetilde{\emptyset }$.

(3) By Definitions 2.6 and 3.1, $\forall x\in U$,

$$\begin{aligned} T_{\underline{\widetilde{R}}(\widetilde{A}\Cap \widetilde{B})}(x)= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee T_{\widetilde{A}\Cap \widetilde{B}}(y))\\= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee (T_{\widetilde{A}}(y)\wedge T_{\widetilde{B}}(y)))\\= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee T_{\widetilde{A}}(y))\\&\wedge \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee T_{\widetilde{B}}(y))\\= & {} T_{\underline{\widetilde{R}}(\widetilde{A})}(x)\wedge T_{\underline{\widetilde{R}}(\widetilde{B})}(x),\\ I_{\underline{\widetilde{R}}(\widetilde{A}\Cap \widetilde{B})}(x)= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge I_{\widetilde{A}\Cap \widetilde{B}}(y))\\= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge (I_{\widetilde{A}}(y)\vee I_{\widetilde{B}}(y)))\\= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge I_{\widetilde{A}}(y))\\&\vee \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge I_{\widetilde{B}}(y))\\= & {} I_{\underline{\widetilde{R}}(\widetilde{A})}(x)\vee I_{\underline{\widetilde{R}}(\widetilde{B})}(x),\\ F_{\underline{\widetilde{R}}(\widetilde{A}\Cap \widetilde{B})}(x)= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge F_{\widetilde{A}\Cap \widetilde{B}}(y))\\= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y))\wedge (F_{\widetilde{A}}(y)\vee F_{\widetilde{B}}(y)))\\= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge F_{\widetilde{A}}(y))\\&\vee \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge F_{\widetilde{B}}(y))\\= & {} F_{\underline{\widetilde{R}}(\widetilde{A})}(x)\vee F_{\underline{\widetilde{R}}(\widetilde{B})}(x). \end{aligned}$$

Thus, $\underline{\widetilde{R}}(\widetilde{A}\Cap \widetilde{B})=\underline{\widetilde{R}}(\widetilde{A})\Cap \underline{\widetilde{R}}(\widetilde{B})$. Similarly, we can show $\overline{\widetilde{R}}(\widetilde{A}\Cup \widetilde{B})=\overline{\widetilde{R}}(\widetilde{A})\Cup \overline{\widetilde{R}}(\widetilde{B})$.

(5) We only need to show the former part. $\forall x\in U$,

$$\begin{aligned} T_{\underline{\widetilde{R}}(\widetilde{A}^{c})}(x)= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee T_{\widetilde{A}^{c}}(y))\\= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee F_{\widetilde{A}}(y))=F_{\overline{\widetilde{R}}(\widetilde{A})}(x)\\= & {} T_{(\overline{\widetilde{R}}(\widetilde{A}))^{c}}(x),\\ I_{\underline{\widetilde{R}}(\widetilde{A}^{c})}(x)= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge I_{\widetilde{A}^{c}}(y))\\= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge (1-I_{\widetilde{A}}(y)))\\= & {} 1-\bigwedge _{y\in U}(I_{\widetilde{R}}(x,y)\vee I_{\widetilde{A}}(y))\\= & {} 1-I_{\overline{\widetilde{R}}(\widetilde{A})}(x)=I_{(\overline{\widetilde{R}}(\widetilde{A}))^{c}}(x),\\ F_{\underline{\widetilde{R}}(\widetilde{A}^{c})}(x)= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge F_{\widetilde{A}^{c}}(y))\\= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge T_{\widetilde{A}}(y))=T_{\overline{\widetilde{R}}(\widetilde{A})}(x)\\= & {} F_{(\overline{\widetilde{R}}(\widetilde{A}))^{c}}(x).\\ \end{aligned}$$

So $\underline{\widetilde{R}}(\widetilde{A}^{c})=(\overline{\widetilde{R}} (\widetilde{A}))^{c}$.

(6) By Definition 3.1, $\forall x\in U$, we have

$$\begin{aligned} T_{\underline{\widetilde{R}}(\widetilde{A}\Cup \widehat{\alpha _{1},\alpha _{2},\alpha _{3}})}(x)= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee T_{\widetilde{A}\Cup \widehat{\alpha _{1},\alpha _{2},\alpha _{3}}}(y))\\= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee (T_{\widetilde{A}}(y)\vee T_{\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}}(y)))\\= & {} \bigwedge _{y\in U}\left( F_{\widetilde{R}}(x,y)\vee T_{\widetilde{A}}(y)\vee \alpha _{1}\right) \\= & {} \left( \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee T_{\widetilde{A}}(y))\right) \vee \alpha _{1}\\= & {} T_{\underline{\widetilde{R}}(\widetilde{A})}(x)\vee \alpha _{1},\\ I_{\underline{\widetilde{R}}(\widetilde{A}\Cup \widehat{\alpha _{1},\alpha _{2},\alpha _{3}})}(x)= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge I_{\widetilde{A}\Cup \widehat{\alpha _{1},\alpha _{2},\alpha _{3}}}(y))\\= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge (I_{\widetilde{A}}(y)\wedge I_{\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}}(y)))\\= & {} \bigvee _{y\in U}\left( ((1-I_{\widetilde{R}}(x,y))\wedge I_{\widetilde{A}}(y))\wedge \alpha _{2}\right) \\= & {} \left( \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge I_{\widetilde{A}}(y))\right) \wedge \alpha _{2}\\= & {} I_{\underline{\widetilde{R}}(\widetilde{A})}(x)\wedge \alpha _{2},\\ F_{\underline{\widetilde{R}}(\widetilde{A}\Cup \widehat{\alpha _{1},\alpha _{2},\alpha _{3}})}(x)= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge F_{\widetilde{A}\Cup \widehat{\alpha _{1},\alpha _{2},\alpha _{3}}}(y))\\= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge (\widetilde{F_{\widetilde{A}}}(y)\wedge F_{\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}}(y)))\\= & {} \bigvee _{y\in U}\left( T_{\widetilde{R}}(x,y)\wedge F_{\widetilde{A}}(y)\wedge \alpha _{3}\right) \\= & {} \left( \bigvee _{y\in U}\left( T_{\widetilde{R}}(x,y)\wedge F_{\widetilde{A}}(y)\right) \right) \wedge \alpha _{3}\\= & {} F_{\underline{\widetilde{R}}(\widetilde{A})}(x)\wedge \alpha _{3}.\\ \end{aligned}$$

So $\underline{\widetilde{R}}(\widetilde{A}\Cup \widehat{\alpha _{1},\alpha _{2},\alpha _{3}})=\underline{\widetilde{R}}(\widetilde{A})\Cup \widehat{\alpha _{1},\alpha _{2},\alpha _{3}}$.

Similarly, we can show $\overline{\widetilde{R}}(\widetilde{A}\Cap \widehat{\alpha _{1},\alpha _{2},\alpha _{3}})=\overline{\widetilde{R}}(\widetilde{A})\Cap \widehat{\alpha _{1},\alpha _{2},\alpha _{3}}$.

(7) If $\underline{\widetilde{R}}(\widetilde{\emptyset })=\widetilde{\emptyset }$, according to (6), we have $\underline{\widetilde{R}}(\widehat{\alpha _{1},\alpha _{2},\alpha _{3}})= \underline{\widetilde{R}}(\widetilde{\emptyset }\Cup \widehat{\alpha _{1},\alpha _{2},\alpha _{3}})= \underline{\widetilde{R}}(\widetilde{\emptyset })\Cup \widehat{\alpha _{1},\alpha _{2},\alpha _{3}} =\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}$.

Conversely, if $\forall \alpha _{1},\alpha _{2},\alpha _{3}\in [0,1]$, $\underline{\widetilde{R}}(\widehat{\alpha _{1},\alpha _{2},\alpha _{3}})=\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}$, Take $\alpha _{1}=0$ and $\alpha _{2}=\alpha _{3}=1$, i.e., $\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}=\widetilde{\emptyset }$, then we have $\underline{\widetilde{R}}(\widetilde{\emptyset })=\widetilde{\emptyset }$.

Similarly, we can show $\overline{\widetilde{R}}(\widehat{\alpha _{1},\alpha _{2},\alpha _{3}})=\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}\Longleftrightarrow \overline{\widetilde{R}}(U)=U$. $\square$

Theorem 3.2

Let $\widetilde{R_{1}},\widetilde{R_{2}}$ be two SVNRs in U, $\forall \widetilde{A}\in$ SVNS(U), we have

• (1) $\underline{\widetilde{R_{1}}\Cup \widetilde{R_{2}}}(\widetilde{A})= \underline{\widetilde{R_{1}}}(\widetilde{A})\Cap \underline{\widetilde{R_{2}}}(\widetilde{A})$;

• (2) $\overline{\widetilde{R_{1}}\Cup \widetilde{R_{2}}}(\widetilde{A}) =\overline{\widetilde{R_{1}}}(\widetilde{A})\Cup \overline{\widetilde{R_{2}}} (\widetilde{A})$.

Proof

(1) $\forall x\in U$, by Definition 3.1, we have

$$\begin{aligned} T_{\underline{\widetilde{R_{1}}\Cup \widetilde{R_{2}}}(\widetilde{A})}(x)= & {} \bigwedge _{y\in U}(F_{\widetilde{R_{1}}\Cup \widetilde{R_{2}}}(x,y)\vee T_{\widetilde{A}}(y))\\= & {} \bigwedge _{y\in U}([F_{\widetilde{R_{1}}}(x,y)\wedge F_{\widetilde{R_{2}}}(x,y)]\vee T_{\widetilde{A}}(y))\\= & {} \bigwedge _{y\in U}([F_{\widetilde{R_{1}}}(x,y)\vee T_{\widetilde{A}}(y)]\wedge [F_{\widetilde{R_{2}}}(x,y)\vee T_{\widetilde{A}}(y)])\\= & {} \bigwedge _{y\in U}(F_{\widetilde{R_{1}}}(x,y)\vee T_{\widetilde{A}}(y))\wedge \bigwedge _{y\in U} (F_{\widetilde{R_{2}}}(x,y)\vee T_{\widetilde{A}}(y))\\= & {} T_{\underline{\widetilde{R_{1}}}(\widetilde{A})}(x)\wedge T_{\underline{\widetilde{R_{2}}}(\widetilde{A})}(x),\\ I_{\underline{\widetilde{R_{1}}\Cup \widetilde{R_{2}}}(\widetilde{A})}(x)= & {} \bigvee _{y\in U}((1-I_{\widetilde{R_{1}}\Cup \widetilde{R_{2}}}(x,y))\wedge I_{\widetilde{A}}(y))\\= & {} \bigvee _{y\in U}([(1-I_{\widetilde{R_{1}}}(x,y))\vee (1-I_{\widetilde{R_{2}}}(x,y))]\wedge I_{\widetilde{A}}(y))\\= & {} \bigvee _{y\in U}([(1-I_{\widetilde{R_{1}}}(x,y))\wedge I_{\widetilde{A}}(y)]\vee [(1-I_{\widetilde{R_{2}}}(x,y))\wedge I_{\widetilde{A}}(y)])\\= & {} \bigvee _{y\in U}((1-I_{\widetilde{R_{1}}}(x,y))\wedge I_{\widetilde{A}}(y))\vee \bigvee _{y\in U} ((1-I_{\widetilde{R_{2}}}(x,y))\wedge I_{\widetilde{A}}(y))\\= & {} I_{\underline{\widetilde{R_{1}}}(\widetilde{A})}(x)\vee I_{\underline{\widetilde{R_{2}}}(\widetilde{A})}(x),\\ F_{\underline{\widetilde{R_{1}}\Cup \widetilde{R_{2}}}(\widetilde{A})}(x)= & {} \bigvee _{y\in U}(T_{\widetilde{R_{1}}\Cup \widetilde{R_{2}}}(x,y)\wedge F_{\widetilde{A}}(y))\\= & {} \bigvee _{y\in U}([T_{\widetilde{R_{1}}}(x,y)\vee T_{\widetilde{R_{2}}}(x,y)]\wedge F_{\widetilde{A}}(y))\\= & {} \bigvee _{y\in U}([T_{\widetilde{R_{1}}}(x,y)\wedge F_{\widetilde{A}}(y)]\vee [T_{\widetilde{R_{2}}}(x,y)\wedge F_{\widetilde{A}}(y)])\\= & {} \bigvee _{y\in U}(T_{\widetilde{R_{1}}}(x,y)\wedge F_{A}(y))\vee \bigvee _{y\in U} (T_{\widetilde{R_{2}}}(x,y)\wedge F_{\widetilde{A}}(y))\\= & {} F_{\underline{\widetilde{R_{1}}}(\widetilde{A})}(x)\vee F_{\underline{\widetilde{R_{2}}}(\widetilde{A})}(x). \end{aligned}$$

Hence, $\underline{\widetilde{R_{1}}\Cup \widetilde{R_{2}}}(\widetilde{A})=\underline{\widetilde{R_{1}}}(\widetilde{A})\Cap \underline{\widetilde{R_{2}}}(\widetilde{A})$.

(2) By (1) and Theorem 3.1 (5), $\overline{\widetilde{R_{1}}\Cup \widetilde{R_{2}}}(\widetilde{A})=(\underline{\widetilde{R_{1}}\Cup \widetilde{R_{2}}}(\widetilde{A}^{c}))^{c}=(\underline{\widetilde{R_{1}}} (\widetilde{A}^{c})\Cap \underline{\widetilde{R_{2}}}(\widetilde{A}^{c}))^{c}=(\underline{\widetilde{R_{1}}} (\widetilde{A}^{c}))^{c} \Cup (\underline{\widetilde{R_{2}}}(\widetilde{A}^{c}))^{c} =\overline{\widetilde{R_{1}}}(\widetilde{A})\Cup \overline{\widetilde{R_{2}}}(\widetilde{A})$. $\square$

Theorem 3.3

Let $\widetilde{R_{1}}$ and $\widetilde{R_{2}}$ be two SVNRs in U, $\forall \widetilde{A}\in$ SVNS(U), we have

• (1) $\underline{\widetilde{R_{1}}\Cap \widetilde{R_{2}}} (\widetilde{A})\Supset \underline{\widetilde{R_{1}}}(\widetilde{A}) \Cup \underline{\widetilde{R_{2}}}(\widetilde{A})\Supset \underline{\widetilde{R_{1}}}(\widetilde{A}) \Cap \underline{\widetilde{R_{2}}}(\widetilde{A})$;

• (2) $\overline{\widetilde{R_{1}}\Cap \widetilde{R_{2}}}(\widetilde{A})\Subset \overline{\widetilde{R_{1}}}(\widetilde{A}) \Cap \overline{\widetilde{R_{2}}}(\widetilde{A})$.

Proof

(1) $\forall x\in U$, by Definition 3.1,

$$\begin{aligned} T_{\underline{\widetilde{R_{1}}\Cap \widetilde{R_{2}}}(\widetilde{A})}(x)= & {} \bigwedge _{y\in U}(F_{\widetilde{R_{1}}\Cap \widetilde{R_{2}}}(x,y)\vee T_{\widetilde{A}}(y))\\= & {} \bigwedge _{y\in U}([F_{\widetilde{R_{1}}}(x,y)\vee F_{\widetilde{R_{2}}}(x,y)]\vee T_{\widetilde{A}}(y))\\= & {} \bigwedge _{y\in U}([F_{\widetilde{R_{1}}}(x,y)\vee T_{\widetilde{A}}(y)]\vee [F_{\widetilde{R_{2}}}(x,y)\\&\vee \, T_{\widetilde{A}}(y)])\\\ge & {} \bigwedge _{y\in U}(F_{\widetilde{R_{1}}}(x,y)\\&\vee \, T_{\widetilde{A}}(y))\vee \bigwedge _{y\in U} (F_{\widetilde{R_{2}}}(x,y)\vee T_{\widetilde{A}}(y))\\= & {} T_{\underline{\widetilde{R_{1}}}(\widetilde{A})}(x)\vee T_{\underline{\widetilde{R_{2}}}(\widetilde{A})}(x),\\ I_{\underline{\widetilde{R_{1}}\Cap \widetilde{R_{2}}}(\widetilde{A})}(x)= & {} \bigvee _{y\in U}((1-I_{\widetilde{R_{1}}\Cap \widetilde{R_{2}}}(x,y))\wedge I_{\widetilde{A}}(y))\\= & {} \bigvee _{y\in U}([(1-I_{\widetilde{R_{1}}}(x,y))\wedge (1-I_{\widetilde{R_{2}}}(x,y))]\\&\wedge \, I_{\widetilde{A}}(y))\\= & {} \bigvee _{y\in U} ([(1-I_{\widetilde{R_{1}}}(x,y))\wedge I_{\widetilde{A}}(y)]\\&\wedge \, [(1-I_{\widetilde{R_{2}}}(x,y))\wedge I_{\widetilde{A}}(y)])\\\le & {} \bigvee _{y\in U}((1-I_{\widetilde{R_{1}}}(x,y)\wedge I_{\widetilde{A}}(y))\\&\wedge \,\bigvee _{y\in U} ((1-I_{\widetilde{R_{2}}}(x,y)\wedge I_{\widetilde{A}}(y))\\= & {} I_{\underline{\widetilde{R_{1}}}(\widetilde{A})}(x)\wedge I_{\underline{\widetilde{R_{2}}}(\widetilde{A})}(x),\\ F_{\underline{\widetilde{R_{1}}\Cap \widetilde{R_{2}}}(\widetilde{A})}(x)= & {} \bigvee _{y\in U}(T_{\widetilde{R_{1}}\Cap \widetilde{R_{2}}}(x,y)\wedge F_{\widetilde{A}}(y))\\= & {} \bigvee _{y\in U}([T_{\widetilde{R_{1}}}(x,y)\wedge T_{\widetilde{R_{2}}}(x,y)]\wedge F_{\widetilde{A}}(y))\\= & {} \bigvee _{y\in U} ([T_{\widetilde{R_{1}}}(x,y)\wedge F_{\widetilde{A}}(y)]\\&\wedge \, [T_{\widetilde{R_{2}}}(x,y)\wedge F_{\widetilde{A}}(y)])\\\le & {} \bigvee _{y\in U}(T_{\widetilde{R_{1}}}(x,y)\wedge F_{\widetilde{A}}(y))\\&\wedge \,\bigvee _{y\in U} (T_{\widetilde{R_{2}}}(x,y)\wedge F_{\widetilde{A}}(y))\\= & {} F_{\underline{\widetilde{R_{1}}}(\widetilde{A})}(x)\wedge F_{\underline{\widetilde{R_{2}}}(\widetilde{A})}(x). \end{aligned}$$

Hence, $\underline{\widetilde{R_{1}}\Cap \widetilde{R_{2}}}(\widetilde{A})\Supset \underline{\widetilde{R_{1}}}(\widetilde{A})\Cup \underline{\widetilde{R_{2}}}(\widetilde{A})$.

So $\underline{\widetilde{R_{1}}\Cap \widetilde{R_{2}}} (\widetilde{A})\Supset \underline{\widetilde{R_{1}}}(\widetilde{A}) \Cup \underline{\widetilde{R_{2}}}(\widetilde{A})\Supset \underline{\widetilde{R_{1}}}(\widetilde{A}) \Cap \underline{\widetilde{R_{2}}}(\widetilde{A})$.

(2) By (1) and Theorem 3.1 (5),

$$\begin{aligned} \overline{\widetilde{R_{1}}\Cap \widetilde{R_{2}}}(\widetilde{A})= & {} (\underline{\widetilde{R_{1}}\Cap \widetilde{R_{2}}}(\widetilde{A}^{c}))^{c}\Subset (\underline{\widetilde{R_{1}}} (\widetilde{A}^{c})\Cup \underline{R_{2}}(\widetilde{A}^{c}))^{c}\\= & {} (\underline{\widetilde{R_{1}}} (\widetilde{A}^{c}))^{c} \Cap (\underline{R_{2}}(\widetilde{A}^{c}))^{c}= \overline{\widetilde{R_{1}}}(\widetilde{A})\Cap \overline{\widetilde{R_{2}}}(\widetilde{A}). \end{aligned}$$

$\square$

By Theorem 3.3, we have the following corollary:

Corollary 3.1

Let $\widetilde{R_{1}}$ and $\widetilde{R_{2}}$ be two SVNRs in U, $\forall \widetilde{A}\in$ SVNS(U). If $\widetilde{R_{1}}\Subset \widetilde{R_{2}}$, then

$\underline{\widetilde{R_{2}}}(\widetilde{A})\Subset \underline{\widetilde{R_{1}}}(\widetilde{A})$ and $\overline{\widetilde{R_{1}}}(\widetilde{A})\Subset \overline{\widetilde{R_{2}}}(\widetilde{A})$.

The following Theorem 3.4 establishes the relationships between special SVNRs and single valued neutrosophic approximation operators.

Theorem 3.4

Let $(U, \widetilde{R})$ be a single valued neutrosophic approximation space. $\underline{\widetilde{R}}(\widetilde{A})$ and $\overline{\widetilde{R}}(\widetilde{A})$ are the lower and upper approximation in Definition 3.1, then we have

• (1)
  
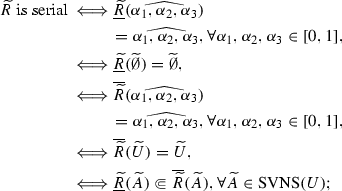
• (2)
  
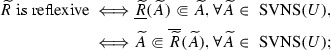
• (3)
  
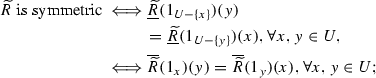
• (4)
  

Proof

By the duality of lower and upper single valued neutrosophic approximation operators, we need only to prove the properties for the upper single valued neutrosophic approximation operator.

(1) According to Theorem 3.1 (1) and (7), we only need to show

$\widetilde{R}$ is serial $\Longleftrightarrow \underline{\widetilde{R}}(\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}) =\widehat{\alpha _{1},\alpha _{2},\alpha _{3}} \Longleftrightarrow \underline{\widetilde{R}}(\widetilde{A})\Subset \overline{\widetilde{R}}(\widetilde{A})$, $\forall \alpha _{1},\alpha _{2},\alpha _{3}\in [0,1]$.

(i) We first show $\widetilde{R}$ is serial $\Longleftrightarrow \underline{\widetilde{R}}(\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}) =\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}$, $\forall \alpha _{1},\alpha _{2},\alpha _{3}\in [0,1]$.

If $\widetilde{R}$ is serial, then $\forall x\in U$, $\bigvee _{y\in U}T_{\widetilde{R}}(x,y)=1$ and $\bigwedge _{y\in U}I_{\widetilde{R}}(x,y)=\bigwedge _{y\in U} F_{\widetilde{R}}(x,y)=0$. $\forall \alpha _{1},\alpha _{2},\alpha _{3}\in [0,1]$, by Definition 3.1, $\forall x\in U$,

$$\begin{aligned} T_{\underline{\widetilde{R}}(\widehat{\alpha _{1},\alpha _{2}, \alpha _{3}})}(x)= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee T_{\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}}(y))\\= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee \alpha _{1})\\= & {} \alpha _{1}\vee \bigwedge _{y\in U}F_{\widetilde{R}}(x,y)=\alpha _{1}\vee 0=\alpha _{1},\\ I_{\underline{\widetilde{R}}(\widehat{\alpha _{1},\alpha _{2},\alpha _{3}})}(x)= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge I_{\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}}(y))\\= & {} \bigvee _{y\in U} ((1-I_{\widetilde{R}}(x,y))\wedge \alpha _{2})\\= & {} \alpha _{2}\wedge \left( 1-\bigwedge _{y\in U}I_{\widetilde{R}}(x,y)\right) =\alpha _{2}\wedge (1-0)\\= & {} \alpha _{2},\\ F_{\underline{\widetilde{R}}(\widehat{\alpha _{1},\alpha _{2},\alpha _{3}})}(x)= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge F_{\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}}(y))\\= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y))\wedge \alpha _{3})\\= & {} \alpha _{3}\wedge \bigvee _{y\in U}T_{\widetilde{R}}(x,y)=\alpha _{3}\wedge 1 =\alpha _{3}. \end{aligned}$$

Therefore, $\forall \alpha _{1},\alpha _{2},\alpha _{3}\in [0,1]$, $\underline{\widetilde{R}}(\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}) =\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}.$

Conversely, if $\forall \alpha _{1},\alpha _{2},\alpha _{3}\in [0,1]$, $\underline{\widetilde{R}}(\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}) =\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}.$ Take $\alpha _{1}=0, \alpha _{2}=\alpha _{3}=1$, according to Definition 3.1, $\forall x\in U$,

$$\begin{aligned} 0= & {} T_{\underline{\widetilde{R}}(\widehat{0,1,1})}(x)= \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee T_{\widehat{0,1,1}}(y))\\= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee 0)=\bigwedge _{y\in U}F_{\widetilde{R}}(x,y),\\ 1= & {} I_{\underline{\widetilde{R}}(\widehat{0,1,1})}(x)=\bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge I_{\widehat{0,1,1}}(y))\\= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge 1)=1\\&-\bigwedge _{y\in U}I_{\widetilde{R}}(x,y),\text { it follows that }\bigwedge _{y\in U}I_{\widetilde{R}}(x,y)=0,\\ 1= & {} F_{\underline{\widetilde{R}}(\widehat{0,1,1})}(x)=\bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge F_{\widehat{0,1,1}}(y))\\= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge 1)=\bigvee _{y\in U}T_{\widetilde{R}}(x,y). \end{aligned}$$

Then, $\widetilde{R}$ is serial.

So $\widetilde{R}$ is serial $\Longleftrightarrow \underline{\widetilde{R}}(\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}) =\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}$, $\forall \alpha _{1},\alpha _{2},\alpha _{3}\in [0,1]$.

(ii) Next, we show $\widetilde{R}$ is serial $\Longleftrightarrow \underline{\widetilde{R}}(\widetilde{A})\Subset \overline{\widetilde{R}}(\widetilde{A})$, $\forall \widetilde{A}\in$ SVNS(U).

Assume that $\widetilde{R}$ is serial. As U is finite, there exists $z\in U$ such that $T_{\widetilde{R}}(x,z)=1$ and $I_{\widetilde{R}}(x,z)=F_{\widetilde{R}}(x,z)=0$. By Definition 3.1, $\forall x\in U$,

$$\begin{aligned} T_{\underline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee T_{\widetilde{A}}(y))\\= & {} \bigwedge _{y\in U-\{z\}}(F_{\widetilde{R}}(x,y)\vee T_{\widetilde{A}}(y))\wedge (F_{\widetilde{R}}(x,z)\vee T_{\widetilde{A}}(z))\\= & {} \bigwedge _{y\in U-\{z\}}(F_{\widetilde{R}}(x,y)\vee T_{\widetilde{A}}(y))\wedge T_{\widetilde{A}}(z)\le T_{\widetilde{A}}(z).\\ T_{\overline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge T_{\widetilde{A}}(y))\\= & {} \bigvee _{y\in U-\{z\}}(T_{\widetilde{R}}(x,y)\wedge T_{\widetilde{A}}(y))\vee (T_{\widetilde{R}}(x,z)\wedge T_{\widetilde{A}}(z))\\= & {} \bigvee _{y\in U-\{z\}}(T_{\widetilde{R}}(x,y)\wedge T_{\widetilde{A}}(y))\vee T_{\widetilde{A}}(z)\ge T_{\widetilde{A}}(z), \end{aligned}$$

Then, $T_{\underline{\widetilde{R}}(\widetilde{A})}(x)\le T_{\overline{\widetilde{R}}(\widetilde{A})}(x)$.

Similarly, we can show $I_{\underline{\widetilde{R}}(\widetilde{A})}(x)\ge I_{\overline{\widetilde{R}}(\widetilde{A})}(x)$ and $F_{\underline{\widetilde{R}}(\widetilde{A})}(x)\ge F_{\overline{\widetilde{R}}(\widetilde{A})}(x)$. So $\underline{\widetilde{R}}(\widetilde{A})\Subset \overline{\widetilde{R}}(\widetilde{A})$.

Conversely, if $\forall \widetilde{A}\in$ SVNS(U), $\underline{\widetilde{R}}(\widetilde{A})\Subset \overline{\widetilde{R}} (\widetilde{A})$. Take $\widetilde{A}=\widetilde{U}$, by Theorem 3.1 (1) and Definition 3.1, then we have

$1=T_{\widetilde{U}}(x)=T_{\underline{\widetilde{R}}(\widetilde{U})}(x)\le \overline{\widetilde{R}}(\widetilde{U})(x) =\bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge T_{\widetilde{U}}(y))=\bigvee _{y\in U}T_{\widetilde{R}}(x,y)$, which means $\bigvee _{y\in U}T_{\widetilde{R}}(x,y)=1$,

$0=I_{\widetilde{U}}(x)=I_{\underline{\widetilde{R}}(\widetilde{U})}(x)\ge \overline{\widetilde{R}} (\widetilde{U})(x)=\bigwedge _{y\in U}(I_{\widetilde{R}}(x,y)\vee I_{\widetilde{U}}(y))=\bigwedge _{y\in U}I_{\widetilde{R}}(x,y)$, which implies that $\bigwedge _{y\in U}I_{\widetilde{R}}(x,y)=0$,

$0=F_{\widetilde{U}}(x)=F_{\underline{\widetilde{R}}(\widetilde{U})}(x) \ge \overline{\widetilde{R}}(\widetilde{U})(x)= \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee F_{\widetilde{U}}(y))=\bigwedge _{y\in U}F_{\widetilde{R}}(x,y)$, which means $\bigwedge _{y\in U}F_{\widetilde{R}}(x,y)=0$.

Hence, $\widetilde{R}$ is serial.

(2) “$\Longrightarrow$” If $\widetilde{R}$ is reflexive, then $\forall x\in U$, we have $T_{\widetilde{R}}(x,x)=1$ and $I_{\widetilde{R}}(x,x)=F_{\widetilde{R}}(x,x)=0$. By Definition 3.1, $\forall \widetilde{A}\in$ SVNS(U), $\forall x\in U$,

$T_{\underline{\widetilde{R}}(\widetilde{A})}(x)=\bigwedge _{y\in U} (F_{\widetilde{R}}(x,y)\vee T_{\widetilde{A}}(y)) \le F_{\widetilde{R}}(x,x)\vee T_{\widetilde{A}}(x)= 0\vee T_{\widetilde{A}}(x)=T_{\widetilde{A}}(x)$,

$I_{\underline{\widetilde{R}}(\widetilde{A})}(x)= \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge I_{\widetilde{A}}(y))\ge (1-I_{\widetilde{R}}(x,x)) \wedge I_{\widetilde{A}}(x)=(1-0)\wedge I_{\widetilde{A}}(x)=I_{\widetilde{A}}(x)$,

$F_{\underline{\widetilde{R}}(\widetilde{A})}(x)=\bigvee _{y\in U} (T_{\widetilde{R}}(x,y)\wedge F_{\widetilde{A}}(y))\ge T_{\widetilde{R}}(x,x) \wedge F_{\widetilde{A}}(x)=1\wedge F_{\widetilde{A}}(x)=F_{\widetilde{A}}(x)$.

So $\underline{\widetilde{R}}(\widetilde{A})\Subset \widetilde{A}$.

“$\Longleftarrow$” Assume $\forall \widetilde{A}\in$ SVNS(U), $\underline{\widetilde{R}}(\widetilde{A})\Subset \widetilde{A}$. $\forall x\in U$, take $\widetilde{A}=1_{U-\{x\}}$, then we have

$0=T_{1_{U-\{x\}}}(x)\ge T_{\underline{\widetilde{R}}(1_{U-\{x\}})}(x)= \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee T_{1_{U-\{x\}}}(y))=(F_{\widetilde{R}}(x,x) \vee T_{1_{U-\{x\}}}(x))\wedge \bigwedge _{y\in U-\{x\}} (F_{\widetilde{R}}(x,y)\vee T_{1_{U-\{x\}}}(y))=(F_{\widetilde{R}}(x,x) \vee 0)\wedge 1=F_{\widetilde{R}}(x,x),$ then $F_{\widetilde{R}}(x,x)=0$,

$1=I_{1_{U-\{x\}}}(x)\le I_{\underline{\widetilde{R}}(1_{U-\{x\}})}(x) =\bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge I_{1_{U-\{x\}}}(y))= ((1-I_{\widetilde{R}}(x,x))\wedge I_{1_{U-\{x\}}}(x))\vee \bigvee _{y\in U-\{x\}}((1-I_{\widetilde{R}}(x,y)) \wedge I_{1_{U-\{x\}}}(y))=((1-I_{\widetilde{R}}(x,x))\wedge 1) \vee 0=1-I_{\widetilde{R}}(x,x),$ then $I_{\widetilde{R}}(x,x)=0$,

$1=F_{1_{U-\{x\}}}(x)\le F_{\underline{\widetilde{R}}(1_{U-\{x\}})}(x)=\bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge F_{1_{U-\{x\}}}(y))=(T_{\widetilde{R}}(x,x)\wedge F_{1_{U-\{x\}}}(x))\vee \bigvee _{y\in U-\{x\}}(T_{\widetilde{R}}(x,y)\wedge F_{1_{U-\{x\}}}(y))=(T_{\widetilde{R}}(x,x)\wedge 1)\vee 0=T_{\widetilde{R}}(x,x),$ then $T_{\widetilde{R}}(x,x)=1$.

Thus, $\widetilde{R}$ is reflexive.

So $\widetilde{R}$ is reflexive $\Longleftrightarrow \underline{\widetilde{R}}(\widetilde{A})\Subset \widetilde{A}$, $\forall \widetilde{A}\in$ SVNS(U).

(3) By Definition 3.1, $\forall x,y\in U$

$$\begin{aligned}&T_{\underline{\widetilde{R}}(1_{U-\{x\}})}(y)=\bigwedge _{z\in U}(F_{\widetilde{R}}(y,z)\vee T_{1_{U-\{x\}}}(z))\\&\quad =[F_{\widetilde{R}}(y,x)\vee T_{1_{U-\{x\}}}(x)]\wedge \bigwedge _{z\in U-\{x\}}(F_{\widetilde{R}}(y,z)\vee T_{1_{U-\{x\}}}(z))\\&\quad =[F_{\widetilde{R}}(y,x)\vee 0] \wedge 1=F_{\widetilde{R}}(y,x),\\&T_{\underline{\widetilde{R}}(1_{U-\{y\}})}(x)=\bigwedge _{z\in U}(F_{\widetilde{R}}(x,z)\vee T_{1_{U-\{y\}}}(z))\\&\quad =[F_{\widetilde{R}}(x,y)\vee T_{1_{U-\{y\}}}(y)] \wedge \bigwedge _{z\in U-\{y\}}(F_{\widetilde{R}}(x,z)\vee T_{1_{U-\{y\}}}(z))\\&\quad =[F_{\widetilde{R}}(x,y)\vee 0] \wedge 1=F_{\widetilde{R}}(x,y),\\&I_{\underline{\widetilde{R}}(1_{U-\{x\}})}(y)=\bigvee _{z\in U}((1-I_{\widetilde{R}}(y,z))\wedge I_{1_{U-\{x\}}}(z))\\&\quad =[(1-I_{\widetilde{R}}(y,x))\wedge I_{1_{U-\{x\}}}(x)]\\&\qquad \vee \bigvee _{z\in U-\{x\}}((1-I_{\widetilde{R}}(y,z))\wedge I_{1_{U-\{x\}}}(z))=[(1-I_{\widetilde{R}}(y,x))\wedge 1]\\&\qquad \vee \, 0=1-I_{\widetilde{R}}(y,x),\\&I_{\underline{\widetilde{R}}(1_{U-\{y\}})}(x)=\bigvee _{z\in U}((1-I_{\widetilde{R}}(x,z))\wedge I_{1_{U-\{y\}}}(z))\\&\quad =[(1-I_{\widetilde{R}}(x,y))\wedge I_{1_{U-\{y\}}}(y)]\\&\qquad \vee \bigvee _{z\in U-\{y\}}((1-I_{\widetilde{R}}(x,z))\wedge I_{1_{U-\{y\}}}(z))\\&\quad =[(1-I_{\widetilde{R}}(x,y))\wedge 1]\vee 0=1-I_{\widetilde{R}}(x,y),\\&F_{\underline{\widetilde{R}}(1_{U-\{x\}})}(y)=\bigvee _{z\in U}(T_{\widetilde{R}}(y,z)\wedge F_{1_{U-\{x\}}}(z))\\&\quad =[T_{\widetilde{R}}(y,x)\wedge F_{1_{U-\{x\}}}(x)]\\&\qquad \vee \bigvee _{z\in U-\{x\}}(T_{\widetilde{R}}(y,z)\wedge F_{1_{U-\{x\}}}(z))\\&\quad =[T_{\widetilde{R}}(y,x)\wedge 1]\vee 0=T_{\widetilde{R}}(y,x),\\&F_{\underline{\widetilde{R}}(1_{U-\{y\}})}(x)=\bigvee _{z\in U}(T_{\widetilde{R}}(x,z)\wedge F_{1_{U-\{y\}}}(z))\\&\quad =[T_{\widetilde{R}}(x,y)\wedge F_{1_{U-\{y\}}}(y)]\vee \bigvee _{z\in U-\{y\}}(T_{\widetilde{R}}(x,z)\wedge F_{1_{U-\{y\}}}(z))\\&\quad =[T_{\widetilde{R}}(x,y)\wedge 1]\vee 0=T_{\widetilde{R}}(x,y). \end{aligned}$$

Note that $\widetilde{R}$ is symmetric iff $\forall x,y\in U$, $T_{\widetilde{R}}(x,y)=T_{\widetilde{R}}(y,x)$, $I_{\widetilde{R}}(x,y)=I_{\widetilde{R}}(y,x)$, and $F_{\widetilde{R}}(x,y)=F_{\widetilde{R}}(y,x)$. Then $\widetilde{R}$ is symmetric iff $\forall x,y\in U$, $T_{\underline{\widetilde{R}}(1_{U-\{x\}})}(y)=T_{\underline{\widetilde{R}}(1_{U-\{y\}})}(x)$, $I_{\underline{\widetilde{R}}(1_{U-\{x\}})}(y)=I_{\underline{\widetilde{R}}(1_{U-\{y\}})}(x)$, and $F_{\underline{\widetilde{R}}(1_{U-\{x\}})}(y)=F_{\underline{\widetilde{R}}(1_{U-\{y\}})}(x)$, which implies that $\widetilde{R}$ is symmetric iff $\forall x,y\in U$, $\underline{\widetilde{R}}(1_{U-\{x\}})(y)=\underline{\widetilde{R}}(1_{U-\{y\}})(x)$.

(4) “$\Longrightarrow$” If $\widetilde{R}$ is transitive, then $\forall x,y,z\in U$, $\bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge T_{\widetilde{R}}(y,z))\le T_{\widetilde{R}}(x,z)$, $\bigwedge _{y\in U}(I_{\widetilde{R}}(x,y)\vee I_{\widetilde{R}}(y,z))\ge I_{\widetilde{R}}(x,z)$, and $\bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee F_{\widetilde{R}}(y,z))\ge F_{\widetilde{R}}(x,z)$. By Definition 3.1, $\forall x\in U$, we have

$$\begin{aligned} T_{\underline{\widetilde{R}}(\underline{\widetilde{R}}(\widetilde{A}))}(x)= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee T_{\underline{\widetilde{R}}(\widetilde{A})}(y))\\= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee \bigwedge _{z\in U}(F_{\widetilde{R}}(y,z)\vee T_{\widetilde{A}}(z)))\\= & {} \bigwedge _{z\in U}\bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee F_{\widetilde{R}}(y,z)\vee T_{\widetilde{A}}(z))\\= & {} \bigwedge _{z\in U}\left( \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee F_{\widetilde{R}}(y,z))\vee T_{\widetilde{A}}(z)\right) \\\ge & {} \bigwedge _{z\in U}(F_{\widetilde{R}}(x,z)\vee T_{\widetilde{A}}(z))\\= & {} T_{\underline{\widetilde{R}}(\widetilde{A})}(x),\\ I_{\underline{\widetilde{R}}(\underline{\widetilde{R}}(\widetilde{A}))}(x)= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge I_{\underline{\widetilde{R}}(\widetilde{A})}(y))\\= & {} \bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge \bigvee _{z\in U}((1-I_{\widetilde{R}}(y,z))\wedge I_{\widetilde{A}}(z)))\\= & {} \bigvee _{z\in U}\bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge (1-I_{\widetilde{R}}(y,z))\wedge I_{\widetilde{A}}(z))\\= & {} \bigvee _{z\in U}\left( \left[ 1-\bigwedge _{y\in U}(I_{\widetilde{R}}(x,y)\vee I_{\widetilde{R}}(y,z))\right] \wedge I_{\widetilde{A}}(z)\right) \\\le & {} \bigvee _{z\in U}((1-I_{\widetilde{R}}(x,z))\wedge I_{\widetilde{A}}(z))\\= & {} I_{\underline{\widetilde{R}}(\widetilde{A})}(x),\\ F_{\underline{\widetilde{R}}(\underline{\widetilde{R}}(\widetilde{A}))}(x)= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge F_{\underline{\widetilde{R}}(\widetilde{A})}(y))\\= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge \bigvee _{z\in U}(T_{\widetilde{R}}(y,z)\wedge F_{\widetilde{A}}(z)))\\= & {} \bigvee _{z\in U}\bigvee _{y\in U}(T_{\widetilde{R}}(x,y) \wedge T_{\widetilde{R}}(y,z)\wedge F_{\widetilde{A}}(z))\\= & {} \bigvee _{z\in U}\left( \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge T_{\widetilde{R}}(y,z))\wedge F_{\widetilde{A}}(z)\right) \\\le & {} \bigvee _{z\in U}(T_{\widetilde{R}}(x,z)\wedge F_{\widetilde{A}}(z))\\= & {} F_{\underline{\widetilde{R}}(\widetilde{A})}(x). \end{aligned}$$

$\square$

Hence, $\underline{\widetilde{R}}(\widetilde{A})\Subset \underline{\widetilde{R}}(\underline{\widetilde{R}}(\widetilde{A}))$.

“$\Longleftarrow$” If $\forall \widetilde{A}\in$ SVNS(U), $\underline{\widetilde{R}}(\widetilde{A})\Subset \underline{\widetilde{R}}(\underline{\widetilde{R}}(\widetilde{A}))$. $\forall x,y,z\in U$, take $\widetilde{A}=1_{U-\{z\}}$, we have

$$\begin{aligned} F_{\widetilde{R}}(x,z)= & {} T_{\underline{\widetilde{R}}(1_{U-\{z\}})}(x)\le T_{\underline{\widetilde{R}}(\underline{\widetilde{R}}(1_{U-\{z\}}))}(x)\\= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee T_{\underline{\widetilde{R}}(1_{U-\{z\}})}(y))\\= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee F_{\widetilde{R}}(y,z)), \end{aligned}$$

$1-I_{\widetilde{R}}(x,z)=I_{\underline{\widetilde{R}}(1_{U-\{z\}})}(x)\ge I_{\underline{\widetilde{R}}(\underline{\widetilde{R}}(1_{U-\{z\}}))}(x) =\bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge I_{\underline{\widetilde{R}}(1_{U-\{z\}})}(y))=\bigvee _{y\in U}((1-I_{\widetilde{R}}(x,y))\wedge (1-I_{\widetilde{R}}(y,z)))=1-\bigwedge _{y\in U}(I_{\widetilde{R}}(x,y)\vee I_{\widetilde{R}}(y,z))$, then $I_{\widetilde{R}}(x,z)\le \bigwedge _{y\in U}(I_{\widetilde{R}}(x,y)\vee I_{\widetilde{R}}(y,z))$,

$$\begin{aligned} T_{\widetilde{R}}(x,z)= & {} F_{\underline{\widetilde{R}}(1_{U-\{z\}})}(x)\ge F_{\underline{\widetilde{R}}(\underline{\widetilde{R}}(1_{U-\{z\}}))}(x)\\= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge F_{\underline{\widetilde{R}}(1_{U-\{z\}})}(y))\\= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge T_{\widetilde{R}}(y,z)). \end{aligned}$$

So $\widetilde{R}$ is transitive.

4 Axiomatic characterizations of single valued neutrosophic rough sets

In this section, we will give axiomatic characterizations of single valued neutrosophic rough sets by defining a pair of abstract operators. For single valued neutrosophic rough sets, we consider a system (SVNS$(U),\Cup ,\Cap ,c,L,H)$, where L, H :  SVNS$(U)\longrightarrow$ SVNS(U) are two operators from SVNS(U) to SVNS(U). Let T(U), I(U) and F(U) be the family of truth-membership function, indeterminacy membership functions, and falsity-membership functions, respectively. L and H can be represented by $L=(L_{T}, L_{I},L_{F})$ and $H=(H_{T},H_{I},H_{F})$, respectively, where $L_{T}, H_{T}: T(U)\longrightarrow T(U)$, $L_{I},H_{I}: I(U)\longrightarrow I(U)$ and $L_{F},H_{F}: F(U)\longrightarrow F(U)$. For $\widetilde{A}\in$ SVNS(U), $L(\widetilde{A})=(L_{T}(T_{\widetilde{A}}),L_{I}(I_{\widetilde{A}})$, $L_{F}(F_{\widetilde{A}}))$ which means that $T_{L(\widetilde{A})}=L_{T}(T_{\widetilde{A}})$, $I_{L(\widetilde{A})}=L_{I}(I_{\widetilde{A}})$, and $F_{L(\widetilde{A})}=L_{F}(F_{\widetilde{A}})$. $H(\widetilde{A})=(H_{T}(T_{\widetilde{A}}),H_{I}(I_{\widetilde{A}}), H_{F}(F_{\widetilde{A}}))$ which means that $T_{H(\widetilde{A})}=H_{T}(T_{\widetilde{A}})$, $I_{H(\widetilde{A})}=H_{I}(I_{\widetilde{A}})$, and $F_{H(\widetilde{A})}=H_{F}(F_{\widetilde{A}})$.

Definition 4.1

Let L, H :  SVNS$(U)\longrightarrow$ SVNS(U) be two single valued neutrosophic set operators. $\forall \widetilde{A}=\{\langle x, T_{\widetilde{A}}(x),I_{\widetilde{A}}(x),F_{\widetilde{A}}(x)\rangle \mid x\in U\}\in$ SVNS(U), L and H are called dual operators if they satisfy the following axioms:

• (SVNSL1) $L(\widetilde{A})=(H(\widetilde{A}^{c}))^{c}$, i.e., $\forall x\in U$, $L_{T}(T_{\widetilde{A}})(x)=H_{F}(T_{\widetilde{A}})(x)$, $L_{I}(I_{\widetilde{A}})(x)=1-H_{I}(\overline{1}-I_{\widetilde{A}})(x)$, $L_{F}(F_{\widetilde{A}})(x)=H_{T}(F_{\widetilde{A}})(x)$;

• (SVNSU1) $H(\widetilde{A})(x)=(L(\widetilde{A}^{c}))^{c}(x)$, i.e., $\forall x\in U$, $H_{T}(T_{\widetilde{A}})(x)=L_{F}(T_{\widetilde{A}})(x)$, $H_{I}(I_{\widetilde{A}})(x)=1-L_{I}(\overline{1}-I_{\widetilde{A}})(x)$, $H_{F}(F_{\widetilde{A}})(x)=L_{T}(F_{\widetilde{A}})(x)$,

where $\overline{1}$ is a constant fuzzy set in U satisfying $\forall x\in U$, $\overline{1}(x)=1$.

It is easy to see that axioms (SVNSL1) and (SVNSU1) are equivalent.

Theorem 4.1

Let L, H :  SVNS$(U)\longrightarrow$ SVNS(U) be two dual operators. Then, there exists a SVNR $\widetilde{R}$ in U such that $L(\widetilde{A})=\underline{\widetilde{R}}(\widetilde{A})$ and $H(\widetilde{A})=\overline{\widetilde{R}}(\widetilde{A})$ for all $\widetilde{A}\in$ SVNS(U) iff L satisfies the following axioms (SVNSL2) and (SVNSL3), or equivalently, H satisfies axioms (SVNSU2) and (SVNSLU3): $\forall \widetilde{A},\widetilde{B}\in$ SVNS(U), $\forall \alpha _{1},\alpha _{2},\alpha _{3}\in [0,1]$,

(SVNSL2) $L(\widetilde{A}\Cup \widehat{\alpha _{1},\alpha _{2},\alpha _{3}})=L(\widetilde{A}) \Cup \widehat{\alpha _{1},\alpha _{2},\alpha _{3}}$, i.e., $\forall x\in U$, $L_{T}(T_{\widetilde{A}}\Cup \overline{\alpha _{1}})(x)=L_{T}(T_{\widetilde{A}})(x)\vee \alpha _{1}$, $L_{I}(I_{\widetilde{A}}\Cap \overline{\alpha _{2}})(x)=L_{I}(I_{\widetilde{A}})(x)\wedge \alpha _{2}$, $L_{F}(F_{\widetilde{A}}\Cap \overline{\alpha _{3}})(x)=L_{F}(F_{\widetilde{A}})(x)\wedge \alpha _{3}$, where $\overline{\alpha _{i}}$ is a constant fuzzy set in U satisfying $\forall x\in U$, $\overline{\alpha _{i}}(x)=\alpha _{i} (i=1,2,3)$;

(SVNSL3) $L(\widetilde{A}\Cap \widetilde{B})=L(\widetilde{A})\Cap L(\widetilde{B})$, i.e., $\forall x\in U$, $L_{T}(T_{\widetilde{A}\Cap \widetilde{B}})(x)=L_{T}(T_{\widetilde{A}}\Cap T_{\widetilde{B}})(x)=L_{T}(T_{\widetilde{A}})(x)\wedge L_{T}(T_{\widetilde{B}})(x)$, $L_{I}(I_{\widetilde{A}\Cap \widetilde{B}})(x)=L_{I}(I_{\widetilde{A}}\Cup I_{\widetilde{B}})(x)=L_{I}(I_{\widetilde{A}})(x)\vee L_{I}(I_{\widetilde{B}})(x)$, $L_{F}(F_{\widetilde{A}\Cap \widetilde{B}})(x)=L_{F}(F_{\widetilde{A}}\Cup F_{\widetilde{B}})(x)=L_{F}(F_{\widetilde{A}})(x)\vee L_{F}(F_{\widetilde{B}})(x)$;

(SVNSU2) $H(\widetilde{A}\Cap \widehat{\alpha _{1},\alpha _{2},\alpha _{3}})=H(\widetilde{A})\Cap \widehat{\alpha _{1},\alpha _{2},\alpha _{3}}$, i.e., $\forall x\in U$, $H_{T}(T_{\widetilde{A}}\Cap \overline{\alpha _{1}})(x)=H_{T}(T_{\widetilde{A}})(x)\wedge \alpha _{1}$, $H_{I}(I_{\widetilde{A}}\Cup \overline{\alpha _{2}})(x)=H_{I}(I_{\widetilde{A}})(x)\vee \alpha _{2}$, $H_{F}(F_{\widetilde{A}}\Cup \overline{\alpha _{3}})(x)=H_{F}(F_{\widetilde{A}})(x)\vee \alpha _{3}$, where $\overline{\alpha _{i}}$ is a constant fuzzy set in U satisfying $\forall x\in U$, $\overline{\alpha _{i}}(x)=\alpha _{i} (i=1,2,3)$;

(SVNSU3) $H(\widetilde{A}\Cup \widetilde{B})=H(\widetilde{A})\Cup H(\widetilde{B})$, i.e., $\forall x\in U$, $H_{T}(T_{\widetilde{A}\Cap \widetilde{B}})(x)=H_{T}(T_{\widetilde{A}}\Cap T_{\widetilde{B}})(x)=H_{T}(T_{\widetilde{A}})(x)\wedge H_{T}(T_{\widetilde{B}})(x)$, $H_{I}(I_{\widetilde{A}\Cap \widetilde{B}})(x)=H_{I}(I_{\widetilde{A}}\Cup I_{\widetilde{B}})(x)=H_{I}(I_{\widetilde{A}})(x)\vee H_{I}(I_{\widetilde{B}})(x)$,

$H_{F}(F_{\widetilde{A}\Cap \widetilde{B}})(x)=H_{F}(F_{\widetilde{A}}\Cup F_{\widetilde{B}})(x)=H_{F}(F_{\widetilde{A}})(x)\vee H_{F}(F_{\widetilde{B}})(x)$.

Proof

“$\Longrightarrow$” It follows immediately from Theorem 3.1.

“$\Longleftarrow$” Suppose that the operator H satisfies axioms (SVNSU2) and (SVNSU3). By using H, we can define a SVNR $\widetilde{R}=\{\langle (x,y),T_{\widetilde{R}}(x,y),I_{\widetilde{R}}(x,y),F_{\widetilde{R}}(x,y)\rangle \mid x,y\in U\}$ as follows,

$\forall x,y\in U$, $T_{\widetilde{R}}(x,y)=H_{T}(T_{1_{y}})(x)$, $I_{\widetilde{R}}(x,y)=H_{I}(I_{1_{y}})(x)$, and $F_{\widetilde{R}}(x,y)=H_{F}(F_{1_{y}})(x)$.

Obviously, $\forall \widetilde{A}\in$ SVNS(U), we have

$T_{\widetilde{A}}=\bigcup _{y\in U}(T_{1_{y}}\Cap \overline{T_{\widetilde{A}}(y)} )$, $I_{\widetilde{A}}=\Cap _{y\in U}(I_{1_{y}}\Cup \overline{I_{\widetilde{A}}(y)})$, and $F_{\widetilde{A}}=\bigcap _{y\in U}(F_{1_{y}}\Cup \overline{F_{\widetilde{A}}(y)})$.

By Definition 3.1, (SVNSU2) and (SVNSU3), we have

$$\begin{aligned} T_{\overline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigvee _{y\in U}(T_{\widetilde{R}}(x,y)\wedge T_{\widetilde{A}}(y))\\= & {} \bigvee _{y\in U}(H_{T}(T_{1_{y}})(x)\wedge T_{\widetilde{A}}(y))\\= & {} \bigvee _{y\in U}H_{T}(T_{1_{y}}\Cap \overline{T_{\widetilde{A}}(y)})(x)\\= & {} H_{T}\left( \bigcup _{y\in U}(T_{1_{y}}\Cap \overline{T_{\widetilde{A}}(y)})\right) (x)\\= & {} H_{T}(T_{\widetilde{A}})(x)\\= & {} T_{H(\widetilde{A})}(x),\\ I_{\overline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigwedge _{y\in U}(I_{\widetilde{R}}(x,y)\vee I_{\widetilde{A}}(y))\\= & {} \bigwedge _{y\in U}(H_{I}(I_{1_{y}})(x)\vee I_{\widetilde{A}}(y))\\= & {} \bigwedge _{y\in U}H_{I}(I_{1_{y}}\Cup \overline{I_{\widetilde{A}}(y)})(x)\\= & {} H_{I}\left( \bigcap _{y\in U}(I_{1_{y}}\Cup \overline{I_{\widetilde{A}}(y)})\right) (x)\\= & {} H_{I}(I_{\widetilde{A}})(x)\\= & {} I_{H(\widetilde{A})}(x),\\ F_{\overline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigwedge _{y\in U}(F_{\widetilde{R}}(x,y)\vee F_{\widetilde{A}}(y))\\= & {} \bigwedge _{y\in U}(H_{F}(F_{1_{y}})(x)\vee F_{\widetilde{A}}(y))\\= & {} \bigwedge _{y\in U}H_{F}(F_{1_{y}}\Cup \overline{F_{\widetilde{A}}(y)})(x)\\= & {} H_{F}\left( \bigcap _{y\in U}(F_{1_{y}}\Cup \overline{F_{\widetilde{A}}(y)})\right) (x)\\= & {} H_{F}(F_{\widetilde{A}})(x)\\= & {} F_{H(\widetilde{A})}(x).\\ \end{aligned}$$

Therefore, $H(\widetilde{A})=\overline{\widetilde{R}}(\widetilde{A})$. As L and H are dual operators and $H(\widetilde{A})=\overline{\widetilde{R}}(\widetilde{A})$, we can easily obtain $L(\widetilde{A})=\underline{\widetilde{R}}(\widetilde{A})$. $\square$

From Theorem 4.1, it follows that axioms (SVNSU1), (SVNSL1)–(SVNSL3), (or equivalently, axioms (SVNSL1), (SVNSU1)–(SVNSU3)) are the basic axioms of single valued neutrosophic approximation operators. Then, we have the following definition.

Definition 4.2

Let L, H :  SVNS$(U)\longrightarrow$ SVNS(U) be two dual operators, if L satisfies axioms (SVNSL2) and (SVNSL3), or equivalently H satisfies axioms (SVNSU2) and (SVNSU3), then the system (SVNS$(U),\Cup ,\Cap ,c,L,H$ ) is called a single valued neutrosophic rough set algebra, and L and H are called single valued neutrosophic lower and upper approximation operators, respectively.

Next, we explore axiomatic characterizations of some special classes of single valued neutrosophic approximation operators.

Theorem 4.2

Let L, H :  SVNS$(U)\longrightarrow$ SVNS(U) be two dual operators, then there exists a serial SVNR $\widetilde{R}$ in U such that $\forall \widetilde{A}\in$ SVNS(U), $L(\widetilde{A})=\underline{\widetilde{R}}(\widetilde{A})$, $H(\widetilde{A})=\overline{\widetilde{R}}(\widetilde{A})$ if and only if L satisfies axioms (SVNSL2), (SVNSL3), and one of the following equivalent axioms, or equivalently H satisfies axioms (SVNSU2), (SVNSU3), and one of the following equivalent axioms:

• (SVNSL4) $L(\widetilde{\emptyset })=\widetilde{\emptyset }$;

• (SVNSU4) $H(\widetilde{U})=\widetilde{U}$;

• (SVNSL5) $L(\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}) =\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}$;

• (SVNSU5) $H(\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}) =\widehat{\alpha _{1},\alpha _{2},\alpha _{3}}$;

• (SVNSLU5) $L(\widetilde{A})\Subset H(\widetilde{A})$, $\forall \widetilde{A}\in$ SVNS(U).

Proof

It follows from Theorems 3.4 (1) and 4.1. $\square$

Theorem 4.3

Let L, H :  SVNS$(U)\longrightarrow$ SVNS(U) be two dual operators, then there exists a reflexive SVNR $\widetilde{R}$ in U such that $\forall \widetilde{A}\in$ SVNS(U), $L(\widetilde{A})=\underline{\widetilde{R}}(\widetilde{A})$, $H(\widetilde{A})=\overline{\widetilde{R}}(\widetilde{A})$ if and only if L satisfies axioms (SVNSL2), (SVNSL3), and one of the following equivalent axioms, or equivalently H satisfies axioms (SVNSU2), (SVNSU3), and one of the following equivalent axioms:

• (SVNSL6) $L(\widetilde{A})\Subset \widetilde{A}$, $\forall \widetilde{A}\in$ SVNS(U);

• (SVNSU6) $\widetilde{A}\Subset H(\widetilde{A})$, $\forall \widetilde{A}\in$ SVNS(U).

Proof

It follows from Theorems 3.4 (2) and 4.1. $\square$

Theorem 4.4

Let L, H :  SVNS$(U)\longrightarrow$ SVNS(U) be two dual operators, then there exists a symmetric SVNR $\widetilde{R}$ in U such that $\forall \widetilde{A}\in$ SVNS(U), $L(\widetilde{A})=\underline{\widetilde{R}}(\widetilde{A})$ and $H(\widetilde{A})=\overline{\widetilde{R}}(\widetilde{A})$ if and only if L satisfies axioms (SVNSL2), (SVNSL3), and one of the following equivalent axioms, or equivalently H satisfies axioms (SVNSU2), (SVNSU3), and one of the following equivalent axioms:

• (SVNSL7) $L(1_{U-\{x\}})(y)=L(1_{U-\{y\}})(x)$, $\forall x,y\in U$;

• (SVNSU7) $H(1_{x})(y)=H(1_{y})(x)$, $\forall x,y\in U$.

Proof

It follows from Theorems 3.4 (3) and 4.1.

Theorem 4.5

Let L, H :  SVNS$(U)\longrightarrow$ SVNS(U) be two dual operators, then there exists a transitive SVNR $\widetilde{R}$ in U such that $\forall \widetilde{A}\in$ SVNS(U), $L(\widetilde{A})=\underline{\widetilde{R}}(\widetilde{A})$, $H(\widetilde{A})=\overline{\widetilde{R}}(\widetilde{A})$ if and only if L satisfies axioms (SVNSL2), (SVNSL3), and one of the following equivalent axioms, or equivalently H satisfies axioms (SVNSU2), (SVNSU3), and one of the following equivalent axioms:

• (SVNSL8) $L(\widetilde{A})\Subset L(L(\widetilde{A}))$, $\forall \widetilde{A}\in$ SVNS(U);

• (SVNSU8) $H(H(\widetilde{A}))\Subset H(\widetilde{A})$, $\forall \widetilde{A}\in$ SVNS(U).

Proof

It follows from Theorems 3.4 (4) and 4.1.

5 An application of single valued neutrosophic rough sets

As an efficient tool of dealing with inaccurate information and data, rough sets especially rough sets on two different universes have applications in many fields such as multi-attribute decision making, clustering, data mining and medical diagnosis. In order to explore the application of single valued neutrosophic rough sets, we first extend the single valued neutrosophic rough sets to two-universes case.

Definition 5.1

Let U, V be two space of points (objects). A SVNS $\widetilde{R}$ in $U\times V$ is called a single valued neutrosophic relation (SVNR) from U to V, denoted by $\widetilde{R}=\{\langle (x,y),T_{\widetilde{R}}(x,y),I_{\widetilde{R}}(x,y),F_{\widetilde{R}}(x,y)\rangle \mid (x,y)\in U\times V\}$, where $T_{\widetilde{R}}: U\times V\longrightarrow [0,1]$, $I_{\widetilde{R}}: U\times V\longrightarrow [0,1]$ and $F_{\widetilde{R}}: U\times V\longrightarrow [0,1]$ denote the truth-membership function, indeterminacy membership function and falsity-membership function of $\widetilde{R}$, respectively.

Definition 5.2

Let $\widetilde{R}$ be a SVNR from U to V, the triple $(U,V,\widetilde{R})$ is called a generalized single valued neutrosophic approximation space on two-universes. $\forall \widetilde{A}\in$ SVNS(V), the lower and upper approximations of $\widetilde{A}$ with respect to $(U, V,\widetilde{R})$, denoted by $\underline{\widetilde{R}}(\widetilde{A})$ and $\overline{\widetilde{R}}(\widetilde{A})$, are two SVNSs whose membership functions are defined as: $\forall x\in U$,

$$\begin{aligned} T_{\underline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigwedge _{y\in V}(F_{\widetilde{R}}(x,y)\vee T_{\widetilde{A}}(y)),\\ I_{\underline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigvee _{y\in V}((1-I_{\widetilde{R}}(x,y))\wedge I_{\widetilde{A}}(y)),\\ F_{\underline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigvee _{y\in V}(T_{\widetilde{R}}(x,y)\wedge F_{\widetilde{A}}(y));\\ T_{\overline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigvee _{y\in V}(T_{\widetilde{R}}(x,y)\wedge T_{\widetilde{A}}(y)),\\ I_{\overline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigwedge _{y\in V}(I_{\widetilde{R}}(x,y)\vee I_{\widetilde{A}}(y)),\\ F_{\overline{\widetilde{R}}(\widetilde{A})}(x)= & {} \bigwedge _{y\in V}(F_{\widetilde{R}}(x,y)\vee F_{\widetilde{A}}(y)). \end{aligned}$$

The pair $(\underline{\widetilde{R}}(\widetilde{A}),\overline{\widetilde{R}}(\widetilde{A}))$ is called a single valued neutrosophic rough set on two-universes.

Peng et al. (2014) introduced the operations of simplified neutrosophic numbers and gave a outranking approach of simplified neutrosophic numbers. Similarly, we can define the operations of single valued neutrosophic numbers and give a outranking approach of single valued neutrosophic numbers.

Definition 5.3

Let $n_{1}=(T_{n_{1}},I_{n_{1}}, F_{n_{1}})$ and $n_{2}=(T_{n_{2}},I_{n_{2}}, F_{n_{2}})$ be two single valued neutrosophic numbers, the operations of single valued neutrosophic numbers can be defined as follows:

• (1) $\lambda n_{1}=(1-(1-T_{n_{1}})^{\lambda },(I_{n_{1}})^{\lambda }, (F_{n_{1}})^{\lambda })$;

• (2) $n_{1}^{\lambda }=((T_{n_{1}})^{\lambda },1-(1-I_{n_{1}})^{\lambda }, 1-(1-F_{n_{1}})^{\lambda })$;

• (3) $n_{1}\oplus n_{2}=(T_{n_{1}}+T_{n_{2}}-T_{n_{1}}\cdot T_{n_{2}},I_{n_{1}}\cdot I_{n_{2}}, F_{n_{1}}\cdot F_{n_{2}})$;

• (4) $n_{1}\odot n_{2}=(T_{n_{1}}\cdot T_{n_{2}},I_{n_{1}}+I_{n_{2}}-I_{n_{1}}\cdot I_{n_{2}}, F_{n_{1}}+F_{n_{2}}-F_{n_{1}}\cdot F_{n_{2}})$.

By Definition 5.3 (3), we can define the sum of two SVNSs in U as follows.

Definition 5.4

Let $\widetilde{A}$ and $\widetilde{B}$ be two SVNSs in U, we define the sum of $\widetilde{A}$ and $\widetilde{B}$ as

$$\begin{aligned} \widetilde{A}\boxplus \widetilde{B}= \{\langle x,\widetilde{A}(x)\oplus \widetilde{B}(x)\mid x\in U\}. \end{aligned}$$

To rank single valued neutrosophic numbers in the decision-making process, Ye (2013) proposed the cosine similarity measure between single valued neutrosophic numbers.

Definition 5.5

(Ye 2013). Let $n=(T_{n},I_{n}, F_{n})$ be a single valued neutrosophic number, $n^{*}=(T_{n^{*}},I_{n^{*}}, F_{n^{*}})=(1,0,0)$ be an ideal single valued neutrosophic number, then the cosine similarity measure between n and $n^{*}$ is defined as follows:

$$\begin{aligned} S(n,n^{*})=\frac{T_{n}\cdot T_{n^{*}}+I_{n}\cdot I_{n^{*}}+F_{n}\cdot F_{n^{*}}}{\sqrt{T_{n}^{2}+I_{n}^{2}+F_{n}^{2}} \ \cdot \sqrt{(T_{n^{*}})^{2}+(I_{n^{*}})^{2}+(F_{n^{*}})^{2}}}. \end{aligned}$$

By Definition 5.5, the bigger the measure value $S(n,n^{*})$ is, the bigger the single valued neutrosophic number n is, because n is close to the ideal value $n^{*}$. Through comparing the cosine similarity measure between each single valued neutrosophic number and the ideal single valued neutrosophic number, the ranking of all single valued neutrosophic numbers can be determined.

Table 4 Single valued neutrosophic relation $\widetilde{R}$ between the symptoms and diseases

For the multi-attribute decision-making problem under single valued neutrosophic environment, the characteristics of the alternatives $x_{i}(i=1, 2,\ldots ,n)$ are represented by single valued neutrosophic numbers $n_{x_{i}}$. Define the alternative $x^{*}$ with the idea characteristics value $n^{*}=(1,0,0)$ as the ideal alternative (Ye 2013, 2014b). The bigger the value of the cosine similarity measure $S(n_{x_{i}},n^{*})$ is, the better the alternative $x_{i}$ is, because the alternative $x_{i}$ is close to the ideal alternative $x^{*}$. By comparing the cosine similarity measure value, the ranking of all alternatives can be determined and we can obtain the optimal alternative.

Next, we present the whole medical diagnosis decision procedure based on single valued neutrosophic rough sets on two-universes.

Assume that the universe $U=\{x_{1},x_{2},\ldots , x_{n}\}$ denotes a set of diseases, and the universe $V =\{y_{1},y_{2},\ldots ,y_{m}\}$ denotes a set of symptoms. Let $R\in$ SVNR$(U\times V)$ be a SVNR from U to V, where $\forall (x_{i},y_{j})\in U\times V$, $R(x_{i},y_{j})$ denotes the degree that the disease $x_{i}(x_{i}\in U)$ has the symptom $y_{j} (y_{j}\in V)$. R can be obtained according to a medical knowledge statistic data. Given a patient $\widetilde{A}$, symptoms of the patient (we also use $\widetilde{A}$ to denote it) are described by a SVNS $\widetilde{A}$ in the universe V according to a doctor’s evaluation. By use of the following algorithm, we can determine what kind of the diseases the patient $\widetilde{A}$ is suffering from.

Algorithm

Step 1. By Definition 5.2, we calculate the lower and upper approximations $\underline{\widetilde{R}}(\widetilde{A})$ and $\overline{\widetilde{R}}(\widetilde{A})$ of $\widetilde{A}$.

Step 2. By Definition 5.4, we get $\underline{\widetilde{R}}(\widetilde{A})\boxplus \overline{\widetilde{R}}(\widetilde{A})$.

Step 3. By Definition 5.5, we compute $S(n_{x_{i}},n^{*})(i=1,2,\ldots ,n)$.

Step 4. The optimal decision is to select $x_{k}$ (which means that the most possible disease is $x_{k}$) if $S(n_{x_{k}},n^{*})=$ max $_{i\in \{1,2,\ldots ,n\}}(S(n_{x_{i}},n^{*}))$.

Step 5. If k has more than one value, then each $x_{k}$ will be the optimal decision. In this case, the patient may suffer more than one disease and each $x_{k}$ will be chosen as the most possible disease, or we need other methods to make a further decision.

In the following, we give a numerical example to illustrate the application of single valued neutrosophic rough sets on two-universes by use of the algorithm above.

Example 5.1

Let $U=\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\}$ be five diseases, where $x_{i}(i=1,2,3,4,5)$ stand for “common cold,” “viral fever,” “malaria,” “typhoid” and “stomach problem,” respectively. $V=\{y_{1}, y_{2}, y_{3}, y_{4}, y_{5}, y_{6}, y_{7}\}$ be five symptoms in clinic, where $y_{j}(j=1,2,3,4,5,6,7)$ stand for “tired,” “a stuffed-up nose,” “headache,” “chill,” “stomach pain,” “dry cough” and “chest-pain,” respectively. $\widetilde{R}$ is a medical knowledge statistic data of the relationship of the disease $x_{i}$ ($x_{i}\in U$) and the symptom $y_{j}(y_{j}\in V)$, and $\widetilde{R}$ is actually a SVNR from U to V (given in Table 4).

Suppose the symptoms of a patient $\widetilde{A}$ are described by a SVNS in the universe V, and

$$\begin{aligned} \widetilde{A}= & {} \{\langle y_{1},0.2, 0.6,0.7\rangle ,\langle y_{2},0.5, 0.2,0.1\rangle ,\langle y_{3},0.1, 0.8,0.6\rangle ,\\&\langle y_{4},0.9, 0.3,0.1\rangle ,\langle y_{5},0, 1,0.5\rangle ,\\&\langle y_{6},0.7, 0.7,0.4\rangle ,\langle y_{7},0.5, 0.8,0.9\rangle \}. \end{aligned}$$

By Definition 5.2, we calculate the lower and upper approximations $\underline{\widetilde{R}}(\widetilde{A})$ and $\overline{\widetilde{R}}(\widetilde{A})$ of the patient $\widetilde{A}$ as follows:

$$\begin{aligned} \underline{\widetilde{R}}(\widetilde{A})= & {} \{\langle x_{1},0.1, 1,0.6\rangle ,\langle x_{2},0.1, 0.8,0.7\rangle ,\\&\langle x_{3},0.2, 0.9,0.9\rangle ,\langle x_{4},0.2, 0.8,0.7\rangle ,\\&\langle x_{5},0, 0.8,0.7\rangle \},\\ \overline{\widetilde{R}}(\widetilde{A})= & {} \{\langle x_{1},0.8, 0.2,0.1\rangle ,\langle x_{2},0.7, 0.2,0.4\rangle ,\\&\langle x_{3},0.5, 0.3,0.5\rangle ,\langle x_{4},0.7, 0.2,0.4\rangle ,\\&\langle x_{5},0.5, 0.2,0.5\rangle \}. \end{aligned}$$

By Definition 5.4, we have

$$\begin{aligned} \underline{\widetilde{R}}(\widetilde{A})\boxplus \overline{\widetilde{R}}(\widetilde{A})= & {} \{\langle x_{1},0.82, 0.02,0.06\rangle ,\langle x_{2},0.73, 0.16,0.28\rangle ,\\&\langle x_{3},0.6,0.27, 0.45\rangle ,\\&\langle x_{4},0.76, 0.16,0.28\rangle ,\langle x_{5},0.5, 0.16,0.35\rangle \}. \end{aligned}$$

Then, by Definition 5.5, we can compute the cosine similarity measure between the single valued neutrosophic number $n_{x_{i}}$ corresponding to $x_{i}$ and the ideal single valued neutrosophic number $n^{*}$ as follows:

$$\begin{aligned} S(n_{x_{1}},n^{*})= & {} 0.997, S(n_{x_{2}},n^{*})=0.915, S(n_{x_{3}},n^{*})=0.753,\\ S(n_{x_{4}},n^{*})= & {} 0.921, S(n_{x_{5}},n^{*})=0.792. \end{aligned}$$

Then, we have

$$\begin{aligned} S(n_{x_{1}},n^{*})>&S(n_{x_{4}},n^{*})>S(n_{x_{2}},n^{*})>S(n_{x_{5}},n^{*})\\> & {} S(n_{x_{3}},n^{*}). \end{aligned}$$

So, the optimal decision is to select $x_{1}$. That is, we can conclude that the patient $\widetilde{A}$ is suffering from common cold $x_{1}$.

To explore the effectiveness of the method proposed in this paper, we compare it with the method proposed in Yang et al. (2012). The method given in Yang et al. (2012) only deals with the decision-making problems with bipolar fuzzy (i.e., intuitionistic fuzzy) information, but not the decision-making problems with the single valued neutrosophic information, while the model proposed in the present paper can handle the decision-making problems not only with bipolar fuzzy (i.e., intuitionistic fuzzy) information (since intuitionistic fuzzy sets can be regarded as an especial case of SVNSs) but also with single valued neutrosophic information. Thus, the proposed method is more general and its application domain is wider than that of the method in Yang et al. (2012).

6 Conclusion

Neutrosophic sets and rough sets are two hot research topics. In this paper, we propose a hybrid model of single valued neutrosophic sets and rough sets, named single valued neutrosophic rough sets. We present a general framework of the study of single valued neutrosophic rough sets through constructive and axiomatic approaches. The single valued neutrosophic rough sets on two-universes are also introduced. We present an algorithm of decision making based on single valued neutrosophic rough sets on two-universes. We also give a numerical example to show the usefulness of single valued neutrosophic rough sets on two-universes.

As far as future directions are concerned, these will include studying other types of fusions of rough sets and neutrosophic sets, and reducts of these model. We will address these issues in our forthcoming research.