Abstract
In this study, using the neutrosophic soft definitions, we define some new concept such as the neutrosophic soft lattice, neutrosophic soft sublattice, complete neutrosophic soft lattice, modular neutrosophic soft lattice, distributive neutrosophic soft lattice, neutrosophic soft chain then we study the relationship and observe some common properties.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Most of the problems in engineering, medical science, economics and social science etc. have vagueness and various uncertainties. To overcome these uncertainties, some kinds of theories were given which we can use as mathematical tools for dealing with uncertainties. However, these theories have their own difficulties. In 1999, Molodtsov [1] initiated a novel concept of soft set theory, which is a completely new approach for modeling vagueness and uncertainty. From then on, works on the soft set theory are progressing rapidly. After Molodtsov’s work, same different applications of soft sets were studied in [2, 3]. Furthermore Maji, Biswas and Roy worked on soft set theory in [4, 5]. Roy et al. presented some applications of this notion to decision making problems in [6]. The algebraic structures of soft sets have been studied by some authors [7–14]. Birkhoff’s work in 1930 started the general development of lattice theory [15]. The lattice theory has been applied to many kinds of fields. Recently, the work introducing the soft set theory to the lattice theory and the fuzzy set theory have been initiated. Fu [16] and Çağman et al. [17] presented the nation of the soft lattice and derived the properties of the soft lattice and discussed the relationship between the soft lattices. Karaaslan et al. [18] introduced the fuzzy soft lattice theory, some related properties on it. Florentine Smarandache for the first time introduced the concept of neutrosophy in 1995 [19, 20]. Maji [21] had combined the neutrosophic set with soft sets and introduced a new mathematical model neutrosophic soft set. Later Broumi and Smarandache defined the concepts interval-valued neutrosophic soft sets and intuitionistic neutrosophic soft sets in [22, 23]. Different algebraic structures and their applications were studied in the neutrosophic soft set context [24–31].
In this paper, we apply the notion of neutrosophic soft sets introduced by [21] to the lattice theory and present the notion of neutrosophic soft lattice, which is different from the one presented by [16–18]. The organization of this paper is as follows: in Sect. 2, some basic concepts and some related properties are introduced. In Sect. 3, the notion of neutrosophic soft lattice is presented and some related properties are defined, then the neutrosophic soft sublattice, complete neutrosophic soft lattice, distributive neutrosophic soft lattice, modular neutrosophic soft lattice, neutrosophic soft chain are presented and their related properties are studied. Section 4 concludes the paper.
2 Preliminaries
Definition 2.1
[19] Let U be a space of points (objects), with a generic element in U denoted by u. A neutrosophic set (N-set) Ain U is characterized by a truth-membership function \(T_A \), an indeterminacy-membership function \(I_A \)and a falsity-membership function \(F_A \). \(T_A (u)\); \(I_A (u)\) and \(F_A \)(u) are real standard or nonstandard subsets of [0, 1]. It can be written as
There is no restriction on the sum of \(T_A \)(u); \(I_A \)(u) and \(F_A \)(u), so
0 \(\le \)sup \(T_A (u)\) + sup \(I_A (u)\) + sup \(F_A (u) \quad \le \) 3.
Definition 2.2
[21] Let U be an initial universe set and E be a set of parameters. Consider E. Let P(U) denote the set of all neutrosophic sets of U. The collection \(\left( {F,A} \right) \) is termed to be the soft neutrosophic set over U, where F is a mapping given by \(F:A\rightarrow P(U)\).
Definition 2.3
[32] Let P be a non-empty ordered set.
-
(i)
If \(x y\) and \(x\wedge y\) exist for all \(x,y\in P\), then P is called a lattice,
-
(ii)
If
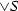 and \(\wedge S\) exist for all \(S\subseteq P\), then P is called a complete lattice.
and \(\wedge S\) exist for all \(S\subseteq P\), then P is called a complete lattice.
Definition 2.4
[15] An algebra  is called a lattice if L is a nonempty set,
is called a lattice if L is a nonempty set,  are binary operations on L, both \(\wedge \) and \(\vee \) are idempotent, commutative and associative, and they satisfy the two absorption identities. That is, for all \(a,b,c\in L\)
are binary operations on L, both \(\wedge \) and \(\vee \) are idempotent, commutative and associative, and they satisfy the two absorption identities. That is, for all \(a,b,c\in L\)
-
1.
\(a\wedge a=a;a\vee a=a\),
-
2.
\(a\wedge b=b\wedge a;a\vee b=b\vee a\),
-
3.
\((a\wedge b)\wedge c=a\wedge (b\wedge c);(a\vee b)\vee c=a\vee (b\vee c)\),
-
4.
\(a\wedge \left( {a\vee b} \right) =a;a\vee \left( {a\wedge b} \right) =a\).
Definition 2.5
[21] Let (F, A) and (G, B) be two neutrosophic soft sets over the common universe U.(F, A) is said to be a neutrosophic soft subset of (G, B) if \(A\subset B,\) and\(T_F \)(e)(x) \(\le T_G (\hbox {e})(\hbox {x}),\hbox {}I_F (\hbox {e})(\hbox {x})\) \(\le I_G (\hbox {e})(\hbox {x}),F_F (\hbox {e})(\hbox {x})\hbox {}\) \(\ge F_G (\hbox {e})(\hbox {x}),\hbox {}\forall e\in A,x\in U.\)We denote it by \((F,A)\subseteq (G,B).\)
Definition 2.6
[21] The complement of a neutrosophic soft set (F, A) denoted by \((F,A)^{c}=(F^{c},\lnot A)\) where \(F^{c}:\lnot A\rightarrow P\left( U \right) \) is a mapping given by \(F^{c}\left( \alpha \right) =\)neutrosophic soft complement with \(T_{F^{c}} \left( x \right) =F_F \left( x \right) ,I_{F^{c}} \left( x \right) =I_F \left( x \right) \hbox {and} F_{F^{c}} \left( x \right) =T_F \left( x \right) .\)
Definition 2.7
[21] Let \(\left( {H,A} \right) \) and \(\left( {G,B} \right) \) be two NSSs over the common universe U. Then the union of \(\left( {H,A} \right) \) and \(\left( {G,B} \right) \) is denoted by “\(\left( {H,A} \right) \tilde{\cup } \left( {G,B} \right) \)” and is defined by\(\left( {H,A} \right) \tilde{\cup } \left( {G,B} \right) =(K,C)\), where \(C=A \cup B\) and the truth-membership, indeterminacy-membership and falsity-membership of (K, C) are as follows:
Definition 2.8
[21] Let \(\left( {H,A} \right) \) and \(\left( {G,B} \right) \) be two NSSs over the common universe U. Then the intersection of \(\left( {H,A}\right) \) and \(\left( {G,B} \right) \) is denoted by “\(\left( {H,A} \right) \tilde{\cap } \left( {G,B} \right) \)” and is defined by\(\left( {H,A} \right) \tilde{\cap } \left( {G,B} \right) =(K,C)\), where \(C=A \cap B\) and the truth-membership, indeterminacy-membership and falsity-membership of (K, C) are as follows:
3 Lattice structures of neutrosophic soft sets
In this section, the notion of neutrosophic soft lattice is defined and several related properties are investigated.
Definition 3.1
Let \(N^{L}\) be a neutrosophic soft set over \(U,{\tilde{\vee }}\) and \(\tilde{\wedge } \) be two binary operation on \( N^{L}\). If elements of \(N^{L}\) are equipped with two commutative and associative binary operations \(\tilde{\vee } \) and \(\tilde{\wedge } \) which are connected by the absorption law, then algebraic structure \(( {N^{L},\tilde{\vee } ,\tilde{\wedge }} )\) is called a neutrosophic soft lattice.
Example 3.2
Let \(U=\left\{ {u_1 ,u_2 ,u_3 ,u_4 } \right\} \) be a universe set and \(N^{L}=\left\{ {F_A ,F_B ,F_C ,F_D } \right\} \tilde{\subseteq } NS (U)\).
Suppose that
Then,\(\left( {N^{L},\tilde{\cup } ,\tilde{\cap } } \right) \)is a neutrosophicsoft lattice. Here binary operations are neutrosophic union and neutrosophic intersection. Hasse diagram of \(N^{L}\)is shown in Fig. 1.
Theorem 3.3
\(( {N^{L},{\tilde{\vee }},\tilde{\wedge }} )\) be a neutrosophic soft lattice and \(F_A ,F_B \in NS (U)\). Then
Proof
Conversely,
\(\square \)
Theorem 3.4
\(( {N^{L},\tilde{\vee } ,\tilde{\wedge } })\) be a neutrosophic soft lattice and \(F_A ,F_B \in NS (U)\). Then the relation \(\tilde{\le } \) which is defined by
is an ordering relation on NS (U).
Proof
-
(i)
\(\forall F_A \in N^{L}, \tilde{\le } \) is reflexive, \(F_A \tilde{\le } F_A \Leftrightarrow F_A \tilde{\wedge } F_A =F_A \)
-
(ii)
\(\forall F_A ,F_B \in N^{L}, \tilde{\le } \) is antisymmetric. Let \(F_A \tilde{\le } F_B \) and \(F_B \tilde{\le } F_A .\) Then
$$\begin{aligned} F_A= & {} F_A \tilde{\wedge } F_B\\= & {} F_B \tilde{\wedge } F_A\\= & {} F_{B.} \end{aligned}$$ -
(iii)
\(\forall F_A ,F_B and F_C \in N^{L},\tilde{\le } \) is transitive. If \(F_A \tilde{\le } F_B \) and \(F_B \tilde{\le } F_C \Rightarrow F_A \tilde{\le } F_C \). Indeed
$$\begin{aligned} F_A \tilde{\wedge } F_C= & {} \left( {F_A \widetilde{\wedge } F_B } \right) \tilde{\wedge } F_C\\= & {} \left( {F_A } \right) \tilde{\wedge } \left( {F_B \tilde{\wedge } F_C } \right) \\= & {} F_A \tilde{\wedge } F_B\\= & {} F_A . \end{aligned}$$
\(\square \)
Theorem 3.5
\(( {N^{L},\tilde{\vee },\tilde{\wedge } })\) be a neutrosophic soft lattice and \(F_A ,F_B \in NS (U)\). Then \(F_A \tilde{\vee } F_B \) and \(F_A \tilde{\wedge } F_B \)are the least upper and the greatest lower bound of \(F_A \hbox {and}F_B \), respectively.
Proof
Suppose that \(F_A \tilde{\wedge } F_B \) is not the greatest lower bound of \(F_A \hbox {and}F_B \). Then there exists \(F_C \in NS (U)\) such that \(F_A \tilde{\wedge } F_B \tilde{\le } F_C \tilde{\le } F_A \)and \(F_A \tilde{\wedge } F_B \tilde{\le } F_C \tilde{\le } F_B \). Hence \(F_C \tilde{\wedge } F_C \tilde{\le } F_A \tilde{\wedge } F_B \). Thus \(F_C \tilde{\le } F_A \tilde{\wedge } F_B \). Therefore \(F_C =F_A \tilde{\wedge } F_{B} \).But this is a contradiction.\(F_A \tilde{\vee } F_B \) being the least upper bound of \(F_A \hbox {and}F_B \) can be shown similarly. \(\square \)
Lemma 3.6
Let \(N^{L}\in NS (U)\). Then neutrosophic soft lattice inclusion relation \(\tilde{\subseteq } \) that is defined by
is an ordering relation on \(N^{L}\).
Proof
For all \(F_A ,F_B and F_C \in N^{L}\),
-
(i)
\(F_A \in N^{L},\tilde{\subseteq } \) is reflexive, \(F_A \tilde{\subseteq } F_A \Leftrightarrow F_A {\tilde{\cap } } F_A =F_A \)
-
(ii)
\(F_A ,F_B \in N^{L},\tilde{\subseteq } \) is antisymmetric. Let \(F_A \tilde{\subseteq } F_B \) and \(F_B \tilde{\subseteq } F_A \Leftrightarrow F_A =F_B \).
-
(iii)
\(F_A ,F_B and F_C \in N^{L},\tilde{\subseteq } \) is transitive. If \(F_A \tilde{\subseteq } F_B \) and \(F_B \tilde{\subseteq } F_C \Rightarrow F_A \tilde{\subseteq } F_C \).
\(\square \)
Corollary 3.7
\(( {N^{L}, {\tilde{\cup } } \hbox {},\hbox {} {\tilde{\cap } },\tilde{\subseteq } })\) is a neutrosophic soft lattice.
Definition 3.8
Let \(( {N^{L},\tilde{\vee } \hbox {},\hbox {}\tilde{\wedge } \hbox {},\tilde{\le } })\) be a neutrosophic soft lattice and let \(F_A \in N^{L}\). If \(F_A \tilde{\le } F_B \) for all \(F_B \in N^{L}\), then \(F_A \) is called the minimum element of \(N^{L}\). If \(F_B \tilde{\le } F_A \) for all \(F_B \in N^{L}\), then \(F_A \) is called the maximum element of \(N^{L}\).
Definition 3.9
Let \(({N^{L},\tilde{\vee } \hbox {},\hbox {}\tilde{\wedge } \hbox {},\tilde{\le } })\) be a neutrosophic soft lattice and let \(F_A \in N^{L}\). If \(F_B \tilde{\le } F_A \hbox {or}F_A \tilde{\le } F_B \) for all \(F_A ,F_B \in N^{L}\), then \(N^{L}\) is called a neutrosophic soft chain.
Example 3.10
Consider the neutrosophic soft lattice in Example 3.2. A neutrosophic soft subset \(N^{S}=\{ {F_A ,F_B ,F_D }\}\tilde{\subseteq } NS (U)\) of \(N^{L}\) is a neutrosophic soft chain. But \(( {N^{L}, {\tilde{\cup } } \hbox {},\hbox {}\mathop {\tilde{\cap }}\ ,\tilde{\subseteq } })\) is not a neutrosophic soft chain since \(F_B \) and \(F_C \)can not be comparable.
Definition 3.11
Let \(({N^{L},\tilde{\vee } \hbox {},\hbox {}\tilde{\wedge } \hbox {},\tilde{\le } })\) be a neutrosophic soft lattice. If every subset of \(N^{L}\) have both a greatest lowers bound and a least upper bound, then \(N^{L}\) is called a complete neutrosophic soft lattice.
Example 3.12
Let \(U=\{ {u_1 ,u_2 ,u_3 ,u_4 ,u_5 }\}\) be a universe set and \(N^{L}=\{ {F_A ,F_B ,F_C ,F_D } \}\tilde{\subseteq } NS (U)\).
Then \(( {N^{L}, {\tilde{\cup } } \hbox {},\hbox {}\mathop {\tilde{\cap }} ,\tilde{\subseteq } })\) is a complete neutrosophic soft lattice
Definition 3.13
Let \(({N^{L},\tilde{\vee } \hbox {},\hbox {}\tilde{\wedge } \hbox {},\tilde{\le } })\) be a neutrosophic soft lattice and \(N^{M}\tilde{\subseteq } N^{L}\). If \(N^{M}\) is a neutrosophic soft lattice with the operations of\(N^{L}\), then \(N^{M}\) is called a neutrosophic sublattice of\(\hbox {}N^{\hbox {L}}\).
Theorem 3.14
Let \(({N^{L},\tilde{\vee } \hbox {},\hbox {}\tilde{\wedge } \hbox {},\tilde{\le } })\) be a neutrosophic soft lattice and \(N^{M}\tilde{\subseteq } N^{L}\). If\(F_A \tilde{\vee } F_B \in N^{M}\) and \(F_A \tilde{\wedge } F_B \in N^{M}\) for all \(F_A , F_B \in N^{M}\), then \(N^{M}\) is a neutrosophic soft lattice.
Proof
It is obvious from Definition 3.13. \(\square \)
Example 3.15
Let \(U= \{ {u_1 ,u_2 ,u_3 ,u_4 ,u_5 }\}\) be a universe set and \(N^{L}= \{ {F_A ,F_B ,F_C ,F_D }\} \tilde{\subseteq } NS (U)\).
Then, if \(N^{M}=\{ {F_A ,F_B ,F_D }\}\tilde{\subseteq } NS (U)\), then \(N^{M}\)is a neutrosophic soft sublattice.
Definition 3.16
Let \(( {N^{L},\tilde{\vee } \hbox {},\hbox {}\tilde{\wedge } \hbox {},\tilde{\le } })\) be a neutrosophic soft lattice and \(F_A ,F_B \hbox {and}F_C \in N^{L}\). If
or
then \(N^{L}\) is called a one-sided distributive neutrosophic soft lattice.
Theorem 3.17
Every neutrosophic soft lattice is a one-sided distributive neutrosophic soft lattice.
Proof
Let \(F_A ,F_B \hbox {and} F_C \in N^{L}.\) \(\square \)
Since \(F_A \tilde{\wedge } F_B \tilde{\le } F_A \) and \(F_A \tilde{\wedge } F_B \tilde{\le } F_B \tilde{\le } F_B \tilde{\vee } F_C \),
\(F_A \tilde{\wedge } F_B \tilde{\le } F_A \) and \(F_A \tilde{\wedge } F_B \tilde{\le } F_B \tilde{\wedge } F_C \) .
Therefore,
And also we have \(F_A \tilde{\wedge } F_C \tilde{\le } F_A \) and \(F_A \tilde{\wedge } F_C \tilde{\le } F_C \tilde{\le } F_B \tilde{\vee } F_C \) . Since \(F_A \tilde{\wedge } F_C \tilde{\le } F_A \) and \(F_A \tilde{\wedge } F_C \tilde{\le } F_B \tilde{\vee } F_C \), then
from \((a) \hbox {and} (b)\), we get the desired result,
Definition 3.18
\(( {N^{L},\tilde{\vee } \hbox {},\hbox {}\tilde{\wedge } \hbox {},\tilde{\le } })\) be a neutrosophic soft lattice. If \(N^{L}\) satisfies the following axioms, it is called a distributive neutrosophic soft lattice;
-
(i)
\(F_A \tilde{\vee } \left( {F_B \tilde{\wedge } F_C } \right) =\left( {F_A \tilde{\vee } F_B } \right) \tilde{\wedge } \left( {F_A \tilde{\vee } F_C } \right) \)
-
(ii)
\(F_A \tilde{\wedge } \left( {F_B \tilde{\vee } F_C } \right) =\left( {F_A \tilde{\wedge } F_B } \right) \tilde{\vee } \left( {F_A \tilde{\wedge } F_C } \right) \)
for all \(F_A ,F_B \hbox {and}F_C \in N^{L}\).
Example 3.19
Let \(U=\{ {u_1 ,u_2 ,u_3 ,u_4 ,u_5 }\}\) be a universe set and \(N^{L}=\{ F_\emptyset ,F_A ,F_B ,F_C ,F_D ,F_E \} \tilde{\subseteq } NS (U).\) Then \(N^{L}\tilde{\subseteq } NS(U)\) is a neutrosophic soft lattice with the operations \({\tilde{\cup } } \hbox {and} {\tilde{\cap }} \). Suppose that
\(\left( {N^{L}, {\tilde{\cup } } \hbox {},\hbox {} {\tilde{\cap }} ,\tilde{\subseteq } } \right) \) is a distributive neutrosophic soft lattice. The Hasse diagram of it is shown in Fig. 2.
Definition 3.20
\(( {N^{L},\tilde{\vee } \hbox {},\hbox {}\tilde{\wedge } \hbox {},\tilde{\le } })\) be a neutrosophic soft lattice. Then \(N^{L}\)is called a neutrosophic soft modular lattice, if it is satisfies the following property:
for all \(F_A ,F_B \hbox {and}F_C \in N^{L}\).
Example 3.21
Let \(U=\{ {u_1 ,u_2 ,u_3 ,u_4 ,u_5 ,u_6 }\}\) be a universe set and \(N^{L}= \{ F_\emptyset ,F_A ,F_B ,F_C ,F_D \}\,\tilde{\subseteq }\,NS (U).\) Then \(N^{L}\,\tilde{\subseteq }\,NS(U)\) is a neutrosophic soft lattice with the operations \({\tilde{\cup } } \ \hbox {and} \ {\tilde{\cap }} \). Suppose that
\(\left( {N^{L}, {\tilde{\cup } }\hbox {},\hbox {} {\tilde{\cap } } ,\tilde{\subseteq } } \right) \)is a neutrosophic soft modular lattice. The Hasse diagram of it is shown in Fig. 3
4 Conclusion
In this paper, we defined the concept of neutrosophic soft lattice as an algebraic structure and showed that these definitions are equivalent. We then investigated some related properties and some characterization theorems. To extend this work one can study the properties of neutrosophic soft set in other algebraic structures and fields. In addition, based on these results, we can further probe the applications of neutrosophic soft lattice.
References
Molodtsov, D.A.: Soft set theory-first results. Comput. Math. Appl. 37, 19–31 (1999)
Chen, D., Tsang, E.C.C., Yeung, D.S., Wang, X.: The parameterization reduction of soft set and its applications. Comput. Math. Appl. 49, 757–763 (2005)
Maji, P.K., Biswas, R., Roy, A.R.: Fuzzy soft sets. J. Fuzzy Math. 9(3), 589–602 (2001)
Maji, P.K., Biswas, R., Roy, A.R.: Soft set theory. Comput. Math. Appl. 45, 555–562 (2003)
Maji, P.K., Roy, A.R.: An application of soft set in decision making problem. Comput. Math. Appl. 44, 1077–1083 (2002)
Roy, A.R., Maji, P.K.: A fuzzy soft set theoretic approach to decision making problems. J. Comput. Appl. Math. 203, 412–418 (2007)
Aktas, H., Cagman, N.: Soft sets and soft groups. Inf. Sci. 177, 2726–2735 (2007)
Feng, F., Jun, Y.B., Zhao, X.: Soft semirings. Comput. Math. Appl. 56(10), 2621–2628 (2008)
Babitha, K.V., Sunil, J.J.: Soft set relations and functions. Comput. Math. Appl. 60(7), 1840–1849 (2010)
Jun, Y.B.: Soft BCK/BCI-algebras. Comput. Math. Appl. 56, 1408–1413 (2008)
Jun, Y.B., Park, C.H.: Applications of soft sets in ideal theory of BCK/BCIalgebras. Inf. Sci. 178, 2466–2475 (2008)
Jun, Y.B., Lee, K.J., Park, C.H.: Soft set theory applied to commutative ideals in BCK-Algebras. J. Appl. Math. Inform. 26, 707–720 (2008)
Gong, K., Xiao, Z., Zhang, X.: The bijective soft set with its operations. Comput. Math. Appl. 60(8), 2270–2278 (2010)
Nagarajan, R., Meenambigai, G.: An application of soft sets to lattices. Kragujevac J. Math. 35(1), 61–73 (2011)
Birkhoff, G.: Lattice Theory. Transactions of the American Mathematical Society, New York (1967)
Li, F.: Soft lattices. Glob. J. Sci. Front. Res. 10(4), 56–58 (2010)
Cagman, N., Karaaslan, F., Enginoglu, S.: Soft lattices. J. New Results Sci. 1, 5–17 (2012)
Karaaslan, F., Cagman, N.: Fuzzy soft lattice theory. ARPN. J. Sci. Technol. 3(3), 248–253 (2013)
Smarandache, F.: A Unifying Field in Logics. Neutrosophy: Neutrosophic Probability Set and Logic. American Research Press, Rehoboth (1999)
Smarandache, F.: Neutrosophic set, a generalisation of the intuitionistic fuzzy sets. Int. J. Pure Appl. Math. 24, 287–297 (2005)
Maji, P.K.: Neutrosophic soft set. Ann. Fuzzy Math. Inform. 5(1), 2287–2623 (2013)
Broumi, S., Smarandache, F.: Intuitionistic neutrosophic soft set. J. Inf. Comput. Sci. England, UK 8(2), 130–140 (2013)
Broumi, S.: Generalized neutrosophic soft set. Int. J. Comput. Sci. Eng. Inf. Technol. 3(2), 17–30 (2013)
Broumi, S., Deli, I., Smarandache, F.: Relations oninterval valued neutrosophic soft sets. J. New Results Sci. 5, 1–20 (2014)
Broumi, S., Smarandache, F.: More on intuitionistic neutrosophic soft sets. Comput. Sci. Inf. Technol. 1(4), 257–268 (2013). doi:10.13189/csit.2013.010404
Broumi, S., Deli, I., Smarandache, F.: Neutrosophic parametrized soft set theory and its decision making problem. Ital. J. Pure Appl. Math. N 32, 1–12 (2014)
Broumi, S., Smarandache, F.: On neutrosophic implications. Neutrosophic Sets Syst. 2, 9–17 (2014)
Ali, M., Smarandache, F.: Complex neutrosophic set. Neural Comput. Appl. 25, 1–18 (2016). doi:10.1007/s00521-015-2154-y
Deli, I., Ali, M., Smarandache, F.: Bipolar neutrosophic sets and their application based on multi-criteria decision making problems. In: Proceeding of the 2015 International Conference on Advanced Mechatronic Systems, IEEE Xplore, Beijing, China, August 22–24 (2015). doi:10.1109/ICAMechS.2015.7287068
Ali, M., Deli, I., Smarandache, F.: The theory of neutrosophic cubic sets and their applications in pattern recognition. J. Intell. Fuzzy Syst. 30(4), 1957–1963 (2016). doi:10.3233/IFS-151906
Smarandache, F., Ali, M.: Neutrosophic Triplet Group. Neural Comput. Appl. (2016) (Accepted)
Davey, B.A., Priestley, H.A.: Introduction to Lattices and Order. Cambridge University Press, Cambridge (1999)
Acknowledgments
The authors would like to thank the referees for giving useful suggestions for improving the work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Uluçay, V., Şahin, M., Olgun, N. et al. On neutrosophic soft lattices. Afr. Mat. 28, 379–388 (2017). https://doi.org/10.1007/s13370-016-0447-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13370-016-0447-7
Keywords
- Neutrosophic soft sets
- Neutrosophic soft lattice
- Neutrosophic soft chain
- Modular neutrosophic soft lattice



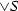 and
and 

