1 Introduction

The decision-making process to ensure reliability is critical in both complex engineering systems, such as power plants, offshore oil platforms, chemical production factories, and public transportation networks, as well as in large-scale environments involving multiple stakeholders, such as water distribution networks, regional power grids, and railway and air transportation systems. Reliability analysis of intricate dynamical systems usually employs stochastic discrete event models like Markov models and stochastic Petri nets (SPNs) (Bobbio et al., 1998; El-Moumen et al., 2023). Consequently, it becomes imperative to tailor existing techniques and tools to suit the specificities of these systems. Nonetheless, conventional analytical methods, such as the Markov model (El Moumen et al., 2023b), are no longer viable for systems that comprise a multitude of interdependent components. The combinatorial explosion problem of state numbers in discrete event systems poses a significant challenge for reliability analysis and dynamic system synthesis (Pinto et al., 2021; Vázquez-Serrano et al., 2021). The exponential growth in the number of states results in a highly complex calculation of the marking graph for the Markov model, which in turn makes the Markov analysis impractical (Ribeiro et al., 2018). Instead, SPNs are used as an estimator for the Markov model (Vázquez et al., 2008). The main advantage of this estimator is that it eliminates the need to determine the marking graph required by the Markov model method (Kalaiarasi et al., 2017; Moumen et al., 2022). However, this approach results in a longer convergence time to reach steady-state probabilities (del Foyo & Silva, 2017; Moumen et al., 2022). In general, this phenomenon is because information throughput is discrete (Bobbio et al., 1998; Florin et al., 1991). Most solutions to this problem aim to approximate SPNs with continuous approaches.

The continuous Petri net (CPN) is an extension of the SPN aimed at finding an acceptable continuous approximation of the discrete behavior of the latter. The CPN has several advantages over its discrete counterpart, including the ability to model continuous changes and time-dependent behaviors, and the ability to handle a large amount of information. To achieve this, several researchers have studied the fluidization of the SPN by the CPN (El Moumen et al., 2023a; Lefebvre et al., 2009; Recalde et al., 1999; Vazquez & Silva, 2009). Fluidization refers to the process of converting an SPN based on discrete events into a CPN based on deterministic continuous time (Recalde et al., 1999). The main goal of this conversion is to obtain a continuous behavior that approximates the behavior of systems modeled by SPNs, which will allow for a more accurate and exact analysis of these systems.

The process of fluidization involves adding continuous variables and differential equations to describe the evolution of the markings in each place of the SPN. This technique requires the use of control theory and numerical analysis to obtain performance calculations such as steady-state behavior of average markings and fast response time. However, fluidization can be challenging as it necessitates defining a continuous representation of the underlying system dynamics while preserving the stochastic behavioral structural properties (El-Moumen et al., 2023; Vazquez & Silva, 2009). It also involves solving information loss problems during the fluidization process and ensuring the coherence of the resulting continuous model.

Fluidization of SPNs can result in unexpected outcomes where the structural and behavioral properties may not be identical ((Lefebvre et al., 2009; Recalde et al., 1999). For instance, a PN can be live as a discrete system but non-live after fluidization (Vazquez & Silva, 2015), and a discretized bounded system can become non-boundary after fluidization (El Moumen et al., 2023a). The average throughput of the CPN may not always be an upper bound on that of the SPN (El Moumen et al., 2023a). While some methods exist for finding steady-state majors for CPN and SPN by solving linear programming problems (Giua & Silva, 2018); (David, 1993), no direct comparison exists between the two obtained majors (discrete and continuous). Additionally, the equilibrium points of SPN cannot be approximated directly by those of CPN. Standard fluidization under the semantics of infinite servers does not always lead to the same behavior (El Moumen et al., 2023a). The average markings and asymptotic average throughputs of SPN and CPN with similar structure and initial marking may not be identical in the general case (Akchioui, 2018). Researchers (El Akchioui, 2017; Lefebvre et al., 2009) have developed numerical approaches to obtain comparable behaviors between different models in this context. The first approach called "adaptive" (El & Choukrad, 2016; El Akchioui, 2017), and the second, "piecewise linear", were developed by (Akchioui, 2018; Lefebvre & Leclercq, 2012). The piecewise linear approach is described in the literature as a numerical method for approximating solutions to ordinary differential equations using piecewise linear functions over adaptively chosen time intervals. We added sufficient conditions, such as subdividing the marking trajectory into multiple intermediate phases, to ensure that the continuous fluid model converges to that of the stochastic model. The adaptive approach is also a numerical method for approximating solutions to ordinary differential equations, but it uses a strategy based on minimizing errors due to variations in markings and average throughputs. We also added conditions to ensure monotonic convergence. These two approaches solve the problem of the difference between asymptotic average markings and throughputs between stochastic and CPN. Finally, a more concise comparison and discussion of the results will be established and analyzed using simulations. The adaptive approach shows better convergence toward the steady state of stochastic models compared to the other approach.

The document is organized into four sections. Section 2 presents basic definitions of Petri nets (PNs), SPN and CPN. Section 3 discusses the limitations of using SPN and standard fluidization in a single region and multiple regions, with examples from the literature presented as a case study to illustrate these problems through numerical simulations. Section 4 describes two fluidization approaches: the piecewise linear and adaptive approaches. The same example is studied for the application of these two approaches, to compare them, discuss the results, and provide perspectives for future work.

2 Background

2.1 Petri nets (PNs)

A PN is a robust mathematical model used to represent a variety of systems operating on discrete variables. Its applications include the analysis, design, and reliability assessment of distributed systems, communication protocols, and other complex systems (Arzola et al., 2020; Rozenberg & Engelfriet, 1998). The original PN model did not incorporate the concept of time, which consists of places, arcs, transitions, and tokens, providing a foundation for modeling various properties of systems (David & Alla, 1994; Desel & Juhás, 2001; Murata, 1989).

In a formal context, a PN is defined by a quintuple = (P, T, W, A, M), where (Desel & Juhás, 2001; Esparza, 1998):

  • P = {Pi}, i = 1, …, n, constitutes a finite set of n places, typically depicted as circles.

  • T = {Tj}, j = 1, …, q, represents a finite set of q transitions, often depicted as lines.

  • W ⊆ (P × T) ∪ (T × P), signifies a set of arcs connecting places and transitions. The incidence matrix W = (WPO − WPR) ∈ (Z)n×q, with WPR = (wijPR) ∈ (IN)n×q containing values of arcs directed from Pi to Tj, and WPO = (wijpo) ∈ (IN)n×q containing values of arcs directed from Tj to Pi.

  • A: W → {1, 2, 3, …}, signifies the weight associated with arcs in W.

  • M: P → {0, 1, 2, …}, represents the marking, indicating the number of tokens, often depicted as dots or positive integers, in each place in Pi.

Timed PNs are a significant extension of conventional PNs designed to incorporate temporal variables into discrete event dynamic systems. They encompass the network's topological structure, labeling elements with temporal values, and establishing triggering rules based on time. Various approaches have been developed to model these timed dependencies, including deterministic timed transition PNs (Ramchandani, 1974), timed PNs by (Merlin, 1974), which define minimum and maximal wait times for transitions, deterministic timed place PNs (Coolahan & Roussopoulos, 1983), and deterministic timed arcs PNs (Zhu & Denton, 1988). Among these approaches, deterministic timed transition PNs, which associate time labels with transitions, stand out for their ability to link timing directly with transitions, providing flexibility for precise control over transition firing times. They are particularly suitable for evaluating system performance, especially in scenarios where time management is critical (Marsan, 1990; Seatzu, 2005).

A transition \({T}_{j}\) is considered enabled when the current marking satisfies the enabling conditions. When enabled, a transition can fire, leading to the transfer of tokens from input places to output places based on the arc multiplicities. The sequencing of transitions becomes crucial when multiple transitions are enabled simultaneously. Determining the firing order is essential in such cases, while others may be delayed. The evolution of a PN is depicted through the marking graph, also recognized as the accessibility graph. Each node within this graph symbolizes a marking, and arcs illustrate potential transitions between markings, with transition labels indicating changes in marking. Place markings are denoted as M(Pi) or simply mi. The initial marking is represented as MI, and the marking at time t is defined by M(t). Ej(M(t)), signifies the enabled degree of transition \({T}_{j}\), determined for marking M(t) according to (Júlvez et al., 2005; Lefebvre et al., 2010):

$$ E_{j} \left( {M\left( t \right)} \right) = \min \left( {M\left( {P_{i} } \right)/w_{ij}^{PR} } \right), {\text{for}}\;{\text{all}}\;{ }P_{i} \in {^\circ T_{j}} . $$
(1)

where °Tj represents the set of places upstream of Tj. For any Pk ∈ °Tj, Pi is a critical place at t (time) for Tj with \(i\) = arg(min (mk (t)/wkjPR)) (Moumen et al., 2022).

Let Y = {yiP}, iP = 1…, K1, denote the set of P-semi-flows, and Z = {ziT}, iT = 1…, K_2, denote the set of T-semi-flows. A P-semi-flow y ∈ (Z+)n, satisfying the relation yT. W = 0, corresponds to a marking invariant: yT.M = YT.MI = C, where C is a constant vector. This relation signifies the conservation of the weighted quantity of markings. A PN that accommodates one or more P-semi-flows in which all places occur at least once is termed conservative. Conversely, a T-semi-flow z ∈ (Z+)q, satisfying the relation W. z = 0, defines a potential cycle involving repetitive transitions while maintaining the marking invariant. A PN that admits one or more T-semi-flows in which all transitions occur at least once is referred to as consistent (Lefebvre & Leclercq, 2012).

2.2 Stochastic Petri Nets (SPNs)

The original PN model did not include the concept of time, leading to limitations in analyzing system performance and reliability. As a result, the notion of event duration associated with PN transitions needed to be introduced. Timed PNs provide the capability to not only depict a logical sequencing of occurrences but also account for their temporal aspects. They are useful for modeling systems where activations synchronize with external events and where system dynamics are influenced by temporal factors (David & Alla, 1994). To address this need, two main approaches were pursued. The first approach, timed PN, models event durations deterministically or within defined intervals. The second approach, SPN, represents event durations as random variables (Heiner et al., 2009; Karamanolis, 1999). Incorporating temporal information into transitions, timed PNs result in a more comprehensive representation. A specific case of timed PNs is SPN, where the firing times of transitions are considered random variables. More specifically, a particular case of SPN involves exponential distributions for firing times (Ajmone Marsan & Chiola, 1987; Haas & Shedler, 1989), with a parameter varying according to (round(Ej(M)) × μj), where Ej(M) represents the enabling degree of transition Tj for a given marking M, and the function "round(.)" denotes the integer part of a number. The concept of SPN models was independently proposed by (Natkin, 1980; Molloy, 1981) in their respective doctoral dissertations. These models aimed to integrate formal description, correctness verification, and performance evaluation in the field of applied stochastic modeling (Marsan, 1990). The foundational idea of associating exponentially distributed random delays with PN transitions, crucial to SPNs, was prefigured by (Symons, 1980) in his work on Numerical PNs, offering a historical perspective on the evolution of these models.

An SPN, denoted as < PN, μ > , associates the underlying PN with a firing rate vector μ = (μj) ∈ (R+)q. Each transition Tj in the SPN is characterized by a firing rate μj, representing the likelihood of Tj firing within a small-time interval dt, given that it has been activated with degree 1 at time t. The marking process of SPN is described using various elements, including the PN incidence matrix, the initial marking, the firing rates, the firing policy, the server policy, and the execution policy (Lefebvre et al., 2009; Silva & Recalde, 2002). These characteristics are all utilized to describe the marking process of an SPN. The vector of the average throughput and average marking of an SPN depending on time, are named, respectively, Xs (t) and Ms (t). SPNs in this work have satisfied the hypotheses (A1–A5) (El Moumen et al., 2023a; Júlvez et al., 2005):

  • (A1) The labeled SPNs are limited by the bounds.

  • (A2) The labeled SPNs can be reset.

  • (A3) The firing policy follows a race policy, where the transition with the shortest firing time is considered to be the one that will fire next.

  • (A4) The server policy is infinite, meaning that each transition Tj has a minimal period (dm) determined by a stochastic length characterized by an exponential distribution with a parameter that varies according to (round(Ej(M)) × μj). This policy is characterized by the influence of the enabling degree.

  • (A5) The execution policy is of the form of "resampling memory," where at the start of labeling, all transitions that were previously enabled have their remaining firing time reset.

These assumptions collectively provide a solid foundation for effectively modeling and analyzing SPN behavior, specifically concerning how markings evolve and the precise timing of transition firings. When focusing on the average marking and average throughput of SPNs, SPNs are configured to encompass an accessibility graph denoted as A(SPN, MI) with finite states. This graph's labeling process aligns seamlessly with a Markov model that exhibits an isomorphism to A(SPN, MI). Consequently, this configuration allows us to calculate the asymptotic behavior of the SPN based on the probability of reaching the steady state within the Markov model (El-Moumen et al., 2023; Moumen et al., 2022).

In the context of operational SPNs adhering to the aforementioned assumptions and operating within a finite state space, the SPN presents a marking graph that is isomorphic to the state space of a Markov model. Within this framework, determining the SPN's steady state becomes feasible by evaluating the probabilities associated with the Markov model states. The vector of steady-state probabilities is defined by the solution of (El & Choukrad, 2016):

$$ \Pi_{S} \cdot A\left( \mu \right) = 0 \;{\text{and}} \;\Pi_{S} \cdot 1_{N} = 1. $$
(2)

with ПS = (πSk)1 × N, the vector of steady-state probabilities of the Markov model related to N states. A(µ), as the Markov model generator associated with the SPN, is a square matrix of dimension N × N, N being the finite number of states of the linked Markov model and 1N = (1,….,1)T represents a vector of dimension N whose all components are equal to 1.

Let Xs = (xsj ∈ (R+)q) represent the average throughput vector of SPN and MS = (mSi) ∈ (R+)n represent the average markings vector of SPN. As a consequence, from the vector ПS, we will deduce the average throughputs of transitions as well as the average markings of places as (Lefebvre et al., 2010):

$$ x_{sj} = \mu_{j} \cdot \mathop \sum \limits_{k = 1}^{N} \left( {E_{j} \left( {M_{k} } \right) \cdot \pi_{k} } \right). $$
(3)
$$ m_{si} = \mathop \sum \limits_{k = 1}^{N} m_{ki} \cdot \pi_{k} . $$
(4)

where MK = (mki) ∈ (R+)n signifies the vector of marking matching the state k of the Markov model. When it comes to the ergodic Markov Model, this method gives an analytical solution of the steady state of the SPN, but it necessitates computing the transition matrix A(µ) (Lefebvre et al., 2009; Vazquez & Silva, 2015), as a result, the SPNs accessibility graph A(SPN, MI) is isomorphic to the Markov model (Vázquez et al., 2008). N rises exponentially. For large-scale systems, the calculation time and storage needs to evaluate A(SPN, MI) become more relevant. In this case, for the Markov model, SPN can be thought of as a stochastic estimator. The benefit of this estimator is that it eliminates the need to determine A(SPN, MI), but, the stochastic estimator is slow to converge, especially for rare events.

In the realm of SPNs, analysis involves the exploration of two distinct yet mutually reinforcing aspects. The first aspect delves into the preservation properties within a PN, derived from P-semi flows and T-semi flows, providing valuable insights into system behavior. The second aspect focuses on the analysis of a continuous-time, discrete-state space Markov process, commonly recognized as a bounded PN (Marsan, 1990; Silva & Recalde, 2002). These two complementary methods together enable a comprehensive exploration of system dynamics within the domain of SPNs. This framework not only facilitates the simulation of complex systems but also offers a practical alternative to state graph-based Markov analysis, especially for large systems where the combinatorial explosion can render traditional methods impractical (Kuntz et al., 2021). Furthermore, SPNs serve as estimators of Markov models, assisting in the comparison and evaluation of system performance indicators.

To facilitate the determination of system performance indicators and the comparison of the random behavior of the SPN with that of a homogeneous Markov model with a finite state space, the algorithm of the stochastic estimator is depicted in Fig. 1 (El Moumen et al., 2023a).

Fig. 1
figure 1

Steady state by SPNs algorithm

Full size image

2.3 Timed Continuous Petri Nets (CPNs)

Timed continuous Petri nets (TCPNs) represent an extension of PN designed for modeling and analyzing dynamic systems that evolve over time. They are utilized to capture systems that exhibit both temporal and continuous characteristics, making them particularly well-suited for modeling reactive systems in fields such as industrial automation, communication, and robotics (El Moumen et al., 2023a). TCPNs combine the features of PNs, timed systems, and continuous systems to accurately depict the dynamic behavior of systems (Silva & Recalde, 2002). While TCPNs are commonly denoted as CPNs, they have been deliberately developed to provide continuous approximations of the discrete behaviors of PNs. CPNs are distinguished by their consistent maximal firing speeds and employ an infinite server semantic to facilitate a seamless transition between discrete and continuous modeling paradigms. The marking of each place is represented as a continuous, non-negative real-valued function of time, as described by (Lefebvre et al., 2010; Seatzu, 2005; Silva & Recalde, 2004). A CPN is formally defined as < PNs, Xmax > , where Xmax = diag(xmaxj) ∈ (R+)q×q is the diagonal matrix of the maximal firing speeds xmaxj, with j = 1,..,q.

Let Mc(t) = (mci) ∈ (R+)n be the vector representing the continuous markings mci(t) of place Pi, with i = 1,..,n. Likewise, let Xc(t) = (xcj) ∈ (R+)q be the vector representing the continuous throughputs of transition Tj. The evolution of the marking in CPN can be described by (Lefebvre et al., 2010):

$$ {{dM_{c} } \mathord{\left/ {\vphantom {{dM_{c} } {dt}}} \right. \kern-0pt} {dt}} = W \cdot X_{C} \left( t \right), M_{c} \left( 0 \right) = M_{I} . $$
(5)

The equation governing the instantaneous velocity of the transition Tj is given by (Lefebvre & Leclercq, 2012):

$$ x_{cj} = x_{{{\text{max}}j}} \cdot E_{j} \left( {M_{c} \left( t \right)} \right). $$
(6)

3 SPNs and CPNs: Problem Statements

3.1 Complexity of the Reachability Graph for SPN

As an example, we will consider the example modeled by (Júlvez et al., 2005) presented in Fig. 2. This PN is used to model a manufacturing system with 5 machineries (T1–T5), and 3 resources limited tools (P1–P3). In this PN model, the vector of the parameters of the transitions µ and the initial marking MI, are given by, μ = (1,1,1,1,1)T, MI = k(6, 6, 2, 0, 3, 0, 3, 0, 0)T where k ∈ IN.

Fig. 2
figure 2

Manufacturing system

Full size image

Table 1 shows the variation in the number of states \(N\) and the computation time required to calculate the reachability graph, based on the parameter k (Silva & Recalde, 2002). We consider two cases: the first has M(P3) = 2, and the second has M(P3) = 4. These cases clearly illustrate the complexity associated with the reachability graph.

Table 1 Number of states and calculation time of the reachability graph in function of k
Full size table

Table 1 indicates that as the parameter k increases, particularly when the marking of place \({P}_{3}\) increases, the number of states in the marking graph increases exponentially (Akchioui, 2018; Murata, 1989). Although the SPN does not need to compute the marking graph, the increase in the number of states leads to a longer computation time.

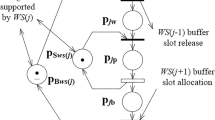
Consider the SPN described in Fig. 3 (Lefebvre & Leclercq, 2012) that contains two joint synchronizations in T1 and T2 with initial marking MI = (5, 0, 0, 0, 4)T and firing rate µ with µ = (3 1 1 10)T. This PN has a single firing invariant defined by the T-semi flow z1 = (1 1 1 1)T and two marking invariants defined by the P-semi flows y1 = (0 0 0 1 1)T, and y2 = (1 1 2 1 0)T.

Fig. 3
figure 3

Non-ordinary SPN with two joins and MI = (5 0 0 0 4)T

Full size image

Figure 4 illustrates the evolution of the estimated marking of place P1 in blue and the average marking in red, as obtained by the SPN simulator using the firing rate µ = (3 1 1 10)T shown in Fig. 3.

Fig. 4
figure 4

Markings evolution Ms1 (t) of SPN in function of time for example of Fig. 3

Full size image

Simulation using SPNs leads to longer calculation times to reach a steady-state behavior, especially when the initial marking generates a large number of states. Therefore, we can explore a solution to expedite this calculation time by employing CPN simulation to estimate the evolution of average markings and throughputs. Unfortunately, SPNs and CPNs exhibit different asymptotic behaviors.

3.2 Standard Approximation of SPNs

The standard approximation of SPNs by CPNs involves replacing the input and output arcs of each place with continuous arcs to model uncertain dynamic systems using differential equations (Júlvez et al., 2005; Vázquez et al., 2008). However, this approach often results in structural and behavioral differences between the two models (Benaya et al., 2018; Silva & Recalde, 2004). For example, a PN can be live as a discrete model but non-live after fluidization (Lefebvre & Leclercq, 2012; Navarro-Gutiérrez et al., 2022), and a discretized bounded system can become non-bounded after fluidization (Horton et al., n.d.). The average throughput of the CPN is not always an upper bound on that of the SPN (Recalde et al., 1999). While there are methods for finding steady-state majors for both CPN and SPN, obtained through solving linear programming problems (Lefebvre et al., 2009; Seatzu, 2005; Vazquez & Silva, 2009), there is no direct comparison between the two majors, discrete and continuous. Additionally, equilibrium points of the SPN cannot be directly approximated by those of the CPN due to differences in behavior resulting from standard fluidization approaches. As a result, the average markings and asymptotic average throughput of SPN and CPN with similar structures and initial markings may not be identical in general. To interpret this issue, we will provide a concrete example and ensure that we are in the same context as the problem. Then, we will establish a proof base to reach the actual solution. This approach will enable us to gain a better understanding of the situation and propose an effective solution to resolve the issue, which involves finding a direct convergence solution between the two models.

Consider the example presented in Fig. 3. Table 2 presents the results of the standard approximation under the infinite server semantics.

Table 2 Markings and throughputs of stochastic and continuous behaviors in Fig. 3
Full size table

Figure 5 shows the simulation of SPN of Fig. 3 with standard approximation (xmaxj = µj), we only consider the marking of the places P1, P4 and P5.

Fig. 5
figure 5

Markings evolution Mc(t) and Ms(t) of CPN and SPN in function of time for example of Fig. 3

Full size image

Figure 5 displays the evolution of markings by SPN and CPN from Fig. 3, enabling a comparison between the two models. In this context, CPN simulation is conducted under the infinite server semantics with xmaxj = μj. Figure 5 clearly illustrates that the behaviors of continuous and stochastic average markings are distinct. This discrepancy arises due to the presence of weighted arcs and synchronization, leading to the emergence of multiple distinct regions, as indicated by the "min(..)" function in the activation degree expression. It is worth noting that the standard approximation method does not guarantee identical behavior between SPNs and CPNs (Silva & Recalde, 2004).

3.3 Region in the Reachability Graph for CPN

In this section, we delve deeper into the concept of regions, which play a pivotal role in our analyses. The notion of the region appears because of the "min(..)" function in the activation degree expression (El Akchioui, 2017; Lefebvre et al., 2010). These regions are vital for understanding the behavior of our model and its various configurations. The marking area is separated into k regions LK (Akchioui, 2018) (some regions may remain empty). Each LK region is defined by its unique combination or configuration (El Moumen et al., 2023a), which is also referred to as the PT-sum (LK) = {(Pi, Tj)}\(.\) The PT-sum for a given LK can be expressed as {(Pi, Tj)}, where Pi represents the critical place of Tj within LK (Silva & Recalde, 2002). The number of configurations is closely tied to the number of synchronizations and the count of places leading to synchronization transitions, denoted as K =|°T1| x … x |°Tq|. The PT-sum (Lk), is formally defined as the sum of all combinations (Pi, Tj), specified below:

$$\begin{aligned} PT - {\text{sum}}\left( {L_{K} } \right) &= \Big[\left( {P_{i} , T_{j} } \right) s \cdot m \cdot \forall M_{c} \left( t \right) \in L_{K} , x_{cj} \left( t \right) \\ &= x_{{{\text{max}}j}} \left( t \right) \cdot {{m_{ci} \left( t \right)} \Big/ {w_{ij}^{PR} }} \Big].\end{aligned} $$
(7)

Each LK region is uniquely characterized by a matrix constraint Lk = (lijk) ∈ (R+)qxn, where i = 1,…, q, k = 1,…,K and j = 1,…, n. The constraints within Lk are as follows:

  • for all Tj ∈ T, ljik (k,j) = 1/wi(k,j)jPR,

  • Otherwise, ljik = 0.

Consequently, within each LK, we can represent the maximal firing speeds vector as Xc(t) = Xmax. LK. Mc(t), as follows:

$$ {{dM_{c} \left( t \right)} \mathord{\left/ {\vphantom {{dM_{c} \left( t \right)} {dt}}} \right. \kern-0pt} {dt}} = W \cdot X_{{{\text{max}}}} \cdot L_{K} \cdot M_{c} \left( t \right), \; \forall M_{c} \left( t \right) \in L_{K} . $$
(8)

Consider the PN illustrated in Fig. 3, which is a non-ordinary PN that contains two joint synchronizations in T1 and T2 with µ = (3, 1, 1, 10)T and MI = (5 0 0 0 4)T. The existence of synchronizations leads to the presence of multiple distinct regions, with the number of regions dependent on the number of synchronizations in the PN. The CPN in Fig. 3 contains two synchronizations, reflected in the choice of maximal firing speed corresponding to the validation degree expression. The maximal firing speeds are determined as follows:

$$ \left\{ {\begin{array}{*{20}l} {X_{c1} \left( t \right) = x_{{{\text{max1}}}} \cdot \min \left( {m_{c1} {{\left( t \right)} \mathord{\left/ {\vphantom {{\left( t \right)} 2}} \right. \kern-0pt} 2}, m_{c5} \left( t \right)} \right)} \hfill \\ {X_{c2} \left( t \right) = x_{{{\text{max2}}}} \cdot \min \left( {m_{c1} \left( t \right),m_{c4} \left( t \right)} \right)} \hfill \\ {X_{c3} \left( t \right) = x_{{{\text{max3}}}} \cdot m_{c2} \left( t \right) } \hfill \\ {X_{c4} \left( t \right) = x_{{{\text{max4}}}} \cdot m_{c3} \left( t \right) } \hfill \\ \end{array} } \right.. $$
(9)

The existence of the “min” operator in the calculation of xc1(t) and xc2(t), leads to the existence of four regions L1 to L4. Each region is linked to a PT-sum(LK) (Silva & Recalde, 2002), k = 1,..,4. Table 3 summarizes the results obtained from each region LK.

Table 3 Regions and configurations for the CPN in Fig. 3
Full size table

Note that P1 is a critical place for both transitions T1 and T2; therefore, L1 is a critical region. The speeds of the two transitions (T1, T2), depend on the same place P1. The following constraint matrix serves as indicators for the regions L1 to L4:

$$ \begin{aligned} L_{1} = & \left[ {\begin{array}{*{20}l} {\quad 1/2} \hfill & {\quad 0} \hfill & {\quad 0} \hfill & {\quad 0} \hfill & {\quad 0} \hfill \\ {\quad 1} \hfill & {\quad 0} \hfill & {\quad 0} \hfill & {\quad 0} \hfill & {\quad 0} \hfill \\ {\quad 0} \hfill & {\quad 1} \hfill & {\quad 0} \hfill & {\quad 0} \hfill & {\quad 0} \hfill \\ {\quad 0} \hfill & {\quad 0} \hfill & {\quad 1} \hfill & {\quad 0} \hfill & {\quad 0} \hfill \\ \end{array} } \right]L_{3} = \left[ {\begin{array}{*{20}c} {\quad 0} & {\quad 0} & {\quad 0} & {\quad 0} & {\quad 1} \\ {\quad 1} & {\quad 0} & {\quad 0} & {\quad 0} & {\quad 0} \\ {\quad 0} & {\quad 1} & {\quad 0} & {\quad 0} & {\quad 0} \\ {\quad 0} & {\quad 0} & {\quad 1} & {\quad 0} & {\quad 0} \\ \end{array} } \right] \\ L_{2} = & \left[ {\begin{array}{*{20}c} {\quad 1/2} & {\quad 0} & {\quad 0} & {\quad 0} & {\quad 0} \\ {\quad 0} & {\quad 0} & {\quad 0} & {\quad 1} & {\quad 0} \\ {\quad 0} & {\quad 1} & {\quad 0} & {\quad 0} & {\quad 0} \\ {\quad 0} & {\quad 0} & {\quad 1} & {\quad 0} & {\quad 0} \\ \end{array} } \right]L_{4} = \left[ {\begin{array}{*{20}c} {\quad 0} & {\quad 0} & {\quad 0} & {\quad 0} & {\quad 1} \\ {\quad 0} & {\quad 0} & {\quad 0} & {\quad 1} & {\quad 0} \\ {\quad 0} & {\quad 1} & {\quad 0} & {\quad 0} & {\quad 0} \\ {\quad 0} & {\quad 0} & {\quad 1} & {\quad 0} & {\quad 0} \\ \end{array} } \right] \\ \end{aligned} $$

The region L1 is a critical region reachable from the initial marking MI. In the following, we subdivide CPN into different classes, depending on the nature of the synchronizations.

3.4 Approximation in Multiple Regions and in the Critical Region

Let us consider the example in Fig. 3, where five SPNs with different firing rates, namely SPN1 through SPN5, denoted as β1 to β5, are available. In this study, we have selected three SPNs from the critical region L1, namely β2, β3 and β5, to highlight the pivotal role played by this specific region in delineating the distinctions between SPNs and CPNs. The choice of these particular SPNs was made to focus our analysis on the region that exhibits unique characteristics and challenges within the context of our study. This selection allows us to explore and better understand the influence of the critical region on the differences between SPNs and CPNs.

Table 4 gathers the results of the standard approximation of SPNs in Fig. 3 in different firing rates under the infinite server semantics with the same structure and the same MI.

Table 4 Stochastic and continuous markings and throughputs of the SPN and CPN in Fig. 3 for different values of Xmaxj = µj
Full size table

Figures 6 and 7 show the projections in the \(\left( {m_{1} , m_{2} + 2 \cdot m_{3} } \right)\) plane of the stochastic and continuous average markings, respectively, in different accessible regions as a function of five random draws of transition rates and maximal firing speeds.

Fig. 6
figure 6

Marking Ms(t) for different firing rates of the SPN for example of Fig. 3

Full size image
Fig. 7
figure 7

Marking Mc(t) for different maximal firing speeds of the CPN for example of Fig. 3

Full size image

The SPN and CPN regions are different. For example, in Fig. 6, β2, β3, and β5 are located in region L1, but after fluidization presented in Fig. 7, they move to region L3. This difference is due to the more sincere division into several regions due to the presence of the "min(..)" function in the definition of the degree of activation, resulting in the CPNs behavior being piecewise linear (Lefebvre & Leclercq, 2012). Note that in Fig. 6, SPN β1 and β4 are located outside of the critical region L1. According to fluidization, in Fig. 7 they remain in the same region as the SPNs. However, other SPNs such as β2, β3, and β5 do not remain in the same region as the SPNs. This shows that the critical region plays an important role in this difference. These results show that the standard approximation of SPNs by CPNs with multiple regions and particularly the critical region does not lead to the same behavior of the asymptotic average marking and that the behavior of SPNs is not always accurately approximated by CPNs.

To overcome this problem, two numerical approaches of fluidization have been studied in (El Moumen et al., 2023a; Júlvez et al., 2005; Lefebvre & Leclercq, 2012; Lefebvre et al., 2009) to obtain a CPN whose average behavior in steady state is equivalent to the average behavior of a given SPN, under the semantics of the infinite server. We will apply these approaches to the previous example, Fig. 3, to compare and discuss them.

4 Numerical Approaches to Fluidization and Comparison

Fluidization is an interesting alternative for estimating the asymptotic behavior of stochastic processes using CPNs. The synchronization is a key element of this approximation. Specifically, the presence of multiple regions, and particularly the existence of critical regions, complicates the standard approximation of the SPNs. In this section, we investigate two different approximation approaches: the piecewise linear approach (Lefebvre & Leclercq, 2012) and the adaptive approach ( El Akchioui, 2017; El Moumen et al., 2023a). The piecewise linear approach is described in the literature as a numerical method for approximating solutions to ordinary differential equations using piecewise linear functions over adaptively chosen time intervals. We have shown that fluidization is not guaranteed when the initial marking exists in the critical region, and therefore we have added sufficient conditions, such as subdividing the marking trajectory into multiple intermediate phases, to ensure convergence in all regions, especially in the critical region. The adaptive approach is also a numerical method that compensates for errors due to variations in marking and throughput rates and necessary conditions will be added to ensure monotone convergence. Both of these approaches solve the problem of the difference between asymptotic markings and throughputs between stochastic and CPN models. Finally, a more concise comparison and discussion of results will be established and analyzed using simulations.

The first one is characterized by maximal firing speeds of transitions defined and different in each region, allowing us to define a new piecewise linear CPN. The second one is characterized by maximal firing speeds of transitions modified by a nonlinear adaptive law, based on minimizing errors due to variations of marking and average firing throughput. Finally, we will apply these approaches to the previous example shown in Fig. 3. We will choose the case of SPN β3, from the critical region L1 as our case for comparison and discussion of these two approaches is grounded in its significance within the context of the study. This choice allows us to effectively illustrate the implications and outcomes of applying these two distinct approaches in a region known for its critical characteristics.

4.1 Piecewise Linear Approach (CPN-PW)

The piecewise linear approach is a modeling tool that divides the approximation of markings into several phases, making it suitable for systems with multiple phases. The maximal firing speed is defined as a piecewise continuous function, allowing the CPN to converge to the stochastic marking. Sufficient conditions are established for the fluid model to converge to the stochastic average marking in both the single region and multiple region cases. Convergence is guaranteed for the single region, but for the multiple region case, particularly the critical region, sufficient conditions are established. This results in the definition of a new piecewise linear CPN (Lefebvre & Leclercq, 2012), where the marking evolves in each region and has different maximal firing speeds of transitions from other regions.

Definition 1

Equivalent average marking.

Let us consider a CPN. Let \({M}_{c}\) be the vector of markings and Xc the vector of stationary state speeds. Xc verifies:

$$ W \cdot X_{c} = 0\quad {\text{with}}\;X_{c} > 0. $$
(10)

In the LK region, (8) can be rewritten, aiding in the characterization of the stationary state of the CPN as:

$$ W \cdot X_{{{\text{max}}}} \cdot L_{k} \cdot M_{c} = 0. $$
(11)

The system of equations obtained from (11) is however insufficient to determine Xmax. When considering the marking invariants, we derive the compatible system as:

$$ \underbrace {{\left( {\begin{array}{*{20}c} {W \cdot X_{{{\text{max}}}} \cdot L_{k} } \\ {Y^{T} } \\ \end{array} } \right)}}_{{S\left( {X_{{{\text{max}}}} } \right)}} \cdot M_{c} = \underbrace {{\left( {\begin{array}{*{20}c} 0 \\ {Y^{T} \cdot M_{I} } \\ \end{array} } \right)}}_{C}. $$
(12)

In the case where the determination of the steady-state marking has a unique non-negative solution, the expression of the marking as a function of Xmax can be obtained as:

$$ M_{c} = f\left( {X_{{{\text{max}}}} } \right). $$
(13)

The function f depends on the maximal firing speeds and can be obtained by the resolution of the (12) provided that the matrix (LKT. Xmax. WT|Y)T is of full rank in columns (i.e., of rank n). In this scenario, the maximal speed matrix can be determined, and the average throughputs can be calculated as follows:

$$ X_{{{\text{max}}}} \cdot L_{k} \cdot M_{c} = X_{c} . $$
(14)

Definition 2

Global asymptotic equivalence.

Consider as SPN < MI, µ, Ms > with MI ∈ Lk and a CPN with the same structure, the same MI and different maximal firing speeds of SPN firing rates. In each Lk, Mc(t) satisfy (8). Consequently, when the marking trajectory remains in the MI region it tends to Mc that satisfies (8). As long as rank(S(Xmax)) = rank(S(Xmax). C) = q, the system of (12) becomes invertible, whose solution allows determining the continuous average marking which verifies (15). As long as Mc converges to Ms satisfy Mc = Ms, the solution of (12) also allows computing Mc = f(Xmax). The long-term exact solution for Mc is as follows:

$$ \left\{ {\begin{array}{*{20}l} {M_{c} = (S^{T} \left( {X_{{{\text{max}}}} } \right) \cdot S\left( {X_{{{\text{max}}}} } \right))^{ - 1} \cdot S^{T} \left( {X_{{{\text{max}}}} } \right)} \hfill \\ {M_{s} = (S^{T} \left( {X_{{{\text{max}}}} } \right) \cdot S\left( {X_{{{\text{max}}}} } \right))^{ - 1} \cdot S^{T} \left( {X_{{{\text{max}}}} } \right) \cdot C} \hfill \\ \end{array} } \right.. $$
(15)

When Mc(t) and Xc(t) converge to Ms and Xs, respectively, as t tends to infinity, and if Mc(t) satisfies the condition, then the rank of S(Xmax) = q, and Xmax satisfies (Lefebvre & Leclercq, 2012):

$$ \left\{ {\begin{array}{*{20}l} {X_{s} = X_{{{\text{max}}}} \cdot L_{k} \cdot (S^{T} \left( {X_{{{\text{max}}}} } \right) \cdot S\left( {X_{{{\text{max}}}} } \right))^{ - 1} \cdot S^{T} \left( {X_{max} } \right) \cdot C} \hfill \\ {M_{s} = (S^{T} \left( {X_{max} } \right) \cdot S\left( {X_{max} } \right))^{ - 1} \cdot S^{T} \left( {X_{max} } \right) \cdot C } \hfill \\ \end{array} } \right.. $$
(16)

In each LK, Xc(t) satisfies Xc(t) = Xmax. LK. Mc (t). In particular, if Ms ∈ LK, Xs holds:

$$ X_{s} = X_{{{\text{max}}}} \cdot L_{k} \cdot M_{s} . $$
(17)

Definition 3

Piecewise Continuous Petri net (CPN-PW).

A CPN-PW is seen as a combination of several timed CPN: {CPNk, k = 1,.., K} with CPNk = {P, T, WPO, WPR, Xmaxk} that evolves only in the region Lk. Xmaxk, k = 1,.., K represents the matrix of maximal firing speeds defined in each region (Lefebvre & Leclercq, 2012).

The CPN-PW behaves like a collection of several CPNs in a single CPN. The matrixes of maximal firing speeds Xmaxk, k = 1,…,K of a CPN-PW are calculated for each region Lk. Each CPN has different maximal firing speeds. The asymptotic average markings of a CPN-PW satisfy the form of (11) in each region Lk. We continue with the example in Fig. 3 to illustrate the global asymptotic equivalence in the β3 SPN that exists in the Lk critical region.

4.2 Adaptive Approach

The adaptive approach is aimed at adapting all maximal firing speeds of the CPNs through an adaptive controller. These speeds are considered time-varying functions and are updated to ensure the modified CPN converges to the SPN. It corrects errors in throughput and marking by referring to the asymptotic stochastic average throughput and average marking to be reached. Therefore, the adaptive maximal firing speeds for the nonlinear CPN (NL-CPN) are defined.

Definition 4

Nonlinear CPN.

A Nonlinear CPN: (NL-CPN) = (P, T, WPR, WPO, Ms, Xs), is governed by the adaptation law of the maximal firing speeds. This law constitutes a system of (n + q) differential equations under the constraint Xmax ≥ 0, as proposed by (El Akchioui, 2017; Lefebvre et al., 2009):

$$ \dot{X}_{{{\text{max}}}} = \eta \cdot {\text{diag}}\left( \mu \right) \cdot \left( {\left( {W^{T} } \right) \cdot \left( {M_{s} - M_{c} \left( t \right)} \right) + \left( {X_{s} - X_{c} \left( t \right)} \right)} \right). $$
(18)

where diag(µ) is the diagonal matrix SPN firing rates, η is the adaptation parameter, (Xs−Xc(t)) represents the error related to the continuous and stochastic average throughput, and the vector (Ms−Mc(t)) the error due to variations in the stochastic and continuous average markings.

To determine the variations of the maximal firing speed associated with the transition Tj, we considered the transition Tj and wj which defines the column j of the W. The variations of the maximal firing speeds of transition Tj depend on the places (°Tj) and downstream (Tj°) of the transition in consideration, in the following different cases:

  • If at time t, all places Pi ∈°Tj, verify msi−mci(t) > 0 and all places Pk ∈ Tj°, verify msk−mck(t) < 0 then wjT.(ms–mc(t)) < 0, this leads to decrease the maximal firing speeds xmaxj of Tj.

  • If at time t, all places Pi ∈°Tj, verify msi−mci(t) < 0 and all places Pk ∈ Tj°, verify msk−mck(t) > 0 then wjT.(ms−mc(t)) > 0, this leads to increase the speed xmaxj of Tj.

On the other hand, the direction of variation of the speed Xmax also depends on the instantaneous firing speed associated with the transition Tj, in the following cases:

  • If xsj−xcj(t) < 0, the maximal firing speeds xmaxj of Tj decreases.

  • If xsj −xcj(t) > 0, the maximal firing speeds xmaxj of \({T}_{j}\) increases.

But when these previously mentioned criteria are not satisfied concurrently, the convergence is no more monotonous. Finally, we will illustrate and compare these different approaches in an example.

4.3 Comparison and Discussion

In this sub-section, we will study the results of the two different fluidization approaches presented previously to illustrate and compare them.

In the first approach studied in this section, the CPN-PW converges to the stochastic average marking in a single region with no problem, and its continuous path remains in the same region as the initial marking. In this case, the steady state converges directly to the stochastic target points. However, when convergence occurs in multiple regions, a problem of converging this model toward the stochastic target points will arise. This problem is manifested by the existence of the critical region, which directly complicates the fluidization by this approach. In this case, we subdivide the marking trajectory into multiple phases and intermediate points to move from one region to another to achieve convergence in the critical region. Table 5 gives the modified continuous average behavior obtained from CPN-PW fluidization of SPN β3 in Fig. 3.

Table 5 Modified continuous behaviors after fluidization by CPN-PW in Fig. 3
Full size table

Table 5 shows that fluidization CPN-PW is not achieved directly; for this purpose, the marking trajectory is divided into several phases and intermediate points Mint to move from one region to another, to achieve stochastic marking of β3. The SPN β3 and the initial marking MI are in two different regions, to reach β3 from MI, two successive phases appear, first, to reach the common intersection of the two regions L2 and L1 whose Mint = (2.1 0.3 0.3 1. 6 2.4)T, we applied the constant positive matrix velocity Xmax1 = xmax4.diag(0.3 0.2 0.9 1)T, where xmax4 represents one degree of freedom, in the second stage we apply the velocity Xmax2 = diag(3.6 1.8 5.1)T to achieve the final value β3 = (1.03 0.80 0.08 3.01 0.98)T (Fig. 8).

Fig. 8
figure 8

Continuous piecewise approximation of the stochastic average marking of the SPN in Fig. 3

Full size image

In the last approach studied in this section, we proposed to modify the definition of the parameters that characterize the maximal firing speeds of the transitions for the CPN, using multiplicative coefficients applied to the maximal firing speeds of all transitions. These coefficients are considered as time dependent functions according to the adaptive law (18). This law minimizes the errors due to variations in markings and throughputs over time in order to have a continuous steady state equivalent to that of the SPN. Table 6 gives the modified continuous average behavior obtained by adapting all the maximal firing speeds of the SPN β3 in Fig. 3.

Table 6 Modified continuous behaviors after adaptation of all maximal firing speeds of CPN in Fig. 3
Full size table

Each maximal firing speed will be corrected by a multiplicative factor. Therefore, only the marking of place \({P}_{1}\) will be represented. Figure 9 shows the continuous average marking and the asymptotic stochastic average marking of the square P1, after the modification of the maximal firing speeds of CPN in Fig. 3.

Fig. 9
figure 9

Evolution of the continuous and stochastic markings of the place P1 in function of time

Full size image

Minimizing the errors due to variations in markings and throughput allows for a new CPN whose average behavior is equivalent to that of the SPN. The implementation of this approach requires knowledge of the asymptotic stochastic behavior β3 = (1.03 0.8 0.08 3.01 0.98)T that is desired to be achieved.

This approach is the most effective for approximating the throughput and average markings of the SPN using the CPN. The first approach requires a critical step to achieve convergence, which involves subdividing the marking trajectory into multiple phases and intermediate points. This results in multiple phases for transitioning from the region of the initial marking to the critical region in the presence of a large number of synchronizations, or in the presence of multiple regions and critical regions. On the other hand, the adaptive approach minimizes errors caused by variations in the throughput and average markings, regardless of the initial marking and the number of synchronizations. This enables it to achieve behavior identical to that of the SPN.

5 Conclusions

In this work, two approaches were studied and compared for fluidization, sufficient conditions were added to achieve identical behavior between the CPN and SPN models. The piecewise linear approach is useful when the approximation of markings is divided into several phases and the maximal firing speeds is defined as a piecewise continuous function. The adaptive approach, on the other hand, adapts all the maximal firing speeds through an adaptive controller to correct errors in throughput and marking by referring to the asymptotic stochastic average throughput and average marking to be reached. The adaptive approach was found to be better than the piecewise linear approach for obtaining average marking and throughput estimates of the SPNs. In future research, new fluid model semantics will be utilized to study the approximation of timed CPNs by partially homothetic SPN approximations, and alternative optimal models will be investigated to address the shortcomings of directly related continuous approaches concerning the SPN transition firing rates.