Throughput maximization of complex resource allocation systems through timed-continuous-Petri-net modeling

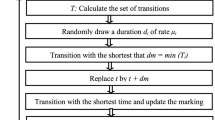
Abstract

Fluid-relaxation-based scheduling is a powerful scheduling method for complex resource allocation systems and other stochastic networks. However, this method has been pursued through rather ad hoc representations and arguments in the past. This paper establishes that timed-continuous Petri nets provide a structured and natural framework for the implementation of this method in the context of complex resource allocation, and highlights the potential advantages of such a more structured approach.

1 Introduction

Complex resource allocation systems (RAS) is a modeling abstraction for the operations that take place in many contemporary application domains (Reveliotis 2017). These environments support the concurrent execution of a number of process types through a set of reusable resources, with each resource being available at a certain number of units that defines the corresponding resource capacity. Process types execute sequentially, through a certain set of processing stages, and the execution of each processing stage requires the exclusive allocation of some “bundle” of the system resources that will be released only when the process secures the resources required for its next processing stage. In this work, we want to coordinate the resource allocation among the contesting processes in order to optimize some time-related performance measure; typical such performance measures are the maximization of the system “throughput” or the minimization of some index of the congestion that is experienced by the running processes.

The resulting scheduling problem is characterized by a very high complexity. In fact, typically this problem is decomposed into two major subproblems, with the first subproblem trying to establish deadlock-free operation for the underlying system, and the second subproblem addressing the considered scheduling problem within the operational – or “behavioral” – subspace that is defined by the first subproblem. The second subproblem can be formulated, in principle, as a Markov Decision Process (MDP) (Puterman 1994), but the practical solution of this MDP is challenged by the very large size of the underlying state space. One way to address this last issue is by using some method from the burgeoning area of Approximate Dynamic Programming (ADP) (Bertsekas 2012); some past endeavors in this direction can be found in Choi and Reveliotis (2003), Li and Reveliotis (2015, 2016). But a more recent development that appeared in (Ibrahim and Reveliotis 2019), has tried to address this scheduling problem by adapting to it the technique of “fluid relaxation (FR)”-based scheduling (Weiss 2000; Bertsimas et al. 2015). Generally speaking, at each decision point, this technique tries to come up with an optimized decision as follows: (i) First, the discrete workflow of the considered operation is approximated by acontinuous flow of similar structure and operational limitations, that is known as the “fluid relaxation” of the original workflow. (ii) Next, a scheduling problem that encodes the gist of the dynamics that determine the optimal decision at the current decision point, is formulated and solved in the approximating representation of the “fluid” relaxation. This new scheduling problem usually takes the form of a linear program (LP) and is known as the corresponding “LP (fluid) relaxation”. (iii) Finally, the information provided in the obtained optimal solution for the LP relaxation is used in order to determine an optimized decision for the current decision point of the original system. Extensive numerical experimentation reported in Ibrahim and Reveliotis (2019) shows that this scheduling method has the potential to provide very high-quality policies for the considered scheduling problem, and, in this way, it defines the “state of art” when it comes to the scheduling of complex RAS.

This technical note intends to show that the developments of Ibrahim and Reveliotis (2019) can be enhanced by leveraging the modeling and analytical power of timed-continuous Petri nets (tc-PNs) (Mahulea 2007). More specifically, the fluid relaxation models and the corresponding relaxing LPs that are used in the implementation of the FR-based scheduling method in Ibrahim and Reveliotis (2019), have been developed through some ad hoc representations and arguments. This work intends to show that timed-continuous Petri nets provide a natural and more structured medium for the representation of these fluid relaxations, and that the existing theory for the tc-PN model also enables (i) a more systematic derivation of the relaxing LP, and (ii) an analytical study of the solution space of this LP and the structure of its optimal solutions. Besides their theoretical interest, these results further enable (iii) a more informed parameterization of the relaxing LP, and (iv) a systematic extension of the methodology to RAS with very complex structure and dynamics.

We should also notice, for completeness, that there is another line of past works that have sought the optimization of the operations of certain contemporary workflows by leveraging some of the modeling and analytical capabilities of timed continuous Petri nets. More specifically, these works employ the particular model of the “first-order hybrid Petri net”, which was introduced and studied in Balduzzi et al. (2000); as characteristic examples, we mention the works of Balduzzi and Di Febbraro (2001), Dotoli et al. (2009), and Cavone et al. (2016). However, the perusal of this material will reveal that except for the fact that they also employ a fluidized representation of the dynamics of the underlying workflow in the form of a continuous Petri net model, the scheduling methods that are pursued in those past works are very different, in their defining philosophy and their underlying operational assumptions, from the FR-based scheduling method that is pursued in this paper.

The rest of the paper is organized as follows: Section 2 provides a more systematic characterization of the RAS scheduling problem that was outlined in the previous paragraphs, using the modeling framework of generalized stochastic Petri nets (GSPNs) (Ajmone Marsan et al. 1994). In an effort to simplify and concretize the presented developments, this scheduling problem is focused on the maximization of the long-term throughput of a capacitated re-entrant line (CRL), which was also the RAS scheduling problem addressed in Ibrahim and Reveliotis (2019). Section 3 introduces the fluid relaxation of the considered scheduling problem and of the underlying GSPN dynamics, through a naturally induced tc-PN model. This section also establishes certain properties for this tc-PN, and employs these properties in order to provide a pertinent formulation of the relaxing LP. The last part of the section discusses the definition of the necessary decision rule for the original scheduling problem, which is based on the optimal solution of the relaxing LP. On the other hand, Section 4 discusses the extension of the results of Sections 2 and 3 to RAS classes with more complex structure and dynamics than the CRL class. Finally, Section 5 concludes the paper and suggests potential future work.

Due to the imposed space limitations for this article, the subsequent developments have been limited to the minimal material that ensures a concise treatment of the paper content; a more expansive treatment of these developments, that provides all the necessary background material and a more leisurely coverage of the presented results, can be found in Ibrahim and Reveliotis (2018), which is accessible through the personal webpage of the second author.

2 GSPN-based modeling of the CRL operation and the throughput maximization problem

The basic CRL model

As stated in the closing part of the previous section, in order to simplify the exposition of the subsequent developments and provide more specificity, we focus on the scheduling problem of maximizing the long-term throughput of a particular RAS class that is known as the capacitated re-entrant line (Reveliotis 2000). This line consists ofL workstations, WS₁,WS₂,…,WS_L, with each workstation possessing (i) a single server, and (ii) a finite buffering capacity of B_i slots. A part visiting some workstation W_i is allocated one of its buffer slots, and it will hold this slot throughout its sojourn at that station; in particular, the part will release this buffer slot only when it has completed its entire processing and exits the system, or it has been allocated a buffer slot at another workstation. The line supports a single process type with the corresponding process plan consisting of M processing stages, J₁, J₂,…,J_M. Each processing stage J_j is carried out at one of the line workstations which will be denoted by WS(j). We further assume that L < M, an assumption that manifests there-entrant nature of the line. Finally, we refer the reader to Reveliotis (2000), Ibrahim and Reveliotis (2019, 2018) for some interesting discussion on the motivation of this CRL model, and on the role of the “re-entrant line” abstraction in the context of the current scheduling theory and practice.

GSPN-based modeling of the considered CRL

In the following, we shall model the above CRL as a GSPN to be denoted by ${\mathcal N}$. The main building block for this GSPN model is the process-resource subnet that is depicted in Fig. 1, and models the workflow and the supporting resource allocation for some processing stage J_j that takes place at the corresponding workstationWS(j).

Fig. 1

The GSPN subnet modeling a single processing stage,J_j, of the considered CRL

Tokens in place p_jw of this subnet rsepresent process instances waiting for the execution of processing stage J_j at workstation WS(j); tokens in placep_jp represent process instances executing processing stage J_j; and tokens in place p_jb represent process instances that have completed the execution of processing stage J_j but are still located at workstation WS(j). In the following, we shall denote these three substages respectively by J_jw, J_jp and J_jb. Furthermore, assuming that the considered CRL starts idle and empty of any jobs, the initial marking m₀(p_jx) of all places p_jx, j = 1,…,M,x ∈{w,p,b}, must be set equal to zero.

The places $p_{B_{WS}(j)}$ and $p_{S_{WS}(j)}$ depicted in Fig. 1 are “resource(-modeling)” places. Tokens in place $p_{B_{WS}(j)}$ model the free buffer slots at the workstation WS(j); as already stated, a process instance entering this workstation for the execution of processing stage J_j must be allocated one of the free buffer slots, and this buffer slot will be released when this process instance leaves the workstation. The initial marking of place $p_{B_{WS}(j)}$ is $\textbf {m}_{0}(p_{B_{WS}(j)}) = B_{WS(j)}$, i.e., the buffering capacity of workstation WS(j). Place $p_{S_{WS}(j)}$ models the server availability at workstation WS(j); the tokens in this place are required only for the execution of the corresponding substage J_jp. Furthermore, since we assume single-server workstations, we shall also have $\textbf {m}_{0}(p_{S_{WS}(j)}) = 1$.

Finally, in the GSPN model of Fig. 1, the thinner black transitions are considered to be untimed, since they essentially model decisions pertaining to the corresponding resource allocation process, The white barred transition is a timed transition, with the corresponding firing delay representing the processing time of the enabling process instance. Following standard practice in GSPN modeling, these firing delays are drawn from an exponential distribution with rate μ_j.

Figure 2 provides the complete GSPN model, ${\mathcal N}$, for a CRL with two single-server workstations, WS₁, WS₂, that support a process type with three processing stages, J₁, J₂, J₃. The servers of the two workstations are modeled by places p₇ and p₉, while the available buffering capacity at each workstation is modeled by places p₈ and p₁₀. On the other hand, the sequential logic that defines the process plan for this CRL is modeled by the path 〈t₀, p₀, t₁, p₁, t₂, p₂, t₃, p₃, t₄, p₄, t₅, p₅, t₆, p₆, t₇〉; the interpretation of the corresponding places p₀,…,p₆ is according to the logic of Fig. 1, with the further understanding that, for the economy of the overall representation, we have dropped the two places corresponding to the processing substages J_1w and J_3b. Finally, place p₁₁ is a “monitor” place that enforces the requirement that the combined number of process instances executing processing stage J₁ and J₂ must be no more than three. In the operational context of this CRL, the enforcement of this restriction is necessary in order to prevent the formation of any deadlock. Indeed, the re-entrant nature of the considered CRLs makes them susceptible to deadlock, and the necessary control logic for deadlock avoidance can be provided through the corresponding theory of deadlock avoidance for complex RAS that is presented in Reveliotis (2017). Furthermore, as detailed in Ibrahim and Reveliotis (2019, 2018), for the considered CRLs it is always possible to obtain deadlock avoidance policies that take the form of a (small) number of linear inequalities on the net sub-marking that is defined by the placesp_jx, j = 1,…,M,x ∈{w,p,b}, and these inequalities can be represented in the employed GSPN framework through the superimposition of an equal number of “monitor” places (Giua et al. 1992; Moody and Antsaklis 1998) (as in the case of the depicted example). Finally, it can also be shown that these “monitor” places play a role in the dynamics of the controlled system that is equivalent to the role of the resource-modeling places (this is also obvious in the controlled GSPN that is depicted in Fig. 2). In the following, we shall assume that the considered GSPN model has been augmented with a set of “monitor” places that will ensure deadlock-free operation for the resulting net.

Fig. 2

The GSPN model for an example CRL

The considered scheduling problem and its MDP formulation

As is the case with any GSPN model (Ajmone Marsan et al. 1994), the set of reachable markings of a CRL-modeling GSPN ${\mathcal N}$ can be partitioned into tangible markings, that enable only timed transitions, andvanishing markings, that enable at least one untimed transition. Furthermore, the sojourn time and the transitional dynamics out of a tangible marking are completely determined by the “exponential race” that is defined by the enabled (timed) transitions. On the other hand, since untimed transitions can fire instantaneously, vanishing markings have zero sojourn times. More importantly, the selection among the set of enabled untimed transitions at a vanishing marking must be arbitrated by some externally specified logic; this logic usually takes the form of a probability distribution that is defined on these enabled transitions, and it is known as the corresponding “random switch”. Hence, in the GSPN-based representation of the CRL dynamics, the scheduling problem of maximizing the CRL throughput reduces to the problem of determining accordingly the random switches at each vanishing marking of the net.

Furthermore, in Li and Reveliotis (2016), Ibrahim and Reveliotis (2018, 2019) it is shown that the last problem defined in the previous paragraph can be further simplified by focusing only on the set X of vanishing markings that result from the firing of some timed transition at some tangible marking. Consider a vanishing marking m ∈ X, and let ${\mathcal T}{\mathcal R}(\textbf {m})$ denote those tangible markings $\textbf {m}^{\prime }$ that are reachable from m through the firing of a sequence of untimed transitions, σ; we shall refer to ${\mathcal T}{\mathcal R}(\textbf {m})$ as the corresponding “tangible reach” of m. Since the time-based performance of the line is determined by the way that it allocates its time among the various tangible markings, the main issue to be resolved at the considered vanishing marking m ∈ X, is the selection of the tangible marking $\textbf {m}^{\prime } \in {\mathcal T}{\mathcal R}(\textbf {m})$. This realization reduces the original scheduling problem to an MDP (Puterman 1994), to be denoted by ${\mathcal MDP(N)}$ in the following. The decision points of ${\mathcal MDP(N)}$ are defined by the aforementioned marking set X, and the possible decisions associated with each decision point m ∈ X are defined by the corresponding tangible reach ${\mathcal T}{\mathcal R}(\textbf {m})$. The transitional dynamics of ${\mathcal MDP(N)}$ upon the execution of a decision at marking m are determined by the exponential race corresponding to the selected tangible state $\textbf {m}^{\prime } \in {\mathcal T}{\mathcal R}(\textbf {m})$. State $\textbf {m}^{\prime }$ also defines the immediate reward, $r(\textbf {m}, \textbf {m}^{\prime })$, that is associated with this decision; $r(\textbf {m}, \textbf {m}^{\prime })$ is equal to the firing probability in state $\textbf {m}^{\prime }$ of the timed transition t_M (i.e., the transition corresponding to the completion of the last processing stage J_M by a running part and the unloading of this part from the line). Finally, let ${\Pi }({\mathcal N})$ denote the set of deterministic policies for this MDP, i.e., the policies that are specified by the selection of a single decision $\textbf {m}^{\prime } \in {\mathcal T}{\mathcal R}(\textbf {m})$ for each decision point m ∈X. Also, let π denote any such deterministic policy. The ultimate objective of ${\mathcal MDP(N)}$ is to determine a deterministic policy π^∗ such that

$$ \pi^{*} = \arg\max_{\pi\in {\Pi}({\mathcal N})} \lim_{N\rightarrow \infty} \frac{1}{E[\tau_{N}]} E\left[ \sum\limits_{i=1}^{N} r(\textbf{m}_{i}, \textbf{m}^{\prime}_{i})\ \left|\ \textbf{m}_{0}, \pi \right.\right] $$

(1)

In Eq. 1, τ_N denotes the time of the N-th state transition for the underlying stochastic process. Hence, in plain terms, the considered MDP seeks to maximize the average reward collected over an infinite operational horizon, which according to the above definition of the immediate reward, corresponds to the long-term throughput of the underlying CRL. The presumed absence of deadlock from the underlying CRL – which is established through the augmentation of the GSPN ${\mathcal N}$ with the necessary monitor places – implies that this MDP problem is well posed, and guarantees the existence of an optimal deterministic policy. But as remarked in the introductory section, the practical solution of ${\mathcal MDP(N)}$ is challenged by the explosive nature of the underlying state space. Hence, next we discuss how we can generate a good suboptimal solution for this problem, by leveraging a fluidized version of the GSPN ${\mathcal N}$.

3 Fluid-relaxation-based scheduling of CRLs through tc-PN-based modeling and analysis

Some notation, semantics and properties for the employed tc-PN models

As explained in the introductory section, FR-based scheduling resolves the decision to be taken at each decision point m ∈ X of the MDP that is induced by the considered CRL model, by formulating and solving an LP relaxation of the original problem. This LP relaxation is obtained through a continuous-flow approximation of the discrete workflow that takes place in the original system. In this section, we shall derive the sought LP relaxation by employing a tc-PN model that is induced from the GSPN model ${\mathcal N}$; this tc-PN model will be denoted by ${\mathcal N}^{(tc)}$ in the following.

${\mathcal N}^{(tc)}$ inherits the basic structure of the GSPN model ${\mathcal N}$, but it operates under the semantics and the transition-fireability rules of timed-continuous Petri nets. In particular, the net ${\mathcal N}^{(tc)}$ has the same “flow” matrix Θ with net ${\mathcal N}$, and the same “pre-flow” and “post-flow” matrices Θ⁻ and Θ⁺. On the other hand, the marking m of the net ${\mathcal N}^{(tc)}$ lies in $\mathbb {R}^{+}_{0}$, and it evolves according to a “flow vector” f(m), that defines a firing rate for very transition t ∈ T at marking m, as follows:¹

$$ \forall t\in T,\ \ \textbf{f}(t;\textbf{m}) = \boldsymbol{\mu}(t) \cdot enab(t,\textbf{m}) = \boldsymbol{\mu}(t) \cdot \min_{p\in^{\bullet{t}}} \left\{ \frac{\textbf{m}(p)}{{\Theta}^{-}(p,t)} \right\} $$

(2)

In particular, the flow vector f(m) defines the rate of change of marking m when the net transitions are fired at their maximum possible speed; for each transition t ∈ T, this maximum speed is defined by (i) the corresponding firing rate μ(t), and (ii) the “enabling degree” of this transition at markingm. Hence, if we let τ denote the absolute time, and we consider the net markingm as a function of τ, we shall have that

$$ \textbf{m}(\tau) = \textbf{m}_{0}+{\Theta} \cdot \boldsymbol{\sigma}(\tau) $$

(3)

Differentiating both sides of the last equation with respect toτ, eventually we get

$$ \dot{\textbf{m}}(\tau) = {\Theta}\cdot \dot{\boldsymbol{\sigma}}(\tau) = {\Theta} \cdot \textbf{f}(\textbf{m}(\tau)) $$

(4)

In the subsequent developments, we shall further allow that $\boldsymbol {\mu }(t) = \infty$ for some transitions t ∈T, which will enable us to replicate the notion of “untimed” transitions of the GSPN modeling framework in the tc-PN context. It is clear from Eq. 2 that, for these transitions, $\textbf {f}(t; \textbf {m}) = \infty$, for all markings m, and therefore, these transitions can fire instantaneously at marking m at any level that does not exceed enab(t,m) (i.e., their enabling degree at that marking).

In addition, we shall consider a “controlled” version of the tc-PN ${\mathcal N}^{(tc)}$, where

$$ \forall t\in T,\ \ \textbf{f}(t;\textbf{m}) \leq \boldsymbol{\mu}(t) \cdot enab(t,\textbf{m}) = \boldsymbol{\mu}(t) \cdot \min_{p\in^{\bullet{t}}} \left\{ \frac{\textbf{m}(p)}{{\Theta}^{-}(p,t)} \right\} $$

(5)

i.e., transitions t ∈ T can be “slowed down” with respect to their maximal firing speeds. The resulting controlled tc-PN has similar reachability dynamics to the corresponding untimed continuous (uc-) PN ${\mathcal N}^{(uc)}$ (Mahulea 2007), and it inherits the structural and behavioral properties of the latter. In particular, both nets have the same reachability space lim–$R^{uc}({\mathcal N}, \textbf {m}_{0})$, where this reachability space also contains all these markings that are reachable from the initial marking m₀ in the limit, i.e., through the firing of some infinite transition sequence. Finally, it can be easily checked that the CRL-modeling GSPN ${\mathcal N}$ is quasi-live, consistent and conservative, and these properties are inherited by the uc-PN ${\mathcal N}^{(uc)}$. But then, the results of Recalde et al. (1999) and Silva et al. (1998) imply that

$$ \textbf{m} \in \text{lim--}R^{uc}({\mathcal N}, \textbf{m}_{0}) \Longleftrightarrow \exists \boldsymbol{\sigma} \geq \textbf{0}\ \text{s.t.}\ \textbf{m} = \textbf{m}_{0}+{\Theta}\cdot \boldsymbol{\sigma} \Longleftrightarrow \forall\ \text{\textit{p}-semiflow}\ \textbf{y},\ \textbf{y}\cdot \textbf{m} = \textbf{y}\cdot \textbf{m}_{0} $$

(6)

Equation 6 implies that the set of reachable markings of the uc-PN ${\mathcal N}^{(uc)}$ is succinctly characterized by the set of markings that satisfy the p-semiflows of this net, or, equivalently, by the minimalp-semiflows. For the CRL-modeling GSPN ${\mathcal N}$, the minimal p-semiflows correspond to the net invariants that are defined by (i) the reusable nature of the various resource types (Reveliotis 2017), and (ii) the control logic that implements the linear inequalities of the applied deadlock avoidance policy through the corresponding “monitor” places (Moody and Antsaklis 1998); in particular, there is one minimal p-semiflow associated with each resource and each “monitor” place. In order to facilitate the subsequent discussion, we shall assume that all these minimal p-semilfows are collected in the rows of a matrix that will be denoted by $B_{y}({\mathcal N})$.

Finally, an additional property that will play a significant role in the following, is that the CRL-modeling GSPN ${\mathcal N}$ has a single minimal t-semiflow, namely the |T|-dimensional vector 1. This property is a straightforward implication of the single and completely sequential process plan that is supported by the underlying CRL model, and when combined with the consistent and conservative nature of the considered net ${\mathcal N}$, it places this net in the particular class of mono-t-semiflow nets (Mahulea 2007).

Steady-state markings of the controlled tc-PN ${\mathcal N}^{(tc)}$

For the needs of the subsequent developments, we define a notion of “steady-state operation” for the controlled tc-PN ${\mathcal N}^{(tc)}$ as follows:

Definition 1

The controlled tc-PN ${\mathcal N}^{(tc)}$can be operated at a steady-state regime at some marking m iff

$$ \exists\ \textbf{f} \in \mathbb{R}^{|T|}\ \text{s.t.}\ \left( \forall t\in T,\ \textbf{0} < \textbf{f}(t;\textbf{m}) \leq \boldsymbol{\mu}(t) \cdot enab(t,\textbf{m}) \right)\ \wedge\ \left( {\Theta} \cdot \textbf{f} = \textbf{0} \right) $$

(7)

Marking m itself is characterized asa potential steady-state marking.

In other words, a given marking m of tc-PN ${\mathcal N}^{(tc)}$ is a potential steady-state marking, if there is a strictly positive t-semiflow of ${\mathcal N}^{(tc)}$ that constitutes a feasible flow vector f for marking m under the controlled dynamics of ${\mathcal N}^{(tc)}$. Then, marking m will remain unaltered under the firing of the net transitions according to the considered flow vector f. Furthermore, the strict positivity off implies that this operation will keep active the entire network. The next proposition provides a complete characterization of the set of steady-state markings of net ${\mathcal N}^{(tc)}$.

Proposition 1

The set of the potential steady-state markings for the controlled tc-PN ${\mathcal N}^{(tc)}$ is given by:

$$ SS({\mathcal N}^{(tc)}) \equiv \left\{\textbf{m}\in \mathbb{R}^{+}_{0}\ \left|\ \left( B_{y}({\mathcal N}) \cdot \textbf{m} = B_{y}({\mathcal N}) \cdot \textbf{m}_{0} \right)\right. \wedge \left( \forall j=1,\ldots,M,\ \textbf{m}(p_{jp}) > 0\right) \right\} $$

(8)

Proof

According to Eq. 6, the first condition in the conjunction in the right-hand-side of Eq. 8 is a necessary and sufficient condition for the reachability of any given marking $\textbf {m}\in \mathbb {R}^{+}_{0}$ in the dynamics of the controlled tc-PN ${\mathcal N}^{(tc)}$.

Next we show that the second condition in this conjunction is equivalent to the condition of Definition 1. For this, first we notice that the mono-t-semiflow structure of the considered network that was discussed in the previous paragraphs, further implies that any flow vector f that satisfies the condition of Definition 1, will bef = f ⋅1, for some scalar f > 0. This result, together with (i) the untimed transitions that are present in ${\mathcal N}^{(tc)}$, and (ii) the inflow relation of the timed transitionst_jj = 1,…,M, of net ${\mathcal N}$ to their corresponding input places p_jp (c.f. Figure 1), further imply that the condition of Definition 1 reduces to the condition

$$ \exists\ f \in \mathbb{R}^{+}\ \text{s.t.}\ \forall t_{j}\in T_{t},\ f\leq \mu(t_{j}) \cdot \textbf{m}(p_{jp}) $$

(9)

where $\mathbb {R}^{+}$ denotes the set of strictly positive reals. The proof concludes by noticing that the second condition in the conjunction in the right-hand-side of Eq. 8 is essentially a rewriting of the condition of Eq. 9. □

The marking set $OSS({\mathcal N}^{(tc)})$ and its reachability

In the following, we are particularly interested in those elements of the marking set $SS({\mathcal N}^{(tc)})$ that will enable a maximal steady-state flow f^∗ for the underlying tc-PN ${\mathcal N}^{(tc)}$; we shall denote this set of markings by $OSS({\mathcal N}^{(tc)})$. In view of Proposition 1 and the arguments in the proof of this proposition, the requested marking set $OSS({\mathcal N}^{(tc)})$, and the corresponding maximal flow f^∗, can be obtained as optimal solutions to the following linear program (LP):

$$ \max f $$

(10)

s.t.

$$ B_{y}({\mathcal N}) \cdot \textbf{m} = B_{y}({\mathcal N}) \cdot \textbf{m}_{0} $$

(11)

$$ \forall t_{j}\in T_{t},\ f\leq \mu(t_{j}) \cdot \textbf{m}(p_{jp}) $$

(12)

$$ f \geq 0 $$

(13)

The reader should notice that the required non-negativity for the vector variable m that appears in the above LP, is enforced by the combination of Eqs. 12 and 13 and the strict positivity of the rates μ(t_j), ∀t_j ∈ T_t. Also, the existence of an optimal solution (f^∗, m^∗) for this LP withf^∗ > 0 is guaranteed by (i) the resource availability that is presumed by the CRL model that is considered in this work, and (ii) the applied deadlock avoidance policy; these two elements define the effective content of Eq. 11. In fact, in Ibrahim and Reveliotis (2018) it is shown that the LP of Eqs. 10–13 can be reduced to an equivalent LP with the same objective function, and with its constraints expressing the restrictions on the flow valuef that are imposed by (i) the limited processing capacity of the workstation servers, and (ii) the “virtual bottlenecks” (Dai and Vande Vate 2000) of the underlying CRL that are defined by the applied deadlock avoidance policy.

The next result establishes that the marking set $OSS({\mathcal N}^{(tc)})$ can be reached in finite time from any marking $\textbf {m} \in {lim-}R^{uc}({\mathcal N},\textbf {m}_{0})$.

Proposition 2

Let f^∗ denote the maximal steady-state flow for the considered net ${\mathcal N}^{(tc)}$, and define the marking $\tilde {\textbf {m}}$ of this net as follows:

$$ \forall \in P,\ \tilde{\textbf{m}}(p) = \left\{ \begin{array}{ll} \frac{f^{*}}{\mu(t_{j})}, & \text{if}\ p = p_{jp}\ \text{for some}\ j\!\in\!\{1,\ldots,M\} \\ 0, & \text{if}\ p = p_{jw}\ \text{or}\ p_{jb}\ \text{for some}\ j\!\in\!\{1,\ldots,M\} \\ \textbf{m}_{0}(p) - {\sum}_{p^{\prime}\in P\setminus\{p\}} \textbf{y}_{p}(p^{\prime}) \cdot \tilde{\textbf{m}}(p^{\prime}), & \text{for every place} \ p\ \text{modeling a resource or} \\ & \text{a monitor place with corresponding} \\ & p\text{-semiflow}\ \textbf{y}_{p} \end{array} \right. $$

(14)

Then, marking $\tilde {\textbf {m}}$ satisfies the following two properties:

• 1. $\tilde {\textbf {m}} \in OSS({\mathcal N}^{(tc)})$.

• 2. $\forall \textbf {m} \in \text {lim--}R^{uc}({\mathcal N},\textbf {m}_{0}),\ \exists \sigma = a_{1} t_{1} {\ldots } a_{k} t_{k}$ for some $k\in \mathbb {Z}^{+}_{0}$, s.t. HCode $\textbf {m} [\sigma \rangle \tilde {\textbf {m}}$.

Proof

In order to prove the first part of Proposition 2, it suffices to show that marking $\tilde {\textbf {m}}$ satisfies the constraints of the LP of Eqs. 10–13, for f = f^∗. The constraint of Eq. 12 is satisfied immediately by the definition of marking $\tilde {\textbf {m}}$. Furthermore, since f^∗ is the maximal steady-state flow of net ${\mathcal N}^{(tc)}$, there exists a marking m^∗ such that (f^∗, m^∗) is an optimal solution to the LP of Eqs. 10–13. Also, Eqs. 12 and 14 imply that $\tilde {\textbf {m}}(p) \leq \textbf {m}^{*}(p)$, ∀p ∈{p_jw, p_jp, p_jb :j = 1,…,M}. Therefore,

$$\textbf{m}_{0}(p) - \sum\limits_{p^{\prime}\in P\setminus\{p\}} \textbf{y}_{p}(p^{\prime}) \cdot \tilde{\textbf{m}}(p^{\prime})\ \geq\ \textbf{m}_{0}(p) - \sum\limits_{p^{\prime}\in P\setminus\{p\}} \textbf{y}_{p}(p^{\prime}) \cdot \textbf{m}^{*}(p^{\prime})\ \geq\ 0$$

and marking $\tilde {\textbf {m}}$ satisfies the constraints of Eq. 11, as well.

Next, we shall establish the second part of Proposition 2 by providing a finite transition sequence σ =σ₁σ₂σ₃σ₄ that will lead from any given marking $\textbf {m} \in \text {lim--}R^{uc}({\mathcal N},\textbf {m}_{0})$ to the target marking $\tilde {\textbf {m}}$.

Transition subsequence σ₁ will first establish a “corridor” of free capacity $\delta < \min \nolimits \{ \tilde {\textbf {m}}(p_{jp}): j=1,\ldots ,M\}$ with respect to each resource or monitor place q across the entire line. This can be attained in an iterative manner, starting from the place p_Mp and unloading the necessary amount of fluid from this place in order to attain the aforestated free-capacity requirement with respect to any resource or monitor place q that includes place p_Mp in the corresponding p-semiflow. Subsequently, we employ the free capacity established through this fluid removal from place p_Mp, in order to satisfy the same free-capacity requirement with respect to the resource and the monitor places that are engaged by the places p_M− 1,w, p_M− 1,p, p_M− 1,b, that model stage J_M− 1; we omit the relevant details to the reader. Sequence σ₁ is completed by proceeding in a similar manner through the remaining stagesJ_M− 2,…,J₁, in this order. Let $\textbf {m}^{\prime }$ denote the marking that will result from this draining.

Transition subsequence σ₂ will employ the “corridor of free capacity” established by sequence σ₁ in order to drain the line from the following quantities:

• For each place p ∈{p_jp|j = 1,…,M} with $\textbf {m}^{\prime }(p) > \tilde {\textbf {m}}(p)-\delta$, transition subsequence σ₂ will remove an amount of fluid equal to $\textbf {m}^{\prime }(p) - \tilde {\textbf {m}}(p) + \delta$.

• For each place p ∈{p_jw, p_jb|j = 1,…,M} with $\textbf {m}^{\prime }(p) > \tilde {\textbf {m}}(p) = 0$, transition subsequence σ₂ will empty completely this place by removing the corresponding amount of fluid $\textbf {m}^{\prime }(p)$.

For all these places, the corresponding drainage will occur in chunks no larger than δ. Then, since the original marking m satisfies all the minimalp-semiflows of net ${\mathcal N}$, all the markings that will be generated by the fluid advancement through the line during this drainage will satisfy these p-semiflows, as well (i.e., they will respect the resource availability of the line and the imposed deadlock avoidance policy). Let us denote the marking that will result from the execution of transition subsequence σ₂ by $\textbf {m}^{\prime \prime }$.

Transition subsequence σ₃ will add to places p ∈{p_jp : j = 1,…,M} with $\textbf {m}^{\prime \prime }(p) < \tilde {\textbf {m}}(p)-\delta$, the quantities $\tilde {\textbf {m}}(p) -\delta - \textbf {m}^{\prime \prime }(p)$. For each such place p, the corresponding quantity will be loaded from the beginning of the line, in chunks no larger than δ. Let us denote the marking that will result from the execution of transition subsequence σ₃ by $\textbf {m}^{\prime \prime \prime }$.

Finally, transition subsequence σ₄ will bring to each place p_jp, j = 1,…,M, a fluid amount equal to δ, starting with placep_Mp, and proceeding with places p_M− 1,p,…,p_1p, in this order. The plausibility of this operation with respect to the p-semiflows of net ${\mathcal N}$ is guaranteed by the specification of (i) marking $\tilde {\textbf {m}}$ in Eq. 14, and (ii) the intermediate target markings $\textbf {m}^{\prime \prime }$ and $\textbf {m}^{\prime \prime \prime }$. □

The proposed LP relaxation for the considered scheduling problem

In the previous parts of this section we have provided a complete characterization of (i) the maximal steady-state throughput, f^∗, that can be attained by the fluidized dynamics of the considered CRL that are encoded by the tc-PN ${\mathcal N}^{(tc)}$, and (ii) the set of markings $OSS({\mathcal N}^{(tc)})$ that can support this steady-state operation. Also, Proposition 2 has established that the marking set $OSS({\mathcal N}^{(tc)})$ is reachable, in finite time, from any reachable markingm of this network. Hence, given a marking $\hat {\textbf {m}}$ that constitutes a decision point of the ${\mathcal MDP(N)}$ of Section 2, the corresponding LP relaxation, to be formulated in the fluidized dynamics of the controlled net ${\mathcal N}^{(tc)}$, must drive these dynamics from marking $\hat {\textbf {m}}$ to some marking $\tilde {\textbf {m}}\in OSS({\mathcal N}^{(tc)})$, in a way that minimizes the experienced loss with respect to the target throughput f^∗ during this transition. The resulting optimal control problem belongs to the class of optimal control problems for the considered tc-PN models that has been investigated in Chapter 7 of Mahulea (2007). Next we adapt the results of that work to the tc-PN ${\mathcal N}^{(tc)}$ that is considered in this paper, and to the particular optimal control problem that was stated in the previous part of this paragraph.

As in Mahulea (2007), we shall derive the sought LP formulation in discretized time, where the time-discretizing (or “sampling”) period will be set equal to some value Δt sartisfying

$$ {\Delta} t < \min_{j=1,\ldots,M} \left\{\frac{1}{\mu(t_{j})} \right\} $$

(15)

The above discretization of time induces a discrete-time controlled continuous PN, ${\mathcal N}^{(dt)}$, from the original tc-PN model of ${\mathcal N}^{(tc)}$. Letting m(k) denote the marking of net ${\mathcal N}^{(dt)}$ at period k, the one-time-step transitional dynamics of this new net satisfy the following state equation:

$$ \textbf{m}(k+1) = \textbf{m}(k) + {\Delta} t \cdot {\Theta} \cdot \textbf{w}(k) $$

(16)

In Eq. 16, Θ denotes the flow matrix of the underlying net ${\mathcal N}$, and w(k) denotes the instantaneous firing levels for the various transitions t ∈ T, that are presumed to be kept constant during the considered time interval Δt. Then, Proposition 7.6 and Theorem 7.9 of Mahulea (2007) imply the following properties for the dynamics of the dt-PN ${\mathcal N}^{(dt)}$:

Proposition 3

Consider the dt-PN ${\mathcal N}^{(dt)}$ that is induced from the ct-PN ${\mathcal N}^{(ct)}$ under time discretization with a sampling period Δt that satisfies the condition of Eq. 15. Furthermore, suppose that the one-time-step transitional dynamics of net ${\mathcal N}^{(dt)}$ observe the enabling condition of Eq. 5.

Then, net ${\mathcal N}^{(dt)}$ possesses the following properties:

• 1. All the markings m(k),k = 1,2,…,that are reached by net ${\mathcal N}^{(dt)}$, when initialized at any initial markingm₀ ≥0, are nonnegative.

• 2. A marking m is reachable in the net ${\mathcal N}^{(dt)}$ if and only if it is reachable in the untimed dynamics of the net ${\mathcal N}^{(tc)}$ with a sequence that never empties an already marked place.

Property 1 of Proposition 3 guarantees that, under the condition of Eq. 15, the dt-PN ${\mathcal N}^{(dt)}$ is a valid approximation of the dynamics of the ct-PN ${\mathcal N}^{(ct)}$ with respect to the preservation of the non-negativity of the net marking. On the other hand, Property 2 of this proposition is a reachability condition in the discretized dynamics of net ${\mathcal N}^{(dt)}$. Fortunately, it can be easily checked that the transition sequence σ that was employed in the proof of Proposition 2, satisfies the condition of Proposition 3, and therefore, Proposition 3 enables the extension of the reachability result of Proposition 2 to the operational context of net ${\mathcal N}^{(dt)}$; i.e., starting from any initial marking m of net ${\mathcal N}^{(dt)}$, we can drive this net to the marking set $OSS({\mathcal N}^{(tc)})$ in a finite number of periods Δt. This realization, when combined with (i) the motivational logic for the pursued LP relaxation that was outlined in the previous paragraphs, and (ii) the above specification of the discrete dynamics of net ${\mathcal N}^{(dt)}$, result in the following form of this LP:

$$ \min \sum\limits_{k=0}^{H} (f^{*}- \textbf{w}(t_{M} ; k)) $$

(17)

s.t.

$$ \forall k=0,1,\ldots, H,\ \ \textbf{m}(k+1) = \textbf{m}(k) + {\Delta} t \cdot {\Theta} \cdot \textbf{w}(k) $$

(18)

$$ \forall k=0,1,\ldots, H,\ \forall j=1,\ldots,M,\ \ \textbf{w}(t_{j}; k) \leq \mu(t_{j}) \cdot \textbf{m}(p_{jp};k) $$

(19)

$$ \forall k=0,1,\ldots, H,\ \textbf{w}(k) \geq \textbf{0} $$

(20)

$$ \forall k=0,1,\ldots, H,\ \forall j=1,\ldots,M,\ \ \textbf{m}(p_{jw}; k+1) \geq 0\ \ ;\ \ \textbf{m}(p_{jb}; k+1) \geq 0 $$

(21)

$$ \textbf{m}(0) = \hat{\textbf{m}} $$

(22)

The LP of Eqs. 17–22 is formulated over a finite time-horizonH + 1 that is selected a priori as one of the problem parameters. During this time-horizon, the considered LP tries to determine the control variables w(k), k = 0,…,H, for the underlying dt-PN ${\mathcal N}^{(dt)}$ so that the total amount of fluid output by this net over the considered time-horizon is maximized. But, as already noticed, under the assumption of a sufficiently long time-horizon H + 1, this objective is equivalently attained by trying to drive the net ${\mathcal N}^{(dt)}$ from its current marking $\hat {\textbf {m}}$ to a marking $\tilde {\textbf {m}} \in OSS({\mathcal N}^{(tc)})$, while minimizing the loss experienced during this transition with respect to the total fluid that would be output by net ${\mathcal N}^{(dt)}$ if it was operated at the maximal flow rate f^∗. The LP objective that is stated in Eq. 17 adopts this last perspective, since this selection also provides a very natural rule for selecting a pertinent value for the parameter H; more specifically, H should be selected such that the optimal value of the LP will remain invariant to any extensions of the employed time horizon H + 1 by one or more periods.

The constraints of Eqs. 18–21 in the above LP essentially stipulate the validity of the one-step transitional dynamics of the net ${\mathcal N}^{(dt)}$ that are implied by any tentative solution. Finally, the constraint of Eq. 22 sets the initial marking for net ${\mathcal N}^{(dt)}$ in the optimal control problem that is addressed by the considered LP, equal to the marking $\hat {\textbf {m}}$ that corresponds to the current decision point of the underlying ${\mathcal MDP(N)}$.

The induced scheduling policy for ${\mathcal MDP(N)}$

The solution of the LP relaxation of Eqs. 17–22 at any decision point $\hat {\textbf {m}}$ of ${\mathcal MDP(N)}$ can “guide” the selection of the next tangible marking $\tilde {\textbf {m}}$ from the tangible reach ${\mathcal T}{\mathcal R}(\hat {\textbf {m}})$ of marking $\hat {\textbf {m}}$, according to the following logic:

Let m^∗(1) be the marking in the obtained optimal solution for the LP relaxation for k = 1.

Then, the proposed scheduling policy will select the next tangible marking $\tilde {\textbf {m}} \in {\mathcal T}{\mathcal R}(\hat {\textbf {m}})$ for the CRL-modeling GSPN ${\mathcal N}$, through the following rule:

$$ \tilde{\textbf{m}} \in \arg\min_{\textbf{m}\in {\mathcal T}{\mathcal R}(\hat{\textbf{m}})} \sum\limits_{j=1,\ldots,M} |\textbf{m}(p_{j}) - \textbf{m}^{*}(p_{j};1)| $$

(23)

In more natural terms, the criterion of Eq. 23 seeks to select a tangible marking $\textbf {m} \in {\mathcal T}{\mathcal R}(\hat {\textbf {m}})$ that matches the marking m^∗(1) at the places p_jp that enable the timed transitions t_j, j = 1,…,M, as much as possible (with respect to the employed l₁-norm), and thus, to attain a utilization for the various servers of the line that is similar to utilization that is implied by marking m^∗(1).

Furthermore, a secondary criterion that we have used in Ibrahim and Reveliotis(2018, 2019) in order to break any ties that are generated through the criterion of Eq. 23, is as follows:

$$ \tilde{\textbf{m}} \in \arg\min_{\textbf{m}\in {\mathcal T}{\mathcal R}(\hat{\textbf{m}})} \sum\limits_{\forall p_{\in} \{p_{jx} : j=1,\dots,M; x=w,p,b\}} |\textbf{m}(p) - \textbf{m}^{*}(p;1)| $$

(24)

This new criterion selects a tangible marking $\textbf {m} \in {\mathcal T}{\mathcal R}(\hat {\textbf {m}})$ that has the smallest l₁-distance from the marking m^∗(1) with respect to the sub-marking that is defined by the places p of net ${\mathcal N}$ that model the processing substages of the underlying CRL; i.e., this criterion tries to attain a spatial arrangement of the active process instances that is as similar to the corresponding arrangement that is implied by marking m^∗(1).²

Extensive numerical experimentation reported in Ibrahim and Reveliotis (2018) reveals that the scheduling methodology that results from all the previous developments that were presented in this section, preserves the ability of the corresponding methodology of Ibrahim and Reveliotis (2019) to identify very high-quality (near-optimal) scheduling policies for the underlying CRLs. The derived methodology is also computationally very efficient, since it is based on: (i) the formulation and solution of the LP of Eqs. 10–13 only once, at the beginning of the entire implementation, in order to compute f^∗; and (ii) the formulation and solution of the LP of Eqs. 17–22 at each decision point m ∈ X of the underlying ${\mathcal MDP(N)}$. Both of these LPs are derived straightforwardly from the underlying GSPN ${\mathcal N}$, and they involve a number of variables and constraints that is a polynomial function of the size of the underlying CRL.³

At the same time, the developments of this section provide a very succinct characterization of the defining logic and the fluidized dynamics that drive this methodology. Next, we discuss briefly how the insights that have been obtained from these developments, enable their extension to some more complex RAS.

4 Extending the presented methodology to other RAS classes

In this section we briefly discuss the extension of the FR-based scheduling method for the CRL throughput maximization problem that has been developed in this work, to the scheduling problem of maximizing the throughput of more complex RAS. In particular, we focus on the class of Disjunctive–Conjunctive (DC–) RAS, that has been studied extensively in Reveliotis (2017).

From a modeling standpoint, the class of DC-RAS supports the concurrent execution of a number of process types. Furthermore, for each such process type, this new class allows for (i) more arbitrary resource allocation requests by the corresponding processing stages than the CRL model considered in this work, and (ii) routing flexibility (i.e., an instance of these process types can execute through more than one sequences of processing stages). The monograph of Reveliotis (2017) provides (a) a detailed characterization of the structure and the operation of these RAS by means of the PN modeling framework, and (b) extensive methodology for the synthesis of efficient deadlock avoidance policies that take the form of linear inequalities on the net marking, and can be implemented through “monitor” places superimposed on the RAS-modeling PN.

A first complication for any attempted extension of the considered scheduling problem to the DC-RAS context arises from the fact that the notion of throughput maximization itself is ill-defined, since there are more than one process types. A reasonable way to circumvent this complication is by assuming that the production rates of all these process types must observe some predefined ratios; then, it is possible to maximize the total production rate, across all process types, by maximizing the production rate of any one of them. Furthermore, the work of Hu et al. (2012) discusses how to encode these production-ratio requirements in the underlying PN model, while preserving all the corresponding theory of deadlock avoidance for these nets.

A second complication for the extension of the results that were developed in the previous parts of this paper to DC-RAS, even when they are operated under the production-ratio constraints that were mentioned in the previous paragraph, arises from the presence of routing flexibility for the supported process types. When viewed in the light of the technical developments that were pursued in the earlier parts of this document, this routing flexibility implies that the underlying GSPN ${\mathcal N}$ will not possess the mono-t-semiflow property. This fact, in turn, requires the redefinition of the steady-state regime for the fluidized version of net ${\mathcal N}$ so that it allows the potential “shut down” of certain parts of this net, in particular, those routes of the different process types that might not be competitive. Once this new convention has been established, the computation of a maximizing flow vector f^∗ for the controlled fluidized net ${\mathcal N}^{(tc)}$ can be attained through an LP formulation that is similar, in terms of its informational content, to the LP of Eqs. 10–13.⁴

A last point that needs some further discussion regarding the proposed extension of our main results to the DC-RAS model, concerns the second part of Proposition 3. We remind the reader that this part implies that in the operation of the discrete-time PN model ${\mathcal N}^{(dt)}$ that is induced from the fluidized net ${\mathcal N}^{(tc)}$, a marked place that feeds a timed transition of the net will never get empty. This could be a potential complication in view the aforementioned need to “shut down” certain parts of the net in the steady-state markings that support its optimized operation.

But this issue is immediately resolved in any real-time implementation of the proposed method that starts the underlying RAS in its empty state, and consistently guides it through those markings that are competitive markings according to the selection logic of Eqs. 23–24. Such an operational scheme will never route any process instances in the direction of those processing stages that are not competitive according to the flow-maximizing LP of Eqs. 10–13, and therefore, the underlying network ${\mathcal N}$ will never mark any places that will have to be emptied by the considered LP relaxation.

Based on all the above discussion, it should be clear that the FR-based scheduling method that has been developed in this work, is effectively extensible to the broader class of DC-RAS. This discussion also reveals the structure, as well as the modeling and analytical capabilities, that are attained when the FR-based scheduling methodology is pursued through the PN-based modeling framework, according to the lines that were specified in this paper.

5 Conclusions

This work has adapted the FR-based scheduling method for complex resource allocation that was initially developed in Ibrahim and Reveliotis (2019), to a new version that takes advantage of the modeling and the analytical power of the PN modeling framework. The presented developments have shown that by making use of the various PN classes that are currently offered by the corresponding PN theory, it is possible (i) to derive the necessary components of this method in a very structured and disciplined manner, and also (ii) to reason about various structural and behavioral aspects of these components with certain rigor that cannot be supported by any ad hoc implementation of this scheduling methodology. This last capability further enables a more profound understanding of the FR-based scheduling method itself, and it can also be used for (a) the further tuning of the method in order to enhance various aspects of its performance (as it was the case with the selection of the time-discretizing parameter Δt and the time-horizon length H that were employed by the proposed LP relaxation of Eqs. 17–22), or (b) the extension of its applicability (as it was the case in the discussion of Section 4). In fact, another interesting extension of the presented developments would be the systematic investigation of the reasons that the FR-based scheduling method will fail to reach an optimal decision in the operational context of the CRL and the other complex RAS classes that have motivated this work; a first set of results along this line can be found in Chapter 5 of Ibrahim (2019).