Design of Optimal Fractional-Order PID Controllers Using Particle Swarm Optimization Algorithm for Automatic Voltage Regulator (AVR) System

Abstract

In practical applications, the pure derivative action is never used, due to the “derivative kick” produced in the control signal for a step input, and to the undesirable noise amplification. It is usually replaced by a first-order low-pass filter. In this paper, we use a $\mu$-order fractional low-pass filter and define a practical fractional-order controller. The proposed approach with new defined fitness function has very easy implementation and the most control performance. We present a method for optimum tuning of practical fractional PID controllers for automatic voltage regulator system using particle swarm optimization (PSO) algorithm. PSO is a robust stochastic optimization technique based on the movement and intelligence of swarm, applies the concept of social interaction to problem solving. From the comparison this technique with the other methods, its influence and efficiency are illustrated. Simulations and comparisons with other FOPID/PID controllers illustrate that the proposed PSO-FOPID controller can provide good control performance with respect to reference input and also improve the system robustness with respect to model uncertainties.

1 Introduction

In the last decade, fractional-order dynamic systems and controllers have been studying widely in many areas of engineering and science (Oldham and Spanier 1974; Lubich 1986; Miller and Ross 1993; Oustaloup 1981; Chengbin and Hori 2004). The concept of the fractional-order PID controllers was proposed by Podlubny et al. (1997). He also demonstrated the better response of this type of controllers, in comparison with the classical PID controllers, when used for the control of fractional-order systems. He was demonstrated the major role of fractional-order calculus in a smart mechatronic system (Podlubny 1999). Hardware and digital realizations of fractional-order systems can be followed in Chen et al. (2004), Nakagawa and Sorimachi (1992), Valério and Sàda Costa (2011). A frequency-domain approach based on given phase margin and crossover frequency is studied in Vinagre et al. (2000). In Monje et al. (2004), an optimization method is presented such that predefined design specifications are satisfied. A method is presented based on the pole distribution of the characteristic equation in the complex plane (Petras 1999). A state-space design approach is presented based on feedback pole placement in Dorcak et al. (2001). A method is presented based on differential evolution (DE) technique in Biswas et al. (2009). Also, a method is presented based on idea of the Ziegler–Nichols and the Astrom–Hagglund methods in Yeroglu and Tan (2011). A method is presented based on the asymptotic behavior of fractional algebraic equations and applies a delicate property of the root loci of the system in Merrikh-Bayat and Karimi-Ghartemani (2010). A fractional-order $(\hbox {PI})^{\lambda }$ controller is designed to improve the flight control performance of a small fixed-wing unmanned aerial vehicle (UAV) in Luo et al. (2011). In Zhou et al. (2013) a series of practical distributed order, robust PI control strategies are presented. In Luo and Chen (2009) is focused on a given type of simple model of fractional-order system and is proposed a fractional-order [proportional derivative] (FO-[PD]) controller for this class of fractional-order system. An experimental study of the fractional order proportional and derivative (FO-PD) controller for the fractional-order systems with generalized fractional capacitor membrane model is presented in Luo et al. (2011) to validate the control performance. In Barbosa et al. (2010) as an application of fractional-order PID controllers is demonstrated effect of fractional orders in the velocity control of a servo system.

Optimal tuning of classical PID controller parameters is done in some paperbut with proposed fitness functions, and classical PID cannot achieve a high-quality solution that effectively improve the transient response of the controlled system. In Devaraj and Selvabala (2009), a method is presented based on real-coded genetic algorithm and fuzzy logic. In Gaing (2004), Rahimian and Raahemifar (2011), Shabib et al. (2005), Amer et al. (2008) is proposed a optimal design method for determining the PID controller parameters of the automatic voltage regulator (AVR) system using the particle swarm optimization (PSO). Other methods such as genetic algorithm (GA), simulated annealing (SA), bee colony algorithm and chaotic algorithm are used for achieving high efficiency and searching global optimal solution in problem space (Wong et al. 2009; Coelho 2007; Krohling and Rey 2001; Gozde and Taplamacioglu 2010). Recently, swarm intelligence, that is another optimization procedure based on social system or the collective behaviors of simple individuals interacting with their environment and each other, has gained popularity. Ant colony optimization (ACO) and particle swarm optimization (PSO) are two popular swarm inspired methods. ACO is inspired by the behaviors of ants and has many successful applications in discrete optimization problems. PSO is a population-based stochastic optimization technique that is inspired by behavior of a bird flock or a school of fish in search of food. PSO is similar to evolutionary techniques such as genetic algorithm (GA), but PSO has few advantages toward GA. Indeed, PSO only has one operator called velocity calculation, so the computation time is decreased significantly. It does not require operators such as crossover and mutation in evolutionary process; thus, PSO implementation is easier than GA. In PSO, the potential solutions, called particles, fly through the problem space by following the current optimum particles. In GAs, chromosomes share information with each other. So, the whole population moves like a one group toward an optimal area. In PSO, only gBest (the best value obtained so far by any particle in the neighborhood of that particle) spreads the information to others. It is a one-way information sharing mechanism i.e., the evolution only looks for the best solution. PSO has memory, that is, the knowledge of good solutions is retained by all particles, whereas in GA, previous knowledge of the problem is destroyed once the population is changed. Unlike GA’s, PSO is the only algorithm that does not depend on the principle of “survival of the fittest” (Gaing 2004). Therefore, compared to other techniques, PSO has a well-balanced mechanism to enhance the global and local exploration abilities and it is an excellent optimization methodology and a simple approach but promising for solving the engineering optimization problems.

In Zamani et al. (2009), a fractional-order controller for AVR system is presented based on a new criterion function with eight terms. However, it is not convenient to select appropriated weighted factors for these eight terms. An optimum fractional-order PID controller is presented in Tang et al. (2012) using chaotic ant swarm (CAS) optimization method and the same fitness function existence in Gaing (2004), and then high performance of proposed method in comparison with Gaing (2004) is illustrated.

In this paper, a novel optimal practical fractional-order controller consist of a $\mu$-order fractional low-pass filter in derivative by using PSO algorithm for a new nonlinear fitness function is presented. High control performance of the proposed practical PSO-FOPID controller for AVR system is compared with other optimal FOPID/PID controllers that are presented in Gaing (2004), Tang et al. (2012). The system robustness using proposed practical PSO-FOPID controller for model uncertainties is compared to CAS-FOPID controller available in Tang et al. (2012).

This paper is organized as follows. Section 2 discusses a brief review to fractional calculus especially fractional-order PID controller. In Sect. 3, brief introduction to particle swarm optimization algorithm is given. Also, the purposed fitness function is illustrated in this section, and its application in $PI^{\lambda }D^{\mu }$ PSO-controller is discussed. In Sect. 4, the model of AVR system is presented. In Sect. 5, simulation results are presented. Section 6 is the conclusion.

2 Review on Fractional Calculus

2.1 Fractional-Order PID Controllers (FOPID)

The fractional PID controller is a generalization of the PID controller. The transfer function of this controller is given by the following function:

$$\begin{aligned} {C}{\left( {s} \right) }={k}_{p} +\frac{{k}_{i}}{{s}^{\lambda }}+{k}_{d} {s}^{\mu } \end{aligned}$$

(1)

In practical applications, the pure derivative action is never used, due to the “derivative kick” produced in the control signal for a step input, and to the undesirable noise amplification. It is usually replaced by a first-order low-pass filter. We use a $\mu$-order fractional low-pass filter; thus, the Laplace transformation of the fractional PID controller can be written as:

$$\begin{aligned} {C}{\left( {s} \right) }={k}_{{p}} +\frac{{k}_{{i}}}{{s}^{\lambda }}+{k}_{{d}} \frac{{N}}{1+\frac{{N}}{{s}^{{\mu }}}} \end{aligned}$$

(2)

where ${s}= {j}\omega$ is the complex frequency, ${k}_{p}$ is the proportional constant, ${k}_{i}$ is the integration constant, ${k}_{d}$ is the differentiation constant, and $\lambda$ and $\mu$ are positive real numbers. Thus, fractional power of ${j}\omega$ is:

$$\begin{aligned} {s}^{\alpha }=\omega ^{\alpha }\left( {\cos \frac{\pi }{2}\alpha +{j}\sin \frac{\pi }{2}\alpha } \right) \end{aligned}$$

(3)

where $\alpha$ is a positive real number. The most popular definitions of fractional derivatives or integrals in fractional calculus are Grünwald–Letnikov (GL), Riemann–Liouville (RL) and Caputo statements. The Grünwald-Letnikov expressed the fractional-order derivative by the following equation (Caponetto et al. 2010)

$$\begin{aligned} _{{a}} {D}_{{t}}^{\gamma }\!{f}\left( {t} \right) =\lim _{{h}\rightarrow 0} {h}^{-\gamma }\sum _{{ j}=0}^{[{t}-{a}/{h}]} \left( {-1} \right) ^{{j}}\left( {{\begin{array}{l} \gamma \\ {j} \\ \end{array}}} \right) {f}\left( {{t}-{jh}} \right) \end{aligned}$$

(4)

where $(-1)^{j}\left( {{\begin{array}{l} r \\ j \\ \end{array} }} \right)$ are (Dorcak 1994):

$$\begin{aligned} {c}_0^{({r})} =1 ,{c}_{j}^{({r})} =\left( {1-\frac{1+{r}}{{j}}} \right) {c}_{{j}-1}^{\left( {r} \right) } ,\quad {j}=0,1,2,\ldots \end{aligned}$$

(5)

And used for recursive computation, these are weights.

Reimann–Liouville (RL) expression for fractional-order derivative is given by:

$$\begin{aligned} _{{a}}{{D}}_{t}^{\gamma }\!{f}\left( {t} \right) =\frac{1}{{{\Gamma }}({n}-\gamma )}\frac{\hbox {d}^{{n}}}{\hbox {d}t^{{n}}}\int \limits _{a}^{t} \frac{{f}^{({n})}(\tau )}{({t}-\tau )^{\gamma -{n}+1}}\mathrm{d}\tau \end{aligned}$$

(6)

where ${\varGamma }(.)$ is Euler’s gamma function that generalizes the factorial, and allows operator, to take noninteger values.

An another definition is the Caputo definition given by

$$\begin{aligned} _{{a}}{{D}}_{{t}}^{\gamma }\!{f}\left( {t} \right) =\frac{1}{{\Gamma }(\gamma -{{n}})}\int \limits _{{a}}^{{t}} \frac{{{f}}^{{\left( {{n}} \right) }(\tau )}}{({t}-\tau )^{\gamma -{{n}}+1}}\hbox {d}\tau \end{aligned}$$

(7)

More detail is available in Das (2011).

2.2 Oustaloup Approximation Algorithm

Oustaloup’s approximation method uses a band-pass filter to approximate the fractional-order operator ${s}^{\lambda }$ based on frequency-domain response (Oustaloup et al. 1996). The approximate transfer function of a continuous fractional-order operator ${s}^{{\lambda }}$ with Oustaloup Algorithm is as follows:

$$\begin{aligned} G_f\left( s\right) =K \prod _{k=-N}^N \frac{s+\omega _k^{\prime }}{s+\omega _k}, \end{aligned}$$

(8)

where the zeros, poles and the gain can be evaluated, respectively, as:

$$\begin{aligned} \omega _k^{\prime }&= \omega _b \left( {\frac{\omega _h }{\omega _b}} \right) ^{\frac{k+N+\frac{1}{2}(1-\gamma )}{2N+1}}, \end{aligned}$$

(9)

$$\begin{aligned} \omega _k&= \omega _b \left( {\frac{\omega _h }{\omega _b }} \right) ^{\frac{k+N+\frac{1}{2}(1+\gamma )}{2N+1}}, \end{aligned}$$

(10)

$$\begin{aligned} K&= \left( {\frac{\omega _h }{\omega _b }} \right) ^{-\frac{\gamma }{2}}\prod \limits _{k=-N}^N \frac{\omega _k }{\omega _k^{\prime }}. \end{aligned}$$

(11)

In our simulation, for approximation of ${s}^{\lambda }$, frequency range is closed as: $\omega \in [\omega _{{b}}, \omega _{{h}}]$ and $\omega _{{b}}= 0.001,\omega _{{h}}=1000, {N}=2$.

3 Design of $\hbox {PI}^{\lambda }D^{\mu }$ PSO-Controller

3.1 Particle Swarm Optimization (PSO)

PSO was developed in 1995 by James Kennedy (social-psychologist) and Russell Eberhart (electrical engineer) (Kennedy and Eberhart 1995). PSO is the only algorithm that does not implement the survival of the fittest. It uses a number of agents (particles) that constitute a swarm moving around in the search space looking for the best solution. Jth particle $(k_j)$ is treated as a point in a $N$-dimensional space $(k_j = k_{j,1}, k_{j,2}, \ldots , k_{j,N})$ which adjusts its “flying” according to its own flying experience as well as the flying experience of other particles. Each particle keeps track of its coordinates in the solution space which are associated with the best solution (fitness) that has achieved so far by that particle. This value is called personal best, $\hbox {Pbest}.\hbox {pbest}_j =\left( {\hbox {pbest}_{j,1}, \hbox {pbest}_{j,2}, \ldots , \hbox {pbest}_{j,N}}\right)$ is previous position of the $j$th particle in a $N$-dimension space. Another best value that is tracked by the PSO is the best value obtained so far by any particle in the neighborhood of that particle. This value is called gbest. The basic concept of PSO lies in accelerating each particle toward its pbest and the gbest locations, with a random weighted acceleration at each time step. The modification of the particle’s position can be mathematically modeled according the following equations.

$$\begin{aligned} v_{j,N}^{(t+1)}&= \omega .v_{j,N}^{(t)} +c_1 \hbox {rand}_1 \left( \ldots \right) \left( {\hbox {pbest}_{j,N}-K_{j,N}^{\left( t\right) }}\right) \nonumber \\&\quad +\,c_2 \hbox {rand}_2 \left( \ldots \right) \left( {\hbox {gbest}-K_{j,N}^{\left( t \right) } } \right) \end{aligned}$$

(12)

$$\begin{aligned} K_{j,N}^{\left( {t+1} \right) }&= K_{j,N}^{\left( t \right) } +v_{j,N}^{(t+1)}\end{aligned}$$

(13)

$$\begin{aligned} v_{j,N}^{(t+1)}&= \left\{ {{\begin{array}{l@{\quad }l} V_N^\mathrm{max} &{} v_{j,N}^{\left( {t+1} \right) } >V_N^\mathrm{max}\\ V_N^\mathrm{min} &{} v_{j,N}^{\left( {t+1} \right) } >V_N^\mathrm{min} \\ \end{array} }} \right. \end{aligned}$$

(14)

where $j=1,2,{\ldots },n$ and $N=1,2,{\ldots },m$, and $n$ number of particles in the population(population size); $m$ dimension of problem (number of members in a particle) that there is five; $t$ pointer of iterations(generations); $v_{j,N}^{(t)}$ velocity of particle $j$ at iteration $t$, $V_N^\mathrm{min} \le v_{j,N}^{(t)} \le V_N^\mathrm{max}$; $\omega$ weighting function; $c_1, c_2$ acceleration factors; $\hbox {rand}_1 \left( \ldots \right) ,\hbox {rand}_1 \left( \ldots \right)$ uniformly distributed random numbers between 0 and 1; $K_{j,N}^{\left( t \right) }$ Current position of particle $j$ at iteration $t$; $\hbox {pbest}_{j,N}$ pbest position of particle $j$; $\hbox {gbest}$ gbest position of swarm.

3.2 Purposed Fitness Function

We define a new fitness function as follows

$$\begin{aligned} \hbox {Min}\,{J}({k}_{{p}}, {k}_{{i}}, \lambda , {k}_{{d}}, \mu = e^{-\beta }(T_{{s}}+{T}_{{r}})\nonumber \\+(1-e^{-\beta })(\hbox {ITSE}+M_p ) \end{aligned}$$

(15)

where ${T}_{{s}}\,\hbox {settling} \,\hbox {time}, \,{T}_{{r}} \,\hbox {rise}\, \hbox {time},\,M_{p} \hbox {overshoot},\beta$ is weighting factor and ITSE is integral of the time multiplied square error criterion given by:

$$\begin{aligned} \hbox {ITSE}=\int \limits _{0}^{{t}_\mathrm{sim}} te^{2}(t)\mathrm{d}t \end{aligned}$$

(16)

where $t_\mathrm{sim}$ is total simulation time and $e(t)=V_\mathrm{ref}-V_S$ is the tracking error. The PID controller design method using the integral of absolute error (IAE), or integral of square error (ISE), or integral of time multiplied square error (ITSE) is often employed in control system design. The IAE, ISE performance indices are as follows:

$$\begin{aligned} \hbox {IAE}=\int \limits _0^{\infty } \left| {e(t)} \right| \mathrm{d}t\end{aligned}$$

(17)

$$\begin{aligned} \hbox {ISE}=\int \limits _0^{\infty }e^{2}(t)\mathrm{d}t \end{aligned}$$

(18)

the ITSE performance indices have excellences of smaller overshoot and oscillation than the IAE or the ISE performance indices and it is the most sensitive, then ITSE has the best selectivity. The most important parameter in this fitness function is ITSE. Minimization of this parameter forces $t_s, t_r \,\hbox {and} \,M_p$ parameters to be optimum. In the other word, with this fitness function $t_{s}, t_{r} \,\hbox {and} \,M_p$ parameters are optimized directly and indirectly. ITSE performance index is calculated using the multiple-application Simpson’s 1/3 rule (Chapra and Canale 1998). Our goal is obtaining the best step response, We minimize $J(k_p, k_i, \lambda , k_d, \mu )$ using PSO algorithm and obtain optimum parameters of $\hbox {PI}^{\lambda }D^{\mu }$ pso-controller. In this paper, PSO parameters is selected as:

$$\begin{aligned} c_1 = c_2 =2, \quad \omega =0.729,\nonumber \\ \hbox {maxIter}=100, \hbox {population size}=100 \end{aligned}$$

(19)

4 Modeling of AVR System

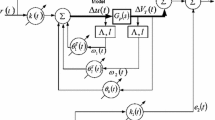
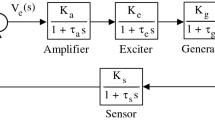
An AVR system holds the terminal voltage magnitude of a synchronous generator at a specified level. Therefore, the stability of the AVR system would seriously affect the security of the power system, and design of a controller for an AVR system is necessary to improve its stability and transient performance. A simpler AVR system comprises four main components, such as amplifier, exciter, generator and sensor. The real model of such a system is shown in Fig. 1. A small signal model of this system including fractional PSO-PID controller is shown in Fig. 2, and the limits of the parameters used in it are presented in Table 1.

Fig. 1

A real model of AVR system

Fig. 2

Block diagram of AVR system

Table 1 Components of AVR system model with transfer function and parameters limits

5 Simulation Results

5.1 Performance of AVR System Without Fractional PID Controller

AVR system has a very poor performance without a Fractional PID controller. Unit step response of AVR system without controller is shown in Fig. 3. That has large overshoot, long settling time and oscillation. An AVR system with PSO-FOPID is shown in Fig. 4.

Fig. 3

Terminal voltage step response of an AVR system without Fractional PID controller

Fig. 4

Block diagram of an AVR system with PSO-FOPID

5.2 Performance of AVR System with PSO-FOPID Controller

In this section, we examine the performance of PSO-FOPID. Terminal voltage step response of the AVR system controlled by optimum PSO-FOPID controller is shown in Fig. 5. The gained best controller parameters are presented in Table 2. It can be seen from Fig. 5 that the step response of the AVR system controlled by PSO-FOPID controller has very good performance. The performance indices in the time domain of the step responses shown in Figs. 3 and 5 are presented in Table 3.

Fig. 5

Terminal voltage step response of the AVR system controlled by optimum PSO-FOPID controller

Table 2 The optimum PSO-FOPID controller parameters with different $\beta$ values

Table 3 Performance indices of the AVR system without controller and with PSO-FOPID Controller for different $\beta$ values

5.3 Comparison with other FOPID Controllers

In this section, we compare PSO-FOPID with other FOPID controllers. For comparison, we consider designed fractional controller in Tang et al. (2012) that is based on chaotic ant swarm (CAS) algorithm (CAS-FOPID) and GA-FOPID controller. The GA algorithm is implemented as in Tang et al. (2012).

The GA algorithm is performed ten runs to obtain the best controller parameters using the same fitness function is given in (15). The step responses of the AVR system controlled by CAS-FOPID controller, GA-FOPID controller and PSO-FOPID controller are shown in Figs. 6 and 7. The best controller parameters and the performance indices are shown in Table 4. With observe Figs. 6, 7 and Table 4, we derive that proposed PSO-FOPID controller has better performance than the CAS-FOPID controller and GA-FOPID controller. The convergence characteristic of the practical PSO-fractional PID controller is shown in Fig. 8.

Fig. 6

Terminal voltage step response of AVR system controlled by PSO-FOPID and CAS-FOPID controllers. a $\beta = 1.0$, b $\beta = 1.5$

Fig. 7

Terminal voltage step response of AVR system controlled by PSO-FOPID, CAS-FOPID and GA-FOPID controllers. a $\beta = 1.0$, b $\beta = 1.5$

Fig. 8

The convergence characteristic of the PSO-fractional PID controller, $\beta = 1.0$

Table 4 Best controller parameters and performance indices different FOPID controllers

5.4 Comparison with other PID Controllers

In this section, we compare PSO-FOPID with other PID controllers. For comparison, we consider designed optimum controllers in Tang et al. (2012), Gaing (2004). In Gaing (2004) is designed a controller based on PSO algorithm (PSO-PID) and in Tang et al. (2012) is designed a controller based on chaotic ant swarm (CAS) algorithm (CAS-PID).

The step responses of theAVR system controlled by PSO-PID controller, CAS-PID controller and PSO-FOPID controller are shown in Fig. 9. The best controller parameters and the performance indices are expressed in Table 5. With observe Fig. 9, and Table 5, we derive that proposed PSO-FOPID controller has better performance than the CAS-PID controller and PSO-PID controller. It shows high performance of fractional-order PID controllers in comparison with integer order PID controllers.

Fig. 9

Terminal voltage step response of AVR system controlled by PSO-FOPID, CAS-PID and PSO-PID controllers. a $\beta$ = 1.0, b $\beta$ = 1.5

Table 5 Best controller parameters and performance indices different PID controllers

5.5 Robustness of PSO-FOPID Controller

To demonstrate robustness of the proposed PSO-FOPID controller strategy against parametric uncertainties, simulations are carried out for three number of operating conditions with previously designed FOPID is considered as follows:

Case 1: $K_g =0.7,\tau _g =1.6$ :

In Fig. 10 we compare proposed PSO-FOPID controller in Table 2 (for $\beta =1)$ with CAS-FOPID controller is designed in Tang et al. (2012). With observe Fig. 10, we derive that proposed PSO-FOPID controller has better performance than CAS-FOPID controller in Tang et al. (2012) with generator uncertainty.

Fig. 10

Terminal voltage step response of AVR system controlled by PSO-FOPID and CAS-FOPID controllers $\beta = 1.0$ with case 1

Case 2: $K_e =1.2,\tau _e =0.5$:

In Fig. 11 we compare proposed PSO-FOPID controller in Table 2 (for $\beta =1$) with CAS-FOPID controller is designed in Tang et al. (2012). With observe Fig. 11, we derive that proposed PSO-FOPID controller has better performance than CAS-FOPID controller in Tang et al. (2012) with exciter uncertainty.

Fig. 11

Terminal voltage step response of AVR system controlled by PSO-FOPID and CAS-FOPID controllers $\beta = 1$ with case 2

Case 3:$K_a =14,\tau _a =0.07$:

In Fig. 12 we compare proposed PSO-FOPID controller in Table 2 (for $\beta =1$) with CAS-FOPID controller is designed in Tang et al. (2012). With observe Fig. 12, we derive that proposed PSO-FOPID controller has better performance than CAS-FOPID controller in Tang et al. (2012) with amplifier uncertainty.

Fig. 12

Terminal voltage step response of AVR system controlled by PSO-FOPID and CAS-FOPID controllers $\beta = 1.0$ with case 3

6 Conclusions

In this paper, a novel optimal practical fractional-order controller using PSO algorithm is presented that has a $\mu$-order fractional low-pass filter in derivative to prevent the “derivative kick” produced in the control signal for a step input, and the undesirable noise amplification. The parameters of optimal practical fractional order controller are determined through optimizing a new nonlinear function consisting of overshoot, integral of time multiplied square error (ITSE), raising time and settling time. These measures are calculated from the step response of AVR system. The simulation results illustrate that the proposed practical PSO-FOPID controller for AVR system has best control performance than other optimal FOPID/PID controllers that so far is presented, and also, for model uncertainties, the practical PSO-FOPID controller is more robust. The proposed technique may apply as an efficient method to design robust optimal practical fractional-order controllers for practical systems to reject external disturbances.