Nomenclature

a r :

= semi-major axis of the instantaneous relative ellipse

\(a_{T_{x}}=\) :

radial component of acceleration resulting from external forces

\(a_{T_{y}}=\) :

along-track component of acceleration resulting from external forces

\(a_{T_{z}}=\) :

cross-track component of acceleration resulting from external forces

A x :

= amplitude of the motion in the LVLH radial direction

A y :

= amplitude of the motion in the LVLH along-track direction

A z :

= amplitude of the motion in the LVLH cross-track direction

E r :

= relative eccentric anomaly

i r :

= relative inclination

n :

= mean motion of the chief’s orbit

\(\bar {n}_{r}=\) :

vector normal to the instantaneous relative orbit

\(\hat {n}_{r}=\) :

unit vector normal to the instantaneous relative orbit

r :

= magnitude of deputy position vector with respect to center of central body

\(\bar {\boldsymbol {r}}=\) :

deputy position vector with respect to center of central body

\(\bar {\boldsymbol {r}}^{C}=\) :

chief position vector with respect to center of central body

\(\bar {\boldsymbol {r}}_{1}=\) :

position vector from the instantaneous center of motion to the point where E r = 0

\(\bar {\boldsymbol {r}}_{2}=\) :

position vector from the instantaneous center of motion to the point where E r = π/2

t :

= time

x = :

relative position vector component in LVLH radial direction

\(\dot {x}=\) :

derivative with respect to time of relative position vector component in LVLH radial direction, taken in LVLH frame

\(\ddot {x}=\) :

second derivative with respect to time of relative position vector component in LVLH radial direction, taken in LVLH frame

\(\hat {x}=\) :

LVLH coordinate unit vector in radial direction

x r = :

radial coordinate of instantaneous center of motion

x q :

= radial coordinate of point Q on circle that circumscribes instantaneous relative orbit ellipse

y :

= relative position vector component in LVLH along-track direction

\(\dot {y}=\) :

derivative with respect to time of relative position vector component in LVLH along-track direction, taken in LVLH frame

\(\ddot {y}=\) :

second derivative with respect to time of relative position vector component in LVLH along-track direction, taken in LVLH frame

\(\hat {y}=\) :

LVLH coordinate unit vector in along-track direction

y r :

= along-track coordinate of instantaneous center of motion

y q :

= along-track coordinate of point Q on circle that circumscribes instantaneous relative orbit ellipse

y s :

= secular drift in LVLH along-track direction

\(\dot {y}_{s}=\) :

secular drift rate in LVLH along-track direction

z :

= relative position vector component in LVLH cross-track direction

\(\dot {z}=\) :

derivative with respect to time of relative position vector component in LVLH cross-track direction, taken in LVLH frame

\(\ddot {z}=\) :

second derivative with respect to time of relative position vector component in LVLH cross-track direction, taken in LVLH frame

\(\hat {z}=\) :

LVLH coordinate unit vector in cross-track direction

γ :

= phase difference between relative eccentric anomaly and cross-track motion phase angle

μ :

= gravitational parameter of central body

ν r :

= relative true anomaly

\(\bar {\boldsymbol {\rho }}=\) :

deputy relative position vector with respect to chief

\(\bar {\boldsymbol {\rho }}^{IC}=\) :

position vector from LVLH origin to instantaneous center of relative motion

\(\bar {\boldsymbol {\rho }}_{1}=\) :

position vector from LVLH origin to location on relative orbit where E r = 0

\(\bar {\boldsymbol {\rho }}_{2}=\) :

position vector from LVLH origin to location on relative orbit where E r = π/2

ψ :

= cross-track motion phase angle

0:

= subscript indicating initial condition

Introduction

The close proximity flight of two or more spacecraft in orbit has been increasingly utilized in order to achieve mission objectives spanning on-orbit inspection [1], formation flight [2, 3], space station resupply [4], and satellite servicing [5, 6], for commercial and defense applications. The increasing prevalence of nano- and micro-spacecraft and emerging architectures including fractionated spacecraft have added to the priority of robust close proximity trajectory design and control [7, 8]. While the mission objectives related to close proximity operations are diverse, there exists a set of relative trajectory control behaviors that are common to most close proximity mission architectures, including rendezvous and station-keeping. Cooperative formation missions often must satisfy a stringent requirement on the relative spacing of the satellites in the cluster. For on-orbit inspection applications, circumnavigation of the targeted space object may be desired. For satellite servicing or resupply missions, close approach and mating must occur. Underlying all of these behaviors is the requirement to maintain safe relative trajectories, where collision avoidance is assured [10–13].

For the above applications, the relative motion between spacecraft is of interest. Analytical models for relative motion appeared as early as 1878 [14], while in more recent history, the past five decades have seen a wealth of literature on the subject. Two of the most widely accepted models developed during that era are that of Tschauner and Hempel [15] and that of Clohessy and Wiltshire [16]. Both models linearize the motion of a “deputy” spacecraft about a “chief” spacecraft, with the latter model assuming a circular chief orbit.

In addition to possessing an analytical model, a clear understanding of the physical motion between close proximity spacecraft on orbit is critical to the design of safe, robust mission plans [17]. Previous works have identified constants of the relative motion. Schaub and Junkins [18] and Vallado [19] defined scalar offsets in the orbit radial and along-track directions, representing the instantaneous center of the motion in the plane of the chief’s inertial orbit. Vallado described the amplitude of the oscillatory motion in the chief’s orbital plane, and he defined a constant that is consistent with the amplitude of the motion in the cross-track direction. Kaplan defined a relative eccentricity parameter of the chase orbit [20]. Gustafson and Kriegsman utilized dynamics of the relative motion to develop parametric equations for automated station-keeping in Earth orbit [21].

Previous works have defined and utilized geometric parameterizations of relative motion. One such common formulation is to represent the differences in classical orbital elements between the deputy and chief as the relative states [18, 22]. A relative parameter set that has seen extensive mission application is that developed by D’Amico and Montenbruck [23]. These particular parameters consist of either orbital element differences between the deputy and chief, or nonlinear combinations thereof. Ref. [24] showed that these parameters match the integration constants of the Clohessy-Wiltshire equations. This parameter set has been applied to several close-proximity missions, most notably PRISMA [25, 26]. Han and Yin [27] put forward a set of geometric relative coordinates very similar to those of Ref. [14], and demonstrate their use for elliptical chief relative motion.

This investigation advances the development of a parameterization called relative orbital elements (ROEs) for close proximity mission planning. ROEs represent a direct re-parameterization of the solutions to the Clohessy-Wiltshire equations. Lovell, Tragesser and Tollefson initially formulated ROEs in 2004 [28, 29], defining six elements that fully characterize the Clohessy-Wiltshire relative motion, and establishing the transformation between ROEs and Cartesian coordinates in the local vertical-local horizontal (LVLH) coordinate frame. They also showed the effect of one or more instantaneous maneuvers on ROEs, and developed a multiple-impulse guidance methodology for relative trajectory control. These advancements provide a useful framework for relative orbit mission planning. Analogous to classical orbital elements, ROEs provide a geometric interpretation of the relative motion of a deputy spacecraft with respect to a chief spacecraft that is in a circular orbit. ROEs allow the characterization of the deputy spacecraft relative motion in an unforced (free-motion) trajectory, and provide a direct visualization of the effects of maneuvers on the relative motion geometry.

Since the introduction of ROEs in 2004, the formulation has been used for the development of several analytical guidance strategies. Bevilacqua and Lovell [30] developed relative motion guidance solutions applying continuous, on-off thrust, and utilizing ROEs as a geometrical representation of the dynamics. Phillips [31] utilized ROEs for determination of satellite collision probability. Aubin [32] employed ROEs to generate solution vectors for a particle swarm evolutionary algorithm. Schwartz et al [33, 34] developed an ROE-based controller for station-keeping of a cluster of spacecraft as part of the DARPA System F6 flight program. The Prox-1 small satellite mission will apply impulsive control strategies based upon ROEs to implement formation flight and circumnavigation maneuvers [35].

This article formally documents the derivation of the ROE parameterization. Through this work, a geometric interpretation of the angular ROEs is provided, leading to a strong analogy between ROEs and classical orbital elements. Additional parameters related to ROEs are described, including the newly defined parameters relative true anomaly and relative inclination. It should be noted that other geometric formulations for relative motion exist in the literature (e.g., Ref. [23]), but the formulation presented herein is beneficial in terms of the visualization of the motion and relative orbit design for mission planning.

This article provides a detailed description of the ROE formulation. “Definition of Relative Orbital Elements” provides an overview of the derivation of ROEs, and describes the geometric interpretation of each element. The transformation between ROEs and the Cartesian states in the LVLH coordinate frame is developed, and the evolution of ROEs with time is evaluated. “Characteristics of the Unforced Motion”describes the three primary modes of the motion, determined based upon the values of the ROEs. Concluding remarks are given in “Conclusions”.

Definition of Relative Orbital Elements

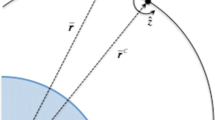
In order to describe the ROE formulation, it is assumed that both the chief and deputy spacecraft travel in two-body motion about the central body, with the chief constrained to be on a circular orbit. The central body, chief, and deputy are treated as point masses, and all perturbations are neglected. It is further assumed that the distance from the chief to the deputy is small relative to the chief’s orbit radius. The Clohessy-Wiltshire equations may be expressed in terms of LVLH coordinates. The LVLH frame is defined in Fig. 1. The origin for the LVLH coordinate system is at the chief location. The \(\hat {x}\)-axis is in the radial direction, the \(\hat {z}\)-axis is in the chief’s angular momentum (cross-track) direction, and the \(\hat {y}\)-axis is obtained by \(\hat {z} \times \hat {x}\). Note that for a circular chief orbit, the \(\hat {y}\)-axis is in the chief’s along-track direction, i.e., aligned with its instantaneous velocity vector. In Fig. 1, the radius vector from the central body to the chief is denoted by \(\bar {\boldsymbol {r}}^{C}\), the radius to the deputy is denoted by \(\bar {\boldsymbol {r}}\), and the relative position vector from the chief to the deputy is denoted by \(\boldsymbol {\bar {\rho }}\).

Fig. 1
figure 1

Coordinate system definition for LVLH frame

Full size image

The Clohessy-Wiltshire equations of motion for the deputy spacecraft relative to the chief are shown in Eqs. 1–3, where n represents the mean motion of the chief spacecraft, and a T x , a T y and a T z are the components of acceleration resulting from external forces acting upon the deputy:

$$ \ddot{x} - 2n\dot{y} - 3n^{2}x = a_{T_{x}} $$
(1)
$$ \ddot{y} + 2n\dot{x} = a_{T_{x}} $$
(2)
$$ \ddot{z} + n^{2}z = a_{T_{z}} $$
(3)

For unforced motion, where no thrust is applied to the deputy spacecraft, the Clohessy-Wiltshire equations reduce to Eqs. 4–6:

$$ \ddot{x} - 2n\dot{y} - 3n^{2}x = 0 $$
(4)
$$ \ddot{y} + 2n\dot{x} = 0 $$
(5)
$$ \ddot{z} + n^{2}z = 0 $$
(6)

A detailed derivation of the solutions to the Clohessy-Wiltshire equations using Laplace transforms is given in Ref. [19]. If the initial conditions for the LVLH Cartesian state are denoted by the subscript 0, then the position and velocity solutions to the Clohessy-Wiltshire equations are given by Eqs. 7–12:

$$\begin{array}{@{}rcl@{}} x(t) &=& \left(4x_{0} + \frac{2\dot{y}_{0}}{n} \right) - \left(3_{x_{0}} + \frac{2\dot{y}_{0}}{n}\right) \cos \left[n\left(t-t_{0}\right)\right] + \frac{\dot{x}_{0}}{n}\sin \left[n(t-t_{0})\right] \\ y(t) &=& y_{0} - \frac{2\dot{x}_{0}}{n} - \left(6nx_{0} + 3\dot{y}_{0}\right)(t-t_{0}) + \frac{2\dot{x}_{0}}{n} \cos \left[n\left(t-t_{0}\right)\right]\end{array} $$
(7)
$$ + \left(6x_{0} + \frac{4\dot{y}_{0}}{n}\right) \sin \left[n\left(t-t_{0}\right)\right] $$
(8)
$$ z(t) z_{0} \cos \left[n\left(t-t_{0}\right)\right] + \frac{\dot{z}_{0}}{n} \sin \left[n\left(t-t_{0}\right)\right] $$
(9)
$$ \dot{x}(t) = \left(3nx_{0} + 2\dot{y}_{0}\right) \sin \left[n\left(t-t_{0}\right)\right] + \dot{x}_{0}\cos \left[n\left(t - t_{0}\right)\right] $$
(10)
$$ \dot{y}(t) = - \left(6nx_{0} + 3\dot{y}_{0}\right) - 2\dot{x}_{0} \sin \left[n\left(t-t_{0}\right)\right]\! +\! \left(6nx_{0} + 4\dot{y}_{0}\right) \cos \left[n\left(t-t_{0}\right)\right] $$
(11)
$$ \dot{z}(t) = - nz_{0} \sin \left[n\left(t - t_{0}\right)\right] + \dot{z}_{0} \cos \left[n\left(t - t_{0}\right)\right] $$
(12)

Derivation of Relative Orbital Elements

Similar to classical orbital elements that convey the orbit geometry of a single space object in orbit about a central body in an inertially-fixed reference frame, ROEs provide a geometric interpretation of the relative orbit between two objects expressed in the LVLH frame. The six ROE parameters fully define the relative orbital state of the deputy with respect to the chief. The ROEs are derived from the solution to the Clohessy-Wiltshire equations. Application of the Harmonic Addition Theorem to Eqs. 7–9 results in the equations:

$$\begin{array}{@{}rcl@{}} x(t) = \left\{ \begin{array}{lll} 4x_{0} + \frac{2\dot{y}_{0}}{n} + \frac{1}{2}\text{sgn} \left[ - \left(3x_{0} + \frac{2\dot{y}_{0}}{n}\right)\right]\left[\left(6x_{0} + \frac{4\dot{y}_{0}}{n}\right)^{2} + \left(\frac{2\dot{x}_{0}}{n}\right)^{2}\right]^{1/2}.\\ \cos\left[n(t-t_{0}) + \tan^{-1}\left(\frac{\dot{x}_{0}/n}{3x_{0} + \frac{2\dot{y}_{0}}{n}}\right)\right], 3x_{0} + \frac{2\dot{y}_{0}}{n} \neq 0\\ 4x_{0} + \frac{2\dot{y}_{0}}{n} + \frac{\dot{x}_{0}}{n} \sin \left[n(t-t_{0})\right], 3x_{0} + \frac{2\dot{y}_{0}}{n} = 0 \end{array}\right. \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} y(t) = \left\{ \begin{array}{lll} y_{0} - \frac{2\dot{x}_{0}}{n} - \left(6nx_{0} + 3\dot{y}_{0}\right)(t-t_{0}) + \text{sgn} \left(\frac{2\dot{x}_{0}}{n}\right).\\ \cos \left[n\left(t-t_{0}\right)\right] + \tan^{1} \left(-\frac{6\dot{x}_{0} + 4\dot{y}_{0}/n}{2\dot{x}_{0}/n}\right), \dot{x}_{0} \neq 0\\ y_{0} - \frac{2\dot{x}_{0}}{n} - \left(6nx_{0} + 3\dot{y}_{0}\right)\left(t-t_{0}\right) \,+\, \left(6\dot{x}_{0} + \frac{4\dot{y}_{0}}{n}\right)\sin \left[n\left(t-t_{0}\right)\right], \dot{x}_{0} = 0 \end{array}\right. \end{array} $$
(14)
$$\begin{array}{@{}rcl@{}} z(t) = \left\{ \begin{array}{ll} \text{sgn}(z_{0})\left[z_{0}^{2} + \left(\frac{\dot{z}_{0}}{n}\right)^{2}\right]^{1/2}\cos\left[n\left(t-t_{0}\right) + \tan^{-1}\left(-\frac{\dot{z}_{0}/n}{z_{0}}\right)\right], z_{0} \neq 0\\ \frac{\dot{z}_{0}}{n}\sin\left[n\left(t-t_{0}\right)\right], z_{0} = 0 \end{array}\right. \end{array} $$
(15)

Through introduction of the atan2 function, it can be shown that Eqs. 13–15 may be expressed as:

$$\begin{array}{@{}rcl@{}} x(t) &=& 4x_{0} + \frac{2\dot{y}_{0}}{n} - \frac{1}{2} \sqrt{\left(6x_{0} + \frac{4\dot{y}_{0}}{n}\right)^{2} + \left(\frac{2\dot{x}_{0}}{n}\right)^{2}}\\ &&\qquad\times\cos\left[n\left(t-t_{0}\right) + \text{atan}2\left(\frac{2\dot{x}_{0}}{n}, 6x_{0} + \frac{4\dot{y}_{0}}{n}\right)\right] \end{array} $$
(16)
$$\begin{array}{@{}rcl@{}} y(t)\!\! &=&\!\! y_{0} - \frac{2\dot{x}_{0}}{n} - \left(6nx_{0} + 3\dot{y}_{0}\right) \left(t-t_{0}\right) \\ &&\!\!\! +\! \sqrt{\left(6x_{0} \,+\, \frac{4\dot{y}_{0}}{n}\right)^{2}\! \!\!+ \left(\frac{2\dot{x}_{0}}{n}\right)}\sin\left[(t-t_{0}) + \text{atan}2 \left(\frac{2\dot{x}_{0}}{n}, 6x_{0} + \frac{4\dot{y}_{0}}{n}\right)\right] \end{array} $$
(17)
$$ z(t) = \sqrt{{z}_{0}^{2} + \left(\frac{\dot{z}_{0}}{n}\right)^{2}}\sin\left[n(t-t_{0}) + \text{atan}2\left(z_{0}, \frac{\dot{z}_{0}}{n}\right)\right] $$
(18)

In Eqs. 16–18, the atan2(a, b) function is related to the arctangent function \(\tan ^{-1}\left (\frac {a}{b}\right )\), where −π < atan2(a, b) ≤ π based upon which quadrant contains the two arguments a and b. The atan2 function eliminates the need for the sgn function, as well as the need to account for two different cases that appear in each of Eqs. 13–15. Note that for each equation, if both arguments of the atan2(a, b) function are equal to zero, the coefficient of the sinusoid also equates to zero, resulting in a zero value for the periodic term.

The expressions for the deputy spacecraft position in the orbital plane of the chief spacecraft, (16–17), each have periodic terms and constant terms. The along-track expression (17) also has a term that varies linearly with time, resulting in a secular drift motion. The first two ROEs describe the deputy spacecraft’s instantaneous center of motion relative to the chief, encompassing the constant and linear time-varying terms. Expressed in terms of the LVLH Cartesian state initial conditions, the instantaneous center of motion ROEs are defined as:

$$ x_{r} = 4x_{0} + \frac{2\dot{y}_{0}}{n} $$
(19)
$$ y_{r} = y_{0} - \frac{2\dot{x}_{0}}{n} - \left(6nx_{0} + 3\dot{y}_{0}\right)(t-t_{0}) $$
(20)

Equations 19–20 indicate how the instantaneous center of the relative motion moves with time.

From Eq. 17, the amplitude of the sinusoidal motion in the along-track direction is given by:

$$ A_{y} = \sqrt{\left(6x_{0} + \frac{4\dot{y}_{0}}{n}\right)^{0} + \left(\frac{2\dot{x}_{0}}{n}^{2}\right)} $$
(21)

From Eq. 16, the amplitude of the sinusoidal motion in the radial direction is:

$$ A_{x} = \frac{1}{2}\sqrt{\left(6x_{0} + \frac{4\dot{y}_{0}}{n}\right)^{2} + \left(\frac{2\dot{y}_{0}}{n}\right)^{2}} $$
(22)

Note that the amplitude of the sinusoidal motion in the radial direction is half of that in the along-track direction. Thus, the motion in the \(\hat {x} - \hat {y}\) plane is always along an “instantaneous ellipse” with the major axis in the along-track direction and with a length that is twice that of the minor axis in the radial direction. Therefore, a single parameter can specify the shape of the instantaneous ellipse in the \(\hat {x} - \hat {y}\) plane. This parameter, a r , is the ROE representing the semi-major axis of the instantaneous relative orbit ellipse, equal to the along-track amplitude of the sinusoidal motion, A y :

$$ a_{r} = \sqrt{\left(6x_{0} + \frac{4\dot{y}_{0}}{n}\right)^{2} + \left(\frac{2\dot{x}_{0}}{n}\right)^{2}} $$
(23)

The fourth ROE parameterizes the angular position of the chaser spacecraft as it moves along the instantaneous relative orbit ellipse in the \(\hat {x} - \hat {y}\) plane. For reasons that are explained below (and shown graphically in Fig. 2) this ROE is termed the relative eccentric anomaly, E r . It represents the argument of the sine and cosine functions in Eqs. 16 and 17, and can be written:

$$ E_{r} = E_{r_{0}} + n \left(t-t_{0}\right) $$
(24)

where

$$ E_{r_{0}} = \text{atan}2\left(\frac{2\dot{x}_{0}}{n}, 6x_{0} + \frac{4\dot{y}_{0}}{n}\right) $$
(25)
Fig. 2
figure 2

Relative orbit geometry in the LVLH \(\hat {x} - \hat {y}\) plane

Full size image

A geometric interpretation of the first four ROE’s is shown on an instantaneous relative motion ellipse in Fig. 2. The semi-major axis of the ellipse is given by a r . The instantaneous center of the ellipse is given by x r and y r , and the deputy’s periapsis is annotated as point P. The instantaneous deputy position along the ellipse is annotated as point D, with coordinates (x, y). A circle of radius a r is circumscribed about the ellipse, and a dashed line, perpendicular to the major axis, is extended through point D, intersecting with the circumscribed circle at point Q. Relative eccentric anomaly, E r , measures the angle centered on (x r , y r ), between the periapsis point P and point Q. Relative eccentric anomaly increases from zero at periapsis with motion in the counter-clockwise direction.

The fifth ROE, A z , is defined as the amplitude of the sinusoidal motion in the cross-track direction. The cross-track component of the relative motion is a simple harmonic oscillator that is independent of the \(\hat {x} - \hat {y}\) motion under the Clohessy-Wiltshire assumptions. From Eq. 18, the amplitude of the cross-track motion is:

$$ A_{z} = \sqrt{z_{0}^{2} + \left(\frac{\dot{z}_{0}}{n}\right)^{2}} $$
(26)

The sixth ROE, ψ, is defined as the phase angle in the cross-track harmonic motion, representing the argument of the sine function in Eq. 18:

$$ \psi = \psi_{0} + n(t-t_{0}) $$
(27)

where

$$ \psi_{0} = \text{atan}2 \left(z_{0}, \frac{\dot{z}_{0}}{n}\right) $$
(28)

A geometric interpretation of A z and ψ is shown in Fig. 3, where the three-dimensional relative motion is projected onto the \(\hat {x} - \hat {z}\) plane. The deputy position along the relative motion ellipse is annotated as initial condition D 0 at time t 0 and as point D at time t. A circle of radius A z is drawn, with the center of the circle coincident with the center of the ellipse at point C. A dashed line, perpendicular to the \(\hat {z}\)-axis, is extended through point D 0, intersecting with the circumscribed circle at point F 0. Point G 0 is shown where a line parallel to the \(\hat {z}\)-axis through point F 0 intersects the \(\hat {x}\)-axis. The angle ψ then represents the angle, centered on point C with coordinates (x r , y r ,0), between the \(- \hat {x}\)-axis and the segment CF on the circle. The deputy’s relative motion intersects the chief’s orbit plane at ψ = 0 and ψ = π. These points are referred to as the relative ascending and descending nodes, respectively [28, 29]. The relative ascending node is the point where the deputy spacecraft passes through z = 0 with \(\dot {z} > 0\); the direction of the deputy’s motion is indicated by an arrow in Fig. 3. At t = t 0, the cross-track motion phase angle is ψ 0. As the deputy progresses in its relative motion about the chief, the cross-track motion phase angle changes according to Eq. 27 as point F progresses at a constant rate (equal to the chief’s mean motion) about the circle. At the point in the ellipse where \(z = A_{z}, \psi = \frac {\pi }{2}\). The relative descending node occurs at ψ = π, and z = −A z at \(\psi = - \frac {\pi }{2}\).

Fig. 3
figure 3

Cross-track motion phase angle geometry, projected onto the \(\hat {x} - \hat {z}\) plane

Full size image

Expressions for ROEs in terms of the time-varying Cartesian state elements may be found as follows. Equation 19 may be combined with Eqs. 7 and 11 to show that:

$$ x_{r} = 4x + \frac{2\dot{y}}{n} $$
(29)

(For Cartesian state elements without the subscript 0, time dependence is implied.) Likewise, Eq. 20 may be combined with Eqs. 8 and 10 to give:

$$ y_{r} = y - \frac{2\dot{x}}{n} $$
(30)

For unforced motion, the time derivative of x r may be taken using Eq. 29, and by substituting for the \(\ddot {y}\) acceleration term using Eq. 5, \(\dot {x}_{r}\), is shown to be equal to zero. Therefore, x r is invariant with time. However, taking the time derivative of y r in Eq. 30 and substituting for the \(\ddot {x}\) acceleration term using Eq. 4 shows that y r has a secular drift that varies linearly with time.

Equation 23 may be combined with Eqs. 7, 10, and 11 to show that:

$$ a_{r} = \sqrt{\left(6x + \frac{4\dot{y}}{n}\right)^{2} + \left(\frac{2\dot{x}}{n}\right)^{2}} $$
(31)

Taking the time derivative of a r as expressed in Eq. 31 and substituting for \(\ddot {x}\) using Eq. 4 and for \(\ddot {y}\) using Eq. 5, it is shown that \(\dot {a}_{r}\) is equal to zero. Therefore, a r is a constant for unforced motion. Equations 29 – 31 indicate that while the instantaneous center of the motion in the \(\hat {x} - \hat {y}\) plane may drift in the along-track direction, its radial component and size are invariant with time.

Equations 24 and 25 may be combined with Eqs. 7, 10, and 11 to show that:

$$ E_{r} = \text{atan}2\left(\frac{2\dot{x}}{n}, 6x + \frac{4\dot{y}}{n}\right) $$
(32)

From Eq. 24, it is seen that the time derivative of E r is equal to n.

Equation 26 may be combined with Eqs. 9 and 12 to show that:

$$ A_{z} = \sqrt{z^{2} + \left(\frac{\dot{z}}{n}\right)^{2}} $$
(33)

Taking the time derivative of A z as expressed in Eq. 33, and substituting for the \(\ddot {z}\) term using Eq. 6, it is shown that \(\dot {A}_{z}\) is equal to zero. Therefore, A z is a constant of the unforced motion.

Equations 27 and 28 may be combined with Eqs. 9 and 12 to show that:

$$ \psi = \text{atan}2 \left(z, \frac{\dot{z}}{n}\right) $$
(34)

From Eq. 27, it is seen that the time derivative of ψ is equal to n.

Table 1 summarizes the expressions for the six ROEs in terms of the LVLH Cartesian states, both at the initial time and at any instantaneous time.

Table 1 Expressions for ROEs in terms of LVLH Cartesian state elements
Full size table

Transformation from Relative Orbital Elements to LVLH Cartesian State

It is frequently desirable to be able to transform from ROEs to LVLH Cartesian states. These transformations are developed here. The position components of the LVLH Cartesian state can be found as follows: Eqs. 19, and 23–25 may be substituted into Eq. 16 to yield:

$$ x = x_{r} - \frac{1}{2} a_{r} \cos~E_{r} $$
(35)

Similarly, Eqs. 20 and 23–25 may be substituted into Eq. 17 to give:

$$ y = y_{r} + a_{r} \sin E_{r} $$
(36)

Equations 26–28 may be substituted into Eq. 18 to give:

$$ z = A_{z} \sin \psi $$
(37)

The velocity LVLH state components can be found as follows. Equation 30 may be substituted into Eq. 36 and rearranged to yield:

$$ \dot{x} = \frac{n}{2} a_{r} \sin E_{r} $$
(38)

Equation 29 can be substituted into Eq. 35 and rearranged to give:

$$ \dot{y} = - \frac{3}{2}nx + na_{r} \cos E_{r} $$
(39)

Equation 29 can be rewritten as:

$$ x = \frac{x_{r}}{4} - \frac{\dot{y}}{2n} $$
(40)

Substituting Eq. 40 into 39 and solving for \(\dot {y}\) gives:

$$ \dot{y} = - \frac{3}{2} nx_{r} + na_{r} \cos E_{r} $$
(41)

Rearranging Eq. 33 gives:

$$ \dot{z}^{2} = n^{2} \left(A_{z}^{2} - z^{2}\right) $$
(42)

Substituting Eq. 37 into 42 gives:

$$ \dot{z} = n^{2} A_{z}^{2} \cos^{2} \psi $$
(43)

Taking the square root of both sides of Eq. 43 gives:

$$ \dot{z} = \pm nA_{z} \cos \psi $$
(44)

Referencing Fig. 3, because \(\dot {z} > 0\) when ψ = 0, then

$$ \dot{z} = nA_{z} \cos \psi $$
(45)

A summary of the transformation from ROEs to LVLH Cartesian state elements is given in Table 2.

Table 2 Expressions for LVLH Cartesian state elements in terms of ROEs
Full size table

Evolution of Relative Orbital Elements with Time

Previously, expressions for the time variation of ROEs were developed in terms of LVLH Cartesian state elements. In this section, expressions for the time variation of each ROE are developed in terms of initial ROE values. The initial condition for each ROE at time t 0 is denoted with a subscript 0.

Equations 19 and 20 express the variation of the instantaneous center of motion with time, given initial conditions expressed in terms of the LVLH Cartesian state. From Eq. 19, it is clear that at t = t 0:

$$ x_{r_{0}} = 4x_{0} + \frac{2\dot{y}_{0}}{n} $$
(46)

As described in “Derivation of Relative Orbital Elements”, the radial coordinate of the instantaneous center of the motion is shown to be constant for unforced motion:

$$ x_{r} = x_{r{0}} $$
(47)

Evaluating (20) at t = t 0 yields:

$$ y_{r_{0}} = y_{0} - \frac{2\dot{x}_{0}}{n} $$
(48)

Multiplying (19) by a factor of \(\frac {3n}{2}\), and substituting with Eq. 48 into Eq. 20 gives:

$$ y_{r} = y_{r_{0}} - \left(\frac{3}{2}\right)nx_{r_{0}}\left(t-t_{0}\right) $$
(49)

As discussed in “Derivation of Relative Orbital Elements”, for unforced motion a r does not vary as a function of time:

$$ a_{r} = a_{r_{0}} $$
(50)

Relative eccentric anomaly varies with time as expressed in Eq. 24, and repeated here:

$$ E_{r} = E_{r_{0}} + n\left(t-t_{0}\right) $$
(51)

The amplitude of the cross-track motion, A z , is given by Eq. 26 as a function of the LVLH Cartesian state initial conditions. Once established by the initial conditions, A z does not vary with time, therefore:

$$ A_{z} = A_{z_{0}} $$
(52)

Finally, the phase angle in the cross-track harmonic motion is given by Eq. 27, repeated here:

$$ \psi = \psi_{0} + n\left(t-t_{0}\right) $$
(53)

In summary, for unforced motion the ROEs x r , a r and A z remain constant, y r varies linearly with time proportional to the secular drift rate, while the angular ROEs E r and ψ vary at a constant angular rate equal to the chief’s mean motion, n. A summary of the expressions for ROEs in terms of the ROE initial conditions is provided in Table 3.

Table 3 Expressions for ROEs in terms of ROE initial conditions
Full size table

Additional Parameters Related to Relative Orbital Elements

In addition to the ROEs summarized in Table 1, there are several related parameters that provide insight into the relative motion. The additional parameters described here include along-track secular drift and drift rate, relative true anomaly, phase angle difference, and relative inclination.

Along-Track Secular Drift and Drift rate

The linear time-varying along-track secular drift term in Eq. 17 indicates the direction and rate of the instantaneous center of motion in the \(\hat {x} - \hat {y}\) plane. The secular drift parameter y s is defined as:

$$ y_{s} = - \left(6nx_{0} + 3\dot{y}_{0}\right) \left(t -t_{0}\right) $$
(54)

In Eq. 54, y s equals the distance in the along-track direction that the instantaneous center of motion has moved during the time period t − t 0. At a given time, the secular drift rate can be written as:

$$ \dot{y}_{s} = \left(6nx_{0} + 3\dot{y}_{0}\right) $$
(55)

For unforced motion, the secular drift rate is a constant. By taking the time derivative of Eq. 20, it is clear that \(\dot {y}_{s}\) is equivalent to \(\dot {y}_{r}\). From Eqs. 19 and 55, it is apparent that:

$$ \dot{y}_{s} = \frac{3}{2}nx_{r} $$
(56)

Thus, the secular drift rate of the instantaneous ellipse in the \(\hat {x} - \hat {y}\) plane is negatively proportional to the radial coordinate of the instantaneous center of motion; if x r is greater than zero, the secular drift is in the negative along-track direction, and vice-versa. If x r equals zero, there is no drift. From Eqs. 20 and 55 it can be seen that:

$$ y_{r} = y_{r_{0}} + \dot{y}_{s} \left(t-t_{0}\right) $$
(57)

where

$$ y_{r_{0}} = y_{0} - \frac{2\dot{x}_{0}}{n} $$
(58)

An example is shown in Fig. 4. The initial coordinates of the instantaneous center of motion in the \(\hat {x} - \hat {y}\) plane at t − t 0 are \(\left (x_{r_{0}}, y_{r_{0}}\right )\). Three orbit periods later, the instantaneous center coordinates are (x r , y r ). In this case, \(x_{r_{0}} > 0\), so \(\dot {y}_{s}\) is negative, and the secular drift is from right to left, in the negative along-track direction. Secular drift rate may be used as an alternative to x r within the set of ROEs.

Fig. 4
figure 4

Secular along-track drift in the \(\hat {x} - \hat {y}\) plane

Full size image

Relative true Anomaly

An angle termed relative true anomaly may be defined that is analogous to the classical orbital element true anomaly, except that it is defined strictly in the \(\hat {x} - \hat {y}\) plane. As shown in Fig. 5, relative true anomaly, ν r , is the angle, centered on (x r , y r ), between the periapsis point P and point D, the instantaneous deputy position along the ellipse. Point Q on the circumscribed circle is always twice as far as point D from the semi-major axis of the instantaneous relative motion ellipse. This can be shown as follows. From the standard equation of an ellipse, the instantaneous relative motion ellipse equation is:

$$ \frac{\left(y-y_{r}\right)^{2}}{a_{r}^{2}} + \frac{\left(x-x_{r}\right)^{2}}{\left(\frac{a_{r}}{2}\right)^{2}}=1 $$
(59)

Solving (38) for x − x r gives:

$$ x-x_{r} = \frac{1}{2}\sqrt{a_{r}^{2} - \left(y-y_{r}\right)^{2}} $$
(60)

From the standard equation for a circle, the equation for the circumscribed circle can be written as:

$$ \frac{\left(y_{q} - y_{r}\right)^{2}}{a_{r}^{2}} + \frac{\left(x_{q} - x_{r}\right)^{2}}{a_{r}^{2}}=1 $$
(61)

Solving (61) for x q −x r , and noting that y q = y, gives:

$$ x_{q} - x_{r} = \sqrt{a_{r}^{2} - \left(y - y_{r}\right)^{2}} $$
(62)

From Eqs. 60 and 62, the desired result is obtained:

$$ x - x_{r} = \frac{1}{2}\left(x_{q} - x_{r}\right) $$
(63)

From Fig. 5 it is clear that:

$$ \tan E_{r} = \frac{y-y_{r}}{2\left(x_{r} - x\right)} $$
(64)

Substituting for x r and y r in Eq. 64 using Eqs. 29 and 30 and simplifying gives:

$$ \tan E_{r} = \frac{\dot{x}}{3nx + 2\dot{y}} $$
(65)

From Fig. 5, it is apparent that:

$$ \tan \upsilon_{r} = \frac{y-y_{r}}{x_{r}-x} $$
(66)

Substituting for x r and y r in Eq. 66 using Eqs. 29 and 30 and simplifying, yields:

$$ \tan\upsilon_{r} = \frac{2\dot{x}}{3nx + 2\dot{y}} $$
(67)

Therefore, relative true anomaly can be expressed as:

$$ \upsilon_{r} = \tan^{-1}\left(\frac{2\dot{x}}{3nx + 2\dot{y}}\right) $$
(68)

Comparing Eq. 68 with Eq. 65, the relationship between relative eccentric anomaly and relative true anomaly is then:

$$ \upsilon_{r} = \tan^{-1}\left(2\tan E_{r}\right) $$
(69)

Relative true anomaly may be used as an alternative to relative eccentric anomaly within the set of ROEs.

Fig. 5
figure 5

Geometry of relative eccentric anomaly and relative true anomaly

Full size image

Phase Angle Difference

The phase angle difference between the relative eccentric anomaly, E r , and the cross-track motion phase angle, ψ, can be expressed as:

$$ \gamma = \psi - E_{r} $$
(70)

The cross-track motion phase angle and relative eccentric anomaly both change at a rate that is equal to the chief’s mean motion, as seen in Eqs. 24 and 27. Therefore, the phase difference γ is a constant, equal to the difference between the two angles at any chosen instant in time. Equation 70 may be used to replace ψ with γ + E r . The advantage of this approach is that four of the six ROEs are then constant, with y r and E r being the only time-varying ROEs. (Note that one could alternatively replace E r with ψ − γ and also achieve four constant ROEs.) The phase difference may be written in terms of LVLH Cartesian state elements as:

$$ \gamma = \text{atan}2\left(z, \frac{\dot{z}}{n}\right) - \text{atan}2 \left(\frac{2\dot{x}}{n}, 6x + \frac{4\dot{y}}{n}\right) $$
(71)

Relative Inclination

An important parameter related to the three-dimensional relative motion is the relative inclination, the angle between the relative orbit plane and the chief’s orbit plane (i.e., the \(\hat {x} - \hat {y}\) plane). As shown in Fig. 6, the normal vector to the instantaneous relative orbit plane, \(\bar {n}_{r}\), is found by taking the cross-product of two position vectors on the relative orbit, corresponding to E r = 0 and \(E_{r} = \frac {\pi }{2}\). In Fig. 6, the LVLH \(\hat {z} - \hat {y} - \hat {z}\) coordinate system is translated to parallel axes \(\hat {z}^{\prime } - \hat {y}^{\prime } - \hat {z}^{\prime }\) with the origin at (x r , y r ,0). The relative inclination is the angle between the relative orbit normal, \(\hat {n}_{r}\) and the \(\hat {z}^{\prime }\) axis.

Fig. 6
figure 6

Geometry of relative inclination

Full size image

The position of the instantaneous center (IC) of the relative motion with respect to the origin of the LVLH coordinate system is given by the vector:

$$ \bar{\rho}^{IC} = \left[x_{r}, y_{r}, 0\right]^{T} $$
(72)

The vector from the origin of the LVLH coordinate system to the relative orbit position corresponding to E r = 0 (periapsis) is given by Eqs. 35 – 37 as:

$$\begin{array}{@{}rcl@{}} \bar{\rho}_{1} = \left[ \begin{array}{cc} x_{r}- \frac{1}{2} a_{r}\\ y_{r}\\ A_{z} \sin \gamma \end{array}\right] \end{array} $$
(73)

where, from Eq. 70, γ is equal to ψ for E r = 0. The position vector from the instantaneous center to the location on the relative orbit corresponding to E r = 0 is given by:

$$ \bar{r}_{1} = \bar{\rho}_{1} - \bar{\rho}^{IC} $$
(74)

From Eqs. 72 – 74, \(\bar {r}_{1}\) can be evaluated as:

$$ \bar{r}_{1} = \left[ \begin{array}{cc} - \frac{1}{2}a_{r}\\ 0\\ A_{z} \sin \gamma \end{array}\right] $$
(75)

The vector from the origin of the LVLH coordinate system to the relative orbit position corresponding to \(E_{r} = \frac {\pi }{2}\) is:

$$ \bar{\rho}_{2} = \left[ \begin{array}{cc} x_{r}\\ y_{r} + a_{r}\\ A_{z} \cos \gamma \end{array}\right] $$
(76)

Note that for \(E_{r} = \frac {\pi }{2}, \gamma = \psi - \frac {\pi }{2}\). From Eq. 37, the \(\hat {z}\)-component of the position vector is equal to A z sinψ, which equates to \(A_{z} \sin \left (\gamma + \frac {\pi }{2}\right )\) for \(E_{r} = \frac {\pi }{2}\). This is simplified to A z cosγ in Eq. 76. The position vector from the instantaneous center to the deputy at \(E_{r} = \frac {\pi }{2}\) is given by:

$$ \bar{r}_{2} = \bar{\rho}_{2} - \bar{\rho}^{IC} $$
(77)

From Eqs 72, 76 and 77, \(\bar {r}_{2}\) can be evaluated as:

$$ \bar{r}_{2} = \left[ \begin{array}{cc} 0\\ a_{r}\\ A_{z} \cos \gamma \end{array}\right] $$
(78)

Using the two position vectors on the instantaneous relative orbit, the cross-product can be taken to find the relative orbit normal, \(\bar {n}_{r}\):

$$ \bar{n}_{r} = \bar{r}_{1} \times \bar{r}_{2} $$
(79)

Using Eqs. 75 and 78, the relative orbit normal vector can be evaluated as:

$$ \bar{n}_{r} = \left[ \begin{array}{cc} -a_{r} A_{z} \sin \gamma\\ \frac{1}{2}a_{r}A_{z} \cos \gamma\\ -\frac{1}{2} a_{r}^{2} \end{array}\right] $$
(80)

The unit vector in the direction of the relative orbit normal is given by:

$$ \hat{n}_{r} = \frac{\bar{n}_{r}}{\left|\bar{n}_{r}\right|} $$
(81)

The relative inclination, i r , is the angle between the instantaneous relative orbit plane and the chief orbit plane. The angle between the relative orbit normal and the chief’s orbit normal, \(\hat {z}\), can be found through the dot product of the two normal unit vectors:

$$ \hat{n}_{r} \cdot \hat{z} = \cos~i_{r} $$
(82)

The relative inclination is given by:

$$ i_{r} = \cos^{-1} \left(\hat{n}_{r} \cdot \hat{z}\right) $$
(83)

Substituting Eqs. 80 and 81 into 83 and simplifying yields:

$$ i_{r} =\cos^{-1}\left( {\frac{-a_{r} }{\sqrt {3A_{z}^{2}\sin^{2}\gamma +A_{z}^{2}\cos^{2}\gamma +a_{r}^{2}}}} \right) $$
(84)

From Eq. 84, it is seen that relative inclination is a function of the semi-major axis of the instantaneous relative ellipse in the \(\hat {x} - \hat {y}\) plane, a r , the amplitude of the cross-track motion, A z , and the phase difference, γ. For unforced motion, each of these parameters is constant, so relative inclination is a constant as well. If the relative ellipse has a secular along-track drift rate due to a non-zero value for x r , the instantaneous relative ellipse lies in a plane that is translating in the along-track direction, with a constant relative inclination angle. Note that for relative motion constrained to the direction, resulting in a relative inclination of 180 deg. Because i r is a function of a r , A z , and γ, it may be used to replace any of these three quantities within the set of ROEs.

To express relative inclination in terms of LVLH Cartesian state elements, Eqs. 31, 33 and 71 are substituted into Eq. 84 to give:

$$ i_{r} =\cos^{-1}\left\{ \frac{-\sqrt {\left( {6x+\frac{4\dot{y}}{n}} \right)^{2}+\left( \frac{2\dot{{x}}}{n} \right)^{2}} }{\sqrt {3\left[ {z^{2}+\left( \frac{\dot{{z}}}{n} \right)^{2}} \right]\sin^{2}\left[ {\text{atan}2\left( z,\frac{\dot{{z}}}{n} \right)-\text{atan}2\left( \frac{2\dot{{x}}}{n},6x+\frac{4\dot{{y}}}{n} \right)} \right]+z^{2}+\left( \frac{\dot{{z}}}{n} \right)^{2}+\left( 6x+\frac{4\dot{y}}{n} \right)^{2}+\left( \frac{2\dot{x}}{n} \right)^{2}} } \right\} $$
(85)

A summary of the useful parameters that are related to ROEs is provided in Table 4.

Table 4 Expressions for useful parameters related to ROEs
Full size table

Characteristics of the Unforced Motion

Utilizing the ROEs defined in “Definition of Relative Orbital Elements”, the unforced “free drift” deputy spacecraft trajectory relative to the chief can be easily characterized. Similar to classical orbital elements, ROEs provide a physical understanding of the relative motion that is not obvious from the relative Cartesian state.

The relative motion is characterized in terms of three primary modes of the motion, based upon the values of the ROEs x d , a r , and A z . As seen in Table 5, the first mode of the relative motion is dependent upon the value for x r . If x r = 0 (Mode 1A), then there is no secular drift of the relative motion in the along-track direction. If x r ≠ 0 (Mode 1B), then the instantaneous relative ellipse in the \(\hat {x} - \hat {y}\) plane will have a secular drift with a rate that is dependent upon the value for x r : a negative value for x r results in a positive secular drift rate in the along-track direction, and a positive value for x r results in a negative rate for secular along-track drift. Note that this behavior makes physical sense when one considers that x r = 0 implies that the chief and deputy possess the same orbit period, x r > 0 implies that the deputy is on a larger inertial orbit (longer period) than the chief, and x r < 0 implies that the deputy is on a smaller orbit (shorter period) than the chief.

Table 5 Modes of unforced relative motion
Full size table

The second mode of the relative motion depends upon the value for a r . If a r = 0 (Mode 2A), then there is no instantaneous relative ellipse in the \(\hat {x} - \hat {y}\) plane. Stated differently, the instantaneous relative ellipse devolves to a point. If a r > 0 (Mode 2B), then the instantaneous relative ellipse in the \(\hat {x} - \hat {y}\) plane has the typical 2:1 ratio of semi-major axis in the along-track direction to semi-minor axis in the radial direction. This behavior makes physical sense when one considers that a r = 0 implies that the chief and deputy are both on circular orbits, whereas a r > 0 implies that the deputy is on an elliptical inertial orbit.

The third mode of the relative motion is dependent upon the value for A z . If A z = 0 (Mode 3A), then there is no cross-track motion. If A z > 0 (Mode 3B), then there is simple harmonic oscillatory motion in the cross-track direction. It is noted that the initial value for y r does not define a primary mode for the relative motion; y r simply gives the initial along-track coordinate of the instantaneous relative ellipse in the \(\hat {x} - \hat {y}\) plane. The angular ROEs E r and ψ are used to define the location of the deputy on the relative orbit in-plane and out-of-plane of the chief’s orbit, respectively. The phasing between these angles impacts the three-dimensional shape of the relative orbit, and determines the locations of the relative ascending and descending nodes where the deputy’s inertial trajectory intersects the chief’s orbit plane.

Each of the three primary modes of relative motion can be superposed to capture the full motion of the deputy spacecraft relative to the chief. For Mode 1A, there is no secular drift in the along-track direction, so the motion in the \(\hat {x} - \hat {y}\) plane is either a stationary point with x = 0 (Mode 1A, 2A), or a stationary ellipse (Mode 1A, 2B) with the characteristic 2:1 ratio of the major-axis to minor-axis length in the \(\hat {x} - \hat {y}\) plane.

For Mode 1B, where there is a secular drift of the instantaneous ellipse in the along-track direction, the \(\hat {x} - \hat {y}\) projection of the deputy’s motion will take on one of four different shapes. Figure 7 shows an example of each of these relative motion shapes, for a case where the chief’s circular orbit altitude is 500 km, the initial along-track coordinate for the deputy is 100 m, and x r for the deputy is 5 m, resulting in a negative secular drift rate in the along-track direction. One orbit period is shown. The shape of the relative drifting motion in the \(\hat {x} - \hat {y}\) plane is determined by the value of a r relative to x r . For a r = 0 (Mode 1B, 2A), the deputy is on a circular orbit, and the motion with respect to the chief is a straight line in the LVLH frame, with a fixed radial component. For a r > 0 (Mode 1B, 2B), the relative motion may be a quasi-sinusoidal curve, a cycloid-like curve that cusps at the extrema, or a cycloid-like curve that curls at the extrema. For all three of the cases in Mode 1B, 2B, the minimum radial coordinate occurs at perigee in the deputy’s orbit, and the maximum radial coordinate occurs at apogee. The quasi-sinusoidal curve is produced when the along-track component of the LVLH Cartesian state increases or decreases monotonically.

Fig. 7
figure 7

Four types of relative drifting motion in the \(\hat {x} - \hat {y}\) plane. Mode 1B, 2A: solid line, a r = 0. Mode 1B, 2B: dashed quasi-sinusoidal curve, \(a_{r} < \frac {3}{2} \left |x_{r}\right |\); bolded cycloid-like curve with cusp, \(a_{r} = \frac {3}{2}\left |x_{r}\right |\); bold-dashed cycloid-like curve with curl, \(a_{r} > \frac {3}{2} \left |x_{r}\right |\). In all cases, motion is from right to left

Full size image

Substituting Eq. 35 into Eq. 39, and using Eq. 56 it is found that:

$$ \dot{y} = \dot{y}_{s} + na_{r} \cos E_{r} $$
(86)

For the case where the along-track component is monotonically decreasing (as shown by the dashed curve in Fig. 7),

$$ \dot{y}_{s} + na_{r} < 0 $$
(87)

Substituting for \(\dot {y}_{s}\) with Eq. 56 gives:

$$ a_{r} < \frac{3}{2} x_{r} $$
(88)

Written generally, to account for both the monotonically increasing and decreasing cases, the condition for a quasi-sinusoidal curve can be written as:

$$ a_{r}\frac{3}{2}\left|x_{r}\right| $$
(89)

For a cycloid-like curve that cusps, \(\dot {y} = 0\) at either periapsis or apoapsis in the deputy’s orbit (i.e., at E r or E r = π). From Eq. 86, it is found that the condition reduces to:

$$ a_{r} = \frac{3}{2}\left|x_{r}\right| $$
(90)

It is noted that for the case where the secular drift rate in the along-track direction is negative, cusps occur at perigee (as shown by the bolded curve in Fig. 8), while for a positive secular drift rate cusps occur at apogee. Finally, cycloid-like curves that curl occur for all other values of a r , when:

$$ a_{r} = \frac{3}{2}\left|x_{r}\right| $$
(91)
Fig. 8
figure 8

Mode 1A, 2B, 3B motion with varying phase difference, γ. Bold solid line: γ = 0; dashed line: \(\gamma = \pi \diagup 2\); solid line: γ = π; dotted line: \(\gamma = 3\pi \diagup 2\). a \(\hat {y} - \hat {x}\) projection, b \(\hat {z} - \hat {x}\) projection, c \(\hat {y} - \hat {z}\) projection, d 3D plot

Full size image

For Mode 3A, there is no cross-track motion and z = 0. For the combination of Modes 1A, 2A, 3B, the motion is a simple oscillation in the cross-track direction, and there is no motion in the \(\hat {x} - \hat {y}\) plane.

For Mode 1A, 2B, 3B, the relative orbit is stationary and in a fixed plane. The angular difference between the relative eccentric anomaly and cross-track phase angle (equal to the parameter γ defined in “Derivation of Relative Orbital Elements”) determines the shape and orientation of the projection of the motion in the \(\hat {z} - \hat {x}\) and \(\hat {z} - \hat {y}\) planes, as shown in Fig. 8. The motion in the \(\hat {x} - \hat {z}\) plane is an ellipse centered on x = 0, z = 0. The motion in the \(\hat {y} - \hat {z}\) plane is an ellipse centered on y = y r , z = 0. Figure 8 shows an example where x r = 0, y r = 100 m, a r = 20 m, and A z = 10 m. Relative orbits associated with four different values for γ are shown: 0, π/2, π, and 3π/2. While the motion in the \(\hat {x} - \hat {y}\) plane is unchanged for each case, the shape and orientation of the ellipses in the \(\hat {x} - \hat {z}\) and \(\hat {y} - \hat {z}\) planes are determined by the value of γ. Note that for \(\gamma = \pi \diagup 2\) and \(\gamma = 3\pi\diagup 2\), the projection of the motion onto the \(\hat {x} - \hat {z}\) and \(\hat {y} - \hat {z}\) planes are straight lines.

For Mode 1B, 2B, 3B, a secular along-track drift is superimposed upon the three-dimensional relative motion. Figure 9 shows an example where x r = 1 m, y r = 100 m, a r = 20 m, A z = 10 m, and γ = 0. The “corkscrew” motion apparent in the three-dimensional plot, Fig. 9d, results from the translation of the instantaneous plane of the motion in the along-track direction.

Fig. 9
figure 9

Mode 1B, 2B, 3B motion. a \(\hat {y} - \hat {x}\) projection, b \(\hat {z} - \hat {x}\) projection, c \(\hat {y} - \hat {z}\) projection, d 3D plot

Full size image

Conclusions

Relative orbital elements provide a useful formulation for characterizing the geometry of relative motion between a chief and deputy space object, leading to an intuitive understanding of the unforced relative motion within the context of the Clohessy-Wiltshire assumptions. Through this work, ROEs have been derived, and the geometric interpretation of each element has been established. It is noted that there is a strong analogy between classical orbital elements, which provide the orbital geometry of a spacecraft about a central body in an inertial reference frame under the two-body assumption, and ROEs which provide the geometry of a relative orbit in the LVLH reference frame under the Clohessy-Wiltshire assumptions.

A direct transformation between ROEs and the relative Cartesian state has been developed. Expressions for the time-variation of ROEs, in terms of both relative Cartesian state parameters and initial ROEs, have been derived. Additional useful parameters related to ROEs have been defined.

Utilizing the ROE parameters, categories of relative motion can be visualized based upon three modes, depending upon values for three particular ROEs: the radial coordinate of the instantaneous center of motion, semi-major axis of the instantaneous relative ellipse, and amplitude of the cross-track motion. By superposing the modes, the behavior of the free-drift trajectory can be determined.