The equations of relative motion in the orbital reference frame

Abstract

The analysis of relative motion of two spacecraft in Earth-bound orbits is usually carried out on the basis of simplifying assumptions. In particular, the reference spacecraft is assumed to follow a circular orbit, in which case the equations of relative motion are governed by the well-known Hill–Clohessy–Wiltshire equations. Circular motion is not, however, a solution when the Earth’s flattening is accounted for, except for equatorial orbits, where in any case the acceleration term is not Newtonian. Several attempts have been made to account for the $J_2$ effects, either by ingeniously taking advantage of their differential effects, or by cleverly introducing ad-hoc terms in the equations of motion on the basis of geometrical analysis of the $J_2$ perturbing effects. Analysis of relative motion about an unperturbed elliptical orbit is the next step in complexity. Relative motion about a $J_2$-perturbed elliptic reference trajectory is clearly a challenging problem, which has received little attention. All these problems are based on either the Hill–Clohessy–Wiltshire equations for circular reference motion, or the de Vries/Tschauner–Hempel equations for elliptical reference motion, which are both approximate versions of the exact equations of relative motion. The main difference between the exact and approximate forms of these equations consists in the expression for the angular velocity and the angular acceleration of the rotating reference frame with respect to an inertial reference frame. The rotating reference frame is invariably taken as the local orbital frame, i.e., the RTN frame generated by the radial, the transverse, and the normal directions along the primary spacecraft orbit. Some authors have tried to account for the non-constant nature of the angular velocity vector, but have limited their correction to a mean motion value consistent with the $J_2$ perturbation terms. However, the angular velocity vector is also affected in direction, which causes precession of the node and the argument of perigee, i.e., of the entire orbital plane. Here we provide a derivation of the exact equations of relative motion by expressing the angular velocity of the RTN frame in terms of the state vector of the reference spacecraft. As such, these equations are completely general, in the sense that the orbit of the reference spacecraft need only be known through its ephemeris, and therefore subject to any force field whatever. It is also shown that these equations reduce to either the Hill–Clohessy–Wiltshire, or the Tschauner–Hempel equations, depending on the level of approximation. The explicit form of the equations of relative motion with respect to a $J_2$-perturbed reference orbit is also introduced.

1 Introduction

The integration of the equations of motion of a space vehicle is usually carried out in an inertial reference system. In rare cases the integration is performed in a reference system which is rigidly connected with the body of the Earth, and thus rotating with it. This is mainly used to simplify the computation of the extended-body gravitational acceleration and its gradient, which appears in the variational equations for estimation problems. There is a case, however, in which the equations of motion are generally integrated in a non-inertial reference system, and this is the case of the relative motion of two or more space vehicles for rendezvous or formation flying purposes. The problem of relative motion is now perceived to have originated in the 1950s with the pioneering contributions of Lawden (1954), Clohessy and Wiltshire (1960), de Vries (1963) and Tschauner and Hempel (1964). In Celestial Mechanics, however, the equations of relative motion have been used since perturbation theory was introduced, which takes us back to the time of Euler. More specifically, the perturbation equations always imply that the motion, or trajectory, of a body is known to some degree of accuracy through what is known as a reference orbit, with respect to which we introduce a machinery to compute perturbations—which, in fact, describe a relative orbit. The difference with the current attitude of investigators seems to lie in the fact that whereas perturbation theory adopts a non-realistic reference orbit, present-day problems deal with the actual physical separation between two space vehicles.

Investigations of relative motion currently rely on two main paradigms. The simpler one is referred to as the HCW, or Hill–Clohessy–Wiltshire equations (Hill 1878; Clohessy and Wiltshire 1960), which assumes a circular reference orbit. The more complicated one is the de Vries (de Vries 1963), and the Tschauner–Hempler (Tschauner and Hempel 1964) equations, which are formulated with respect to a Keplerian elliptical orbit. Both paradigms admit of an analytical solution (Prussing and Conway 2012; Yamanaka and Ankersen 2002), which is the ultimate reason for their popularity. In fact, they are the basis for many extensions to include the effects of perturbations, most notably those associated with the oblateness of the Earth—whose precessional effects induce relative secular drifts of the mean angular elements of a satellite pair with consequent formation disruption—and the presence of atmospheric drag (e.g., Sengupta et al. 2007; Jiang et al. 2007; Wnuk and Golebiewska 2005).

By construction, these paradigms are approximations to the equations that describe the true relative motion. They are approximations because they are formulated in rotating reference systems and are not the exact transformation of the quite simple form that the equations of relative motion assume in an inertial reference system. As a matter of fact, the non-inertial form of the equations of relative motion is very well known, but only in a form which is not directly usable for integration unless the angular velocity and the angular acceleration of the non-inertial reference frame are given in terms of (functions of) the dynamical state of the (possibly virtual) body at the origin of this frame. Some approximations are known and used in the literature, but they generally refer to the circular or elliptical motion paradigms, with a few extensions to include the precessional effects of the Earth’s oblateness.

We draw special attention to the formulation of the equations of relative motion introduced by Kechichian (1998). This is the most thorough treatment currently available. It provides the full equations of motion in the orbital reference frame (RF) in what may be defined as a mixed-variable formulation, which is the prototype of many subsequent, approximate formulations (e.g., Xu and Wang 2008; Chen and Jing 2012; Ross 2003). What we mean by mixed-variable, or hybrid, formulation is that the equations are given for the dynamical state expressed in Cartesian coordinates, but with all ancillary variables appearing in the coefficients expressed as Keplerian elements of the reference orbit.

It is the purpose of this contribution to formulate the exact equations of relative motion in general terms, i.e., under no restriction as to the character of the motion of the reference body, nor the type of force field in which the pair of bodies revolve. The equations will consistently be developed using only Cartesian coordinates. In the following Sections the inertial equations of relative motion will be introduced, the orbital frame associated with the reference body will be defined and its angular motion expressed in terms of its dynamical state. The general equations of relative motion in the orbital frame will then be developed and their reduction to the simple paradigms introduced above will be derived to show that the resulting equations are identical with those already known. Finally, the full and the linearized equations will be developed for the relative motion of a $J_2$-perturbed orbit pair.

2 The equations in the inertial frame

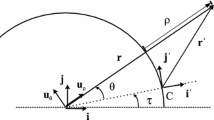
Consider the Earth and two objects S (the primary) and $S_{1}$ (the secondary) in orbit around it. We adopt an inertial, geocentric reference frame $\left\{ \mathbf {i},\mathbf {j},\mathbf {k} \right\} ,$ where the unit vectors $\mathbf {i},\ \mathbf {j},\ \mathbf {k}$ form a right-handed triad. Under the assumption that the mass of each object is so small as to make their mutual gravitational interaction negligible, the equations of motion of each body in the framework of Newtonian mechanics is

$$\begin{aligned} {\ddot{\mathbf{r}}}=\mathbf{N}( \mathbf {r};\mu ) +\mathbf {P}( \mathbf {r},{\dot{\mathbf{r}}},t;\varvec{\sigma }), \end{aligned}$$

(1)

which shows that the acceleration is the sum of a Newtonian term $\mathbf {N} ( \mathbf {r};\mu )$ and a perturbation term $\mathbf {P}( \mathbf {r},{\dot{\mathbf{r}}},t;\varvec{\sigma })$ depending on the position $\mathbf {r},$ the velocity ${\dot{\mathbf{r}}},$ and possibly the time t. The Newtonian term is simply the point-mass acceleration, or

$$\begin{aligned} \mathbf {N}=-\mu \frac{\mathbf {r}}{r^{3}}, \end{aligned}$$

(2)

where $\mu =G( M+m)$ is the two-body gravitational parameter with M the mass of the Earth and m the mass of the object. The perturbation $\mathbf {P}( \mathbf {r},{\dot{\mathbf{r}}},t;\varvec{ \sigma })$ contains acceleration terms associated with non-central gravitational effects, including the tides, due to the mass distribution of the real Earth, the presence of external bodies such as the Sun, the Moon, and the planets, as well as any non-conservative accelerations due to surface interactions such as atmospheric drag, solar radiation pressure, etc. The set of model parameters describing these interaction terms has been explicitly represented with the vector $\varvec{\sigma }$.

In practical applications the perturbation term of greatest interest is that due to the oblateness of the Earth as described by the second zonal harmonic coefficient $J_{2}$. The acceleration due to $J_{2}$ is (Kaplan 1976)

$$\begin{aligned} \mathbf {P}_{J_{2}}=-\frac{3}{2}\frac{\mu }{a_{e}^{2}}J_{2}\left( \frac{a_{e} }{r}\right) ^{4}\left\{ 2( {\hat{\mathbf{r}}}\cdot \mathbf {k}) \mathbf {k}+\left[ 1-5( {\hat{\mathbf{r}}}\cdot \mathbf {k}) ^{2} \right] {\hat{\mathbf{r}}}\right\} , \end{aligned}$$

(3)

where $a_{e}$ is a scale parameter associated with the specific value of $J_{2},$ usually taken as an average equatorial radius of the Earth, $\mathbf { k}$ is the unit vector along the symmetry axis of the Earth, which coincides with the third axis of the inertial reference frame adopted, and ${\hat{\mathbf{r}}}$ is the unit vector in the radial direction out of the origin to the field point occupied by the body. In the case of atmospheric drag the perturbation is

$$\begin{aligned} \mathbf {P}_{D}=-\frac{1}{2}\delta ( \mathbf {r}) C_{D}( {\dot{\mathbf{r}}}-{\varvec{\upomega } }_{e}\times \mathbf {r}) ^{2}, \end{aligned}$$

(4)

where $\delta ( \mathbf {r})$ is the local atmospheric density, $C_{D}$ the drag coefficient, ${\varvec{\upomega } }_{e}$ the angular velocity of the Earth (no-wind assumption) so that the expression in parenthesis is the velocity of the spacecraft with respect to the atmosphere.

The equations of relative motion in the inertial frame are simply obtained by differencing the equations of motion of the two bodies. If we define the separation vector $\varDelta \mathbf {r}$ as the difference $\mathbf {r}_{1}- \mathbf {r}$ between the position vectors $\mathbf {r}$ and $\mathbf {r}_{1}$ of S and $S_1$, respectively, then

where

$$\begin{aligned} \varDelta \mathbf {N}( \mathbf {r},\mathbf {r}_{1};\mu ) =\mathbf {N} ( \mathbf {r}_{1};\mu ) -\mathbf {N}( \mathbf {r};\mu ), \end{aligned}$$

(6)

and

$$\begin{aligned} \varDelta \mathbf {P}( \mathbf {r},\mathbf {r}_{1},{\dot{\mathbf{r}}},{\dot{\mathbf{r}}}_{1},t;\varvec{\sigma }) =\mathbf {P}( \mathbf {r}_{1}, {\dot{\mathbf{r}}}_{1},t;\varvec{\sigma }) -\mathbf {P}( \mathbf { r},{\dot{\mathbf{r}}},t;\varvec{\sigma }). \end{aligned}$$

(7)

For high accuracy computations the Encke formulation can be used, which entails expressing the differential Newtonian acceleration in the form (Battin 1999)

$$\begin{aligned} \varDelta \mathbf {N}=-\frac{\mu }{r^{3}}\left\{ f( q) \mathbf {r}+ \left[ \,1+f( q) \right] \varDelta \mathbf {r}\right\} , \end{aligned}$$

(8)

where

$$\begin{aligned} q= & {} -\frac{\left( 2\mathbf {r}+\varDelta \mathbf {r}\right) \cdot \varDelta \mathbf { r}}{\left( \mathbf {r}+\varDelta \mathbf {r}\right) \cdot ( \mathbf {r} +\varDelta \mathbf {r}) }, \end{aligned}$$

(9)

$$\begin{aligned} f( q)= & {} q\frac{3( 1+q) +q^{2}}{1+( 1+q) ^{3{/}2}}. \end{aligned}$$

(10)

3 The equations in the RTN frame

Assume now that the orbit of the primary is known, i.e., that its state vector and associated functionals (e.g., its acceleration) are known, or can be computed. Introduce the orbital reference frame $\{ {\hat{\mathbf{r}}},{\hat{\mathbf{t}}},{\hat{\mathbf{n}}}\}$ defined by the three unit vectors respectively in the radial, the transverse and the normal directions. These are easily computed from available information as¹

$$\begin{aligned} {\hat{\mathbf{r}}}= & {} \mathbf {r}{/}r, \end{aligned}$$

(11)

$$\begin{aligned} {\hat{\mathbf{t}}}= & {} {\hat{\mathbf{n}}\times \hat{\mathbf{r}},} \end{aligned}$$

(12)

$$\begin{aligned} {\hat{\mathbf{n}}}= & {} \mathbf {r}\times \dot{\mathbf {r}}{/}\left| {\mathbf{r}}\times \dot{\mathbf{r}}\right| . \end{aligned}$$

(13)

Note that the normal direction is parallel to the angular momentum vector—thus normal to the instantaneous orbital plane,—and that the transverse direction is perpendicular to both the normal and radial directions, thus completing a right-handed triad.

The orbital RF, also known as the RTN, or Hill reference frame, is naturally associated with the orbit of a point particle, as we are assuming our orbiting bodies to be. The RTN frame must not be confused with the Frenet–Serret frame associated with a space curve, or trajectory. The fundamental difference between the two frames is that while the Frenet–Serret frame is defined by intrinsic geometric properties of the curve, like its osculating plane, its center of curvature, etc., the RTN frame has its radial axis forced to be constantly directed to the origin of the inertial RF where the trajectory of the primary is described. In general, the inertial RF is centered at the approximate center of force, which normally is at the center of mass of the Earth. The RTN RF is a non-inertial RF and is ideally suited to model local relative dynamics.

In order to write the equations of motion of body $S_{1}$ in the RTN frame of the primary it is necessary to have an expression for its inertial acceleration ${\ddot{\mathbf{r}}}_{1}$ as determined by an observer fixed in, or comoving with, the RTN axes associated with body S. Let us introduce new notation to indicate the relative position vector between S and $S_{1}$ by defining ${ \varvec{\uprho } }=\varDelta \mathbf { r}$. It is well known that in a non-inertial reference frame the inertial acceleration of $S_{1}$ can be expressed as the sum of its acceleration ${\ddot{\varvec{\uprho }}}$ as measured in the non-inertial frame, the (translational) acceleration ${\ddot{\mathbf{r}}}$ of the origin S of the frame, plus three terms associated with the rotation of the non-inertial axes. This leads to the expression²

$$\begin{aligned} {\ddot{\mathbf{r}}}_{1}={\ddot{\mathbf{r}}}+{\ddot{\varvec{\uprho }}}+2{\varvec{\upomega } }\times {\dot{\varvec{\uprho }}}+{\dot{\varvec{\upomega }}\times \varvec{\uprho } }+{\varvec{\upomega } }\times ( {\varvec{\upomega } }\times {\varvec{\uprho } }), \end{aligned}$$

(14)

where the third term $2{\varvec{\upomega } }\times {\dot{\varvec{\uprho }}}$ on the r.h.s. is known as the Coriolis acceleration, the fourth term $\dot{\varvec{\upomega }}\times \varvec{\uprho }$ is the Eulerian acceleration and the final term ${\varvec{\upomega } }\times ( {\varvec{\upomega } }\times {\varvec{\uprho } })$ is the centripetal acceleration. Here the axial vector ${\varvec{\upomega } }$ is the angular velocity of the RTN frame with respect to the inertial frame and ${\dot{\varvec{\upomega }}}$ the corresponding angular acceleration.

Recall that a similar relationship exists between velocities. In fact, the inertial velocity ${\dot{\mathbf{r}}}_{1}$ of $S_{1}$ is the sum of the velocity ${\dot{\varvec{\uprho }}}$ of $S_{1}$ as measured by S plus the velocity ${\dot{\mathbf{r}}}$ of the origin, or of S itself, and the velocity ${\varvec{\upomega } }\times {\varvec{\uprho } }$ due to the rotation of the non-inertial axes, so that

$$\begin{aligned} {\dot{\mathbf{r}}}_{1}={\dot{\mathbf{r}}}+{\dot{\varvec{\uprho }}}+{\varvec{\upomega } } \times {\varvec{\uprho }}. \end{aligned}$$

(15)

The equations of motion of $S_{1}$ can then be written in the RTN reference frame with origin at S by replacing the relative inertial acceleration ${\ddot{\mathbf{r}}} _{1}-{\ddot{\mathbf{r}}}$ as provided by (14) into Eq. (5) to yield

where the forcing terms $\varDelta \mathbf {N}$ and $\varDelta \mathbf {P}$ are given respectively by Eqs. (6) and (7). In order to integrate these equations it is necessary to express the angular velocity and the angular acceleration in terms of the state variables.

3.1 The angular velocity

The angular velocity of the moving axes defining the RTN reference frame can be obtained from simple kinematical considerations. First compute the time rate of change of each of the unit vectors defining the axes. From (11) we find

$$\begin{aligned} \frac{d\,{\hat{\mathbf{r}}}}{dt}= & {} \frac{{\dot{\mathbf{r}}}}{r}-\frac{\mathbf {r} }{r^{2}}\dot{r} \nonumber \\= & {} \frac{1}{r}\left[ {\dot{\mathbf{r}}}-( {\dot{\mathbf{r}}\cdot \hat{\mathbf{r}}} ) {\hat{\mathbf{r}}}\right] \nonumber \\= & {} \frac{1}{r}\left[ ( {\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) {\hat{\mathbf{t}}}+( {\dot{\mathbf{r}}\cdot \hat{\mathbf{n}}}) {\hat{\mathbf{n}}}\right] \nonumber \\= & {} \frac{1}{r}({\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) {\hat{\mathbf{t}}}, \end{aligned}$$

(17)

where the last step follows from the fact that by construction the normal unit vector is perpendicular to the osculating orbital plane. Then from (13), using the definition of the angular momentum

$$\begin{aligned} \mathbf {h}=\mathbf {r}\times \dot{\mathbf {r}}, \end{aligned}$$

(18)

follows

$$\begin{aligned} \frac{d\,{\hat{\mathbf{n}}}}{dt}= & {} \frac{{\mathbf{r}\times \ddot{\mathbf{r}}}}{ \left| {\mathbf{r}}\times \dot{\mathbf{r}}\right| }-\frac{\mathbf {r}\times \dot{\mathbf {r}}}{\left| {\mathbf{r}}\times \dot{\mathbf{r}}\right| ^{2}}\frac{d\,}{dt} \left| {\mathbf{r}}\times \dot{\mathbf{r}}\right| \nonumber \\= & {} \frac{1}{\left| \mathbf {h}\right| }\left\{ {\mathbf{r}\times \ddot{\mathbf{r}}}-\left[ {\hat{\mathbf{n}}}\cdot ( {\mathbf{r}\times \ddot{\mathbf{r}}}) \right] {\hat{\mathbf{n}}}\right\} \nonumber \\= & {} \frac{1}{h}\left\{ ( {\hat{\mathbf{r}}\cdot \mathbf{r}\times \ddot{\mathbf{r}}}) {\hat{\mathbf{r}}+( {\hat{\mathbf{t}}\cdot \mathbf{r}\times \ddot{\mathbf{r}}}) \hat{\mathbf{t}} +( {\hat{\mathbf{n}}\cdot \mathbf{r}\times \ddot{\mathbf{r}}}) \hat{\mathbf{n}}}-( {\hat{\mathbf{n}}}\cdot {\mathbf{r}\times \ddot{\mathbf{r}}}) {\hat{\mathbf{n}}} \right\} \nonumber \\= & {} \frac{1}{h}{( {\hat{\mathbf{t}}\cdot \mathbf{r}\times \ddot{\mathbf{r}}})\hat{\mathbf{t}}} \nonumber \\= & {} \frac{1}{h}{( {\ddot{\mathbf{r}}\cdot \hat{\mathbf{t}}\times \mathbf{r}}) \hat{\mathbf{t}}} \nonumber \\= & {} -\frac{r}{h}{( {\ddot{\mathbf{r}}\cdot \hat{\mathbf{n}}}) \hat{\mathbf{t}}}. \end{aligned}$$

(19)

Then, from (12),

$$\begin{aligned} \frac{d\,{\hat{\mathbf{t}}}}{dt}= & {} \frac{d\,{\hat{\mathbf{n}}}}{dt}\times {\hat{\mathbf{r}}}+{\hat{\mathbf{n}}}\times \frac{d\,{\hat{\mathbf{r}}}}{dt} \nonumber \\= & {} -\frac{r}{h}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) \, {\hat{\mathbf{t}}}\times {\hat{\mathbf{r}}}+\frac{1}{r}( {\dot{\mathbf{r}} \cdot \hat{\mathbf{t}}}) {\hat{\mathbf{n}}}\times {\hat{\mathbf{t}}} \nonumber \\= & {} \frac{r}{h}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) {\hat{\mathbf{n}}}-\frac{1}{r}( {\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) {\hat{\mathbf{r}}}. \end{aligned}$$

(20)

Collecting results, we finally have that the time rates of change of the three unit vectors of the mobile axes are given by the formulae

Now we also know from (15) that the inertial time derivative of a vector fixed in the moving trihedron can be obtained as the result of a vector product with the angular velocity, i.e., for the three vectors at hand as

$$\begin{aligned} \frac{d\,{\hat{\mathbf{r}}}}{dt}= & {} {\varvec{\upomega } }\times {\hat{\mathbf{r}}}, \end{aligned}$$

(22)

$$\begin{aligned} \frac{d\,{\hat{\mathbf{t}}}}{dt}= & {} {\varvec{\upomega } }\times {\hat{\mathbf{t}}}, \end{aligned}$$

(23)

$$\begin{aligned} \frac{d\,{\hat{\mathbf{n}}}}{dt}= & {} {\varvec{\upomega } }\times {\hat{\mathbf{n}}}. \end{aligned}$$

(24)

If we now left-multiply vectorially each time derivative of a vector by the vector itself and do so on both sides of each of the preceding equations we obtain

$$\begin{aligned} {\hat{\mathbf{r}}}\times \frac{d\,{\hat{\mathbf{r}}}}{dt}= & {} {\hat{\mathbf{r}}} \times ( {\varvec{\upomega } }\times {\hat{\mathbf{r}}}) =( {\varvec{\upomega } \cdot \hat{\mathbf{t}}}) {\hat{\mathbf{t}}}+( {\varvec{\upomega } }\cdot {\hat{\mathbf{n}}}) {\hat{\mathbf{n}},} \end{aligned}$$

(25)

$$\begin{aligned} {\hat{\mathbf{t}}}\times \frac{d\,{\hat{\mathbf{t}}}}{dt}= & {} {\hat{\mathbf{t}}} \times ( {\varvec{\upomega } }\times {\hat{\mathbf{t}}}) =( \mathbf { \varvec{\upomega } }\cdot {\hat{\mathbf{r}}}) {\hat{\mathbf{r}}}+( {\varvec{\upomega } }\cdot {\hat{\mathbf{n}}}) {\hat{\mathbf{n}},} \end{aligned}$$

(26)

$$\begin{aligned} {\hat{\mathbf{n}}}\times \frac{d\,{\hat{\mathbf{n}}}}{dt}= & {} {\hat{\mathbf{n}}} \times ( {\varvec{\upomega } }\times {\hat{\mathbf{n}}}) =( \mathbf { \varvec{\upomega } }\cdot {\hat{\mathbf{r}}}) {\hat{\mathbf{r}}}+( {\varvec{\upomega } \cdot \hat{\mathbf{t}}}) {\hat{\mathbf{t}}.} \end{aligned}$$

(27)

Summing these three equations and solving for ${\varvec{\upomega }}$ leads to

$$\begin{aligned} 2{\varvec{\upomega } }={\hat{\mathbf{r}}}\times \frac{d{\hat{\mathbf{r}}}}{dt}+ {\hat{\mathbf{t}}}\times \frac{d{\hat{\mathbf{t}}}}{dt}+{\hat{\mathbf{n}}}\times \frac{d{\hat{\mathbf{n}}}}{dt}. \end{aligned}$$

(28)

This can now be rewritten using the expressions for the times rate of change of the unit vectors given by (21) as

$$\begin{aligned} 2{\varvec{\upomega } }=\frac{1}{r}( {\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) ( {\hat{\mathbf{r}}\times \hat{\mathbf{t}}}) +\frac{r}{h}({\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) ({\hat{\mathbf{t}}\times \hat{\mathbf{n}}} ) -\frac{1}{r}({\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) ( {\hat{\mathbf{t}}\times \hat{\mathbf{r}}}) -\frac{r}{h}{( {\ddot{\mathbf{r}}\cdot \hat{\mathbf{n}}}) }( {\hat{\mathbf{n}}\times \hat{\mathbf{t}}}), \end{aligned}$$

(29)

which leads finally to expressing the angular velocity vector as

in terms of functions of the dynamical state and the instantaneous acceleration acting on the origin of the RTN reference frame, i.e., on body S. Note that the angular velocity has no transverse component, as required by the constraint that the radial axis of the RTN frame always be directed to the origin of the inertial RF. Thus,

$$\begin{aligned} {\varvec{\upomega } }= {\omega } _{r}{\hat{\mathbf{r}}}+ {\omega } _{n}{\hat{\mathbf{n}},} \end{aligned}$$

(31)

with

$$\begin{aligned} \omega _{r}= & {} \dfrac{r}{h}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}} ), \end{aligned}$$

(32)

$$\begin{aligned} \omega _{n}= & {} \dfrac{1}{r}( {\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}). \end{aligned}$$

(33)

3.2 The angular acceleration

The angular acceleration can be computed by taking directly the time derivative of Eq. (30), or from

$$\begin{aligned} 2{\dot{\varvec{\upomega }}}={\hat{\mathbf{r}}}\times \dfrac{d^{2}\,{\hat{\mathbf{r}}} }{dt^{2}}+{\hat{\mathbf{t}}}\times \dfrac{d^{2}\,{\hat{\mathbf{t}}}}{dt^{2}}+ {\hat{\mathbf{n}}}\times \dfrac{d^{2}\,{\hat{\mathbf{n}}}}{dt^{2}}, \end{aligned}$$

(34)

which follows from (28). Less labor is required with the first option. The result is

Notice that, as in the case of the angular velocity, the angular acceleration has no component in the transverse direction. We can also write for ease of use

$$\begin{aligned} {\dot{\varvec{\upomega }}}=\dot{ {\omega }}_{r}{\hat{\mathbf{r}}}+\dot{{\omega }}_{n} {\hat{\mathbf{n}},} \end{aligned}$$

(36)

with

$$\begin{aligned} \dot{ {\omega }}_{r}= & {} \dfrac{r}{h}\left[ \dfrac{\dot{r}}{r}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) -2\frac{r}{h}( {\ddot{\mathbf{r}}} \cdot {\hat{\mathbf{t}}}) ( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}} ) +( {\dddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) \right] , \end{aligned}$$

(37)

$$\begin{aligned} \dot{ {\omega }}_{n}= & {} \dfrac{1}{r}\left[ ( {\ddot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) -2\dfrac{\dot{r}}{r}({\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) \right] . \end{aligned}$$

(38)

It is a matter of some interest that the angular acceleration involves the third time derivative of position, or what is known as the jerk. This can be computed by taking the time derivative of the acceleration as

$$\begin{aligned} {\dddot{\mathbf{r}}}=\dfrac{\partial \,{\ddot{\mathbf{r}}}}{\partial t}+( \nabla _{{\mathbf{r}}} {\ddot{\mathbf{r}}}) \,{\dot{\mathbf{r}}}+( \nabla _{{\dot{\mathbf{r}}}}\,{\ddot{\mathbf{r}}}) \,{\ddot{\mathbf{r}},} \end{aligned}$$

(39)

where the operator $\nabla$ represents the gradient with respect to the indicated subscript (in the following, the lack of an index on this operator will implicitly mean that the gradient is to be taken with respect to the position $\mathbf {r}$). Equation (39) shows that the time rate of change of the acceleration can occur intrinsically through the time variation of the parameters defining the force field, or simply because the body changes its position in the field because of its motion, or through a change of its velocity in the case of a dissipative force field (i.e., a force depending on the velocity), or through any combination of these three reasons.

Note that the partial derivative of the acceleration with respect to the time can be computed from the acceleration model used on the r.h.s. of Eq. (1) as

$$\begin{aligned} \dfrac{\partial \,{\ddot{\mathbf{r}}}}{\partial t}=\dfrac{\partial \,\mathbf {N} ( \mathbf {r};\mu ) }{\partial \mu }\dfrac{d\mu }{dt}+\dfrac{ \partial \,\mathbf {P}( \mathbf {r},{\dot{\mathbf{r}}},t;\varvec{\sigma }) }{\partial \varvec{\sigma }}\dfrac{d\varvec{\sigma }}{dt}. \end{aligned}$$

(40)

In general, these time variations are due to changes in the mass or the mass distribution of the bodies involved, which is the reason for having earlier introduced the model parameters.

In the case of constant mass distributions and conservative fields, the radial component of the angular acceleration can be written as

$$\begin{aligned} \dot{ {\omega }}_{r}=\dfrac{r}{h}\left[ \dfrac{\dot{r}}{r}({\ddot{\mathbf{r}} }\cdot {\hat{\mathbf{n}}}) -2\frac{r}{h}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{t}}}) ( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}} ) +{\hat{\mathbf{n}}}^{T}( \nabla {\ddot{\mathbf{r}}}) {\dot{\mathbf{r}}}\right] . \end{aligned}$$

(41)

It should be observed that the acceleration ${\ddot{\mathbf{r}}}$ appearing in the expressions for the angular velocity and the angular acceleration can be effectively reduced to the disturbing acceleration $\mathbf {P}$ since the Newtonian term $\mathbf {N}$ has no transverse nor normal components and therefore contributes nil to the expressions. This is also true for the quadratic form appearing in the radial component of the angular acceleration (41). This implies that the angular velocity and the angular acceleration have no radial components if the force is central.

3.3 The equations of relative motion in the RTN frame

Now that we have the expressions for the angular velocity and acceleration in terms of the dynamical state variables and functions thereof, we can proceed to compute the terms in the non-inertial expression of the acceleration as they appear in Eq. (16). We only need to focus on the centripetal acceleration term and use the identity

$$\begin{aligned} {\varvec{\upomega } }\times ( {\varvec{\upomega } }\times {\varvec{\uprho } }) =\left( {\varvec{\upomega } }\cdot {\varvec{\uprho } }\right) {\varvec{\upomega } }-{\omega } ^{2}{\varvec{\uprho }}, \end{aligned}$$

(42)

with

$$\begin{aligned} {\omega } ^{2}=\frac{1}{r^{2}}({\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) ^{2}+\left( \frac{r}{h}\right) ^{2}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) ^{2}, \end{aligned}$$

(43)

to find

$$\begin{aligned} {\varvec{\upomega } }\times ( {\varvec{\upomega } }\times {\varvec{\uprho } })= & {} \left[ \frac{1}{h}( {\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) ( {\hat{\mathbf{n}}}\cdot {\varvec{\uprho } }) +\left( \frac{r}{h}\right) ^{2}({\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) ( {\hat{\mathbf{r}}}\cdot {\varvec{\uprho } }) \right] ( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) \,{\hat{\mathbf{r}}} \nonumber \\&+\,\left[ \frac{1}{r^{2}}( {\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) ({\hat{\mathbf{n}}}\cdot {\varvec{\uprho } }) +\frac{1}{h}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) ({\hat{\mathbf{r}}}\cdot {\varvec{\uprho } } ) \right] ( {\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) \,{\hat{\mathbf{n}}} \nonumber \\&-\,\left[ \frac{1}{r^{2}}( {\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) ^{2}+\left( \frac{r}{h}\right) ^{2}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) ^{2}\right] {\varvec{\uprho }}. \end{aligned}$$

(44)

Performing the required substitutions in (14) we find that the inertial acceleration $\varDelta {\ddot{\mathbf{r}}}$ of $S_{1}$ can be expressed in terms of the relative position vector ${\varvec{\uprho } }$ and velocity ${\dot{\varvec{\uprho }}}$ in the RTN frame as

$$\begin{aligned} \varDelta {\ddot{\mathbf{r}}}= & {} {\ddot{\varvec{\uprho }}}+2\frac{1}{r}({\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) ( {\hat{\mathbf{n}}}\times {\dot{\varvec{\uprho }} }) +2\frac{r}{h}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) ( {\hat{\mathbf{r}}}\times {\dot{\varvec{\uprho }}}) \nonumber \\&+\,\left\{ -\dfrac{2}{r^{2}}({\dot{\mathbf{r}}\cdot \hat{\mathbf{r}}}) ( {\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) +\dfrac{1}{r}( \ {\ddot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) \right\} ( {\hat{\mathbf{n}}\times \varvec{\uprho } } ) \nonumber \\&+\,\left\{ \left[ \dfrac{1}{h}( {\dot{\mathbf{r}}\cdot \hat{\mathbf{r}}}) -2\left( \frac{r}{h}\right) ^{2}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{t}} }) \right] ( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) + \dfrac{r}{h}{\hat{\mathbf{n}}}^{T}( \nabla {\ddot{\mathbf{r}}}) {\dot{\mathbf{r}}}\right\} ( {\hat{\mathbf{r}}\times \varvec{\uprho } }) \nonumber \\&+\left[ \frac{1}{r^{2}}( {\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) ( {\hat{\mathbf{n}}}\cdot {\varvec{\uprho } }) +\frac{1}{h}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) ( {\hat{\mathbf{r}}}\cdot {\varvec{\uprho } }) \right] ( {\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) {\hat{\mathbf{n}}} \nonumber \\&+\,\left[ \frac{1}{h}( {\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) ({\hat{\mathbf{n}}}\cdot {\varvec{\uprho } }) +\left( \frac{r}{h}\right) ^{2}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) ( {\hat{\mathbf{r}}}\cdot {\varvec{\uprho } }) \right] ( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) {\hat{\mathbf{r}}} \nonumber \\&-\,\left[ \frac{1}{r^{2}}({\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) ^{2}+\left( \frac{r}{h}\right) ^{2}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) ^{2}\right] {\varvec{\uprho } }. \end{aligned}$$

(45)

Introduce the following variables to indicate the scalar coefficients appearing in this equation

$$\begin{aligned} A= & {} \frac{1}{r^{2}}( {\dot{\mathbf{r}}}\cdot {\hat{\mathbf{t}}}) ^{2}, \end{aligned}$$

(46)

$$\begin{aligned} B= & {} \left( \frac{r}{h}\right) ^{2}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) ^{2}, \end{aligned}$$

(47)

$$\begin{aligned} C= & {} \frac{1}{h}( {\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) ( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}), \end{aligned}$$

(48)

$$\begin{aligned} D= & {} \left[ \dfrac{1}{h}( {\dot{\mathbf{r}}\cdot \hat{\mathbf{r}}}) -2\frac{r^{2}}{h^{2}}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{t}}}) \right] ( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}) +\dfrac{r}{h}\left[ {\hat{\mathbf{n}}}^{T}( \nabla {\ddot{\mathbf{r}}}) {\dot{\mathbf{r}}} \right] , \end{aligned}$$

(49)

$$\begin{aligned} E= & {} -\dfrac{2}{r^{2}}\ ( {\dot{\mathbf{r}}\cdot \hat{\mathbf{r}}}) ({\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) +\dfrac{1}{r}( {\ddot{\mathbf{r}} \cdot \hat{\mathbf{t}}}), \end{aligned}$$

(50)

$$\begin{aligned} L= & {} 2\frac{1}{r}( {\dot{\mathbf{r}}}\cdot {\hat{\mathbf{t}}}), \end{aligned}$$

(51)

$$\begin{aligned} M= & {} 2\frac{r}{h}( {\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}), \end{aligned}$$

(52)

and note that they are all expressed in terms of the dynamical state and the acceleration of the reference body S. The evaluation of these coefficients is easily done when the dynamical variables are available in the inertial reference frame and use is made of the definitions (11), (12) and (13) of the RTN unit vectors.

We can now write the inertial acceleration difference as

$$\begin{aligned} \varDelta {\ddot{\mathbf{r}}}= & {} {\ddot{\varvec{\uprho }}}-( A+B) {\varvec{\uprho } }+D\,{\hat{\mathbf{r}}\times \varvec{\uprho } }+E\,{\hat{\mathbf{n}}\times \varvec{\uprho } }+L\, {\hat{\mathbf{n}}}\times {\dot{\varvec{\uprho }}}+M\,\,{\hat{\mathbf{r}}}\times {\dot{\varvec{\uprho }}} \nonumber \\&+\,\left[ C( {\hat{\mathbf{n}}}\cdot {\varvec{\uprho } }) +B( {\hat{\mathbf{r}}}\cdot {\varvec{\uprho } }) \right] {\hat{\mathbf{r}}}+\left[ A( {\hat{\mathbf{n}}}\cdot {\varvec{\uprho } }) +C( {\hat{\mathbf{r}}} \cdot {\varvec{\uprho } }) \right] {\hat{\mathbf{n}}}. \end{aligned}$$

(53)

Introducing the coordinates $( \xi ,\ \eta ,\ \zeta )$ for the position ${\varvec{\uprho }}$ of $S_{1}$ in the RTN reference frame allows us to write the position, the velocity and the acceleration of $S_{1}$ as

$$\begin{aligned} {\varvec{\uprho } }= & {} \xi {\hat{\mathbf{r}}}+\eta {\hat{\mathbf{t}}}+\zeta {\hat{\mathbf{n}},} \end{aligned}$$

(54)

$$\begin{aligned} {\dot{\varvec{\uprho }}}= & {} \dot{\xi }{\hat{\mathbf{r}}}+\dot{\eta }{\hat{\mathbf{t}}}+\dot{\zeta }{\hat{\mathbf{n}},} \end{aligned}$$

(55)

$$\begin{aligned} {\ddot{\varvec{\uprho }}}= & {} \ddot{\xi }{\hat{\mathbf{r}}}+\ddot{\eta }{\hat{\mathbf{t}}}+\ddot{\zeta }{\hat{\mathbf{n}}.} \end{aligned}$$

(56)

These lead to the useful expressions

$$\begin{aligned} {\hat{\mathbf{r}}\times \varvec{\uprho } }= & {} \eta {\hat{\mathbf{n}}}-\zeta {\hat{\mathbf{t}}} \end{aligned}$$

(57)

$$\begin{aligned} {\hat{\mathbf{r}}\times \dot{\varvec{\uprho }}}= & {} \dot{\eta }{\hat{\mathbf{n}}}-\dot{\zeta } {\hat{\mathbf{t}}} \end{aligned}$$

(58)

$$\begin{aligned} {\hat{\mathbf{n}}\times \varvec{\uprho } }= & {} \xi {\hat{\mathbf{t}}}-\eta {\hat{\mathbf{r}}} \end{aligned}$$

(59)

$$\begin{aligned} {\hat{\mathbf{n}}}\times {\dot{\varvec{\uprho }}}= & {} \dot{\xi }{\hat{\mathbf{t}}}-\dot{ \eta }{\hat{\mathbf{r}}} \end{aligned}$$

(60)

for the various terms appearing in the acceleration formula (53).

Thus

$$\begin{aligned} \varDelta {\ddot{\mathbf{r}}}= & {} ( \ddot{\xi }-A\xi -E\eta +C\zeta -L\dot{\eta }) {\hat{\mathbf{r}}} \nonumber \\&+\,( \ddot{\eta }+E\xi -( A+B) \eta -D\zeta +L\dot{\xi }-M\dot{ \zeta }) {\hat{\mathbf{t}}} \nonumber \\&+\,(\ddot{\zeta }+C\xi +D\eta -B\zeta +M\dot{\eta }) {\hat{\mathbf{n}}} \end{aligned}$$

(61)

We can now write the equations of relative motion (16) in the RTN frame as

where we have added a thrust acceleration term $\mathbf {T}$ to account for possible controls applied to spacecraft $S_{1}$. Component-wise, these equations take the form

Alternatively, the same equations can be put in matrix form as

where $\mathsf {0}$ and $\mathsf {I}$ are respectively the null and the identity matrix of order 3, and the matrices $\mathsf {H}$ and K have been defined as

$$\begin{aligned} \mathsf {H}= & {} \left( \begin{array}{ccc} A &{}\quad E &{}\quad -C \\ -E &{}\quad A+B &{}\quad D \\ -C &{}\quad -D &{}\quad B \end{array}\right) , \end{aligned}$$

(65)

$$\begin{aligned} \mathsf {K}= & {} \left( \begin{array}{ccc} 0 &{}\quad L &{}\quad 0 \\ -L &{}\quad 0 &{}\quad M \\ 0 &{}\quad -M &{}\quad 0 \end{array} \right) . \end{aligned}$$

(66)

These equations are exact, in the sense that no approximation has been made in deriving them. They are completely equivalent to the equations of motion (5) written in the inertial system.

For higher numerical accuracy, recall that the Newtonian differential acceleration term should be computed according to the Encke formulation given in Eq. (8). In this case

$$\begin{aligned} \varDelta \mathbf {N}=-\frac{\mu }{r^{3}}\left\{ f( q) \,r\,{\hat{\mathbf{r}}}+\left[ \,1+f( q) \right] {\varvec{\uprho } }\right\} , \end{aligned}$$

(67)

and the auxiliary variable q can be computed in the RTN frame as

$$\begin{aligned} q=-\frac{[ ( 2r+\xi ) {\hat{\mathbf{r}}}+\eta {\hat{\mathbf{t}}} +\zeta {\hat{\mathbf{n}}}] \cdot ( \xi {\hat{\mathbf{r}}}+\eta {\hat{\mathbf{t}}}+\zeta {\hat{\mathbf{n}}}) }{[ ( r\,+\xi ) {\hat{\mathbf{r}}}+\eta {\hat{\mathbf{t}}}+\zeta {\hat{\mathbf{n}}}] ^{2}}=-\frac{( 2r+\xi ) \xi +\eta ^{2}+\zeta ^{2}}{( r\,+\xi ) ^{2}+\eta ^{2}+\zeta ^{2}} \end{aligned}$$

(68)

while f( q) is still given by Eq. (10). Then the RTN components of the Newtonian differential acceleration are given explicitly by

$$\begin{aligned} ( \varDelta \mathbf {N}) _{\xi }= & {} -\frac{\mu }{r^{3}}\left\{ f( q) \,r\,+\left[ \,1+f( q) \right] \xi \right\} , \end{aligned}$$

(69)

$$\begin{aligned} ( \varDelta \mathbf {N}) _{\eta }= & {} -\frac{\mu }{r^{3}}\left[ \,1+f( q) \right] \eta , \end{aligned}$$

(70)

$$\begin{aligned} ( \varDelta \mathbf {N}) _{\zeta }= & {} -\frac{\mu }{r^{3}}\left[ \,1+f( q) \right] \zeta \end{aligned}$$

(71)

for use within equations (63).

Equation (62), or equivalently their forms (63) and (64), are obviously non-linear. In fact, although linear terms appear, they are simply due to the non-inertial components of the acceleration which are the result of the application of linear operators—functions of the angular velocity operator—the nonlinearity creeps in through the differential Newtonian acceleration, as explicitly shown by Eq. (67), given the nonlinearity of both $q=q({\varvec{\uprho }})$ and f(q). These equations are fully written in Cartesian coordinates. The motion of the two spacecraft is obtained through the integration of a 12th-order system of ODE’s constituted by Eqs. (1) and (62). Integration of the former set of equations provides the dynamical state vector, and functions thereof, of spacecraft S in the inertial reference frame that are required for the simultaneous integration of the latter set of ODE’s, which provides the relative dynamical state vector directly in the RTN reference frame.

4 Approximate formulations

In many cases it is not advisable, nor necessary, to integrate the exact equations of motion. When the differential accelerations are small and the relative motion is sought over short intervals of time, a linearized set of equations may be used. In the following we first derive a linearized set of equations through a first-order expansion of both the differential Newtonian and perturbation terms. We then show that under more restrictive assumptions these linearized equations reduce to two well-known sets of equations which are widely used to model relative motion. We will end with a critical analysis of the terms of use of these equations.

4.1 Linearization

It is usual to adopt an approximate formulation for the differential Newtonian term which is obtained by a first order expansion about the position of the primary body S. In this case we have that $\varDelta \mathbf {N }=\nabla \mathbf {N}(\mathbf {r}_{1}-\mathbf {r}),$ or

$$\begin{aligned} \varDelta \mathbf {N}=\frac{\,\mu }{r^{5}}\left( 3\mathbf {r\,r}^{T}-r^{2}\mathsf { I}\right) {\varvec{\uprho }}, \end{aligned}$$

(72)

and the matrix form of the equations of relative motion in the RTN RF simplifies to

where

$$\begin{aligned} \mathsf {G}=\nabla \mathbf {N}=\frac{\,\mu }{r^{3}}\left( 3{\hat{\mathbf{r}}\, \hat{\mathbf{r}}}^{T}-\mathsf {I}\right) \end{aligned}$$

(74)

is the gravity gradient matrix. In the RTN frame this takes the form

$$\begin{aligned} \left. \mathsf {G}\right| _{ RTN }=\left( \begin{array}{ccc} 2g &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -g &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -g \end{array}\right) , \end{aligned}$$

(75)

where $g=\mu {/}r^{3}$ is the absolute value of the Newtonian gravity gradient at the origin S of the Hill frame. In component form the equations of motion are now

At the same time the differential perturbation term $\varDelta \mathbf {P}$ should also be linearized, since $\left\| \varDelta \mathbf {P}\right\| \ll \left\| \varDelta \mathbf {N}\right\|$. Then

$$\begin{aligned} \varDelta \mathbf {P}\cong \nabla {\mathbf{P}\,\varvec{\uprho } }=\left( \begin{array}{c} \frac{\partial P_{\xi }}{\partial {\varvec{\uprho } }} \\ \frac{\partial P_{\eta }}{\partial {\varvec{\uprho } }} \\ \frac{\partial P_{\zeta }}{\partial {\varvec{\uprho } }} \end{array} \right) \left( \begin{array}{c} \xi \\ \eta \\ \zeta \end{array} \right) =\left( \begin{array}{c} \frac{\partial P_{\xi }}{\partial \xi }\xi +\frac{\partial P_{\xi }}{ \partial \eta }\eta +\frac{\partial P_{\xi }}{\partial \zeta }\zeta \\ \frac{\partial P_{\eta }}{\partial \xi }\xi +\frac{\partial P_{\eta }}{ \partial \eta }\eta +\frac{\partial P_{\eta }}{\partial \zeta }\zeta \\ \frac{\partial P_{\zeta }}{\partial \xi }\xi +\frac{\partial P_{\zeta }}{ \partial \eta }\eta +\frac{\partial P_{\zeta }}{\partial \zeta }\zeta \end{array}\right) \end{aligned}$$

(77)

and

or, after resolving components, we find the linearized equation of relative motion in the RTN reference frame to be

These are the linearized equations that describe the relative motion between two non-interacting spacecraft, each subject to the same force field. As with their full counterparts, these equations are expressed using Cartesian coordinates and the motion of the spacecraft pair implies the integration of a 12th order system of ODE’s constituted by either Eqs. (76), (78), or (79), and Eq. (1).

4.2 Reduction to circular reference orbit

In the case of the primary S in circular orbit of radius $r=R$ the equations of motion simplify considerably. In fact, with the absolute value of the radial gravity gradient, the acceleration and the transverse component of velocity respectively given by

$$\begin{aligned} g= & {} \frac{\mu }{R^{3}}=n^{2} \end{aligned}$$

(80)

$$\begin{aligned} {\ddot{\mathbf{r}}}= & {} -\frac{\mu }{R^{2}}{\hat{\mathbf{r}}}=-n^{2}R\,{\hat{\mathbf{r}}}, \end{aligned}$$

(81)

$$\begin{aligned} {\dot{\mathbf{r}}}\cdot {\hat{\mathbf{t}}}= & {} nR \end{aligned}$$

(82)

and since from the gravity gradient (74), now simplified to

$$\begin{aligned} \mathsf {G}=\nabla {\ddot{\mathbf{r}}}= \frac{\,\mu }{R^{3}}\left( 3{\hat{\mathbf{r}}\,\hat{\mathbf{r}}}^{T}- \mathsf {I}\right) =n^{2}\left( 2{\hat{\mathbf{r}}\hat{\mathbf{r}}}^{T}-{\hat{\mathbf{t}} \hat{\mathbf{t}}}^{T}-{\hat{\mathbf{n}}\hat{\mathbf{n}}}^{T}\right) , \end{aligned}$$

(83)

follows that the quadratic form

$$\begin{aligned} {\hat{\mathbf{n}}}^{T}(\nabla {\ddot{\mathbf{r}}} ) {\dot{\mathbf{r}}}=n^{2}{\hat{\mathbf{n}}}^{T}\left( 2{\hat{\mathbf{r}}\,\hat{\mathbf{r}}}^{T}-{\hat{\mathbf{t}}\hat{\mathbf{t}}}^{T}-{\hat{\mathbf{n}}\hat{\mathbf{n}}} ^{T}\right) {\dot{\mathbf{r}}}=-n^{2}\left( {\hat{\mathbf{n}}}\cdot {\dot{\mathbf{r}}}\right) =0, \end{aligned}$$

(84)

we find that the auxiliary quantities (46)–(52) simplify to

$$\begin{aligned} A= & {} n^{2}, \end{aligned}$$

(85)

$$\begin{aligned} L= & {} 2n, \end{aligned}$$

(86)

$$\begin{aligned} B= & {} C=D=E=M=0. \end{aligned}$$

(87)

Therefore the Eq. (76) take the form

which are identical to the Hill–Clohessy–Wiltshire (HCW) equations (Clohessy and Wiltshire 1960; Prussing and Conway 2012) forced by the additional modelling of the non-Newtonian force field and the thrust acceleration component. In these equations the perturbation $\mathbf {P}$ (and of course the thrust $\mathbf {T}$) are to be computed at ${\varvec{\uprho },}$ since they both act on $S_{1}$.

4.3 Reduction to Keplerian reference orbit

In the case of S following a general Keplerian orbit the equations of motion in the RTN frame simplify less dramatically. In this case we have

$$\begin{aligned} {\dot{\mathbf{r}}\cdot \hat{\mathbf{r}}}= & {} \dot{r}, \end{aligned}$$

(89)

$$\begin{aligned} {\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}= & {} r\dot{\theta }, \end{aligned}$$

(90)

where $\theta$ represents the true anomaly. The term involving the full gravity gradient is still zero, as indicated by Eq. (84), since the dyadic structure of the quadratic form does not change. In fact, since ${\hat{\mathbf{n}}}^{T}( \nabla \mathbf {N}) {\dot{\mathbf{r}}}= 0,$ as was proved above, we can write in general that

$$\begin{aligned} {\hat{\mathbf{n}}}^{T}( \nabla {\ddot{\mathbf{r}}}) {\dot{\mathbf{r}}} \equiv {\hat{\mathbf{n}}}^{T}( \nabla \mathbf {P}) {\dot{\mathbf{r}}}, \end{aligned}$$

(91)

Equation (49) can be modified accordingly and $\nabla {\ddot{\mathbf{r}}}$ replaced with $\nabla \mathbf {P}$ in its last term. Recall that Eq. (49) remains valid only under conditions of constant mass distributions and conservative fields, as previously remarked.

Then the coefficients (46)–(52) simplify to

$$\begin{aligned} A= & {} \dot{\theta }^{2}, \end{aligned}$$

(92)

$$\begin{aligned} E= & {} -2\frac{\dot{r}}{r}\dot{\theta }, \end{aligned}$$

(93)

$$\begin{aligned} L= & {} 2\dot{\theta }, \end{aligned}$$

(94)

$$\begin{aligned} B= & {} C=D=M=0 \end{aligned}$$

(95)

and we have

$$\begin{aligned} \ddot{\xi }= & {} ( 2g+A) \xi +E\eta +L\dot{\eta }+P_{\xi }+T_{\xi }, \end{aligned}$$

(96)

$$\begin{aligned} \ddot{\eta }= & {} -E\xi +( A-g) \eta -L\dot{\xi }+P_{\eta }+T_{\eta }, \end{aligned}$$

(97)

$$\begin{aligned} \ddot{\zeta }= & {} -g\zeta +P_{\zeta }+T_{\zeta }. \end{aligned}$$

(98)

Recalling that $g=\mu {/}r^{3},$ these equations can also be written in the form

which are the de Vries equations (de Vries 1963). If we again stipulate that the orbit of the reference body be circular, then as before $\dot{r}=0,\,\dot{\theta }=n,$ and $\mu {/}r^{3}=n^{2},$ and the de Vries equations reduce to the HCW equations, as expected. The de Vries equations, through the application of the Nechville transformation (Nechville 1926)

$$\begin{aligned}&\displaystyle \xi =r\tilde{\xi },\quad \eta =r\tilde{\eta },\quad \zeta =r\tilde{\zeta }, \end{aligned}$$

(100)

$$\begin{aligned}&\displaystyle h\,dt =r^{2}d\theta , \end{aligned}$$

(101)

can be reduced to an alternate form, known as the Tschauner–Hempel equations, which read (Tschauner and Hempel 1964)

where p is the semilatus rectum of the reference orbit. Here the independent variable is the true anomaly so that the prime signs indicate differentiation with respect to $\theta$. Notice how these equations, while retaining the same form of the HCW equations, represent a generalization to a non-circular, Keplerian reference orbit of those equations, to which they reduce when the variable ratio r / p becomes unity.

4.4 Critique

The restriction of the linearized equations (76) to the case of a Keplerian reference orbit needs to be analyzed in some detail. In particular, it must be kept in mind that in their original form equations (76) describe the relative motion of two physical objects subject to exactly the same force field. Now, since Keplerian orbits naturally develop only in a strictly Newtonian field, the non-Newtonian pertubation $\mathbf {P}$ does not affect the motion of the reference body S and should for consistency be deleted from the force field—which means that it is inconsistent to keep it, as we have done, in the HCW equations (88) or the de Vries equations (99), except for very special cases like a circular equatorial orbit in a purely zonal field. Considerations along similar lines have been made by Ross (2003). However, the term as we have written it, appears in these equations in full, not just through its differential action with respect to body S as indicated in equations (76). This makes the equations consistent, in the sense that they do describe relative motion, but only with respect to a virtual center, which cannot be occupied by a physical body (unless the body is itself controlled). The true relative motion can still be modelled with the use of the HCW or the de Vries equations, but they should be applied to each of the bodies involved—while clearly keeping the vitual center the same—and the results differenced. Clearly, this procedure has some drawbacks since its apparent simplicity makes it harder, for instance, to implement relative navigation techniques.

5 Comparison with previous work

It is of interest to examine if the equations of relative motion given here are equivalent to the equations of motion as formulated by other authors. As it was mentioned earlier, previous authors have adopted a mixed system of variables—i.e., a combination of Cartesian coordinates and Keplerian elements—to express the equations of relative motion with respect to elliptical, possibly precessing, orbits. The difference is found in their expressions for the angular velocity and the angular acceleration, which are invariably given in terms of rates and accelerations of the angular Keplerian elements of the orbit of the reference body. In particular, the radial and normal components of the angular velocity are given as (Kechichian 1998; Chen and Jing 2012)

$$\begin{aligned} {\omega } _{r}= & {} \dot{\varOmega }\sin i\sin u\,+\dfrac{di}{dt}\cos u, \end{aligned}$$

(103)

$$\begin{aligned} {\omega } _{n}= & {} \dot{u}+\dot{\varOmega }\cos i, \end{aligned}$$

(104)

where $\varOmega$ is the longitude of the ascending node, i is the inclination and $u=\theta + {\omega }$ is the argument of latitude. We will show that these expressions are equivalent to those found here, Eqs. (32) and (33). There are two methods to carry out the proof. One is based on kinematics, the other on dynamics. It may be of interest to examine both.

5.1 Dynamical method

Let us first address the dynamical method. Consider the radial component ${\omega } _{r}$. Since ${\ddot{\mathbf{r}}}\cdot {\hat{\mathbf{n}}}=\mathrm {N}$ is the normal component of the disturbing acceleration, so that ${\omega }_{r}=(r{/}h)\mathrm {N},$ we need to show that

$$\begin{aligned} \dfrac{r}{h}\mathrm {N}=\dot{\varOmega }\sin i\sin u\,+\dfrac{di}{dt}\cos u. \end{aligned}$$

(105)

But this follows immediately if we consider the Lagrange planetary equations (LPE) for the inclination and the longitude of the node in their Gaussian form (Kaplan 1976)

$$\begin{aligned} \frac{di}{dt}= & {} \frac{r}{h}\cos u\,\mathrm {N,} \end{aligned}$$

(106)

$$\begin{aligned} \frac{d\varOmega }{dt}= & {} \frac{r\sin u}{h\sin i}\ \mathrm {N,} \end{aligned}$$

(107)

isolate the quantity $( r{/}h) \mathrm {N}$ on the r.h.s. of each, multiply through the first by $\cos ^{2}u,$ the second by $\sin ^{2}u$ and sum side by side.

Consider now the normal component ${\omega } _{n}$ which we write as

$$\begin{aligned} \dfrac{1}{r} ({\dot{\mathbf{r}}\cdot \hat{\mathbf{t}}}) =\dfrac{1}{r}\left( \dot{r}{\hat{\mathbf{r}}}+\frac{h}{r}{\hat{\mathbf{t}}}\right) \cdot {\hat{\mathbf{t}}}=\frac{h}{r^{2}}, \end{aligned}$$

(108)

where the use of the Keplerian decomposition of the velocity is legal in view of the fact that the components are to be expressed in terms of osculating elements, which also appear in the LPE. In order to prove that the expressions (33) and (104) are equivalent we thus need to show that

$$\begin{aligned} \frac{h}{r^{2}}=\frac{du}{dt}+\frac{d\varOmega }{dt}\cos i. \end{aligned}$$

(109)

To this end consider the LPE for the true anomaly and the argument of perigee ${\omega }$ (not to be confused with the absolute value of the angular velocity) in their Gaussian form (Kaplan 1976)

$$\begin{aligned} \frac{d\theta }{dt}= & {} \frac{h}{r^{2}}+\frac{p}{he}\left[ \cos f\ \mathrm {R} -\left( 1+\frac{r}{p}\right) \sin f\ \mathrm {T}\right] , \end{aligned}$$

(110)

$$\begin{aligned} \frac{d {\omega } }{dt}= & {} \frac{p}{he}\left[ -\cos f\;\mathrm {R}+\left( 1+\frac{ r}{p}\right) \sin f\ \mathrm {T}\right] -\dfrac{r}{h}\cot i\,\sin u\,\mathrm {N.} \end{aligned}$$

(111)

Substituting (107) into (111) and using the result to replace the term in square bracket of equation (110) leads immediately to the result (109).

5.2 Kinematical method

Another way of proving (103) and (104) is to write the angular velocity vector in terms of its components along the third inertial axis $\mathbf {k},$ the nodal vector $\mathbf {N}={\hat{\mathbf{k}}} \times {\hat{\mathbf{n}}},$ and the normal axis ${\hat{\mathbf{n}}}$ as

$$\begin{aligned} {\varvec{\upomega } }=\dot{\varOmega }\,{\hat{\mathbf{k}}}+\dfrac{di}{dt}{\hat{\mathbf{N}} }+\dot{u}\,{\hat{\mathbf{n}},} \end{aligned}$$

(112)

where ${\hat{\mathbf{N}}}=\mathbf {N}{/}|\mathbf {N}|$. Recall that the nodal vector has a length equal to the sine of the inclination, $\left| \mathbf {N}\right| =\sin i$. Then the components of $\mathbf {\varvec{\upomega } }$ along the RTN axes can be obtained as

$$\begin{aligned} {\omega } _{r}= & {} {\varvec{\upomega } }\cdot {\hat{\mathbf{r}}} \nonumber \\= & {} \left( \dot{\varOmega }\,{\hat{\mathbf{k}}}+\dfrac{di}{dt}{\hat{\mathbf{N}}}+\dot{u}\, {\hat{\mathbf{n}}}\right) \cdot {\hat{\mathbf{r}}} \nonumber \\= & {} \dot{\varOmega }\,({\hat{\mathbf{k}}}\cdot {\hat{\mathbf{r}}})+\dfrac{di}{dt}({\hat{\mathbf{N}}}\cdot {\hat{\mathbf{r}}}). \end{aligned}$$

(113)

But the direction cosines between the two reference frames show that ${\hat{\mathbf{k}}}\cdot {\hat{\mathbf{r}}}=\sin i\sin u$ and ${\hat{\mathbf{N}}} \cdot {\hat{\mathbf{r}}}=\cos u,$ which, upon substitution into the preceding equation, proves the validity of (103). Similarly, for the normal component we find

$$\begin{aligned} {\omega } _{n}= & {} {\varvec{\upomega } }\cdot {\hat{\mathbf{n}}} \nonumber \\= & {} \left( \dot{\varOmega }\,{\hat{\mathbf{k}}}+\dfrac{di}{dt}{\hat{\mathbf{N}}}+\dot{u}\, {\hat{\mathbf{n}}}\right) \cdot {\hat{\mathbf{n}}} \nonumber \\= & {} \dot{\varOmega }\,({\hat{\mathbf{k}}}\cdot {\hat{\mathbf{n}}})+\dot{u}, \end{aligned}$$

(114)

which, on recalling that ${\hat{\mathbf{k}}}\cdot {\hat{\mathbf{n}}}=\cos i,$ proves the validity of (104).

The kinematical method is also employed by Kechichian (1998) and appears to be originally due to Breakwell (1974). As a side note, the transverse component of the angular velocity can be obtained by the projection of (112) as

$$\begin{aligned} {\omega } _{t}=\dot{\varOmega }\,({\hat{\mathbf{k}}}\cdot {\hat{\mathbf{t}})}+\dfrac{di }{dt}({\hat{\mathbf{N}}}\cdot {\hat{\mathbf{t}}}). \end{aligned}$$

(115)

But we know that ${\omega } _{t}=0,$ so, recalling that ${\hat{\mathbf{k}}}\cdot {\hat{\mathbf{t}}}=\sin i\cos u$ and that ${\hat{\mathbf{N}}}\cdot {\hat{\mathbf{t }}}=-\sin u,$ it follows that

$$\begin{aligned} \dot{\varOmega }\sin i\cos u=\dfrac{di}{dt}\sin u. \end{aligned}$$

(116)

This same relationship between the time derivatives of the longitude of the node and the inclination also follows from the Gauss form of the LPE’s: it is sufficient to eliminate $( r{/}h) \mathrm {N}$ between (106) and (107).

6 The linearized equations of motion in the presence of the oblateness perturbation

From the expression of the oblateness perturbation (3) we find the gradient with respect to the position to be given by

$$\begin{aligned} \nabla _{\mathbf {r}}\mathbf {P}_{J_{2}}= & {} -\dfrac{3}{2}\dfrac{\mu }{a_{e}^{3} }J_{2}\left( \dfrac{a_{e}}{r}\right) ^{5}\left\{ 2\mathbf {kk} ^{T}-10( {\hat{\mathbf{r}}}\cdot \mathbf {k}) \left( \mathbf {k}\hat{\mathbf{r}}^{T}+ \hat{\mathbf{r}}{} \mathbf{k}^{T}\right) \right. \nonumber \\&+\left. \left[ 1-5( {\hat{\mathbf{r}}}\cdot \mathbf {k}) ^{2}\right] -5\left[ 1-7( {\hat{\mathbf{r}}}\cdot \mathbf {k}) ^{2}\right] {\hat{\mathbf{r}}\hat{\mathbf{r}}}^{T}\right\} \end{aligned}$$

(117)

In order to adapt this dyadic expression for immediate use in RTN frame coordinates, it is expedient to replace the unit vector $\mathbf {k}$ with its expression

$$\begin{aligned} \mathbf {k}=k_{r}{\hat{\mathbf{r}}}+k_{t}{\hat{\mathbf{t}}}+k_{n}{\hat{\mathbf{n}}} \end{aligned}$$

(118)

in the RTN basis,³ where

$$\begin{aligned} k_{r}=\mathbf{k}\cdot \hat{\mathbf{r}},\quad k_{t}=\mathbf{k}\cdot \hat{\mathbf{t}},\quad k_{n}=\mathbf{k}\cdot \hat{\mathbf{n}}, \end{aligned}$$

(119)

are direction cosines directly computable from information available from the numerical integration of the inertial motion of S. Note that in inertial coordinates $k_{r}=z{/}r,\,k_{t}=( h_{x}y-h_{y}x){/}hr,$ and $k_{n}=h_{z}{/}h$. The gravity perturbation gradient can thus be expressed as a dyadic in the RTN basis as

$$\begin{aligned} \nabla \mathbf {P}_{J_{2}}= & {} K\left\{ 4\left( 1-3k_{r}^{2}\right) {\hat{\mathbf{r}}\hat{\mathbf{r}}}^{T}- \left( 1-5k_{r}^{2}+2k_{t}^{2}\right) {\hat{\mathbf{t}} \hat{\mathbf{t}}}^{T}- \left( 1-5k_{r}^{2}+2k_{t}^{2}\right) {\hat{\mathbf{n}}\hat{\mathbf{n}}} ^{T}\right. \nonumber \\&+\,\left. 8k_{r}k_{t}\left( {\hat{\mathbf{r}}\hat{\mathbf{t}}}^{T}+{\hat{\mathbf{t}}\hat{\mathbf{r} }}^{T}\right) +8k_{r}k_{n}\left( {\hat{\mathbf{r}}\hat{\mathbf{n}}}^{T}+{\hat{\mathbf{n}}\hat{\mathbf{r}}} ^{T}\right) -2k_{t}k_{n}\left( {\hat{\mathbf{t}}\hat{\mathbf{n}}}^{T}+{\hat{\mathbf{n}}\hat{\mathbf{t}}} ^{T}\right) \right\} , \end{aligned}$$

(120)

where the function K has been defined as

$$\begin{aligned} K= \frac{3}{2}\frac{\mu }{a_{e}^{3}}J_{2}\left( \frac{a_{e}}{r}\right) ^{5}. \end{aligned}$$

(121)

The equations of relative motion for the $J_{2}$-perturbed case can now be easily written down. We first need to complete the expression for the angular acceleration by including the quadratic form appearing in the expression (49) of the D coefficient. Making use of expression (120) and accounting for the identity (91) we find

$$\begin{aligned} {\hat{\mathbf{n}}}^{T}(\nabla \mathbf {P}_{J_{2}}) {\dot{\mathbf{r}}} = K\left[ 8k_{r}k_{n}( {\hat{\mathbf{r}}}\cdot {\dot{\mathbf{r}}}) -2k_{t}k_{n} ( {\hat{\mathbf{t}}}\cdot {\dot{\mathbf{r}}}) - \left( 1-5k_{r}^{2}+2k_{n}^{2}\right) ({\hat{\mathbf{n}}}\cdot {\dot{\mathbf{r}}}) \right] , \end{aligned}$$

(122)

since the Newtonian part of the acceleration contributes nil, as was already shown above. This expressions, of course, must be used in the equations of relative motion even when the perturbation term is not linearized. The linearization can easily be carried out by forming the term $\nabla \mathbf{P}\,{\varvec{\uprho }}$ appearing in (7). By multiplying (120) and (54) we obtain the linearized $J_{2}$ acceleration as

$$\begin{aligned} \nabla \mathbf {P}_{J_{2}}{\varvec{\uprho } }= & {} K\left\{ \left[ 4\left( 1-3k_{r}^{2}\right) \xi +8k_{r}k_{t}\eta +8k_{r}k_{n}\zeta \right] {\hat{\mathbf{r}}}\right. \nonumber \\&+\left[ 8k_{r}k_{t}\xi -\left( 1-5k_{r}^{2}+2k_{t}^{2}\right) \eta -2k_{t}k_{n}\zeta \right] {\hat{\mathbf{t}}} \nonumber \\&\left. +\left[ 8k_{r}k_{n}\xi -2k_{t}k_{n}\eta -\left( 1-5k_{r}^{2}+2k_{n}^{2}\right) \zeta \right] {\hat{\mathbf{n}}}\right\} , \end{aligned}$$

(123)

which is conveniently expressed in the RTN basis.

The full, linearized equations of relative motion including the differential effects of $J_{2}$ can then be written as

where the quantities $A,\,B,\,C,\,D,\,L$ and M have been defined in Eqs. (46) through (52). Equations (124) are the specialized version of Eqs. (78) or (79) for the case of the $J_{2}$ oblateness perturbation.

7 Conclusions

A derivation of the equations of relative motion for two non-mutually interacting spacecraft in Earth orbit has been presented in the orbital reference frame. These equations are subject to no other restriction, and they are valid for any force field describing their motion. This has been done by application of straightforward expressions derived for the angular velocity and the angular acceleration of the orbital reference frame associated with the reference spacecraft. It has been shown that these two vectors can be expressed in terms of the dynamical state vector of the reference body, without recourse to the time rates of change of its angular orbital elements. This leads to a novel, self-contained formulation of the 12th order set of the equations of motion of the spacecraft pair based on Cartesian coordinates. A linearized formulation of these equations has also been derived, which reduces to the well-known Hill–Clohessy–Wiltshire equations or to the de Vries, or the Tschauner–Hempel equations when the reference spacecraft is respectively in a circular or elliptical Keplerian orbit. An explicit form of the linearized equations has been derived for the case of Keplerian orbits perturbed by the Earth’s $J_2$ zonal harmonic.