1 Introduction

Coaxial waveguide consists of a hollow conductive shell and a solid conductor rod that is coaxial with the shell. The cross section of the shell and rod can be designed in circular and elliptical shapes, etc. The coaxial devices are capable of generating higher power than conventional cylindrical devices. Recently, a method has been proposed to achieve high power at a given wavelength with lower beam energy. In this method, a free laser electron can be used using an annular electron beam in a coaxial waveguide [1,2,3].

Coaxial waveguides have many applications and many studies have been done about them [4,5,6,7]. The high-frequency eigenmodes of a coaxial waveguide including a magnetized annular plasma have been analysed [4]. Propagation of electromagnetic waves in a magnetized plasma coaxial waveguide has been studied [5]. Electron energy gain in the transverse electric mode of a coaxial plasma waveguide has been studied [6]. Furthermore, propagation of space-charge waves through a coaxial waveguide with circular cross section and containing an annular magnetized plasma has been investigated [7].

Geometrically, waveguides have different cross sections, such as rectangles, circles and ellipses are filled with different materials and have different applications [8,9,10,11,12,13]. Furthermore, elliptical cross-sectional waveguides have advantages over circular cross-sectional waveguides. It has been shown that converting a dielectric waveguide with a circular cross section to an elliptical waveguide, considering the same cross-sectional area, reduces damping in the dominant mode [14] and modal degeneracy, allows practical guidance of traveling electromagnetic waves. In addition, attenuation and power flow effects are obtained in a surface wave transmission line with an elliptical cross section for wave propagation [15]. It has been recognized that some existing modes in an elliptical waveguide have less attenuation than the corresponding modes in a circular waveguide.

On the other hand, by applying a constant and static magnetic field to an electron plasma, plasma is converted to magnetized plasma, and its dispersion curves find four branches as: an electron Langmuir and cyclotron modes, ordinary and extraordinary modes.

In this paper, we considered two configurations: one is a coaxial elliptical waveguide including an annular vacuum-magnetized plasma-vacuum and another is an elliptical waveguide filled by magnetized plasma. We consider magnetized collisionless cold plasma. In two structures propagation of space-charge waves was studied. The potentials for the annular plasma region and the two annular vacuum regions in the coaxial elliptical waveguide and in the plasma waveguide in terms of Mathieu functions in the electrostatic approximation were presented. Dispersion relation, components of electric field and electron velocity in two configurations were calculated. Numerical computations were made and results were graphically presented.

We study the propagation of space charge waves considering the appropriate approximations,including electrostatic approximation and ignoring the effects of ion motions and electron temperature. Then we calculate perturbed potential, electron density, electron velocity, and dispersion relation in the two considered structures.

In the previous work, the propagation of space-charge waves in a coaxial waveguide with circular cross section including an annular plasma in an axial magnetic field has been studied [7]. Here we consider the waveguide with elliptical cross section and examine the space charge waves in these configurations. The results obtained are different from the previous results and the calculated quantities are expressed in terms of Mathieu functions. In this work, the Introduction is presented as Sect. 1. In Sect. 2, we use the Poisson, continuity, and momentum transfer equations in the appropriate form, and combining these equations, we obtain dispersion relation. The appropriate solutions for the distribution of potentials as Mathieu functions in all spatial regions are presented. In Sect. 3, space-charge waves in an elliptical magnetized plasma waveguide are studied. The perturbed potential, electron density, electron velocity, and dispersion relation in this configuration are calculated. In Sect. 4, numerical results are graphically presented. A conclusion is expressed in Sect. 5.

2 Electrostatic Space-Charge in the Coaxial Elliptical Waveguide Including An Annular Magnetized Plasma

Fig. 1
figure 1

Two different waveguide structures with elliptical cross section, a The cross section of the coaxial elliptical waveguide, b Metallic elliptical waveguide filled by plasma

Full size image

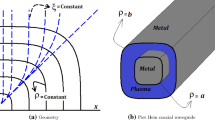
In this section, the configuration under study is a coaxial elliptical waveguide. This waveguide structure consists of a metallic elliptical shell as cladding, so that in its center is a solid metallic cylinder with an elliptical cross section and coaxial with it as a core. This coaxial elliptical waveguide contains an annular plasma in an axial magnetic field. The cross section of this configuration is shown in Fig. 1a.

Here it is noted that we can write the conversion relations between the elliptic coordinate system, \((\xi ,\eta ,z)\)  and cartesian system (x, y, z) as following forms: [16]:

$$\begin{aligned} x=d\cosh \xi \cos \eta , \quad y=d\sinh \xi \sin \eta , \quad z=z, \end{aligned}$$

where \(d=\sqrt{a_{\mathrm{bound.}}^2-b_{\mathrm{bound.}}^2} ~\) and \(a_{\mathrm{bound.}}\), \(b_{\mathrm{bound.}}\)  introduce the elliptic boundary as:  \(\xi _{\mathrm{bound.}}=\tanh ^{-1}(b_{\mathrm{bound.}}/a_{\mathrm{bound.}})\).

Therefore in Fig. 1 the boundary of inner solid metal is defined by: \(\xi =\xi _a\)  and the boundary of metallic cylindrical shell is indicated by: \(\xi =\xi _b\). We define the boundary of inner of elliptical annular plasma by: \(\xi =\xi _i\) and the boundary of outer of elliptical annular plasma by: \(\xi =\xi _o\).Furthermore the regions of \(\xi _a<\xi <\xi _i\) and  \(\xi _o<\xi <\xi _b\) are vacuum and  \(B_0\hat{z}\) is external magnetic field. It is mentioned that we consider the electrostatic approximation for investigations of the space-charge mode. In the considered approximation, the wavenumber in the axial direction is satisfied in: \(k \gg \omega /c \),and k is wavenumber. Therefore we consider  \( {\mathbf {E}} = -\mathbf {\nabla }\phi \) as a relation between the electrostatic potential and electric field. We use the Poisson equation as follows:

$$\begin{aligned} \nabla ^2\delta \phi =\frac{e}{\varepsilon _0}\delta n~, \end{aligned}$$
(1)

and use the continuity and momentum transfer equations in the below forms:

$$\begin{aligned}&\frac{\partial \delta n}{\partial t}+n_0\mathbf {\nabla }.\delta {\mathbf {v}}=0~, \end{aligned}$$
(2)
$$\begin{aligned}&\quad \frac{\partial \delta {\mathbf {v}}}{\partial t}=\frac{e}{m_e}\mathbf {\nabla }\delta \phi -\omega _c \delta {\mathbf {v}}\times \hat{z}~, \end{aligned}$$
(3)

where \(\delta \phi \), \(\delta n\) and \( \delta {\mathbf {v}}\) are the perturbed potential, velocity and density of electrons.

Therefore, we obtain Helmholtz equations for the vacuum regions: \(\xi _a<\xi <\xi _i\) and \(\xi _o<\xi <\xi _b\)  in the following forms:

$$\begin{aligned} \nabla ^2_\bot \delta \tilde{\phi }^{(I,III)}-k^2\delta \tilde{\phi }^{(I,III)}=0~, \end{aligned}$$
(4)

and for the plasma region: \(\xi _i<\xi <\xi _o\) as:

$$\begin{aligned} \nabla ^2_\bot \delta \tilde{\phi }^{(II)}+\kappa ^2\delta \tilde{\phi }^{(II)}=0, \end{aligned}$$
(5)

with:

$$\begin{aligned} \kappa ^2=\frac{k^2(\omega _c^2-\omega ^2)(\omega _p^2-\omega ^2)}{\omega ^2(\omega _p^2+\omega ^2-\omega ^2)},~ \omega _c=\frac{eB_0}{m_e}~,~\omega _p^2=\frac{n_0e^2}{\varepsilon _0m_e}, \end{aligned}$$
(6)

where \(\omega _c\) and \(\omega _p\) indicate the cyclotron and plasma frequencies of electron, respectively.

\(\omega _c\) and \(\omega _p\) are the cyclotron and plasma frequencies of electron, respectively, and are defined as \(\omega _c=\frac{eB_0}{m_e}\) and \(\omega _p=\sqrt{\frac{n e^2}{\varepsilon _0m_e}}\), where \(m_e\) and \(-e\) are defined as the electron mass and the electron charge and \(n_0\) is the unperturbed electron density that it is assumed uniform and constant throughout the plasma.

Here we study space-charge waves and thus the perturbed potential is introduced by: \(\delta \phi =\delta \tilde{\phi }e^{i(kz-\omega t)}\). By considering the z axis as propagating direction, the form of potential is \(\delta \phi =\delta \tilde{\phi }e^{i(kz-\omega t)}\), where k and \(\omega \) indicate the wavenumber and the angular frequency. However in the elliptical cylinder coordinates  \(\delta \tilde{\phi }\) satisfies in the following equation:

$$\begin{aligned} \frac{1}{h^2}(\frac{\partial ^2}{\partial \xi ^2}+\frac{\partial ^2}{\partial \eta ^2})\delta \tilde{\phi }^{(I,II,III)}(\xi ,\eta ) +k^2_{(I,II,III)}\delta \tilde{\phi }^{(I,II,III)}(\xi ,\eta )=0, \end{aligned}$$
(7)

where: \(h=d\sqrt{\cosh ^2\xi -\cos ^2\eta }\), \(k^2_{(I,III)}=-k^2~,~k^2_{(II)}=\kappa ^2\) and  \(q_{(I,II,III)}=k^2_{(I,II,III)}d^2/4\). Equation (7)is a Mathieu equation and it has the even and odd solutions [15]. Therfore we obtain:

$$\begin{aligned}&\delta \phi ^{(I,III)}(\xi ,\eta ,z,t)=\sum _{m=0}^\infty [C_m^{(I,III)}Ce_m(\xi ,-q_{(I,III)})+F_m^{(I,III)}Fek_m(\xi ,-q_{(I,III)})] ce_m(\eta ,-q_{(I,III)}) \exp [i(kz-\omega t)] \nonumber \\&\quad +\sum _{m=1}^\infty [S_m^{(I,III)}Se_m(\xi ,-q_{(I,III)})+G_m^{(I,III)}Gek_m(\xi ,-q_{(I,III)})]se_m(\eta ,-q_{(I,III)}) \exp [i(kz-\omega t)], \end{aligned}$$
(8)

and:

$$\begin{aligned}&\delta \phi ^{(II)}(\xi ,\eta ,z,t)=\sum _{m=0}^\infty [C_m^{(II)}Ce_m(\xi ,q_{(II)})+F_m^{(II)}Fey_m(\xi ,q_{(II)})]ce_m(\eta ,q_{(II)}) \exp [i(kz-\omega t)]\nonumber \\&\quad +\sum _{m=1}^\infty [S_m^{(II)}Se_m(\xi ,q_{(II)})+G_m^{(II)}Gey_m(\xi ,q_{(II)})]se_m(\eta ,q_{(II)}) \exp [i(kz-\omega t)], \end{aligned}$$
(9)

where \(ce_m(\eta ,q_i)\) ,\(se_m(\eta ,q_i)\) are the even and odd solutions of the angular Mathieu equation, and \(Ce_m(\xi ,q_i)\) ,\(Se_m(\xi ,q_i)\)  are the even and odd solutions of the radial Mathieu equation.

\(Ce_m(\xi ,q_i)\) ,\(Se_m(\xi ,q_i)\) are the radial solutions of the first kind and  \(Fey_m(\xi ,q_i)\), \( Gey_m(\xi ,q_i)\)  are the radial solutions of the second kind,for \(q_i>0\) and for \(q_i<0\) the solutions of the second kind are converted to \(Fek_m\) and \(Gek_m\) [16]. We consider the even solution of Mathieu equation in three regions as follows:

$$\begin{aligned}&\delta \tilde{\phi }_{m}^{(I)}=\delta \tilde{\phi }_{m(even)}^{(I)}(\xi ,\eta )= [C_m^{(I)}Ce_m(\xi ,-q_{(I)})+F_m^{(I)}Fek_m(\xi ,-q_{(I)})] ce_m(\eta ,-q_{(I)})~for~~\xi _a<\xi <\xi _i~, \end{aligned}$$
(10)
$$\begin{aligned}&\quad \delta \tilde{\phi }_{m}^{(II)}=\delta \tilde{\phi }_{m(even)}^{(II)}(\xi ,\eta )= [C_m^{(II)}Ce_m(\xi ,q_{(II)})+F_m^{(II)}Fey_m(\xi ,q_{(II)})] ce_m(\eta ,q_{(II)})~for~~\xi _i<\xi <\xi _o~, \end{aligned}$$
(11)
$$\begin{aligned}&\quad \delta \tilde{\phi }_{m}^{(III)}=\delta \tilde{\phi }_{m(even)}^{(III)}(\xi ,\eta )= [C_m^{(III)}Ce_m(\xi ,-q_{(III)}) +F_m^{(III)}Fek_m(\xi ,-q_{(III)})]ce_m(\eta ,-q_{(III)})~for~~\xi _o<\xi <\xi _b~, \end{aligned}$$
(12)

Furthermore, it is mentioned that the potential must vanish at the surfaces  \(\xi _a\)  and \(\xi _b\). Therefore:

$$\begin{aligned}&\delta \tilde{\phi }_{m}^{(I)}=\,\delta \tilde{\phi }_{m(even)}^{(I)}(\xi ,\eta )= C_m^{(I)}[Ce_m(\xi ,-q_{(I)})-\alpha _aFek_m(\xi ,-q_{(I)})] ce_m(\eta ,-q_{(I)}), \end{aligned}$$
(13)
$$\begin{aligned}&\quad \delta \tilde{\phi }_{m}^{(II)}=\,\delta \tilde{\phi }_{m(even)}^{(II)}(\xi ,\eta )= [C_m^{(II)}Ce_m(\xi ,q_{(II)})+F_m^{(II)}Fey_m(\xi ,q_{(II)})] ce_m(\eta ,q_{(II)}), \end{aligned}$$
(14)
$$\begin{aligned}&\quad \delta \tilde{\phi }_{m}^{(III)}=\,\delta \tilde{\phi }_{m(even)}^{(III)}(\xi ,\eta )= C_m^{(III)}[Ce_m(\xi ,-q_{(III)}) -\alpha _bFek_m(\xi ,-q_{(III)})]ce_m(\eta ,-q_{(III)}), \end{aligned}$$
(15)

where:

$$\begin{aligned} \alpha _a=\, & {} \frac{Ce_m(\xi _b,-q_{(I)})}{Fek_m(\xi _b,-q_{(I)})},\nonumber \\ \alpha _b=\, & {} \frac{Ce_m(\xi _b,-q_{(III)})}{Fek_m(\xi _b,-q_{(III)})}. \end{aligned}$$
(16)

The latter boundary conditions are obtained from the fact that, the potential must be continuous in the interfaces of the plasma and vacuum at the elliptical boundaries of \(\xi _i\)  and  \(\xi _o\).

Now we obtain another boundary condition to complete the calculations. Using Eqs. (2) and (3), we can obtain:

$$\begin{aligned} -\mathbf {\nabla }.(en_0\delta {\mathbf {v}}+\varepsilon _0\frac{\partial }{\partial t}\mathbf {\nabla }\delta \phi )=0 \end{aligned}$$
(17)

By integrating Eq. (17) , it can be shown that  \(-en_0\delta v_\xi +\frac{i\omega }{h}\frac{\partial }{\partial \xi }\delta \phi \) , must be continuous across interface of plasma-vacuum .

The components of velocity perturbations are:

$$\begin{aligned}&\delta {\tilde{v}}_\xi ^{(II)}=\frac{e}{m_e(\omega ^2-\omega _c^2)h} \left[ i\omega [C_m^{(II)}Ce_m'(\xi ,q_{(II)})+F_m^{(II)}Fey_m'(\xi ,q_{(II)})] ce_m(\eta ,q_{(II)})\right. \nonumber \\&\quad +\left. \omega _c[C_m^{(II)}Ce_m(\xi ,q_{(II)})+F_m^{(II)}Fey_m(\xi ,q_{(II)})]ce'_m(\eta ,q_{(II)})\right] \exp [i(kz-\omega t)]~, \end{aligned}$$
(18)
$$\begin{aligned}&\quad \delta {\tilde{v}}_\eta ^{(II)}=\frac{e}{m_e(\omega ^2-\omega _c^2)h} \left[ i\omega [C_m^{(II)}Ce_m(\xi ,q_{(II)})+F_m^{(II)}Fey_m(\xi ,q_{(II)})ce'_m(\eta ,q_{(II)})\right. \nonumber \\&\quad -\left. \omega _c[C_m^{(II)}Ce'_m(\xi ,q_{(II)})+F_m^{(II)}Fey'_m(\xi ,q_{(II)})]ce_m(\eta ,q_{(II)})\right] \exp [i(kz-\omega t)]~, \end{aligned}$$
(19)
$$\begin{aligned}&\quad \delta {\tilde{v}}_z^{(II)}=\frac{ike}{m_e}[C_m^{(II)}Ce_m(\xi ,q_{(II)})+F_m^{(II)}Fey_m(\xi ,q_{(II)})]ce_m(\eta ,q_{(II)}) \exp [i(kz-\omega t)]~, \end{aligned}$$
(20)

and the density perturbation in the plasma region calculate in the following form:

$$\begin{aligned} \delta {\tilde{n}}^{(II)}=\frac{\varepsilon _0}{e}(\kappa ^2+k^2)[C_m^{(II)}Ce_m(\xi ,q_{(II)})+F_m^{(II)}Fey_m(\xi ,q_{(II)})]ce_m(\eta ,q_{(II)})\exp [i(kz-\omega t)]. \end{aligned}$$
(21)

Furthermore, the components of the electric field in vacuum and plasma regions are calculated as follows:

$$\begin{aligned} E_\xi ^{(I,III)}= & {} -\frac{1}{h} C_m^{(I,III)}[Ce'_m(\xi ,-q_{(I,III)})-\alpha _{a,b} Fek'_m(\xi ,-q_{(I,III)})]ce_m(\eta ,-q_{(I,III)})\exp [i(kz-\omega t)]~, \end{aligned}$$
(22)
$$\begin{aligned} E_\eta ^{(I,III)}= & {} -\frac{1}{h} C_m^{(I,III)}[Ce_m(\xi ,-q_{(I,III)})-\alpha _{a,b}Fek_m(\xi ,-q_{(I,III)})]ce'_m(\eta ,-q_{(I,III)})\exp [i(kz-\omega t)]~, \end{aligned}$$
(23)
$$\begin{aligned} E_z^{(I,III)}= & {} -ik C_m^{(I,III)}[Ce_m(\xi ,-q_{(I,III)})-\alpha _{a,b}Fek_m(\xi ,-q_{(I,III)})]ce_m(\eta ,-q_{(I,III)})\exp [i(kz-\omega t)]~, \end{aligned}$$
(24)

and

$$\begin{aligned} E_\xi ^{(II)}= & {} -\frac{1}{h}[C_m^{(II)}Ce'_m(\xi ,q_{(II)})+F_m^{(II)}Fey'_m(\xi ,q_{(II)})]ce_m(\eta ,q_{(II)})\exp [i(kz-\omega t)]~, \end{aligned}$$
(25)
$$\begin{aligned} E_\eta ^{(II)}= & {} -\frac{1}{h}[C_m^{(II)}Ce_m(\xi ,q_{(II)})+F_m^{(II)}Fey_m(\xi ,q_{(II)})]ce'_m(\eta ,q_{(II)})\exp [i(kz-\omega t)]~, \end{aligned}$$
(26)
$$\begin{aligned} E_z^{(II)}= & {} -ik[C_m^{(II)}Ce_m(\xi ,q_{(II)})+F_m^{(II)}Fey_m(\xi ,q_{(II)})]ce_m(\eta ,q_{(II)})\exp [i(kz-\omega t)]~. \end{aligned}$$
(27)

2.1 Dispersion Equation in the Considered Configuration

The dispersion function in the supposed elliptical coaxial waveguide is obtained by applying the mentioned suitable boundary conditions in the separating boundaries. By applying boundary conditions , the dispersion equation is achieved by setting the determinant of the coefficients equal to zero: By applying the right boundary conditions, we can achieve the dispersion relation in the coaxial elliptical waveguide, as:

$$\begin{aligned} \bigg | \begin{array}{cccc} \alpha _{11} &{} \alpha _{12} &{} \alpha _{13} &{} \alpha _{14} \\ \alpha _{21} &{} \alpha _{22} &{} \alpha _{23} &{} \alpha _{24} \\ \alpha _{31} &{} \alpha _{32} &{} \alpha _{33} &{} \alpha _{34} \\ \alpha _{41} &{} \alpha _{42} &{} \alpha _{43} &{}\alpha _{44} \\ \end{array} \bigg |=0, \end{aligned}$$
(28)

The elements of above determinate are defined by:

$$\begin{aligned} \alpha _{11}&=x_1s_1 , \alpha _{12}=-x_2s_2 , \alpha _{13}=-x_3s_2 , \alpha _{14}=0, \alpha _{21}=0 , \alpha _{22}=-x_4s_2 , \alpha _{23}=-x_5s_2 , \alpha _{24}=x_6s_1, \end{aligned}$$
(29a)
$$\begin{aligned} \alpha _{31}&=ix_7s_1 , \alpha _{32}=-iT_1x_8s_2-T_2x_2s_4, \alpha _{33}=-iT_1x_9s_2-T_2x_3s_4 , \alpha _{34}=0, \end{aligned}$$
(29b)
$$\begin{aligned} \alpha _{41}=0 , \alpha _{42}=-iT_1x_{11}s_2-T_2x_4s_4, \alpha _{43}=-iT_1x_{12}s_2-T_2x_5s_4 , \alpha _{44}=0ix_{10}s_1, \end{aligned}$$
(29c)

where

$$\begin{aligned} T_1=\frac{\omega (\omega ^2-\omega _c^2-\omega _p^2)}{\omega ^2-\omega _c^2}~,~T_2=-\frac{\omega _c(\omega _p^2)}{\omega ^2-\omega _c^2}, \end{aligned}$$
(30)

and:

$$\begin{aligned} x_1&=Ce_m(\xi _i,-q_{(I)})-\alpha _aFek_m(\xi _i,-q_{(I)}), x_2=Ce_m(\xi _i,q_{(II)}), x_3=Fek_m(\xi _i,q_{(II)}), \end{aligned}$$
(31a)
$$\begin{aligned} x_4&=Ce_m(\xi _o,q_{(II)}) , x_5=Fek_m(\xi _o,q_{(II)}), x_6=Ce_m(\xi _o,-q_{(I)})-\alpha _bFek_m(\xi _o,-q_{(I)}), \end{aligned}$$
(31b)
$$\begin{aligned} x_7&=Ce'_m(\xi _i,-q_{(I)})-\alpha _aFek'_m(\xi _i,-q_{(I)}), x_8=Ce'_m(\xi _i,q_{(II)}), x_9=Fek'_m(\xi _i,q_{(II)}), \end{aligned}$$
(31c)
$$\begin{aligned} x_{10}=Ce'_m(\xi _o,-q_{(I)})-\alpha _bFek'_m(\xi _o,-q_{(I)}), x_{11}=Ce'_m(\xi _o,q_{(II)}), x_{12}=Fek'_m(\xi _o,q_{(II)}), \end{aligned}$$
(31d)

and so:

$$\begin{aligned} s_1= & {} \int _0^{2\pi }ce_m(\eta ,-q_{(I)})ce_n(\eta ,q_{(II)}) {\mathrm{d}}\eta ~, \end{aligned}$$
(32)
$$\begin{aligned} s_2= & {} \int _0^{2\pi }ce_m(\eta ,q_{(II)})ce_n(\eta ,q_{(II)}) {\mathrm{d}}\eta ~, \end{aligned}$$
(33)
$$\begin{aligned} s_3= & {} \int _0^{2\pi }ce'_m(\eta ,-q_{(I)})ce_n(\eta ,q_{(II)}) {\mathrm{d}}\eta ~, \end{aligned}$$
(34)
$$\begin{aligned} s_4= & {} \int _0^{2\pi }ce'_m(\eta ,q_{(II)})ce_n(\eta ,q_{(II)}) {\mathrm{d}}\eta ~. \end{aligned}$$
(35)
Fig. 2
figure 2

Plot of the dispersion curves in the elliptical plasma waveguide. The solid curve is for the normalized \(\frac{\omega _+}{\omega _p}\) and the dashed curve is for the normalized \(\omega _-\) , a \(\frac{\omega _c}{\omega _p}=1.86\), b \(\frac{\omega _c}{\omega _p}=0.5\)

Full size image
Fig. 3
figure 3

Plot of the normalised \(\omega _-\)  as a function of the normalized wavenumber and  \(\frac{\omega _c}{\omega _p}\) in the elliptical plasma waveguide, a higher normalized frequency, b lower normalized frequency

Full size image
Fig. 4
figure 4

Plot of the normalised potential versus  \(\xi ~,~\eta \) in the elliptical plasma waveguide, a Even mode, b Odd mode

Full size image
Fig. 5
figure 5

Plot of the normalised  \(E_\xi \)  versus  \(\xi ,~\eta \) in the elliptical plasma waveguide for  \(m=r=1\), a Even mode, b Odd mode

Full size image
Fig. 6
figure 6

Plot of the normalised \(E_\eta \) versus \(\xi , \eta \) in the elliptical plasma waveguide for  \(m=r=1\), a Even mode, b Odd mode

Full size image
Fig. 7
figure 7

Plot of the normalised potential versus  \(\xi ~,~\eta \) in the coaxial elliptical waveguide consisting of vacuum-plasma-vacuum ,for even mode, a \(\phi ^{(I)}-\xi ~,~\eta \), b \(\phi ^{(II)}-\xi ~,~\eta \), c \(\phi ^{(III)}-\xi ~,~\eta \)

Full size image
Fig. 8
figure 8

Plot of the normalized components of electric field versus  \(\xi , \eta \) in the coaxial elliptical waveguide consisting of vacuum-plasma-vacuum, for even mode, a \(E_\xi ^{(I)}-\xi ~,~\eta \), b \(E_\eta ^{(I)}-\xi ~,~\eta \)

Full size image
Fig. 9
figure 9

Plot of the normalized components of electric field versus  \(\xi , \eta \) in the coaxial elliptical waveguide consisting of vacuum-plasma-vacuum,for even mode, a \(E_\xi ^{(II)}-\xi , \eta \), b \(E_\eta ^{(II)}-\xi , \eta \)

Full size image
Fig. 10
figure 10

Plot of the normalized components of electric field versus \(\xi , \eta \) in the coaxial elliptical waveguide consisting of vacuum-plasma-vacuum,for even mode, a \(E_\xi ^{(III)}-\xi , \eta \), b \(E_\eta ^{(III)}-\xi , \eta \)

Full size image

3 Space-Charge Waves in the Metallic Elliptical Waveguide Filled by Plasma

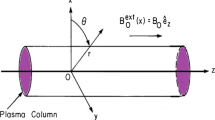
In this section, we consider an elliptical waveguide filled by plasma with elliptical boundary \(\xi _b\). The constant static magnetic field is along the axis of the waveguide, \(B_0\hat{z}\). This configuration is shown in Fig. 1. We use the linearized Poisson,continuity and momentum equations. Therefore, for space-charge waves propagating in the z direction,the perturbed potential, \(\delta \tilde{\phi }\), satisfies in the following equation:

$$\begin{aligned} \frac{1}{h^2}(\frac{\partial ^2}{\partial \xi ^2}+\frac{\partial ^2}{\partial \eta ^2})\delta \tilde{\phi }(\xi ,\eta ) +\kappa ^2\delta \tilde{\phi }(\xi ,\eta )=0. \end{aligned}$$
(36)

Equation (36) has the even and odd solutions [11]as follows:

$$\begin{aligned} \delta \phi (\xi ,\eta ,z,t)=\sum _{m=0}^\infty \sum _{r=1}^\infty C_mCe_m(\xi ,q_{m.r})ce_m(\eta ,q_{m.r})\exp [i(kz-\omega t)] +\sum _{m=1}^\infty \sum _{r=1}^\infty S_mSe_m(\xi ,\bar{q}_{m,r})se_m(\eta ,\bar{q}_{m,r})\exp [i(kz-\omega t)] \end{aligned}$$
(37)

The boundary condition is \(\delta \phi =0\)  at the boundary of elliptical \(\xi _b\). It means \(Ce_m(\xi _b,q)=0~,~Se_m(\xi _b,q)=0\). Therefore the even solution is:

$$\begin{aligned} \delta \tilde{\phi }_{m}(\xi ,\eta )= C_m Ce_m(\xi ,q_{m,r})ce_m(\eta ,q_{m,r}) \end{aligned}$$
(38)

In the electrostatic approximation, the dispersion relation for space-charge waves in the considered structure for even mode is given by:

$$\begin{aligned} \frac{k^2(\omega _c^2-\omega ^2)(\omega _p^2-\omega ^2)}{\omega _p^2(\omega _p^2+\omega ^2-\omega ^2)}-\frac{4q_{m,r}}{d^2}=0~, \end{aligned}$$
(39)

The solutions of Eq. (39) are expressed as higher and lower frequency:

$$\begin{aligned} \omega _{\pm }^2=\frac{1}{2}\left[ (\omega _p^2+\omega _c^2)\pm \sqrt{(\omega _p^2+\omega _c^2)^2-\frac{4k^2d^2\omega _p^2\omega _c^2}{k^2d^2+4q_{m,r}}}\right] , \end{aligned}$$
(40)

In the electrostatic approximation, the electric field components can be expressed as:

$$\begin{aligned} E_\xi= & {} -\frac{1}{h} C_m Ce'_m(\xi ,q_{m,r})ce_m(\eta ,q_{m,r})\exp [i(kz-\omega t)] \end{aligned}$$
(41)
$$\begin{aligned} E_\eta= & {} -\frac{1}{h} C_m Ce_m(\xi ,q_{m,r})ce'_m(\eta ,q_{m,r})\exp [i(kz-\omega t)] \end{aligned}$$
(42)
$$\begin{aligned} E_z= & {} -ik C_m Ce_m(\xi ,q_{m,r})ce_m(\eta ,q_{m,r})\exp [i(kz-\omega t)] \end{aligned}$$
(43)

and the velocity perturbations are:

$$\begin{aligned}&\delta {\tilde{v}}_\xi =\frac{e}{m_e(\omega ^2-\omega _c^2)h} \left[ i\omega C_m Ce'_m(\xi ,q_{m,r})ce_m(\eta ,q_{m,r})\omega _c C_mCe_m(\xi ,q_{m,r})ce'_m(\eta ,q_{m,r})\right] \exp [i(kz-\omega t)], \end{aligned}$$
(44)
$$\begin{aligned}&\quad \delta {\tilde{v}}_\eta =\frac{e}{m_e(\omega ^2-\omega _c^2)h} \left[ i\omega C_m Ce_m(\xi ,q_{m,r})'_m(\eta ,q_{m,r})\omega _c C_mCe'_m(\xi ,q_{m,r})ce_m(\eta ,q_{m,r})\right] \exp [i(kz-\omega t)], \end{aligned}$$
(45)
$$\begin{aligned}&\quad \delta {\tilde{v}}_z=\frac{ike}{m_e} C_m Ce_m(\xi ,q_{m,r})ce_m(\eta ,q_{m,r})\exp [i(kz-\omega t)]~, \end{aligned}$$
(46)

and so the density perturbation is calculated as follows:

$$\begin{aligned} \delta {\tilde{n}}=\frac{\varepsilon _0}{e}(\kappa ^2+k^2)C_m Ce_m(\xi ,q_{m,r})ce_m(\eta ,q_{m,r})\exp [i(kz-\omega t)]. \end{aligned}$$
(47)

4 Numerical Results

In this section, we investigate the numerical results for two considered configurations.

We consider the typical values for the elliptic boundary in the considered configuration and so we choose the special mode \(m=1\).

Figure 2a, b illustrates the dispersion curves for space-charge waves in the elliptical magnetized plasma waveguide for \(\frac{\omega _c}{\omega _p}=1.86\) and \(\frac{\omega _c}{\omega _p}=0.5\), respectively.

Variations of the normalized frequency \(\frac{\omega }{\omega _p}\) as functions of  \(\frac{\omega _c}{\omega _p}\) and normalized wave number in a completely filled plasma elliptical waveguide for the normalized higher and lower frequency are seen in Fig. 3a, b, respectively.

The plots of the normalized potential as functions of \(\xi , \eta \) in the completely filled plasma elliptical waveguide, for even and odd modes are seen in Fig. 4a, b, respectively.

We plot the normalized \(\xi \) component of electric field, \(E_\xi \), versus \(\xi , \eta \) in the completely filled plasma elliptical waveguide, for even and odd modes, in Fig. 5a, b, respectively.

Figure 6a, b illustrates the normalized \(E_\eta \)  as functions of  \(\xi ~,~\eta \) in the completely filled plasma elliptical waveguide, for even and odd modes, respectively.

Figure 7a–c shows the plots of the normalized potential versus \(\xi , \eta \) in the coaxial elliptical waveguide including an annular vacuum-plasma-vacuum, for even mode, in I, II and III regions, respectively.

Figure 8a, b illustrates the normalized \(E_\xi \) and \(E_\eta \) versus \(\xi , \eta \) in the coaxial elliptical waveguide including an annular vacuum-plasma-vacuum, for even mode in the vacuum region (I).

Figure 9a, b illustrates the normalized \(E_\xi \) and \(E_\eta \) versus \(\xi ~,~\eta \) in the coaxial elliptical waveguide including an annular vacuum-plasma-vacuum, for even mode in the plasma region (II).

Figure 10a, b illustrates the normalized \(E_\xi \) and \(E_\eta \)  versus \(\xi , \eta \) in the coaxial elliptical waveguide including an annular vacuum-plasma-vacuum, for even mode in the vacuum region (III).

For waves to propagate: it is necessary that \(\kappa ^2>0\). For the case  \(\omega _c > \omega _p\), the mode \(\omega < \omega _p\)  is predicted from the case of  \(B_0=\infty \), and so the upper hybrid mode \(\omega _c<\omega < \sqrt{\omega _p^2+\omega _c^2}\) is appeared as a characteristic frequency in the plasma. This mode has is a backward wave. When the magnetic field is further reduced  \(\omega _p > \omega _c\), it is seen that waves propagate for \(\omega < \omega _c\). The backward wave mode now propagates in the frequency range \(\omega _p<\omega < \sqrt{\omega _p^2+\omega _c^2}\). For the case of  \(B_0=0\), the upper pass band reduces to the plasma resonance at \(\omega _p\) and the lower pass band reduces towards \(\omega =0\). In both cases, the waves cease to propagate. That is, surprisingly, a plasma-filled waveguide without an external magnetic field will not propagate a space-charge wave. However, the waves will propagate even when \(B_0=0\)  if the plasma does not fill the waveguide. This is because filling the waveguide had eliminated the possibility of surface waves [17].

5 Conclusions

In this paper, we considered two configurations: one is a coaxial elliptical waveguide, including an annular vacuum-magnetized plasma-vacuum, and another is an elliptical waveguide filled by magnetized plasma. We considered magnetized collisionless cold plasma and applied the electrostatic approximation and neglected the effects of ion motions and electron temperature. In two structures, the propagation of space-charge waves was studied. The electric potentials and fields for the all spatial regions in the coaxial elliptical waveguide and the elliptical plasma waveguide in terms of Mathieu functions in the electrostatic approximation were presented. Dispersion relation, components of the electric field, and electron velocity in two configurations were calculated. Numerical calculations were done, and the results were plotted. We ignored from different effects. We considered the mode with \(m=1\). It is possible excitation of surface wave modes at the boundaries of structures, but in this investigation we ignored from effect of surface waves. Furthermore, we note that in this study, we investigated the space charge waves in the two elliptical structures only via the considered mode. We have assumed the different approximates and neglected the different effects and so the results are approximately analysed in these structures. Regardless of the fact that they are approximate, the results presented in this article are still useful for the analysis of the considered problem, although.