1 Introduction

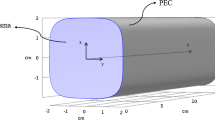
The Piet Hein coaxial waveguide consists of an internal solid metallic rod cylinder with a Piet Hein curve cross section surrounded by a hollow cylindrical metal shell having a Piet Hein curve cross section. The space between two conductors can be filled with vacuum, dielectric, plasma, etc.

Various waveguides have cross sections with different shapes such as rectangular, circular, elliptical, triangular, annular, Piet Hein, cardiodic and other cross sections [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. Since rectangular and circular waveguides are necessary for different systems, a waveguide with a cross-sectional located in the middle between the circle and the rectangle will be very attractive. A waveguide with the cross section of the Piet Hein curve only satisfies these conditions and offers interesting results. The special feature of such a structure is that it basically has the properties of the circular waveguide and elliptical waveguide. These waveguides will be very useful, because due to the special structure of such waveguides, adverse effects such as wave scattering, etc., are not expected to happen. These effects may be present in rectangular waveguides due to the sharp corners, which have some effect on the wave propagation. Of course, a new cross section is not chosen arbitrarily for the waveguide, but it is a systematic choice. Some geometries are modified or distorted cross sections of circles and rectangles. The geometry of Piet Hein is in the middle of the two. Configurations are determined so that mathematical analysis is possible. The main issue is to understand how distorting the cross section of a waveguide or introducing a new substance can change modal behavior. A comparative study has been conducted on the subject of modal properties and scattering of optical waveguides with Piet Hein section [12]. For a structure consisting of an annular optical Piet Hein waveguide, theoretical analysis and scattering curves are investigated [13]. The dispersion properties of an optical Piet Hein waveguide that has a conductive sheath helical have been investigated [14]. On the other hand, plasma can be used to support very high electric fields. Therefore, to accelerate the charged particles, waveguides containing plasma can be used. One of the interesting applications of plasma waveguides is their use in charged particle accelerators. It is clear that the type of waveguide cross section can play an important role in this goal. Much research has been done by researchers on the acceleration and dynamics of charged particles in waveguides with rectangular, triangular, circular and elliptical cross sections [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30].

However, the coaxial waveguide consists of a hollow conductive shell and a solid conductor rod that is coaxial with the shell. The cross section of the shell and rod can be designed in circular, elliptical, Piet Hein curve shapes, etc. The coaxial devices are capable of generating higher power than conventional cylindrical devices. Recently, a method has been proposed to achieve high power at a given wavelength with lower beam energy. In this method, a free laser electron can be used using an annular electron beam in a coaxial waveguide [31,32,33]. Coaxial waveguides have many applications and many studies have been done about them [34,35,36,37]. The high-frequency eigenmodes of a coaxial waveguide including a magnetized annular plasma have been analyzed [34]. Propagation of electromagnetic waves in a magnetized plasma coaxial waveguide has been studied [35]. Electron energy gain in the transverse electric mode of a coaxial plasma waveguide has been studied [36]. Furthermore, propagation of space-charge waves through a coaxial waveguide with circular cross section and containing an annular magnetized plasma has been investigated [37].

It is mentioned that Piet Hein waveguide has already been studied in the field of optical works, but the main and novel idea of our work is to use these types of waveguides containing plasma and in the microwave range.

In this work, we consider a metallic Piet Hein coaxial waveguide that it is contained cold unmagnetized plasma. The basic equations and the wave equation are presented in this structure and its solutions are expressed, approximately. Here, the propagating waves can be divided into two basic sets of modes. For transverse magnetic modes (TM), the magnetic field component along the propagation direction is equal to zero. For the transverse electric field modes (TE), the electric field has a zero component along the propagation direction. The dispersion relation and fields for TM and TE modes are obtained in the considered structure and plotted. The motion of an electron injected into the structure was investigated and analyzed numerically and graphically. In the paper, Introduction is presented as Sect. 1. In Sect. 2, basic equations in the Piet Hein waveguide and wave equation in this geometry considering a suitable approximation are presented. In Sect. 3, the electromagnetic field for TM mode and dispersion relation in the Piet Hein plasma coaxial waveguide are obtained and plotted. Electron movement injected into the considered coaxial waveguide was investigated and analyzed for TM mode numerically and graphically. In Sect. 4, the electromagnetic field for TE mode and dispersion relation in the structure are obtained and plotted. Electron movement injected into the Piet Hein waveguide was investigated and analyzed for TE mode numerically and graphically. Conclusion is expressed in Sect. 5.

Fig. 1
figure 1

Geometry of cross-sectional of Piet Hein coaxial waveguide

Full size image

2 Basic equations in the Piet Hein waveguide

We consider a Piet Hein waveguide and the following equation is defined as:

$$\begin{aligned} \left( {\frac{x}{{a_{0} }}} \right) ^{n} + \left( {\frac{y}{{b_{0} }}} \right) ^{n} = 1 , \end{aligned}$$
(1)

\(a_0\)  and  \(b_0\)  introduce as the semi diameters of the curve and we have considered  \(n = 4\) , \(a_0=b_0=a\) . The Piet Hein curve as the shape of the cross section of the considered waveguide is presented by the relation:

$$\begin{aligned} x^4+y^4=a^4, \end{aligned}$$
(2)

We introduce a suitable coordinate  \((\rho ,\xi ,z)\)  for the study of the considered cross section. Furthermore, we introduce the curves as follow:

$$\begin{aligned} x^4+y^4=\rho ^4, \end{aligned}$$
(3)

and the curves perpendicular to above curves as:

$$\begin{aligned} \frac{1}{x^2}-\frac{1}{y^2}=\frac{1}{\xi ^2}, \end{aligned}$$
(4)

Therefore, \(\rho =constant\) shows a Piet Hein curve. Figure 1 shows curves of, \(\rho =constant\) and, \(\xi =constant\) for different values of, \(\rho \) and, \(\xi \). The scale factors \(h_\rho , h_\xi \) and \(h_z\) can be calculated as follows:

$$\begin{aligned}&\displaystyle h_\rho =\frac{\rho ^3}{\sqrt{A[\xi ^2+\rho ^2-\xi ^2\sqrt{\xi ^2+\rho ^2}]}}, \end{aligned}$$
(5)
$$\begin{aligned}&\displaystyle h_\xi =\frac{\sqrt{\xi ^2+\rho ^2}-\xi ^2}{\sqrt{A(\xi ^2+\rho ^2)}}, \end{aligned}$$
(6)
$$\begin{aligned}&\displaystyle h_z=1, \end{aligned}$$
(7)

where we introduce parameter A as:

$$\begin{aligned} A=\sqrt{\left[ \sqrt{\xi ^2+\rho ^2}+\xi ^2\right] ^2-4\xi ^4}, \end{aligned}$$
(8)
Fig. 2
figure 2

Dispersion curves for electromagnetic waves of purposed TM mode in the plasma Piet Hein coaxial waveguide

Full size image
Fig. 3
figure 3

Electric and magnetic fields for purposed TM mode in the plasma Piet Hein coaxial waveguide as function of \(\rho \) and  \(\xi =const.\), for first solution of Eq. (14)

Full size image
Fig. 4
figure 4

Electric and magnetic fields for purposed TM mode in the plasma Piet Hein coaxial waveguide as function of \(\rho \) and  \(\xi =const.\), for second solution of Eq. (14)

Full size image
Fig. 5
figure 5

Electric and magnetic fields for purposed TM mode in the plasma Piet Hein coaxial waveguide as functions of \(\rho \) and z and  \(\xi =const.\), for first solution of Eq. (14)

Full size image
Fig. 6
figure 6

Electric and magnetic fields for purposed TM mode in the plasma Piet Hein coaxial waveguide as functions of \(\rho \) and z and  \(\xi =const.\), for second solution of Eq. (14)

Full size image

Using the Maxwell equations and considering the time dependence as \(e^{i\omega t}\) , one can obtain the longitudinal component of electric or magnetic fields by solving the Helmholtz wave equation inside the waveguide [12, 13, 38]:

$$\begin{aligned} \left[ \nabla ^2+\frac{\omega ^2}{c^2}\varepsilon \right] \left( \begin{array}{c} E_z(\rho ,\xi ,z)\\ B_z(\rho ,\xi ,z)\\ \end{array} \right) =0, \end{aligned}$$
(9)

where \(\omega \) is the angular frequency, and  \(\varepsilon \)  is the dielectric constant of the waveguide region. When the medium inside the waveguide is filled with a homogeneous cold plasma, the dielectric constant of cold plasma is defined as:  \(\varepsilon =(1-\frac{\omega _p^2}{\omega ^2})\) where  \(\omega _p=( n_0e^2/m_e \varepsilon _0)^{\frac{1}{2}}\) is the plasma frequency and  \(n_0\)  is the density of electrons in the plasma and  \(\varepsilon _0\)  is the electric permittivity in free space and for free space  \(\varepsilon =1\) . It is assumed that \(E_z=E_z(\rho ,\xi )e^{i(\omega t-\beta z)}\) and \(B_z=B_z(\rho ,\xi )e^{i(\omega t-\beta z)}\), therefore:

$$\begin{aligned}&\frac{3A\sqrt{\xi ^4+\rho ^4}}{\rho ^7} \left[ \sqrt{\xi ^4+\rho ^4}-\xi ^2 \right] \frac{\partial E_z(B_z)}{\partial \rho } +\frac{A\xi ^2}{\rho ^6} \left[ \sqrt{\xi ^4+\rho ^4}-\xi ^2 \right] \frac{\partial ^2E_z(B_z)}{\partial \rho ^2}\nonumber \\&\quad +\frac{3A\xi }{\left[ \sqrt{\xi ^4+\rho ^4}-\xi ^2 \right] }\frac{\partial E_z(B_z)}{\partial \xi } \nonumber \\&\quad +\frac{A\sqrt{\xi ^4+\rho ^4}}{\left[ \sqrt{\xi ^4+\rho ^4}-\xi ^2 \right] }\frac{\partial ^2 E_z(B_z)}{\partial \xi ^2} +\left( \frac{\omega ^2}{c^2}\varepsilon -\beta ^2 \right) E_z(B_z)_z=0, \end{aligned}$$
(10)

By applying the approximation  \(\rho \ll \xi \) and using the technique of separation of variables and considering  \( E_z(B_z)=F(\rho )G(\xi )\), the above equation is converted to two following equations as:

$$\begin{aligned}&\displaystyle \frac{\rho ^6}{\sqrt{2}}\frac{1}{F(\rho )}\frac{\partial ^2 F(\rho )}{\partial \rho ^2}+\frac{3\rho ^5}{\sqrt{2}}\frac{1}{F(\rho )}\frac{\partial F(\rho )}{\partial \rho }+(\frac{\omega ^2}{c^2}\varepsilon -\beta ^2)F(\rho )=\alpha , \end{aligned}$$
(11)
$$\begin{aligned}&\displaystyle 4\sqrt{2}\xi ^6\frac{1}{G(\xi )}\frac{\partial ^2 G(\xi )}{\partial \xi ^2}+12\sqrt{2}\xi ^5\frac{1}{G(\xi )}\frac{\partial G(\xi )}{\partial \xi }=-\alpha , \end{aligned}$$
(12)

where \(\alpha \) is separation constant. Here, we consider the simplest solution with \(\alpha =0\), and considering this assumption, two differential equations are obtained as follows:

$$\begin{aligned}&\displaystyle \frac{\partial ^2 F(\rho )}{\partial \rho ^2}+\frac{3}{\rho }\frac{\partial F(\rho )}{\partial \rho }+\sqrt{2}(\frac{\omega ^2}{c^2}\varepsilon -\beta ^2)F(\rho )=0, \end{aligned}$$
(13)
$$\begin{aligned}&\displaystyle \frac{\partial ^2 G(\xi )}{\partial \xi ^2}+\frac{3}{\xi }\frac{\partial G(\xi )}{\partial \xi }=0, \end{aligned}$$
(14)

The second-order differential Eq. (14) has two solutions. The first solution is equivalent to a constant amount and the second solution is a function of  \(\xi \).

Fig. 7
figure 7

Trajectory of electron in the plasma Piet Hein coaxial waveguide for purposed TM mode

Full size image
Fig. 8
figure 8

Changes of kinetic energy of electron in the plasma Piet Hein coaxial waveguide with for purposed TM mode

Full size image
Fig. 9
figure 9

Changes of angle \(\theta \)  versus z  in the plasma Piet Hein coaxial waveguide with for purposed TM mode

Full size image
Fig. 10
figure 10

Dispersion curves for electromagnetic waves of purposed TE mode in the plasma Piet Hein coaxial waveguide

Full size image
Fig. 11
figure 11

Electric and magnetic fields for purposed TE mode in the plasma Piet Hein coaxial waveguide as function of \(\rho \) and  \(\xi =const.\), for first solution of Eq. (14)

Full size image
Fig. 12
figure 12

Electric and magnetic fields for purposed TE mode in the plasma Piet Hein coaxial waveguide as function of \(\rho \) and  \(\xi =const.\), for second solution of Eq. (14)

Full size image
Fig. 13
figure 13

Electric and magnetic fields for purposed TE mode in the plasma Piet Hein coaxial waveguide as functions of \(\rho \) and z and  \(\xi =const.\), for first solution of Eq. (14)

Full size image
Fig. 14
figure 14

Electric and magnetic fields for purposed TE mode in the plasma Piet Hein coaxial waveguide as functions of \(\rho \) and z and  \(\xi =const.\), for second solution of Eq. (14)

Full size image
Fig. 15
figure 15

Trajectory of electron in the plasma Piet Hein coaxial waveguide for purposed TE mode

Full size image
Fig. 16
figure 16

Changes of kinetic energy of electron in the plasma Piet Hein coaxial waveguide with for purposed TE mode

Full size image
Fig. 17
figure 17

Changes of angle \(\theta \)  versus z  in the plasma Piet Hein coaxial waveguide with for purposed TE mode

Full size image

3 Electromagnetic fields in the Piet Hein coaxial waveguide containing plasma for TM mode

Now we consider a Piet Hein coaxial waveguide [13] filled by cold unmagnetized homogeneous plasma with inner Piet Hein metallic boundary \(\rho =a\) and outer Piet Hein metallic boundary \(\rho =b\). We assume an electromagnetic radiation for excitation of the  TM  mode in the direction of the z-axis. We use Maxwell’s equation, boundary conditions  \(E_z|_{\rho =a}=0\) , \(E_z|_{\rho =b}=0\) , considered approximation in Sect. 2, \(\rho \ll \xi \), and Eqs. (13, 14). Then, we calculate the electromagnetic field components of the TM mode as follows:

$$\begin{aligned} E_z= & {} \frac{A}{Y_1(ka)}\frac{1}{\rho }[ Y_1(ka)J_1(k\rho )- J_1(ka)Y_1(k\rho )]G(\xi )exp(i(\omega t-\beta z+\delta )), \end{aligned}$$
(15)
$$\begin{aligned} E_\rho= & {} -\frac{i\beta }{h_\rho (\frac{\omega ^2}{c^2}\varepsilon -\beta ^2)}\frac{A}{Y_1(ka)}\left[ -\frac{1}{\rho ^2}[ Y_1(ka)J_1(k\rho )- J_1(ka)Y_1(k\rho )\right] \nonumber \\&+\frac{1}{\rho }[ Y_1(ka)J'_1(k\rho )- J_1(ka)Y'_1(k\rho )]]G(\xi )exp(i(\omega t-\beta z+\delta )), \end{aligned}$$
(16)
$$\begin{aligned} E_\xi= & {} -\frac{i\beta }{h_\xi (\frac{\omega ^2}{c^2}\varepsilon -\beta ^2)}\frac{A}{Y_1(ka)}\frac{1}{\rho }[ Y_1(ka)J_1(k\rho )- J_1(ka)Y_1(k\rho )]\nonumber \\&\times G'(\xi )exp(i(\omega t-\beta z+\delta )), \end{aligned}$$
(17)
$$\begin{aligned} B_\rho= & {} \frac{i\omega \varepsilon _0\mu _0\varepsilon }{h_\xi (\frac{\omega ^2}{c^2}\varepsilon -\beta ^2)}\frac{A}{Y_1(ka)}\frac{1}{\rho }[ Y_1(ka)J_1(k\rho )- J_1(ka)Y_1(k\rho )]\nonumber \\&\times G'(\xi )exp(i(\omega t-\beta z+\delta )), \end{aligned}$$
(18)
$$\begin{aligned} B_\xi= & {} -\frac{i\omega \varepsilon _0\mu _0\varepsilon }{h_\rho (\frac{\omega ^2}{c^2}\varepsilon -\beta ^2)}\frac{A}{Y_1(ka)}\bigg [-\frac{1}{\rho ^2}\left[ Y_1(ka)J_1(k\rho )- J_1(ka)Y_1(k\rho )\right] \nonumber \\&+\frac{1}{\rho }\left[ Y_1(ka)J'_1(k\rho )- J_1(ka)Y'_1(k\rho )\right] \bigg ]G(\xi )exp(i(\omega t-\beta z+\delta )), \end{aligned}$$
(19)

where

$$\begin{aligned} k=\sqrt{\sqrt{2}(\frac{\omega ^2}{c^2}\varepsilon -\beta ^2)}~,~\varepsilon =1-\frac{\omega _p^2}{\omega ^2}, \end{aligned}$$
(20)

\(\omega _P=\sqrt{\frac{ne^2}{\varepsilon _0 m_e}}\) is plasma frequency, n is electrons density, \(-e\)  is the charge of electron, \(m_e\)  is the electron mass, and  \(\beta \) is wavenumber.

The dispersion function in the supposed plasma Piet Hein coaxial waveguide is obtained by applying the mentioned suitable boundary conditions in the boundaries \(\rho =a\)  \(\rho =b\). Then, the dispersion equation is calculated as:

$$\begin{aligned} J_1(ka)Y_1(kb)- J_1(kb)Y_1(ka)=0 \end{aligned}$$
(21)

We plotted the dispersion relation related to these waves in Fig. 2.

Figures 3, 4, 5 and 6 show the components of electric and magnetic fields for the considered TM mode.

3.1 Electron movement in the plasma-containing Piet Hein coaxial waveguide for TM mode

In this subsection, we assume that an electron is injected in the cold plasma Piet Hein coaxial waveguide and accelerate under the purposed TM mode of electromagnetic wave. We want to study the variation of energy and the path of an electron in the purposed coaxial waveguide. The Lorentz and energy equations are written in the purposed coaxial waveguide. To investigate the behavior of electrons inside this coaxial waveguide, we solve the following equations by the fourth-order Runge–Kutta numerical method. The Lorentz and energy equations for electrons in Cartesian coordinates are written as follows:

$$\begin{aligned} \frac{d(\gamma m_ev_x) }{dt}= & {} -e[E_x+v_y B_z-v_z B_y], \end{aligned}$$
(22)
$$\begin{aligned} \frac{d(\gamma m_ev_y) }{dt}= & {} -e[E_y+v_z B_x-v_x B_z)], \end{aligned}$$
(23)
$$\begin{aligned} \frac{d(\gamma m_ev_z) }{dt}= & {} -e[E_z+v_x B_u-v_y B_x], \end{aligned}$$
(24)

and:

$$\begin{aligned} \frac{d(\gamma m_ec^2)}{dt}=-e(v_x E_x+v_y E_y+v_z E_z), \end{aligned}$$
(25)

It is mentioned that we consider the first solution of Eq. (14). In Fig. 7, we plotted the path of the electron in the purposed coaxial waveguide. Figure 8 illustrates the kinetic energy in the plasma Piet Hein coaxial waveguide for different values of  \(\delta \). Figure 9 presents the angle \(\theta =\arctan \sqrt{p_x^2+p_y^2}/p_z\) in the plasma Piet Hein waveguide for different values of \(\delta \).

4 Electromagnetic fields in the Piet Hein coaxial waveguide containing plasma for TE mode

Similar to Sect. 3, we consider a Piet Hein coaxial waveguide filled by cold unmagnetized plasma and an electromagnetic radiation for excitation of the TE mode in the direction of the z-axis. We use Maxwell’s equation, boundary condition  \(E_\xi |_{\rho =a}=0\) , considered approximation Sect. 2 , \(\rho \ll \xi \), and Eqs. (13, 14). Then, we calculate the field components of for TE mode as follows:

$$\begin{aligned} E_\rho =-\frac{i\omega \mu _0}{h_\xi (\frac{\omega ^2}{c^2}\varepsilon -\beta ^2)}\frac{A}{\alpha _2}\frac{1}{\rho }[\alpha _2J_1(k\rho )-\alpha _1Y_1(k\rho )]G'(\xi )exp(i(\omega t-\beta z+\delta )), \end{aligned}$$
(26)
$$\begin{aligned} E_\xi= & {} \frac{i\omega \mu _0}{h_\rho (\frac{\omega ^2}{c^2}\varepsilon -\beta ^2)}\frac{A}{\alpha _2}[-\frac{1}{\rho ^2}[\alpha _2J_1(k\rho )- \alpha _1Y_1(k\rho )]+\frac{1}{\rho }[\alpha _2J'_1(k\rho )-\alpha _1Y'_1(k\rho )]]\nonumber \\&\times G(\xi )exp(i(\omega t-\beta z+\delta )), \end{aligned}$$
(27)
$$\begin{aligned} B_\rho= & {} -\frac{i\beta \mu _0}{h_\rho (\frac{\omega ^2}{c^2}\varepsilon -\beta ^2)}\frac{A}{\alpha _2} [-\frac{1}{\rho ^2}[\alpha _2J_1(k\rho )-\alpha _1Y_1(k\rho )]+\frac{1}{\rho }[\alpha _2J'_1(k\rho )- \alpha _1Y'_1(k\rho )]]\nonumber \\&\times G(\xi )exp(i(\omega t-\beta z+\delta )), \end{aligned}$$
(28)
$$\begin{aligned} B_\xi =-\frac{i\beta \mu _0}{h_\xi (\frac{\omega ^2}{c^2}\varepsilon -\beta ^2)}\frac{A}{\alpha _2}\frac{1}{\rho }[\alpha _2J_1(k\rho )-\alpha _1Y_1(k\rho )]G'(\xi )exp(i(\omega t-\beta z+\delta )), \end{aligned}$$
(29)
$$\begin{aligned} B_z=\frac{A}{\alpha _2}\mu _0\frac{1}{\rho }[\alpha _2J_1(k\rho )-\alpha _1Y_1(k\rho )]G(\xi )exp(i(\omega t-\beta z+\delta )), \end{aligned}$$
(30)

where:

$$\begin{aligned} \alpha _1=-\frac{1}{a}J_1(ka)+J'_1(ka)~,~\alpha _2=-\frac{1}{a}Y_1(ka)+Y'_1(ka), \end{aligned}$$
(31)
$$\begin{aligned} \alpha _3=-\frac{1}{b}J_1(kb)+J'_1(kb)~,~\alpha _4=-\frac{1}{b}Y_1(kb)+Y'_1(kb), \end{aligned}$$
$$\begin{aligned} k=\sqrt{\sqrt{2}(\frac{\omega ^2}{c^2}\varepsilon -\beta ^2)}~,~\varepsilon _p=1-\frac{\omega _p^2}{\omega ^2}, \end{aligned}$$

By applying boundary condition, the dispersion equation is calculated as:

$$\begin{aligned} \alpha _1\alpha _4-\alpha _2\alpha _3=0 \end{aligned}$$
(32)

We plotted the dispersion relation related to these waves in Figs. 10, 11, 12, 13 and 14 show the variations of the real part of electric and magnetic fields components for considered TE mode.

4.1 Electron movement in the plasma-containing Piet Hein coaxial waveguide for TE mode

Similar to Subsect. 3.1, we examine the electron movement in the cold plasma Piet Hein waveguide that accelerates under the purposed TE mode of electromagnetic wave. Here again, we choose the first solution of Eq. (14). In Fig. 15 we plotted the path of the electron in the purposed waveguide. Figure 16 illustrates the kinetic energy in the plasma Piet Hein waveguide for different values of \(\delta \) . Figure 17 presents the angle \(\theta =\arctan \sqrt{p_x^2+p_y^2}/p_z\) in the plasma Piet Hein waveguide for different values of  \(\delta \).

5 Conclusions

In this work, solutions of wave equation a metallic Piet Hein coaxial waveguide containing cold unmagnetized plasma were approximately presented. The components of electromagnetic field for TM and TE modes in the plasma coaxial waveguide with Piet Hein cross section were obtained and fields are plotted for different cases. Using the boundary conditions in the considered coaxial waveguide, the dispersion relations for two considered modes were derived. Dispersion relation and obtained fields were plotted. The motion of an electron injected in the metallic Piet Hein coaxial waveguide including cold homogeneous unmagnetized plasma in the presence of TM and TE modes excited by electromagnetic radiation wave graphically investigated. The differential equations appeared to be solved using the Runge–Kutta numerical method. Numerical calculations were done, and the results were plotted. It is mentioned that we consider a suitable approximation and ignored from different effects. We used the special modes. It is possible excitation of surface wave modes at the boundaries of structures, but in this investigation, we ignored the effect of surface waves and so on. Here, we assume that the nonlinear effects to be negligible in this work. We have assumed the different approximates and neglected the different effects and so the results in these structures are investigated approximately. Regardless of their approximation, the results presented in this paper are still useful for problem analysis.