1 Introduction

The perfect electromagnetic conductor (PEMC) [1, 2] is the generalization of a perfect electric conductor (PEC) and perfect magnetic conductor (PMC) [3]. Electromagnetic energy and power cannot enter into the PEMC medium because the real values of the admittance M, the complex Poynting vector becomes imaginary [4,5,6]. The boundary conditions at the surface of the PEMC are expressed in the forms [2]:

$$\begin{aligned} \hat{n} \times (\vec{H} + M\vec{E}) = 0 \end{aligned}$$
$$\begin{aligned} \hat{n}\cdot (\vec{D}-M\vec{B})=0 \end{aligned}$$

where M is the admittance parameter, and it determines the PEMC. In the limits \(M = 0\) and \(M \rightarrow \pm \infty\), the PEMC converts to PMC and PEC, respectively.

Waveguides with different materials have different applications in terahertz, microwave, millimeter, and light waves. Depending on the application of the waveguide, they have different cross-sections and are filled with different materials. Waveguides with PEMC boundaries are of particular importance in the field of wave propagation description [7,8,9]. A lot of research has been done on the use of PEMC materials [10,11,12]. Much research has been performed by researchers on particulate acceleration and electron dynamics in the different types of waveguides with various cross-sections and different materials, considering various effects. Some researchers have investigated the acceleration and dynamics of electrons with different EM modes of microwave propagation inside elliptical, circular, and rectangular waveguides containing cold plasma, warm plasma, magnetized plasma, collision plasma, collisionless plasma, homogeneous plasma, inhomogeneous plasma, etc. [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27].

It is mentioned that PMC boundaries ensure two useful and interesting features. First, PMC cannot allow EM waves and currents to enter the surface. Second, PMC surfaces have a very high surface impedance in a certain limited frequency range, and PMC surfaces reflect EM waves without phase change of the electric field [28].

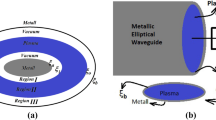
In the present work, we study wave propagation in the elliptical and circular waveguides filled with a magnetized plasma core and a PEMC boundary as a wall.

We investigate the effect of the PEMC boundary on the EM field propagation and the power flux density in the mentioned waveguides. We investigate the effect of the PEMC boundary on the energy and dynamics of an injected electron in elliptical and circular waveguides filled with magnetized plasma. We calculate the dispersion functions applied to get the modes.

The present paper is formed into four sections, of which Sect. 1 is the Introduction. Section 2 deals with the calculation of the fields and power flux, and also the dispersion relation, of the hibrid modes in an elliptical waveguide filled by magnetized plasma (MPEW): magnetized plasma elliptical waveguide, core, and a cover PEMC boundary, considering the appropriate boundary conditions. The results are plotted. The effect of the PEMC boundary on the energy and trajectory of an injected electron in the considered configuration is investigated. In Sect. 3, we investigate the fields and power flux, and also the dispersion relation, of the hybrid modes in a circular waveguide filled by magnetized plasma (MPCW): magnetized plasma circular waveguide, core, and a cover PEMC boundary, considering the appropriate boundary conditions. The results are plotted. The effect of the PEMC boundary on the energy and dynamics of an injected electron in the considered configuration is investigated. Finally, the conclusion is stated in Sect. 4.

2 Investigation of the Effect of PEMC Wall in the MPEW Coated with a PEMC

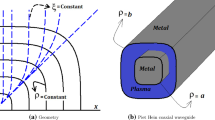
We consider an MPEW coated with a PEMC. An elliptical boundary bounds the plasma, indicated by \(\zeta =\zeta _0\), and the plasma is in the constant magnetic field \(\vec{B}=B_0\hat{z}\).

Elliptical coordinates are indicated by \((\zeta ,\vartheta ,z)\) and are expressed as [29]

$$\begin{aligned} x=l\cosh \zeta \cos \vartheta ~,~~y=l\sinh \zeta \sin \vartheta ~~,~~z=z, \end{aligned}$$
(1)

where \(l=\sqrt{a_{xB}^2-a_{yB}^2}~\) is the semi-focal length, \(a_{xB}\) and \(a_{yB}\) are defined as the semi-major and minor axes of the boundary with ellipse form, and the boundary is indicated by \(\zeta _{B}=arctanh(a_{yB}/a_{xB})\).

The wave equations for \(E_z\) and \(H_z\) are calculated as

$$\begin{aligned} \left[ \nabla _T^4 + \varsigma 1\nabla _T^2 +\varsigma _2\right] \left( \begin{array}{c} E_z(\zeta ,\vartheta ) \\ H_z(\zeta ,\vartheta )\\ \end{array} \right) =0 \end{aligned}$$
(2)

where

$$\begin{aligned} \varsigma _1=-\frac{\beta ^2\varepsilon _P}{\varepsilon _T}+\frac{\omega ^2\varepsilon _P}{c^2}+\frac{\omega ^2}{c^2}\frac{\varepsilon _T^2-g^2}{\varepsilon _T}-\beta ^2 \end{aligned}$$
(3)
$$\begin{aligned} \varsigma _2=(-\frac{\beta ^2\varepsilon _P}{\varepsilon _T}+\frac{\omega ^2\varepsilon _P}{c^2})(\frac{\omega ^2}{c^2}\frac{\varepsilon _T^2-g^2}{\varepsilon _T}-\beta ^2)-\frac{g^2\varepsilon _P\beta ^2\omega ^2}{c^2\varepsilon _T^2} \end{aligned}$$
(4)
$$\begin{aligned} \nabla _T=\frac{1}{h^2}\frac{\partial ^2}{\partial \zeta ^2}+\frac{1}{h^2}\frac{\partial ^2}{\partial \vartheta ^2} \end{aligned}$$
(5)

Here, \(h=l\sqrt{cosh^2\xi -cos^2\eta }\), and \(\beta\) is the axial component of the wave number vector of the propagating wave. Furthermore, the dielectric tensor \(\tilde{\varepsilon }\) of the magnetized plasma is indicated as

$$\begin{aligned} \tilde{\varepsilon }=\left( \begin{array}{ccc} \varepsilon _T &{} ig&{} 0 \\ -ig&{} \varepsilon _T &{} 0 \\ 0 &{} 0 &{} \varepsilon _P \\ \end{array} \right) \end{aligned}$$
(6)

where g, \(\varepsilon _T\), and \(\varepsilon _P\) are defined as follows:

$$\begin{aligned} \varepsilon _T=1-\frac{\omega _p^2}{\omega ^2-\omega _c^2}~~,~~ g=-\frac{\omega _p^2\omega _c}{\omega (\omega ^2-\omega _c^2)}~~,~~\varepsilon _P=1-\frac{\omega _p^2}{\omega ^2} \end{aligned}$$
(7)

Here, \(\omega _p=(n_0e^2/m_e \varepsilon _0)^{\frac{1}{2}}\) and \(\omega _c=eB_0/m_e\) are defined as the electron plasma and cyclotron frequencies, respectively.

The EM fields can be written in the form of transverse and longitudinal components as

$$\begin{aligned} \vec{E}=\vec{E}_T+\hat{e}_zE_z \end{aligned}$$
(8)
$$\begin{aligned} \vec{H}=\vec{H}_T+\hat{e}_zH_z \end{aligned}$$
(9)

We consider the longitudinal and transverse filed components for the hybrid mode in the magnetized plasma region as

$$\begin{aligned} E_z(\zeta ,\vartheta ,z,t) =&\;\sum _{m=0}^\infty [C_{1m} Ce_m(\zeta ,q_1)ce_m(\vartheta ,q_1)\\&+ C_{2m} Ce_m(\zeta ,q_2)ce_m(\vartheta ,q_2)]e^{i(\omega t -\beta z+\delta )}, \end{aligned}$$
(10)
$$\begin{aligned} H_z(\zeta ,\vartheta ,z,t) =&\;\sum _{m=0}^\infty -i[h_1C_{1m} Ce_m(\zeta ,q_1)ce_m(\vartheta ,q_1)\\&+h_2C_{2m} Ce_m(\zeta ,q_2)ce_m(\vartheta ,q_2)]e^{i(\omega t -\beta z+\delta )}, \end{aligned}$$
(11)
$$\begin{aligned} \left( \begin{array}{c} E_\zeta (\zeta ,\vartheta )\\ E_\vartheta (\zeta ,\vartheta )\\ H_\zeta (\zeta ,\vartheta ) \\ H_\vartheta (\zeta ,\vartheta )\\ \end{array} \right) =\left( \begin{array}{cccc} \varrho _{11} &{} \varrho _{12} &{} \varrho _{13} &{} \varrho _{14} \\ \varrho _{21} &{} \varrho _{22} &{} \varrho _{23} &{} \varrho _{24} \\ \varrho _{31} &{} \varrho _{32} &{} \varrho _{33} &{} \varrho _{34} \\ \varrho _{41} &{} \varrho _{42} &{} \varrho _{43} &{}\varrho _{44} \\ \end{array} \right) \left( \begin{array}{c} \frac{1}{h}\frac{\partial H_z(\zeta ,\vartheta )}{\partial \zeta } \\ \frac{1}{h} \frac{\partial H_z(\zeta ,\vartheta )}{\partial \vartheta } \\ \frac{1}{h}\frac{\partial E_z(\zeta ,\vartheta )}{\partial \zeta }\\ \frac{1}{h}\frac{\partial E_z(\zeta ,\vartheta )}{\partial \vartheta } \\ \end{array} \right) \end{aligned}$$
(12)

where \(C_{1m}\) and \(C_{2m}\) are constants, and so \(Ce_m(\vartheta ,q_i)\) and \(Ce_m(\zeta ,q_i)\) are defined as the even solutions of the angular and radial Mathieu equations [29]. Furthermore,

$$\begin{aligned} \varrho _{11}=\frac{\omega ^3}{c^2}\mu _0g\chi _2~~,~~ \varrho _{12}=-i\omega \mu _0\chi _1\chi _2~~,~~ \end{aligned}$$
(13)
$$\begin{aligned} \varrho _{13}=-i\beta \chi _1\chi _2~~,~~\varrho _{14}=-\frac{\omega ^2}{c^2}\beta g\chi _2~~,~~ \end{aligned}$$
$$\begin{aligned} \varrho _{21}=i\omega \mu _0g\chi _1\chi _2~~,~~ \varrho _{22}=\frac{\omega ^3}{ c^2}\mu _0g\chi _2~~,~~ \end{aligned}$$
$$\begin{aligned} \varrho _{23}=\frac{\omega ^2}{c^2}\beta g\chi _2~~,~~\varrho _{24}=-i\beta \chi _1\chi _2~~,~~ \end{aligned}$$
$$\begin{aligned} \varrho _{31}=-i\beta \chi _1\chi _2~~,~~ \varrho _{32}=-\frac{\omega ^2}{ c^2}g\chi _2~~,~~\end{aligned}$$
(14)
$$\begin{aligned} \varrho _{33}=-\frac{\omega \beta ^2}{\mu _0c^2}g\chi _2~~,~~\varrho _{34}=\frac{i}{\omega \mu _0}\chi _3 \chi _2~~,~~ \end{aligned}$$
$$\begin{aligned} \varrho _{41}=\frac{\omega ^2}{c^2}\beta \chi _2~~,~~\varrho _{42}=-i\beta \chi _1\chi _2~~,~~ \end{aligned}$$
$$\begin{aligned} \varrho _{43}=-i\frac{1}{\mu _0c^2}\chi _3\chi _2~~,~~\varrho _{44}=-\frac{\omega \beta ^2}{\mu _0}g \chi _2~~,~~ \end{aligned}$$

where

$$\begin{aligned} \chi _1=-\beta ^2+\frac{\omega ^2\varepsilon _T}{c^2}~~,~~\chi _2=\frac{1}{\chi _1^2-\frac{g^2\omega ^4}{c^4}}~~,~~ \chi _3=\chi _1\frac{\omega ^2\varepsilon _T}{c^2}-\frac{\omega ^4g^2}{c^4}, \end{aligned}$$
(15)

and also

$$\begin{aligned} \iota _{1,2}^2=\frac{1}{2\varepsilon _T}\left[ -(\varepsilon _T+\varepsilon _P)\beta ^2+\frac{\omega ^2}{c^2}(\varepsilon _T\varepsilon _P+\varepsilon _T^2-g^2)\right] \end{aligned}$$
(16)
$$\begin{aligned} \pm \frac{1}{2\varepsilon _T}\left\{ \left[ -(\varepsilon _P-\varepsilon _T)\beta ^2+\frac{\omega ^2}{c^2}(\varepsilon _T\varepsilon _P-\varepsilon _T^2+g^2)\right] ^2+\frac{4\omega ^2\beta ^2}{c^2}\varepsilon _T^2\varepsilon _P\right\} ^{\frac{1}{2}} \end{aligned}$$
$$\begin{aligned} h_{1,2}=\frac{\varepsilon _T}{\mu _0\omega \beta g}(\frac{\omega ^2\varepsilon _P}{c^2}-\frac{\beta ^2\varepsilon _P}{\varepsilon _T}-p_{1,2}^2) \end{aligned}$$
(17)

where \(q_1=\frac{l^2\iota _1^2}{4}\) and \(q_2=\frac{l^2\iota _2^2}{4}\). In this study we choose \(\iota ^2_{1,2}~>0\). It is noted that the frequency-wavenumber plane can be divided into regions in which \(\iota _{1,2}^2>0\), \(\iota _{1,2}^2<0\), and \(\iota _{1,2}^2\) are complex [30].

2.1 Dispersion Equation

Using the correct and appropriate boundary conditions, the dispersion equation is derived. The PEMC boundary conditions are expressed as [2, 9]

$$\begin{aligned} H_z|_{\zeta =\zeta _0}+M E_z|_{\zeta =\zeta _0}=0 \end{aligned}$$
(18)
$$\begin{aligned} H_\vartheta |_{\zeta =\zeta _0}+M E_\vartheta |_{\zeta =\zeta _0}=0 \end{aligned}$$
(19)

The dispersion equation is derived from the above boundary by setting the condition that the determinant of the coefficients of these equations becomes equal to zero:

$$\begin{aligned} DR=a_{11}a_{22}-a_{12}a_{21} \end{aligned}$$
(20)

where

$$\begin{array}{l} a_{11}=T_1s_1~,\\ a_{12}=T_2s_2~,\\ a_{21}=(T_3+T_5)s_1+(T_4+T_6)s_3~,\\ a_{22}=(T_7+T_9)s_2+(T_8+T_{10})s_4~,~ \end{array}$$
(21)
$$\begin{array}{l} T_1=(-ih_1+M)Ce_m(\zeta _0,q_1)~,\\ T_2=(-ih_2+M)Ce_m(\zeta _0,q_2)~,~ \end{array}$$
(22)
$$\begin{aligned} T_3=-i(\beta k_0^2+M\omega \mu _0k_0^2)g\chi _2h_1Ce'_m(\zeta _0,q_1)~,~ \end{aligned}$$
(23)
$$\begin{aligned} T_4=-(\beta +M\omega \mu _0)\chi _1\chi _2h'_1Ce_m(\zeta _0,q_1)~,~ \end{aligned}$$
(24)
$$\begin{aligned} T_5=-i(\frac{\chi _3}{\omega \mu _0} +M\beta \chi _1)\chi _2Ce'_m(\zeta _0,q_1)~,~ \end{aligned}$$
(25)
$$\begin{aligned} T_6=-(\frac{\beta ^2k_0^2}{\omega \mu _0} +M\beta k_0^2)g\chi _2Ce_m(\zeta _0,q_1)~,~ \end{aligned}$$
(26)
$$\begin{aligned} T_7=-i(\beta k_0^2+M\omega \mu _0k_0^2)g\chi _2h_2Ce'_m(\zeta _0,q_2)~,~ \end{aligned}$$
(27)
$$\begin{aligned} T_8=-(\beta +M\omega \mu _0)\chi _1\chi _2h_2Ce_m(\zeta _0,q_2)~,~ \end{aligned}$$
(28)
$$\begin{aligned} T_9=-i(\frac{\chi _3}{\omega \mu _0} +M\beta \chi _1)\chi _2Ce'_m(\zeta _0,q_2)~,~ \end{aligned}$$
(29)
$$\begin{aligned} T_{10}=-(\frac{\beta ^2k_0^2}{\omega \mu _0} +M\beta k_0^2)g\chi _2Ce_m(\zeta _0,q_2)~,~ \end{aligned}$$
(30)

and

$$\begin{aligned} s_1=\int _0^{2\pi }ce_n(\vartheta ,q_1)ce_m(\vartheta ,q_1) d\vartheta , \end{aligned}$$
(31)
$$\begin{aligned} s_2=\int _0^{2\pi }ce_n(\vartheta ,q_1)ce_m(\vartheta ,q_2) d\vartheta , \end{aligned}$$
(32)
$$\begin{aligned} s_3=\int _0^{2\pi }ce_n(\vartheta ,q_1)ce'_m(\vartheta ,q_1) d\vartheta , \end{aligned}$$
(33)
$$\begin{aligned} s_4=\int _0^{2\pi }ce_n(\vartheta ,q_1)ce'_m(\vartheta ,q_2) d\vartheta . \end{aligned}$$
(34)

2.2 Injected Electron Dynamics in the MPEW with PEMC Wall

Now, we study the effect of the PEMC wall on the dynamics of injected electrons in the MPEW. For this aim, we use the Lorentz and energy equations for electrons:

$$\begin{aligned} \frac{d(\gamma m_ev_x) }{dt}=-e[E_x+v_y B_z+v_y B_0-v_z B_y], \end{aligned}$$
(35)
$$\begin{aligned} \frac{d(\gamma m_ev_y) }{dt}=-e[E_y+v_z B_x-v_x B_z-v_x B_0)], \end{aligned}$$
(36)
$$\begin{aligned} \frac{d(\gamma m_ev_z) }{dt}=-e[E_z+v_x B_u-v_y B_x], \end{aligned}$$
(37)

and

$$\begin{aligned} \frac{d(\gamma m_ec^2)}{dt}=-e(v_x E_x+v_y E_y+v_z E_z), \end{aligned}$$
(38)

\(-e\) is the electron charge and \(m_e\) is the rest mass of the electron. We solve the above equations by the fourth-order Runge–Kutta method.

For numerical investigation, we consider that an electron with an initial energy of  20 keV  is injected into the waveguide with plasma density \(\sim 10^{17} m^{-3}\), and assume \(m=1, n=1\).

In Fig. 1, we plotted dispersion curves for different values of the PEMC admittance parameter, M , in the MPEW coated with a PEMC. Figure 2 shows the variation of the power flux density versus \(\zeta\) and \(\vartheta\) in the MPEW coated with a PEMC. The power flux density can be calculated as follows: \(S_z=\frac{1}{2}Re(E_\zeta H^*_\vartheta -E_\vartheta H^*_\zeta )\).

Fig. 1
figure 1

Plot of DR versus normalized wave number, \(\beta l\), for different values of M in the MPEW coated with a PEMC

Full size image
Fig. 2
figure 2

Plot of the power flux density versus \(\zeta\) and \(\vartheta\) in the MPEW coated with a PEMC

Full size image

In Fig. 3, we plotted the three-dimensional trajectory of the electron in the MPEW coated with a PEMC, for different values of the M parameter. We considered \(M_1=0.002\), \(M_2=0.006\), and \(M_3=0.01\).

Fig. 3
figure 3

Electron trajectory for different values of M in the MPEW coated with a PEMC

Full size image

Figure 4 illustrates the energy of the electron in the MPEW coated with a PEMC for different values of the M parameter. We considered \(M_1=0.002\), \(M_2=0.01\), and \(M_3=0.1\).

Fig. 4
figure 4

Electron energy for different values of M in the MPEW coated with a PEMC

Full size image

3 Investigation of the Effect of PEMC Wall in the MPCW Coated with a PEMC

The wave equations for \(E_z\) and \(H_z\) are obtained as the following forms:

$$\begin{aligned} E_z(\rho ,\phi ,z,t) =\sum _{m=0}^\infty [J_{1m} J_m(p_1\rho )+ J_{2m} J_m(p_2\rho )]e^{i(\omega t -\beta z+m\phi +\delta )}, \end{aligned}$$
(39)
$$\begin{aligned} H_z(\rho ,\phi ,z,t) =\sum _{m=0}^\infty -i[h_1J_{1m} J_m(p_1\rho )+h_2J_{2m} J_m(p_2\rho )]e^{i(\omega t -\beta z+m\phi +\delta )}, \end{aligned}$$
(40)

Furthermore, transverse electric and magnetic field components are obtained in the following forms:

$$\begin{aligned} \left( \begin{array}{c} E_\rho (\rho ,\phi )\\ E_\phi (\rho ,\phi )\\ H_\rho (\rho ,\phi ) \\ H_\phi (\rho ,\phi )\\ \end{array} \right) =\left( \begin{array}{cccc} \varrho _{11} &{} \varrho _{12} &{} \varrho _{13} &{} \varrho _{14} \\ \varrho _{21} &{} \varrho _{22} &{} \varrho _{23} &{} \varrho _{24} \\ \varrho _{31} &{} \varrho _{32} &{} \varrho _{33} &{} \varrho _{34} \\ \varrho _{41} &{} \varrho _{42} &{} \varrho _{43} &{}\varrho _{44} \\ \end{array} \right) \left( \begin{array}{c} \frac{\partial H_z(\rho ,\phi )}{\partial \rho } \\ \frac{1}{\rho } \frac{\partial H_z(\rho ,\phi )}{\partial \phi } \\ \frac{\partial E_z(\rho ,\phi )}{\partial \rho }\\ \frac{1}{\rho }\frac{\partial E_z(\rho ,\phi )}{\partial \phi } \\ \end{array} \right) \end{aligned}$$
(41)

Using the boundary conditions,

$$\begin{aligned} H_z|_{\rho =\rho _0}+M E_z|_{\rho =\rho _0}=0 \end{aligned}$$
(42)
$$\begin{aligned} H_\phi |_{\rho =\rho _0}+M E_\phi |_{\rho =\rho _0}=0, \end{aligned}$$
(43)

we obtain the dispersion relation

$$\begin{aligned} DR=a_{11}a_{22}-a_{12}a_{21} \end{aligned}$$
(44)

where we calculate

$$\begin{array}{l} a_{11}=T_1~,\\ a_{12}=T_2~,\\ a_{21}=(T_3+T_5)+(T_4+T_6)\frac{im}{\rho }~,\\ a_{22}=(T_7+T_9)s_2+(T_8+T_{10})\frac{im}{\rho }~,~ \end{array}$$
(45)
$$\begin{aligned} T_1=(-ih'_1+M)J_m(p_1\rho _0)~,~ T_2=(-ih'_2+M)J_m(p_2\rho _0)~,~ \end{aligned}$$
(46)
$$\begin{aligned} T_3=-i(\beta k_0^2+M\omega \mu _0k_0^2)g\chi _2h'_1J'_m(p_1\rho _0)~,~ \end{aligned}$$
(47)
$$\begin{aligned} T_4=-(\beta +M\omega \mu _0)\chi _1\chi _2h'_1J_m(p_1\rho _0)~,~ \end{aligned}$$
(48)
$$\begin{aligned} T_5=-i(\frac{\chi _3}{\omega \mu _0} +M\beta \chi _1)\chi _2J'_m(p_1\rho _0)~,~ \end{aligned}$$
(49)
$$\begin{aligned} T_6=-(\frac{\beta ^2k_0^2}{\omega \mu _0} +M\beta k_0^2)g\chi _2J_m(p_1\rho _0)~,~ \end{aligned}$$
(50)
$$\begin{aligned} T_7=-i(\beta k_0^2+M\omega \mu _0k_0^2)g\chi _2h'_2J'_m(p_2\rho _0)~,~ \end{aligned}$$
(51)
$$\begin{aligned} T_8=-(\beta +M\omega \mu _0)\chi _1\chi _2h'_2J_m(p_2\rho _0))~,~ \end{aligned}$$
(52)
$$\begin{aligned} T_9=-i(\frac{\chi _3}{\omega \mu _0} +M\beta \chi _1)\chi _2J'_m(p_2\rho _0)~,~ \end{aligned}$$
(53)
$$\begin{aligned} T_{10}=-(\frac{\beta ^2k_0^2}{\omega \mu _0} +M\beta k_0^2)g\chi _2J_m(p_2\rho _0)~.~ \end{aligned}$$
(54)

For numerical investigation, similar to the previous section, we calculate and plot the obtained results in the MPCW coated with a PEMC.

In Fig. 5, we plotted the three-dimensional trajectory of the electron in the MPCW coated with a PEMC, for different values of the PEMC admittance parameter. We considered \(M_1=0.001\) and \(M_2=0.004\). Figure 6 illustrates the energy of the electron in the MPCW coated with a PEMC, for different values of the M parameter. We considered \(M_1=0.001\), \(M_2=0.004\), and \(M_3=0.01\).

Fig. 5
figure 5

Electron trajectory for different values of M in the MPCW coated with a PEMC

Full size image
Fig. 6
figure 6

Electron energy for different values of M in the MPCW coated with a PEMC

Full size image

4 Conclusions

In this work, we considered MPEW and MPCW coated with a PEMC boundary as cover. The EM wave propagation in two considered waveguides was studied. Considering appropriate boundary conditions, dispersion relations for the hybrid modes were derived. The EM fields and the power flux density in the mentioned waveguides were presented. The effect of a PEMC boundary on the energy and dynamics of an injected electron in the two considered configurations was graphically studied. In the end, it seems necessary to mention that the obtained results are approximate and in the considered frequency and parameter range. Various effects may appear in practical applications. We omitted some effects. However, the results are good and acceptable.