1 Introduction

The generating mechanism of nerve impulse is one of most actively investigated problems in Neuroscience [1–16]. The interest in this problem is motived by the crucial need to understand characteristic properties of the action potential, assumed to be a propagating form of the transmembrane voltage along the axon. Pioneer in this endeavor, the Hodgkin–Huxley model [1, 2] rests on the picture of a reaction–diffusion process, in which the nerve impulse is an electric voltage propagating in form of an asymmetric pulse along the nerve fiber. Originally, this model was introduced to explain data obtained from measurements of conductive parameters of a nerve fiber, and particularly to show how these data could be used to directly calculate both the shape and velocity of an action potential on the squid giant axon [17].

From a general standpoint, the Hodgkin–Huxley model can be regarded as a cable model for the nerve [6, 19]. In this specific cable model, the nerve impulse is an electric wave associated with the flow of ion currents (Na\(^+\) and K\(^+\)) through specific ion channels. This self-regenerative wave propagates with a constant shape, through a mechanism that can be summarized as follows: during the generation and transmission of the nerve impulse, the leading edge of the depolarization region of the nerve triggers adjacent membranes to depolarize, causing a self-propagation of the excitation related to the transmembrane voltage down the nerve fiber [1, 18, 21]. Hodgkin and Huxley suggested that a most convenient way to describe the propagation of this transmembrane voltage is to view the nerve fiber as an electric cable. Thus, in its most conventional formulation, the Hodgkin–Huxley model assumes currents in intracellular and extracellular fluids to be ohmic, such that the net transmembrane current is the sum of ionic and capacitive currents. In this picture, the conservation law for currents passing through the membrane can be expressed [1]:

$$\begin{aligned} C_m\frac{\partial V}{\partial t}=D\frac{\partial ^2 V}{\partial x^2}-F(V), \end{aligned}$$
(1)

where V is the transmembrane voltage, \(C_m\) is the capacitance of the membrane capacitor, D is the diffusion coefficient and F accounts for contributions from some ion currents.

Besides the well-established electrical activity of the nerve membrane, observations [22–26] have also revealed the existence of mechanical constraints related to pressures due to fluid flows through the membrane. In ref. [27], these mechanical constraints have been associated with electromechanical forces responsible for mechanotransduction processes in the nerve. Concretely in the latter processes, pressures exerted by fluids across the cell membrane are assumed to trigger excitations of electrical natures that play important role in the control of various stimuli-responsive organs as well as in homeostasis of living organisms [27].

Heimburg and Jackson [7, 28] formulated the idea that mechanical forces, related to pressure waves, could play a major role in the nerve membrane excitation and subsequently in the buildup process of the nerve impulse. In this respect, they postulated that pressure waves associated with the propagation of the density difference between fluids flowing through the nerve membrane could actually be a mechanical manifestation of the action potential. Much recently there have been other attempts to revisit the mathematical description of the nerve impulse [29–33], with the common aim to combine electrical and mechanical processes in order to gain a better understanding of the mechanism underlying the nerve impulse generation.

In the present work, we consider a model describing an electromechanical process in the generation of the action potential. The model combines the cable model for the nerve impulse [6, 19], and the pressure-wave model proposed by Heimburg and Jackson [7]. The model assumes that the membrane capacitance changes with the difference in densities of ionic fluids simultaneously crossing the membrane, leading to a modified cable equation where the membrane capacitor now behaves like a “feedback” component reminiscent of a capacitive diode (i.e., VARACTOR) in a transmission line [34, 35]. Though our assumption of a density-dependent membrane capacitance is not supported by sound experimental evidences, it is relevant to recall that the membrane capacitance is well-known to strongly depend on diameter of the nerve assumed to be a cylindrical cable [6]. Therefore, since the nerve membrane is a non-rigid porous wall that undergoes structural deformations (i.e., expansion and contraction) due to mechanical (i.e., or pressure) forces created by the flow of ionic fluids along the nerve (see discussions e.g., of ref. [20]), it is reasonable to think that the nerve diameter is actually not constant as usually assumed, and consequently the membrane capacitance should change in response to the change in densities of the fluids flowing along the nerve.

In Sect. 2, we present the model, which consists of two nonlinear partial differential equations, namely the modified cable equation for the action potential and the Boussinesq-type equation for the density-difference wave [7]. In Sect. 3, we first consider the stationary regime for the modified cable equation. In this purpose, we use the exact one-soliton solution to the Korteweg-de Vries (KdV) equation, derived from the Boussinesq-type equation for the soliton model of the nerve [7], to recast the modified cable equation into a linear operator problem with zero eigenvalue. Three exact bound-state solutions to this linear operator problem are obtained analytically, for specific values of characteristic parameters of the model. In Sect. 4, numerical simulations of the modified cable equation are carried out assuming the three stationary solutions as initial profiles for the action potential. Section 5 presents a conclusion of our study.

2 The Model

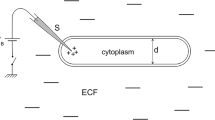
The axon can be regarded as a long cylinder with walls made of cell membrane surrounded by intracellular and extracellular fluids [2, 33]. The intracellular fluid stands for a conductive liquid with a high concentration of potassium ions but a low concentration of sodium and chlorine ions, while the cell membrane acts like a barrier preventing ions in the intracellular liquid from mixing with external solutions. Due to the difference in ion concentrations in intracellular and extracellular fluids, a resting potential is expected to set up through the membrane. If the nerve is depolarized, e.g., due to the presence of a stimulus of any kind, the axon membrane will become selectively permeable to ionic currents which flow rapidly into the cell, reversing the polarity of the action potential [1, 2].

In general, for a fixed number of charged lipids around the cell membrane, the charge density will be different because the respective lipid areas are different [27]. Therefore we can expect changes in the electrostatic potential of the membrane during a propagating pressure wave, indicating a possibility of an electromechanical coupling between the net fluid density and the electrostatic potential on the cell membrane. This electromechanical coupling, first reported by Petrov [36] and widely observed in recent experiments in neurophysiology [27, 29, 30, 37–39], can also be linked with changes in membrane capacitance as a result of variation of the fluid density through the membrane.

The model proposed in this study retains key ingredients of the cable model for the nerve [6, 19], except the membrane capacitance that will be assumed to vary instantly with the net fluid density crossing the membrane at a given time t. With these considerations the system dynamics can be described by the following set of two nonlinear space-time partial differential equations:

$$\begin{aligned} D\frac{\partial ^2 V}{\partial x^2}= & {} \frac{\partial }{\partial t} \bigg ( C_m(x,t) \,V\bigg ), \end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial ^2 U}{\partial t^2}&=c_0^2&\frac{\partial }{\partial x}\Bigg (B(U)\frac{\partial U}{\partial x}\Bigg )-h\frac{\partial ^4 U}{\partial x^4}. \end{aligned}$$
(3)

Equation (3), in which \(c_0\) is a characteristic velocity and h is a dispersion coefficient [40], is actually the most general form of density pulse equation [40], where the dimensionless variable \(U=\Delta \rho ^A/\rho _0^A\) represents the density difference \(\Delta \rho ^A=\rho ^A-\rho _0^A\) per unit of the homogeneous density \(\rho _0^A\). In this equation, the function B(U), which accounts for the phase transition in the so-called soliton model [7], was postulated to stand for an empirical function that can be expanded in powers of U as [40] \(B(U)\approx 1 + B_1 U + B_2U^2 + ...\), where \(B_1\) should be a negative real parameter and \(B_2\) a positive real parameter [40]. In the present study and as assumed in most studies on the soliton model, we shall retain only the linear term and set \(B_1=-1\), for simplicity. With this assumption, Eq. (3) reduces to:

$$\begin{aligned} \frac{\partial ^2 U}{\partial t^2}=c_0^2\frac{\partial }{\partial x}\Bigg ((1-U)\frac{\partial U}{\partial x}\Bigg )-h\frac{\partial ^4 U}{\partial x^4}. \end{aligned}$$
(4)

To represent the instantaneous change of the capacitance \(C_m\) of the membrane capacitor, due to variation of the ion-carrying fluid density [24, 25] across the membrane, we suppose that when the nerve is active, the rate of change of the membrane capacitance is proportional to the net density of ion-carrying fluid \(\Delta \rho ^A\) across the membrane, i.e.,

$$\begin{aligned} \frac{\partial C_m(x,t)}{\partial t}=\kappa \Delta \rho ^A, \end{aligned}$$
(5)

where \(\kappa\) is assumed positive. With assumption (5) Eq. (2) becomes:

$$\begin{aligned} C_m(x,t)\frac{\partial V}{\partial t}=D\frac{\partial ^2 V}{\partial x^2}-\kappa \Delta \rho ^A(x,t)V, \end{aligned}$$
(6)

where the membrane capacitance \(C_m(x,t)\) is now given by:

$$\begin{aligned} C_m(x,t)=C_a+\kappa \int {\Delta \rho ^A(x,t)dt}. \end{aligned}$$
(7)

Instructively, the value \(\kappa =0\) reproduces the familiar cable model for the nerve [6, 19]. However, for nonzero values of \(\kappa\), Eq. (6) gives rise to a modified cable equation whose solution depends on the spatiotemporal profile of the density-difference wave \(\Delta \rho ^A(x,t)\). In the next section, using the exact one-soliton solution to Eq. (4), we seek for possible analytical solutions to the modified cable Eq. (2). In this respect, we shall see that the modified cable equation is analytically tractable only in the steady-state regime. Indeed in this regime, the modified cable equation reduces to a linear-operator problem with zero eigenvalue, the bound states of which are Legendre polynomials [41].

3 Stationary Solutions to the Action-potential Equation

Introducing new coordinates, namely

$$\begin{aligned} U(x,t)=\psi (\xi ,T), \xi =c(\frac{x}{c_0}-t), T=\frac{h}{c}t, \end{aligned}$$
(8)

and integrating once with respect to the new variable \(\xi\), Eq. (4) reduces to the KdV equation [42]:

$$\begin{aligned} \frac{\partial \psi }{\partial T}=\alpha \psi \frac{\partial \psi }{\partial \xi }-\beta \frac{\partial ^3 \psi }{\partial \xi ^3}, \end{aligned}$$
(9)

where \(\alpha\) and \(\beta\) are constants depending on \(c_0\), h and c. In principle, the parameters \(\alpha\) and \(\beta\) can be set to any values through judicious coordinate transformations; however, we shall retain the most widely used values of these parameters, i.e., \(\alpha =6\) and \(\beta =-1\) [42]. For these specific values, Eq. (9) admits exact one and n-soliton solutions [42]. Focusing on the one-soliton solution, the inverse-scattering transform suggests the following analytical expression:

$$\begin{aligned} U(x,t)=-2sech^2(x-4t), \end{aligned}$$
(10)

which is a localized wave of compression. Using this localized pressure wave, associated with the difference in densities of fluids across the membrane, we can re-express the modified cable Eq. (6) as:

$$\begin{aligned} C_m(x,t)\frac{\partial V}{\partial t}=D\frac{\partial ^2 V}{\partial x^2}-\varepsilon U(x,t)V, \end{aligned}$$
(11)

where we defined \(\varepsilon =\kappa \rho _0\). Equation (11) needs to be fully solved in order to gain a consistent picture of the spatiotemporal evolution of the action potential V(x, t). But this equation is complex as it stands, and no exact analytical solution can be obtained. Nonetheless it is remarkable that at steady state, this equation reduces to the linear eigenvalue problem:

$$\begin{aligned} \Bigg ( \vartheta (x) -\frac{\partial ^2}{\partial x^2} \Bigg ) V(x)=0, \quad \vartheta (x)= -\mu \, sech^2 x, \end{aligned}$$
(12)

in which \(\mu =\frac{2\varepsilon }{D}\), and where we introduced the new voltage variable \(V(x)=V(x,0)\). By setting \(\tau =\tanh x\), Eq. (12) can be transformed into a Legendre equation of order n [41]:

$$\begin{aligned} \frac{d}{d\tau }\left\{ (1-\tau ^2)\frac{dV}{d\tau }\right\} +n(n+1)V=0, \end{aligned}$$
(13)

where \(n(n+1)=\mu\), n being a positive integer. Solutions to Eq. (13), for an arbitrary value of the positive integer n, are the Legendre polynomials:

$$\begin{aligned} V_n(\tau )=\frac{1}{2^n n!}\frac{d^n}{d\tau ^n}(\tau ^2-1)^n, \quad n=1,2,3, \cdots . \end{aligned}$$
(14)

The three first solutions, corresponding to \(n=\) 1, 2 and 3, respectively, are:

$$\begin{aligned} V_1(x)= & {} \tanh x, \quad D=2\epsilon , \end{aligned}$$
(15)
$$\begin{aligned} V_2(x)= & {} \frac{1}{2}(3 \tanh ^2 x - 1), \quad D=6\epsilon , \end{aligned}$$
(16)
$$\begin{aligned} V_3(x)= & {} \frac{1}{2}(5 \tanh ^2 x -3)\tanh x, \quad D=12\epsilon , \end{aligned}$$
(17)

These solutions are sketched in Fig. (1). Note that higher-order solutions (i.e., solutions corresponding to higher values of n) can be found analytically from the general formula Eq. (14), but here we consider only the above three solutions. In the next section, they will be used as initial profiles in numerical simulations of the modified cable Eq. (11) in the dynamic regime.

Fig. 1
figure 1

Sketches of the first three solutions to the action-potential Eq. (12) in stationary regime. From left to right: \(n=1\), 2, 3

Full size image

4 Travelling-wave Solutions to the Modified Cable Equation

The modified cable equation (11) is an initial-value problem, as such it can be solved numerically using a finite-difference algorithm. In our case, we adopt a finite-difference scheme that combines a central-difference approximation for time derivative and a forward-difference approximation for the second-order derivative in space [43]. The diffusion coefficient D, the bare membrane capacitance \(C_a\), the electromechanical coupling coefficient \(\kappa\) and the quantity \(\epsilon\) were chosen arbitrary in the simulations, for the present study is more descriptive than a quantitative analysis of the problem.

Figures 2, 3 and 4 show profiles of the transmembrane voltage V(x, t) at six different times t, generated numerically from the modified cable Eq. (11) for three distinct initial conditions corresponding to the stationary solutions (15) (Fig. 2), (16) (Fig. 3) and (17) (Fig. 4), respectively. Values of parameters are \(D=6\), \(C_a=2\), \(\kappa =0.3\) and \(\epsilon =3.3\).

Fig. 2
figure 2

(Color online) Profiles of the transmembrane voltage at different times t, obtained from numerical simulations of Eq. (11) with the bound state Eq. (15) used as initial solution: \(D=6.0\), \(C_a=2.0\), \(\kappa =0.3\), \(\epsilon =3.3\)

Full size image
Fig. 3
figure 3

(Color online) Profiles of the transmembrane voltage at different times t, obtained from numerical simulations of Eq. (11) with the bound state Eq. (16) used as initial condition: \(D=6.0\), \(C_a=2.0\), \(\kappa =0.3\), \(\epsilon =3.3\)

Full size image
Fig. 4
figure 4

(Color online) Profiles of the transmembrane voltage at different times t, obtained from numerical simulations of Eq. (11) with the bound state Eq. (17) used as initial condition: \(D=6.0\), \(C_a=2.0\), \(\kappa =0.3\), \(\epsilon =3.3\)

Full size image

In Fig. 2, where the initial profile of the transmembrane voltage \(V(x,t=0)\) is a kink given exactly by Eq. (15), it is seen that kink transforms gradually into a pulse upon propagation. At long term, the transmembrane voltage stabilizes in a typical asymmetric pulse characterized by a long trailing tail but a steep front [44,45,46,47,48]. A similar behaviour is also observed for the two other cases where the initial profiles of the transmembrane voltage are a pulse given by Eq. (16), and the kink-pulse structure given by Eq. (17). In clear, for the present model, the long-term shape of the propagating transmembrane voltage will always be an asymmetric pulse with a steep front and a trailing tail as observed in most experiments, irrespective of the initial profile determined by the stationary solution to the modified cable Eq. (12).

The spacetime evolutions of the three different numerical solutions shown in Figs. 2, 3 and 4 are represented in Figs. 5, 6 and 7 respectively. These three-dimensional representations provide more evidence of a similar shape profile for the three initial solutions, at long term.

Fig. 5
figure 5

(Color online) Spatiotemporal shape of the transmembrane voltage V(x, t), obtained numerically with the initial profile Eq. (15): \(\epsilon =2\), \(\kappa =0.3\), \(C_a=2.9\)

Full size image
Fig. 6
figure 6

(Color online) Spatiotemporal shape of the transmembrane voltage V(x, t), obtained numerically with the initial profile Eq. (16): \(\epsilon =2\), \(\kappa =0.3\), \(C_a=2.9\)

Full size image
Fig. 7
figure 7

(Color online) Spatiotemporal shape of the transmembrane voltage V(x, t), obtained numerically with the initial profile Eq. (17): \(\epsilon =2\), \(\kappa =0.3\), \(C_a=2.9\)

Full size image

5 Conclusion

Exploiting experimental evidences of the influence of electromechanical processes in the generation and propagation of the action potential [16, 27, 33, 46–48], we have proposed a model for this physiological phenomenon which combines two existing pictures, namely the electrical picture [1, 6, 19], which describes the nerve impulse as a pure electrical wave related to the voltage difference created by ions around the nerve membrane, and the hydrodynamic picture of Heimburg and Jackson [7] according to which the nerve membrane is instead a pressure wave, associated with the density difference of fluids flowing across the membrane. In the proposed model we kept the cable picture of the action potential, but assumed that the net charge stored in the membrane capacitor at a given time, was controlled by mechanosensory processes associated with pressure waves that are generated by the difference in densities of ion-carrying fluids flow across the membrane. In this respect, the mathematical formulation corresponding to the proposed model involves a combination of the KdV equation [7], and the cable equation but with a capacitor whose capacitance is a function of the net density of fluid crossing the nerve membrane. By assuming a simple linear relationship between the membrane capacitance and the density difference, we obtained that in steady-state regime, the modified cable equation governing the spacial profile of the action potential, can be reduced to the Legendre equation whose exact solutions are the familiar Legendre polynomials. Solving the full partial differential equation describing the spatiotemporal evolution of the transmembrane voltage, assuming the first three modes of the Legendre polynomials as initial profiles for the transmembrane voltage, we found that at long term, the transmembrane voltage always stabilizes in a typical pulse shape characterized by a long tail and a steep front.

We would like to point out that although there is no direct experimental evidence of some dependence of the membrane capacitance on the fluid density, it should be recalled that the membrane capacitance is well known to depend on the nerve diameter (assuming that the nerve is an electrical cable). It turns out that since the nerve membrane undergoes structural deformations, namely is expanded and contracted alternately as ionic fluids flow along the nerve cable, the nerve diameter cannot be constant as usually assumed. Hence, the membrane capacitance cannot be constant, instead the membrane capacitance should depend on the effective density of fluid flowing across the membrane. In the present study, a linear dependence of the membrane capacitance on the density difference was considered, of course we do not expect this linear dependence to reflect the exact physical reality. This simple case was considered to highlight the novel qualitative features expected from an account of electromechanical processes.