1 Introduction

Dusty plasmas have received a great deal of interest in the last few decades. Dust is ubiquitous in nebulas, in asteroid zones, in planetary magnetospheres, in interstellar clouds, in cometary environments (e.g. cometary comae and tails), on the surfaces of the Mars’ and Earth’s moon, and in the Earth’s polar mesosphere [1–5]. A dusty plasma is an electron-ion plasma with an additional component of small micron- sized highly charged dust [5]. This introduction of massive, charged dust component modify the existing linear wave modes and introduces new waves such as dust-acoustic (DA) wave, dust-ion-acoustic (DIA) wave, etc.

Rao et al. [6] first theoretically predicted the existence of dust-acoustic waves (DAWs) in an unmagnetized dusty plasma. After 5 years, Barkan et al. [7] experimentally studied the DAWs and verified the theoretical prediction of Rao et al. [6]. The DAWs which are now found to be very common in both space and laboratory devices [6–10], in which the inertia is provided by the dust particle mass and the restoring force, are provided by the pressures of the inertialess electrons and ions. A number of authors have studied nonlinear DAWs both theoretically [11–14] and experimentally [15–17] during the last few years.

A nonextensive distribution (q distribution) [18] is the most generalized distribution to study the linear and the nonlinear properties of shock waves (SHWs) in different plasma systems, where the non-equilibrium stationary states exist. The experimental results for electrostatic plane wave propagation in a collisionless thermal plasma have shown a transition to a class of Tsallis velocity distribution characterized by a nonextensive parameter q that is usually smaller than one [19]. Nowadays, the study of nonextensive plasma [18] has been received a great deal of interest to the plasma physics researchers due to its wide relevance in astrophysical and cosmological scenarios like protoneutron stars [20], stellar polytropes [21], hadronic matter and quark-gluon plasma [22], dark-matter halos [23], etc. Different types of waves such as DIAWs or DAWs or ion-acoustic waves or positron-acoustic waves have been studied in nonextensive plasmas by many authors considering one or two components to be nonextensive [24–26].

The shock structures arise due to the balance between the nonlinear effect and the dissipation. The dissipation arises due to Landau damping, kinematic viscosity among the plasma species, wave particle interaction, etc., which is responsible to form the shock structures in a plasma system [27]. The shock structures were found by Andersen et al. [28] in laboratory experiments such as Q-machine experiment. First observation of DASHWs was reported by Samsonov et al. [29] in a three-dimensional dusty plasma under microgravity condition. Already a large number of scientists have investigated SHWs both theoretically and experimentally in different plasma system. Shahmansouri and Tribeche [30] have studied the DASHWs in a charge varying dusty plasma with nonextensive ions as well as electrons. Tasnim et al. [31] considered two-temperature nonthermal ions and discussed the properties of SHWs. In the same year, Masud et al. [32–34] considered two-temperature electrons following Maxwellian distributions in a dusty plasma environment and analyzed both the solitary waves and the SHWs in respective articles. Recently, Alam et al. [35] considered kappa distributed electrons with two distinct temperatures and discussed the properties of DIASHWs. Very recently, Emamuddin et al. [24, 36] have studied the DA solitary structures in both magnetized and unmagnetized dusty plasma system with two-temperature nonextensive electrons and Maxwellian ions.

In our present manusript, we have considered the same plasma system considered by Emamuddin et al. [24, 36] but we have studied the shock structures in this plasma system. Our aim here is to investigate the shock wave properties and also to analyze their basic features (polarity, amplitude, width, etc.) in such a dusty plasma with two-temperature electrons.

The manuscript is organized as follows. The governing equations of the plasma fluid model are given in Section 2. In Section 3, the characteristics of linear waves are briefly summarized. In Section 4, we have derived Burgers equation using the reductive perturbation method. The numerical solution of Burgers equation is presented in Section 5. A brief discussion is finally presented in Section 6.

2 Governing Equations

We consider the nonlinear propagation of the DAWs in a collisionless and unmagnetized dusty plasma system consisting of negatively charged mobile dust, two-temperature electrons of temperature T e1 and T e2, and Maxwellian ions with temperature T i . The concept of two-temperature electrons (electrons with two distinct temperatures) is now well established from the theoretical [34–38] and experimental [39, 40] points of view. Thus, at equilibrium the quasi-neutrality condition implies, n i0=n e10+n e20+Z d n d0, where n s0 is the unperturbed number densities of the species s (here s=i, e1, e2, d for ion, electrons with temperature T e1, electrons with temperature T e2, and immobile dust, respectively) and Z d is the number of electrons residing onto the dust grain surface. We assume that T e2>T e1 so that the electron with temperature T e2 can be called a hot electron and the electron with temperature T e1 can be called a cold electron. The dynamics of the DAWs, whose phase speed is much smaller (larger) than the electrons (ions) thermal speed, can be described by using normalized equations of the forms

$$\begin{array}{@{}rcl@{}} &&\frac{\partial n_{d}}{\partial t}+\frac{\partial }{\partial x}(n_{d}u_{d})=0, \end{array} $$
(1)
$$\begin{array}{@{}rcl@{}} &&\frac{\partial u_{d}}{\partial t} + u_{d} \frac{\partial u_{d}} {\partial x} =\frac{\partial \psi} {\partial x}+\eta\frac{\partial^{2}u_{d}}{\partial x^{2}}, \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} &&\frac{\partial^{2}\psi}{\partial x^{2}}= -\mu_{i}e^{-\psi}+\left[\mu_{1}\{{1+(q-1)\sigma_{1}\psi}\}^{\frac{1+q}{2(q-1)}}\right]\\ &&+\left[\mu_{2}\{{1+(q-1)\sigma_{2}\psi}\}^{\frac{1+q}{2(q-1)}}\right] + n_{d}. \end{array} $$
(3)

where n d is the ion number density normalized by its equilibrium value n d0, u d is the dust fluid speed normalized by C d , ψ is the electrostatic wave potential normalized by T e /e, and η is the viscosity coefficient normalized by \(m_{d}n_{do}\omega _{pd}\lambda _{Dm}^{2}\). The time variable t is normalized by \(\omega _{pd}^{-1}=\left (m_{d}/4\pi e^{2}n_{d0}{Z_{d}^{2}}\right )^{1/2}\) and the space variable x is normalized by λ D m =(T i /4π e 2 n d0 Z d )1/2. We have defined the parameters μ s =n s0/Z d n d0 (here, s=i, e1, e2), σ 1=T i /T e1, and σ 2 = T i /T e2. Furthermore, T i; T e1, and T e2 are, respectively, the temperatures of the ions, the cold electrons, and the hot electrons in the units of energy. Consequently, the number densities [24, 41] of two-temperature nonextensive electrons, n e1 and n e2, are given respectively as

$$\begin{array}{@{}rcl@{}} n_{e1}=n_{e10}[(1+(q-1)e\psi/T_{e1}]^{\frac{1+q}{2(q-1)}}, \end{array} $$
(4)
$$\begin{array}{@{}rcl@{}} n_{e2}=n_{e20}[(1+(q-1)e\psi/T_{e2}]^{\frac{1+q}{2(q-1)}}. \end{array} $$
(5)

Here, q is the nonextensive parameter characterizing the degree of nonextensivity, and it is larger than −1. It is very important to note that when we take q→1, the particle density reduces to the well-known Maxwell-Boltzmann density. q<1 refers to the case of superextensivity [24–26], whereas q>1 refers to subextensivity [42].

3 Linear Waves

To analyze the characteristics of linear waves, we derive the linear dispersion relation for the plasma system under consideration here. We expand the dependent variables in (1)–(3) in a power series of 𝜖, as described below in (7)–(9), with the terms containing 𝜖 2 or higher neglected, and by replacing ∂/∂ t→−i ω and ∂/∂ x→i k, we get ω 2+i ω η k 2=k 2 C, where the parameter C is defined as C=1/2k 2+2μ i +(q+1)μ 1 σ 1+(q+1)μ 2 σ 2.

Now, we separate the dispersion relation into its real and imaginary parts by setting ω=ω R +i ω I , then we obtain \({\omega _{R}^{2}}-{\omega _{I}^{2}}-\omega _{I}\eta k^{2}=k^{2}C\) and ω R (2ω I +η k 2)=0 as the real and the imaginary parts, respectively. For nonzero real frequency, the imaginary part reduces to ω I =−k 2 η/2. This reflects the energy dissipation associated with the viscosity. Again substituting ω I =−k 2 η/2, we get the real angular frequency \(\omega _{R}=\sqrt {k^{2}C-k^{4}\eta ^{2}/4}\).

We first consider the nondissipative case (η=0), which leads to the dispersion relation ω 2=k 2 C \(\equiv {\omega _{0}^{2}}\), then we consider η=0.5 and 0.9, respectively. In Fig. 1, we have shown the real (positive, upper curves) and imaginary (negative, lower curves) parts of the linear dispersion relation for DAWs. It is observed that the real part of the wave frequency decreases (in absolute magnitude), while the imaginary part of the wave frequency increases (in absolute magnitude) with the increasing values of kinematic viscosity (i.e., dissipative effect) η (see Fig. 1).

Fig. 1
figure 1

Variation of the wave frequency ω with the wave vector k for different viscosity coefficient η. The upper (positive ω) curves are for real and the lower (negative ω) curves are for imaginary parts of the DAWs linear dispersion relation

Full size image

4 Nonlinear Waves

To derive a dynamical equation for the electrostatic DASHWs from our basic system of equations (1)–(3), we employ the reductive perturbation technique. We first introduce the stretched coordinates as [25, 34]

$$\begin{array}{@{}rcl@{}} &&\xi=\epsilon(x - V_{p}t),\qquad \tau={\epsilon}^{2}t. \end{array} $$
(6)

where 𝜖 is a smallness parameter measuring the weakness of the dispersion and V p is the phase speed of the DAWs. We can expand the perturbed quantities n d , u d , and ψ about the equilibrium values in power series of 𝜖 as

$$\begin{array}{@{}rcl@{}} &&n_{d}=1+\epsilon n_{d}^{(1)}+\epsilon^{2}n_{d}^{(2)}+\cdot \cdot \cdot, \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} &&u_{d}=0+\epsilon u_{d}^{(1)}+\epsilon^{2}u_{d}^{(2)}+\cdot \cdot \cdot, \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} &&\psi=0+\epsilon\psi^{(1)}+\epsilon^{2}\psi^{(2)}+\cdot \cdot \cdot, \end{array} $$
(9)

and develop equations in various powers of 𝜖. To the lowest order in 𝜖, (1)–(3) give

$$\begin{array}{@{}rcl@{}} &&u_{d}^{(1)}=-\frac{\psi^{(1)}}{V_{p}}, \end{array} $$
(10)
$$\begin{array}{@{}rcl@{}} &&n_{d}^{(1)}=-\frac{\psi^{(1)}}{{V_{p}^{2}}}, \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} &&V_{p}=\sqrt{\frac{1}{\mu_{i}}+\frac{2}{(q+1)(\mu_{1}\sigma_{1}+\mu_{2}\sigma_{2})}}. \end{array} $$
(12)

Equation (12) describes the phase speed of DAWs regarding the dusty plasma under consideration. To the next higher order of 𝜖, i.e., taking the coefficients of 𝜖 3 from (1) and (2), and 𝜖 2 (3), one may obtain another set of simultaneous equations for ψ (1)=ϕ, ψ (2), \(n_{d}^{(2)}\), and \(u_{d}^{(2)}\). After some algebraic calculation (omitted here), one may obtain the nonlinear Burgers type equation as

$$\begin{array}{@{}rcl@{}} &&\frac{\partial \phi}{\partial \tau}+A\phi\frac{\partial \phi}{\partial \xi}=C\frac{\partial^{2} \phi}{\partial\xi^{2}}, \end{array} $$
(13)

where the nonlinear coefficient A and the dissipative coefficient C are given by

$$\begin{array}{@{}rcl@{}} \left. \begin{array}{l} \!\!\!A=\!\frac{{V_{p}^{3}}}{2}\left[\mu_{i}\,+\,\frac{1}{ 4}(q\,+\,1)(q\,-\,3)\!\left(\mu_{1}{\sigma_{1}^{2}}\,+\,\mu_{2}{\sigma_{2}^{2}}\right)\,-\,\frac{3}{{V_{p}^{4}}}\right],\\ {\kern2pt} B=\frac{\eta}{2}. \end{array} \right\} \end{array} $$
(14)

5 Steady-State Solution of the Burgers Equation

The stationary shock wave solution of the Burgers equation (13) is obtained by transforming the independent variables to ζ=ξ−U 0 τ ′ and τ ′=τ, where U 0 is the speed of the shock waves, and imposing the appropriate boundary conditions, viz. ψ→0, d ψ/d ξ→0, d 2 ψ/d ζ 2→0 at ξ→±∞. Thus, one can express the stationary shock wave solution of the Burgers equation (13) as

$$\begin{array}{@{}rcl@{}} \psi=\psi_{m}{[1-\tanh}(\xi/\delta)], \end{array} $$
(15)

where the amplitude ψ m , and the width δ are given by

$$ \psi_{m}=U_{0}/A,\,\,\delta={2B/U_{0}}. $$
(16)

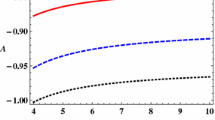
It is obvious from (15)–(16) that for vanishing nonlinear effect (i.e., for A=0), the amplitude of the SHWs approaches to infinity. This means that our theory is not valid when A∼0 which makes the amplitude extremely large and breaks down the validity of the reductive perturbation method. Thus, A=0 gives the critical value of the plasma parameters above/below which positive/negative potential structures may exist. We note that the nonlinearity coefficient A is a function of μ i , μ 1, μ 2, σ 1, σ 2, and q for the model under consideration in this manuscript. So, to find the parametric regimes corresponding to A=0, we have to express one (viz. q) of these parameters in terms of the others (viz. μ i , μ 1, μ 2, σ 1, and σ 2). Therefore, A(q = q c = 0) leads to the critical value of q (long expression →omitted here).

We find the critical value q=q c=−0.6 for a set of plasma parameters (viz. μ 1=0.2, μ 2=0.65, μ i =0.1, σ 1=0.5, and σ 2=0.25) [24] that means q<1 which is referred to the case of superextensivity [24–26]. The parametric regime for this set of values is shown in Fig. 2. Figures 3, 4, 5, 6, 7, 8, and 9 show how the nonextensivity of electrons and Maxwellian ions, electron-to-dust number density ratio, ion-to-dust number density ratio, and ion-to-electron temperature ratio affect on the formation of DASHWs. Figures 3 and 4 show the variation of amplitude of positive (at q<q c) and negative (at q>q c) SHWs with σ 2 and μ 2 keeping other plasma parameters fixed at σ 1=0.5, μ 1=0.2, μ i =0.1, and U 0=0.01. In Figs. 5 and 6 we observe the positive and negative shock structures for different values of the nonextensive index q for σ 1 = 0.5, σ 2 = 0.25, μ 1 = 0.2, μ 2 = 0.65, μ i =0.1, η = 0.1, and U 0=0.01. Figures 7 and 8 show the positive and negative potential SHWs for different values of μ 1. Figure 9 shows the variation of the width △ of the SHWs with kinematic viscosity η.

Fig. 2
figure 2

The A=0 graph which represent the variation of q c with σ 1 and σ 2, where q c is the critical value of nonextensive index q above or below which positive or negative shock structures are formed

Full size image
Fig. 3
figure 3

Showing the variation of amplitude of the positive shock potential with σ 2 and μ 2. The other plasma parameters are fixed at q = −0.85, σ 1 = 0.5, μ 1 = 0.2, μ i =0.1, and U 0 = 0.01

Full size image
Fig. 4
figure 4

Showing the variation of amplitude of the negative shock potential with σ 2 and μ 2. The other plasma parameters are fixed at q=−0.5, σ 1=0.5, μ 1=0.2, μ i =0.1, and U 0=0.01

Full size image
Fig. 5
figure 5

Showing the variation of positive potential shock profile with ξ and q. The other plasma parameters are fixed at σ 1=0.5, σ 2=0.25, μ 2=0.65, μ i =0.1, η=0.1, and U 0=0.01

Full size image
Fig. 6
figure 6

Showing the variation of negative potential shock profile with ξ and q. The other plasma parameters are fixed at σ 1 = 0.5, σ 2 = 0.25, μ 2 = 0.65, μ i = 0.1, η = 0.1, and U 0 = 0.01

Full size image
Fig. 7
figure 7

Showing the variation of electrostatic potential ψ of the positive shock profile with ξ for different values of μ 1. The other plasma parameters are fixed at q=−0.7, σ 1=0.5, σ 2=0.25, μ 2=0.65, μ i =0.1, η=0.1, and U 0=0.01

Full size image
Fig. 8
figure 8

Showing the variation of electrostatic potential ψ of the negative shock profile with ξ for different values of μ 1. The other plasma parameters are fixed at q=−0.5, σ 1=0.5, σ 2=0.25, μ 2=0.65, μ i =0.1, η=0.1, and U 0=0.01

Full size image
Fig. 9
figure 9

Variation of the shock wave width △ with U 0 for different viscosity coefficient η

Full size image

6 Discussion

The basic features of the DASHWs in an unmagnetized dusty plasma containing negatively charged mobile dust fluids, nonextensive electrons with two distinct temperatures, and Maxwellian ions are investigated theoretically and numerically. The propagation of the small amplitude DASHWs in nonextensive plasmas has been considered by analyzing the solution of the Burgers equation. It should also be noted that the Burgers equation derived here is valid [25, 31] only for the limits A ≠ 0, A > 0, and A < 0. The results which have been found from this investigation are summarized as follows:

  1. 1.

    The wave frequency (real part) is observed to increase with the increasing values of wave vector. On the other hand, the wave frequency is found to decrease with the increasing values of kinematic viscosity effect (via η) for fixed values of wave vector, that is, the phase speed decreases with increasing kinematic viscosity (shown in Fig. 1).

  2. 2.

    The nonextensive plasmas under consideration support finite-amplitude shock structures, whose basic features (viz. polarity, amplitude, width, etc.) strongly depend on different plasma parameters, particularly, ion-to-dust number density ratio (via μ i ), cold electron-to-dust number density ratio (via μ 1), hot electron-to-dust number density ratio (via μ 2), ion-to-cold electron temperature ratio (via σ 1), ion-to-hot electron temperature ratio (via σ 2), and nonextensive index q.

  3. 3.

    We have obtained the critical value q=q c=−0.6 for a fixed set of parametric values (viz. μ 1=0.2, μ 2=0.65, μ i =0.1, σ 1=0.5, and σ 2=0.25) [24] (shown in Fig. 2).

  4. 4.

    We have observed that at q<q c, positive SHWs exist, whereas at q>q c, negative SHWs exist (shown in Figs. 5, 6, 7, and 8).

  5. 5.

    The height of the positive (negative) potential shock structure increases (decreases) with the increase of σ 2 and μ 2, as shown in Figs. 3 and 4.

  6. 6.

    The amplitude of positive and negative potential SHWs increases with the increase of q (see Figs. 5 and 6).

  7. 7.

    It is observed that the amplitude of positive (negative) potential SHWs decreases (increases) with the increase of μ 1, as shown in Fig. 7 (Fig. 6). Our results agree with the results of Masud et al. [34].

  8. 8.

    Figure 9 shows the variation of width △ with U 0 for different values of the kinematic viscosity η, where △ increases with the increase of η and decreases with the increase of dust fluid speed U 0. The later is consistent with the result of Masud et al. [32] obtained in a dusty plasma with two distinctive temperatures Maxwellian electrons.

Therefore, our findings should clarify the nonlinear electrostatic structures that propagate in astrophysical and cosmological plasma scenarios where unmagnetized nonextensive plasma with two-temperature electrons and ions may exist: like stellar polytropes [21], hadronic matter and quark-gluon plasma [22], protoneutron stars [20], dark-matter halos [23], etc. It can be noted here that the analysis of shock structures in such plasmas in the presence of external magnetic field is also a problem of great importance and outside the scope of our present study. The laboratory experiment of SHWs in different plasma models have been performed by a number of authors. Luo et al. [43] have examined the shock formation in negative ion plasma. Nakamura [44] has examined DIASHWs in a homogeneous unmagnetized dusty double-plasma device. To conclude, we propose to perform a new laboratory experiment to verify the results of theory (i.e., to observe such DASHWs with two distinct temperature nonextensive electrons and Maxwellian ions in both laboratory and space plasma) that is presented in this manuscript by using the experimental set up of Luo et al. [43] or Nakamura [44].