1 Introduction

Over the last few decades, the study of linear and nonlinear propagation of dust ion-acoustic (DIA) waves (Shukla and Silin 1992; Moslem et al. 2005; Alinejad 2010, 2011a, 2011b; EI-Taibany et al. 2011; Rahman and Mamun 2011; Das et al. 2012; El-Labany et al. 2012) are the hot point of interest in recent development in dusty plasma physics. In 1992, Shukla and Silin (1992) first reported theoretically the existence of low frequency DIA waves. From the seminal paper of Shukla and Silin (1992), it has been concluded that the addition of immovable massive and heavier charged dust in electron-ion plasma can significantly modify the wave dynamics. Due to the conservation of equilibrium charge density and strong inequality n i0≫n e0 (where n i0 (n e0) is the equilibrium ion (electron) number density) the dusty plasma system can not support the usual ion-acoustic (IA) waves, but can do the DIA waves of Shukla and Silin (1992). In the DIA waves, the restoring force comes from the pressures of inertialess electrons, whereas the ion mass provides the inertia similar to the usual ion acoustic waves, and the phase speed of the DIA waves is much smaller (larger) than electron (ion) thermal speed. The evolution of low frequency DIA waves arises on a time scale which is much shorter than the dust plasma period. The theoretical prediction of Shukla and Silin (1992) has been observed in laboratory experiments (Barkan et al. 1996; Merlino and Goree 2004; Nakamura et al. 1999). The nonlinear propagation of DIA waves, particularly the DIA solitary waves (SWs) (Shukla and Silin 1992; Moslem et al. 2005; Alinejad 2010, 2011a, 2011b; EI-Taibany et al. 2011; Rahman and Mamun 2011; Das et al. 2012; El-Labany et al. 2012) mentioned here, are consistent with equilibrium plasma system. Total energy of such plasma system is considered to be extensive, i.e., Maxwellian distribution in Boltzmann Gibbs statistics is believed to be valid universally for the macroscopic ergodic equilibrium systems (Shukla and Silin 1992; Moslem et al. 2005; Rahman and Mamun 2011). However, space plasmas (Vasyliunas 1968; Leubner 1982; Plastino and Plastino 1993; Feron and Hjorth 2008; Gervino et al. 2012; Lavagno and Pigato 2011) clearly indicate the particles which follow non-Maxwellian distribution function with high energy tail. Such particles, following non-Maxwellian distribution function point to a class of Tsallis’s velocity distribution (Tsallis 1988) are very important to describe the non-equilibrium stationary states such as long-range interactions (Plastino and Plastino 1993; Nobre and Tsallis 1995) among the plasma species, global correlations (Sakagami and Taruya 2004) among the self-gravitating systems, long-time memory effects, or in a fractal-multi fractal space, etc. This type of velocity distribution (Tsallis 1988) is well known as q-distribution which characterizes the nonextensivity of any plasma species.

Very recently, nonextensive (Renyi 1955; Tsallis 1988) plasmas are hot point of current scientific researches in dusty plasmas. The rapidly growing interest to survey the effect of nonextensivity of plasma particles on any nonequilibrium plasma system is due to the fact that such effects of nonextensivity of plasma constituents are quite common in astrophysical and cosmological scenarios like stellar polytropes (Plastino and Plastino 1993), hadronic matter and quark-gluon plasma (Gervino et al. 2012), protoneutron stars (Lavagno and Pigato 2011), dark-matter halos (Feron and Hjorth 2008), etc. as well as its laboratory applications in nanomaterials, microdevices, and microstructures (Vladimirov and Ostrikov 2004), etc. After, the rudimentary concept of nonextensive entropy proposed by Renyi (Renyi 1955), and subsequently proposed by Tsallis (Tsallis 1988), the nonextensive behavior of electrons and ions (characterizing by a parameter q) have been successfully employed in plasma physics (Lima et al. 2000; Du 2004; Bacha and Tribeche 2011; Tribeche et al. 2010; Pakzad and Tribeche 2011; Sahu 2012; Sahu and Tribeche 2012; Bains et al. 2011). It is important to note that q=1 corresponds to Maxwellian distribution and q≠1 denotes the q distribution point to a class of Tsallis’s velocity distribution (Tsallis 1988). The distribution for q≠1 follows a power law distribution instead of usual exponential law. The nonextensive parameter q is taken to be constant and very close to the value for which ordinary statistical mechanics is obtained (q=1), meaning that all calculations can be performed in the leading order to (q−1), with no considerable loss of information (Vergou 2009).

We now turn to the point of SWs (Tribeche et al. 2010; Pakzad and Tribeche 2011; Tribech and Shukla 2011; Pakzad 2011a, 2011b; Eslami et al. 2011a, 2011b, 2012; El-Awady and Moslem 2011; Tribeche and Merriche 2011; Pakzad 2011; Tribeche and Djebarni 2010) which are formed due to delicate balance between nonlinearity and dispersion. Motivated by the work of Lima et al. (2000) who have discussed the effect of nonextensivity characterizing by nonextensive q-parameter (Tsallis 1988) smaller than unity on the propagation of plane wave in a collisionless thermal plasma, extensive works have been devoted to the sake of nonextensive behaviors of electrons, ions, etc. in different plasma environment (Tribeche et al. 2010; Pakzad 2011, 2011a, 2011b; Tribech and Shukla 2011; Eslami et al. 2011a, 2011b, 2012; El-Awady and Moslem 2011; Tribeche and Merriche 2011; Tribeche and Djebarni 2010). For example, Eslami et al. (2011a) have investigated the nature of the head-on collision of ion-acoustic SWs in a collisionless plasma and discussed the impacts of electron nonextensivity on the phase shifts of both the colliding SWs. Large amplitude IA SWs have also been addressed by Tribeche et al. (2010) following q-nonextensive electron distribution. Using pseudo-potential approach, Pakzad (2011b) formulated electron acoustic solitary waves (EASWs) which exhibits a rarefactive spatially localized (soliton-like) structure. Moreover, nonplanar geometric effects have also been discussed in such a EASWs by Pakzad (2011a). Tribeche and Merriche (2011) stressed about nonextensive dust-acoustic (DA) SWs where soliton exhibits compression for q<0 and rarefaction for q>0 by assuming ion noextensivity. Very recently, Eslami et al. (2012) have investigated the geometric effects on DIA SWs by assuming adiabatic ion-fluid and nonextensive electrons, and they inferred that both compressive and rarefactive type solitons are significantly modified by electron nonextensivity.

All of these theoretical investigations (Tribeche et al. 2010; Pakzad and Tribeche 2011; Tribech and Shukla 2011; Pakzad 2011, 2011a, 2011b; Eslami et al. 2011a, 2012; El-Awady and Moslem 2011; Tribeche and Merriche 2011; Tribeche and Djebarni 2010) are consistent when dispersion effect is much more dominant over dissipation and that is neglected. However, for a plasma medium with significant dissipative properties, supports the formation of shock structures. The Landau damping, kinematic viscosity among the plasma species, the collision between ion-neutral, dust-neutral, etc. are the major cause for arising the dissipation which is responsible for the formation of shock structures in plasma system. Sahu and Tribeche (2012) discussed about the different aspects of DA shock waves by taking into account the ion nonextensivity and dust kinematic viscosity. Basic features of IA shock waves in presence of nonextensive electrons and ion kinematic viscosity are also pronounced by Sahu (2012). But no evidence yet has been found point to the subject of DIA shock waves in a nonextensive dissipative plasma system. Therefore, we have considered the electron nonextensivity and ion kinematic viscosities along with stationary charged dust and have studied the basic features of DIA shock waves by deriving the Burgers equation. The manuscript is organized as follows. The governing equations are provided in Sect. 2. The Burgers equation is derived and numerically solved in Sect. 3. A brief discussion is finally provided in Sect. 4.

2 Governing equations

We consider nonlinear propagation of the DIA waves in an unmagnetized dusty plasma system consisting of negatively charged stationary dust, inertial ions, and electrons following q-nonextensive distribution. Thus, at equilibrium we have n i0=n e0+Z d n d0, where n i0 (n e0) is the equilibrium ion (electron) number density and n d0 such of dust density. The nonlinear dynamics of the DIA waves, whose phase speed is much smaller (larger) than the electron (ion) thermal speed, is described by the normalized equations of the form

(1)
(2)
(3)
(4)

where q is the nonextensive parameter characterizing the degree of nonextensivity, i.e. q=1 corresponds to Maxwellian distribution and q<(>)1 denotes the nonextensive q-distribution, n i is the ion number density normalized by its equilibrium value n i0, u i is the ion fluid speed normalized by C i =(T e /m i )1/2, ϕ is the electrostatic wave potential normalized by T e /e, Z d (normalized by its equilibrium value Z d0) is the number of electrons residing on the stationary dust grain surface, μ=Z d n d0/n i0, η is the viscosity coefficient normalized by \(m_{i}n_{io}\omega_{pi}\lambda_{Dm}^{2}\), T e is the electron temperature in energy units, t is the time variable normalized by the ion plasma period \(\omega_{pi}^{-1}=(m_{i}/4\pi n_{io}e^{2})^{1/2}\), r is the radial space variable normalized by λ Dm =(T e /4πn io e 2)1/2.

3 Shock waves

To derive a dynamical equation for the electrostatic DIA shock waves from our basic equations (1)–(4), we employ the reductive perturbation technique. We construct a weakly nonlinear theory of DIA waves with small but finite amplitude which leads to a scaling (Mamun 2008) of the independent variables

(5)

where ϵ is a smallness parameter measuring the weakness of the dispersion and V p is the phase speed of the DIA waves. We can expand the perturbed quantities n i , u i , and ϕ about the equilibrium values in power series of ϵ as

(6)
(7)
(8)

and develop equations in various powers of ϵ. To the lowest order in ϵ, (1)–(4) give

(9)
(10)

Equation (10) represents the linear dispersion relation for the DIA wave which is significantly modified by the nonextensive electron in such a nonextensive dusty plasma system under consideration where ion mass provides the inertia and electron thermal pressure provides the restoring force, and stationary charged dust plays a crucial role because of their extremely mass and charge. It is very important to note that when we take q→1, the particle density reduces to the well known Maxwell-Boltzmann density distribution. q<1 refers to the case of superextensivity (Tribeche and Merriche 2011) whereas q>1 refers to the subextensivity (Tribeche and Merriche 2011). To the next higher order of ϵ, i.e., taking the coefficients of ϵ 3 from both sides of Eqs. (1) and (2), and ϵ 2 from both sides of Eqs. (3) and (4), one may obtain another set of simultaneous equations for \(n_{i}^{(2)}\), \(u_{i}^{(2)}\), and ϕ (2). Invoking this different set of equations which contain coupled set of parameters viz. as first and second order perturbed quantities of the ion density, as well as ion fluid speed and characterizing wave potential, we finally, deduce the Burgers equation for the propagarton of DIA shock waves in nonextensive plasma as

(11)

where ϕ (1)=ψ, A is the nonlinear coefficient, and C is the dissipative coefficient. The expressions for the coefficients of A and C can be represented as

(12)
(13)

Equation (11) is the well-known Burgers equation, derived for the DIA shock waves in a dusty plasma with nonextensive electrons.

4 Shock wave solution of the Burgers equation

The stationary shock wave solution of the Burgers equation (11) is obtained by transforming the independent variables to ζ=ξ−U 0 τ′ and τ′=τ, where U 0 is the speed of the shock waves in a moving frame, and imposing the appropriate boundary conditions, viz. ψ→0, dψ/dζ→0, d 2 ψ/dζ 2→0 at ζ→±∞. Thus, one can express the stationary shock wave solution of the Burgers equation (11) as

(14)

where the amplitude ψ m , and the width δ are given by

(15)

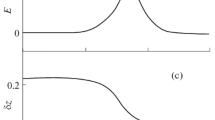
It is obvious from Eqs. (14) and (15) that the dusty plasma system under consideration supports the DIA shock waves with positive (negative) potential, i.e. with the compression (rarefaction) of the ion number density if the nonlinear coefficient A>0 (A<0). This means that for q>(<)0.6 by inserting a typical values of μ=0.5 in the expression (q=q c =3μ/(4−3μ)), we have obtained compressive (rarefactive) type shock structures. q c is the minimum value of nonextensive parameter q for which shock structures transit from negative to positive potential proceeding from the value of q below the minimum to that above minimum. Figure 1 indicates us that how q c varies with μ. It is clear from the expression of q c that the shock wave transition from compression to rarefaction is rigorously depended on the parameter μ. In case of Maxwellian distribution q=1, the parameter μ can be retrieved as 2/3. It is also clear from the Eqs. (12)–(15) along with the figure 1 that the formation of DIA shock waves are due to kinematic viscosity of ions with stationary negatively charged dust, and the basic properties of shock waves are significantly modified by the nonextensive behavior of electron. We have plotted the A=0 curve which separates the shock waves into two regimes: the parametric regime above (below) the curve corresponds to A>0 (A<0) [shown in Fig. 1] are associated with positive (negative) potential.

Fig. 1
figure 1

Showing how q c [obtained from A(q=q c )=0] varies with μ

Full size image

We also observed that shock structures can not be formed, corresponding to q=0.6 or q→0.6. The shock waves are formed far above or below the minimum value of q. At q≃0.6 the shock amplitude goes to infinite value for which the structure is collapsed. Compressive shock structure is found for a parametric regime corresponds to q=0.7–0.9 at μ=0.5. However, rarefactive shock waves are formed within the range of q=0.01–0.3 which is much below q c . We choose our parameter μ=0.5 to attain the minimal values of q c =0.6. Since our parametric choice of degree of nonextensive electrons is greatly impelled by its convenience rather than its precise fitting of the observations. However, one has to choose any other value of μ to reorganize the minimal value of q, is obviously within the range −1<q<1 (Tribeche and Merriche 2011), and the variation of q c shown in Fig. 1, is also within the range. It may be concluded that due to nonextensivity of electrons one has to find the shock structures in presence of a lower amount of dust, and this prediction is shown in Fig. 1 [nonextensive parameter q c decreases with the decrease of μ]. Figures 2, 3, 4, 5 and 6 show how the nonextensivity of electrons affects on the formation of DIA shock structures. The variation of thickness with η and U 0 is shown in Fig. 4, where △ increases with increasing η and decreases with U 0. It is clear from (13) and (15) that the shock height is independent of the viscosity coefficient but the shock width is directly proportional to the viscosity coefficient, η. This has been already reported in Eq. (15) and numerically shown in Fig. 4. Figures 5 and 6 show the behavior of compressive (rarefactive) shock waves structures with the variation of q, and it is found that the strength of the shock waves decreases (increases) with the increase of q. The interesting findings from our present investigation is that, the amplitude of the negative (positive) potential shock waves is increased (decreased) with the increase of electron nonextensivity. The rarefactive DIA shock structures still have not been observed by the laboratory experiments (Nakamura 1999, 2001; Luo et al. 1999). But due to nonextensivity of electrons, we have found both rarefactive and compressive shock waves. The rarefactive shock waves may originate due to electron nonextensivity, and that waves may be observed in laboratory experiments. It may be stressed here that the results of this investigation should be useful for understanding the nonlinear features of electrostatic disturbances in laboratory plasmas since DIA waves (Nakamura et al. 1999) are more suitable than the DA (Barkan et al. 1995; D’Angelo 1995) waves to observe in laboratory dusty plasma conditions.

Fig. 2
figure 2

Showing the variation of amplitude of the positive shock structure with q and U 0 for μ=0.5 (Color figure online)

Full size image
Fig. 3
figure 3

Showing the variation of amplitude of the negative shock structure with q and U 0 for μ=0.5 (Color figure online)

Full size image
Fig. 4
figure 4

Showing the variation of the width (△) with η and U 0 (Color figure online)

Full size image
Fig. 5
figure 5

Showing the positive potential (ψ m >0) shock profile with q for μ=0.5, and U 0=0.1 (Color figure online)

Full size image
Fig. 6
figure 6

Showing the negative potential (ψ m <0) shock profile with q for μ=0.5, and U 0=0.1 (Color figure online)

Full size image

5 Discussion

We have carried out the analysis of the DIA shock waves by deriving the Burgers equation in an unmagnetized, collisionless, dissipative dusty plasma system containing nonextensive electrons, inertial ions, and negatively charged stationary dust. It has been found that shock compression or rarefaction are sensitive to the degree of nonextensivity of electrons. For exceeding or proceeding towards the minimum value of q, we have shown the existence of compressive and rarefactive shock structures, respectively. DIA shock structures are formed far above (below) the minimum value of q. This makes sense that for q=0.6 the amplitude of the shock waves breaks down due to the vanishing of the nonlinear co-efficient A. We note that we get positive (negative) shock waves for q>0.6 (q<0.6). Comparing to electrons distribution in extensive limit (q=1), it has been found that due to nonextensivity of electrons the shock structures are formed in presence of a lower amount of dust. We stress that shock polarity switch may be attributed to the electron nonextensivity which may originate from the global correlation (Sakagami and Taruya 2004) or long range interactions (Plastino and Plastino 1993; Nobre and Tsallis 1995) among the dusty plasma system under consideration. The basic features (amplitude, width, etc.) of the positive and negative potential shock waves are significantly modified by the electron nonextensivity. Our investigation may be useful to study the nonextensive effects in different astrophysical environments like interstellar and space plasmas (Ferro et al. 2004; Vergou 2009), particularly in stellar polytropes (Plastino and Plastino 1993), hadronic matter and quark-gluon plasma (Gervino et al. 2012), protoneutron stars (Lavagno and Pigato 2011), dark-matter halos (Feron and Hjorth 2008) etc. where nonextensivity can play the vital roles. The shock analysis proposed here, is valid for small but finite amplitude limit. Shock structures will be more general and bounded by taking into account the external magnetic field (Shukla 2005). Further it can be said that the analysis of vortices, double-layers, etc. with or without the effects of obliqueness and external magnetic field in a planar and nonplanar geometries by deriving K-dv, Burgers or higher order nonlinear equation, where the nonextensivity can play a significant role, are also the problems of great importance but beyond the scope of the present work. To conclude, we propose to perform a laboratory experiment which can satisfy the observation of the rarefactive DIA shock structures in such a nonextensive plasma.