Radiation, Velocity and Thermal Slips Effect Toward MHD Boundary Layer Flow Through Heat and Mass Transport of Williamson Nanofluid with Porous Medium

Abstract

The thermal radiation impact of MHD boundary layer flow of Williamson nanofluid along a stretching surface with porous medium taken into account of velocity and thermal slips is discussed numerically. This model aims to examine the phenomena of heat and mass transport caused by thermophoresis and Brownian motion. Through the help of similarity transformations, the governing system of PDEs is converted to a set of nonlinear ODE’s. Here, ordinary differential equations provide the mathematical formulation. The coupled system obtained has been analyzed using the Keller-Box technique; Newton's system dictates that the coefficients must be accurate and refined. To get a full understanding of the present situation, the effect of the flow regulating factors on relevant profiles is quantified and qualitatively assessed. The wall friction factor, heat, and mass transport coefficients are calculated graphically and tabulated. The findings reveal that when the slip and heat factor parameters improve, the boundary layer's thickness drops. Furthermore, the present findings indicate that raising the Williamson parameter enhances the concentration and temperature of the nanofluid. The validity of the outcomes is further shown by comparison to previously published data, which demonstrate good agreement.

1 Introduction

Magnetohydrodynamics is the science that scrutinizes the magnetic properties of electrically accompanying materials and has become the basis for a variety of industrial, scientific, and technical applications, including production of chemicals, liquid metals, automobile cooling systems, electrolytes, plasma, electronic chip cooling, nuclear power plant heat extraction, and saltwater, among others. In the fields of metallurgy and polymer technology, it appears to be frequently utilized. Magnetic drug targeting, astrophysical sensing, and engineering may all benefit from MHD applications [1, 2]. Magnetic fields, in particular, are critical in the formation of stars. Based on all these significant benefits, analysts and researchers monitor MHD flows on a continuous basis. Metri et al. [3] explore the impact of heat sink/source over MHD forced convective visco-elastic fluid flow subjected to dissipation with porous medium. Akbar et al. [4] numerically studied the influence of MHD heat transport nanofluid flow over a stretched surface for the new heat flux concept. Numerous authors Rashidi et al. [5], Rashidi and Erfani [6], Khedr et al. [7], Fang and Zhang [8], Magyari and Chamkha [9], Ishak et al. [10], Yasin et al. [11], Falodun and Omowaye [12], Madhusudan et al. [13] have recently examined the problems on MHD impact of magnetic fields on stretching sheet and various aspects of flow issues. Magnetic effect is said to have a key impact in heat control applications.

Nanofluids have become a topic of wide spread research due to the fact that the inclusion of nanoparticles is utilized in novel ways to improve thermal conductivity and hence heat transmission process. Colloidal suspensions of nanomaterials in a base liquid are utilized to create these fluids. A nanofluid is a fluid that contains tiny volumetric amounts of nanometer-sized particles (0–100 nm) called nano-particles. Typically, the nanomaterials used in nanofluids include carbides, carbon nanotubes, metals, and oxides. Ethylene glycol, water, and oil are all components of basic base fluids. There are additional thermo-physical characteristics that also influence nanofluid heat transfer enhancement. The dispersion, amorphous movement, thermophoresis effects, Brownian motion, and thermophoresis impacts are a few of these physical properties. The examination of nanofluid flow has piqued the interest of researchers in recent years, due to a rise in applications in many sectors of science & technology, bio-mechanics, nuclear, and chemical sectors. For instance, food materials (mayonnaise, chocolate, ketchup, alcoholic beverages, yoghurt, milk and apple sauce in liquefied form), chemical materials (paints, cosmetics, pharmaceutical chemicals, toothpastes, oil, reservoirs, shampoos, grease, etc.), and biological materials (synovial fluid, syrups, vaccines, blood, etc.). The term nanofluid was first coined by Choi [14]. The thermal conductivity of copper nanoparticles embedded in a nanofluid of ethylene glycol was explored by Eastmann et al. [15]. Since then, thermophoresis and Brownian diffusion demonstrations have fueled the advancement of mathematical modeling of nanofluids. The free convective flow of a nanoliquid was investigated by Kuznetsov and Nield [16] using an analytical approach.

The stagnation-point flow of a nanofluid toward a nonlinear stretching sheet was explored with Anwar et al. [17]. Azimi and Riazi [18] discussed heat transmission between two parallel disks of Go-water Nanofluid. Bhargava et al. [19] described an effective hybrid method for modeling MHD nanofluid flow through a permeable stretched sheet. [20] Raza et al. scrutinized MHD Flow of nano-Williamson liquid caused via multiple slips on a stretched plate. Khan [21] investigated the stability of magneto convective flow of SiO₂–MoS₂/C₂H₆O₂ hybrid nanoliquids using a shrinking/stretching wedge. Chamkka et al. [22] investigated the laminar MHD mixed convection flow of a nanoliquid over a stretched permeable area with heat production or absorption. Turkyilmazoglu [23] investigated an accurate analytical solution for heat and mass transport in nanofluids with MHD slip flow. Wubshet and Shankar [24] studied the flow and heat transfer of a nanofluid via a permeable stretched sheet under a variety of boundary conditions, including velocity, temperature, and solutal slip. Nagendra et al. [25] investigated the numerical simulation of hydromagnetic heat and mass transport in a nano-Williamson liquid passing through a vertical plate through thermal and momentum slip effects. Garoosi et al. [26] studied numerical modeling of natural convection in heat exchangers utilizing the Buongiorno model. Konda et al. [27] analyzed the performance of a non-uniform heat sink/source on the MHD boundary layer flow and melting heat transport of a Williamson nanoliquid in a porous media. Yahaya et al. [28] explored nanofluid hydromagnetic slip flow with thermal stratification and convective heating. Acharya et al. [29] investigated the impact of numerous slips and chemical reactions on the radiative MHD Williamson nanoliquid flow in porous media: A computational approach. Mishra and Mathur [30] used a semi-analytical technique to investigate Williamson nanofluid flow in porous media with melting heat transport boundary conditions.

Asogwa et al. [31] investigated the comparative analysis of water-based Al₂O₃ nanoparticles via H₂O-based CuO nanoparticles through heat transport toward an exponentially accelerated radiative Riga plate area. Warke et al. [32] investigated nonlinear radiation through magnetomicropolar stagnation point flow over a heated stretching sheet using a numerical investigation.

The thermal radiation effect has piqued the interest of academics due to its vast range of scientific, technical uses, and industrial sectors. It encompasses electric power, food, solar cell panels, gas turbines, different propulsion mechanisms for aeroplanes, and the medical sector. The impact of radiation and mixed convection on nanofluid flow over a vertical plate with melting heat transport was investigated by Mahanthesh et al. [33]. FazleMabood et al. [34] investigated the radiation impact on MHD Williamson nanoliquid flow with a heated surface. On a shrinking/stretching porous sheet, thermo-diffusion and radiation effects on Williamson nanofluid were investigated by Bhatti and Rashidi [35]. The influence of radiation on nanofluid flow across a stretched surface was inspected by Krishnamurthy et al. [36], Dulal Pal et al. [37], Ghadikolaei et al. [38], and Almakki et al. [39]. This work is based on several recent articles as [40,41,42,43,44,45,46].

Inspired by above reputed researchers, the present work discusses the Williamson nanofluid flowing via a porous media with a constant stretching sheet. In this case, the influence of radiation plays an important role in temperature control, and the technique of convective heat transport is very important in issues where comparatively higher temperature has happened. According to the aforementioned literatures, no study has been conducted on MHD nanofluid via a stretching sheet when thermal radiation and slip conditions are present. The solution of coupled nonlinear equations is obtained by numerical computing. For numerous values of physical restrictions, the consequence of dimensionless parameters has been evoked. The originality of this observation is to consider the behavior of the radiation, velocity, and thermal slips on MHD boundary layer flow through heat and mass transport in a Williamson nanoliquid with porous media.

2 Mathematical Formulation

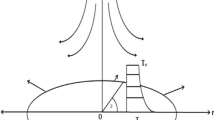
Assume that the steady-state 2-D and incompressible MHD Williamson nanofluid flow toward a horizontal stretching sheet with porous medium and radiation. Figure 1 illustrates the physical model of the problem. The plate is expanded along the direction of the coordinated axis ‘$x$’and it has a velocity $U_{w} \left( x \right) = bx$, $(b > 0)$. $y$ is the coordinate measured vertical to the sheet at $y = 0$. The temperature at the wall is denoted by $T_{w} = T_{\infty } + ax^{2}$ and the constant along the stretching sheet is delineated as the nanoparticles volume fraction $C_{w}$. The volume fraction of nanoparticles and ambient values of temperature are represented with $C_{\infty }$ and $T_{\infty }$ as $y \to \infty$. In thermal equilibrium, the nanoliquid is assumed to have been a single phase, and slip velocity among base liquid and particles exists. Nanoparticles are considered to be consistent in size and shape.

Fig. 1

Physical model of the problem

In the occurrence of magnetic field and radiation, the boundary layer equations (Ref. [48]) that regulate two-dimensional flow are:

$$\frac{\partial u }{{\partial x}} + \frac{\partial v }{{\partial y}} = 0$$

(1)

$$u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = \nu \frac{{\partial^{2} u}}{{\partial y^{2} }} + \sqrt 2 \nu {\Gamma }\frac{\partial u}{{\partial y}}\frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\sigma B^{2}_{0} }}{\rho }u - \frac{v}{{k^{\prime}}}u$$

(2)

$$u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\left( {\rho c} \right)_{p} }}{{\left( {\rho c} \right)_{nf} }}\left[ {D_{{\text{B}}} \frac{\partial C}{{\partial y}}\frac{\partial T}{{\partial y}} + \frac{{D_{{\text{T}}} }}{{D_{\infty } }}\left( {\frac{\partial T}{{\partial y}}} \right)^{2} } \right] - \frac{1}{{\left( {\rho c} \right)_{nf} }}\frac{{\partial q_{r} }}{\partial y}$$

(3)

$$u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} = D_{{\text{B}}} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{{\text{T}}} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }}$$

(4)

The following are subject to the appropriate conditions at the boundary:

$$\begin{aligned} & u = u_{w} + A^{*} \mu \left( {\frac{\partial u}{{\partial y}}} \right),\quad v = 0, \\ & \quad T = T_{w} + B^{*} \frac{\partial T}{{\partial y}},\quad C = C_{w} \;{\text{at}}\;y = 0 \\ & u \to 0,\quad T = T_{\infty } ,\quad C = C_{\infty } \;{\text{as}}\;y \to \infty \\ \end{aligned}$$

(5)

where $A^{*}$ and $B^{*}$ are velocity and thermal slip factors.

When the Rosseland approximation for radiation is used, the radiative heat flux is simplified as follows,

$$q_{r = } \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{4} }}{\partial y},$$

(6)

where $\sigma^{*}$ represents the constant of Stefan-Boltzmann, and $k^{*}$ indicates the coefficient of mean absorption. Assumed that there are small temperature variations in the fluid flow so that $T^{4}$ can be represented as a function of $T$ which is in linear form with the help of truncated Taylor's series about the temperature at free stream $T_{\infty }$, and omitting the terms which are in higher-order then we get,

$$T^{4} \approx 4TT_{\infty }^{3} - 3T_{\infty }^{3} ,$$

(7)

Now substitute (6) and (7) in (3), we have

$$u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\left( {\rho c} \right)_{p} }}{{\left( {\rho c} \right)_{f} }}\left[ {D_{{\text{B}}} \frac{\partial C}{{\partial y}}\frac{\partial T}{{\partial y}} + \frac{{D_{{\text{T}}} }}{{D_{\infty } }}\left( {\frac{\partial T}{{\partial y}}} \right)^{2} } \right] + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} \left( {\rho c} \right)_{f} }}\frac{{\partial^{2} T}}{{\partial y^{2} }}$$

(8)

Employing the following similarity transformations:

$$u = bxf^{\prime}\left( \eta \right),\quad v = - \left( {b\nu } \right)^{\frac{1}{2}} f\left( \eta \right),\quad \eta = \sqrt {\frac{b}{\nu }} y$$

(9)

$$\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\quad \phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }}$$

(10)

Using transformations in (9, 10), Eqs. (2), (4), and (8) subject to the constraints in (5) will be in the following form:

$$f^{\prime\prime\prime} - \left( {f^{\prime}} \right)^{2} + ff^{\prime\prime} + \lambda f^{\prime\prime}f^{\prime\prime\prime} - \left( {M + Kp} \right)f^{\prime} = 0$$

(11)

$$\left( {\frac{3 + 4R}{3}} \right)\theta^{\prime\prime} + \Pr .f\theta^{\prime} - 2\Pr .f^{\prime}\theta + \left( {\frac{{{\text{Nc}}}}{{{\text{Le}}}}} \right)\theta^{\prime}\phi^{\prime} + \frac{{{\text{Nc}}}}{{\left( {{\text{Le}}} \right)\left( {{\text{Nbt}}} \right)}}\left( {\theta^{\prime}} \right)^{2} = 0$$

(12)

$$\phi^{\prime\prime} + {\text{Sc}}.f\phi^{\prime} + \left( {\frac{1}{{{\text{Nbt}}}}} \right)\theta^{\prime\prime} = 0$$

(13)

where

$$\begin{aligned} & \lambda = \sqrt {\frac{{2b^{3} }}{\nu }} \Gamma x,\;\Pr = \frac{\nu }{\alpha }, \\ & \quad {\text{Nc}} = \frac{{\left( {\rho c} \right)_{p} }}{{\left( {\rho c} \right)_{f} }}\left( {C_{w} - C_{\infty } } \right),\;{\text{Nbt}} = \frac{{T_{\infty } D_{{\text{B}}} \left( {C_{w} - C_{\infty } } \right)}}{{D_{{\text{T}}} \left( {T_{w} - T_{\infty } } \right)}}, \\ & {\text{Le}} = \frac{\alpha }{{D_{{\text{B}}} }},\;{\text{Sc}} = \frac{\nu }{{D_{{\text{B}}} }},\;M = \frac{{\sigma B_{0}^{2} }}{\rho b}, \\ & \quad Kp = \frac{\nu }{k^{\prime}b},\;{\text{and}}\;R = \frac{{4\sigma^{*} T_{\infty }^{3} }}{{kk^{*} }} \\ \end{aligned}$$

where $f,\theta \;{\text{and}}\;\phi$ are functions of $\eta$ and prime designates diff. w.r.to $\eta$. The equivalent transformed boundary conditions are

$$\left. {\begin{array}{*{20}l} \theta \left( 0 \right) = 1 + \beta \theta^{\prime}\left( 0 \right), \;f^{\prime}\left( 0 \right) = 1 + \delta f^{\prime\prime}\left( 0 \right),\; \phi \left( 0 \right) = 1,\\ \quad f\left( 0 \right) = 0\;{\text{at}}\;\eta = 0 \hfill \\ {\theta \left( \infty \right) = 0,\;f^{\prime}\left( \infty \right) = 0, \;\phi \left( \infty \right) = 0} \hfill \\ \end{array} } \right\}$$

(14)

The quantities of physical interest are described as the coefficient of friction factor $C_{f}$, Nu, the local Nusselt number, and ${\text{Sh }}$ the local Sherwood number, are specified as

$$C_{f} \!=\! \frac{{\tau_{w} }}{{\rho U_{w}^{2} }},\quad {\text{Nu}} \!=\! \frac{{xq_{w} }}{{k\left( {T_{w} \!-\! T_{\infty } } \right)}} {\text{and}}\;{\text{Sh}} = \frac{{xq_{m} }}{{D_{{\text{B}}} \left( {C_{w} - C_{\infty } } \right)}}$$

(15)

where $\tau_{w}$ is the shear stress, $q_{w}$ is the heat flux and $q_{m}$ is the mass flux volume fraction of the nanoparticle at the plate surface, which are specified by

$$\tau_{w} = \mu \left[ {\frac{\partial u}{{\partial y}} + \frac{{\Gamma }}{\sqrt 2 }\left( {\frac{\partial u}{{\partial y}}} \right)^{2} } \right],\quad q_{w} = - k\left. {\frac{\partial T}{{\partial y}}} \right|_{y = 0} \;{\text{and}}\; q_{m} = - D_{{\text{B}}} \left. {\frac{\partial C}{{\partial y}}} \right|_{y = 0}$$

(16)

finally, using Eqs. (16) and (10), Eq. (15) becomes

$$C_{f} \sqrt {\text{Re}} = f^{\prime\prime}\left( 0 \right) + \frac{\lambda }{2}f^{{\prime\prime}{2}} \left( 0 \right),\quad \frac{{{\text{Nu}}}}{{\sqrt {\text{Re}} }} = - \theta^{\prime}\left( 0 \right)\;{\text{and}}\; \frac{{{\text{Sh}}}}{{\sqrt {\text{Re}} }} = - \phi ^{\prime}\left( 0 \right),$$

(17)

where ${\text{Re}} = \frac{{U_{w} \left( x \right)}}{\nu }x$ is the Reynold’s number.

3 Method of Solution

Due to the model's extreme nonlinearity, an exact solution of the set of Eqs. (11)–(13) subject to boundary constraints via Eq. (14) is implausible. The approach based on implicit differences is utilized for numerical evaluation. The following are the steps which are involved in this method:

• In order to get the finite difference nonlinear algebraic equations with the second-order truncation error, use the central difference derivatives and the average mid points of the rectangle to figure out the nonlinear equations.

• The resultant differential equations are first expressed in finite difference form, and then linearized by Newton's technique.

• After using the finite difference scheme and Newton's technique, a block tridiagonal matrix is created that has square blocks on the upper, main, and lower diagonals and zero blocks on the remaining diagonals. It also contains submatrices in lieu of scalars.

• The tridiagonal matrix factorization technique is used to solve block matrix problems. The LU decomposition method is based on forward and backward sweeps.

This procedure is continued until convergence occurs.

3.1 Keller Box Procedure

In this scheme, the below set of steps are implicated to attain numerical solutions:

• Transform Eqs. (11)–(13) ODE’s of higher order into set of first-order ODE’s. We add new independent variables in this circumstances, $p\left( \eta \right),\;q\left( \eta \right),\;\theta \left( \eta \right) = v\left( \eta \right),\;g\left( \eta \right),\;\phi \left( \eta \right) = s\left( \eta \right)\;{\text{and}}\;n\left( \eta \right)$ and Eqs. (11)–(13) and (14) change to the following form

  $f^{\prime} = p,\;p^{\prime} = q,\;v^{\prime} = g\;{\text{and}}\;s^{\prime} = n$ so that Eqs. (11)–(13) can be written as

  $$q^{\prime}\left( {1 + \lambda .q} \right) + fq - p^{2} - \left( {M + Kp} \right)p = 0$$

  (18)
  $$\quad\left( {1 + \frac{4R}{3}} \right)g^{\prime} + \Pr .fg - 2\Pr .pv \quad+ \left( {\frac{{{\text{Nc}}}}{{{\text{Le}}}}} \right).gn - \left( {\frac{{{\text{Nc}}}}{{{\text{Le}}.{\text{Nbt}}}}} \right)g^{2} = 0$$

  (19)
  $$n^{\prime} + {\text{Sc}}.fn + \left( {\frac{1}{{{\text{Nbt}}}}} \right)g^{\prime} = 0$$

  (20)

  In Eq. (14) the terms have been modified.

  $$\begin{aligned} & f\left( 0 \right) = 0,\;p\left( 0 \right) = 1 + \delta .q\left( 0 \right),\\ & v\left( 0 \right) = 1 + \beta .g\left( 0 \right),\;s\left( 0 \right) = 1 \;{\text{and}} \\ & p\left( \eta \right) \to 0,\;v\left( \eta \right) \to 0,\;s\left( \eta \right) \to 0\;{\text{as}}\;\eta \to \infty \\ \end{aligned}$$

  (21)

  Determine the finite differences with first-order differential equations ODE’s.

  For instance the finite differences at any point of the form are

  $$\qquad\left( {}\, \, \, \right)_{j}^{{n - \frac{1}{2}}} = \frac{1}{2}\left[ {\left( {}\, \, \, \right)_{j}^{n} + \left( {}\, \, \, \right)_{j}^{n - 1} } \right], \left( {}\, \, \, \right)_{{j - \frac{1}{2}}}^{n} = \frac{1}{2}\left[ {\left( {}\, \, \, \right)_{j}^{n} + \left( {}\, \, \, \right)_{j - 1}^{n} } \right]\qquad\qquad$$

  (22)
  $$\quad\qquad\qquad\left( {\frac{\partial u}{{\partial x}}} \right)_{{j - \frac{1}{2}}}^{{n - \frac{1}{2}}} = \frac{1}{{k_{n} }}\left[ {\left( u \right)_{{j - \frac{1}{2}}}^{n} - \left( u \right)_{{j - \frac{1}{2}}}^{n - 1} } \right], \left( {\frac{\partial u}{{\partial \eta }}} \right)_{{j - \frac{1}{2}}}^{{n - \frac{1}{2}}} = \frac{1}{{h_{j} }}\left[ {\left( u \right)_{{j - \frac{1}{2}}}^{{n - \frac{1}{2}}} - \left( u \right)_{{j - \frac{1}{2}}}^{{n - \frac{1}{2}}} } \right]$$

  (23)

  • Obtaining linearized algebraic equations through the help of Newton’s technique.

    $${\text{Ex:}}\;f_{j}^{{\left( {i + 1} \right)}} = f_{j}^{\left( i \right)} + \delta f_{j}^{\left( i \right)} .$$

    (24)

  • To find the solution, the set of linear equations can be arranged into the matrix form and implement the procedure of block tri-diagonal elimination technique.

    $$\begin{aligned} & {\text{Ex}}{.:}\;\left[ {\begin{array}{*{20}l} {[A_{1} ]} \hfill & {[C_{1} ]} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {[B_{2} ]} \hfill & {[A_{2} ]} \hfill & {[C_{1} ]} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & \cdots \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & \cdots \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {[B_{i - 1} ]} \hfill & {[C_{i - 1} ]} \hfill & {[B_{2} ]} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {[B_{j} ]} \hfill & {[A_{j} ]} \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {[\delta_{1} ]} \hfill \\ {[\delta_{2} ]} \hfill \\ \cdots \hfill \\ \cdots \hfill \\ {[\delta_{j - 1} ]} \hfill \\ {[\delta_{j} ]} \hfill \\ \end{array} } \right] \\ & \quad = \left[ {\begin{array}{*{20}l} {[r_{1} ]} \hfill \\ {[r_{2} ]} \hfill \\ \cdots \hfill \\ \cdots \hfill \\ {[r_{j - 1} ]} \hfill \\ {[r_{j} ]} \hfill \\ \end{array} } \right], \\ & {\text{i}}{\text{.e}}{.,}\;[A][\delta ] = [r] \\ \end{aligned}$$

    (25)

  • In accordance with the convergence criterion and compliance with the B.C’s (14), the following starting assumptions are acceptable guesses:

  $$\qquad f\left( \eta \right) = \frac{1}{{\left( {1 + \delta } \right)}}\left( {1 - e^{ - \eta } } \right),\;\theta \left( \eta \right) = \frac{1}{{\left( {1 + \beta } \right)}}e^{ - \eta } ,\;\phi \left( \eta \right) = e^{ - \eta }$$

  (26)

The presented method is completely trustworthy, has second-order consistency, and is simple to programme, all of which contribute to a highly desirable conclusion. The adaption of the accompanying initial estimations is one of the factors affecting the consistency of the scheme. To solve the aforementioned difference equations in block-matrix form, the Thomas method is utilized. The current research uses a consistent grid size of ${\Delta }\eta =$ 0.001, which provides four decimal places of accuracy for the majority of the indicated values in the table, with a tolerance for error 10⁻⁵ in every circumstance, MATLAB software was utilized to program.

4 Validation and Convergence of the Numerical Technique

The convergence of the Keller-Box method gets after 100 iterations. The accuracy of the current numerical solution is taken as 10⁻⁵. Table 1 shows an outstanding agreement between our procedure outcomes and the works of Hayat et al. [47] (Analytical Method) and Kho et al. [48] (Shooting Method).

Table 1 Comparison of Nusselt number values for various $\Pr$ when ${\text{Nc}} = 2.5,\;{\text{Nbt}} = 2.0,\;{\text{Le}} = 10,\;Kp = R = {\text{Sc}} = \beta = \lambda = \delta = 0.5,\;M = 0.3$

5 Results and Discussion

To gain a physical understanding of the present investigation of MHD heat and mass transport Williamson nanofluid flow with thermal radiation and porous medium, extensive numerical computations are accomplished using the Keller-Box approach. The findings validate the impact of various non-dimensional factors on the standard profiles, including the thermal radiation parameter, the magnetic field, and others. Additionally, evaluated the same on the coefficient of friction factor, rate of heat transport, and mass transfer using tables and diagrams. In this investigation the non-dimensional parameter values $\delta = 0.25,\;\lambda = 0.5,\;M = 0.3,\;Kp = 0.2, \;\beta = 0.5,\;\Pr = 7.0,\;{\text{Nc}} = 2.5,\;{\text{Nbt}} = 2.0,\;{\text{Le}} = 10,\;{\text{Sc}} = 5.0\;{\text{and}}\;R = 0.5$ were used. These variables are treated as constants throughout this research, except for the changed parameters shown in the graphs. The results are visually shown in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23 and 24. To validate the current numerical outcomes, a comparison with Hayat et al. [47] and Kho et al. [48] was performed, and a good agreement was found, as shown in Table 1.

Fig. 2

Variations of slip parameter on velocity profile

Fig. 3

Variations of slip parameter on temperature profile

Fig. 4

Variations of slip parameter on concentration profile

Fig. 5

Variations of thermal slip parameter on temperature profile

Fig. 6

Variations of thermal slip parameter on concentration profile

Fig. 7

Variation of the Williamson parameter on velocity profile

Fig. 8

Variation of the Williamson parameter on temperature profile

Fig. 9

Variation of the Williamson parameter on concentration profile

Fig. 10

Variation of Prandtl number on temperature

Fig. 11

Variations of heat capacitance ratio parameter on temperature

Fig. 12

Variation of Lewis number on temperature profile

Fig. 13

Variations of the diffusivity ratio parameter on temperature profile

Fig. 14

Variations of the diffusivity ratio parameter on concentration profile

Fig. 15

Variations of Schmidt number on concentration profile

Fig. 16

Variations of magnetic parameter on velocity profile

Fig. 17

Variations of magnetic parameter on temperature

Fig. 18

Variations of magnetic parameter on contration profile

Fig. 19

Variations of radiation parameter on temperature profile

Fig. 20

Variations of the permeability parameter on velocity profile

Fig. 21

The variations of thermal slip parameter and Prandtl number on temperature gradient

Fig. 22

The variations of diffusivity ratio parameter and heat capacitance ratio parameter on temperature gradient

Fig. 23

The variations of Lewis number and Prandtl number on temperature gradient

Fig. 24

The variations of radiation and Prandtl number on temperature gradient

Figure 2 demonstrates that velocity patterns decrease with slip parameter δ. Slip means that the fluid velocity in the vicinity of the sheet is no longer equivalent to the stretched sheet velocity. Increasing δ lowers the velocity because only a portion of the tugging on the sheet can be transferred to the fluid. Additionally, slip parameter δ reduces boundary layer width. Additionally, as the slip parameter δ grows, the width of the boundary layer decreases. The slip parameter, δ, rises, the fluid temperature increases, thereby increasing the thermal boundary layer thickness (See Fig. 3). Increasing the slip parameter produces friction at the surface, which, in turn, provides a frictional force to enable more fluid to flow over the stretched surface, decreasing the fluid velocity. Figure 4 pictorially represents for escalating values δ, enhances the species concentration gradients.

Figure 5 explains the outcome of the thermal slip factor (δ) on temperature curves. This figure indicates that when the thermal slip factor grows, the temperature field and its associated boundary layer width drop. This augmentation is very substantial in the area immediately next to the wall, but it has a minor impact farther away from the wall. Figure 6 depicts the concentration fluctuation as a function of β. It reveals that when the value of β rises, the concentration $\phi \left( \eta \right)$ declines.

Figures 7, 8, 9 explore the consequence of the Williamson parameter (λ) on the curves of velocity, temperature, and species concentration. It is noted that the growing values of λ, enhance the fluid velocity close to the wall and fall it at the free stream. As a result, as the Williamson parameter is raised, the width of the momentum boundary layer near the wall grows. It has been discovered that enhancing the values of λ raises the temperature and concentration distributions.

The influence of the Prandtl number (Pr) over the temperature curve is depicted in Fig. 10. When a rise in Pr causes a temperature drop, this indicates that the liquid’s thermal conductivity is significantly smaller than its viscosity. It's worth noting that increasing Pr values pointedly lowers the temperature. Thus, variable thermal conductivity is an excellent tool for determining the rate of transmission in heat. During the process of heat transfer, Pr is utilized to regulate the thickness of the thermal boundary layer. The effects of Nc on temperature distributions are depicted in Fig. 11. It is discovered that boosting Nc improves temperature gradients, resulting in a thicker boundary layer. Nc is defined as the ratio of nanoparticle’s and nanofluid's heat capacities. Generally, nanoparticles have a lower specific heat capacity (Cp) than liquids. Thus, the inclusion of solid particles raises the specific heat of the base fluid, resulting in a rise in the temperature profile.

Figure 12 describes the evolution of the temperature gradient as a function of the Lewis number (Le). Temperature diffusivity divided by nanoparticle mass species diffusivity is known as the Lewis number. As illustrated in Fig. 12, enhancing the Lewis number lowers temperature magnitudes, hence decreasing the thickness of the thermal boundary layer. Due to the fact that mass diffusivity is dependent on the species of nanoparticles present in the base fluid, proper selection of nanoparticles by polymer doping has a significant influence on the thermophysical behavior of enrobing flow. In Figs. 13 and 14, several values of the diffusivity ratio parameter (Nbt) were plotted against thermal and species concentration fields, respectively. Both profiles degraded as the Nbt value increased. It is important to note that the temperature and breadth of the thermal boundary layer decline as the value of Nbt grows. Because Nbt is defined as the ratio of Brownian to thermophoretic diffusivities, an increase in Nbt suggests that nanofluid particles are becoming more actively dispersed.

Figure 15 portrays the variance in the concentration profile for higher Schmidt indices. The concentration field is shown to be diminishing as the Schmidt volume rises. This is due to the fact that the Schmidt number is inversely proportional to the mass diffusivity. As a result, a liquid flow regime via a higher Sc has lower mass diffusion values as the concentration distribution becomes more focused.

Figure 16 depicts a plot of a velocity profile to assess the influence of the magnetic parameter. In this study, it was discovered that there is a verse relationship between positive changes in the magnetic parameter and the velocity curve. This is because of a resistive force known as the Lorentz force, which is triggered as the size of the magnetic field rises, opposing liquid flow and so diminishing the liquid's velocity. The applied magnetic field substantially raises the temperature of the fluid and, as shown in Fig. 17, the density of the classical thermal nanofluid boundary layer. Increased magnetic parameter values have a substantial effect on nanoparticle concentration gradients. As shown in Fig. 18, classical nanofluid occupies a larger volume percentage than non-Newtonian nanofluid.

Figure 19 exemplifies the impact of the radiation parameter on temperature scattering. An important observation demonstrates that escalate temperature sketches with modified values of R. Physically, R denotes the ratio of heat transmission by thermal radiation to heat transfer via conduction. Thermal radiation takes precedence over conduction at greater levels of R. The greater the R value, the more heat enters the system, causing an increase in θ(η).

The impact of the permeability parameter on the profiles of velocity is displayed in Fig. 20. It is evident that the occurrence of porous media restricts fluid flow, causing it to move more slowly. As a result, as the permeability parameter increases, the resistance to liquid motion rises and hence drops in velocity.

The fluctuation of the thermal slip parameter, Nusselt number for Prandtl number Pr is shown in Fig. 21. It has been revealed that with the rise of values for the thermal slip and Prandtl numbers Pr, the Nusselt number is enhanced. The variation of the Nusselt number through Nc and Nbt is seen in Fig. 22. It is noticed that when the amounts of both parameters rise, the Nusselt number increases as well. Figure 23 depicts the change in Nusselt number for incremental values of Pr and Le. Incremental levels of Le and Pr are accompanied by an increase in the temperature gradient. Figure 24 reveals the combined influence of the Prandtl number and the Radiation term R on the Nusselt number. It's worth noting that the magnitude of the Nusselt number increases via rising Pr and R values.

The variation in the skin friction coefficient $- f^{\prime\prime}\left( 0 \right)$ for various pertinent flow, parameters are shown in Table 2. According to Table 2, the skin friction coefficient is a decreasing function of λ. Furthermore, $- f^{\prime\prime}\left( 0 \right)$ rises, while δ, and M increase. Moreover, as the permeability parameter increases, the coefficient of skin friction $- f^{\prime\prime}\left( 0 \right)$ increases as well. This is because increasing the $Kp$ at the wall slows the fluid motion, resulting in a drop in velocity at the surface. The variation of the Nusselt and Sherwood numbers with respect to various physical parameters is shown in Table 3. As shown in this table, increasing the values of $\lambda ,\delta ,\beta$ and $Nc$ lowers the Nusselt number, while increasing the values of $\Pr$ and ${\text{Nbt}}$ has the opposite effect observed. Enhancing values of $\lambda , \delta \;{\text{and}}\;\Pr$ drops the values of local Sherwood number, but a reverse trend is observed in the case of $\beta ,{\text{Nc}},$ and ${\text{Nb}}$. Table 4 illustrates the variation of the Nusselt number and Sherwood number with respect to ${\text{Le}},{\text{Sc}},M,R\;{\text{and}}\; Kp$ while the other governed flow factors are fixed. As the rising values of Schmidt number Sc, the local Nusselt number $- \theta^{\prime}\left( 0 \right)$ decreases, however, the local Sherwood number $- \phi^{\prime}\left( 0 \right)$ increases. An accumulated values of Lewis number Le and Radiation parameterR escalates the rate of heat transfer and the opposite trend is noticed in the values of wall nanoparticle volume fraction. The variation of both $- \theta^{\prime}\left( 0 \right)$ and $- \phi^{\prime}\left( 0 \right)$ diminishes for noticeable values of M and Kp.

Table 2 Computational values of -$f^{\prime\prime}\left( 0 \right)$ for various values of $\delta ,\lambda ,M,Kp$ when $\beta = 1.0,\;\Pr = 7.0,\;{\text{Nc}} = 2.5,\;{\text{Nbt}} = 2.0,\;{\text{Le}} = 10,\;{\text{Sc}} = 5.0,\;R = 0.5$

Table 3 Computational values of $- \theta^{\prime}\left( 0 \right)$ and $- \varphi^{\prime}\left( 0 \right)$ for various values of $\delta ,\beta ,\lambda ,\Pr ,{\text{Nc}},{\text{Nbt}}$ when ${\text{Le}} = 10,\;{\text{Sc}} = 5,\;M = 0.5,\;R = 0.5\;{\text{and}}\; Kp = 0.2$

Table 4 Numerical computations of $- \theta^{\prime}\left( 0 \right)$ and $- \varphi^{\prime}\left( 0 \right)$ for different values of ${\text{Le}},{\text{Sc}},M,R,Kp$

6 Final Remarks

A numerical study of MHD Williamson nanofluid passing through a stretched surface is performed, taking into consideration the effects of heat radiation and the porous medium. The findings are obtained using the Keller-Box approach. The influence of several critical flow parameters on three fluid flow profiles is described using a graphical representation form. The following are the major conclusions drawn from the preceding discussion:

• In the presence of increasing magnetic field (M) and permeability parameter values, it is predicted that the velocity profile would diminish.

• While an increase in the value of $\delta$ reduces the velocity, but heat and mass transfer gradients exhibit the opposite pattern

• For larger values of Williamson parameter, a drop in velocity field is seen, along with an upsurge in temperature and concentration.

• As the values of Nc and R increase, the fluid temperature increases; however, the reverse trend is seen as the values of Pr, Le, and Nbt increase.

• The temperature and concentration profiles become more pronounced as M increases, but thermal slip factor $\beta$ has the reverse trend.

• The fluid concentration gradients diminish as enhanced values of Nbt and Schmidt number (Sc).

• Enhancement in the values of Pr against Le, and Nc versus Nbt, all contribute to an increase in the magnitude of heat transfer rate.

Appendix

After using the similarity transformations

$$\begin{aligned} & u = bxf^{\prime}\left( \eta \right),\quad v = - \left( {b\nu } \right)^{\frac{1}{2}} f\left( \eta \right),\quad \eta = \sqrt {\frac{b}{\nu }} y \\ & \theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\quad \phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }} \\ \end{aligned}$$

The following Partial differential Eqs. (1)–(4) are transformed into Ordinary differential equations:

First we need to find the following differentials of $\eta , u,v,T\;{\text{and}}\;C$ with respect to $x \& y.$

$$\begin{aligned} & \frac{\partial \eta }{{\partial x}} = 0,\quad \frac{\partial \eta }{{\partial y}} = \sqrt {\frac{b}{\nu }} , \\ & \quad \frac{\partial u}{{\partial x}} = bf^{\prime}\left( \eta \right),\quad \frac{\partial u}{{\partial y}} = bxf^{\prime\prime}\left( \eta \right)\sqrt {\frac{b}{\nu }} \\ & \frac{\partial v}{{\partial x}} = 0, \quad \frac{\partial v}{{\partial y}} = - bf^{\prime}\left( \eta \right),\quad \frac{{\partial^{2} u}}{{\partial y^{2} }} = \frac{{xb^{2} }}{\nu }f^{\prime\prime\prime}\left( \eta \right), \\ & \quad \frac{\partial T}{{\partial x}} = 2ax\theta^{\prime}\left( \eta \right), \quad \frac{\partial T}{{\partial y}} = \sqrt {\frac{b}{\nu }} ax^{2} \theta ^{\prime}\left( \eta \right) \\ & \frac{{\partial^{2} T}}{{\partial y^{2} }} = \frac{b}{\nu }ax^{2} \theta^{\prime\prime}\left( \eta \right),\quad \frac{\partial C}{{\partial x}} = 2ax\phi \left( \eta \right) , \\ & \quad \frac{\partial C}{{\partial y}} = \sqrt {\frac{b}{\nu }} ax^{2} \phi^{^{\prime}\left( \eta \right)} ,\quad \frac{{\partial^{2} C}}{{\partial y^{2} }} = \frac{b}{\nu }ax^{2} \phi^{\prime\prime}\left( \eta \right) \\ \end{aligned}$$

Then Eq. (1) itself satisfies

$$\frac{\partial u }{{\partial x}} + \frac{\partial v }{{\partial y}} = bf^{\prime}\left( \eta \right) + ( - bf^{\prime}\left( \eta \right) = 0$$

Equation (2) $u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = \nu \frac{{\partial^{2} u}}{{\partial y^{2} }} + \sqrt 2 \nu {\Gamma }\frac{\partial u}{{\partial y}}\frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\sigma B^{2}_{0} }}{\rho }u - \frac{v}{{k^{\prime}}}u$ transformed to the following form.

$$\begin{aligned} & \Rightarrow bxf^{\prime}\left( \eta \right).bf^{\prime}\left( \eta \right) + \left[ { - \left( {b\nu }\right)^{\frac{1}{2}} f\left( \eta \right)} \right].\left[ {bx\sqrt {\frac{b}{\nu }} f^{\prime\prime}\left( \eta \right)} \right]\\&\quad = \nu \left[ {\frac{{b^{2} x}}{\nu }f^{\prime\prime\prime}\left( \eta \right)} \right ] \\ & \qquad +\sqrt 2 \nu {\Gamma} {bx\sqrt {\frac{b}{\nu }} }f^{\prime\prime}( \eta ) {\frac{{b^{2} x}}{\nu }}f^{\prime\prime\prime}\left( \eta \right) - \frac{{\sigma B_{0}^{2} }}{\rho }bxf^{\prime}\left( \eta \right)\\ &\qquad -\frac{\nu }{{k^{\prime}}}bxf^{\prime}\left( \eta \right) \\ &\Rightarrow b^{2} xf^{{\prime}{2}} \left( \eta \right) - b^{2}xf\left( \eta \right)f^{\prime\prime}\left( \eta \right) = b^{2}xf^{\prime\prime\prime}\left( \eta \right) \\ & \quad + \sqrt {\frac{{2b^{3} }}{\nu }} b^{2} x{\Gamma }f^{^{\prime\prime}} \left(\eta \right)f^{\prime\prime\prime}\left( \eta \right) - \frac{{b^{2}x\sigma B_{0}^{2} }}{\rho b}f^{\prime}\left( \eta \right) -\frac{{\nu b^{2} x}}{{k^{\prime}b}}f^{\prime}\left( \eta \right) \\& \Rightarrow f^{{\prime}{2}} \left( \eta \right) - f\left( \eta \right)f^{\prime\prime}\left( \eta \right) =f^{\prime\prime\prime}\left( \eta \right) + \sqrt {\frac{{2b^{3}}}{\nu }} {\Gamma }f^{\prime\prime}\left( \eta \right)f^{\prime\prime\prime}\left( \eta \right)\\ &\quad -\frac{{\sigma B_{0}^{2} }}{\rho b}f^{\prime}\left( \eta \right) -\frac{\nu }{{k^{\prime}b}}f^{\prime}\left( \eta \right) \\ &\Rightarrow \user2{f^{\prime\prime\prime}}\left( {\varvec{\eta}}\right) + \user2{\lambda f^{\prime\prime}}\left( {\varvec{\eta}}\right)\user2{f^{\prime\prime\prime}}\left( {\varvec{\eta}} \right)\\ &\quad - \user2{f^{\prime}}^{2} \left( {\varvec{\eta}} \right) +{\varvec{f}}\left( {\varvec{\eta}}\right)\user2{f^{\prime\prime}}\left( {\varvec{\eta}} \right) -\user2{Mf^{\prime}}\left( {\varvec{\eta}} \right) -\user2{Kpf^{\prime}}\left( {\varvec{\eta}} \right) = 0 \\\end{aligned}$$

The Energy Eq. (3)

$u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\left( {\rho c} \right)_{p} }}{{\left( {\rho c} \right)_{f} }}\left[ {D_{{\text{B}}} \frac{\partial C}{{\partial y}}\frac{\partial T}{{\partial y}} + \frac{{D_{T} }}{{D_{\infty } }}\left( {\frac{\partial T}{{\partial y}}} \right)^{2} } \right] + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} \left( {\rho c} \right)_{f} }}\frac{{\partial^{2} T}}{{\partial y^{2} }}$ is transformed to the following form:

$$\begin{aligned} & \Rightarrow bxf^{\prime}\left( \eta \right). 2ax\theta^{\prime}\left( \eta \right) + \left[ { - \left( {b\nu } \right)^{\frac{1}{2}} f\left( \eta \right)} \right].\left[ {ax^{2} \sqrt {\frac{b}{\nu }} \theta^{^{\prime}\left( \eta \right)} } \right]\\ & \quad = \alpha \left[ {\frac{{abx^{2} }}{\nu }\theta^{^{\prime\prime}\left( \eta \right)} } \right] \\ & \qquad + \frac{{\left( {\rho C} \right)_{p} }}{{\left( {\rho C} \right)_{f} }}\left[ {D_{{\text{B}}} ax^{2} \sqrt {\frac{b}{\nu }} \theta^{\prime}\left( \eta \right).ax^{2} \sqrt {\frac{b}{\nu }} \phi^{\prime}\left( \eta \right) + \frac{{D_{{\text{T}}} }}{{T_{\infty } }}\left( {ax^{2} \sqrt {\frac{b}{\nu }} \theta^{\prime}\left( \eta \right)} \right)^{2} } \right]\\ & \qquad + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{\left( {\rho C} \right)_{f} 3k^{*} \nu }}ax^{2} b \theta ^{\prime\prime}\left( \eta \right). \\ & \Rightarrow 2abx^{2} f^{\prime}\theta^{\prime} - abx^{2} f\theta^{\prime} = \alpha \frac{{abx^{2} }}{\nu }\theta^{\prime\prime} + \frac{{\left( {\rho C} \right)_{p} }}{{\left( {\rho C} \right)_{f} }}D_{{\text{B}}} a^{2} x^{4} \frac{b}{\nu }\theta^{\prime}\phi^{\prime} \\ & \qquad + \frac{{\left( {\rho C} \right)_{p} }}{{\left( {\rho C} \right)_{f} }}a^{2} x^{4} \frac{b}{\nu }\frac{{D_{{\text{T}}} }}{{T_{\infty } }}\theta^{{^{{\prime}{2}} }} + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{\left( {\rho C} \right)_{f} 3k^{*} \nu }}ax^{2} b \theta ^{\prime\prime} \\ & \Rightarrow 2f^{\prime}\theta - f\theta^{\prime} = \frac{\alpha }{\nu }\theta^{\prime\prime} + \frac{{\left( {\rho C} \right)_{p} }}{{\left( {\rho C} \right)_{f} }}D_{{\text{B}}} \frac{{ax^{2} }}{\nu }\theta^{\prime}\phi^{\prime} \\ &\qquad + \frac{{\left( {\rho C} \right)_{p} }}{{\left( {\rho C} \right)_{f} }}\frac{{ax^{2} }}{\nu }\frac{{D_{{\text{T}}} }}{{T_{\infty } }}\theta^{{^{{\prime}{2}} }} + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{\left( {\rho C} \right)_{f} 3k^{*} \nu }} \theta ^{\prime\prime} \\ & \Rightarrow 2f^{\prime}\theta - f\theta^{\prime} = \frac{1}{\Pr }\theta^{\prime\prime} + \frac{{{\text{Nc}}}}{{{\text{Le}}.\Pr }}\theta^{\prime}\phi^{\prime} + \frac{{{\text{Nc}}}}{{\Pr .{\text{Le}}.{\text{Nbt}}}}\theta^{{^{{\prime}{2}} }} + \frac{4}{3\Pr }R \theta ^{\prime\prime} \\ & \Rightarrow 2f^{\prime}\theta - f\theta^{\prime} = \frac{1}{\Pr }\theta^{\prime\prime} + \frac{4}{3\Pr }R \theta ^{\prime\prime} + \frac{{{\text{Nc}}}}{{\Pr .{\text{Le}}}}\theta^{\prime}\phi^{\prime} + \frac{{{\text{Nc}}}}{{\Pr .{\text{Le}}.{\text{Nbt}}}}\theta^{{^{{\prime}{2}} }} \\ & \Rightarrow 2f^{\prime}\theta - f\theta^{\prime} = \frac{1}{\Pr }\left( {1 + \frac{4}{3}R} \right) \theta ^{\prime\prime} + \frac{{{\text{Nc}}}}{{\Pr .{\text{Le}}}}\theta^{\prime}\phi^{\prime} + \frac{{{\text{Nc}}}}{{\Pr .{\text{Le}}.{\text{Nbt}}}}\theta^{{^{{\prime}{2}} }} \\ & \Rightarrow \left( {\frac{{3 + 4{\varvec{R}}}}{3}} \right)\user2{\theta^{\prime\prime}} + {\varvec{Pr}}.\user2{f\theta^{\prime}} - 2{\varvec{Pr}}.\user2{f^{\prime}\theta } + \left( {\frac{{{\varvec{Nc}}}}{{{\varvec{Le}}}}} \right)\user2{\theta^{\prime}}\phi^{\prime}\\ &\qquad + \frac{{{\varvec{Nc}}}}{{\left( {{\varvec{Le}}} \right)\left( {{\varvec{Nbt}}} \right)}}\left( {\user2{\theta^{\prime}}} \right)^{2} = 0\user2{ } \\ \end{aligned}$$

Similarly, we get

Species concentration equation from (4) in the following form

$$\phi^{\prime\prime} + {\varvec{Sc}}.{\varvec{f}}\phi^{\prime} + \left( {\frac{1}{{{\varvec{Nbt}}}}} \right)\user2{\theta^{\prime\prime}} = 0$$