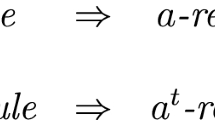The locally nilradical for modules over commutative rings

Abstract

Let R be a commutative unital ring and $a\in R.$ We introduce and study properties of a functor $a\Gamma _{a}(-),$ called the locally nilradical on the category of R-modules. $a\Gamma _{a}(-)$ is a generalisation of both the torsion functor (also called section functor) and Baer’s lower nilradical for modules. Several local–global properties of the functor $a\Gamma _{a}(-)$ are established. As an application, results about reduced R-modules are obtained and hitherto unknown ring theoretic radicals as well as structural theorems are deduced.

1 Introduction

Radicals are a good tool to study the structure of rings and modules over rings. There are several radicals in the literature about rings and modules which include among others; Baer’s lower nilradical (also called the prime radical), Köthe’s upper nilradical, Andrunakievich’s generalised nilradical (also called the completely prime radical), Jacobson radical and Brown–McCoy radical. In this article, we introduce and study a radical called the locally nilradical for modules over commutative rings. Radical theory also exists for abelian categories, and it is what is termed as torsion theory.

Throughout this paper, all rings R are commutative and unital. The category of all left R-modules is denoted by R-Mod. If $M \in R$-Mod, then $\sqrt{(0:M)}$ denotes the radical ideal of (0 : M),  i.e., $\sqrt{(0:M)}= \left\{ r\in R~|~r^{k}\in (0:M) ~\text {for some } k\in {\mathbb {Z}}^{+} \right\} .$ Let M be an R-module and ${{\mathfrak {a}}}$ an ideal of R. The $\mathbf {\mathfrak {a}}$-torsion (also called the section) functor is defined by:

$$\begin{aligned}&\Gamma _{{{\mathfrak {a}}}}:R\text {-Mod} \rightarrow R\text {-Mod}\\&M\mapsto \Gamma _{{{\mathfrak {a}}}}(M), \end{aligned}$$

where $\Gamma _{{{\mathfrak {a}}}}(M)$ is the submodule of M given by $\Gamma _{{\mathfrak {a}}}(M):= \left\{ m\in M ~| ~{{\mathfrak {a}}}^{k}m= 0 ~\text {for some}~ k\in {\mathbb {Z}}^{+} \right\} .$ On modules defined over Noetherian rings, this functor is left exact and a radical, see Rohrer (2018). Its right derived functor $H_{\mathfrak {a}}^i(-)$ is what is called the local cohomology functor with respect to $\mathfrak {a}.$ For more information about local cohomology, see Brodmann and Sharp (2013). If R is a ring, $a\in R$ and $\mathbf {\mathfrak {a}}$ an ideal of R generated by a,  then it is easy to see that $\Gamma _{{\mathfrak {a}}}(M)= \Gamma _{a}(M),$ where $\Gamma _{a}(M):= \left\{ m\in M ~| ~a^{k}m= 0 ~\text {for some } k\in {\mathbb {Z}}^{+} \right\} .$

By generalising the torsion functor, we define a new functor:

$$\begin{aligned}&a\Gamma _{a}:R\text {-Mod} \rightarrow R\text {-Mod}\\&M\mapsto a\Gamma _{a}(M) , \end{aligned}$$

called the locally nilradical which associates to every R-module M a submodule $a\Gamma _{a}(M)$ for every $a\in R$, where $a\Gamma _{a}(M):=\left\{ am~| ~a^{k}m=0, ~m\in M, \text {for some}~k\in {\mathbb {Z}}^{+} \right\}$, i.e., left multiplication by a of the submodule $\Gamma _a(M)$.

$a\Gamma _{a}(M)$ is contained in the envelope $E_{M}(0)$ of M which has been considered in the literature as a module analogue of the set of nilpotent elements of a ring. Secondly, we observe that if M is the R-module R,  then $a\Gamma _{a}(-)$ associates to R a nil ideal $a\Gamma _{a}(R)$ of R. For if $x\in a\Gamma _{a}(R),$ then $x= ar$ and $a^{k}r =0$ for some $k\in {\mathbb {Z}}^{+}.$ It follows that $x^{k}= (ar)^{k}= a^{k}r^{k}=0.$ So, x is nilpotent and $a\Gamma _{a}(R)$ is nil. We use the adjective “locally” because $a\Gamma _{a}(-)$ gives the local behaviour for a given element $a\in R$ as opposed to the global picture which is for all $a\in R$ given by the nilradical ${\mathcal {N}}(R).$ To be precise, we show that $\bigcup \nolimits _{a\in R} a\Gamma _{a}(R)= {\mathcal {N}}(R).$

This paper is devoted to studying properties of the functor $a\Gamma _{a}(-)$. We list some of them below.

• $a\Gamma _{a}(-)$ is a radical on the category R-Mod (Proposition 3.1).

• For a Noetherian local ring R of characteristic p,  the Frobenius functor $F_{R}(-)$ is exact on R-Mod if and only if for any $a\in R$, the functor $a\Gamma _{a}(-)$ is trivial on R-Mod (Theorem 3.1).

• For any ring R,  and $a\in R,$ $a\Gamma _{a}(R)[x]= a\Gamma _{a}(R[x])$ (Theorem 3.2).

• For any R-module M,  $\bigcup \nolimits _{a\in R} a\Gamma _{a}(M) = E_{M}(0)$ where $E_{M}(0)$ is the envelope of the zero submodule of M,  (Proposition 4.1) and $\bigcup \nolimits _{a\in R} a\Gamma _{a}(R)= {\mathcal {N}}(R)$ (Corollary 4.1).

• For any R-module M,  $\sqrt{(0:M)}M= \sum \nolimits _{a\in \sqrt{(0:M)} }a\Gamma _{a}(M)$ (Theorem 5.2).

• If M is a finitely generated multiplication R-module, then $\sum \nolimits _{a\in \sqrt{(0:M)} }a\Gamma _{a}(M)=\beta (M)$, where $\beta (M)$ is the prime radical of M (Corollary 5.4).

• If M is a reduced R-module and $\mathfrak {a}$ is the ideal of R generated by $a\in R$, then for any $a\in R$, the i-th local cohomology of M with respect to $\mathfrak {a}$ is given by $H_{\mathfrak {a}}^i(M)\cong \text {Ext}_{R}^i(R/\mathfrak {a}, M)$, (Theorem 6.1).

For more information about radical theory of rings, see Gardner and Wiegandt (2004); while for torsion theory, see Bican et al. (1982), Stenstroem (2012) among others.

2 Reduced modules

Lee and Zhou (2004) introduced reduced modules. It is clear that an R-module M is reduced if and only if for all $a\in R,$ $a\Gamma _{a}(M)=0.$ The functor $a\Gamma _{a}(-)$ therefore can be seen as a measure of how far a module is from being reduced.

Definition 2.1

Let R be a ring, M an R-module and $a\in R$. M is a-reduced if for all $m\in M$,

$$\begin{aligned} a^{2}m=0~ \text { implies that}~am=0. \end{aligned}$$

Definition 2.2

An R-module M is reduced if it is a-reduced for all $a\in R.$

It then follows that an R-module is (globally) reduced if and only if it is locally reduced.

Proposition 2.1

Every free module defined over a reduced ring is reduced.

Proof

It follows from Lee and Zhou (2004, Example 1.3). $\square$

Corollary 2.1

Any vector space is a reduced module.

Corollary 2.2

A projective module defined over a reduced ring is reduced.

For an R-module M,  $a\in R$ and $k\in {\mathbb {Z}}^{+},$ we write $(0:_{M}{a}^{k})$ to denote the submodule of M given by $\left\{ m\in M~|~a^{k}m=0\right\} .$

Proposition 2.2

Let M be an R-module, $a\in R$ and ${{\mathfrak {a}}}$ the ideal of R generated by a. The following statements are equivalent:

• 1. M is a-reduced,

• 2. $a\Gamma _{a}(M)= 0$,

• 3. $(0:_{M}{a})~=~(0:_{M}{a}^{k})~\text {for all} ~k\in {\mathbb {Z}}^{+}$,

• 4. $\lim \limits _{\overrightarrow{k}}\text{ Hom }_{R}(R/{{\mathfrak {a}}}^{k},M)\cong \text { Hom}_{R}(R/{{\mathfrak {a}}},M)$,

• 5. $\Gamma _{a}(M)\cong \text { Hom}_{R}(R/{{\mathfrak {a}}},M)$,

• 6. $0\rightarrow \Gamma _{a}(M) \rightarrow M \rightarrow aM \rightarrow 0$ is a short exact sequence.

Proof

$1\Rightarrow 2$ :

Let $n \in a\Gamma _{a}(M).$ Then $n=am$ for some $m \in \Gamma _{a}(M).$ So, there exists $k\in {\mathbb {Z}}^{+}$ such that $a^{k}m=0.$ From 1,  we have $am=0.$ Thus, $n=0$ and $a\Gamma _{a}(M)=0.$

$2\Rightarrow 3$ :

In general, $(0:_{M}{a})\subseteq (0:_{M}{a}^{k}).$ Now, let $m\in (0:_{M}{a}^{k}),$ i.e., $a^{k}m = 0.$ It follows that $m \in \Gamma _{a}(M).$ So, by 2,  $am \in a\Gamma _{a}(M)=0$ which implies that $m \in (0:_{M}{a}).$

$3\Rightarrow 4$ :

It is known that $\text {Hom}_{R}(R/{{\mathfrak {a}}}^{k},M)\cong (0:_{M}{a}^{k})$ and $\lim \limits _{\overrightarrow{k}}\text{ Hom }_{R}(R/{{\mathfrak {a}}}^{k},M)$ $\cong \bigcup \nolimits _{k\in {\mathbb {Z}}^{+}} (0:_{M}{a}^{k}),$ see (Brodmann and Sharp 2013, page 6). Since by 3,  $(0:_{M}{a}^{k})=(0:_{M}{a})$ for all $k\in {\mathbb {Z}}^{+},$ we have $\lim \limits _{\overrightarrow{k}}\text{ Hom }_{R}(R/{{\mathfrak {a}}}^{k},M) \cong \text { Hom}_{R}(R/{{\mathfrak {a}}},M).$

$4\Rightarrow 5$ :

Since $\Gamma _{a}(M)\cong \lim \limits _{\overrightarrow{k}}\text{ Hom }_{R}(R/{{\mathfrak {a}}}^{k},M),$ 4 implies that $\Gamma _{a}(M)\cong \text { Hom}_{R}(R/{{\mathfrak {a}}},M).$

$5\Rightarrow 6$ :

The R-module epimorphism $M \rightarrow aM$ defined by $m\mapsto am$ has kernel $(0:_{M}{a}).$ So, $0\rightarrow (0:_{M}{a}) \rightarrow M \rightarrow aM \rightarrow 0$ is a short exact sequence. From 5,  $\Gamma _{a}(M)\cong \text { Hom}_{R}(R/{{\mathfrak {a}}},M)\cong (0:_{M}{a})$. So, $0\rightarrow \Gamma _{a}(M) \rightarrow M \rightarrow aM \rightarrow 0$ is a short exact sequence.

$6\Rightarrow 1$ :

Let $a\in R$ and $m\in M$ such that $a^{2}m=0.$ Then $m\in \Gamma _{a}(M).$ From 6,  $\Gamma _{a}(M)$ is the kernel of the epimorphism $M\rightarrow aM$ given by $m\mapsto am .$ It follows that $am=0$ which establishes 1. $\square$

Proposition 2.3

Let M be an R-module and $\mathfrak {a}$ an ideal of R generated by a. The following statements are equivalent:

• 1. M is reduced;

• 2. $a\Gamma _{a}(M)= 0~\text {for all}~ a\in R;$

• 3. $(0:_{M}{a})=(0:_{M}{a}^{k})~\text {for all} ~a\in R, k\in {\mathbb {Z}}^{+};$

• 4. $\lim \limits _{\overrightarrow{k}}\text{ Hom }_{R}(R/{{\mathfrak {a}}}^{k},M)\cong \text { Hom}_{R}(R/{{\mathfrak {a}}},M)~\text {for all}~ a\in R;$

• 5. $\Gamma _{a}(M)\cong \text { Hom}_{R}(R/{{\mathfrak {a}}},M)~\text{ for } \text{ all } a\in R;$

• 6. $0\rightarrow \Gamma _{a}(M) \rightarrow M \rightarrow aM \rightarrow 0$ is a short exact sequence for all $a\in R$.

Proof

This follows from Proposition 2.2 and the fact that an R-module is reduced if and only if it is a-reduced for all $a \in R.$ $\square$

Proposition 2.2 (resp. Proposition 2.3) shows that being a-reduced (resp. reduced) is a categorical property, i.e., it can be expressed entirely in terms of objects and morphisms. Therefore, if R and S are rings and $F: R\text {-Mod} \rightarrow S\text {-Mod}$ is a category equivalence, then an R-module M is a-reduced (resp. reduced) if and only if so is the S-module F(M).

We now give a new characterisation of reduced rings.

Corollary 2.3

Let R be a ring and $\mathfrak {a}$ an ideal of R generated by a. The following statements are equivalent:

• 1. R is reduced;

• 2. $a\Gamma _{a}(R)= 0~\text {for all}~ a\in R;$

• 3. $(0:_{R}{a})=(0:_{R}{a}^{k})~\text {for all} ~a\in R, k\in {\mathbb {Z}}^{+};$

• 4. $\lim \limits _{\overrightarrow{k}}\text{ Hom }_{R}(R/{{\mathfrak {a}}}^{k},R)\cong \text { Hom}_{R}(R/{{\mathfrak {a}}},R)~\text {for all}~ a\in R;$

• 5. $\Gamma _{a}(R)\cong \text { Hom}_{R}(R/{{\mathfrak {a}}},R)~\text{ for } \text{ all } a\in R;$

• 6. $0\rightarrow \Gamma _{a}(R) \rightarrow R \rightarrow aR \rightarrow 0$ is a short exact sequence for all $a\in R$.

Proof

This follows from Proposition 2.3 and the fact that a ring R is reduced if and only if the R-module R is reduced. $\square$

For a given ring R and $a\in R$, the submodule $a\Gamma _{a}(M)$ is a measure of how far the R-module M is from being a-reduced.

Example 2.1

Let p be a prime number, $k\in {\mathbb {Z}}^{+}$ and ${\mathbb {Z}}_{p^{k}}$ a group of integers modulo $p^{k}.$ ${\mathbb {Z}}_{p^{k}}$ is a ${\mathbb {Z}}$-module and $\Gamma _{p}({\mathbb {Z}}_{p^{k}})= {\mathbb {Z}}_{p^{k}}.$ It follows that for $k=1,~\Gamma _{p}({\mathbb {Z}}_{p})= {\mathbb {Z}}_{p}$ and hence $p\Gamma _{p}({\mathbb {Z}}_{p})= 0,$ i.e., every ${\mathbb {Z}}$-module ${\mathbb {Z}}_{p}$ is p-reduced.

Proposition 2.4

If $\{M_{i}\}_{i\in I}$ is a family of R-modules and $M =\prod \nolimits _{i\in I} M_{i}$, then M is a reduced $(\text {resp.}~ a\text {-reduced})$ R-module if and only if each $M_i$ is a reduced $(\text {resp.}~a {\text {-reduced}})$ R-module.

Proof

Follows from (Lee and Zhou 2004, Example 1.3). $\square$

Proposition 2.5

For any R-module M and $a\in R,$ the R-module $M/a\Gamma _{a}(M)$ is a-reduced.

Proof

Suppose that $M/a\Gamma _{a}(M)$ is not a-reduced, i.e., there exists $m\in M$ and $k\in {\mathbb {Z}}^{+}$ such that $a^{k}m\in a\Gamma _{{\mathfrak {a}}}(M)$ but $am\notin a\Gamma _{a}(M).$ $a^{k}m\in a\Gamma _{a}(M)$ implies that $a^{k-1}m\in \Gamma _{{\mathfrak {a}}}(M).$ So, $a^{s}(a^{k-1}m)=0$ for some $s\in {\mathbb {Z}}^{+}$ and $a^{s+k-1}m=0 .$ However, $am\notin a\Gamma _{a}(M)$ implies that $m\notin \Gamma _{a}(M)$ and as such $a^{l}m \ne 0$ for all $l\in {\mathbb {Z}}^{+},$ which is a contradiction since $a^{s+k-1}m=0.$ $\square$

Corollary 2.4

For any R-module M and $a\in R,$

$$\begin{aligned} a\Gamma _{a}(M/a\Gamma _{a}(M))=0. \end{aligned}$$

Proof

By Proposition 2.5, the R-module $M/a\Gamma _{a}(M)$ is a-reduced. The desired result follows from Proposition 2.2. $\square$

3 Properties of the locally nilradical

A functor $\gamma :R\text {-Mod} \rightarrow R\text {-Mod}$ is a preradical if for every R-homomorphism $f:M \rightarrow N,~ f(\gamma (M))\subseteq \gamma (N)$. $\gamma$ is a radical if it is a preradical and for all $M \in R$-Mod, $\gamma (M/\gamma (M))=0.$ A radical $\gamma$ is hereditary or left exact if for every submodule N of a module $M \in R$-Mod, $\gamma (N)= N \cap \gamma (M).$ Equivalently, if for any exact sequence $0 \rightarrow N \rightarrow M \rightarrow K$ of R-modules, the sequence $0 \rightarrow \gamma (N) \rightarrow \gamma (M) \rightarrow \gamma (K)$ is also exact.

Proposition 3.1

For any ring R and $a\in R$, the functor

$$\begin{aligned}&a\Gamma _{a}:R{\text {-Mod}} \rightarrow R{\text {-Mod}} \\&M\mapsto a\Gamma _{a}(M) \end{aligned}$$

is a radical.

Proof

Let $f: M \rightarrow N$ be an R-module homomorphism. Let $x\in f(a\Gamma _{a}(M)).$ Then $x=af(m)$ for some $m\in \Gamma _{a}(M).$ This implies that $a^{k}m=0$ for some $k \in {\mathbb {Z}}^{+}.$ So, $a^{k}f(m)=f(a^{k}m)=f(0)=0.$ This shows that $f(m)\in \Gamma _{a}(N)$ and $x= af(m)\in a\Gamma _{a}(N).$ Hence, $f(a\Gamma _{a}(M))\subseteq a\Gamma _{a}(N).$ This shows that the functor $a\Gamma _{a}(-)$ is a preradical. Corollary 2.4 shows that $a\Gamma _{a}(-)$ is a radical. $\square$

The radical $a\Gamma _{a}(-)$ is in general not left exact. Consider $M:={\mathbb {Z}}_{8}$ and $N:=2{\mathbb {Z}}_{8}.$ By Example 2.1, if $a= 2\in {\mathbb {Z}},$ then $2\Gamma _{2}(M)= 2{\mathbb {Z}}_{8}$ and $2\Gamma _{2}(N)= 4{\mathbb {Z}}_{8} \subsetneq 2{\mathbb {Z}}_{8}= N\cap 2\Gamma _{2}(M).$ However, on the subcategory of reduced R-modules, $a\Gamma _{a}(-)$ is a left exact radical.

A submodule N of an R-module M is characteristic if for all automorphisms f of M, $f(N)\subseteq N$.

Proposition 3.2

Let R be a ring, $a\in R$ and M an R-module. The following statements hold.

• 1. $a\Gamma _{a}(R)$ is an ideal of R.

• 2. For each $M \in R$-Mod, $a\Gamma _{a}(M)$ is a characteristic submodule of M and

  $$\begin{aligned} a\Gamma _{a}(R)M \subseteq a\Gamma _{a}(M). \end{aligned}$$

• 3. If M is projective, then $a\Gamma _{a}(M)= a\Gamma _{a}(R)M.$

Proof

Since $a\Gamma _{a}(-)$ is a (pre)radical, the proof follows from Bican et al. (1982, Proposition 1.1.3). $\square$

From Proposition 3.2, we can recover Corollary 2.2, i.e., a projective module M over a reduced ring R is reduced. For if R is reduced, then so is the module ${}_RR.$ As such, $a\Gamma _{a}(R)=0$ for all $a\in R.$ By Proposition 3.2, $a\Gamma _{a}(M)=0$ for all $a\in R$ and therefore by Proposition 2.3, M is reduced.

Proposition 3.3

Let M be an R-module, $a\in R$ and N a submodule of M.

• 1. $a\Gamma _{a}(N) \subseteq N\cap a\Gamma _{a}(M)$ and $(a\Gamma _{a}(M) + N)/N \subseteq a\Gamma _{a}(M/N).$

• 2. If $a\Gamma _{a}(N)= N,$ then $N \subseteq a\Gamma _{a}(M).$

• 3. If $a\Gamma _{a}(M/N)=0,$ then $a\Gamma _{a}(M) \subseteq N.$

Proof

It follows from Bican et al. (1982, Proposition 1.1.1) since $a\Gamma _{a}(-)$ is a (pre)radical. $\square$

Proposition 3.4

Let $\{M_{i}\}_{i\in I}$ be a family of R-modules. Then

$$\begin{aligned} a\Gamma _{a}\left( \bigoplus \limits _{i\in I} M_{i}\right) =\bigoplus \limits _{i\in I}a\Gamma _{a}(M_{i}) \end{aligned}$$

and

$$\begin{aligned} a\Gamma _{a}\left( \prod \limits _{i\in I} M_{i}\right) \subseteq \prod \limits _{i\in I}a\Gamma _{a}(M_{i}). \end{aligned}$$

Proof

It follows from Bican et al. (1982, Proposition 1.1.2). $\square$

The radical $a\Gamma _{a}(M)$ is not idempotent. Take for instance $M:= {\mathbb {Z}}_{4}$ as a ${\mathbb {Z}}$-module. $2\Gamma _{2}({\mathbb {Z}}_{4})= 2{\mathbb {Z}}_{4}$ but $2\Gamma _{2}(2\Gamma _{2}({\mathbb {Z}}_{4})) = 2\Gamma _{2}(2{\mathbb {Z}}_{4})=0.$ So $2\Gamma _{2}(2\Gamma _{2}({\mathbb {Z}}_{4})) \ne 2\Gamma _{2}({\mathbb {Z}}_{4}).$

Let R be a Noetherian ring of prime characteristic p and $f: R \rightarrow R$ the Frobenius ring homomorphism, i.e., $f(r)= r^{p},~ \text {for} ~r\in R.$ Let $R^{f}$ be the ring with the $R\text {-}R$ bimodule structure given by $r.s := rs$ and $s.r := sf(r)$ for $r\in R$ and $s\in R^{f}.$ $F_{R}(-):= R^{f} \otimes _{R}-$ is a right exact functor on the category R-Mod and is called the Frobenius functor on R; see Marley (2014).

Theorem 3.1

Let R be a Noetherian local ring of characteristic p. The following statements are equivalent:

• 1. $F_{R}(-)$ is exact on R-Mod,

• 2. $a\Gamma _{a}(-)$ is a zero functor on R-Mod for all $a\in R$,

• 3. R is a regular ring,

• 4. every R-module is reduced.

Proof

By Kunz (1969), the functor $F_{R}(-)$ is exact on R-Mod if and only if R is a regular ring. However, by Rege and Buhphang (2008, Theorem 2.16), R is a regular ring if and only if every R-module is reduced, i.e., if and only if $a\Gamma _{a}(-)$ is the zero functor on R-Mod for all $a\in R.$ $\square$

Theorem 3.1 gives a subcategory of R-Mod on which the Frobenius functor is exact, i.e., the subcategory of all reduced R-modules when R is a Noetherian local ring of characteristic p. This highlights the importance of the subcategory of reduced modules over a Noetherian local ring of characteristic p. They are doing to the Frobenius functor what a projective module (resp. injective module and flat module) M does to the functor $\hbox {Hom}_{R}(M,-),$ (resp. $\hbox {Hom}_{R}(-,M)$ and $-\bigotimes _{R}M)$, i.e., transforming them into exact functors.

Since for a commutative ring R,  ${\mathcal {N}}(R)$ is the prime radical of R, ${\mathcal {N}}(R)[x]= {\mathcal {N}}(R[x]),$ see Lam (2013, Theorem 10.19). Theorem 3.2 gives the local behavior of this.

Theorem 3.2

For any ring R and $a\in R,$

$$\begin{aligned} a\Gamma _{a}(R)[x]= a\Gamma _{a}(R[x]). \end{aligned}$$

Proof

• Let $f(x)\in a\Gamma _{a}(R)[x].$ Then $f(x)= \sum \nolimits _{i=0}^{n}r_{i}x^{i}$ with $r_{i}\in a\Gamma _{a}(R).$ This implies that for each $r_{i},~ i\in \{0,1,2,\ldots ,n\},$ there exists $s_{i}\in \Gamma _{a}(R)$ and $k_{i} \in {\mathbb {Z}}^{+}$ such that $r_{i}=as_{i}$ and $a^{k_{i}}s_{i}=0.$ $f(x)= \sum \nolimits _{i=0}^{n}(as_{i})x^{i} =a\sum \nolimits _{i=0}^{n}s_{i}x^{i}.$ To show that $f(x)\in a\Gamma _{a}(R[x]),$ it is enough to show that $g(x)=\sum \nolimits _{i=0}^{n}s_{i}x^{i}\in \Gamma _{a}(R[x])$ since $f(x)= ag(x).$ Let $k:= \text {max}\{k_{i}\}_{i=0}^{n}.$ Then $a^{k}g(x)=\sum \nolimits _{i=0}^{n}a^{k}s_{i}x^{i}=0.$ Hence $g(x)\in \Gamma _{a}(R[x])$ as required. This proves that $a\Gamma _{a}(R)[x] \subseteq a\Gamma _{a}(R[x]).$

• Now, suppose that $f(x)\in a\Gamma _{a}(R[x]).$ Then $f(x)= ag(x)$ and there exists $k\in {\mathbb {Z}}^{+}$ such that $a^{k}g(x)=0.$ If $g(x)= r_{0}+\cdots +r_{n}x^{n},$ then $f(x)= ar_{0}+\cdots +ar_{n}x^{n}.$ We show that each $ar_{i}\in a\Gamma _{a}(R)$ for $i \in \{0,1,\ldots ,n\}.$ If $ar_{i}=0,~ ar_{i}\in a\Gamma _{a}(R).$ Suppose that $ar_{i}\ne 0.$ Then $a^{k}r_{i}=0$ for all $i\in \{0,1,\ldots ,n\}$ since $a^{k}g(x)=0.$ Then, each $r_{i}\in \Gamma _{a}(R)$ and $ar_{i}\in a\Gamma _{a}(R)$ for all $i\in \{0, 1, \cdots , n\}$. So, $f(x)\in a\Gamma _{a}(R)[x]$ and $a\Gamma _{a}(R[x])\subseteq a\Gamma _{a}(R)[x].$ $\square$

${\mathcal {N}}(R)=0,$ (i.e., R is reduced) if and only if $a\Gamma _{a}(R)=0$ (i.e., R is a-reduced) for each $a\in R.$ ${\mathcal {N}}(R)[x]= {\mathcal {N}}(R[x])$ and $a\Gamma _{a}(R)[x]= a\Gamma _{a}(R[x])$ for all $a\in R$. However, ${\mathcal {N}}(-)$ is hereditary, see Gardner and Wiegandt (2004, Example 3.2.12) but the “local” radical $a\Gamma _{a}(-)$ is not hereditary.

A proper submodule N of an R-module M is prime if for all $a\in R ~\text {and}~ m\in M$, $am\in N$ implies that either $m\in N$ or $aM\subseteq N.$ A module is prime if its zero submodule is prime. A prime module is reduced. Let $\beta (M)$ denote the intersection of all prime submodules of M. We call $\beta (M)$ the prime radical of M. Since $a\Gamma _{a}(R)\subseteq {\mathcal {N}}(R)$ for any ring R and $a\in R$; and $a\Gamma _{a}(M) \subseteq \beta (M)$ for any R-module M and $a\in R$, the locally nilradical can also be seen as a generalisation of the Baer’s lower nilradical for modules.

Let R be a ring and $a \in R.$ By Bican et al. (1982, Proposition 1.1.4), ${\mathcal {T}}_{a} := \left\{ M\in R\text {-Mod} ~| ~ a\Gamma _{a}(M)= M \right\}$ is a torsion class and ${\mathcal {F}}_{a} := \left\{ M\in R\text {-Mod} ~ | ~ a\Gamma _{a}(M)= 0 \right\}$ is a pretorsion-free class. In general, a-reduced modules are not closed under extension. ${\mathbb {Z}}_{4}$ is not a 2-reduced ${\mathbb {Z}}$-module. However, its submodule $2{\mathbb {Z}}_{4}$ and its quotient ${\mathbb {Z}}_{4}/2{\mathbb {Z}}_{4}$ are 2-reduced. This shows that in general, a-reduced modules form a pretorsion-free class but not a torsion-free class of a torsion theory.

4 Stratifications

Let N be a submodule of an R-module M. The envelope $E_{M}(N)$ of N is the set

$$\begin{aligned} E_{M}(N):= \left\{ am~|~ a^{k}m\in N, ~a\in R,~m\in M,~ \text {for some }k\in {\mathbb {Z}}^{+} \right\} . \end{aligned}$$

The set $E_{M}(N)$ was used by McCasland and Moore (1991), Jenkins and Smith (1992), Azizi (2009) and Azizi (2007) among others while studying modules and rings that satisfy the radical formula. $E_{M}(0)$ was considered as the module analogue of ${\mathcal {N}}(R),$ the collection of all nilpotent elements of the ring R. For any ring R, $E_{R}(0)= {\mathcal {N}}(R).$

Proposition 4.1

(Stratification of the envelope) For any R-module M,

$$\begin{aligned} E_{M}(0)= \bigcup \limits _{a\in R} a\Gamma _{a}(M). \end{aligned}$$

Proof

If $m\in \bigcup \nolimits _{a\in R} a\Gamma _{a}(M),$ then $m = an$ for some $n\in \Gamma _{a}(M).$ This implies that $a^{k}n = 0$ for some $k\in {\mathbb {Z}}^{+}.$ By definition of $E_{M}(0),~m\in E_{M}(0).$ Conversely, if $m\in E_{M}(0),$ then $m = an$ with $a^{k}n = 0$ for some $n\in M, a\in R$ and $k\in {\mathbb {Z}}^{+}.$ So, $n\in \Gamma _{a}(M)$ which implies that $m\in a\Gamma _{a}(M).$ Thus, $m\in \bigcup \nolimits _{a\in R} a\Gamma _{a}(M).$ $\square$

Corollary 4.1

(Stratification of the nilradical) For any ring R,  if ${\mathcal {N}}(R)$ is the collection of all nilpotent elements of R,  then

$$\begin{aligned} {\mathcal {N}}(R)= \bigcup \limits _{a\in R} a\Gamma _{a}(R)= E_{R}(0). \end{aligned}$$

Recall that, for an R-module M, where R is a reduced ring, the torsion submodule t(M) of M is the submodule

$$\begin{aligned} t(M) := \left\{ m\in M~|~am=0~\text {for some } 0 \ne a\in R\right\} . \end{aligned}$$

Proposition 4.2

(Stratification of the torsion submodule) For any reduced module M defined over a reduced ring R,

$$\begin{aligned} t(M)= \bigcup \limits _{0 \ne a\in R} \Gamma _{a}(M). \end{aligned}$$

Proof

If M is a reduced R-module and $0 \ne a\in R$, then $\Gamma _{a}(M)= \left\{ m\in M~|~ am=0 \right\} .$ So $\Gamma _{a}(M)\subseteq t(M)$. The reverse inclusion follows from the definitions of both $\Gamma _{a}(M)$ as well as t(M). $\square$

5 Comparison with other radicals

A proper submodule N of an R-module M is a-semiprime (resp. semiprime) if the R-module M/N is a-reduced (resp. reduced). We denote by Rad(M) (resp. S(M), $S_{a}(M)$) the Jacobson radical (resp. semiprime radical, a-semiprime radical) of M, i.e., the intersection of all maximal (resp. semiprime, a-semiprime) submodules of M.

Proposition 5.1

For any R-module M and $a\in R,$ we have the following inclusions of radical submodules of M:

$$\begin{aligned} \bigcap \limits _{a\in R} a\Gamma _{a}(M) \subseteq a\Gamma _{a}(M)\subseteq S_{a}(M) \subseteq S(M)\subseteq \beta (M) \subseteq {\text {Rad}}(M). \end{aligned}$$

Proof

$\bigcap \nolimits _{a\in R} a\Gamma _{a}(M) \subseteq a\Gamma _{a}(M)$ is trivial. If a submodule N of an R-module M is a-semiprime, then by definition, the module M/N is a-reduced. By Proposition 2.2, $a\Gamma _{a}(M/N)= 0.$ From Proposition 3.3(3),  we get $a\Gamma _{a}(M)\subseteq N,$ i.e., every a-semiprime submodule of M contains the submodule $a\Gamma _{a}(M)$ of M. It follows that the intersection of all a-semiprime submodules of M contains $a\Gamma _{a}(M),$ i.e., $a\Gamma _{a}(M)\subseteq S_{a}(M).$ Since a semiprime submodule of an R-module M is a-semiprime (i.e., M/N reduced implies M/N a-reduced), we have $S_{a}(M)\subseteq S(M).$ $S(M)\subseteq \beta (M)$ is due to the fact that prime submodules are semiprime and $\beta (M) \subseteq {\text {Rad}}(M)$ follows from the fact that maximal submodules are prime. $\square$

Corollary 5.1

For any ring R, 

$$\begin{aligned} \bigcap \limits _{a\in R} a\Gamma _{a}(R) \subseteq a\Gamma _{a}(R)\subseteq S_{a}(R) \subseteq S(R)= {\mathcal {N}}(R) \subseteq {\text {Rad}}(R). \end{aligned}$$

From Proposition 5.1 (resp. Corollary 5.1), we can see that the radical submodule $a\Gamma _{a}(M)$ (resp. ideal $a\Gamma _{a}(R)$) is very small in comparison with other radical submodules of M (resp. ideals of R). In addition, $a\Gamma _{a}(R)$ is a proper ideal of R since it is nil and therefore the unity of R cannot belong to it.

Theorem 5.2

For any R-module M,

$$\begin{aligned} \sqrt{(0:M)}M=\sum \limits _{a\in \sqrt{(0:M)} }a\Gamma _{a}(M). \end{aligned}$$

Proof

Let $m \in \sqrt{(0:M)}M.$ $m= \sum \nolimits _{i=1}^{n}r_{i}m_{i}$ where $r_{i} \in$ $\sqrt{(0:M)},$ $m_{i} \in M$ and $n\in {\mathbb {Z}}^{+}.$ So, $r_{i}^{k_{i}}M= 0$ for all $i\in \{1,2,\ldots ,n\}$ and for some $k_{i} \in {\mathbb {Z}}^{+}.$ It follows that $r_{i}^{k_{i}}m_{i}= 0$ for all $i\in \{1,2,\ldots ,n\}.$ Hence, $r_{i}m_{i}\in r_{i}\Gamma _{r_{i}}(M).$ Therefore $m= \sum \nolimits _{i=1}^{n}r_{i}m_{i} \in \sum \nolimits _{i=1}^{n}r_{i}\Gamma _{r_{i}}(M) \subseteq \sum \nolimits _{a\in \sqrt{(0:M)} }a\Gamma _{a}(M)$ and hence $\sqrt{(0:M)}M \subseteq \sum \nolimits _{a\in \sqrt{(0:M)} }a\Gamma _{a}(M) .$ Now, for any $a\in \sqrt{(0:M)} ,$ $a\Gamma _{a}(M) \subseteq \sqrt{(0:M)}M.$ So, $\sum \nolimits _{a\in \sqrt{(0:M)} }a\Gamma _{a}(M) \subseteq \sqrt{(0:M)}M$ which gives the reverse inclusion. $\square$

Corollary 5.3

If M is an R-module such that (0 : M) is a radical ideal of R,  then

$$\begin{aligned} \sum \limits _{a\in \sqrt{(0:M)} }a\Gamma _{a}(M)=0. \end{aligned}$$

In particular, if $a\in \sqrt{(0:M)}$, then M is a-reduced.

Proof

By Theorem 5.2, $\sqrt{(0:M)}M= \sum \nolimits _{a\in \sqrt{(0:M)} }a\Gamma _{a}(M).$ Since (0 : M) is a radical ideal of R,  $\sqrt{(0:M)}= (0:M).$ It follows that $\sqrt{(0:M)}M= (0:M)M= 0$ which leads to the desired result. $\square$

Corollary 5.4

If the R-module M is a finitely generated multiplication module and $\beta (M)$ is the prime radical of M,  then

$$\begin{aligned} \sum \limits _{a\in \sqrt{(0:M)} }a\Gamma _{a}(M)= \beta (M). \end{aligned}$$

Proof

By McCasland and Moore (1986, Theorem 4), $\sqrt{(0:M)}M= \beta (M).$ However, by Theorem 5.2, $\sqrt{(0:M)}M= \sum \nolimits _{a\in \sqrt{(0:M)} }a\Gamma _{a}(M).$ It follows that $\sum \nolimits _{a\in \sqrt{(0:M)} }a\Gamma _{a}(M)= \beta (M)$ as required. $\square$

6 Computation of local cohomology

In Theorem 6.1, we show that reduced modules simplify computations of local cohomology; the usual direct limits involved in the definition of local cohomology are dropped.

Theorem 6.1

Let R be a Noetherian ring, M be an R-module and $\mathfrak {a}$ an ideal of R generated by $a\in R$. Each of the following statements holds.

• 1. If M is a-reduced, then the i-th local cohomology module $H_{\mathfrak {a}}^i(M)$ is given by

  $$\begin{aligned} H_{\mathfrak {a}}^i(M)\cong \text {Ext}_{R}^i(R/\mathfrak {a}, M). \end{aligned}$$

• 2. If M is a-reduced and $R/\mathfrak {a}$ is a projective R-module, then for all $i\ge 1$

  $$\begin{aligned} H_{\mathfrak {a}}^{i}(M)=0. \end{aligned}$$

• 3. If M is reduced, then for all $a\in R$,

  $$\begin{aligned} H_{\mathfrak {a}}^i(M)\cong \text {Ext}_{R}^i(R/\mathfrak {a}, M). \end{aligned}$$

Proof

By Proposition 2.2, if M is an a-reduced R-module, then $\Gamma _{a}(M)\cong \text { Hom}_{R}(R/{{\mathfrak {a}}}, M)$. The i-th local cohomology of M which is the right derived functor of $\Gamma _{a}(M)$ is the R-module $H_{\mathfrak {a}}^i(M)\cong \text {Ext}_{R}^i(R/\mathfrak {a}, M)$. If the R-module $R/\mathfrak {a}$ is projective, then it follows by general theory that the module $H_{\mathfrak {a}}^i(M)$ vanishes for all $i\ge 1$. 3 is due to the fact that, if M is reduced, then it is a-reduced for all $a\in R$. $\square$