Trace formula and new form of N-soliton to the Gerdjikov–Ivanov equation

Abstract

The Gerdjikov–Ivanov equation is investigated by the Riemann–Hilbert approach and the technique of regularization. The trace formula and new form of N-soliton solution are given. The dynamics of the stationary solitons and non-stationary solitons are discussed.

1 Introduction

The main purpose of this paper is to study the following Gerdjikov–Ivanov (GI) equation [14]

$$\begin{aligned} iq_t+q_{xx}-iq^2q^*_x+\frac{1}{2}q^3{q^*}^2=0 \end{aligned}$$

(1)

by Riemann–Hilbert methods [1, 2, 6, 11, 22, 24, 27, 30] and the technique of regularization. Here $*$ denotes the complex conjugation. This method is a generalization of the dressing methods [28, 29], which now have many development, such as [3, 12, 13].

In this paper, we construct a nonregular Riemann–Hilbert problem, and give a new form of N-soliton solution. For the present Riemann–Hilbert problem, the determination of its solution, which is sectionally analytic, has zeroes in each analytic domain. So the Riemann–Hilbert problem, whose index is not zero, is called a nonregular one. Note that it is very difficult to solve a matrix nonregular Riemann–Hilbert problem. The method of regularization is an efficient way to solve the problem. The regularization of the Riemann–Hilbert problem can be fulfilled by introducing a rational matrix, named the soliton matrix. In this procedure, the zeroes of the Riemann–Hilbert problem are transformed into the poles of the soliton matrix, which plays an important role in deriving the solitons.

The GI equation (1) is the generalization of the derivative nonlinear Schrödinger equation [19,20,21], and is usually called the third type of derivative nonlinear Schrödinger equation, while the second type of derivative nonlinear Schrödinger equation is Chen–Lee–Liu equation [4]. The GI equation is an important integrable model in physics and mathematics, and has been studied extensively. For example, it has been studied via Darboux transformation [8,9,10, 15, 25], the nonlinearization [5, 16, 26], and others [17, 18, 23, 31]. As a result, many properties, such as Hamiltonian structures, N-soliton solution, rogue wave, algebro-gemetric solutions, were investigated. In this work, we give the trace formula and the new form of N-soliton solution of the GI equation. Here, the N-soliton solution is derived by using the block matrix decomposition.

An outline of this paper is as follows: In Sect. 2, we study the direct scattering problems of the GI spectral problem. In Sect. 3, the trace formula and Riemann–Hilbert problem are constructed, and solitons of the GI equation are derived. In addition, for one-soliton, dynamic behaviors of the stationary solitons and non-stationary solitons are investigated.

2 Spectral analysis

In this section, we present the scattering and inverse scattering methods for GI equation using the Riemann–Hilbert formulation. The Lax equations of Eq. (1) are

$$\begin{aligned} \begin{aligned}&J_x=-ik^2[\sigma _3, J]+XJ, \\&J_t=-2ik^4[\sigma _3, J]+YJ, \end{aligned} \end{aligned}$$

(2)

where $[\sigma _3, J]=\sigma _3J-J\sigma _3$ is the commutator and

$$\begin{aligned} X=kQ-\frac{i}{2}Q^2\sigma _3 , \ \ Q=\left( \begin{array}{cc} 0 &{} q(x,t) \\ -q^*(x,t) &{} 0 \end{array} \right) , \end{aligned}$$

$$\begin{aligned} Y=2k^3Q-ik^2Q^2\sigma _3-ikQ_x\sigma _3+\frac{1}{2}(Q_xQ-QQ_x)+\frac{i}{4}Q^4\sigma _3, \end{aligned}$$

with $\sigma _i (i=1,2,3)$ are classical Pauli matrices.

As usual, in the direct scattering process, we only concentrate on the x-part of the Lax pair (2), where t enters as a dummy variable and is omitted. Now we introduce matrix Jost solutions $J_\pm =J_\pm (x,t,k)$ for the x-part of the Lax pair (2) with the asymptotic conditions

$$\begin{aligned} \begin{aligned}&J_\pm \rightarrow \text {I}, \ \ \ x\rightarrow \pm \infty . \\ \end{aligned} \end{aligned}$$

(3)

Here $\text {I}$ is the $2\times 2$ identity matrix. Since $J_+$ and $J_-$ are both solutions of (2), they are linearly related:

$$\begin{aligned} J_-(x,t,k)=J_+(x,t,k)\mathrm{e}^{-i\theta (x,t,k)\sigma _3} T(k)\mathrm{e}^{i\theta (x,t,k)\sigma _3}, \end{aligned}$$

(4)

where

$$\begin{aligned} \theta (x,t,k)=k^2x+2k^4t, \quad T(k)=\begin{pmatrix} a(k) &{} -\tilde{b}(k) \\ b(k) &{} \tilde{a}(k) \end{pmatrix}. \end{aligned}$$

(5)

Since $tr(Q)=0$, $\det J_\pm (x,t,k)$ are independent of x, we have $\det J_\pm (x,t,k)=1$ in view of (3), and $\det T(k)=1$ from (4).

We note that X(x, t, k) in (2) admits the relations $X^\dag (x,t,k^*)=-X(x,t,k)$ and $\sigma _3 X(x,t,-k)\sigma _3=X(x,t,k)$, and Y(x, t, k) has the same properties. So, it is readily verified that the Jost functions $J_\pm (x,t,k)$ satisfy the following symmetry conditions

$$\begin{aligned} J_\pm ^\dag (k^*)=J_\pm ^{-1}(k), \quad \sigma _3J_\pm (-k)\sigma _3=J_\pm (k). \end{aligned}$$

(6)

In fact, if the function $J_\pm (k)$ admits the Eq. (2) and boundary condition (3), then the function $\sigma _3J_\pm (-k)\sigma _3$ also does. The unique solution of the boundary problem implies the second equation in (6). In addition, the functions $J_\pm ^\dag (k^*)$ and $J_\pm ^{-1}(k)$ satisfy the adjoint equation of (2) and boundary condition (3), so the first equation in (6) is produced. We note that Eq. (6) implies that

$$\begin{aligned} T^\dag (k^*)=T^{-1}(k), \quad \sigma _3T(-k)\sigma _3=T(k), \end{aligned}$$

(7)

in terms of (4). Thus, we have

$$\begin{aligned} \begin{aligned} \tilde{a}(k)=a^*(k^*), \quad a(-k)=a(k), \quad \tilde{a}(-k)=\tilde{a}(k),\\ \tilde{b}(k)=b^*(k^*), \quad b(-k)=-b(k), \quad \tilde{b}(-k)=-\tilde{b}(k). \end{aligned} \end{aligned}$$

(8)

Using the large-x asymptotic condition (3), we can turn the x-part of (2) into the Volterra integral equations

$$\begin{aligned} J_\pm (x,t,k)=\text {I}+\int _{\pm \infty }^xe^{ik^2\sigma _3(y-x)}X(y,t,k)J_\pm (y,t,k)e^{ik^2\sigma _3(x-y)}dy. \end{aligned}$$

(9)

By performing the standard procedures on the Volterra integral equations (9), one can prove the existence and uniqueness of the Jost solutions $J_\pm$. Moreover, it is important that $[J_-]_1, [J_+]_2$ can be analytically extended into $D_+$, and $[J_-]_1, [J_+]_2$ into $D_-$, where the regions $D_\pm$ are defined by

$$\begin{aligned} \begin{aligned}&D_+=\{k\in \mathbb {C}|\arg k\in (0,\pi /2)\cup (\pi , 3\pi /2)\},\\&D_-=\{k\in \mathbb {C}|\arg k\in (\pi /2,\pi )\cup (3\pi /2,2\pi )\}. \end{aligned} \end{aligned}$$

Here $[J_\pm ]_l$ $(l=1,2)$ denote the lth column of $J_\pm$.

To construct the Riemann–Hilbert problem on $\mathbb {R}\cup i\mathbb {R}$ by using the analytic properties of the Jost solutions $J_\pm$, it is important to introduce a matrix function $P_1=P_1(x,k)$ which is analytic in $D_+$

$$\begin{aligned} P_1=([J_-]_1, [J_+]_2), \end{aligned}$$

(10)

and solves the linear spectral problem (2). Furthermore, by considering the large-k asymptotic behavior of $P_1$, we have

$$\begin{aligned} P_1\rightarrow \text {I}, \ \ \ k\in D_+ \rightarrow \infty . \end{aligned}$$

(11)

On the other hand, we can define a matrix function $P_2=P_2(x,k)$ which is analytic for k in $D_-$

$$\begin{aligned} P_2=\begin{pmatrix} [J_-^{-1}]^1 \\ [J_+^{-1}]^2 \end{pmatrix}, \end{aligned}$$

(12)

in terms of (4) and (6). Here each superscript denotes the row of a matrix. Moreover, the large-k asymptotic behavior of $P_2$ can be shown to be

$$\begin{aligned} P_2\rightarrow \text {I}, \ \ \ k\in D_- \rightarrow \infty . \end{aligned}$$

(13)

Note that the sectionally analytic functions $P_1$ and $P_2$ admit the following symmetry condition

$$\begin{aligned} P_1^\dag (k^*)=P_2(k), \end{aligned}$$

(14)

in view of the definition (10), (12) and the symmetry condition in (6).

Let us consider the asymptotic expansion of $P_1$

$$\begin{aligned} P_1(k)=\text {I}+k^{-1}P_1^{(1)}+k^{-2}P_1^{(1)}+\cdots , \ \ \ \ k\rightarrow \infty , \end{aligned}$$

(15)

and substitute this expansion into (2), then we find that

$$\begin{aligned} Q=i[\sigma _3, P_1^{(1)}]. \end{aligned}$$

(16)

Thus, the potential q can be reconstructed as

$$\begin{aligned} q=2i(P_1^{(1)})_{12}, \end{aligned}$$

(17)

where $(P_1^{(1)})_{12}$ is the (1, 2)-entry of $P_1^{(1)}$.

3 Trace formula and solitons

From the definitions of $P_1$ and $P_2$ as well as the scattering relations between $J_+$ and $J_-$, we see that

$$\begin{aligned} \det P_1(k)=a(k) , \ \ \ k\in D_+, \end{aligned}$$

(18)

$$\begin{aligned} \det P_2(k)=\tilde{a}(k), \ \ \ k\in D_-, \end{aligned}$$

(19)

which means that the zeros of $\det P_1$ and $\det P_2$ are the same as a(k) and $\tilde{a}(k)$, respectively.

From (8), we find that if $k_j$ is a zero of $\det P_1$, then$-k_j$ is also a zero of $\det P_1$ and $\hat{k}_j=k_j^*$ is a zero of $\det P_2$. Thus we first assume that $\det P_1$ has 2N simple zeros $\{k_j\}_1^{2N}$ satisfying $k_{N+j}=-k_j$, $1\le j\le N$, which all lie in $D_+$. Hence, $\det P_2$ possesses 2N simple zeros $\{\hat{k}_j\}_1^{2N}$ satisfying $\hat{k}_j=k_j^*$, $1\le j\le 2N$, which all lie in $D_-$. By virtue of analyticity, we know that a(k) is independent of the variables x and t, so that the zeros $\{k_j\}$ are constants. Thus, the generating function for the conservation laws is just a(k), and $\log a(k)$ is the generating function for local integrals of the motion [7]. We note that the latter gives the trace formula.

In the following, we discuss the associated trace formula. To this end, we introduce the sectionally analytic functions

$$\begin{aligned} \varOmega ^+(k)=a(k)\prod \limits _{j=1}^N\frac{k^2-\hat{k}_j^2}{k^2-k_j^2},\quad \varOmega ^-(k)=\tilde{a}(k)\prod \limits _{j=1}^N\frac{k^2-k_j^2}{k^2-\hat{k}_j^2}, \end{aligned}$$

(20)

which imply that $\varOmega ^+(k)\varOmega ^-(k)=a(k)\tilde{a}(k), k\in \mathbb {R}\cup i\mathbb {R}$. From $\det T(k)=1$, we find

$$\begin{aligned} \varOmega ^+(k)\varOmega ^-(k)=\frac{1}{1+\rho (k)\tilde{\rho }(k)}, \quad k\in \mathbb {R}\cup i\mathbb {R}, \end{aligned}$$

(21)

where

$$\begin{aligned} \rho (k)=\frac{b(k)}{a(k)},\quad \tilde{\rho }(k)=\frac{\tilde{b}(k)}{\tilde{a}(k)}. \end{aligned}$$

From (8), we find

$$\begin{aligned} \tilde{\rho }(k)=\rho ^*(k^*),\quad \rho (-k)\tilde{\rho }(-k)=\rho (k)\tilde{\rho }(k). \end{aligned}$$

We note that this equation can be used to construct a jump condition on the curve $\mathbb {R}\cup i\mathbb {R}$. Taking logarithms and applying the Cauchy projectors

$$\begin{aligned} \mathcal {P}_\pm [f](k)=\frac{1}{2\pi i}\int _{\Gamma }\frac{f(z)}{z-(k\pm i0)}\mathrm{d}z, \end{aligned}$$

we have

$$\begin{aligned} \log \varOmega ^\pm (k)=\mp \frac{1}{2\pi i}\int _{\Gamma }\frac{1+\rho (z)\rho ^*(z^*)}{z-k}\mathrm{d}z, \quad k\in D^\pm , \end{aligned}$$

where $\Gamma$ is the path consisting of lines from $i\infty$ to 0, from 0 to $\infty$, from $-i\infty$ to 0, and from 0 to $-\infty$. Substituting $\Omega ^+(k)$ for a(k), we obtain the trace formula

$$\begin{aligned} a(k)=\prod \limits _{j=1}^N\frac{k^2-k_j^2}{k^2-\hat{k}_j^2}\exp \left[ -\frac{1}{2\pi i}\int _{\Gamma }\frac{1+\rho (z)\rho ^*(z^*)}{z-k}\mathrm{d}z\right] , \quad k\in D^+. \end{aligned}$$

(22)

Now, it is time to construct the Riemann–Hilbert problem. In fact, $P_1$ and $P_2$ satisfy the jump condition on the curve $\mathbb {R}\cup i\mathbb {R}$

$$\begin{aligned} P_-(x,t,k)P_+(x,t,k)=E_1G(k)E_1^{-1}, \ \ \ k\in \Gamma \end{aligned}$$

(23)

where $E_1=\exp (-i(k^2x+2k^4t))$ and

$$\begin{aligned} G(k)=\begin{pmatrix} 1 &{} \tilde{b}(k) \\ b(k) &{} 1 \end{pmatrix}. \end{aligned}$$

(24)

In this case, each of $\ker [P_1(k_j)]$ and $\ker [P_2(\hat{k}_j)]$ contains only a single column vector $v_j=v_j(x,t)$ and a row vector $\hat{v}_j=\hat{v}_j(x,t)$, respectively

$$\begin{aligned} P_1(k_j)v_j=0 , \ \ \ \ \ \hat{v}_jP_2(\hat{k}_j)=0 , \ \ \ \ \ 1\le j\le 2N. \end{aligned}$$

(25)

It is noted that these vectors satisfy the following relations

$$\begin{aligned} v_j=\sigma _3v_{j-N} , \ \ \ \ \ N+1\le j\le 2N. \end{aligned}$$

(26)

$$\begin{aligned} \hat{v}_j=v_j^\dag , \ \ \ \ \ 1\le j\le 2N. \end{aligned}$$

(27)

Now we shall get the spatial evolutions of the vectors $v_j$, $1\le j\le N$. For this purpose, we take the x-derivative of $P_1(k_j)v_j=0$. Then utilizing the x-part of (2), we obtain the particular spatial evolution

$$\begin{aligned} v_{j,x}=(\alpha _j \text {I}-ik_j^2\sigma _3)\cdot v_j, \end{aligned}$$

(28)

in terms of the fact that the rank of the matrix $P_1(k_j)$ is 1. On the other hand, taking the t-derivative of $P_1(k_j)v_j=0$ and using the t-part of (2), we have the special temporal evolution

$$\begin{aligned} v_{j,t}=(\beta _j \text {I}-2ik_j^4\sigma _3)\cdot v_j. \end{aligned}$$

(29)

Here $\alpha _j$ and $\beta _j$ are arbitrary constant. By solving (28) and (29) explicitly, we get

$$\begin{aligned} v_j=\mathrm{e}^{(\alpha _j \text {I}-ik_j^2\sigma _3)x+(\beta _j \text {I}-2ik_j^4\sigma _3)t}\cdot v_{j,0}, \ \ \ 1\le j\le N, \end{aligned}$$

(30)

where each $v_{j,0}$, $1\le j\le N$ is a nonzero complex constant vector. If we set $k_j=\xi _j+i\eta _j$ and $v_{j,0}=(e^{\alpha _{j0}+i\beta _{j0}},1)^T$, where $\alpha _{j0}$ and $\beta _{j0}$ are some real constants, then $v_j$ is denoted in the following form

$$\begin{aligned} v_j=\mathrm{e}^{\epsilon _j}\left( \mathrm{e}^{(z_j+i\varphi _j)/2}, \mathrm{e}^{-(z_j+i\varphi _j)/2}\right) ^T, \ \ \ 1\le j\le N, \end{aligned}$$

(31)

where

$$\begin{aligned} \begin{aligned} \epsilon _j&=\alpha _j x+\beta _jt+(\alpha _{j0}+i\beta _{j0})/2,\\ z_j&=4\xi _j\eta _j[x+4(\xi _j^2-\eta _j^2)t]+\alpha _{j0},\\ \varphi _j&=-2(\xi _j^2-\eta _j^2)x-4(\xi _j^4-6\xi _j^2\eta _j^2+\eta _j^4)t+\beta _{j0}. \end{aligned} \end{aligned}$$

(32)

It is known that utilizing the methods in Refs. [24, 27] the Riemann–Hilbert problem (23) with the canonical normalization condition can be transformed to a Riemann–Hilbert problem without zeros. we note that the index , 2N, of the non-regular Riemann–Hilbert problem is given by its zeroes. By introducing the soliton matrix, (see $P_2(k)$ below), we get a regular Riemann–Hilbert problem, whose index is zero. To obtain soliton solutions for the GI equation (1), we choose the jump matrix G to be the $2\times 2$ identity matrix which corresponds to the reflection-less case. In this case, the solution of the regular Riemann–Hilbert problem is holomorphic, and can be chosen as the identity matrix in view of the canonical normalization. Consequently, the unique solution for this particular Riemann–Hilbert problem is represented by the soliton matrix and its inverse

$$\begin{aligned} \begin{aligned} P_1(k)=\text {I}-\sum \limits _{m=1}^{2N}\sum \limits _{j=1}^{2N}{{v_mv_j^\dagger (M^{-1})_{mj}}\over {k-\hat{k}_j}}\\ P_2(k)=\text {I}+\sum \limits _{m=1}^{2N}\sum \limits _{j=1}^{2N}{{v_mv_j^\dagger (M^{-1})_{mj}}\over {k-k_m}} \end{aligned} \end{aligned}$$

(33)

where $M=(M_{mj})_{2N\times 2N}$ is a matrix whose entries are

$$\begin{aligned} M_{mj}=\frac{v_m^\dagger v_j}{k_j-\hat{k}_m} , \ \ \ \ 1\le m, j\le 2N. \end{aligned}$$

(34)

In order to eliminate the inverse matrix $M^{-1}$ in (33), we introduce the following vectors

$$\begin{aligned} \begin{aligned} \hat{f}_\alpha&=(v_{1,\alpha }, v_{2,\alpha }, \cdots , v_{2N,\alpha }), \\ g_{\beta }&=(v^\dagger _{1,\beta }, v^\dagger _{2,\beta }, \cdots , v^\dagger _{2N,\beta })^T, \\ \tilde{g}_\beta&=\left( \frac{v^\dagger _{1,\beta }}{k-k_1}, \frac{v^\dagger _{2,\beta }}{k-k_2} \cdots , \frac{v^\dagger _{2N,\beta }}{k-k_{2N}}\right) ^T, \end{aligned} \end{aligned}$$

(35)

where $v_{m,\alpha }$ and $v^\dagger _{j,\beta }, (\alpha ,\beta =1,2)$ denote the elements. Then each element of the matrix $P_1$ in (33) can be rewritten as

$$\begin{aligned} (P_1)_{\alpha \beta }=\frac{\det (\tilde{M}_{\alpha \beta }^a)}{\det M}, \quad \tilde{M}_{\alpha \beta }^a=\left( \begin{matrix} \delta _{\alpha \beta }&{}\hat{f}_\alpha \\ \tilde{g}_\beta &{}M \end{matrix}\right) . \end{aligned}$$

(36)

Furthermore, each element of the matrix $P_1^{(1)}$ in (15) takes the form

$$\begin{aligned} (P_1^{(1)})_{\alpha \beta }=\frac{\det (M_{\alpha \beta }^a)}{\det M}, \quad M_{\alpha \beta }^a=\left( \begin{matrix} 0&{}\hat{f}_\alpha \\ g_\beta &{}M \end{matrix}\right) . \end{aligned}$$

(37)

Note that the representations (36) and (37) can be derived in terms of the following block matrix decomposition

$$\begin{aligned} \begin{aligned} \left( \begin{matrix} A_{m\times m}&{}B_{m\times n}\\ C_{n\times m}&{}D_{n\times n} \end{matrix} \right)&=\left( \begin{matrix} A&{}0\\ C&{}I_{n\times n} \end{matrix} \right) \left( \begin{matrix} I_{m\times m}&{}A^{-1}B\\ 0&{}D-CA^{-1}B \end{matrix} \right) \\&=\left( \begin{matrix} I_{m\times m}&{}B\\ 0&{}D \end{matrix} \right) \left( \begin{matrix} A-BD^{-1}C&{}0\\ D^{-1}C&{}I_{n\times n} \end{matrix} \right) . \end{aligned} \end{aligned}$$

In fact, one may find

$$\begin{aligned} (P_1)_{\alpha \beta }= & {} \delta _{\alpha \beta }-\sum \limits _{m=1}^{2N}\sum \limits _{j=1}^{2N}v_{m,\alpha }(M^{-1})_{mj}\frac{{v_{j,\beta }^\dagger }}{k-\hat{k}_j} =\delta _{\alpha \beta }-\hat{f}_\alpha (M^{-1})\tilde{g}_\beta ,\\ (P_1^{(1)})_{\alpha \beta }= & {} -\sum \limits _{m=1}^{2N}\sum \limits _{j=1}^{2N}v_{m,\alpha }(M^{-1})_{mj}{{v_{j,\beta }^\dagger }} =-\hat{f}_\alpha (M^{-1}){g}_\beta . \end{aligned}$$

Since

$$\begin{aligned} \tilde{M}_{\alpha \beta }^a=\left( \begin{matrix} 1&{}\hat{f}_\alpha \\ 0&{}M \end{matrix}\right) \left( \begin{matrix} \delta _{\alpha \beta }-\hat{f}_\alpha (M^{-1})\tilde{g}_\beta &{}0\\ M^{-1}\tilde{g}_\beta &{}I \end{matrix}\right) , \end{aligned}$$

and $\det (\tilde{M}_{\alpha \beta }^a)=\det (M)(\delta _{\alpha \beta }-\hat{f}_\alpha (M^{-1})\tilde{g}_\beta )$. Thus Eq. (36) is proved. Equation (37) can be shown similarly.

Hence the N-soliton solution of GI equation has the new form

$$\begin{aligned} q=2i\frac{\det (M_{12}^a)}{\det M}, \end{aligned}$$

(38)

where the matrix M is defined by (34) and $M_{12}^a$ by (37). We note that the N-fold Darboux transformation of the GI equation was discussed in [9, 10], and one soliton and two soliton were presented, but no explicit N-soliton solition.

For $N=1$ in formula (38). Consequently, one-soliton solution of the GI equation (1) takes the form

$$\begin{aligned} q=\frac{8\xi _1\eta _1\mathrm{e}^{i\varphi _1}}{k_1\mathrm{e}^{-z_1}+k_1^{*}\mathrm{e}^{z_1}} \end{aligned}$$

(39)

where $k_1=\xi _1+i\eta _1\in D_+$ and

$$\begin{aligned} \begin{aligned}&z_1=4\xi _1\eta _1[x+4(\xi _1^2-\eta _1^2)t]+\alpha , \\&\varphi _1=-2(\xi _1^2-\eta _1^2)x-4(\xi _1^4-6\xi _1^2\eta _1^2+\eta _1^4)t+\beta . \end{aligned} \end{aligned}$$

Here, we have chosen $v_{1,0}=(e^{\alpha _0+i\beta _0},1)^T$.

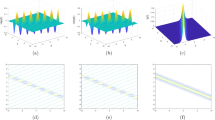
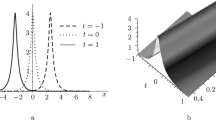
Thus, $\xi _1\eta _1>0$ if $k_1\in D^+$. Moreover, in the subregion $\{\xi _1<\eta _1\}$ of $D^+$, the one-soliton is a right traveling wave (see Fig. 1), and in the subregion $\{\xi _1>\eta _1\}$ of $D^+$, the one-soliton is a left traveling wave (see Fig. 2). On the line $\xi _1=\eta _1$, the one-soliton is a stationary wave (see Fig. 3).

Fig. 1

One-soliton q(x, t) in (39) with the parameters chosen as $\xi _1=0.5, \eta _1=1, \alpha =\beta =0$. Red line absolute value of q, yellow line real part of q and green line imaginary of q (colour figure online)

Fig. 2

One-soliton q(x, t) in (39) with the parameters chosen as $\xi _1=1, \eta _1=0.5, \alpha =\beta =0$

Fig. 3

One-soliton q(x, t) in (40) with the parameters chosen as $\xi _1=0.5, \eta _1=0.5, \alpha =\beta =0$

The stationary soliton can be derived by letting $k_1=\xi (1+i)$,

$$\begin{aligned} q=2\xi \mathrm{e}^{i\phi }\frac{\cosh (z)+i\sinh (z)}{\cosh (2z)}, \end{aligned}$$

(40)

where

$$\begin{aligned} z=4\xi ^2x+\alpha ,\quad \phi =16\xi ^4t+\beta . \end{aligned}$$

Hence $|q|^2=4\xi ^2/\cosh (2z)$.

We note that the real part and imaginary part of the one-soliton have some interesting behaviors (see Figs. 4, 5, 6). For non-stationary solitons, the wave forms of the real part and imaginary part do not change (see Figs. 1, 2). However, for stationary soliton, the waves of the real part and imaginary part are changing over time, but the wave form of the absolute value does not change (see Fig. 3).

Fig. 4

One-soliton q(x, t) in (39) with the parameters chosen as $\xi _1=0.5, \eta _1=1, \alpha =\beta =0$

Fig. 5

One-soliton q(x, t) in (39) with the parameters chosen as $\xi _1=1, \eta _1=0.5, \alpha =\beta =0$

Fig. 6

One-soliton q(x, t) in (40) with the parameters chosen as $\xi _1=0.5, \eta _1=0.5, \alpha =\beta =0$