Effect of flapping frequency, Reynolds number and angle of attack on the aerodynamic force coefficients of a translating wing

Abstract

This study presents a computational investigation of a flapping wing executing to and from horizontal motion with a fixed angle of attack or pitch orientation. The computational results compare well with the experimental results of Lua et al. (Exp Fluids 51(1):177–195, 2011). An attempt has been made to understand the effect of flapping frequency (f), Reynolds number (Re) and angle of attack ($\alpha$) on flow features like vortex structures and wing–wake interaction. The present study is conducted for five different flapping frequencies, namely, f = 0.021, 0.21, 0.315, 0.42 and 2.1 Hz, four different chord-based Reynolds numbers, namely Re = 2000, 5000, 10,000 and 50,000 and two different angles of attack, namely $\alpha = 45^{\circ }$ and $\alpha = 60^{\circ }$. Vorticity contours display variation of vortex structures with change in flapping frequency. The temporal history of resultant force coefficients show distinct characteristics like amplitude modulation, linear growth and decay, inflexional behavior, dual peak behavior, etc. Frequency spectrum of the lift coefficient reveals that the flapping frequency is most dominant and it is accompanied by several harmonics. At higher Reynolds number, the spectrum displays broadband character. The power content of the dominant frequency increases with increase in flapping frequency and decreases with increase in angle of attack. A short investigation on the effect of three-dimensionality of the flow is also presented in this study. Additionally, three-dimensional eddy resolving simulations were performed with IDDES.

1 Introduction

Insects and birds generate lift and thrust force by flapping their wings. The flapping wing kinematics can be broadly classified into three distinct motions, namely heaving (up and down translational motion), sweeping (forward and backward translational motion) and pitching (angular motion about the wing’s longitudinal axis). In a cycle, the flapping wing motion itself can be divided into translational and rotational phases. The translational phase consists of two half strokes, namely the upstroke and the downstroke. At the end of each half stroke, the rotational motion sets in, during which the wing rapidly rotates and reverses its direction of motion (stroke reversal) for the consecutive half stroke. These stroke reversals preceding downstroke and upstroke are termed as pronation and supination, respectively.

Flapping wing MAVs, which are inspired by flapping motion found in natural fliers, have important advantages over conventional fixed and rotary wing aircraft including increased aerodynamic efficiency, enhanced maneuverability and reduced noise. By conventional laws of aerodynamic theory based on steady flow over rigid wings at constant velocities, insects or birds would not be able to perform active flight. Ellington [6] performed experiments on insect wings under steady flow in a wind tunnel over the range of velocities encountered during flapping flight and observed that the measured forces are substantially smaller than those required to maintain active flight. This failure of conventional steady-state theory to explain the aerodynamics of flapping wings paved ways for the search of unsteady mechanisms which can explain these enhanced aerodynamic forces experienced during flapping flight. Weis-Fogh and Jensen [27] in a series of papers established that the energy budget of a wing stroke comprises at least three independent terms, namely, aerodynamic (due to wind forces), inertial term (due to the acceleration of the wing mass), and elastic (due to elastic deformations of the wing and body). Maxworthy [12] is an excellent review of insect aerodynamics which emphasizes the importance of unsteady aerodynamics in insect flight. Spedding [18] emphasizes aerodynamic performance augmentation through unsteady aerodynamics. These three papers have been a source of motivation for the present study to explore the unsteady aerodynamics through numerical simulations of a relatively simple flapping configuration. Some of the important unsteady aerodynamic phenomena pertaining to flapping flight are Wagner effect [22] which concerns the transient lift augmentation produced due to the sudden change of angle of attack of a wing or sudden change of freestream speed; apparent mass effect [6, 21], which concerns a portion of the flow in the vicinity of the wing which gets dragged due to the wing motion; clap and fling mechanism [19, 26] which is a technique by which rigid fling of a pair of wings generates high unsteady lift forces associated with high circulations around the separation vortices; and Kramer effect [8] which deals with a wing rotating from low to high angles of attack which results in a lift coefficient above the steady-stall value. This is associated with dynamic stall. Many of these unsteady aerodynamics concepts are of significant relevance for the present study because of their fundamental and generic nature in the domain of unsteady aerodynamics. However, none of the above mentioned effects could still explain the reason behind the high lift generated to sustain flight until [7] discovered the formation of the leading edge vortex (LEV), a translational mechanism in which a vortical flow structure is formed at the leading edge of the wing at high angle of attack which transiently generates additional lift forces. Birch and Dickinson [3] suggested that the presence of axial flow along spanwise direction stabilizes this leading edge vortex. The stability and role of LEV in lift augmentation has been discussed by Shyy and Liu [17]. Dickinson et al. [5] conducted experiments on a fruit fly, Drosophila melanogaster and his results confirm the contribution of leading edge vortex to the necessary lift during translation portion of the wing stroke. His results also suggested that by properly timing the wing rotation, flapping wing can generate lift through rotational mechanism (rotational circulation) in addition to that produced by the leading edge vortex. However, the most important hypothesis of his study is the wake capture. He proposed that although rotational circulation can explain the increase in forces at stroke reversal, but it is not the only factor. He hypothesized that the wake capture is the mechanism through which, during the early phase of each stroke the wing benefits from the wake of the previous half stroke and hence an increase in lift force is observed. However, a computational study conducted by Sun and Tang [20] on similar flow kinematics suggested the opposite. They found that the wake from the previous stroke actually reduces the lift and they attributed it to the downwash created by the wake vortices. They proposed that the effect of acceleration is responsible for the peak in lift coefficient observed. Lua et al. [11] conducted DPIV experiments on a 3D biconvex flapping wing with end plates, performing translational flapping motion in the form of “acceleration—constant velocity— deceleration” in various phases of flapping motion. Their results showed two possible outcomes from the wing–wake interaction. They termed the first outcome as wing–wake interaction of first kind in which on stroke reversal, the wing faces a pair of counter rotating wake vortices which leads to higher lift. The other outcome is wing–wake interaction of second kind in which wing encounters a single wake vortex and its vortex suction effect results in reduction of lift. They proposed that the outcome depends solely on the flapping motion kinematics and timing of the stroke reversal. Detailed reviews on aerodynamic modelling of flapping flight can be found in Ansari et al. [1] and Shyy et al. [16].

Over the years, several numerical tools have been developed to solve the Navier–Stokes equations with dynamic or moving boundaries to investigate the flow dynamics over a flapping wing. Wang [24] developed a fourth order accurate Navier–Stokes solver to solve hovering insect flight and has extensively discussed the 2D mechanism [23] & role of drag force in hovering flight [25]. The limitations of panel method in predicting aerodynamic forces in a flapping flight have been discussed by Persson et al. [14], in which they compared potential flow solution of flow field over a flapping elliptic planform wing with Navier–Stokes solution. In the last two decades, with advancement of computational power, researchers started investigating effect of wing shape parameters (planform shape, camber, twist, etc.) on flapping flight using numerical simulations [2, 9].

In the present study, the authors have performed a numerical investigation of the translational flapping wing kinematics “acceleration—constant velocity—deceleration” reported by Lua et al. [11] in their experimental work. More specifically, the present study focuses on the effect of variation of flapping frequency, Reynolds number and angle of attack on the aerodynamic forces acting on the wing with elliptic cross section of chord length 60 mm and maximum thickness to chord ratio 2%. Although force measurements on the 2D wing have been reported in Lua et al. [11], as far as the authors are aware, this is probably the first time a computational parametric study on the above mentioned kinematics is being reported.

2 2D computational model

Ansys Fluent is a commercial CFD package and has inbuilt Dynamic mesh algorithms to model translating and rotating boundaries. The efficiency of this solver in the context of flapping wing kinematics has been well documented in the recent years [4, 10]. For the present study, incompressible viscous flow around a flapping wing is solved using Ansys Fluent. The governing equations for such a flow in absence of any source or body forces are the continuity equation and the Navier–Stokes equation in the following form,

$$\begin{aligned}&\nabla .\vec {v}= 0\\&\rho \left( \frac{\partial \vec {v}}{\partial t}+\vec {v}.\nabla \vec {v}\right)= -\nabla p + \mu \nabla ^{2}\vec {v}. \end{aligned}$$

In this study, a two-dimensional elliptic wing profile with a chord of length 60 mm and maximum thickness to chord ratio of 2% is chosen. The airfoil and the computational domain are created and meshed using Gambit. The region in which the above-mentioned governing equations are solved is called the computational domain. The accuracy of the results heavily depends upon the quality of the mesh used in the computational domain. Intensive care has to be taken to maintain high quality of the mesh during simulations. Also, the mesh has to be dynamic to allow and accommodate the motion of the wing. The present flow solver satisfies the geometric conservation law on dynamically deforming mesh. The following section elaborates the computational domain selection for present simulations.

2.1 Computational domain selection

Initially a typical one-domain computational model is considered as shown in Fig. 1a. The elliptic wing is given a rotational motion and the mesh around the wing deforms. Large-scale deformations are observed in the mesh especially near the wing as the wing performs rotational motion as shown in Fig. 1b. While performing flow computations, these large-scale mesh deformations leave prominent flow features unresolved giving rise to a spurious flow field solution around the wing.

Fig. 1

a One-domain computational model and b large-scale deformations of the near wing mesh

To avoid such large-scale mesh deformations near the wing, a two-domain approach with hybrid structured–unstructured mesh is followed. The computational domain is divided into two regions, namely inner and outer, as indicated by concentric circular regions as shown in Fig. 2. The outer region consists of unstructured triangular elements that deform and allow the movement for the inner region. The inner region is meshed with structured quadrilateral elements. Structured quadrilateral elements in the inner region are expected to provide superior accuracy to resolve the boundary layer and vortex generation and interaction processes than unstructured mesh. The inner region moves along with the elliptic wing, i.e. it remains static with respect to the moving body and the outer region deforms. The evolution of the two-domain computational model following the translating motion is shown in Fig. 3.

Fig. 2

Two-domain computational model

Fig. 3

Evolution of the two-domain computational model following translating motion

This approach ensures a consistent high-quality mesh near the wing during its translation, which improves the accuracy of the computations and also significant amount of computational time is saved as only fewer cells have to be deformed and re-meshed at each time step. It is important to have unstructured triangular mesh in the deforming outer region because the Fluent Dynamic Meshing algorithms employed in the present study work only on unstructured triangular grid. The above-described two-domain approach was first suggested by Mueller [13] and was used by Prosser et al. [15], Lua et al. [10] and Dash et al. [4] to obtain accurate results on moving meshes. In the present study, the two-domain approach explained above has been used to compute the flow field around the translating wing.

2.2 Wing kinematics and user defined functions

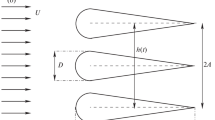
The flapping wing kinematics performed in this study involves two sets of motions similar to that of experiments conducted by Lua et al. [11]. In the first motion, henceforth called as Motion A, the wing is fixed at a constant angle of attack and is first linearly accelerated to a maximum velocity, translates with this maximum velocity for a certain period of time before linearly decelerating to rest. The total duration of this motion is denoted by T. The linear acceleration and deceleration phases of the motion account for 16% of the total time period (T). Angle of attack is defined as the angle between the chord of the wing and the direction of the translational velocity of the wing. In the latter motion, henceforth called as Motion B, the wing is subjected to same motion as Motion A but in back and forth sense. Figure 4 shows the wing kinematics in Motion B. In one complete cycle, the wing begins motion with a downstroke (translational motion along –ve X-axis) and ends with an upstroke (translating motion along +ve X-axis). Since, there is no angular pitching involved at the end of upstroke and downstroke, the role of leading edge and trailing edge is exchanged as the direction of motion of the wing gets reversed. Hence, accordingly, the aerodynamic force coefficients also change their signs during each stroke. In Fig. 4, the direction of arrows indicates the direction of wing translation.

Fig. 4

Wing kinematics of motion B

The parameters governing the above two motions are frequency (f) and Reynolds number (Re). The frequency (f) of Motion B is defined as

$$\begin{aligned} f=\frac{1}{2T}. \end{aligned}$$

The Reynolds number (Re) is defined based on the chord of the wing (c), the kinematic viscosity of the surrounding fluid ($\nu$) and the maximum velocity ($U_\text {max}$) to which the wing is accelerated at the end of acceleration phase, i.e.

$$\begin{aligned} \mathrm{Re}=\frac{U_\text {max}c}{\nu }. \end{aligned}$$

In the present study, Ansys Fluent Version 14, is used to perform dynamic mesh simulation. To provide a desired motion to the wing geometry and mesh, the built-in solver code needs to be complemented with User-Defined Functions (UDFs). UDFs are defined using DEFINE macro provided by Fluent and are dynamically linked to the Dynamic Mesh Zones in Fluent to provide the desired translational and rotational motion to the wing and provide necessary translation and deformation to desired regions of the mesh.

3 Validation study

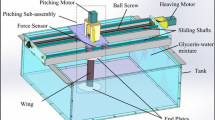
In this section, the above-developed computational model is subjected to a validation study. The validation presented here is a comparison with the DPIV experiments conducted by Lua et al. [11] involving a bi convex flapping wing of chord length 60 mm and wing span of 300 mm, performing wing kinematics identical to that of Motion A and Motion B as specified in Sect. 2.2 at a Reynolds number of 2000. The wing motion is performed in a quiescent medium of glycerin–water mixture. The time period of Motion A is $T = 2.382$ s and the frequency of Motion B is $f = 0.21$ Hz. The above experiment is numerically simulated using the computational model discussed earlier.

The boundary conditions applied at different boundaries indicated in Fig. 2 are briefly discussed below :

• No-slip boundary condition is employed on the translating wing surface.

• Consistent flux transport is enforced at the inner & outer grid interface.

• Zero net convective and diffusive flux transport is enforced at the farfield boundary.

The radius of the inner region of the computational domain is 8c whereas the radius of the outer region is 15c, where c is the wing chord. Some initial simulations were performed to ascertain that the 8c radius of the inner domain was sufficient to contain most of the rapidly evolving flow features. For unsteady transient flow calculations, the pressure-based solver is used, PISO scheme is used for solving pressure velocity coupling, spatial discretization is performed using Green–Gauss Cell-based gradient technique, pressure Poisson’s equation is solved using second-order central differencing scheme and time stepping is performed using first-oder implicit scheme . An attempt has been made to compare the wing force measurements performed by Lua et al. [11] with the present simulation results at angles of attack of $\alpha =45^{\circ }$ and $60^{\circ }$, respectively. The drag ($F_\text {D}$) and lift ($F_\text {L}$) forces are defined as the forces parallel and normal to the wing’s translational motion, respectively, and their corresponding coefficients are defined as follows where S is the wing planform area which is equal to the airfoil chord (c) for the two-dimensional case.

$$\begin{aligned} C_\text {D}&= \dfrac{F_\text {D}}{\frac{1}{2}\rho U^2_\text {max} S}\\ C_\text {L}&= \dfrac{F_\text {L}}{\frac{1}{2}\rho U^2_\text {max} S}. \end{aligned}$$

Fig. 5

Comparison of a coefficient of drag and b coefficient of lift for $\alpha = 45^{\circ }$ for Motion A

Fig. 6

Comparison of a coefficient of drag and b coefficient of lift for $\alpha = 60^{\circ }$ for Motion A

Fig. 7

Comparison of a coefficient of drag and b coefficient of lift for $\alpha = 45^{\circ }$ for Motion B

Fig. 8

Comparison of a coefficient of drag and b coefficient of lift for $\alpha = 60^{\circ }$ for Motion B

From Figs. 5, 6, 7 and 8, it is evident that the simulations and experiment agree reasonably well. However, the minor difference in the force coefficients is expected to be due to the following reasons:

• Three-dimensionality of the flow Lua et al. [11] conducted experiments on a three-dimensional wing with uniform cross-sectional profile with two end plates to minimize three-dimensional effects. Though the flow around the wing tips is restricted, the flow over the leeward as well as windward surfaces of wing has the freedom to move along the wing span. Three-dimensionality of the flow may not be insignificant at large angles of attack when there is significant flow separation and accompanying three-dimensional flow instabilities. Hence, the wing surface flow in an experiment has an extra degree of freedom along spanwise direction which is absent in the two-dimensional simulation model.

• Transitional nature of the flow Though the Reynolds number is low, i.e. 2000, from Figs. 5, 6, 7 and 8, it is observed that the experimental force coefficients exhibit fluctuations whereas the computed force coefficients have a much more smoother character. These oscillations indicate that the flow might have become transitional during experiment and this transition caused fluctuations in the experimental force coefficient values. The smoothness of the simulated data is due to the laminar modeling of the flow.

• Experimental uncertainties Effect of experimental uncertainties and ambient perturbations are very difficult to replicate in a numerical study. Such effects would always contribute towards a difference between experimental and numerical data.

An attempt to examine the three-dimensionality of the flow has been made in the present study and reported in Sect. 5.4. The transitional nature of the flow has not been modeled in the present study. Most of the simulations have been performed assuming laminar flow. The grid was refined appropriately for higher Reynolds number and higher frequency cases to ensure that all the relevant scales and transients are captured with reasonably good fidelity. Three-dimensional eddy resolving simulations have been reported in Sect. 5.5 for one particular case, namely Motion B at Re = 50,000 and $\alpha = 60^{\circ }$, to assess the effect of turbulence at the highest Reynolds number and angle of attack investigated.

4 Parametric study

This section describes the setup for the numerical simulations performed in this study. The two parameters that are varied in this study are frequency (f) & Reynolds number (Re). For the study on effect of frequency, the Reynolds number is held constant at 2000 and the study is performed for a few discrete frequencies, namely 0.021 Hz, 0.21 Hz, 0.315 Hz, 0.42 Hz and 2.1 Hz. For study on effect of Reynolds number, the frequency is held constant at 0.21 Hz and Reynolds number is varied from 2000, 5000, 10,000 to 50,000. The study is conducted at wing angles of attack of $\alpha = 45^{\circ }$ and $\alpha = 60^{\circ }$. The properties of the surrounding quiescent fluid are chosen to match that of glycerin–water mixture with density $\rho = 1076.6$ $\mathrm {kg/ m}^{3}$ and kinematic viscosity of $\nu = 2.722$ x $10^{-6}$ $\mathrm {m}^{2}/\mathrm {s}$ . Since the computational model used in the validation study gave reasonably good results, the same has been used in all the simulations in the parametric study. A grid independence study has been performed and a suitable mesh has been identified for each configuration following guidelines of grid convergence index. In this numerical study, the framework of the experimental work reported by Lua et al. [11] is adopted. Simulation results are initially compared with experiments thereby demonstrating the suitability of the computational method (Sect. 3). Subsequently, the numerical simulations have been conducted over a wider range of parameters (Sect. 5). The highest flapping frequency simulated is 2.1 Hz. However, on the basis of flapping frequency, a comparison with the animal kingdom is difficult, since natural flyers’ wing beat frequencies are significantly higher in the investigated Reynolds numbers range.

5 Results and discussion

5.1 Effect of frequency

Figures 9, 10, 11, 12 and 13 show the instantaneous vorticity contours for Re $= 2000, \alpha = 45^{\circ }$ and five different flapping frequencies, namely $f = 0.021$, 0.21, 0.315, 0.42 and 2.1 Hz, respectively. The flapping frequency reported by Lua et al. [11] is 0.21 Hz. In the present study, the frequency has been varied over a range of two orders, covering a range from one order lower to one order higher of that of the above reference frequency of 0.21 Hz. During the stroke from right to left, i.e. downstroke, a clockwise leading edge vortex forms on the upper edge of the wing and simultaneously a counter clockwise trailing edge vortex forms on the lower edge of the wing. The evolution of these vortex structures is shown in (a)–(e) of Figs. 9, 10, 11, 12 and 13 . The leading edge vortex is comparatively weak with respect to the trailing edge vortex for the lowest frequency. With increase in frequency, the leading edge vortex becomes significantly stronger and remains attached over most of the stroke, while the trailing edge vortex separates during the middle of the stroke. Formation of a secondary vortex near the upper wing tip on the leeward side is observed during the constant velocity phase for $f = 0.21$, 0.315 and 0.42 Hz. This structure is not visible at $f = 2.1$ Hz. Also, the trailing edge vortex remains stable almost throught the stroke for $f = 2.1$ Hz. Towards the end of the stroke, two flow features are noticed. First, fresh leading and trailing edge vortices of opposite nature to those formed during acceleration phase are formed, however, they are much weaker than those formed during the accelerating phase. Second, wing–wake interaction occurs, where the shed vortices tend to slide along the neighboring region of the leeward surface of the wing. This feature is more pronounced for $f = 0.21$, 0.315 and 0.42 Hz. The shed vortices lie further away from the wing for $f = 0.021$ Hz. Vortex structures for the return stroke from left to right are shown in (f)–(j) of Figs. 9, 10, 11, 12 and 13. Wing–wake interaction occurs at the beginning of the return stroke due to the presence of residual vortex structures from previous stroke. During the remaining stroke flow, features predominantly similar to that of the previous stroke are observed. One distinct feature is observed for $f = 2.1$ Hz. Two counter-rotating vortex pairs are formed from the leading and trailing edges. These pairs remain stable almost all through the stroke and shed towards the end of the stroke. Such pair is visible only near the trailing edge for $f=0.42$ Hz.

Fig. 9

Vorticity contours for $\alpha = 45^{\circ }$ for Motion B for $f = 0.021$ Hz

Fig. 10

Vorticity contours for $\alpha = 45^{\circ }$ for Motion B for $f = 0.21$ Hz

Fig. 11

Vorticity Contours for $\alpha = 45^{\circ }$ for Motion B for $f = 0.315$ Hz

Fig. 12

Vorticity Contours for $\alpha = 45^{\circ }$ for Motion B for $f = 0.42$ Hz

Fig. 13

Vorticity Contours for $\alpha = 45^{\circ }$ for Motion B for $f = 2.1$ Hz

Figures 14, 15, 16, 17 and 18 show the time history of the lift and drag coefficients for Re $= 2000, \alpha = 45^{\circ }$ case for the five different frequencies, respectively. Due to the kinematic symmetry produced at this angle of attack, the drag and lift coefficients almost coincide with each other. Also, as the wing sweeps from right to left i.e. downstroke, the drag and lift forces act along positive X and Y directions, respectively, while they change sign during the reverse stroke of the wing when it translates from left to right, i.e. upstroke. As the frequency increases, the peak positive and negative values of the force coefficients increase. If the force coefficient values for $f = 0.021$ Hz and $f = 2.1$ Hz are compared, they differ by approximately one order. The first negative peak is observed at the beginning of the second stroke. This peak has a larger magnitude than the first peak because of wake interaction of the first kind discussed by Lua et al. [11]. It is uniformly observed for the entire frequency range. This is because of the direct interaction of the wing with the residual vortices from previous stroke which leads to enhanced relative velocity and thereby force augmentation. At $f = 0.021$ Hz, during the right to left stroke, there is a sharp spike during the acceleration phase and a sharp fall during deceleration phase. In the uniform velocity phase, an oscillatory behavior of force coefficients is noticed. During the left to right stroke, i.e. upstroke, a rise during the accelerating phase is noted but without a spike and immediately followed by the oscillatory behavior in force coefficients. Starting from the third stroke, inflection points are noticed during both the acceleration and deceleration phase, which implies a momentary reduction in the rate of increase in the lift and drag. It is linked with shedding of leading and trailing edge vortices during different phases of a stroke. Reasonable periodicity is achieved from third stroke onwards. However, certain amounts of variations are noticeable even at later strokes which is expected to be due to nominal aperiodicity in vortex shedding and residual wake structures. For $f = 0.21$ Hz, the first stroke force growth is near linear but for second stroke onwards, the growth shows inflexional nature followed by occasional dual peak. This is followed by an almost linear decay followed by minimum lift point. A dual-negative peak is occasionally observed. Periodic patterns are observed from 6th stroke onwards. These features are illustrated in Fig. 15. For $f = 0.315$ and 0.42 Hz, the inflexional trends persist and dual peaks become a more regular feature at $f = 0.42$ Hz. Periodicity is observed from 6th stroke onwards for $f = 0.315$ Hz and from 4th stroke onwards for $f = 0.42$ Hz. Non-circulatory forces associated with wing acceleration and added mass effects dominate over circulatory or vortex related forces with increase in frequency. This leads to sharper temporal structure of force coefficients.

At this point, it may be worthwhile to relook at features observable separately from the vorticity contours and force–time histories and attempting to correlate them. When the wing accelerates from rest while executing the downstroke, both the lift and drag forces increase rapidly and reach their respective maximum values by the end of the acceleration phase. As seen in Figs. 14, 15, 16, 17 and 18, there is a sharp increase in the forces which is due to the combined effect of acceleration and the generation of the leading and trailing edge vortices from the top and bottom tips of the wing, respectively. As the wing enters the constant velocity phase of the stroke motion, the forces drop sharply during a short initial phase. This could be due to the end of the acceleration and initiation of constant velocity phase. After this short transient, a longer phase of gradual reduction follows until the end of the constant velocity phase. The leading edge vortex separates during this phase. The strength of this vortex, its location and distance from the wing, and wing traverse time influence the overall wing–wake interaction which continues as the wing decelerates and stops. This is the stronger vortex out of the pair for all the frequencies apart from the lowest one. As the wing decelerates at the end of the constant velocity phase, it experiences another sharp reduction in forces caused due to wing deceleration. The first trailing edge vortex which had shed much earlier in the stroke and had diffused gradually was followed by formation of a second trailing vortex, which is more distinctly visible for $f = 0.21$, 0.315 and 0.42 Hz (Figs. 10, 11 and 12). The reduction in the wing translation speed causes the strong leading edge vortex and a weak second trailing edge vortex to travel towards the leeward side of the wing. The proximity of these vortices with the leeward surface leads to impingement of their induced velocity on the wing which results in drag reduction. In particular, for $f = 0.21$ Hz, the close proximity of the strong leading edge vortex and sliding of the second trailing edge vortex over the leeward surface produces an additional inflexion point in the force curves. This is when the forces tend to increase for a short duration before monotonically decreasing to their minimum negative values marking the end of the stroke. This inflexional behavior systematically repeats for $f = 0.21$ Hz (Fig. 15), and intermittently repeats for $f = 0.021$ Hz (Fig. 14). However, it is not observed at higher frequencies. This once again corroborates the fact that proper synchronization between wing movement and vortex interaction can strongly influence the force history, thus indicating the possibility of an optimum frequency at which the effect of vortex induced velocities can be maximized. Since the wing continues to flap within its own wake, the influence of residual structures can be profound. Thus, when the wing reverses the direction and starts the upstroke, residual vortices would interact with the wing. This is also true for the downstroke. For $f = 2$.1 Hz, the residual structures from downstroke remain most coherent as seen in Fig. 13f–j and closely slide past the leading and trailing edges of the wing for the first half of upstroke. The suction peaks produced due to the leading and trailing edge vortices formed during upstroke are augmented by the close proximity of the residual vortices. The longer phase of gradual reduction of forces follows until the end of the constant velocity phase as usual, but least reduction is observed for $f = 2.1$ Hz compared to the other frequencies. This larger retention of forces is possible due to the coherent nature of the newly formed and residual vortex structures. They form strong vortex pairs by the end of the upstroke as seen in Fig. 13j. This effect is not so dominant for $f = 0.315$ and 0.42 Hz and absent at lower frequencies. Thus, we see a close correspondence between the vortex structures and the force time history. In general, for larger frequencies, the non-circulatory forces associated with wing acceleration and added mass effects play a more dominant role over circulatory or vortex related forces as mentioned earlier.

Fig. 14

Time history of force coefficients for $f = 0.021$ Hz & $\alpha = 45^{\circ }$

Fig. 15

Time history of force coefficients for $f = 0.21$ Hz & $\alpha = 45^{\circ }$

Fig. 16

Time history of force coefficients for $f = 0.315$ Hz & $\alpha = 45^{\circ }$

Fig. 17

Time history of force coefficients for $f = 0.42$ Hz & $\alpha = 45^{\circ }$

Fig. 18

Time history of force coefficients for $f = 2.1$ Hz & $\alpha = 45^{\circ }$

Figures 19, 20, 21, 22 and 23 show the time history of the lift and drag coefficients for Re $= 2000$, $\alpha = 60^{\circ }$ case for the five different frequencies, respectively. Due to the kinematic asymmetry produced at this angle of attack, the drag coefficient is larger than the lift coefficient. The force coefficients change sign due to change in wing sweep direction. Like in the case of $\alpha = 45^{\circ }$, as the frequency increases, the peak positive and negative values of the force coefficients increase and the force coefficient values for $f = 0.021$ Hz and $f = 2.1$ Hz differ by approximately one order. Many of the features observed in case of $\alpha = 45^{\circ }$ are repeated. The first negative peak is observed at the beginning of the second stroke. This peak has a larger magnitude than the first peak because of wake interaction of the first kind. This behavior is observed for all frequencies. At $f = 0.021$ Hz, in the uniform velocity phase, an oscillatory behavior of force coefficients is noticed. This oscillatory behavior is not noticed at higher frequencies. Inflexional behavior of force coefficients occurs less frequently at 0.021 Hz, but it is a regular feature at higher frequencies. Dual-negative peaks are observed for $f = 0.21$, 0.315 and 0.42 Hz. For $f = 0.021$ Hz, reasonable periodicity is achieved from 10th stroke onwards. Periodic patterns are observed 9th stroke onwards for $f = 0.21$ and 0.315 Hz, and 8th stroke onwards for $f = 0.42$ and 2.1 Hz. However, marginal variations are visible at later strokes perhaps due to nominal aperiodicity in vortex shedding and residual wake structures. For both $\alpha = 45^{\circ }$ and $60^{\circ }$, the periodicity seems to be achieved within lesser number of strokes as frequency increases. Also, periodicity is achieved earlier at lower angle of attack. Like in the case of $\alpha = 45^{\circ }$, non-circulatory forces dominate with increase in frequency at $\alpha = 60^{\circ }$.

Fig. 19

Time history of force coefficients for $f = 0.021$ Hz & $\alpha = 60^{\circ }$

Fig. 20

Time history of force coefficients for $f = 0.21$ Hz & $\alpha = 60^{\circ }$

Fig. 21

Time history of force coefficients for $f = 0.315$ Hz & $\alpha = 60^{\circ }$

Fig. 22

Time history of force coefficients for $f = 0.42$ Hz & $\alpha = 60^{\circ }$

Fig. 23

Time history of force coefficients for $f = 2.1$ Hz & $\alpha = 60^{\circ }$

5.2 Effect of Reynolds number

Figures 24, 25, 26 and 27 show the time history of the lift and drag coefficients for $\alpha = 45^{\circ }$ and $f = 0.21$ Hz at four different Reynolds numbers, namely Re $= 2000$, 5000, 10,000 and 50,000, respectively. With increase in Reynolds number, there is a reduction in the force coefficients. With increase in Reynolds number, there is an increasing presence of multiple large- and small-scale inflexions and oscillations in the force histories. These are due to vortex shedding and wing–vortex interactions where vortex structures with a wide range of length and time scales are involved, which is typically observed at higher Reynolds numbers. Though the overall temporal history of force coefficients is expected to reach a certain degree of periodicity after a number of strokes, periodicity of small-scale features is unlikely to be achieved at higher Reynolds numbers.

Fig. 24

Time history of force coefficients for Re = 2000 & $\alpha = 45^{\circ }$

Fig. 25

Time history of force coefficients for Re = 5000 & $\alpha = 45^{\circ }$

Fig. 26

Time history of force coefficients for Re = 10,000 & $\alpha = 45^{\circ }$

Fig. 27

Time history of force coefficients for Re = 50,000 & $\alpha = 45^{\circ }$

Figures 28, 29, 30 and 31 show the time history of the lift and drag coefficients for $\alpha = 60^{\circ }$ and $f = 0.21$ Hz at four different Reynolds numbers, namely Re = 2000, 5000, 10,000 and 50,000, respectively. As observed for $\alpha =45^{\circ }$, with increase in Reynolds number, there is increasing presence of multiple large- and small-scale inflexions and oscillations in the force histories. The force coefficients seem to vary temporally in in-phase manner. Reasonably periodic behavior of force coefficients is observed from as early as second stroke for Re = 50,000, however, such periodicity is not achieved at lower Reynolds numbers. This could be due to enhanced robustness of vortex structures at higher Reynolds number. Leading and trailing edge vortices of various scales get shed from time to time which influence the force coefficient time history. The wing–wake interactions of both first and second kind seem to be occurring on multiple occasions during each stroke leading to the oscillatory force behavior.

Fig. 28

Time history of force coefficients for Re = 2000 & $\alpha = 60^{\circ }$

Fig. 29

Time history of force coefficients for Re = 5000 & $\alpha = 60^{\circ }$

Fig. 30

Time history of force coefficients for Re = 10,000 & $\alpha = 60^{\circ }$

Fig. 31

Time history of force coefficients for Re = 50,000 & $\alpha = 60^{\circ }$

5.3 Frequency spectrum analysis

Figures 32, 33, 34, 35 and 36 show the frequency spectrum obtained from the Fast Fourier Transform (FFT) of the lift coefficient of the flapping wing performing motion B at different frequencies for Re = 2000. The spectrum for $f = 0.021$ Hz at $\alpha = 45^{\circ }$ shows the most dominant peak at $\mathrm{St} = 0.021$ which corresponds to the forcing frequency (Fig. 32). Another higher harmonic is observed at $\mathrm{St} = 0.063$. Couple of weaker harmonics with comparable power content are also observed at $\mathrm{St} = 0.105$, 0.147 and 0.189. At the same frequency, when the angle of attack is increased to $\alpha = 60^{\circ }$, it is observed that the peak frequencies remain the same but the power content corresponding to each peak frequency is slightly decreased. For $f = 0.21$ Hz, the most dominant peak for both angle of attacks is observed at $St = 0.21$ with slight decrease in power content at higher angle of attack (Fig. 33). Couple of other harmonics are observed at St = 0.63, 0.48, 1.41, 1.47 and 1.89 with significant decrease in power content at higher angle of attack. At $f = 0.315$ Hz, the most dominant peak is observed at the forcing frequency of $\mathrm{St} = 0.315$ for both angles of attack (Fig. 34). Another higher harmonic is observed at $\mathrm{St} = 0.94$ in both cases but with significant decrease in power content at $\alpha = 60^{\circ }$. In case of $\alpha = 45^{\circ }$, weaker harmonics are observed at $St = 1.57$, 2.20, 2.83, 4.1 and 4.72 whereas for $\alpha = 60^{\circ }$, weaker harmonics are visible at St = 2.2, 2.83 and 4.72. At f = 0.42 Hz, the most dominant peak is observed at St = 0.42 with next higher harmonic at St = 1.26 with enhanced reduction in power content between $\alpha = 45^{\circ }$ and $\alpha = 60^{\circ }$ (Fig. 35). Other weaker harmonics with comparable power content are observed at St = 2.1, 2.94, 3.78 and 6.3 in case of $\alpha = 45^{\circ }$ and at St = 2.94, 3.78 and 6.3 in case of $\alpha = 60^{\circ }$.At f = 2.1 Hz, the most dominant peak is again observed at the forcing frequency of St = 2.1 for both angles of attack with an order of magnitude increase in power content for both angles of attack (Fig. 36). Notably, the decrease in power content of the most dominant frequency for $\alpha = 60^{\circ }$ is observed to be highest for this frequency. Another higher harmonic is observed at St = 6.3 and with weaker harmonics at St = 10.5, 14.69, 18.87 and 31.48 in both the cases.

The forcing frequency is the most dominant frequency visible in the frequency spectrum over the entire frequency range that has been studied. In terms of power content, with increase in frequency, the power content of the most dominant peak increases with highest being at f = 2.1 Hz and least at f = 0.021 Hz. The effect of angle of attack in frequency spectrum is also observed. For a given frequency, the power content of dominant peak decreases at higher angle of attack and this difference is larger at higher frequencies. For a given forcing frequency, a large number of harmonics are observed at both angles of attack. This is expected because as the wing is pitched up to higher angle, the flow field in the wing–wake becomes very unsteady and complex which inturn affects the frequency spectrum of the flow field and consequently the forces acting on the body. It is interesting to note that in all the cases, the energy content of the flow is distributed over a broad frequency spectrum with a richer content of higher frequencies which implies that higher harmonics of the forcing frequency are excited to a greater extent as opposed to the sub-harmonics.

Fig. 32

FFT of lift coefficient for Re = 2000 & f = 0.021 Hz: a $\alpha = 45^{\circ }$ b $\alpha = 60^{\circ }$

Fig. 33

FFT of lift coefficient for Re = 2000 & f = 0.21 Hz: a $\alpha = 45^{\circ }$ b $\alpha = 60^{\circ }$

Fig. 34

FFT of Lift coefficient for Re = 2000 & f = 0.315 Hz: a $\alpha = 45^{\circ }$ b $\alpha = 60^{\circ }$

Fig. 35

FFT of lift coefficient for Re = 2000 & f = 0.42 Hz: a $\alpha = 45^{\circ }$ b $\alpha = 60^{\circ }$

Fig. 36

FFT of lift coefficient for Re = 2000 & $f = 2.1\hbox {Hz}$: a $\alpha = 45^{\circ }$ b $\alpha = 60^{\circ }$

Figures 37, 38, 39 and 40 show the frequency spectrum obtained from the Fast Fourier Transform (FFT) of the lift coefficient of the flapping wing performing motion B at different Reynolds numbers for frequency $f = 0.21$ Hz. For Re = 2000, the most dominant peak for both angle of attacks is observed at $\mathrm{St} = 0.21$ with decrease in power content at higher angle of attack. Couple of other harmonics are observed at $\mathrm{St} = 0.63$, 0.48, 1.41, 1.47 and 1.89 with significant decrease in power content at higher angle of attack. As the Reynolds number is increased to 5000, the most dominant peak still corresponds to the forcing frequency St = 0.21 and in terms of its power content, the difference between $\alpha = 45^{\circ }$ & $\alpha = 60^{\circ }$ becomes much smaller. Compared to Re = 2000, a decrease in power content of the most dominant peak is observed. Another relatively strong harmonic is observed at $\mathrm{St} = 0.63$ in both the cases. Several weaker harmonics are observed for both angles of attack. For $\alpha = 45^{\circ }$, harmonics are visible at St = 0.315, 0.42, 0.84, 0.99, 1.15, 1.26 and 1.68. For $\alpha = 60^{\circ }$, weaker harmonics are observed at St = 0.94, 1.05, 1.21, 1.47, 1.63 and 1.89. For Re= 10,000, the most dominant peak is again the forcing frequency St $= 0.21$ for both angles of attack but with a decrease in power content compared to that of Re = 5000. The power content for $\alpha = 60^{\circ }$ is quite close to that of $\alpha = 45^{\circ }$. At $\mathrm{St} = 0.63$, another dominant peak is observed in both the cases. Weaker harmonics are visible at $\mathrm{St} = 1.05$, 1.42, 1.52, 1.62 and 1.83 for $\alpha = 45^{\circ }$ and at $\mathrm{St} = 0.315$,1.05, 1.36, 1.67, 1.89 and 2.31 for $\alpha = 60^{\circ }$. At Re = 50,000, the forcing frequency $\mathrm{St} = 0.21$ is again the dominant frequency with power content being nearly the same for both angles of attack. However, there is a substantial decrease in its power content when compared to $Re = 2000$, 5000 & 10,000. From above observations, we can say that with increase in Reynolds number, the energy content of the dominant harmonic becomes weaker. More and more harmonics are excited as the Reynolds number increases since the flow becomes more receptive towards perturbations. The same can be confirmed by studying the slope of the least square straight line that can be fit into the FFT curve. For Re = 2000 & $\alpha = 45^{\circ }$, the slope is – 0.1823, whereas for $\alpha = 60^{\circ }$, the slope is – 0.1243. At Re = 50,000, for $\alpha = 45^{\circ }$ and $60^{\circ }$, the slopes are – 0.0889 and – 0.0861, respectively. It appears that the negative slopes are larger for Re = 2000 than Re = 50,000. The broadband nature at higher Re spreads the energy over a larger frequency range. Hence, leading to a shallower slope at higher Re.

Fig. 37

FFT of lift coefficient for $f = 0.21$ Hz & Re = 2000: a $\alpha = 45^{\circ }$ b $\alpha = 60^{\circ }$

Fig. 38

FFT of lift coefficient for $f = 0.21$ Hz & Re = 5000: a $\alpha = 45^{\circ }$ b $\alpha = 60^{\circ }$

Fig. 39

FFT of lift coefficient for $f = 0.21$ Hz & Re = 10,000: a $\alpha = 45^{\circ }$ b $\alpha = 60^{\circ }$

Fig. 40

FFT of lift coefficient for $f = 0.21$ Hz & Re = 50,000: a $\alpha = 45^{\circ }$ b $\alpha = 60^{\circ }$

5.4 Three-dimensionality of the flow

In moving boundary problems such as flapping wing, where the flow dynamics is highly non-linear and unsteady, the effect of three-dimensionality of the flow can be predominant. In experiments, the 2D analysis of a flapping wing is carried out using a 3D wing with end plates [11] to restrict flow from turning around wing tips and thereby minimizing the three-dimensional effect of the flow. However, the flow still has the freedom to move along spanwise direction in either way till the wing tip. Similar is the case with the bottom surface. This kind of motion can be induced in highly unsteady flow such as flapping wing. A 2D simulation of such kind of flows suppresses the extra degree of freedom associated with the flow in experiments. Therefore, to completely replicate the 2D flapping wing experiments, it is more logical to perform simulations over a 3D wing with end plates.

In this section, we try to explore the effect of three dimensionality of the flow over a flapping wing on the aerodynamic force coefficients. The 2D computational model developed above in Sect. 2 is extruded in the third dimension to generate a 3D simulation model with wing tips forming the left and right boundaries of the computational domain. Therefore, in this way, the flow is not allowed to turn around at the wing tips on either sides. Flow over a 3D wing with chord of 60 mm and wing span of 300 mm, similar to the one used by Lua et al. [11] in their experiments, performing wing kinematics Motion A and Motion B as described earlier in Sect. 2.2 is simulated for both angles of attack $\alpha = 45^{\circ }$ and $\alpha = 60^{\circ }$. The 3D aerodynamic force coefficients obtained are compared with the 2D results obtained in validation study (refer Sect. 3) and with experimental data of Lua et al. [11]. Figures 41, 42, 43 and 44 show the comparison of the results.

Fig. 41

Comparison of a coefficient of drag and b coefficient of lift for $\alpha = 45^{\circ }$ for Motion A

Fig. 42

Comparison of a coefficient of drag and b coefficient of lift for $\alpha = 60^{\circ }$ for Motion A

Fig. 43

Comparison of a coefficient of drag and and b coefficient of lift for $\alpha = 45^{\circ }$ for Motion B

Fig. 44

Comparison of a coefficient of drag and b coefficient of lift for $\alpha = 60^{\circ }$ for Motion B

From Figs. 41 and 42, it can be seen that the 2D simulation results and 3D simulation results almost coincide for Motion A at both angles of attack. In case of Motion B, a slight deviation of 3D results from 2D results is observed from $t/T = 2.5$–3.0 for $\alpha = 45^{\circ }$ (refer Fig. 43). For $\alpha = 60^{\circ }$, the deviation from 2D results is clearly visible from t/T = 2.5 (refer Fig. 44). This deviation of 3D simulation results from 2D results indicate a slight change in flow features along spanwise direction. It is quite interesting to note that in case of Motion B at both $\alpha = 45^{\circ }$ & $\alpha =60^{\circ }$, the 3D results are closer to the experimental results of Lua et al. [11] which is consistent and supports our argument about the three-dimensionality of flow in experiments. Also, it is observed that the effect of three-dimensionality of flow becomes dominant at higher angle of attack (in this case for $\alpha = 60^{\circ }$) and for wing kinematics involving to and fro motion such as Motion B.

5.5 Three-dimensional Eddy resolving simulations

Previous sections reported laminar flow computations performed predominantly for two-dimensional configurations and a few on three dimensional configurations (refer Sect. 5.4). It is well known that a large angle of attack translational oscillation of an airfoil would produce large-scale flow separation, vortex shedding, vortex interaction and unsteady wake. Two-dimensional solution precludes the possibility of capturing spanwise unsteadiness for such a complex unsteady flow situation. Additionally, at the highest Reynolds number considered in the present study, Re = 50,000, the flow is expected to manifest turbulent nature. The spanwise fluctuations would be augmented due to the presence of turbulence. An appropriate eddy-resolving turbulence model needs to be employed to study and characterize the flow field. Improved Delayed detached Eddy simulation (IDDES) was performed in the present study. The 2D domain considered for Re = 50,000 was extruded along the spanwise direction. The near wing inner domain was meshed using a fine structured grid with the first cell thickness of 2e–5 m to resolve the finer eddy scales. Satisfactory mesh resolution was used along azimuthal and spanwise directions as well. IDDES essentially solves SST $k-\omega$ RANS equations in the near-wall region and LES equations with Smagorinsky model in the rest of the domain. Symmetry boundary condition has been utilized at the spanwise boundaries and farfield for the three-dimensional laminar simulations reported in Sect. 5.4 as well as the IDDES Simulations.

The cell zones where the RANS equations and the LES equations are solved can be seen in Fig. 45, which show the contours of DES Turbulent Kinetic Energy (TKE) Dissipation Multiplier ($\xi$). For $0< \xi < 1$, RANS equations are solved and for $1< \xi < \xi _\text {max}$, LES equations are solved. From the contours, it is evident that the RANS computations are confined to a small region around the wing section, and beyond that region, the model switches to LES.

Fig. 45

Contours of DES Turbulent Kinetic Energy Dissipation Multiplier in a RANS and b LES solver regions

The transient formulation was limited to a first-order time-stepping implicit scheme because the remeshing of the tetrahedral cells required in the outer region to accommodate the wing movement could be satisfactorily accomplished only using this scheme. Also, higher time steps could be chosen for the implicit scheme without encountering numerical instability and meshing issues. The timestep size for the current simulations is chosen as T/100. The solution at each timestep was considered to be converged when all the transport equation residuals dropped below the value of 1e–5. The accuracy of spatial resolution is second order.

Fig. 46

Comparison of instantaneous vortex structures captured using a 3D laminar simulation b 3D IDDES simulation; For Motion B, Re=50,000, $\alpha = 60^{\circ }$, $t/T=3$

To ascertain the assumptions stated in the first paragraph of Sect. 5.5, laminar flow equations were solved. Figure 46 shows a comparison between instantaneous vortex structures captured by 3D laminar simulation and IDDES for Motion B, Re = 50,000, $\alpha = 60^{\circ }$, $t/T=3$. From the comparison, it is visible that IDDES has been able to better resolve the range of vortex structures that exist at this moderately high Reynolds number. Laminar simulation fails to capture the details. Further, it does not model the energy cascade which exists in turbulent flows, which leads to inaccurate prediction of flow structures. Thus, for effective capturing of the energy cascade that exists in turbulent flows, eddy resolving simulations are necessary. Hence, IDDES simulations were considered and they were carried out up to $t/T=8$.

Fig. 47

Lambda2 isosurfaces at $t/T=6.8$; For Motion B, Re = 50,000, $\alpha =60^{\circ }$

Figure 47 shows the instantaneous Lambda2 contours around the wing at $\alpha = 60^{\circ }$ executing Motion B at $t/T=6.8$. At this location, the wing has completed 80% of the downstroke and is approaching the end of the downstroke. The contours indicate a range of vortex structures spanning from small to large, which is expected due to the increasing scale separation, which occurs with an increase in Reynolds number. It also shows the eddy resolving capability of IDDES. The presence of turbulent fluctuations enables the formation of a strong leading and trailing edge vortex pair at the beginning of a stroke, as seen from the mid-span vorticity contours in Fig. 48. At this location, the wing has started its downstroke and has completed 20% of the stroke. The robustness of the vortex pair sustains all through the stroke, as is visible in Fig. 48 to corresponds to $t/T=6.8$. Waviness in the shear layer indicates Kelvin–Helmholtz instability. However, that does not induce the breakdown of the shear layer. Intermittency in the shear layer appears to be limited.

Fig. 48

a Vorticity contours at mid-span at $t/T=6.2$. b Vorticity contours at mid-span at $t/T=6.8$; For Motion B, Re = 50,000, $\alpha = 60^{\circ }$

Fig. 49

Comparison of coefficient of drag between 2D laminar simulation and IDDES for Motion B, Re = 50,000, $\alpha = 60^{\circ }$

Fig. 50

Comparison of coefficient of lift between 2D laminar simulation and IDDES for Motion B, Re = 50,000, $\alpha = 60^{\circ }$

Figures 49 and 50 show a comparison between 2D laminar simulation and 3D IDDES results for lift and drag coefficients. There is a significant similarity in trend. However, in general, the peak values of IDDES exceed those of laminar simulations. The strong leading and trailing edge vortices produce strong suction peaks, which manifest in the form of a spike in the force coefficients. The enhanced turbulent mixing augments cross-momentum exchange that feeds significant tangential momentum to the near wall layer in the leeward wing surface. This reduces the pressure drag and augments lift. However, it also leads to a higher skin friction coefficient. The interplay of these effects can be seen in the force coefficient history. The cycle-to-cycle variations seem to be larger in the IDDES simulations. There is a slight phase difference between the two results, which exists systematically over several cycles of simulations which have been performed.

To conclude on the relative magnitudes of the transient terms, convective derivative terms, Pressure Gradient (PG) terms and Reynolds Stress (RS) terms, a comparative table (refer Table 1) is shown below. A term of the order of 1e + n is indicated by the number ‘n’ in the table. Following this approach, each of the terms corresponding to X, Y and Z Reynolds averaged momentum equations from the present IDDES simulations are reported.

Table 1 Comparison of relative magnitudes of the transient terms, convective derivative terms, pressure gradient terms and Reynolds Stress terms for Motion B, Re = 50,000, $\alpha = 60^{\circ }$

It is observed that the transient term is a weak term which is possible because its effect is strong only during the end of a stroke and beginning of another, where significant temporal changes occur due to large acceleration. Wake capture and added mass effects could interact in a complex manner during stroke reversal. However, during the steady wing sweep, the transient term remains weak, and therefore in a cycle average sense its effect is not significant. The effect is weakest along the spanwise direction. Convective terms and the Reynolds stress terms are the most dominant and are of comparable magnitude, which clearly indicates the necessity of implementing an eddy resolving simulation for Re = 50,000 case. The pressure gradient is slightly weaker than these terms. Its effect is weakest along the spanwise direction. A detailed budget of turbulent kinetic energy and dissipation for Re = 50,000 could reveal more about the physics. However that falls beyond the scope of the present work.

6 Conclusion

A numerical investigation of the translational flapping wing kinematics reported in the experimental work of Lua et al. [11] was attempted in the present study. The wing executed a to-and-fro horizontal flapping motion with a fixed pitch orientation or angle of attack. The present study focused on the effect of flapping frequency, Reynolds number and angle of attack on various aspects like vortex structures produced by the wing motion, wing–vortex interaction, aerodynamic forces and their frequency spectra. Although force measurements and DPIV results for the above kinematics has been reported in Lua et al. [11], for $f = 0.21$ Hz, Re = 2000 and $\alpha = 45^{\circ }$ & $60^{\circ }$, to the best of the authors’ knowledge, a detailed computational parametric study on the above mentioned kinematics has not been reported earlier. The present study was performed for five different frequencies, namely $f = 0.021$, 0.21, 0.315, 0.42 and 2.1 Hz, four different Reynolds numbers, namely Re = 2000, 5000, 10,000 and 50,000 and two different angles of attack, namely $\alpha = 45^{\circ }$ & $60^{\circ }$ to obtain a greater insight on effects of the above parameters. The properties of the working fluid used in the experiments were exactly replicated in the numerical simulations.

A mesh based on two-domain approach was generated around the moving wing which provided consistently high quality for every phase of the wing motion and was computationally cheap. The numerical procedure was initially validated by comparing the numerical force coefficient data with experimental results of Lua et al. [11] for both Motion A (one time translation of the wing) and Motion B (to-and-fro flapping of the wing). Major features of the force time history could be captured quite well using the Ansys Fluent Version 14 laminar flow solver with the use of dynamic meshing-based two-domain approach for the validation problem. This was achieved without incorporating any transition and turbulence model. After completing the validation study, a set of computational meshes were generated for the entire range of flapping frequencies, Reynolds number and angle of attack in a systematic manner following grid convergence index guidelines.

Subsequently, the instantaneous vorticity contours of the flow were studied for Re = 2000, $\alpha = 45^{\circ }$ and five different flapping frequencies, namely $f = 0.021$, 0.21, 0.315, 0.42 and 2.1 Hz, respectively. Leading and trailing edge vortices are formed from the wing tips during wing stroke and they shed from time to time forming residual vortices. Their frequency-related variations were identified. Wing–wake interaction of first kind which occurs on stroke reversal and the second kind in which wing encounters a single wake vortex were both noticed for these various test cases.

Temporal history of drag and lift coefficients was studied for Re = 2000, $\alpha$ = $45^{\circ }$ and $60^{\circ }$ for five different flapping frequencies to study the effect of flapping frequency. The drag and lift coefficients almost coincided for $\alpha = 45^{\circ }$ while drag was relatively higher for $\alpha = 60^{\circ }$. When the wing changed sweep direction, sign of the force coefficients reversed. As the frequency increased, the peak positive and negative values of the force coefficients increased. The first negative peak was observed at the beginning of the second stroke. This peak had a larger magnitude than the first peak because of wake interaction of the first kind. This effect was observed uniformly over the entire frequency range. For both angles of attack, nominal periodicity of force coefficients was achieved within lesser number of strokes as flapping frequency increased. Also, periodicity was achieved earlier at lower angle of attack. Non-circulatory forces associated with wing acceleration and added mass effects dominated over circulatory or vortex-related forces with increase in frequency. This was visible through the sharper temporal structure of force coefficients.

Temporal history of drag and lift coefficients was studied at $f = 0.21$ Hz, $\alpha = 45^{\circ }$ and $60^{\circ }$ at four different Reynolds numbers, namely Re = 2000, 5000, 10,000 and 50,000, for studying the effect of Reynolds number. With increase in Reynolds number, multiple large- and small-scale inflexions and oscillations were visible in the time history of force coefficients. These were due to vortex shedding and wing–vortex interactions caused by vortex structures comprising a wide range of length and time scales. This is a typical character of high Reynolds number flows.

From the FFT of lift coefficient time history, it was concluded that the forcing frequency is the most dominant frequency over the entire range of frequencies in the spectrum for the different Reynolds numbers and angles of attack studied. With increase in frequency, the power content of the dominant frequency increased while with increase in the angle of attack, its value decreased. The broadband nature of Reynolds number was also observed in the frequency spectra.

The effect of three-dimensionality of the flow was briefly studied by comparing 3D simulation results (wing with end plates) with two-dimensional experimental results. This effect was more clearly visible in to-and-fro wing kinematics, i.e. in Motion B, than in Motion A. Also, the effect became more prominent with increase in angle of attack.

Three-dimensional laminar and eddy resolving simulations using IDDES were performed to study the Motion B at Re = 50,000, $\alpha = 60^{\circ }$. Larger lift and drag force peaks are predicted using IDDES when compared with 2D laminar simulations. Strong and stable leading and trailing edge vortices and a wide range of vortex structures are captured by IDDES compared to 3D laminar simulation. Further, relative comparisons of the order of magnitudes of terms in Reynolds averaged momentum equation indicate that Reynolds stresses are significant at this Reynolds number.