Introduction

Basic statement

Needs assessment proved that one of the vital human needs is access to drinking water. For this reason, human beings have started various works such as digging wells, building dams, aqueducts, and so on. But today, there are many concerns. For example, we have recently seen global warming climate change. The increase in the human population is another cause for concern. But with the advancement of science, the use of new scientific methods to achieve the goal has also increased. Modeling the water quality parameters is one of the fundamental challenges investigated by several studies (Parmar and Bhardwaj 2014; Zhou 2020). One of the crucial human issues is access to drinking water. In this case, AI and LMs, artificial neural networks (ANN), and engineering sciences were tools to help human beings. Due to water scarcity in countries around the world, the study of water resources in different scientific ways has been considered by researchers (Poursaeid et al. 2020; Chang et al. 2021). The following will be reviewed related studies to water resources and their quantitative and qualitative simulations.

Related studies

Today, artificial intelligence methods have been developed for various purposes. In previous research, artificial intelligence techniques have been used for scientific challenges. In addition, several studies have been conducted in the field of water resources and related modeling. In these studies, numerical modeling, analytical modeling, artificial intelligence simulations, etc., have been used. But in this research, we review the articles related to water resources modeling and quantitative and qualitative simulations that have used artificial intelligence.

On the one hand, some studies used ANNs and LMs to model water resources separately. ANNs were applied to simulate water parameters. ANNs such as multi-layer perceptron neural network, backpropagation neural network, Radial basis function neural network, and LMs such as support vector machine, extreme learning machine, and reinforcement learning machine. In mentioned works, the accuracy of ANNs and LMs was compared to similar articles. Finally, the superiority of these models over previous works was confirmed (Gholami et al. 2011; Wu et al. 2014; Yang et al. 2014; Kalteh 2014, 2015; Kheradpisheh et al. 2015; Shahid and Ehteshami 2015; Nema et al. 2017; Manu and Thalla 2017; Wang et al. 2019; Qu et al. 2020; Vijay and Kamaraj 2021; Sada and Ikpeseni 2021; Che Nordin et al. 2021; Sarkar et al. 2021). On the other hand, in some other papers, Optimizer & Heuristic algorithms (OHA) simulated quantitative and qualitative water parameters. OHAs such as genetic algorithm, differential evolution, and particle swarm optimization algorithm implemented to model the water parameters. Specifically, the OHAs proportionally improved the modeling's speed and accuracy in these studies. (Parmar and Bhardwaj 2014; Walker et al. 2015; Guneshwor et al. 2018; Vaheddoost and Aksoy 2018; Elkiran et al. 2019). Besides, other articles combined ANNs & LMs with OHAs to model water parameters. The results showed that hybrid models' simulation, speed, accuracy, and ability were often higher than the original models (Heddam et al. 2019; Zhang et al. 2019, 2021; Majumder and Eldho 2020; Azimi and Azhdary Moghaddam 2020; Poursaeid et al. 2020, 2021).

Contributions

In this paper, quantitative and qualitative groundwater parameters were predicted using LM techniques and mathematical methods. However, there are many articles in this field, but in this study, for the first time in the study area, four AI and mathematical models have been used simultaneously to quantitatively and qualitatively simulate the water of Meghan Wetland located in the Arak plain, Markazi province of Iran. Three models of artificial intelligence SAELM LSSVM, ANFIS, and MLR as a mathematical model, simulated the EC, TDS, GWL, and salinity parameters. It should be noted that there are several parameters in the water resources quality management, including Cl−, EC, TDS, SO42 +, etc. Many researchers have used the most widely used parameters in this field, such as above-mentioned parameters.

The structure of this work in the following sections is as follows: Defining the water quality parameters discussed in the second part. The third part of the article describes materials and methods, including AI models and mathematical models. Moreover, In mentioned section, the characteristics of the study area and the data collection steps are presented. Also, in Sect. 5, the results of the research are discussed. Finally, the general conclusion is summarized in the last section.

Problem statement

In this part, water quality parameters are introduced as follows.

Water quality parameters

This section explains the water quality parameters. Although there are several parameters in this field (Solanki et al. 2015), we have tried to describe the most widely used parameters in this work.

Total dissolved solids (TDS)

Total dissolved solids (TDS) means the numerical sum of solids soluble in water (Jamei et al. 2020). This parameter is measured in milligrams per liter (mgl−1). This parameter includes different types of mineral salts such as soluble bicarbonates (HCO−3), organic matter, magnesium (Mg+2), calcium (Ca+2), sodium (Na+), potassium (K+), chloride (Cl−), sulfate (SO4−2), nitrates (NO−3) (Ahmadianfar et al. 2020).

Salinity

Water salinity is one of the water quality parameters. This parameter is equivalent to salt concentration in water according to the definition. However, some research has defined salinity as the concentration of water-soluble mineral salt in a specific volume or weight per square meter (Sparks 2003). It should be noted that some factors such as increased consumption or high evaporation rate lead to increased salinity (Harris 2009). It should be noted that this parameter is measured in milligrams per liter (mgl−1).

Electrical conductivity (EC)

Electrical conductivity (EC) is one of the quality parameters of water sources and is measured in micro Siemens per centimeter (μScm−1). EC is considered equivalent to the salinity of water (Serrano-Finetti et al. 2019). Because this parameter indicates the number of salts in the water and is equal to the amount of electrical transfer of water, this parameter is an essential factor in drinking water quality and agriculture. However, the amount of ionic salt in water reduces its quality for drinking (Ahmadianfar et al. 2020).

Materials and methods

Study area

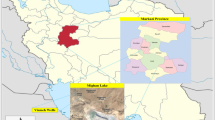
The study area of this research is Meghan Wetland, located in Markazi province in Iran as Fig. 1. According to the statistical results of synoptic stations, the maximum and minimum precipitation varies from 461 mm in the northeast to 208 mm in the center of Arak plain.

Fig. 1
figure 1

Source: Wikimedia and GoogleMap

Meghan wetland.

Full size image

AI models

In the following sections, the AI and MLR models will be explained.

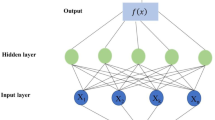
Self Adaptive Extreme Learning Machine (SAELM)

The proposed method in this study is SAELM model. Extreme learning machine was proposed in 2004 by Huang et al. (2004). This model is one of the learning machine types, and in various research, its superiority over other methods (including neural networks and learning machines) has been proved (Huang et al. 2006, 2012). If we have n neurons in the hidden layer, then we can define the single-layer feedforward network of the learning machine based on mathematical relations as follows (Liang et al. 2006; Poursaeid et al. 2020):

$$y_{i} = \sum\limits_{j = 1}^{k} {\beta_{j} g(a_{j} x_{i} + c_{j} )} \, = u_{i} \,\,\,\,,\,\,i = 1,2,3,...,N$$
(1)

So that g, ci, and βi are the transfer function between input and output layers, respectively. The above relation can be rewritten in the form of the following:

$$\begin{gathered} c_{j} = [c_{j1} ,c_{j2} ,...,c_{jn} ]^{T} ,c_{j} \in R,\quad j = 1,2,3,...,k \hfill \\ a_{j} = [a_{j1} ,a_{j2} ,...,a_{jn} ]^{T} ,a_{j} \in R^{t},\quad j = 1,2,3,...,k \hfill \\ \beta_{j} = [\beta_{j1} ,\beta_{j2} ,...,\beta_{jn} ]^{T} ,\beta_{j} \in R^{L},\quad j = 1,2,3,...,k \hfill \\ \end{gathered}$$
(2)
$$\begin{gathered} G\beta = Y \hfill \\ G = \left[ {\begin{array}{*{20}c} {g(x_{1} ;c_{1} ,w_{1} )} & \cdots & {g(x_{1} ;c_{k} ,w_{k} )} \\ \vdots & \ddots & \vdots \\ {g(x_{n} ;c_{1} ,w_{1} )} & \cdots & {g(x_{N} ;c_{k} ,w_{k} )} \\ \end{array} } \right]_{n \times k} \hfill \\ \end{gathered}$$
(3)
$$\beta = (\beta_{1}^{T} ,\beta_{2}^{T} ,...,\beta_{h}^{T} )_{h \times m}^{T}$$
(4)

Finally, the output weights can be calculated using the Moore–Penrose generalized inverse matrix method.

$$\beta = G^{\dag } Y$$
(5)

Least square support vector machine (LSSVM)

LSSVM model is a type of SVMs that can adjust the constant factors of the support vector model with least-square solutions and self-adapting changes. The support vector model was developed by Vapnik (Sapankevych and Sankar 2009). These learning machines operate based on Structural risk minimization. Meanwhile, some other AI methods use the Empirical risk minimization method. (Cristianini and Shawe-Taylor 2000; Dibike et al. 2001). SVM is used in classification problems. In short, an equation is obtained in a Quadratic programming problem in this theory. The fixed parameters of the model are determined, and then with optimization algorithms such as genetic algorithm (GA) or other methods, we can get the optimal values for this equation. The SVM can also be used for regression problems. The mathematical definition of LSSVM is that if xi and yi are the inputs and outputs, then the nonlinear regression function is as follows (Valyon and Horvath 2007):

$$f(x) = \sum\limits_{i = 1}^{n} {w_{i} \varphi_{i} (x) + b =^{{}} } w^{T} .\varphi (x_{i} ) + b$$
(6)

where w is the weight vector, and b is the bias, and φ are nonlinear functions for mapping data into large feature spaces, so:

$$w = \left[ {\begin{array}{*{20}c} {w_{1} } \\ \vdots \\ {w_{n} } \\ \end{array} } \right]\begin{array}{*{20}c} {} & , & {} \\ \end{array} \varphi = \left[ {\begin{array}{*{20}c} {\varphi_{1} } \\ \vdots \\ {\varphi_{n} } \\ \end{array} } \right]$$
(7)

The nonlinear regression problem can be solved by minimizing the following Quadratic programming problem:

$$Min_{w,e,b} \begin{array}{*{20}c} {} & {\left\{ {\lambda (w,e) = \frac{1}{2}w^{T} w + \frac{1}{2}C\sum\limits_{i = 1}^{m} {e_{i}^{2} } } \right\}} \\ \end{array}$$
(8)

where C is the tradeoff variable between two terms of the equation, so:

$$Y_{i} = w^{T} .\varphi (x_{i} ) + b + e_{i}, \begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {\begin{array}{*{20}c} {} & {} & {} \\ \end{array} } & {Y_{i} = y_{i} + \delta } \\ \end{array}_{i}$$
(9)

It should be noted that δi is defined as network noise. Then for each xi, the output is a weighted set of n kernel functions, in which the central variable of the kernel functions is determined using the xi as inputs data. We will have the Lagrangian form of the equation as follows:

$$\psi (w,b,e,\alpha ) = \lambda (w,e) - \sum\limits_{i = 1}^{n} {a_{i} \left( {w^{T} .\varphi (x_{i} ) + b + e_{i} - Y_{i} } \right)}$$
(10)

In Eq. 10, ai are lagrangian multipliers. In the following solution, we solve the problem with a constrained optimization problem. Then we have the optimization with the following conditions as follows:

$$\begin{gathered} \frac{\partial \psi }{{\partial w}} = 0\begin{array}{*{20}c} {} & { \to w = \sum\limits_{i = 1}^{m} {a_{i} \varphi (x_{i} )} } \\ \end{array} \hfill \\ \frac{\partial \psi }{{\partial b}} = 0\begin{array}{*{20}c} {} & { \to \sum\limits_{i = 1}^{m} {a_{i} = 0} } \\ \end{array} \hfill \\ \frac{\partial \psi }{{\partial e_{i} }} = 0\begin{array}{*{20}c} {} & { \to a_{i} = C_{{}} e_{i} ,} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} \\ \end{array} } & {} \\ \end{array} } & {} \\ \end{array}_{{}}^{{}} \begin{array}{*{20}c} {} & {} & {} & {i = 1,2,...,m} \\ \end{array} \hfill \\ \frac{\partial \psi }{{\partial a_{i} }} = 0\begin{array}{*{20}c} {} & { \to w^{T} \varphi (x_{i} ) + b + e_{i} - Y_{i} = 0,} \\ \end{array} \begin{array}{*{20}c} {} & {} & {} & {i = 1,2,...,m} \\ \end{array} \hfill \\ \end{gathered}$$
(11)

And the final solution to the problem is as follows:

$$\begin{gathered} \left[ {\begin{array}{*{20}c} 0 & 1 & 1 & {\begin{array}{*{20}c} \cdots & 1 \\ \end{array} } \\ 1 & {\Phi_{11} + \frac{1}{C}} & {\Phi_{12} } & {\begin{array}{*{20}c} \cdots & {\Phi_{1m} } \\ \end{array} } \\ 1 & {\Phi_{21} } & {\Phi_{12} + \frac{1}{C}} & {\begin{array}{*{20}c} \cdots & {\Phi_{2m} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {\begin{array}{*{20}c} 1 \\ 1 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {\begin{array}{*{20}c} {\Phi_{(m - 1)1} } \\ {\Phi_{m1} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {\begin{array}{*{20}c} {\Phi_{(m - 1)2} } \\ {\Phi_{m2} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \ddots & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdots & {\Phi_{(m - 1)m} } \\ \end{array} } \\ {\begin{array}{*{20}c} \cdots & {\Phi_{mm} + \frac{1}{C}} \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} b \\ {a_{1} } \\ {a_{1} } \\ {\begin{array}{*{20}c} \vdots \\ {a_{m} } \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ {Y_{1} } \\ {Y_{2} } \\ {\begin{array}{*{20}c} \vdots \\ {Y_{m} } \\ \end{array} } \\ \end{array} } \right] \hfill \\ Y = \left[ {Y_{1} ,...,Y_{m} } \right],a = \left[ {a_{1} ,...,a_{m} } \right],1 = \left[ {1,...,1} \right] \hfill \\ \end{gathered}$$
(12)

And in Eq. 12, the Φi,j is the kernel matrix. Also, ϕ(xi,xj) is the kernel functions:

$$\Phi_{i.j} = \phi (x_{i} ,x_{j} )\begin{array}{*{20}c} {} & {\begin{array}{*{20}c} , & {\begin{array}{*{20}c} {} & {\Phi_{i,j} = \varphi^{T} (x_{i} ).\varphi (x_{j} )} \\ \end{array} } \\ \end{array} } \\ \end{array} \begin{array}{*{20}c} {} & {\begin{array}{*{20}c} , & {i,j = 1,...,m} \\ \end{array} } \\ \end{array}$$
(13)

Adaptive neuro-fuzzy inference system (ANFIS)

Adaptive Neuro-Fuzzy Inference System, or ANFIS for short, is a feed neural network that simulates based on fuzzy logic (El-Shafie et al. 2006). In this type of network, two types of inferential systems based on FIS fuzzy logic are used (Tokachichu and Gaddam 2021; Arora and Keshari 2021):

  • A fuzzy inference system-based network, called Mamdani, is known as M-FIS for short.

  • Takagi–Sugeno fuzzy inference system-based network, known as TS-FIS for short.

In these networks, there are at least two inputs I1 and I2, for the network based on TS-FIS fuzzy inference system and two if–then conditional principles for each output Oi and the conditional rules of these fuzzy networks are as follows:

Rule (1): If x is input I1 and output O1, then we have:

$$f_{1} = a_{1} x_{1} + b_{1} y_{1} + \alpha_{1}$$

Rule (2): If x is input I2 and output O2, then we have:

$$f_{2} = a_{2} x_{2} + b_{2} y_{2} + \alpha_{2}$$

Neuro-fuzzy networks are organized of one input layer and the other five layers, which can be a type of multi-layered neural network.

  • Layer 0: Input layer with n Input nodes

  • Layer 1: This layer provides a membership function for points using gaussian rules by fuzzifying each node.

    $$\mu_{Di} (x) = \exp \left\{ { - \left[ {\left( {\frac{{x - h_{i} }}{{\varphi_{i} }}} \right)^{2} } \right]^{{t_{i} }} } \right\}$$
    (14)

    where φi, ti, and hi are adaptive functions in a fuzzy network.

  • Layer 2:all of fuzzified data are passed into operators. Also, Ii and Oi are the membership parameters of the antecedent parameters of rule (1).

    $$w_{i} = \mu_{Di} (x) \times \mu_{Oi} (x)$$
    (15)

  • Layer 3: in this layer, All of the nodes are normalized as below:

    $$\overline{w}_{i} = \frac{{w_{i} }}{{\sum\nolimits_{j = 1}^{m} {w_{j} } }}$$
    (16)

    where the \(\overline{w}_{i}\), in 2nd layer, is the Sum of Operator in the ith order.

  • Layer 4: The corresponding linear function is calculated for each node in this layer. Then the coefficients of the functions are computed using the BNN-error (backpropagation neural network error).

    $$\overline{w}_{i} f_{i} = \overline{w}_{i} (a_{0} x_{0} + a_{1} x_{1} + a_{2} )$$
    (17)

    where ai is the parameter for the input I, also \(\overline{w} i\) as the output parameter of Layer 3.

  • Layer 5: This layer is the sum of the outputs of each node from the 4th layer, which is calculated as follows in Eq. 18:

    $$\sum\limits_{{}}^{{}} {\overline{w}_{i} f_{i} } = \frac{{\sum\limits_{{}}^{{}} {w_{i} f_{i} } }}{{\sum\limits_{{}}^{{}} {w_{i} } }}$$
    (18)

Multiple Linear Regression (MLR)

Multiple linear regression methods are based on statistical and mathematical calculations. These methods can be used to study the relationships between input variables and multi-target variables. The mathematical definition of this model is as follows:

$$f(x_{i} ) = a_{0} + a_{1} x_{1} + a_{2} x_{2} +\cdots + a_{n} x_{n} + \varepsilon$$
(19)

where the f (xi) is a secondary variable, xi ‘s are multiple Primary variables, ai are regression multipliers, and ε is a random error in the equation (Çamdevýren et al. 2005; Asadi et al. 2014).

Data collection and performance indicators

Data analysis

The Input dataset was sampled and collected for 175 months in the study area. This work used the primary dataset of the TDS, salinity, GWL, and EC parameters. After collecting data, the K-Fold cross-validation method was used to randomize the data to improve the accuracy of the models. 70% of the data were used in the training phase, and 30% were assigned for the testing phase.

Performance indicators

In the present study, to evaluate the accuracy of models, the statistical indices: Absolute mean error percent (MAPE), root means square error (RMSE), and coefficient of determination (R2) are used as Eq. 20–22:

$$R^{2} = \frac{{\left( {n\sum\nolimits_{i = 1}^{n} {O_{i} I_{i} - \sum\nolimits_{i = 1}^{n} {O_{i} \sum\nolimits_{i = 1}^{n} {I_{i} } } } } \right)^{2} }}{{\left( {n\sum\nolimits_{i = 1}^{n} {\left( {O_{i} } \right)^{2} - \sum\nolimits_{i = 1}^{n} {\left( {O_{i} } \right)^{2} } } } \right)\left( {n\sum\nolimits_{i = 1}^{n} {\left( {I_{i} } \right)^{2} - \sum\nolimits_{i = 1}^{n} {\left( {I_{i} } \right)^{2} } } } \right)}}$$
(20)
$$RMSE = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {O_{i} - I_{i} } \right)^{2} } }$$
(21)
$$MAPE = \frac{{\sum\nolimits_{i = 1}^{n} {\left| {O_{i} - I_{i} } \right|} }}{n} \times 100$$
(22)

where Ii the input values, Oi output values, \(\overline{I}\) the mean of observational values, and n the number of observational values.

Results and discussions

First, input values were entered for all models. Then EC, TDS, GWL, and Salinity parameters were considered output variables. Moreover, the superior model was selected in each simulation phase for four output variables. Finally, after the simulation, the performance of each model is examined. In this study, models' performance was evaluated by four different methods: performance evaluation with statistical indicators, performance evaluation by uncertainty analysis by Wilson Score Method (WSMUA), performance evaluation with response figures, performance evaluation with discrepancy ratio charts, and error distribution diagrams (Figs. 2 and 3).

Fig. 2
figure 2

Graphical abstract

Full size image
Fig. 3
figure 3

Research flowchart

Full size image

Evaluation indicators

This section investigates the values of evaluation indicators for models performance in the output parameters simulation. In this study, statistical indicators MAPE, RMSE, and R2 have been used for evaluation.

According to Fig. 4 and Table 1, the best model in quantitative and qualitative water simulation were known, and bold fonts show the superior model in each output's simulation. The SAELM in GWL and EC modeling, the LSSVM model in TDS simulation, and the MLR in salinity simulation were determined as the best models and presented the most accurate results.

Fig. 4
figure 4

Models performance indices: MAPE R2

Full size image
Table 1 Models evaluation indices
Full size table

Wilson score method uncertainty analysis (WSMUA)

After simulation, to investigate the prediction error, the amount of uncertainty of models can be calculated, and the performance of models can be evaluated in estimating the targets. The present study performed uncertainty analysis by the WSMUA (Poursaeid et al. 2020; Bonakdari et al. 2020).

Computational parameters in this analysis are prediction error (∆i), mean error (Mean), and standard deviation of error values (Std), each of which is calculated according to Eq. 23–25. The results of the uncertainty analysis with a width of uncertainty band that denoted by the (WUB), with 95% confidence bound (PEI 95%) was calculated. Also, based on the (Mean) values, if its sign is positive, the model will have an overestimation performance. If its mean error is negative, the model will have an underestimation performance.

$$\Delta_{i} = O_{i} - I_{i}$$
(23)
$${\text{Mean}} = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {\Delta_{i} }$$
(24)
$${\text{Std}} = \sqrt {\sum\nolimits_{i = 1}^{n} {\left( {\Delta_{i} - {\text{Mean}}} \right)^{2} /(n - 1)} }$$
(25)

In the above equations, Ii is the input values, Oi is the output values, and n is the number of observational samples. The results of the uncertainty analysis are shown in Table 2.

Table 2 Models uncertainty analysis
Full size table

According to Table 2 results, the SAELM is the superior model in GWL simulation and had the Underestimation performance. The performance of other models was Overestimation, and the SAELM model was the most accurate with the minimum of average error equal to 0.0128.

Response and correlation figures

The models' output was illustrated and presented as response plots in this section. In addition, correlation plots also are displayed.

The proposed model had excellent performance in GWL simulation. Moreover, this model was more accurate than over models for simulating the EC parameters. The SAELM had the most accurate plots with the best correlation between observed_predicted values based on Fig. 5 diagrams (Figs. 6, 7, 8 and 9).

Fig. 5
figure 5

Model performance in GWL simulation

Full size image
Fig. 6
figure 6

Model performance in TDS simulation

Full size image
Fig. 7
figure 7

Model performance in EC simulation

Full size image
Fig. 8
figure 8

Model performance in salinity simulation

Full size image
Fig. 9
figure 9

Discrepancy ratio chart

Full size image

Discrepancy ratio and error distribution

According to the mathematical definition of Discrepancy Ratio (DR) written in Eq. 26, according to this definition, the closeness of DR values to a horizontal line (DR = 1) shows the high accuracy of the simulation.

$${\text{DR}} = \left[ {\frac{{{\text{Value}}_{{{\text{predicted}}}} }}{{{\text{Value}}_{{{\text{observed}}}} }}} \right]$$
(26)

The diagram of the DR shows the high accuracy of the SAELM and the MLR models. The closeness of DR values for SAELM and MLR models to the DR line (DR = 1) shows the high accuracy of the mentioned models in GWL and salinity simulation. Additionally, Error percent is defined as Eq. 27.

$${\text{Error}}\,{\text{Percent}} = \left| {\frac{{{\text{predicted}} - {\text{observed}}}}{{{\text{observed}}}}} \right| \times 100$$
(27)

According to the prediction results error in Fig. 10, The SAELM and MLR model has the most Error-percent (100%) in the range of less than 1%. Meanwhile, the LSSVM has the best accuracy in prediction in the next rank. The SAELM in EC simulation had the worst performance with the most error percent in the range of greater than 2%.

Fig. 10
figure 10

Error percent distribution of models

Full size image

Conclusions

This study collected sampling data related to 175 months for groundwater of Meghan Wetland located in Arak plain in Markazi province in Iran. The primary parameters of this study were sampling (t), (TDS), (EC), (Cl), (Salinity), and (GWL). Then, using three AI models and a mathematical model, water parameters modeling was performed. The proposed method in this article was the SAELM model. Other models are LSSVM, ANFIS, and the mathematical model is MLR. After analyzing the results, the performance of the models was evaluated with five approaches: Based on statistical indicators, the best results were recorded for models SAELMGWL simulation and MLRsalinity, with the lowest value of RMSE and MAPE. Additionally, the mentioned models had the closest R2 values to 1.

Based on the response & correlation plots, the best performance was assigned to the SAELMGWL model with better mapping of simulated values than observed values. Based on the results of the WSMUA, the SAELMGWL model with a minimum mean error value equal to 0.0128 was the best and most accurate model. According to the DR diagram, the SAELMGWL and MLRsalinity models had the highest concentration of output points near the DR = 1 line. Also, based on the error distribution percentage diagram, the best forecast accuracy was assigned to SAELMGWL and MLRsalinity models with the lowest error percent in the range of less than 1%.