Estimation of total dissolved solids, electrical conductivity, salinity and groundwater levels using novel learning machines

Abstract

In this study, the groundwater parameters including electrical conductivity (EC), salinity, total dissolved solids (TDS) and groundwater level (GWL) for a 15-year time series (from 2002 to 2017) of the Mighan Plain, located in Markazi Province, Iran, were simulated using a hybrid meta heuristic artificial intelligence (AI) model called “wavelet self-adaptive extreme learning machine” (WSAELM) for the first time. Initially, the detection of the most significant lags of the time-series data was conducted using the autocorrelation function (ACF) and the partial autocorrelation function (PACF) analyses. By using these lags, four WSAELM models were defined and then the superior models in simulating the TDS, EC, salinity and GWL were introduced. The values of the determination coefficient (R²), Variance Accounted for (VAF) and the Nash–Sutcliffe efficiency coefficient (NSC) for the superior model simulating salinity were computed to be 0.991, 98.124 and 0.980, respectively. Also, approximately 44% of the TDS values modeled by the best model had an error less than 10%, while roughly a third of the TDS values estimated by the model had an error more than 15%. The findings indicated that the proposed hybrid model underestimated the GWL parameter, while it performed in an overestimate way for other parameters. The results of the uncertainty analysis showed the low width of uncertainty for GWL (WUB = ± 0.798), TDS (WUB = ± 5.035), EC (WUB = ± 6.425) and salinity (WUB = ± 66.650).

Introduction

Due to climate change and global warming, different parts of Earth, especially arid and semi-arid regions have been faced by serious challenges for supplying fresh water for various purposes such as urban, industrial and agricultural consumptions. Iran, located in the Southeast Asia region has a semi-arid climate, thus has experienced many problems for supplying drinking water demands in recent years. In this country, the major part of fresh water is supplied from water tables. In recent years, due to excessive withdrawals of water from different aquifers, hazardous problems such as the groundwater scarcity, the formation of sinkholes, salinization of water tables, drying of lakes have raised (Barzegar and Moghaddam 2016; Malekzadeh et al. 2019a). Therefore, investigations of qualitative and quantitative characteristics of aquifers in these regions are enormously important. The calibration of common approaches requires a large number of variables which each of them has errors (i.e. measurement error) and may lead to increase cumulative error. Therefore, the use of artificial intelligence-based approaches such as neural networks that are well-known for predicting complex nonlinear problems can be served as alternatives to existing approaches. Given the generalizability of artificial intelligence-based methods, the use of these methods in practical tasks is reasonable. Furthermore, thanks to high accuracy in modeling as well as saving time, the application of artificial intelligence (AI) techniques is increasingly developing. In comparison to field studies or three-dimensional simulations, AI approaches are considered as time saving, efficient and accurate tools simulating and estimating complex phenomena like groundwater parameters.

Related works

Many researchers have studied groundwater level (GWL) fluctuations as one of the most important quantitative parameters of groundwater systems. Salinity has also been taken into account as a groundwater qualitative parameter. Waters containing chloride ions are categorized as saline. Electrical conductivity (EC) is another groundwater qualitative parameter whose change negatively affects the quality of drinking water and even waters used for agricultural purposes. Further, total dissolved solids (TDS) are an index of the dissolved combined content of all inorganic and organic substances existing in water. This parameter is introduced as an important index of freshwater used for urban demands. Due to the important of the aforementioned variables, many studies had been done on the prediction of GWL (Kholghi and Hosseini, 2009; Chen et al. 2009; Emamgholizadeh et al. 2014; Nourani et al. 2016), Salinity (Alagha et al. 2017), EC (Orouji et al. 2013; Khashei-Siuki and Sarbazi 2015; Jalalkamali 2015) and TDS (Demirdag et al. 2000; Asadollahfardi et al. 2011; Ghavidel and Montaseri 2014; Gholami et al. 2017).

Zhang et al. (2017) employed the radial basis function network (RBF) and ANFIS to predict the water table variations in the city of Jilin, China for a 10-year period from 2000 to 2009. Moreover, Liu et al. (2018) by combining the empirical mode decomposition (EMD), particle swarm optimization (PSO), phase space reconstruction (PSR) and extreme learning machine (ELM) models, developed some hybrid methods estimating GWL fluctuations. They indicated that the EMD and PSO models significantly increased the accuracy of the ELM model.

In addition, Barzegar and Moghaddam (2016) simulated the salinity values of the aquifers in the vicinity of Tabriz, Iran by means of different artificial intelligence techniques such as the multi-layer perceptron neural network (MLP), the generalized regression neural network (GRNN) and the radial basis function neural network (RBFNN). They developed the committee neural network (CNN) through the optimization of the artificial intelligence network and stated that the CNN model approximates objective function values with higher accuracy. Furthermore, Roy and Datta (2017) simulated saltwater intrusion towards a multi-layer aquifer using the ANN. They also used the genetic algorithm to optimize the ANFIS network and indicated that this algorithm markedly increases the modeling accuracy.

In recent years, many researchers modeled EC values in groundwater systems using artificial intelligence methods. Nozari and Azadi (2017) measured EC values in drainage water and aquifers through an experimental study. The ANN results proved that the numerical model is in good agreement with the observed values. It is worth mentioning that Azad et al. (2018) used the ANFIS network by three optimization algorithms including the Genetic Algorithm, the Ant Colony Optimization for Continuous Domains and the Differential Evolution for estimating EC. They expressed that the Differential Evolution algorithm simulates EC values with higher accuracy.

Aryafar et al. (2019) simulated a number of hydro-chemical parameters such as TDS in an aquifer located in the east of Iran using the GP, the ANN and ANFIS. They compared the results obtained from the numerical models and concluded that the GP approximates objective function values with higher accuracy.

Research objective

Owing to importance of groundwater in the country of Iran, the groundwater qualitative and quantitative parameters have been investigated by many researches (Barzegar and Moghaddam 2016; Malekzadeh et al. 2019a). It is worth noted that the Mighan Plain is considered as one of the most important regions in the central part of Iran, where the groundwater sources has been undergone a serious reduction.

On the other hand, artificial intelligence (AI) techniques have been broadly used in modeling the groundwater parameters in different areas of Iran due to high flexibility, good precision and time and cost savings of these technological advancements (Nourani et al. 2016; Malekzadeh et al. 2019b).

Regarding the literature, there is no AI study to estimate the groundwater parameters in the Mighan Plain by using a hybrid meta-heuristic model.

Therefore, in this study, the capability of a hybrid meta-heuristic AI model named “wavelet self-adaptive extreme learning machine” is used to simulate the time series data of total dissolved solids (TDS), electrical conductivity (EC), salinity and groundwater level (GWL) of the Mighan Plain located in Markazi Province, Iran for the first. More details are presented in the coming sections.

Materials and methods

Case study

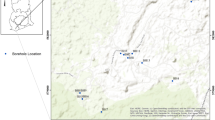
The study area is the Arak Plan with an area of 5520 km² located in the Mighan Desert basin lying between longitude 49°29′ to 50 degrees and 18′ E and latitude 32°48′ to 34°44′ N. According to the results obtained in the stations located in the study area, the highest rainfall is related to the Alraj station with a mean annual of 461 mm in the northeast of the basin and the lowest rainfall in the Davodabad station with a mean annual of 208 mm in the center of the plain. In Fig. 1, the geographical situation of the study area, Mighan Lake and the observational well (Veysameh) are illustrated. The groundwater qualitative parameters and also the quantitative monthly parameters for a 15-year time series from 2002 to 2017 of the Mighan Plain, Iran are applied. Additionally, the maximum, minimum, mean, standard deviation and variance values of the Veysameh well are given in Table 1.

Fig. 1

Geographical location of case study

Table 1 Monthly statistical indices of each parameter

Extreme learning machine

The ELM is a fast convergence, gradient-free technique used for modeling complex nonlinear problems as well as time varying systems (Wang et al. 2016; Huang et al. 2004, 2006; Miche et al. 2010; Cao et al. 2012; Tang et al. 2016). For a set with N multi-inputs/single-output data pairs $\{ (x_{i} ,t_{i} )_{i = 1}^{N} ;\,x_{i} \in R^{d} \,{\text{and}}\,t_{i} \in R^{m} \}$, the ELM algorithm randomly chooses hidden layer biases and input weights. In addition, in this method, output weights are analytically computed through the model learning process by very simple matrix calculations. According to the structure defined for the ELM, it can be concluded that this method has high learning speed and is more accurate than single layer feed forward neural network (SLFFNN) learning algorithms such as back propagation (BP) (Huang et al. 2006). A SLFFNN is defined as follows:

$$ y_{i} = \sum\limits_{j = 1}^{L} {\beta_{j} g(a_{j} x_{i} + b_{j} ) = t_{i} \,\,\,,i = 1,2,3, \ldots ,N} , $$

(1)

where $b_{j} = [b_{j1} ,b_{j2} , \ldots ,b_{jn} ]^{T} \in R\,\,(j = 1,2, \ldots ,L)$ and $a_{j} = [a_{j1} ,a_{j2} , \ldots ,a_{jn} ]^{T} \in R^{d} \,\,(j = 1,2, \ldots ,L)$ are the learning parameters related to the jth hidden node, $\beta_{j} = [\beta_{j1} ,\beta_{j2} , \ldots ,\beta_{jn} ]^{T} \in R^{m} \,\,\,(j = 1,2, \ldots ,L)$ is the output weigh linking the output node to the hidden node and g() is the activation function. Equation (1) can be rewritten in a matrix form as follows (Huang et al. 2006):

$$ H \cdot \beta = T, $$

(2)

where H is the hidden layer matrix, T is the target matrix, β is the output weight matrix and H is calculated as follows:

$$ H = \left[ {\begin{array}{*{20}c} {g(a_{1} .x_{1} + b_{1} )} & \cdots & {g(a_{L} .x_{1} + b_{L} )} \\ \vdots & \ddots & \vdots \\ {g(a_{1} .x_{N} + b_{1} )} & \cdots & {g(a_{L} .x_{N} + b_{L} )} \\ \end{array} } \right], $$

(3)

where jth is an array of the matrix H representing the output vector. It is related to the jth hidden neuron according to x_i which selects the matrix H parameters and meets the parameters a^*_j, b^*_j and β^*_j, so (Huang et al. 2006):

$$ \left\| {H(a_{1}^{*} ,a_{2}^{*} , \ldots ,a_{L}^{*} ,b_{1}^{*} ,b_{2}^{*} , \ldots ,b_{L}^{*} )\beta^{*} - T} \right\| = \min_{\beta } \left\| {H(a_{1}^{{}} ,a_{2}^{{}} , \ldots ,a_{L}^{{}} ,b_{1}^{{}} ,b_{2}^{{}} , \ldots ,b_{L}^{{}} )\beta^{{}} - T} \right\|. $$

(4)

Consequently, the cost function in the ELM tool is mathematically presented as follows (Mahmoud et al. 2018):

$$ {\text{Cos}} t = \sum\limits_{i = 1}^{N} {\left( {\sum\limits_{j = 1}^{L} {\left( {\beta_{j} g()a_{j} .x_{i} + b_{j} } \right) - t_{i} } } \right)}^{2} . $$

(5)

Solving Eq. (2) by means of the least square method leads to the calculation of the output matrix (β) as follows:

$$ \beta = H^{ + } T. $$

(6)

Here H⁺ is the Moore–Penrose (MP) generalized inverse of the matrix H (Moore 1920). To calculated H⁺, the singular value decomposition is employed (Huang et al. 2006).

Self-adaptive extreme learning machine

The differential evolution (DE) algorithm which is a population-based evolutionary algorithm is used to optimize the objective function $f(\theta )\,(\theta \in R^{D} )$. This algorithm considers N_p vectors related to individual parameters for achieving the global minimum during learning and producing G generations until reaching the desired convergence level in a given problem (Man et al. 1996; Liu et al. 2009; Pacifico and Ludermir 2013; Zhang et al. 2015). For a D dimension problem with N_p population, the i^th candidature parameter (θ_i,G) is defined as follows:

$$ \theta_{i,G} = [\theta_{i,G}^{1} ,\theta_{i,G}^{2} , \ldots ,\theta_{i,G}^{D} ]\,\,\,\,\,i = 1,2, \ldots ,N_{p} . $$

(7)

Here D is the dimension of the search space.

The DE procedure in the ELM optimization is expressed as follows:

Step 1. Initialization

In this step, the cover parameter states are initialized by defining the minimum and maximum bonds (θ_min, θ_max, respectively) as follows:

$$ \theta_{i,G} = \theta_{\min } + r\;{\text{and}}\;(0,1) \cdot (\theta_{\max } - \theta_{\min } ). $$

(8)

Step 2: Mutation

In this step, different vectors produced in the provided random population are chosen and the mutated vector is generated. Generally, there are six different strategies used in today's studies to define the mutated vector whose selections depend on the structure and the type of the problem (Qin et al. 2009; Islam et al. 2012; Han et al. 2013; Mohamed and Almazyed 2017; Ebtehaj and Bonakdari 2017; Gholami et al. 2018). The strategies defined to produce the mutated vector are expressed as follows:

Strategy I:

$$v_{i,G} = \theta_{{r_{1} ,G}}^{i} + F \cdot (\theta_{{r_{2} ,G}}^{i} - \theta_{{r_{3} ,G}}^{i} )$$

(9)

Strategy II:

$$v_{i,G} = \,\theta_{{r_{1} ,G}}^{i} + F \cdot (\theta_{{{\text{best}},G}}^{{}} - \theta_{{r_{1} ,G}}^{i} ) + F \cdot (\theta_{{r_{2} ,G}}^{i} - \theta_{{r_{3} ,G}}^{i} ) + F \cdot (\theta_{{r_{4} ,G}}^{i} - \theta_{{r_{5} ,G}}^{i} )$$

(10)

Strategy III:

$$v_{i,G} = \theta_{{r_{1} ,G}}^{i} + F \cdot (\theta_{{r_{2} ,G}}^{i} - \theta_{{r_{3} ,G}}^{i} ) + F \cdot (\theta_{{r_{4} ,G}}^{i} - \theta_{{r_{5} ,G}}^{i} )$$

(11)

Strategy IV:

$$v_{i,G} = \theta_{{r_{1} ,G}}^{i} + K \cdot (\theta_{{r_{1} t,G}}^{i} - \theta_{i,G}^{{}} ) + F \cdot (\theta_{{r_{2} ,G}}^{i} - \theta_{{r_{3} ,G}}^{i} )$$

(12)

Strategy V:

$$v_{i,G} = \theta_{{{\text{best}},G}}^{{}} + F \cdot (\theta_{{r_{1} ,G}}^{i} - \theta_{{r_{2} ,G}}^{i} )$$

(13)

Strategy VI:

$$v_{i,G} = \theta_{{{\text{best}},G}}^{{}} + F \cdot (\theta_{{r_{1} ,G}}^{i} - \theta_{{r_{2} ,G}}^{i} ) + F \cdot (\theta_{{r_{3} ,G}}^{i} - \theta_{{r_{4} ,G}}^{i} ),$$

(14)

where $r_{1}^{i} ,r_{2}^{i} ,r_{3}^{i} ,r_{4}^{i} ,r_{5}^{i}$ are random exclusive integer values in the range of [1, N_p], F is the mutation factor involved to control difference vectors scaling. K is the control parameter defined in the range of [0, 1].

Step 3: Crossover

The crossover operator is used during this stage. The reason for using this operator is to increase the diversity of vectors stimulated by mutation. According to the mutated vector v_i,G = [ v_i,G¹, v_i,G,² …, v_i,G^D] and the trial vector as u_i,G = [u_i,G¹, u_i,G,² …, u_i,G^D, the crossover operator for G different generations is defined as follows:

$$ u_{i,G}^{j} = \left\{ {\begin{array}{*{20}l} {v_{i,G}^{j} } & {{\text{if}}\,({\text{rand}}\,j\, \le {\text{CR}})\,{\text{or}}\,(j = j_{{{\text{rand}}}} )} \\ {\theta_{i,G}^{j} } & {{\text{Otherwise}}} \\ \end{array} } \right., $$

(15)

where CR is the crossover factor. This parameter is defined to control the fraction of values of copied parameters in the new generation using the mutated vector. The value of this parameter is usually considered in the domain [0, 1]. j_rand is an integer random number defined in the domain [0, 1], and the parameter rand j is equal to the evaluation of jth random parameters generated in the domain [0, 1].

Step 4: Selection

Using the fitness function defined for each target and the corresponding trial vector, the selection procedure is done so that each one with values smaller than the fitness function is transferred to the next generation as the population. Subsequently, step2 through step4 continue with the maximum specific iterations until reaching the desired target. To overcome the restrictions raised by the strategy selection, the trial vector production and the determination of control parameter values, the self-adaptive DE method is utilized under the name of "SAELM" in this research to optimize the ELM method. In the SAELM, the DE algorithm parameters as well as the strategies for producing the trial vector are determined as self-adaptive. Using the initial definition of the hidden layer matrix as follows, the ELM optimization using self-adaptive DE is expressed as follows under the name of "SAELM":

$$ \theta_{k,G} = g(a_{1,(k,G)}^{T} ,a_{2,(k,G)}^{T} \ldots ,a_{L,(k,G)}^{T} ,b_{1,(k,G)}^{T} ,b_{2,(k,G)}^{T} \ldots ,b_{L,(k,G)}^{T} ), $$

(16)

where j is a random value generated through the training process (j = 1, 2, …, L), G is the generation number and k is the population number (k = 1, 2, …, N_p). The output matrix optimized by self-adaptive through the SAELM modeling is defined as follows:

$$ \beta_{k,G} = H_{k,G}^{ + } T $$

(17)

$$ {\text{RMSE}}_{k,G} = \sqrt {\frac{{\sum\limits_{i = 1}^{N} {\left\| {\sum\limits_{j = 1}^{L} {\beta_{j} g(a_{j,(k,G)} \cdot x_{i} + b_{j,(k,G)} ) - t_{i} } } \right\|} }}{m.N}} , $$

(18)

where

$$ \theta_{k,G + 1} = \left\{ {\begin{array}{*{20}l} {u_{k,G + 1} } \\ {u_{k,G + 1} } \\ {\theta_{k,G} } \\ \end{array} \begin{array}{*{20}c} {{\text{if}}\,{\text{RMSE}}_{{\theta_{k,G} }} - {\text{RMSE}}_{{u_{k,G} + 1}} > \varepsilon \cdot {\text{RMSE}}_{{\theta_{{k,G^{/} }} }} } \\ {\,\,{\text{if}}\,\left| {{\text{RMSE}}_{{\theta_{k,G} }} - {\text{RMSE}}_{{u_{k,G} + 1}} } \right| < \varepsilon \cdot {\text{RMSE}}_{{\theta_{k,G} }} \,\,\,\,\,{\text{and}}\;\left\| {\beta_{{u_{k,G} + 1}} } \right\|M < \left\| {\beta_{{\theta_{k,G} }} } \right\|\,} \\ {{\text{Otherwise}}} \\ \end{array} } \right. $$

(19)

$$ H_{k,G} = \left[ {\begin{array}{*{20}c} {g(a_{1,(k,G)} \cdot x_{1} + b_{1,(k,G)} )} & \cdots & {g(a_{L,(k,G)} \cdot x_{1} + b_{L,(k,G)} )} \\ \vdots & \ddots & \vdots \\ {g(a_{1,(k,G)} \cdot x_{N} + b_{1,(k,G)} )} & \cdots & {g(a_{L,(k,G)} \cdot x_{N} + b_{L,(k,G)} )} \\ \end{array} } \right]. $$

(20)

All trail vectors (u_k,G+1) produced at the (G + 1)th generation are assessed by the RMSE index (Eq. 18) with the tolerance ε.

Wavelet transform

The Fourier transform provides the function f(x) as infinite sin (ax) and cos (ax). Despite the good ability of the Fourier transform in analyzing signals, this transform has two disadvantages: first, the basic Fourier functions (sin and cos) are not suitable for displaying complex signals and second, this transform removes the time parameter.

Similar to the Fourier transform, the wavelet transform (Grossmann and Morlet 1984) deals with the extension of functions, but this extension is written in terms of wavelet functions. Wavelet is a finite range with a mean of zero, while Fourier is a sinusoidal function extending from − ∞ to + ∞. On the other hand, the sinusoidal curve in Fourier is a predictable soft curve, while wavelets do not follow a certain rule.

The sinusoidal wave is localized in terms of the number and frequency but not in time, while wavelet is localized in terms of both frequency and time. Wavelet transform is capable of considering different features of a time series such as breakdown points, discontinuities and trends (Adamowski and Sun 2010; Singh 2012). Therefore, a transform which decomposes the process into a few horizons makes it different in repetitive periods, oscillating classes and groups, mutation structures and general and local characteristics of the dynamics of the process. Wavelets are mathematical functions dividing data into frequency components and study each component according to its corresponding display. Wavelets have gender. The father wavelet is often represented by ϕ and the mother wavelet by the $\psi$ symbol, as follows:

$$ \phi_{j,k} (t) = S^{{ - \frac{j}{2}}} \phi \left( {\frac{{t - S^{j} k}}{{S^{j} }}} \right) $$

(21)

$$ \psi_{j,k} (t) = S^{{ - \frac{j}{2}}} \psi \left( {\frac{{t - S^{j} k}}{{S^{j} }}} \right). $$

(22)

As can be seen, the scale parameter (S) distinguishes the role of the wavelet analysis from the Fourier analysis. The j alternation alters the range of vision and can change the analysis from global to local and vice versa. The father wavelet has an integral equal to one, while the mother wavelet integral equals zero. The father wavelet represents the smooth section of the signal trend (low frequency), while the mother wavelet indicates partial sections (high frequency). The wavelet transform of a function like f can be displayed by the following equation:

$$ W_{\psi } f(j,k) = 2^{{ - \frac{j}{2}}} \int\limits_{ - \infty }^{ + \infty } {f(t)\psi \left( {2^{{ - \frac{j}{2}}} t - k} \right){\text{d}}t} . $$

(23)

Now, we can establish a relationship between time series and the wavelet display. Each time series like y(y) is expressed as follows:

$$ y(t) = \sum\limits_{k} {S_{j,k} \phi_{j,k} (t) + } \sum\limits_{k} {d_{j,k} \psi_{j,k} (t) + } \sum\limits_{k} {d_{j - 1,k} \psi_{j - 1,k} (t) + } \cdots + \sum\limits_{k} {d_{1,k} \psi_{1,k} (t)} $$

(24)

In these expressions, j = 1, 2, …, J and J represents the maximum desired scale.

In fact, in the wavelet transform, as the Fourier transform, a function or time series is expressed as a set of sentences with the basic wavelet functions, except that the wavelet functions are not like sin and cos and include the scale parameter.

Combination of wavelet transform with SAELM (WSAELM)

Unlike regular sampling data, time-series data are ordered. Thus, there is extra information about a dataset sample that can take advantage of the wavelet transform if there are meaningful temporal patterns. The autocorrelation function (ACF) is one of the devices utilized to recognize patterns in datasets. Particularly, the ACF express the correlation between separated values adopting different time lags. Therefore, regarding how many time steps might be separated, the ACF shows how the values correlate with each other. In order to model the ELM and SAELM models by the wavelet transform, first, data must be divided into various categories. At the beginning, the model input requires to be identified. To this end, the autocorrelation function (ACF) is employed in this study. The ACF diagram related to the training data used in this paper is illustrated in Fig. 2. Based on the diagrams provided in this figure, the trend is clearly observed, thus should be detrended prior to modeling. In fact, the ACF presented for GWL belongs to the detrended data. Unlike GWL, the trend is not seen in other series, thus the drawn ACF belongs to the main data. According to the ACF diagrams and the confidence bonds drawn for each variable, the effective lags related to each of these variables are considered as different models as follows. It should be noted that for learning the artificial intelligence methods, 132 months are taken into account as the training data and the rest (43 months) as the test data.

Fig. 2

ACF diagram for all time series

Salinity, EC, TDS

$$ \begin{gathered} {\text{Model }}\,{\text{l}}:\,\,\,\,\,{\text{TS}}(t) = f({\text{TS}}(t - 1)) \hfill \\ {\text{Model 2}}:\,\,\,\,\,{\text{TS}}(t) = f({\text{TS}}(t - 1),\,{\text{TS}}(t - 2)) \hfill \\ {\text{Model 3}}:\,\,\,\,\,{\text{TS}}(t) = f({\text{TS}}(t - 1),\,{\text{TS}}(t - 2),\,{\text{TS}}(t - 3)) \hfill \\ {\text{Model 4}}:\,\,\,\,\,{\text{TS}}(t) = f({\text{TS}}(t - 1),\,{\text{TS}}(t - 2),\,{\text{TS}}(t - 3),\,{\text{TS}}(t - 4)) \hfill \\ \end{gathered} $$

GWL

$$ \begin{gathered} {\text{Model 1}}:\,\,\,\,\,{\text{GWL}}(t) = f({\text{GWL}}(t - 1)) \hfill \\ {\text{Model 2}}:\,\,\,\,\,{\text{GWL}}(t) = f({\text{GWL}}(t - 1),{\text{GWL}}(t - 12)) \hfill \\ {\text{Model 3}}:\,\,\,\,\,{\text{GWL}}(t) = f({\text{GWL}}(t - 1),\,{\text{GWL}}(t - 2),\,\,{\text{GWL}}(t - 12)) \hfill \\ {\text{Model 4}}:\,\,\,\,\,{\text{GWL}}(t) = f({\text{GWL}}(t - 1),\,{\text{GWL}}(t - 2),\,{\text{GWL}}(t - 3),\,{\text{GWL}}(t - 12)) \hfill \\ \end{gathered} $$

After selecting the learning data and defining different models, there are two basic steps prior to the analysis including the determination of the wavelet function and the decomposition level. These two steps are crucially important in implementing the wavelet transforms. Of the significant and basic notes in selecting the mother wavelet is the nature of the phenomenon occurrence and the type of its time series. Therefore, the patterns of mother wavelet functions which can fit well in terms of the geometric shape over the time series, perform better in mapping operations and subsequently yield better results. The mother wavelet functions used in this study are Coiflets (Coif) chosen among different wavelet functions through numerous trial and error attempts.

Furthermore, in order to determine the decomposition level, the following formula (Malekzadeh et al. 2019a) is used:

$$ DL = {\text{int}} \left[ {\log \left( n \right)} \right], $$

(25)

where int denotes integer parts of the decomposition level, n is the number of training samples and DL is the decomposition level. The wavelet transform process for a mother wavelet with two decomposition levels is depicted in Fig. 3. Also, a flowchart for the current study is provided in Fig. 4.

Fig. 3

Discrete process of a time series using desired mother wavelet by two-level wavelet transforms

Fig. 4

Flowchart for current study

Goodness of fit

In this study, in order to evaluate the accuracy of the numerical models, the determination coefficient (R²), Variance Accounted For (VAF), Root Mean Squared Error (RMSE), and the Nash–Sutcliffe efficiency coefficient (NSC) are used:

$$ R^{2} = \frac{{\left( {n\sum\nolimits_{i = 1}^{n} {P_{i} O_{i} - \sum\nolimits_{i = 1}^{n} {P_{i} \sum\nolimits_{i = 1}^{n} {O_{i} } } } } \right)^{2} }}{{\left( {n\sum\nolimits_{i = 1}^{n} {\left( {P_{i} } \right)^{2} - \sum\nolimits_{i = 1}^{n} {\left( {P_{i} } \right)^{2} } } } \right)\left( {n\sum\nolimits_{i = 1}^{n} {\left( {O_{i} } \right)^{2} - \sum\nolimits_{i = 1}^{n} {\left( {O_{i} } \right)^{2} } } } \right)}} $$

(26)

$$ {\text{VAF}}(\% ) = \left( {1 - \frac{{{\text{var}}\left( {P_{i} - O_{i} } \right)}}{{{\text{var}}\left( {P_{i} } \right)}}} \right) $$

(27)

$$ {\text{RMSE}} = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {P_{i} - O_{i} } \right)^{2} } } $$

(28)

$$ {\text{NSC}} = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {\left( {O_{i} - P_{i} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{n} {\left( {O_{i} - \overline{O} } \right)^{2} } }}, $$

(29)

where $O_{i}$,$P_{i}$, $\overline{O}$ and $n$ denote observational values, values simulated by the numerical models, the average of observational values and the number of observational values, respectively.

In the following, the accuracy of the ELM, SAELM, WELM and WSAELM numerical models for estimating the values of TDS, EC, salinity and GWL in the test mode is examined. In addition, the most effective lags and the superior models are introduced. Then, the results obtained from the superior models are analyzed. Furthermore, an uncertainty analysis is conducted for these models.

Results and discussion

Total dissolved solids (TDS)

In this section, the evaluation of the artificial intelligence based techniques in estimating TDS is assessed. The results of the statistical indices for the ELM, SAELM, WELM and WSAELM models are shown in Fig. 4. In addition, the scatter plots for all artificial intelligence methods are drawn in Fig. 5. The ELM1, SAELM1, WELM1 and WSAELM1 models (Model 1, see Fig. 2) estimate the TDS values in terms of (t-1).

Fig. 5

Results of statistical indices for simulating TDS by different models

Among all models estimating the objective function value in terms of (t-1), the WSAELM1 model has the highest correlation with the observational data. For this model, the values of R2, RMSE and NSC are obtained 0.985, 32.554 and 0.970, respectively. In addition, VAF is computed for this model equal to 97.039. Moreover, the ELM2, SAELM2, WELM2 and WSAELM2 models (Model 2, see Fig. 2) approximate the objective function values in terms of the lags (t-1) and (t-2). According to the modeling results, among all models with two inputs, the WSAELM2 models the TDS values with higher accuracy. For example, the values of VAF and NSC for this model are calculated 98.750 and 0.987, respectively. In addition, using the lags (t-1), (t-2) and (t-3) the TDS values are calculated 98.750, 0.987 and 16.305, respectively. Also, using the lags (t-1), (t-2) and (t-3) the TDS values are forecasted by means of the ELM3, SAELM3 and WELM3 models (Model 3, see Fig. 2). Among these models, the WSAELM3 model estimates the TDS values with higher accuracy and the minimum error. In other words, the values of R², RMSE and NSC for WSAELM3 are calculated 0.996, 17.140 and 0.992, respectively. Additionally, the ELM4, SAELM4, WELM4 and WSAELM4 models (Model 4, see Fig. 2) simulate the objective function values using the lags (t-1), (t-2), (t-3) and (t-4). Analyzing the modeling results indicates that the WSAELM4 model estimates the TDS values with the highest correlation (R2 = 0.996) and the lowest error (RMSE = 16.174). Furthermore, for this model, the values of VAF and NSC are obtained 99.267 and 0.993, respectively. Thus, according to the TDS modeling by the artificial intelligence methods, the WSAELM4 model is detected as the superior model. In addition, the lags (t-1), (t-2), (t-3) and (t-4) are the most effective lags for simulating TDS by these models.

Electrical conductivity (EC)

In this section, the results of the EC modeling by different artificial intelligence methods are evaluated. In Fig. 6, the results obtained from statistical indices are shown for the ELM, SAELM, WELM and WSAELM models. Also, the scatter plots for all models are illustrated in Fig. 7. Among all artificial intelligence methods simulating EC using the lag (t-1), the WSAELM1 estimates this parameter with a reasonable accuracy. For example, R², RMSE and VAF for this model are obtained 0.980, 51.061 and 95.838, respectively. Moreover, the value of NSC for WSAELM1 is 0.952. Furthermore, among all models estimating EC by the lags (t-1) and (t-2), the WSAELM2 model has a good performance. For this model, the values of RMSE, VAF and NSC are equal to 23.657, 99.117 and 0.991, respectively. However, the WSAELM3 which forecasts the objective parameter values in terms of the lags (t-1), (t-2) and (t-3), has a low error and a high correlation. Additionally, the WSAELM4 is introduced as the model with the best performance among the models simulating the EC values by means of the lags (t-1), (t-2), (t-3) and (t-4). For this model, RMSE and NSC are computed 20.653 and 0.933, respectively. Therefore, among all numerical models, the WSAELM4 and the lags (t-1), (t-2), (t-3) and (t-4), respectively, are identified as the superior model and the most effective parameters.

Fig. 6

Scatter plots for simulating TDS by different models

Fig. 7

Statistical indices for simulating EC by different models

Salinity

In this section, the artificial models developed for simulating salinity are evaluated. Based on the modeling results, among all models simulating salinity using the lag (t-1), the WSAELM1 model has the best performance compared to the other methods (i.e. ELM1, WELM1 and SAELM1 as Model 1, see Fig. 2). For example, the values of VAF and NSC for this model are obtained 86.667 and 0.847, respectively. It is worth noting that among all models with two input parameters (t-1, t-2), the WSAELM2 model has the highest accuracy. In other words, the value RMSE for the WSAELM2 is calculated 219.130. Also, for this model, the values of R² and NSC, respectively, are 0.991 and 0.982. In contrast, the WSAELM3 which simulates the salinity values by three input lags, has a good performance. For WSAELM3, the values of VAF and NSC are calculated 97.360, and 0.970, respectively. For example, R2 and RMSE for this mode are approximated 0.991 and 221.298, respectively. The results of the statistical indices as well as the scatter plots for all numerical models are shown in Figs. 8 and 9. Thus, according to the modeling results, the WSAELM4 has the best performance in modeling the salinity values and the lags (t-1), (t-2), (t-3) and (t-4) have the maximum influence.

Fig. 8

Scatter plots for simulating EC by different models

Fig. 9

Results of statistical indices for simulating salinity by different models

Groundwater level (GWL)

In this section, the results obtained from the artificial intelligence methods for estimating GWL are studied. In Figs. 10 and 11, the results of the statistical indices and the scatter plots for these models are illustrated. According to the modeling results, the WSAELM1 which simulates the objective function values in terms of (t-1) has an acceptable performance. For this model, the values of R², VAF and RMSE are calculated 0.842, 70.894 and 0.338, respectively. Furthermore, the value of NSC for the WSAELM1 is estimated 0.564. Also, the WSAELM2 approximate the GWL values in terms of (t-1) and (t-12). The values of R² and VAF for the WSAELM2 are computed 0.878 and 87.743, respectively. For this model, the value of NSC is obtained 0.853. The ELM3, SAELM3, WELM3 and WSAELM3 models simulate the GWL values in terms of the lags (t-1), (t-2) and (t-12). The values of R² and NSC for the WSAELM3 are obtained 0.940 and 0.937, respectively. Furthermore, VAF, for the mentioned model, is 94.024, whereas the ELM4, SAELM4, WELM4 and WSAELM4 models (Model 4, see Fig. 2) simulate the objective function values by the lags (t-1), (t-2), (t-3) and (t-12). The analysis of these models demonstrates that the WSAELM4 has the highest correlation with the observational data. For this model, R², RMSE and VAF are computed 0.995, 0.078 and 98.452, respectively. Additionally, the value of NSC for this model is obtained equal to 0.984.

Fig. 10

Scatter plots for simulating salinity by different models

Fig. 11

Results of statistical indices for simulating GWL by different models

According to the modeling results, the WSAELM4 model is introduced as the best model compared to the other ones and the lags (t-1), (t-2), (t-3) and (t-12) are detected as the most effective lags.

Superior models and effective lags

As shown, using the input lags, four different models for each method (ELM, WELM, SAELM and WSAELM) are defined. For TDS, EC and salinity, the ELM1, WELM1, SAELM1 and WSAELM1 models are as a function of (t-1). The ELM2, WELM2, SAELM2 and WSAELM2 models are in terms of the input lags (t-1) and (t-2), whilst the ELM3, WELM3, SAELM3 and WSAELM3 models estimate TDS, EC and salinity using the lags (t-1), (t-2), (t-3). Also, the ELM4, WELM4, SAELM4, and WSAELM4 models are as a function of the lags (t-1), (t-2), (t-3) and (t-4).

For GWL, the ELM1, WELM1, SAELM1 and WSAELM1 models forecast the target function adopting (t-1), whereas the ELM2, WELM2, SAELM2 and WSAELM2 models predict the GWL values using (t-1) and (t-12). Moreover, the lags (t-1), (t-2), (t-12) are utilized to model the GWL values using the ELM3, WELM3, SAELM3 and WSAELM3 models. However, the ELM4, WELM4, SAELM4, and WSAELM4 models are in terms of the lags (t-1), (t-2), (t-3) and (t-12).

In the previous section, the superior model (WSAELM4) estimated the TDS, EC and salinity values by means of a combination of the lags (t-1), (t-2), (t-3) and (t-4). Also, the WSAELM4 is detected as the superior model in estimating the GWL values by the lags (t-1), (t-2), (t-3), (t-12).

In the following, further evaluation of the superior models is conducted. In Fig. 12, the comparison of the TDS, EC, salinity and GWL values simulated by the superior models with the observational data is shown. As can be seen, the superior numerical models simulate the objective function values with reasonable accuracy. In addition, the error distribution graphs for these models are shown in Fig. 13. According to the modeling results, about 44% of the TDS values simulated by the WSAELM4 have an error less than 10%, while about a third of the TDS values estimated by the WSAELM4 have an error more than 15%. Furthermore, about 14% of the EC values modeled by the WSAELM4 have an error between 10 and 15%. It should be noted that about 37% of the salinity values simulated by the superior WSAELM 4 model have an error more than 15%. In addition, about half of the GWL values modeled by the WSAELM4 have an error less than 10%. Moreover, about 28% of the GWL values modeled by the WSAELM4 have an error between 10 and 15%.

Fig. 12

Scatter plots for simulating GWL by different models

Fig. 13

Comparison of observational qualitative and quantitative parameters with values simulated by superior models

Definitely, groundwater fluctuations are the most important parameter in each aquifer which was evaluated in the current study. Increasing the level of groundwater can affect other parameters like salinity, electrical conductivity and total dissolved solids in a specific period of time. Also, variations of the salinity, TDS and EC was pretty similar, however the GWL undergoes an insignificant change. In order to examine the effects of the parameters on each other precisely, fluctuations of the parameters should be evaluated in a longer period.

Furthermore, to further evaluation of the modeling results, the discrepancy ratio (DR) is used. This index is defined as follows:

$$ {\text{DR}} = \frac{{P_{i} }}{{O_{i} }}. $$

(30)

The closeness of DR to the number 1 reveals the closeness of simulated values to observational ones. For the superior models, the values of DR_max, DR_min and DR_ave denoting the maximum, minimum and average discrepancy ratios are calculated as well. Further, the graphs of the DR variations for the superior models are depicted in Fig. 14. For example, the values of DR_max, DR_min and DR_ave for the TDS modeling by the WSAELM4 model are calculated 1.01, 0.998 and 1.00001, respectively. Also, for simulating EC and salinity by means of the WSAELM4 model, DR_ave is estimated 0.0008 and 0.9995, respectively. It is worth mentioning that DR_max for the GWL approximation by the WSAELM4 is obtained almost equal to 1.003.

Fig. 14

Error distribution of superior models for estimating TDS, EC, salinity and GWL

Uncertainty analysis

In the following, the uncertainty analysis of the superior models is conducted for TDS, EC, salinity and GWL. The uncertainty analysis conducted to evaluate the error predicted by the numerical model and determine the performance of these models. Generally, the predicted error of the numerical model is considered equal to simulated values by the numerical model (P_i) minus observed values (O_i) $\left( {e_{i} = P_{i} - O_{i} } \right)$. In addition, the average of the predicted error is obtained as $\overline{e} = \sum\nolimits_{i = 1}^{n} {e_{i} }$, while the standard deviation value of predicted error values is defined as $S_{e} = \sqrt {\sum\nolimits_{j = 1}^{n} {\left( {e_{j} - \overline{e}} \right)^{2} /n - 1} }$. The negative sign of $\overline{e}$ shows the underestimated performance of the numerical model, while the positive sign exhibits the overestimated performance of the mentioned numerical model. It should be noted that using the $\overline{e}$ and $S_{e}$ parameters, a confidence bound is created around predicted values of an error by the Wilson score method without the continuity correction. Subsequently, applying $\pm 1.64S_{e}$ causes the formation of a 95% confidence bound approximately which is denoted by 95% PEI. The parameters of the uncertainty analysis of the superior models are given in Table 2. In this table, the "width of uncertainty band" is shown by the WUB. According to the uncertainty analysis, the WSAELM4 model has an overestimated performance in simulating TDS, EC and salinity, while the performance of this model in simulating GWL is underestimated. Furthermore, 95% PEI for estimating salinity by the WSAELM4 is between − 48.400 and 88.900. Additionally, the width of uncertainty band for modeling TDS by the superior model is about − 5.035.

Table 2 Uncertainty analysis parameters of superior models for different parameters

To sum up, the WSAELM algorithm is introduced as the premium method compared to other approaches such as the ELM, the WELM and the SAELM in estimating the groundwater parameters, since the WSAELM algorithm is simultaneously optimized by means of the differential evolution (DE) algorithm and also the wavelet transform (WT) (Fig. 15).

Fig. 15

Discrepancy ratio graphs of superior models for estimating TDS, EC, salinity and GWL

Conclusion

In this study, for the first time, the groundwater quantitative (groundwater level) and qualitative (total dissolved solids, electrical conductivity and salinity) parameters of the Mighan Plain located in Markazi Province, Iran, were monthly simulated for a 15-year period from 2002 to 2017 by means of a new artificial intelligence techniques such as the extreme learning machine (ELM) and the self-adaptive extreme learning machine (SAELM) as well as two hybrid methods including the wavelet extreme learning machine (WELM) and the wavelet self-adaptive extreme learning machine (WSAELM). The wavelet transform was utilized to develop the hybrid methods. In this paper, the wavelet transform was implemented for decomposing the time-series data as well as increasing the accuracy of the artificial intelligence methods. In addition, the autocorrelation function (ACF) and the partial autocorrelation function (PACF) analysis were employed to detect the significant lags of the time series. After that, using these lags for each of the ELM, SAELM, WELM and WSAELM models, four distinctive models were developed. Then, by conducting a sensitivity analysis the superior models and the most effective lags for each of TDS, EC, salinity and GWL were introduced. The most important findings of the study are as follows:

• The wavelet transform noticeably enhanced the performance of the ELM and SAELM methods.

• The values of RMSE, R² and NSC for the superior model in estimating EC were calculated 20.653, 0.997 and 0.993, respectively.

• Almost 37% of the salinity values estimated by the superior model (WSAELM4) had an error more than 15%.

• The lags (t-1), (t-2), (t-3) and (t-4) were detected as the most effective lags for simulating TDS, EC and salinity, whereas the lags (t-1), (t-2), (t-3) and (t-12) were the most important ones in modeling the GWL values.

• The results of the error distribution and the discrepancy ratio proved that the superior models have high accuracy.

• An uncertainty analysis was conducted to demonstrate that the superior models have an overestimated performance in estimating TDS, EC and salinity, while their performance for simulating the GWL fluctuations was found underestimate.

The current study presented a good insight into modeling the quantitative and qualitative parameters of groundwater using met-heuristic hybrid artificial intelligence techniques. However, in order to examine the effects of the parameters on each other precisely, fluctuations of the parameters should be evaluated in a longer period. Also, the studied area is one of the critical points in terms of lack of precipitations in the country of Iran so other regions in the country or similar case study can be investigated as well.