1 Introduction

In high power applications like ship propulsion, electric aircraft, and electric traction, the multiphase machines, greater than three-phase, are used for reasons of reliability, power segmentation, and fault tolerance capability (Morawiec et al. 2020; Kamel and Sumner 2019; Levi et al. 2016; Mohammadpour and Parsa 2015). Among the existing multiphase machines, five-phase and six-phase induction or synchronous machines are the most considered in the literature. In synchronous multiphase machines using permanent magnets, known as permanent magnet synchronous machine, both mechanical friction and copper losses are reduced due to the absence of brushes and commutator, and the elimination of the rotor coils. In addition, the machine cooling is more efficient because most of the energy losses are concentrated in the stator; this leads to an improved efficiency. For these reasons, the focus of the present study will be on the control of a five-phase permanent magnet synchronous motor drive (PMSM).

In order to improve the control performance of the five-phase PMSM based multilevel drives, diverse control strategies have been proposed in the literature (Bounasla and Barkat 2020; Zhou et al. 2019; Mehedi et al. 2019). Although they adopt different methods, they reach the same goal by achieving the decoupled control between flux and torque, just like to a DC machine with separate excitation. Direct control torque is one of these strategies, in which the machine stator flux and torque are controlled directly without the need of inner current control loops, modulator block, and with less parameters dependency; this makes its structure quite simple and has a fast dynamic response. However, the variation of switching frequency is the major disadvantage of this control strategy that leads to produce an unwanted high ripple exists in the torque and stator (Hamdi et al. 2018; Payami et al. 2017; Parsa and Toliyat 2007).

This problem can be solved by mixing the space vector modulation (SVM) with DTC to form the so-called DTC-SVM (Mesloub et al. 2020; Reghioui et al. 2019; Ouledali et al. 2015). Indeed, instead of a hysteresis controllers and switching table, two PI controllers and space vector modulation (SVM) block are used. However, despite the previously mentioned merit, the quality of the DTC-SVM control strategy is related to the nature of the controller applied. Commonly, it is based on classical PI controllers that can achieve good performance, but in presence of external disturbances or parameters variations they may lose it.

Another quite interesting DTC structure based on predictive approach known as Model Predictive Control (MPC) has been lately published in the domain of electrical drives (Cho et al. 2018; Siami et al. 2017). It has many advantages including simple principle, fast dynamic response, and multivariable control flexibility. Presently, MPC is extended to multi-phase drives (Bounasla and Barkat 2020; Xiong et al. 2020; Huang et al. 2020; Li et al. 2019; Wu et al. 2018). According to switching frequency, the predictive DTC (PDTC) strategies can be categorized into two groups: variable switching frequency and constant switching frequency. In the first group, the stator voltage vector that can achieve the lowest value of a given cost function is selected and applied to the machine terminals for a whole sampling interval. Although this control approach leads to minimize torque and stator flux ripples, the switching frequency is still variable. In the second group, there are two different proposed strategies that combine predictive control with modulation techniques capable to operate the inverter with constant switching frequency. The first one is known as PDTC-SVM in which the principle is based on the calculation of the average voltage vector using a predictive torque control algorithm. Then, the computed average voltage vector is used to generate the inverter switching states by employing an SVM block (Reguig Berra et al. 2020; Bouafia et al. 2010). The second approach depends on selecting two active and one zero voltage vectors to calculate optimal vector application times, in order to reduce the value of a predefined cost function (Song et al. 2014, 2013; Antoniewicz and Kazmierkowski 2008). This approach can be considered as an effective solution to achieve lower torque and stator flux ripples, and operate the inverter with fixed switching frequency at the same time.

The main purpose of this paper is the extension and application of a constant switching frequency predictive direct power control strategy proposed in (Antoniewicz and Kazmierkowski 2008) on multiphase drive based five-phase PMSM. This extension aims to reduce the torque and stator flux ripples while operating the inverter under a fixed switching frequency. The performance of the proposed constant switching frequency predictive direct torque control (CSF-PDTC) approach will be compared with classical PDTC and PDTC-SVM.

The organization of the rest of the paper is as follows: Sect. 2 presents the mathematical model of the five-phase PMSM. Analysis and design of the predictive DTC with SVPWM are detailed in Sect. 3. In Sect. 4, the proposed constant switching frequency PDTC is presented. Simulation results are shown and discussed in Sect. 5. Finally, the conclusion of the research paper is given in Sect. 6.

2 Five-phase PMSM modeling

The model of the five-phase PMSM is totally defined in a rotating (d-q) through its electrical, magnetic, and mechanical equations (Parsa and Toliyat 2007), (Mukhtar 2010):

  • The stator voltages are as follows:

$$\left\{ \begin{gathered} V_{d} = R_{s} i_{d} + \frac{{d\phi_{d} }}{dt} - \omega_{r} \phi_{q} \hfill \\ V_{q} = R_{s} i_{q} + \frac{{d\phi_{q} }}{dt} + \omega_{r} \phi_{d} \hfill \\ \end{gathered} \right.$$
(1)

where \(V_{d} ,V_{q}\) are the d-q axes stator voltages; \(i_{d} ,i_{q}\) are the d-q axes stator currents; \(\phi_{d} ,\,\,\phi_{q}\) are the d-q axes stator fluxes; \(R_{s}\) is the stator resistance; \(\omega_{r}\) is the rotor speed.

  • The stator flux components in the (d-q) frame are given by:

$$\left\{ \begin{gathered} \phi_{d} = L_{d} i_{d} + \phi_{f} \hfill \\ \phi_{q} = L_{q} i_{q} \hfill \\ \end{gathered} \right.$$
(2)

where \(L_{d} ,L_{q}\) are the d-q axes stator inductances; \(\phi_{f}\) is the permanent magnet flux linkage.

  • The mechanical dynamic and electromagnetic torque equations are expressed by:

$$\left\{ \begin{gathered} \frac{{d\omega_{r} }}{dt} = \frac{1}{J} \, \left( {T_{em} - T_{L} - f\omega_{r} } \right) \hfill \\ \, T_{em} = \frac{5}{2}p(\phi_{d} i_{q} - \phi_{q} i_{d} ) \, \hfill \\ \end{gathered} \right.$$
(3)

where \(T_{em} ,\,\,\,\,T_{L}\) are the electromagnetic and load torque; \(p\) is the pole pair number, \(J\) is the moment inertia; \(f\) is the friction coefficient.

3 Predictive DTC with SVM principle

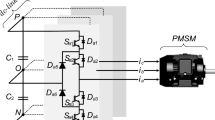
The idea behind designing this strategy is to calculate the average voltage vector using a predictive torque control algorithm, during each switching period, in order to cancel the reference tracking errors of the electromagnetic torque and stator flux. Then, the computed average voltage vector is used to generate the inverter switching states by employing an SVM technique that ensures the inverter operation at a constant switching frequency (Bouafia et al. 2010). This idea is illustrated in Fig. 1.

Fig. 1
figure 1

Predictive DTC with SVM of five-phase PMSM drive

Full size image

In this figure, the PI controller is used to regulate the error between the speed and its reference. The output of PI speed controller presents the reference of electromagnetic torque.

PDTC requires a predictive model of the torque and stator flux behavior, which is described in the following steps.

The estimated torque and stator flux can be expressed by the following formulas:

$$\left\{ \begin{gathered} T_{em} = \frac{5}{2}p(\phi_{d} i_{q} - \phi_{q} i_{d} ) \hfill \\ \phi_{s} = \sqrt {\phi_{d}^{2} + \phi_{q}^{2} } \hfill \\ \end{gathered} \right.$$
(4)

The torque and stator flux derivatives are given as follows:

$$\left[ {\begin{array}{*{20}c} {\frac{{dT_{em} }}{dt}} \\ {\frac{{d\phi_{s} }}{dt}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left( {\frac{5}{2}p} \right)\left( {ca + db} \right)} \\ {\frac{{L_{d} \phi_{d} a + L_{q} \phi_{q} b}}{{2\sqrt {\phi_{d}^{2} + \phi_{q}^{2} } }}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\left( {\frac{5}{2}p} \right)\left( {\frac{c}{{L_{d} }}} \right)} & {\left( {\frac{5}{2}p} \right)\left( {\frac{d}{{L_{q} }}} \right)} \\ {\frac{{\phi_{d} }}{{2\sqrt {\phi_{d}^{2} + \phi_{q}^{2} } }}} & {\frac{{\phi_{q} }}{{2\sqrt {\phi_{d}^{2} + \phi_{q}^{2} } }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {V_{dref} } \\ {V_{qref} } \\ \end{array} } \right]$$
(5)

With

$$\left\{ \begin{gathered} a = - \frac{{R_{s} }}{{L_{d} }}i_{d} + \frac{{L_{q} }}{{L_{d} }}p\omega_{r} i_{q} \hfill \\ b = - \frac{{R_{s} }}{{L_{q} }}i_{q} - \frac{{L_{d} }}{{L_{q} }}p\omega_{r} i_{d} - \frac{{\phi_{f} }}{{L_{q} }}p\omega_{r} \hfill \\ c = L_{d} i_{q} - \phi_{q} \hfill \\ d = \phi_{d} - L_{q} i_{d} \hfill \\ \end{gathered} \right.$$

If the sampling period \(T_{e}\) is infinitely small compared with the fundamental period, the discretization of the Eq. 5 yields:

$$\left[ {\begin{array}{*{20}c} {\frac{{T_{em} \left( {k + 1} \right) - T_{em} \left( k \right)}}{{T_{e} }}} \\ {\frac{{\phi_{s} \left( {k + 1} \right) - \phi_{s} \left( k \right)}}{{T_{e} }}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left( {\frac{5}{2}p} \right)\left( {c_{k} a_{k} + d_{k} b_{k} } \right)} \\ {\frac{{L_{d} \phi_{d} \left( k \right)a_{k} + L_{q} \phi_{q} \left( k \right)b_{k} }}{{2\sqrt {\phi_{d}^{2} \left( k \right) + \phi_{q}^{2} \left( k \right)} }}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\left( {\frac{5}{2}p} \right)\left( {\frac{{c_{k} }}{{L_{d} }}} \right)} & {\left( {\frac{5}{2}p} \right)\left( {\frac{{d_{k} }}{{L_{q} }}} \right)} \\ {\frac{{\phi_{d} \left( k \right)}}{{2\sqrt {\phi_{d}^{2} \left( k \right) + \phi_{q}^{2} \left( k \right)} }}} & {\frac{{\phi_{q} \left( k \right)}}{{2\sqrt {\phi_{d}^{2} \left( k \right) + \phi_{q}^{2} \left( k \right)} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {V_{dref} \left( k \right)} \\ {V_{qref} \left( k \right)} \\ \end{array} } \right]$$
(6)

With

$$\left\{ \begin{gathered} a_{k} = - \frac{{R_{s} }}{{L_{d} }}i_{d} \left( k \right) + \frac{{L_{q} }}{{L_{d} }}p\omega_{r} \left( k \right)i_{q} \left( k \right) \hfill \\ b_{k} = - \frac{{R_{s} }}{{L_{q} }}i_{q} \left( k \right) - \frac{{L_{d} }}{{L_{q} }}p\omega_{r} \left( k \right)i_{d} \left( k \right) - \frac{{\phi_{f} }}{{L_{q} }}p\omega_{r} \left( k \right) \hfill \\ c_{k} = L_{d} i_{q} \left( k \right) - \phi_{q} \left( k \right) \hfill \\ d_{k} = \phi_{d} \left( k \right) - L_{q} i_{d} \left( k \right) \hfill \\ \end{gathered} \right.$$

The control objective is to force the torque and stator flux to track their reference values at the next sampling period; the Eq. (6) can be rewritten using references as follows:

$$\left[ {\begin{array}{*{20}c} {\frac{{T_{emref} \left( {k + 1} \right) - T_{em} \left( k \right)}}{{T_{e} }}} \\ {\frac{{\phi_{sref} \left( {k + 1} \right) - \phi_{s} \left( k \right)}}{{T_{e} }}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left( {\frac{5}{2}p} \right)\left( {c_{k} a_{k} + d_{k} b_{k} } \right)} \\ {\frac{{L_{d} \phi_{d} \left( k \right)a_{k} + L_{q} \phi_{q} \left( k \right)b_{k} }}{{2\sqrt {\phi_{d}^{2} \left( k \right) + \phi_{q}^{2} \left( k \right)} }}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\left( {\frac{5}{2}p} \right)\left( {\frac{{c_{k} }}{{L_{d} }}} \right)} & {\left( {\frac{5}{2}p} \right)\left( {\frac{{d_{k} }}{{L_{q} }}} \right)} \\ {\frac{{\phi_{d} \left( k \right)}}{{2\sqrt {\phi_{d}^{2} \left( k \right) + \phi_{q}^{2} \left( k \right)} }}} & {\frac{{\phi_{q} \left( k \right)}}{{2\sqrt {\phi_{d}^{2} \left( k \right) + \phi_{q}^{2} \left( k \right)} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {V_{dref} \left( k \right)} \\ {V_{qref} \left( k \right)} \\ \end{array} } \right]$$
(7)

Using the Eq. (7), the required average voltage vector is expressed as follows:

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {V_{dref} \left( k \right)} \\ {V_{qref} \left( k \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left( {\frac{5}{2}p} \right)\left( {\frac{{c_{k} }}{{L_{d} }}} \right)} & {\left( {\frac{5}{2}p} \right)\left( {\frac{{d_{k} }}{{L_{q} }}} \right)} \\ {\frac{{\phi_{d} \left( k \right)}}{{2\sqrt {\phi_{d}^{2} \left( k \right) + \phi_{q}^{2} \left( k \right)} }}} & {\frac{{\phi_{q} \left( k \right)}}{{2\sqrt {\phi_{d}^{2} \left( k \right) + \phi_{q}^{2} \left( k \right)} }}} \\ \end{array} } \right]^{ - 1} \hfill \\ \left( {\left[ {\begin{array}{*{20}c} {\frac{{T_{emref} \left( {k + 1} \right) - T_{em} \left( k \right)}}{{T_{e} }}} \\ {\frac{{\phi_{sref} \left( {k + 1} \right) - \phi_{s} \left( k \right)}}{{T_{e} }}} \\ \end{array} } \right]{ - }\left[ {\begin{array}{*{20}c} {\left( {\frac{5}{2}p} \right)\left( {c_{k} a_{k} + d_{k} b_{k} } \right)} \\ {\frac{{L_{d} \phi_{d} \left( k \right)a_{k} + L_{q} \phi_{q} \left( k \right)b_{k} }}{{2\sqrt {\phi_{d}^{2} \left( k \right) + \phi_{q}^{2} \left( k \right)} }}} \\ \end{array} } \right]} \right), \hfill \\ \end{gathered}$$
(8)

The torque and stator flux references at the next sampling period (k + 1) can be estimated using a linear extrapolation as shown in Fig. 2.

Fig. 2
figure 2

Predictive value estimation of torque and stator flux references

Full size image

The estimated torque and stator flux references are given by:

$$\left\{ \begin{gathered} T_{emref} \left( {k + 1} \right) = 2T_{emref} \left( k \right) - T_{emref} \left( {k - 1} \right) \hfill \\ \phi_{sref} \left( {k + 1} \right) = 2\phi_{sref} \left( k \right) - \phi_{sref} \left( {k - 1} \right) \hfill \\ \end{gathered} \right.$$
(9)

Consequently, the final PDPC control law, which provides the required average voltage vector that is applied during each sampling period, is given by the following equation:

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {V_{dref} \left( k \right)} \\ {V_{qref} \left( k \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left( {\frac{5}{2}p} \right)\left( {\frac{{c_{k} }}{{L_{d} }}} \right)} & {\left( {\frac{5}{2}p} \right)\left( {\frac{{d_{k} }}{{L_{q} }}} \right)} \\ {\frac{{\phi_{d} \left( k \right)}}{{2\sqrt {\phi_{d}^{2} \left( k \right) + \phi_{q}^{2} \left( k \right)} }}} & {\frac{{\phi_{q} \left( k \right)}}{{2\sqrt {\phi_{d}^{2} \left( k \right) + \phi_{q}^{2} \left( k \right)} }}} \\ \end{array} } \right]^{ - 1} \hfill \\ \left( {\left[ {\begin{array}{*{20}c} {\frac{{\Delta T_{emref} \left( k \right) - e_{{T_{em} }} \left( k \right)}}{{T_{e} }}} \\ {\frac{{\Delta \phi_{sref} \left( k \right) - e_{{\phi_{s} }} \left( k \right)}}{{T_{e} }}} \\ \end{array} } \right]{ - }\left[ {\begin{array}{*{20}c} {\left( {\frac{5}{2}p} \right)\left( {c_{k} a_{k} + d_{k} b_{k} } \right)} \\ {\frac{{L_{d} \phi_{d} \left( k \right)a_{k} + L_{q} \phi_{q} \left( k \right)b_{k} }}{{2\sqrt {\phi_{d}^{2} \left( k \right) + \phi_{q}^{2} \left( k \right)} }}} \\ \end{array} } \right]} \right) \hfill \\ \end{gathered}$$
(10)

where \(e_{{T_{em} }} \left( k \right)\) and \(e_{{\phi_{s} }} \left( k \right)\) are the actual torque and stator flux tracking errors defined as:

$$\left\{ \begin{gathered} e_{{T_{em} }} \left( k \right) = T_{emref} \left( k \right) - T_{em} \left( k \right) \hfill \\ e_{{\phi_{s} }} \left( k \right) = \phi_{sref} \left( k \right) - \phi_{s} \left( k \right) \hfill \\ \end{gathered} \right.$$
(11)

\(\Delta T_{emref} \left( k \right)\) and \(\Delta \phi_{sref} \left( k \right)\) are the actual changes in torque and stator flux references given by:

$$\left\{ \begin{gathered} \Delta T_{emref} \left( k \right) = T_{emref} \left( k \right) - T_{emref} \left( {k - 1} \right) \hfill \\ \Delta \phi_{sref} \left( k \right) = \phi_{sref} \left( k \right) - \phi_{sref} \left( {k - 1} \right) \hfill \\ \end{gathered} \right.$$
(12)

The reference voltage vector components in stationary frame can be calculated using the following transformation:

$$\left( {\begin{array}{*{20}c} {V_{\alpha ref} } \\ {V_{\beta ref} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos (\theta_{r} )} & { - \sin (\theta_{r} )} \\ {\sin (\theta_{r} )} & {\cos (\theta_{r} )} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {V_{dref} } \\ {V_{qref} } \\ \end{array} } \right)$$
(13)

At this stage, the SVPWM modulator is used to produce the five-phase inverter control signals.

4 Constant switching frequency PDTC approach

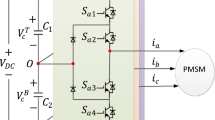
Figure 3 represents a constant switching frequency predictive DTC of five-phase PMSM drive. The proposed control strategy relies on calculating optimal vector application times to generate inverter switching states by selecting three voltage vectors; one of them is zero voltage. This leads to improve the performance and efficiency of predictive torque control in terms of torque and stator flux ripples reduction as well as operating the inverter with a constant switching frequency (Song et al. 2014, 2013; Antoniewicz and Kazmierkowski 2008).

Fig. 3
figure 3

Control scheme of constant switching frequency predictive DTC of a five-phase PMSM drive

Full size image

The CSF-PDTC approach uses the same speed PI controller as that used in the previous control strategy to produce the reference of electromagnetic torque.

This strategy is based on Eq. (5) giving the time derivatives of the torque and stator flux. An increase or decrease in torque and stator flux is the result of applying a voltage vector, which can be defined as follows:

$$\left\{ \begin{gathered} f_{{T_{emi} }} = \left. {\frac{{dT_{em} }}{dt}} \right\|_{{V_{c} = V_{Li} }} \hfill \\ f_{{\phi_{si} }} = \left. {\frac{{d\phi_{s} }}{dt}} \right\|_{{V_{c} = V_{Li} }} \hfill \\ \end{gathered} \right.$$
(14)

where \(i\) is number of applied voltage vector \(V_{Li} /i = 1, \ldots ,10.\)

From (14), the relation between torque, stator flux, and application times can be expressed as:

$$\left\{ \begin{gathered} T_{emi} = T_{em} + f_{{T_{emi} }} t_{i} \hfill \\ \phi_{si} = \phi_{s} + f_{{\phi_{si} }} t_{i} \hfill \\ \end{gathered} \right.$$
(15)

When three voltage vectors are selected within switching period, then the Eq. (15) can be rewritten as follows:

$$\left\{ \begin{gathered} T_{em1} = T_{em} + f_{{T_{em1} }} t_{1} \hfill \\ T_{em2} = T_{em1} + f_{{T_{em2} }} t_{2} \hfill \\ T_{em3} = T_{em2} + f_{{T_{em3} }} t_{3} \hfill \\ \end{gathered} \right.$$
(16)
$$\left\{ \begin{gathered} \phi_{s1} = \phi_{s} + f_{{\phi_{s1} }} t_{1} \hfill \\ \phi_{s2} = \phi_{s1} + f_{{\phi_{s2} }} t_{2} \hfill \\ \phi_{s3} = \phi_{s2} + f_{{\phi_{s3} }} t_{3} \hfill \\ \end{gathered} \right.$$
(17)

where \(t_{1} ,t_{2} ,t_{3}\) are voltage vectors application times.

Figure 4 shows graphical representation of Eqs. (16) and (17).

Fig. 4
figure 4

Torque a and stator flux b changes under three \(V_{i}\) voltage vectors application during one switching time \(T_{s}\)

Full size image

Equations (16) and (17) can be simplified to:

$$\left\{ \begin{gathered} T_{em3} = T_{em} + f_{{T_{em1} }} t_{1} + f_{{T_{em2} }} t_{2} + f_{{T_{em3} }} t_{3} \hfill \\ \phi_{s3} = \phi_{s} + \phi_{s1} t_{1} + \phi_{s2} t_{2} + \phi_{s3} t_{3} \hfill \\ \end{gathered} \right.$$
(18)

The application times fulfill the following constraint:

$$T_{s} = t_{1} + t_{2} + t_{3}$$
(19)

To achieve symmetrical vectors application within one switching time, the Eqs. (16) and (17) can be extended to:

$$\left\{ \begin{gathered} T_{em1} = T_{em} + f_{{T_{em1} }} t_{1} \, T_{em4} = T_{em3} + f_{{T_{em3} }} t_{3} \hfill \\ T_{em2} = T_{em1} + f_{{T_{em2} }} t_{2} \, T_{em5} = T_{em4} + f_{{T_{em2} }} t_{2} \, \hfill \\ T_{em3} = T_{em2} + f_{{T_{em3} }} t_{3} \, T_{em6} = T_{em5} + f_{{T_{em1} }} t_{1} \hfill \\ \end{gathered} \right.$$
(20)
$$\left\{ \begin{gathered} \phi_{s1} = \phi_{s} + f_{{\phi_{s1} }} t_{1} \, \phi_{s4} = \phi_{s3} + f_{{\phi_{s3} }} t_{3} \, \hfill \\ \phi_{s2} = \phi_{s1} + f_{{\phi_{s2} }} t_{2} \, \phi_{s5} = \phi_{s4} + f_{{\phi_{s2} }} t_{2} \, \hfill \\ \phi_{s3} = \phi_{s2} + f_{{\phi_{s3} }} t_{3} \, \phi_{s6} = \phi_{s5} + f_{{\phi_{s1} }} t_{1} \, \hfill \\ \end{gathered} \right.$$
(21)

Figure 5 shows graphical representation of Eqs. (20) and (22).

Fig. 5
figure 5

Torque a and stator flux b changes under symmetrical application of three voltage vectors \(V_{Li}\) during one switching time Ts

Full size image

Equation (20) and (21) can be simplified to:

$$\left\{ \begin{gathered} T_{em6} = T_{em} + 2f_{{T_{em1} }} t_{1} + 2f_{{T_{em2} }} t_{2} + 2f_{{T_{em3} }} t_{3} \hfill \\ \phi_{s6} = \phi_{s} + 2f_{{\phi_{s1} }} t_{1} + 2f_{{\phi_{s2} }} t_{2} + 2f_{{\phi_{s3} }} t_{3} \hfill \\ \end{gathered} \right.$$
(22)

In this case, \(t_{1} ,t_{2} ,t_{3}\) should verify the following condition:

$$T_{s} = 2\left( {t_{1} + t_{2} + t_{3} } \right)$$
(23)

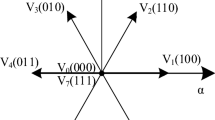
In this strategy, the vector sequence applied to the converter is selected in order to minimize the switching losses. To do this, the \(\alpha ,\beta\) plane is divided into ten sectors as depicted in Fig. 6.

Fig. 6
figure 6

Converter voltage vectors \(V_{Li}\)

Full size image

The predictive torque and stator flux values at the end of the switching period \(T_{em6} ,\,\,\phi_{s6}\) are considered as reference \(T_{emref} ,\phi_{sref}\).

$$\left\{ \begin{gathered} T_{emref} = T_{em6} \hfill \\ \phi_{sref} = \phi_{s6} \hfill \\ \end{gathered} \right.$$
(23)

The torque and stator flux errors \((e_{{T_{em} }} ,e_{{\phi_{s} }} )\) are expressed as follows:

$$\left\{ \begin{gathered} e_{{T_{em} }} = T_{emref} - T_{em} - 2\left( {f_{{T_{em1} }} t_{1} + f_{{T_{em2} }} t_{2} + f_{{T_{em3} }} \left( {\frac{1}{2}T_{s} - t_{1} - t_{2} } \right)} \right) \hfill \\ e_{{\phi_{s} }} = \phi_{sref} - \phi_{s} - 2\left( {f_{{\phi_{s1} }} t_{1} + f_{{\phi_{s2} }} t_{2} + f_{{\phi_{s3} }} \left( {\frac{1}{2}T_{s} - t_{1} - t_{2} } \right)} \right) \hfill \\ \end{gathered} \right.$$
(24)

The goal of control algorithm is to determine the voltage vector application times \(t_{1} ,t_{2} ,t_{3}\) in order to minimize the following cost function defined as sum of squared torque and stator flux errors.

$$F = e_{{T_{em} }}^{2} + e_{{\phi_{s} }}^{2}$$
(25)

After replacing (24) into (25), it results:

$$F = \left[ {T_{emref} - T_{em} - 2\left( {f_{{T_{em1} }} t_{1} + f_{{T_{em2} }} t_{2} + f_{{T_{em3} }} \left( {\frac{1}{2}T_{s} - t_{1} - t_{2} } \right)} \right)} \right]^{2} { + }\left[ {\phi_{sref} - \phi_{s} - 2\left( {f_{{\phi_{s1} }} t_{1} + f_{{\phi_{s2} }} t_{2} + f_{{\phi_{s3} }} \left( {\frac{1}{2}T_{s} - t_{1} - t_{2} } \right)} \right)} \right]^{2}$$
(26)

The optimal application times \(t_{1} ,t_{2}\), which minimize the cost function \(F\), during a switching time \(T_{s}\), satisfy the following minimum condition in which each partial derivative is zero:

$$\left\{ \begin{gathered} \frac{\partial F}{{\partial t_{1} }} = 0 \hfill \\ \frac{\partial F}{{\partial t_{2} }} = 0 \hfill \\ \end{gathered} \right.$$
(27)

First partial derivatives of the cost function F are expressed as:

$$\begin{aligned} \frac{\partial F}{{\partial t_{1} }} & = 4\left[ \begin{gathered} \left( {T_{emref} - T_{em} - f_{{T_{em3} }} T_{s} } \right)\left( {f_{{T_{em3} }} - f_{{T_{em1} }} } \right) \hfill \\ + \left( {\phi_{sref} - \phi_{s} - f_{{\phi_{s3} }} T_{s} } \right)\left( {f_{{\phi_{s3} }} - f_{{\phi_{s1} }} } \right) \hfill \\ \end{gathered} \right] \\ & \quad { + 8}\left[ {\left( {f_{{T_{em3} }} - f_{{T_{em1} }} } \right)^{2} + \left( {f_{{\phi_{s3} }} - f_{{\phi_{s1} }} } \right)^{2} } \right]t_{1} \\ & \quad { + 8}\left[ \begin{gathered} \left( {f_{{T_{em3} }} - f_{{T_{em2} }} } \right)\left( {f_{{T_{em3} }} - f_{{T_{em1} }} } \right) \hfill \\ + \left( {f_{{\phi_{s3} }} - f_{{\phi_{s2} }} } \right)\left( {f_{{\phi_{s3} }} - f_{{\phi_{s1} }} } \right) \hfill \\ \end{gathered} \right]t_{2} \\ \end{aligned}$$
(28)
$$\begin{aligned} \frac{\partial F}{{\partial t_{2} }} & = 4\left[ \begin{gathered} \left( {T_{emref} - T_{em} - f_{{T_{em3} }} T_{s} } \right)\left( {f_{{T_{em3} }} - f_{{T_{em2} }} } \right) \hfill \\ + \left( {\phi_{sref} - \phi_{s} - f_{{\phi_{s3} }} T_{s} } \right)\left( {f_{{\phi_{s3} }} - f_{{\phi_{s2} }} } \right) \hfill \\ \end{gathered} \right] \\ & \quad { + 8}\left[ \begin{gathered} \left( {f_{{T_{em3} }} - f_{{T_{em1} }} } \right)\left( {f_{{T_{em3} }} - f_{{T_{em2} }} } \right) + \hfill \\ \left( {f_{{\phi_{s3} }} - f_{{\phi_{s1} }} } \right)\left( {f_{{\phi_{s3} }} - f_{{\phi_{s2} }} } \right) \hfill \\ \end{gathered} \right]t_{1} \\ & \quad { + 8}\left[ {\left( {f_{{T_{em3} }} - f_{{T_{em2} }} } \right)^{2} + \left( {f_{{\phi_{s3} }} - f_{{\phi_{s2} }} } \right)^{2} } \right]t_{2} \\ \end{aligned}$$
(29)

To find the critical points of \(F\), the first partial derivatives given by Eqs. (28) and (29) should be set equal to zero. The solution of the resulting linear system of equations is given by:

$$t_{1} = \frac{{\left[ \begin{gathered} \left( {T_{emref} - T_{em} } \right)\left( {f_{{\phi_{s2} }} - f_{{\phi_{s3} }} } \right) + \left( {\phi_{sref} - \phi_{s} } \right)\left( {f_{{T_{em3} }} - f_{{T_{em3} }} } \right) \hfill \\ + \left( {f_{{T_{em2} }} f_{{\phi_{s3} }} - f_{{T_{em3} }} f_{{\phi_{s2} }} } \right)T_{s} \hfill \\ \end{gathered} \right]}}{{\left[ {2\left( {\left( {f_{{\phi_{s2} }} - f_{{\phi_{s3} }} } \right)f_{{T_{em1} }} + \left( {f_{{\phi_{s3} }} - f_{{\phi_{s1} }} } \right)f_{{T_{em2} }} + \left( {f_{{\phi_{s1} }} - f_{{\phi_{s2} }} } \right)f_{{T_{em3} }} } \right)} \right]}}$$
(30)
$$t_{2} = \frac{{\left[ \begin{gathered} \left( {T_{emref} - T_{em} } \right)\left( {f_{{\phi_{s3} }} - f_{{\phi_{s1} }} } \right) + \left( {\phi_{sref} - \phi_{s} } \right)\left( {f_{{T_{em1} }} - f_{{T_{em3} }} } \right) \hfill \\ + \left( {f_{{\phi_{s1} }} f_{{T_{em3} }} - f_{{\phi_{s3} }} f_{{T_{em1} }} } \right)T_{s} \hfill \\ \end{gathered} \right]}}{{\left[ {2\left( {\left( {f_{{\phi_{s2} }} - f_{{\phi_{s3} }} } \right)f_{{T_{em1} }} + \left( {f_{{\phi_{s3} }} - f_{{\phi_{s1} }} } \right)f_{{T_{em2} }} + \left( {f_{{\phi_{s1} }} - f_{{\phi_{s2} }} } \right)f_{{T_{em3} }} } \right)} \right]}}$$
(31)

Using (23), the time \(t_{3}\) can be calculated by:

$$t_{3} = \frac{1}{2}T_{s} - t_{1} - t_{2}$$
(32)

To check the nature of the critical point \((t_{1} ,t_{2} )\) of \(F\), which can be a local minimum, local maximum, saddle point, or none of these, second partial derivative test is used; this is done by calculating the Hessian matrix determinant given by (Bittinger et al. 2012):

$$D = = \frac{{\partial^{2} F}}{{\partial t_{1}^{2} }}\frac{{\partial^{2} F}}{{\partial t_{2}^{2} }} - \left( {\frac{{\partial^{2} F}}{{\partial t_{2} \partial t_{1} }}} \right)^{2}$$
(33)

According to the D value, four conditions can be distinguished:

  1. 1.

    If \(D > 0\) and \(\frac{{\partial^{2} F}}{{\partial t_{1}^{2} }} > 0,\) then \(F\) has a local minimum,

  2. 2.

    If \(D > 0\) and \(\frac{{\partial^{2} F}}{{\partial t_{1}^{2} }} < 0,\) then \(F\) has a local maximum,

  3. 3.

    If \(D < 0,\) then \(F\) has a saddle point,

  4. 4.

    If \(D = 0,\) then the test is inconclusive.

The second partial derivatives are given by:

$$\begin{aligned} \frac{{\partial^{2} F}}{{\partial t_{1}^{2} }} & = {8}\left[ {\left( {f_{{T_{em3} }} - f_{{T_{em1} }} } \right)^{2} + \left( {f_{{\phi_{s3} }} - f_{{\phi_{s1} }} } \right)^{2} } \right] \\ \frac{{\partial^{2} F}}{{\partial t_{2}^{2} }} & = {8}\left[ {\left( {f_{{T_{em3} }} - f_{{T_{em2} }} } \right)^{2} + \left( {f_{{\phi_{s3} }} - f_{{\phi_{s2} }} } \right)^{2} } \right] \\ \frac{{\partial^{2} F}}{{\partial t_{1} \partial t_{2} }} & = {8}\left[ \begin{gathered} \left( {f_{{T_{em3} }} - f_{{T_{em2} }} } \right)\left( {f_{{T_{em3} }} - f_{{T_{em1} }} } \right) \hfill \\ + \left( {f_{{\phi_{s3} }} - f_{{\phi_{s2} }} } \right)\left( {f_{{\phi_{s3} }} - f_{{\phi_{s1} }} } \right) \hfill \\ \end{gathered} \right] \\ \end{aligned}$$
(34)

In order to calculate \(D\), it is sufficient to replace (34) into Eq. (33). The resulting expression is simplified to the following:

$$D = 64\left( \begin{gathered} f_{{\phi_{s1} }} f_{{T_{em2} }} - f_{{\phi_{s2} }} f_{{T_{em1} }} - f_{{\phi_{s1} }} f_{{T_{em3} }} \hfill \\ + f_{{\phi_{s3} }} f_{{T_{em1} }} + f_{{\phi_{s2} }} f_{{T_{em3} }} - f_{{\phi_{s3} }} f_{{T_{em2} }} \hfill \\ \end{gathered} \right)^{2}$$
(35)

Note that both Eqs. (35) and the first one of (34) are always positive. This implies that, the critical point \((t_{1} ,t_{2} )\) represents effectively the local minimum of F.

The flowchart of the proposed CSF-PDTC strategy is shown in Fig. 7.

Fig. 7
figure 7

Flowchart of the proposed CSF-PDTC strategy

Full size image

5 Simulation results

In this section, a set of numerical simulations are carried out to illustrate the effectiveness of the proposed control in the steady-state and dynamic, and is compared to PDTC-SVM, and classical PDTC. Parameters of the five-phase PMSM are given in Table 2.

Table 1 Vector sequence to be applied to the inverter
Full size table
Table 2 Five-phase PMSM parameters
Full size table

The control system is carried out under deferent operating conditions such as sudden change of load torque, and step change in reference speed. The five-phase PMSM is accelerated from standstill to speed reference (100 rad/s). The full load torque \(\left( {T_{L} = 5\,{\text{N}}\,{\text{m}}} \right)\) is applied from (t = 0.3 s to t = 0.7 s). After that a sudden reversion in the speed command from (100 rad/s) to-(− 100 rad/s is performed at 1 s.

The five-phase PMSM dynamic responses: motor speed, electromagnetic torque, and stator flux are presented in Figs. 8 and 9 for CSF-PDTC and PDTC-SVM control strategies, respectively.

Fig. 8
figure 8

Dynamic responses of five-phase PMSM controlled by CSF-PDTC: a Motor speed, b Electromagnetic torque, c Stator flux, d Stator flux circle trajectory

Full size image
Fig. 9
figure 9

Dynamic responses of five-phase PMSM controlled by PDTC-SVM: a Motor speed, b Electromagnetic torque, c Stator flux, d Stator flux circle trajectory

Full size image

From Figs. 8a and 9a, the speed follows its reference value. Elimination of the load torque causes a slight variation in speed response. The speed controller intervenes to face this variation and ensures that the system follows its suitable reference speed. When comparing between CSF-PDTC and PDTC-SVM methods, there is no significant difference in term of tracking performance.

Figures 8b and 9b illustrate the electromagnetic torque curves produced by the five-phase PMSM controlled by CSF-PDTC and PDTC-SVM using the same \(PI\) controller. The proposed control shows a significant improvement in reducing torque ripples.

From Figs. 8c and 9c, it can be observed that the stator flux has a fast and good reference tracking, without any influence by the load variation. This indicates that a good decoupled control between flux and electromagnetic torque is achieved. Furthermore, the stator flux ripple in the proposed control is less than that obtained by PDTC-SVM.

From Figs. 8d and 9d, it can note that the stator flux vector forms a circular trajectory for both control methods respectively.

The circular stator flux trajectory in 3D is presented in Fig. 10a, b, it can clearly notice that the proposed control has a faster dynamic response in transient state compared to PDTC, and PDTC-SVM.

Fig. 10
figure 10

Stator flux circle trajectory in 3D presentation for different control strategies of predictive DTC for a five-phase PMSM drive

Full size image

From Fig. 11, it can be seen that CSF-PDTC structure, under the same operating conditions, can achieve smaller ripples compared to classical PDTC, and PDTC-SVM. This result confirms the superiority of the proposed control in terms of ripples reduction.

Fig. 11
figure 11

Comparison between different control strategies of predictive DTC for a five-phase PMSM driver: a Electromagnetic torque ripple, b Stator flux ripple

Full size image

6 Conclusion

This paper proposes an improved version of predictive DTC scheme of a five-phase PMSM fed by a five-leg inverter operating under a constant switching frequency. The obtained simulation results confirm that the proposed CSF-PDTC exhibits good response without overshoot while ensuring the decoupling between the stator flux and the electromagnetic torque. Comparative study confirms that the proposed predictive DTC can decrease considerably the torque and stator flux ripples compared to PDTC-SVM and classical PDTC.