1 Introduction

Finite set model predictive torque control (FS-MPTC) has emerged as a promising derivative structure from direct torque control (DTC) owing to its ease of implementation, fast torque response, and simple inclusion of constraints and nonlinearities [1,2,3,4,5,6]. However, some inherent issues are associated with FS-MPTC because of the finite number of switching states. In general, the application of a single switching state throughout the control cycle increases flux/torque ripples with a variable switching frequency [7]. Several strategies have been introduced to reduce the flux/torque ripple of the FS-MPTC scheme [8].

Over the past decades, the demand for multilevel power converters (ML-PCs) has increased across industries and research communities [9,10,11,12,13,14,15], particularly in high-power applications [13]. One of the most attractive ML-PC structures applied to medium-voltage motor drives is the three-level neutral point clamped inverter (3L-NPCI). Compared with typical two-level voltage source inverters, 3L-NPCIs result in lower output waveform ripples, higher efficiency, less switching stress across switching devices, and lower total harmonic content. Model predictive control (MPC) has been widely applied to 3L-NPCIs [14] because of the aforementioned advantages. However, 3L-NPCI-based MPC systems still have limitations, such as a large computation load, difficult selection of weighting factors, and capacitor voltage deviations.

To decrease the calculation effort of MPC owing to the large number of feasible voltage vectors (VVs), scholars have introduced various solutions [16–18]. The main aim of these predictive torque control (PTC) algorithms is to reduce the number of predicted VVs and/or switching sequences. The issue of weighting factor tuning in MPC has been completely eliminated or reduced in previous studies [19–21]. However, the difficulty with 3L-NPCIs is the neutral point (NP) imbalance owing to the deviation of the capacitor voltage. This issue causes the degradation of output currents and imposes large stress on switching devices. Consequently, several studies have focused on addressing this problem using the opposite effect of redundant switching states on NP potential and alterations in various modulation techniques [11, 22, 23].

Some solutions have been proposed to ensure minimal torque errors using FS-MPTC. One of these solutions is duty cycle control by inserting one or two VVs per sampling interval [24]. Another torque/flux reduction strategy involves applying discrete space vector modulation (DSVM), which synthesizes a large number of virtual VVs [25]. The application of DSVM to MPC results in a relatively high computational burden in actual implementation owing to the large number of virtual VVs. This issue can be solved by applying deadbeat control [13] and using lookup tables [25,26,27].

This study proposes a simple FS-MPTC with DSVM (PTC-DSVM) for a 3L-NPCI-fed permanent magnet synchronous motor (PMSM) while considering the NP voltage deviation. The proposed method generates feasible VVs online using an effective preselection strategy on the basis of flux orientation and torque error. To address the imbalance issue, this study proposes a simple offset voltage to be injected on the best switching VV after the cost function evaluation. In this manner, the control complexity and calculation load are minimized by reducing the number of candidate VVs and control objectives. The feasibility of the proposed method is validated using experimental results.

2 Basic 3L-NPCI-fed PTC of PMSM

2.1 Model of 3L-NPCI

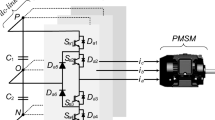
Figure 1 shows the topology of the 3L-NPCI for PMSM. Each phase has four switching devices: Sx1, Sx2, Sx3, and Sx4 (\(x=A, B,\mathrm{ and }C)\). The switching-state vectors for the 3L-NPCI structure are shown in Fig. 2.

Fig. 1
figure 1

Circuit structure of 3L-NPCI of PMSM

Full size image
Fig. 2
figure 2

Space vector diagram of conventional FS-MPTC fed by 3L-NPCI

Full size image

The 3L-NPCI consists of 19 VVs with a combination of 27 switching states. The VVs include three zero VVs (ZVV) \(\overrightarrow{v}\) 0,1,2; six small VVs (SVVs) \(\overrightarrow{v}\) 3,...,\(\overrightarrow{v}\) 8; six medium VVs (MVVs) \(\overrightarrow{v}\) 9,...,\(\overrightarrow{v}\) 14; and six large VVs (LVVs) \(\overrightarrow{v}\) 15,...,\(\overrightarrow{v}\) 20.

Each SVV has two switching states with two opposite connections to the top capacitor voltage (VcT) or bottom capacitor voltage (VcB). The voltage switching states are characterized by P, O, and N, which represent a link to “ + ” DC voltage bus, NP, and “– “ DC bus, respectively. On the basis of the size of the VV, the space VVs are divided into four groups: large (\(\overrightarrow{v}\) L), medium (\(\overrightarrow{v}\) M), small (\(\overrightarrow{v}\) S), and zero (\(\overrightarrow{v}\) Z). To ensure a balanced 3L-NPCI drive system, the voltages for the top and bottom capacitors should be equally distributed.

2.2 Traditional FS-MPTC

The equations for the FS-MPTC of the PMSM in the stationary reference frame are as follows:

$${\overrightarrow{\psi }}_{s}\left(\mathrm{k}\right)={L}_{s}\bullet {\overrightarrow{i}}_{s}\left(k\right)+{\overrightarrow{\psi }}_{pm}\left(k\right),$$
(1)
$${T}_{e}=\frac{3}{2}p\bullet (\overrightarrow{\psi }(\mathrm{k})\bullet {\overrightarrow{i}}_{s}(k)),$$
(2)

where \({\overrightarrow{v}}_{s}\), \({\overrightarrow{i}}_{s}\), and \({\overrightarrow{\psi }}_{\mathrm{s}}\) represent the stator voltage, stator current, and stator flux vectors, respectively. Te represents the electrical torque. \({R}_{s}\) and Ls represent the stator resistance and stator self-inductance, respectively. \({\overrightarrow{\psi }}_{pm}\) represents the permanent magnet flux, and P represents the number of pole pairs.

The predicted quantities of stator flux vector and stator current vector can be, respectively, expressed as follows:

$$ \vec{\psi }_{s} \left( {k + 1} \right) = { }\vec{\psi }_{s} \left( {\text{k}} \right) + T_{s} \cdot \vec{v}_{s} \left( k \right) + T_{s} R_{s} \cdot \vec{i}_{s} \left( k \right) + T_{s} \cdot Y \cdot \omega_{r} \left( k \right), $$
(3)
$$ \vec{i}_{s} \left( {k + 1} \right) = \Lambda \cdot \vec{i}_{s} \left( k \right) + {\rm M} \cdot \vec{v}_{s} \left( k \right) + \Gamma , $$
(4)

where

$$ \vec{i}_{s} = \left[ {\begin{array}{*{20}c} {i_{s\alpha } } \\ {i_{s\beta } } \\ \end{array} } \right],\;\vec{v}_{s} = \left[ {\begin{array}{*{20}c} {v_{s\alpha } } \\ {v_{s\beta } } \\ \end{array} } \right],\;Y = \left[ {\begin{array}{*{20}c} {\psi_{s\beta } } \\ { - \psi_{s\alpha } } \\ \end{array} } \right], $$
$$ \Lambda = \left[ {\begin{array}{*{20}c} {1 - R_{s} \cdot T_{s} /L_{s} } & {L_{s} \cdot T_{s} \cdot \omega_{r} \left( k \right)} \\ { - L_{s} .T_{s} \cdot \omega_{r} \left( k \right)} & {1 - R_{s} \cdot T_{s} /L_{s} } \\ \end{array} } \right], $$
$$ {\rm M} = \left[ {\begin{array}{*{20}c} {T_{s} /L_{s} } & 0 \\ 0 & {T_{s} /L_{s} } \\ \end{array} } \right],\;\Gamma = \left[ {\begin{array}{*{20}c} 0 \\ { - \vec{\psi }_{pm} \cdot \omega_{r} \cdot T_{s} /L_{s} } \\ \end{array} } \right], $$

where \({\omega }_{r}\) represents the motor rotor speed and k and k + 1 denote the present and predicted sampling discrete steps, respectively. Ts represents the sampling time.

On the basis of the predicted values of (3) and (4), the motor torque can be predicted as follows:

$${T}_{e}\left(k+1\right)=6\frac{3}{2}p.\left({ \overrightarrow{\psi }}_{s}\left(k+1\right)\bullet {\overrightarrow{i}}_{s}\left(k+1\right)\right).$$
(5)

The 3L-NPCI structure consists of 19 VVs, as illustrated in Fig. 2. A cost function is formed as follows to determine the optimal VV among the admissible VVs:

$$g=\left|{T}_{ref}-{ T}_{e}(k+1)\right|+{Y}_{\psi }\left|{\psi }_{ref}-\left|{ \overrightarrow{\psi }}_{s}(k+1)\right|\right|,$$
(6)

where \({T}_{ref}\) represents the torque reference and \({\psi }_{ref}\) represents the flux linkage reference at the kth sampling time. \({Y}_{\psi }\) represents the weighting factor that defines the relative importance of the flux control objective. \({Y}_{\psi }\) is found herein as the ratio of rated torque and rated flux (\({T}_{rated}\)/\({\psi }_{rated}\)). Note that the obtained value of the weighting factor still needs further fine-tuning during the experimental implementation.

3 Proposed PTC-DSVM fed by 3L-NPCI

The proposed PTC method uses a DSVM to synthesize VVs. The aim of this study is to achieve a reduction in torque and flux ripple such that the method can be easily applied with reduced complexity and the problem of NP balance for 3L-NPCI systems can be resolved.

3.1 Synthesis of online-generated VVs

Although the conventional PTC fed by 3L-NPC uses only 19 VVs defined by switching states for prediction, the proposed PTC based on the DSVM strategy can extend the prediction to a large number of synthesized virtual VVs to achieve further waveform ripple reductions in steady-state operations.


Figure 3a shows the general voltage space voltage diagram (VSVD), which was initially developed by [24]. This DSVM method consists of 12 VSVD regions and K hexagons of various sizes and numbers of VVs; it is expressed as follows:

Fig. 3
figure 3

Coordinate diagram for a General VSVD; b VV values of R4 when K = 2

Full size image
$$O\left(m\right)=12\bullet m, \left\{\left[m=1:K\right] \because O\left(m\right)=1\right\},$$
(7)

where O is the total number of VVs. In this DSVM, the VSVD is divided into 12 regions (i.e., R1–R12). In each VSVD region, VVs are synthesized upon invoking on the basis of (7). The symmetry of the VSVD regions according to the \(\alpha -\beta \) frame is an attractive feature of the DSVM method. Thus, three mathematical expressions for each group of VSVD regions can be generated online and are expressed as follows:

$$ (v_{\alpha } ,v_{\beta } )^{{\left( {x,y} \right)}} = \left\langle {{{\delta }} \cdot {\raise0.7ex\hbox{${V_{{DC}} }$} \!\mathord{\left/ {\vphantom {{V_{{DC}} } {6K}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${6K}$}}\left( {x + 3y} \right)~,~~\sqrt 3 \cdot {{\xi }} \cdot {\raise0.7ex\hbox{${V_{{DC}} }$} \!\mathord{\left/ {\vphantom {{V_{{DC}} } {6K}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${6K}$}}\left( { - x + y} \right)} \right\rangle , $$
(8)
$$ (v_{\alpha } ,v_{\beta } )^{{\left( {x,y} \right)}} = \left\langle {\delta \cdot {\raise0.7ex\hbox{${V_{{DC}} }$} \!\mathord{\left/ {\vphantom {{V_{{DC}} } {6K}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${6K}$}}\left( {\left( { - x + 3y} \right)} \right),~~\sqrt 3 \cdot \xi \cdot {\raise0.7ex\hbox{${V_{{DC}} }$} \!\mathord{\left/ {\vphantom {{V_{{DC}} } {6K}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${6K}$}}\left( {x + y} \right)} \right\rangle , $$
(9)
$$ (v_{\alpha } ,~v_{\beta } )^{{\left( {x,y} \right)}} = \left\langle {\delta \cdot {\raise0.7ex\hbox{${V_{{DC}} }$} \!\mathord{\left/ {\vphantom {{V_{{DC}} } {3K}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3K}$}}\left( x \right)~,~~\xi \cdot {\raise0.7ex\hbox{${V_{{DC}} }$} \!\mathord{\left/ {\vphantom {{V_{{DC}} } {3K}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3K}$}}\left( {\sqrt 3 \cdot y} \right)} \right\rangle , $$
(10)

where x and y represent the quantities for each coordinate VSVD region from 0 to K. \(\updelta \) and \(\upxi \) represent the coefficients based on the VSVD regions, as listed in Table 1. Thus, the VSVD region sets (\({R}_{3}, {R}_{4}, {R}_{8}, \mathrm{and} {R}_{10}\)), (\({R}_{2}, {R}_{5}, {R}_{8}, \mathrm{and} {R}_{11}\)), and (\({R}_{1}, {R}_{6}, {R}_{7}, \mathrm{and} {R}_{12}\)) correspond to (8), (9), and (10), respectively. On the basis of (7), the number of predicted VVs depends on parameter K of the hexagonal diagrams. Thus, in this study, K can be freely set online, and it can control the number of VVs in the prediction stage.

Table 1 Coefficient values according to VSVD regions
Full size table

Figure 3b shows the coordinate labels of \(\alpha -\beta \) VVs in the VSVD region R4 when K is set to 2 and the coefficients \(\updelta \) and \(\upxi \) are identified to be + 1. Apparently, the same sets of voltage labels in the (x, y) coordinate plane \(\left\{{{v}_{\alpha \beta }}^{\left(\mathrm{0,0}\right)}\right.\), \({{v}_{\alpha \beta }}^{\left(\mathrm{0,1}\right)}, {{v}_{\alpha \beta }}^{\left(\mathrm{1,1}\right)}, {{v}_{\alpha \beta }}^{\left(\mathrm{0,2}\right)}, {{v}_{\alpha \beta }}^{\left(\mathrm{1,2}\right)}\), \(\left.{{v}_{\alpha \beta }}^{\left(\mathrm{2,2}\right)}\right\}\) are employed upon initiation for all VSVD regions. However, the value for each voltage label also depends on the corresponding equations, i.e., (8) to (10), and the coefficients in Table 1.

3.2 Proposed preselection strategy

Considering all the VVs for future torque and flux prediction is known to significantly increase the calculation time. Hence, such a strategy is unsuitable for a real control system. Moreover, storing VVs in predefined lookup tables increases system complexity, as in [25]. In addition, the preselection technique of the conventional DSVM-based PTC [25] can affect torque performance because this method needs to regulate the flux and torque simultaneously. Hence, the candidate VVs in the selected DSVM region for the increase or decrease of flux during the torque transient could have a slow torque dynamic response.

In this study, a new preselection strategy based on flux orientation and torque error is proposed to determine the optimal VSVD region per control cycle. Upon the selection of the VSVD region, the corresponding candidate VVs are generated online for the cost function calculation using (8)–(10) and the coefficients in Table 1.

To find the admissible VVs, the proposed PTC-DSVM applies active VVs that ensure the circular motion of the stator flux on the basis of the stator flux orientation (\({\phi }_{s}\)) and torque error (\({T}_{err}={T}_{ref}-{T}_{e}\)) for the flux direction. The flux position is determined as follows:

$${\phi }_{s}=\mathrm{arctan}\left({\psi }_{\beta }/{\psi }_{\alpha }\right).$$
(11)

Thus, the variation in stator flux is obviously controlled by the VV, as in the DTC algorithm, and is proportional to the direction of the applied VV during \({T}_{s}\).

The designed preselection strategy applies the DSVM region with VVs, which ensure fast toque responses while maintaining good flux regulation.

As the 12 SVD regions in Fig. 3 are strictly symmetrical, the \(\alpha -\beta \) plane of flux rotation is divided into 12 sectors, as defined by

$$({\rm Z}-1)\bullet \pi /6\le {S}_{\psi }\left({\rm Z}\right) \le \mathrm{\rm Z}\bullet \pi /6,$$
(12)

where \({S}_{\psi }\) represents the flux sector and \({\rm Z}=1,\dots ,12.\)


In this manner, each flux sector corresponds to one VSVD region, whose VVs are the closest to the circular trajectory of the stator flux in the anticlockwise direction for an increasing torque (\(\mathrm{TI}\)) and in the clockwise direction for a decreasing torque (TD). Figure 4 shows an example in which the stator flux \({\overrightarrow{\psi }}_{s}\) is located at \({S}_{\psi } (1)\). The VSVD region R6 is the optimum region in the anticlockwise direction, and region \({R}_{1}\) is the optimal VSVD region in the clockwise direction. Table 2 lists the optimum VSVD regions for each flux sector. Upon selection of the VSVD region, the VVs are initiated online. The prediction process begins with the evaluation of these VVs using the cost function in (6) to obtain the optimal VV (\({v}^{opt}\)).

Fig. 4
figure 4

Illustration for the VSVD region selection for both flux rotation at Sψ (1)

Full size image
Table 2 Optimal VSVD region for each flux sector
Full size table

3.3 Proposed neutral point voltage balance

The 3L-NPCI consists of two DC link capacitors linked in series. Although good performance can be achieved with PTC-DSVM, this topology can cause NP voltage deviation, which leads to increased voltage stress on the switching device. For good motor drive performance, the top and bottom voltages of the in-series-linked DC link capacitors should be balanced. A common practice is to treat the problem of capacitor voltage balancing by using a separate cost function; this approach requires an additional weighting factor [19,20,21]. However, this practice involves tedious tuning of the cost function weighting factors, thereby leading to high control complexity.


In this study, the proposed balancing technique involves a simple voltage offset based on the maximum and minimum values of the selected VV \({v}^{opt}\). The main advantage of this proposed capacitor voltage balancing scheme is that it is simple and easily employed, thus eliminating the need for a weighting factor or cost function evaluation. In addition, the proposed method does not consider the redundant switching states of small VVs. The proposed NP voltage balancing scheme applies a compensated voltage offset (voff,cv) on the basis of the top capacitor voltage VcT and bottom capacitor voltage VcB in the linear modulation range; it is expressed as follows:

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} v_{off,cv} = \frac{{V_{dc} }}{2} - v_{\max } , \hfill \\ v_{off,cv} = - \frac{{V_{dc} }}{2} - v_{\min } , \hfill \\ \end{gathered} & \begin{gathered} (V_{C}^{T} \ge V_{C}^{B} ) \hfill \\ \hfill \\ (V_{C}^{T} < V_{C}^{B} ) \hfill \\ \end{gathered} \\ \end{array} } \right., $$
(13)

where \({v}_{max}\) and \({v}_{min}\) are the maximum and minimum values of best switching vector \({v}^{opt}\), respectively. Then, the resultant voltage output (vres) can be obtained by injecting the optimum VV obtained from the cost evaluation using the offset voltage in (13) as follows:

$${v}_{res}={v}^{opt}+{v}_{off,cv.}$$
(14)

For convenience, the resultant VV \({v}_{res}\) is implemented on a carrier-based pulse-width modulator to produce switching signals. The entire control algorithm for the proposed method is illustrated in Fig. 5.

Fig. 5
figure 5

Control diagram for the proposed PTC-DSVM

Full size image

3.4 Implementation and experimental results

The performance of the proposed PTC-DSVM for the 3L-NPCI-fed PMSM coupled with an induction machine (load) was verified experimentally by using a functional DSP (TMS320C28346). The specifications of the PMSM parameters are listed in Table 3. The nominal flux and weighting factor were set at 0.58 Wb and 150, respectively. The DC link voltage was 300 V. Therefore, each capacitor voltage was 150 V.

Table 3 PMSM parameters
Full size table

Figure 6 shows the proposed NP voltage balancing control for the PTC-DSVM when the motor operates at 100 rpm and is loaded with 5 Nm. Before the NP voltage balancing control, a large voltage deviation between the capacitor voltages (i.e., VcT and VcB) was clearly observed. After the proposed offset voltage was applied to the best switching VV obtained from the cost function evaluation, the capacitor voltage deviations immediately converged to 150 V.

Fig. 6
figure 6

Experimental result for the control of capacitor voltages balancing in the proposed PTC-DSVM

Full size image

The performance of the proposed PTC-DSVM was evaluated by comparing it with the traditional PTC-DSVM [25] at different motor operations under the same number of VVs (i.e., 37 VVs) and the same weighting factor.

Figure 7 shows the steady-state performance at 600 rpm with a load of 10 Nm for the proposed PTC-DSVM and the traditional PTC-DSVM [25]. From top to bottom, the waveforms shown in Fig. 7 are the flux amplitude, electromagnetic torque, top and bottom capacitor voltages, line-to-line voltage Vab, and A-phase stator current ia. The torque and flux ripples were calculated online using the equation in [26]. Figure 7b clearly shows that the proposed PTC-DSVM improved the steady-state performance with minimal torque and flux ripples while maintaining excellent capacitor voltage balancing. A feature worth mentioning is that the proposed balancing control is applied to the PTC-DSVM methods. In addition, the line-to-line voltage of the proposed PTC-DSVM algorithm had the best shape with reduced voltage spikes. Figures 7a and 7b show that the traditional PTC-DSVM suffered from large torque spikes, which resulted in undesirable output current surges.

Fig. 7
figure 7

Experimental steady-state response at 600 rpm for: a traditional PTC-DSVM [25]; ( b) proposed PTC-DSVM

Full size image

Figure 8 shows the steady-state performance of the PTC-DSVM methods at 100 rpm with a load of 10 Nm. The proposed method showed an excellent reduction in terms of flux/torque ripples, whereas the conventional PTC-DVSM presented torque spikes and current surges. Relative to the traditional PTC-DSVM, the proposed technique had reduced voltage spikes for the line-to-line voltage. Both methods maintained excellent capacitor voltage balancing using the proposed offset voltage.

Fig. 8
figure 8

Experimental steady-state response at 100 rpm for: a traditional PTC-DSVM [25]; ( b) proposed PTC-DSVM

Full size image

Figure 9 illustrates the torque transient performance from 3 to 30 Nm for the proposed and traditional PTC-DSVM methods when the PMSM ran at 300 rpm. Notably, the proposed method demonstrated excellent torque transient performance relative to the traditional method. The poor torque transient performance of the traditional PTC-DSVM [25] was attributed to the selected region of the VVs and the location of the flux position. Notably, the fast torque response depended on the selected VV during the torque transient [28]. Thus, the selected VV region could have inappropriate candidate VVs to achieve a fast torque performance.

Fig. 9
figure 9

Experimental dynamic torque response for: a traditional PTC-DSVM [25]; ( b) proposed PTC-DSVM

Full size image

4 Conclusion

A DSVM-based PTC algorithm was proposed in this study to enhance the performance of a 3L-NPCI-driven PMSM. The study also achieved NP voltage balancing using a simple offset voltage, which was injected after the cost function calculation.

The proposed PTC-DSVM technique significantly improved the performance of the PMSM fed by 3L-NPCI in terms of a reduction in flux, current, and torque ripples while maintaining NP voltage balancing. The main advantage of the proposed PTC-DSVM algorithm is its simplicity. It is also capable of minimizing the torque/flux ripples and achieving a fast torque dynamic performance.