Reliability modeling of a computer system with preventive maintenance and priority subject to maximum operation and repair times

Abstract

The main focus of this paper is on the reliability modelling of a computer system considering the concepts of redundancy, preventive maintenance and priority in repair activities. Two identical units of a computer system are taken—one unit is initially operative and the other is kept as spare in cold standby. In each unit h/w and s/w work together and may fail independently from normal mode. There is a single server who visits the system immediately as and when needed. Server conducts preventive maintenance of the unit (computer system) after a maximum operation time. Repair of the h/w is done at its failure while s/w is upgraded from time to time as per requirements. If server unable to repair the h/w in a pre-specific time (called maximum repair time), h/w is replaced by new one giving some replacement time. Priority to h/w repair is given over s/w up gradation if, in one unit s/w is under up-gradation and h/w fails in another operative unit. The failure time of h/w and s/w follows negative exponential distributions while the distributions of preventive maintenance, h/w repair/replacement and s/w up-gradation times are taken as arbitrary with different probability density functions. The expressions for several reliability and economic measures are derived in steady state using semi-Markov process and regenerative point technique. The graphical study of mean time to system failure (MTSF) and profit function has also been made giving particular values to various parameters and costs.

1 Introduction

Now a day’s computer systems are of growing importance because of their wide use in many areas such as aerospace, transportation, automobiles, home appliances as well as in most of the clerical works. In computer systems, h/w and s/w work together to complete various tasks in a given period of time with full efficiency. In spite of increasing development and availability of new computer technologies, a little work has been dedicated to the reliability modeling of computer systems with independent failures of h/w and s/w components. And, most of the research work has been carried out either considering h/w or s/w alone. Friedman and Tran (1992) tried to establish a combined reliability model for the whole system including both hardware and software. But the technique of redundancy was not used in that paper in order to improve the performance and reliability of the system. First time, Malik and Anand [2010] developed a reliability model for a computer system with independent h/w and s/w failures using the technique of redundancy.

It is observed that continued operation and ageing of operable systems reduce their performance, reliability and safety. Thus, to slow the deterioration process as well as to restore the system in a younger age or state, the preventive maintenance can be conducted after a maximum operation time. Malik and Nandal (2010) analyzed a cold standby system introducing the concept of preventive maintenance after a maximum operation time. Further, the availability of the system can be increased by making replacement of the failed components by new one in case their repair times are too long. Kumar et al. (2012) discussed a computer system with the aspects of maximum operation and repair times. Furthermore, sometimes it becomes necessary to give priority in repair disciplines to one unit over the other not only to reduce the down time but also to minimize the operating cost. Malik and Sureria (2012) studied probabilistically a computer system with priority to h/w repair over s/w replacement.

While considering above observations and facts in mind, here a reliability model for a computer system is developed using the concepts of redundancy, preventive maintenance and priority. Two identical units of a computer system are taken up—one unit is initially operative and the other is kept as spare in cold standby. In each unit h/w and s/w work together and may fail independently from normal mode. There is a single server who visits the system immediately to conduct preventive maintenance of the unit after a maximum operation time as well as to do h/w repair/replacement and s/w up-gradation. If server unable to repair the h/w in a pre-specific time (called maximum repair time), h/w is replaced by new one giving some replacement time. However, only up-gradation of the s/w is made as per requirements giving some up-gradation time. Priority to h/w repair is given over s/w up gradation if, in one unit s/w is under up-gradation and h/w fails in another operative unit. The failure time of h/w and s/w follows negative exponential distributions while the distributions of preventive maintenance, h/w repair/replacement and s/w up-gradation times are taken as arbitrary with different probability density functions. All random variables are statistically independent to each other. The repairs and switch devices are perfect. The expressions for various reliability measures such as mean time to system failure, availability, busy period of the server due to preventive maintenance, busy period of the server due to h/w repair/replacement, busy period of the server due to software up-gradation, expected number of software up-gradations, expected number of hardware replacements and expected number of visits of the server are derived by using semi-Markov process and regenerative point technique. The graphical study of mean time to system failure (MTSF) and profit function has been made giving particular values to various parameters and costs.

2 Transition probabilities and mean sojourn times

Using Fig. 1, simple probabilistic considerations yield the following expressions for the non-zero elements

$$ p_{ij} = Q_{ij} (\infty ) = \int_{0}^{\infty } {q_{ij} (t)dt} \;\text{as} $$

(1)

${\text{p}}_{0 1} = \frac{{\mathop \alpha \nolimits_{0} }}{A}$, ${\text{p}}_{0 2} = \frac{{\mathop {a\lambda }\nolimits_{1} }}{A}$, ${\text{p}}_{0 3} = \frac{{\mathop {b\lambda }\nolimits_{2} }}{A}$, ${\text{p}}_{ 10} = f^{*} \left( {\text{A}} \right),{\text{ p}}_{ 1 6} = \;\frac{{\mathop {a\lambda }\nolimits_{1} }}{A}\left[ {{ 1} - f^{*} \left( {\text{A}} \right)} \right] \, = {\text{ p}}_{ 1 2. 6}$, ${\text{p}}_{ 1 8} = \frac{{\mathop {b\lambda }\nolimits_{2} }}{A}\,\left[ {{ 1} - f^{*} \left( {\text{A}} \right)} \right] = {\text{ p}}_{ 1 3. 8, }$ ${\text{p}}_{ 1. 1 3} = \frac{{\mathop \alpha \nolimits_{0} }}{A}\left[ {{ 1} - f^{*} \left( {\text{A}} \right)} \right] \, = {\text{p}}_{ 1 1. 1 3}$, ${\text{p}}_{ 20} = g^{*} \left( {\text{B}} \right)$, ${\text{p}}_{ 2 4} = \frac{{\mathop \beta \nolimits_{0} }}{B}\left[ {{ 1} - g^{*} \left( {\text{B}} \right)} \right]$, ${\text{p}}_{ 2 5} = \frac{{\mathop \alpha \nolimits_{0} }}{B}\left[ {{ 1} - g^{*} \left( {\text{ B}} \right)} \right]{\text{p}}_{ 2. 1 1} =$ $\frac{{\mathop {b\lambda }\nolimits_{2} }}{B}\left[ {{ 1} - g^{*} \left( {\text{B}} \right)} \right]$, ${\text{p}}_{ 2. 1 2} = \frac{{\mathop {a\lambda }\nolimits_{1} }}{B}\left[ {{ 1} - g^{*} \left( {\text{B}} \right)} \right]$, ${\text{p}}_{ 30} = h^{*} \left( {\text{A}} \right),{\text{ p}}_{ 3 7} = \frac{{\mathop {a\lambda }\nolimits_{1} }}{A}\left[ {{ 1} - h^{*} \left( {\text{A}} \right)} \right]$ _, ${\text{p}}_{ 3 9} = \frac{{\mathop \alpha \nolimits_{0} }}{A}\left[ {{ 1} - h^{*} \left( {\text{A}} \right)} \right] = {\text{ p}}_{ 3, 1. 9}$, ${\text{p}}_{ 40} = m^{*} \left( {\text{A}} \right)$, ${\text{p}}_{ 3, 10} = \frac{{\mathop {b\lambda }\nolimits_{2} }}{A}\left[ {{ 1} - h^{*} \left( {\text{A}} \right)} \right] = {\text{ p}}_{ 3 3. 10}$ _, ${\text{p}}_{ 5 1} = g^{*} \left( {{{\upbeta}}_{0} } \right)$, ${\text{p}}_{ 5, 1 6} = { 1} - g^{*} \left( {{{\upbeta}}_{0} } \right)$, ${\text{p}}_{ 4. 1 7} = \frac{{\mathop \alpha \nolimits_{0} }}{A}\left[ {{ 1} - m^{*} \left( {\text{A}} \right)} \right] = {\text{ p}}_{ 4, 1. 1 7}$, ${\text{p}}_{ 6 2} = f^{*} \left( 0 \right)$, ${\text{p}}_{ 7 3} = {\text{g}}^{*} \left( 0 \right)$, ${\text{p}}_{ 8 3} = f^{*} \left( 0 \right)$, ${\text{p}}_{ 9 1} = {\text{ h}}^{*} \left( 0 \right)$, ${\text{p}}_{ 10. 3} = h^{*} \left( 0 \right)$, ${\text{p}}_{ 1 1. 3} = g^{*} \left( {{{\upbeta}}_{0} } \right)$, ${\text{p}}_{ 1 1. 1 4} = { 1} - g^{*} \left( {{{\upbeta}}_{0} } \right)$, ${\text{p}}_{ 4, 1 8} = \frac{{\mathop {b\lambda }\nolimits_{2} }}{A}\left[ {{ 1} - m^{*} \left( {\text{A}} \right)} \right] \, = {\text{ p}}_{ 4 3. 1 8}$, ${\text{p}}_{ 1 2. 2} = g^{*} \left( {{{\upbeta}}_{0} } \right)$, ${\text{p}}_{ 1 2. 1 5} = { 1} - g^{*} \left( {{{\upbeta}}_{0} } \right)$, ${\text{p}}_{ 1 3. 1} = f^{*} \left( 0 \right)$,${\text{p}}_{ 1 4. 3} = m^{*} \left( 0 \right)$, ${\text{p}}_{ 4 2. 1 9} = {\text{p}}_{ 4. 1 9} = \frac{{\mathop {a\lambda }\nolimits_{1} }}{A}\left[ {{ 1} - m^{*} \left( {\text{A}} \right)} \right]$, ${\text{p}}_{ 1 5. 2} = m^{*} \left( 0 \right)$, ${\text{p}}_{ 1 6. 1} = m^{*} \left( 0 \right)$,${\text{p}}_{ 1 7. 1} = m^{*} \left( 0 \right)$, ${\text{p}}_{ 1 8. 3} = m^{*} \left( 0 \right)$, ${\text{P}}_{19.2} = m^{*} \left( 0 \right)$, ${\text{p}}_{ 2 1. 5} = \frac{{\mathop \alpha \nolimits_{0} }}{B}\left[ {{ 1} - g^{*} \left( {\text{B}} \right)} \right]g^{*} \left( {{{\upbeta}}_{0} } \right)$, ${\text{p}}_{ 2 1. 1 6, 5} = \frac{{\mathop \alpha \nolimits_{0} }}{B}\left[ {{ 1} - g^{*} \left( {\text{B}} \right)} \right]\left[ { 1- g^{*} \left( {{{\upbeta}}_{0} } \right)} \right]$, ${\text{p}}_{ 2 3. 1 1} = \frac{{\mathop {b\lambda }\nolimits_{2} }}{B}\left[ {{ 1} - g^{*} \left( {\text{B}} \right)} \right]\left[ {g^{*} \left( {{{\upbeta}}_{0} } \right)} \right]$, ${\text{p}}_{ 2 3. 1 1, 1 4} = \frac{{\mathop {b\lambda }\nolimits_{2} }}{B}\left[ {{ 1} - g^{*} \left( {\text{B}} \right)} \right]\left[ { 1- g^{*} \left( {{{\upbeta}}_{0} } \right)} \right]$, ${\text{p}}_{ 2 2. 1 2} = \frac{{\mathop {a\lambda }\nolimits_{1} }}{B}\left[ {{ 1} - g^{*} \left( {\text{B}} \right)} \right]g^{*} \left( {{{\upbeta}}_{0} } \right)$, ${\text{p}}_{ 2 2. 1 2, 1 5} = \frac{{\mathop {a\lambda }\nolimits_{1} }}{B}\left[ {{ 1} - g^{*} \left( {\text{B}} \right)} \right]\left[ { 1- g^{*} \left( {{{\upbeta}}_{0} } \right)} \right]$

Fig. 1

.

where

$$ \text{A} = \mathop {a\lambda }\nolimits_{1} + \mathop {b\lambda }\nolimits_{2} + \mathop \alpha \nolimits_{0} \;{\text{and B}} = {\text{ a}}\lambda_{ 1} + {\text{b}}\lambda_{ 2} + \alpha_{0} + {{\upbeta}}_{0} $$

(2)

It can be easily verified that ${\text{p}}_{0 1} + {\text{p}}_{0 2} + {\text{p}}_{0 3} = {\text{ p}}_{ 10} + {\text{p}}_{ 1 6} + {\text{p}}_{ 1 8} + {\text{p}}_{ 1. 1 3} = {\text{ p}}_{ 20} + {\text{p}}_{ 2 4} + {\text{p}}_{ 2 5} + {\text{ p}}_{ 2, 1 1} + {\text{p}}_{ 2. 1 2}$

$$ \begin{gathered} = {\text{ p}}_{ 30} + {\text{p}}_{ 3 7} + {\text{p}}_{ 3 9} + {\text{p}}_{ 3, 10} = {\text{ p}}_{ 40} + {\text{p}}_{ 4. 1 7} + {\text{p}}_{ 4. 1 8} + {\text{ p}}_{ 4. 1 9} = {\text{ p}}_{ 5. 1} + {\text{ p}}_{ 5. 1 6} = {\text{ p}}_{ 6 2} = {\text{ p}}_{ 7 3} = {\text{ p}}_{ 8 3} = {\text{ p}}_{ 9 1} = {\text{ p}}_{ 10. 3} \hfill \\ = {\text{ p}}_{ 1 1. 3} + {\text{ p}}_{ 1 1. 1 4} =_{{}} {\text{p}}_{ 1 2. 2} + {\text{ p}}_{ 1 2. 1 5} = {\text{ p}}_{ 1 3. 1} = {\text{ p}}_{ 1 4. 1} = {\text{p}}_{ 1 5. 2} = {\text{ p}}_{ 1 6. 1} = {\text{ p}}_{ 1 7. 1} =_{{}} {\text{p}}_{ 1 8. 3} = {\text{p}}_{ 1 9. 4} = {\text{p}}_{ 10} + {\text{p}}_{ 1 2. 6} + {\text{ p}}_{ 1 1. 1 3} + {\text{p}}_{ 1 3. 8} = {\text{p}}_{ 20} + {\text{p}}_{ 2 4} + {\text{p}}_{ 2 1. 5} + {\text{p}}_{ 2 1, 1 6. 5} + {\text{p}}_{ 2 3, 1 1} + {\text{p}}_{ 2 3. 1 1, 1 4} + {\text{p}}_{ 2 2, 1 2} + {\text{p}}_{ 2 2. 1 2, 1 5} \hfill \\ = {\text{p}}_{ 30} + {\text{p}}_{ 3 1. 9} + {\text{p}}_{ 3. 7} + {\text{p}}_{ 3 3. 10} = {\text{p}}_{ 40} + {\text{p}}_{ 4 1. 1 7} + {\text{ p}}_{ 4 2. 1 9} + {\text{ p}}_{ 4 3. 1 8} = 1\hfill \\ \end{gathered} $$

(3)

The Mean Sojourn Times (μ_i) in the state S_i are

$$ \begin{gathered} {{\upmu}}_{0} = \frac{1}{{\mathop {a\lambda }\nolimits_{1} + \mathop {b\lambda }\nolimits_{2} + \mathop \alpha \nolimits_{0} }},\;{{\upmu}}_{ 1} = \frac{1}{{\mathop {a\lambda }\nolimits_{1} + \mathop {b\lambda }\nolimits_{2} + \mathop \alpha \nolimits_{0} + \alpha }},\;{{\upmu}}_{ 2} = \frac{1}{{\mathop {a\lambda }\nolimits_{1} + \mathop {b\lambda }\nolimits_{2} + \mathop \alpha \nolimits_{0} + \theta + \mathop \beta \nolimits_{0} }} \hfill \\ {{\upmu}}_{ 3} = \frac{1}{{\mathop {a\lambda }\nolimits_{1} + \mathop {b\lambda }\nolimits_{2} + \mathop \alpha \nolimits_{0} + \mathop \beta \nolimits_{{}} }},\;{{\upmu}}_{ 4} = \frac{1}{{\mathop {a\lambda }\nolimits_{1} + \mathop {b\lambda }\nolimits_{2} + \mathop \alpha \nolimits_{0} + \mathop \gamma \nolimits_{{}} }} \hfill \\ \end{gathered} $$

(4)

3 Reliability and Mean Time to System Failure (MTSF)

Let ϕ_i(t) be the cdf of first passage time from the regenerative state i to a failed state. Regarding the failed state as absorbing state, we have the following recursive relations for

ϕ_i (t) as

$$ \phi_{i} (t) = \sum\limits_{j} {Q_{i,j} (t)\circledS \phi_{j}(t)} + \sum\limits_{k} {Q_{i,k} (t)} $$

(5)

where j is an un-failed regenerative state to which the given regenerative state i can transit and k is a failed state to which the state i can transit directly.

Taking LT of above relation (5) and solving for $\tilde{\phi }_{0} (s)$

We have

$$ {\text{R}}*\left( {\text{s}} \right) \, = \frac{{1 - \tilde{\phi }_{0} (s)}}{s} $$

(6)

The reliability of the system model can be obtained by taking Laplace inverse transform of (6).

The mean time to system failure (MTSF) is given by

$$ {\text{MTSF }} = \mathop {\lim }\limits_{s \to o} \frac{{1 - \tilde{\phi }_{0} (s)}}{s}\; = \frac{{N_{1} }}{{D_{1} }}\;{\text{where}} $$

(7)

${\text{N}}_{ 1} = \mu_{0} + p_{01} \mu_{1} + p_{02} \mu_{2} + p_{03} \mu_{3} + p_{24} p_{02} \mu_{4}$ and ${\text{D}}_{ 1} = 1 - p_{01} p_{10} - p_{02} p_{20} - p_{03} p_{30} - p_{02} p_{24} p_{40}$

4 Steady state availability

Let A_i(t) be the probability that the system is in up-state at instant ‘t’ given that the system entered regenerative state i at t = 0. The recursive relations for A_i (t) are given as

$$ A_{i} \left( t \right) = M_{i} \left( t \right) + \sum\limits_{j} {q_{i,j}^{(n)} \left( t \right)\copyright\;A_{j} \left( t \right)} $$

(8)

where j is any successive regenerative state to which the regenerative state i can transit through n transitions. M_i(t) is the probability that the system is up initially in state $S_{i} \in E$ is up at time t without visiting to any other regenerative state, we have

$$ \begin{gathered} M_{0} (t) = e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} ,M_{1} (t) = e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} \overline{F(t)} ,M_{2} (t) = e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} + \beta_{0} )t}} \overline{G(t)} \hfill \\ M_{3} (t) = e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} \overline{H(t)} ,\;M_{4} (t) = e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} \overline{M(t)} \hfill \\ \end{gathered} $$

(9)

Taking LT of above relations (8) and solving for $A_{0}^{*} (s)$, the steady state availability is given by

$$ A_{0} (\infty ) = \mathop {\lim }\limits_{s \to 0} sA_{0}^{*} (s)\; = \frac{{N_{2} }}{{D_{2} }}\;{\text{where}} $$

(10)

N₂ = μ₀ {(1 − p_11.13) [(1 − p_33.10 − p₇₃ p₃₇) (1 − p_22.12 − p_22.12.15 − p₂₄p_42.19)] − p_12.6 [(1 − p_33.10 − p₇₃ p₃₇) (p_22.5 + p_21.5.16 + p_41.17p₂₄) + p_31.9(p_23.11 + p_23.11,14 + p_43.18p₂₄)] − p_13.8[(1 − p_22.12 − p_22.12.15 − p₂₄p_42.19)p_31.9]} + $\mu_{1}$ {p₀₁ (1 − p_33.10 − p₇₃ p₃₇) (1 − p_22.12 − p_22.12.15 − p₂₄p_42.19) + p₀₂ [(1 − p_33.10 − p₇₃ p₃₇) (p_21.5 + p_21.5.16 + p_41.17p₂₄) + p_31.9(p_23.11 + p_23.11,14 + p_43.18p₂₄)] + p₀₃[(1 − p_22.12 − p_22.12.15 − p₂₄p_42.19)p_31.9]} + ($\mu_{2}$+p₂₄ $\mu_{4}$){p₀₁ [(1 − p_33.10 − p₇₃ p₃₇)p_12.6 + p₀₂{(1 − p_11.13) (1 − p_33.10 − p₇₃ p₃₇) − p_13.8p_31.9] + p₀₃ p_31.9p_12.6} + ($\mu_{3}$){p₀₁ [p_12.6(p_23.11 + p_23.11,14 + p_43.18p₂₄) + (1 − p_22.12 − p_22.12.15 − p₂₄p_42.19)p_13.8] + p₀₂[(1 − p_11.13) (p_23.11 + p_23.11,14 + p_43.18p₂₄) + p_13.8 (p_21.5 + p_21.5.16 + p_41.17p₂₄)] + p₀₃[(1 − p_11.13) (1 − p_22.12 − p_22.12.15 − p₂₄p_42.19) − p_12.6 (p_21.5 + p_21.5.16 + p_41.17p₂₄)]}

and

D₂ = μ₀ {(1 − p_11.13) [(1 − p_33.10 − p₇₃ p₃₇) (1 − p_22.12 − p_22.12.15 − p₂₄p_42.19)] − p_12.6 [(1 − p_33.10 − p₇₃ p₃₇) (p_22.5 + p_21.5.16 + p_41.17p₂₄) + p_31.9(p_23.11 + p_23.11,14 + p_43.18p₂₄)] − p_13.8[(1 − p_22.12 − p_22.12.15 − p₂₄p_42.19)p_31.9]} + $\mu^{\prime}_{1}$ {p₀₁ (1 − p_33.10 − p₇₃ p₃₇) (1 − p_22.12 − p_22.12.15 − p₂₄p_42.19) + p₀₂ [(1 − p_33.10 − p₇₃ p₃₇) (p_21.5 + p_21.5.16 + p_41.17p₂₄) + p_31.9(p_23.11 + p_23.11,14 + p_43.18p₂₄)] + p₀₃[(1 − p_22.12 − p_22.12.15 − p₂₄p_42.19)p_31.9]} + ($\mu^{\prime}_{2}$+p₂₄ $\mu^{\prime}_{4}$){p₀₁ [(1 − p_33.10 − p₇₃ p₃₇)p_12.6 + p₀₂{(1 − p_11.13) (1 − p_33.10 − p₇₃ p₃₇) − p_13.8p_31.9] + p₀₃ p_31.9p_12.6} + ($\mu^{\prime}_{3}$+p₃₇ $\mu_{7}$){p₀₁ [p_12.6(p_23.11 + p_23.11,14 + p_43.18p₂₄) + (1 − p_22.12 − p_22.12.15 − p₂₄p_42.19)p_13.8] + p₀₂[(1 − p_11.13) (p_23.11 + p_23.11,14 + p_43.18p₂₄) + p_13.8 (p_21.5 + p_21.5.16 + p_41.17p₂₄)] + p₀₃[(1 − p_11.13) (1 − p_22.12 − p_22.12.15 − p₂₄p_42.19) − p_12.6 (p_21.5 + p_21.5.16 + p_41.17p₂₄)]}

5 Busy period analysis for server

Let $B_{i}^{P} (t),$ $B_{i}^{R} (t), \,$ $B_{i}^{S} (t)\,\,{\text{and}}$ $B_{i}^{HRp} (t)$be the probabilities that the server is busy in preventive maintenance of the system, repairing the unit due to hardware failure, up-gradation of the software and hardware replacement at an instant ‘t’ given that the system entered state i at t = 0. The recursive relations for $B_{i}^{P} (t),$ $B_{i}^{R} (t), \,$ $B_{i}^{S} (t)\,\,{\text{and}}$ $B_{i}^{HRp} (t)$ are as follows

$$ \begin{gathered} B_{i}^{p} \left( t \right) = W_{i} \left( t \right) + \sum\limits_{j} {q_{i,j}^{(n)} \left( t \right)\copyright} B_{j}^{p} \left( t \right),\;B_{i}^{R} \left( t \right) = W_{i} \left( t \right) + \sum\limits_{j} {q_{i,j}^{(n)} \left( t \right)\copyright} B_{j}^{R} \left( t \right) \hfill \\ B_{i}^{S} \left( t \right) = W_{i} \left( t \right) + \sum\limits_{j} {q_{i,j}^{(n)} \left( t \right)\copyright} B_{j}^{S} \left( t \right)\,\,\,{\text{and}} B_{i}^{HRp} \left( t \right) = W_{i} \left( t \right) + \sum\limits_{j} {q_{i,j}^{(n)} \left( t \right)\copyright} B_{j}^{HRp} \left( t \right) \hfill \\ \end{gathered} $$

(11)

where j is any successive regenerative state to which the regenerative state i can transit through n transitions. Let W_i(t) be the probability that the server is busy in state S_i due to preventive maintenance, hardware and software failure up to time t without making any transition to any other regenerative state or returning to the same via one or more non-regenerative states. We have$W_{1}^{{}} = e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} \overline{F} (t) + (\alpha_{0} e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} \copyright{ 1)}\overline{{{\text{F}}_{{}} }} (t) + (a\lambda_{1} e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} \copyright{ 1)}\overline{F} (t) + (b\lambda_{2} e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} \copyright{ 1)}\overline{F} (t)$ $W_{2}^{{}} = e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} + \beta_{0} )t}} \overline{G} (t) + (\alpha_{0} e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} + \beta_{0} )t}} )\overline{{{\text{G}}_{{}} }} (t) + (a\lambda_{1} e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} + \beta_{0} )t}} \copyright{ 1)}\overline{G} (t) + (b\lambda_{2} e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} + \beta_{0} )t}} \copyright{ 1)}\overline{G} (t)$ $W_{3}^{{}} = e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} \overline{H} (t) + (\alpha_{0} e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} \copyright 1 )\overline{{{\text{H}}_{{}} }} (t) + (a\lambda_{1} e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} )\overline{H} (t) + (b\lambda_{2} e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} \copyright 1 )\overline{H} (t)$ $W_{4}^{{}} = e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} \overline{M} (t) + (\alpha_{0} e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} \copyright{ 1)}\overline{{{\text{M}}_{{}} }} (t) + (a\lambda_{1} e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} \copyright{ 1)}\overline{M} (t) + (b\lambda_{2} e^{{ - (a\lambda_{1} + b\lambda_{2} + \alpha_{0} )t}} \copyright{ 1)}\overline{M} (t)$, Taking LT of above relations (11). And, solving for $B_{i}^{*P} (s)$,$B_{i}^{*R} (s)$, $B_{i}^{*S} (s)\,\,{\text{and}}$ $B_{i}^{*HRp} (s)$, the time for which server is busy due to preventive maintenance, h/w repair/replacement and s/w up-gradation respectively is given by

$$ B_{0}^{P} = \mathop {\lim }\limits_{s \to 0} sB_{0}^{*P} (s)\;= \;\frac{{N_{3}^{P} }}{{D_{2} }},B_{0}^{S} = \mathop {\lim}\limits_{s \to 0} sB_{0}^{*S} (s) = \frac{{N_{3}^{S} }}{{D_{2}}},B_{0}^{R} = \mathop {\lim }\limits_{s \to 0} sB_{0}^{*R} (s) =\frac{{N_{3}^{R} }}{{D_{2} }} $$

And

$$ B_{0}^{HRp} = \mathop {\lim }\limits_{s \to 0} \,sB_{0}^{*HRp} (s) = \frac{{N_{3}^{HRp} }}{{D_{2} }} $$

(12)

where

$$ \begin{gathered} N_{3}^{P} = \mathop W\nolimits_{1}^{*} (0)\{ {\text{p}}_{0 1} \left( { 1- {\text{ p}}_{ 3 3. 10} - {\text{ p}}_{ 7 3} {\text{p}}_{ 3 7} } \right) \, \left( { 1- {\text{ p}}_{ 2 2. 1 2} - {\text{ p}}_{ 2 2. 1 2. 1 5} - {\text{ p}}_{ 2 4} {\text{p}}_{ 4 2. 1 9} } \right) + \, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,{\text{p}}_{0 2} \left[ {\left( { 1- {\text{ p}}_{ 3 3. 10} - {\text{ p}}_{ 7 3} {\text{p}}_{ 3 7} } \right) \, \left( {{\text{p}}_{ 2 1. 5} + {\text{ p}}_{ 2 1. 5. 1 6} + {\text{ p}}_{ 4 1. 1 7} {\text{p}}_{ 2 4} } \right) + {\text{ p}}_{ 3 1. 9} \left( {{\text{p}}_{ 2 3. 1 1} + {\text{ p}}_{ 2 3. 1 1, 1 4} + {\text{ p}}_{ 4 3. 1 8} {\text{p}}_{ 2 4} } \right)} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\, + {\text{ p}}_{0 3} \left[ {\left( { 1- {\text{ p}}_{ 2 2. 1 2} - {\text{ p}}_{ 2 2. 1 2. 1 5} - {\text{ p}}_{ 2 4} {\text{p}}_{ 4 2. 1 9} } \right){\text{p}}_{ 3 1. 9} } \right]\} \hfill \\ N_{3}^{R} = \mathop W\nolimits_{2}^{*} (0)\{ {\text{p}}_{0 1} \left[ {\left( { 1- {\text{ p}}_{ 3 3. 10} - {\text{ p}}_{ 7 3} {\text{p}}_{ 3 7} } \right){\text{p}}_{ 1 2. 6} + {\text{ p}}_{0 2} \{ \left( { 1-_{{}} {\text{p}}_{ 1 1. 1 3} } \right) \, \left( { 1- {\text{ p}}_{ 3 3. 10} - {\text{ p}}_{ 7 3} {\text{p}}_{ 3 7} } \right) - {\text{ p}}_{ 1 3. 8} {\text{p}}_{ 3 1. 9} } \right] + \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,{\text{ p}}_{0 3} {\text{p}}_{ 3 1. 9} {\text{p}}_{ 1 2. 6} \} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, + \mathop W\nolimits_{7}^{*} (0){\text{p}}_{37} \{ {\text{p}}_{0 1} \left[ {{\text{p}}_{ 1 2. 6} \left( {{\text{p}}_{ 2 3. 1 1} + {\text{ p}}_{ 2 3. 1 1, 1 4} + {\text{ p}}_{ 4 3. 1 8} {\text{p}}_{ 2 4} } \right) + \, \left( { 1- {\text{ p}}_{ 2 2. 1 2} - {\text{ p}}_{ 2 2. 1 2. 1 5} - {\text{ p}}_{ 2 4} {\text{p}}_{ 4 2. 1 9} } \right){\text{p}}_{ 1 3. 8} } \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, + {\text{ p}}_{0 2} [\left( { 1-_{{}} {\text{p}}_{ 1 1. 1 3} } \right) \, \left( {{\text{p}}_{ 2 3. 1 1} + {\text{ p}}_{ 2 3. 1 1, 1 4} + {\text{ p}}_{ 4 3. 1 8} {\text{p}}_{ 2 4} } \right) + {\text{ p}}_{ 1 3. 8} \left( {{\text{p}}_{ 2 1. 5} + {\text{ p}}_{ 2 1. 5. 1 6} + {\text{ p}}_{ 4 1. 1 7} {\text{p}}_{ 2 4} } \right)\left] { + {\text{p}}_{0 3} } \right[ \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\left( { 1-_{{}} {\text{p}}_{ 1 1. 1 3} } \right)\left( { 1- {\text{ p}}_{ 2 2. 1 2} - {\text{ p}}_{ 2 2. 1 2. 1 5} - {\text{ p}}_{ 2 4} {\text{p}}_{ 4 2. 1 9} } \right) - {\text{ p}}_{ 1 2. 6} \left( {{\text{p}}_{ 2 1. 5} + {\text{ p}}_{ 2 1. 5. 1 6} + {\text{ p}}_{ 4 1. 1 7} {\text{p}}_{ 2 4} } \right)]\} \hfill \\ N_{3}^{S} = \mathop W\nolimits_{3}^{*} (0)\{ {\text{p}}_{0 1} \left[ {{\text{p}}_{ 1 2. 6} \left( {{\text{p}}_{ 2 3. 1 1} + {\text{ p}}_{ 2 3. 1 1, 1 4} + {\text{ p}}_{ 4 3. 1 8} {\text{p}}_{ 2 4} } \right) + \, \left( { 1- {\text{ p}}_{ 2 2. 1 2} - {\text{ p}}_{ 2 2. 1 2. 1 5} - {\text{ p}}_{ 2 4} {\text{p}}_{ 4 2. 1 9} } \right){\text{p}}_{ 1 3. 8} } \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, + {\text{ p}}_{0 2} [\left( { 1-_{{}} {\text{p}}_{ 1 1. 1 3} } \right) \, \left( {{\text{p}}_{ 2 3. 1 1} + {\text{ p}}_{ 2 3. 1 1, 1 4} + {\text{ p}}_{ 4 3. 1 8} {\text{p}}_{ 2 4} } \right) + {\text{p}}_{ 1 3. 8} \left( {{\text{p}}_{ 2 1. 5} + {\text{ p}}_{ 2 1. 5. 1 6} + {\text{ p}}_{ 4 1. 1 7} {\text{p}}_{ 2 4} } \right)\left] { + {\text{p}}_{0 3} } \right[ \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\left( { 1-_{{}} {\text{p}}_{ 1 1. 1 3} } \right) \, \left( { 1- {\text{ p}}_{ 2 2. 1 2} - {\text{ p}}_{ 2 2. 1 2. 1 5} - {\text{ p}}_{ 2 4} {\text{p}}_{ 4 2. 1 9} } \right) - {\text{ p}}_{ 1 2. 6} \left( {{\text{p}}_{ 2 1. 5} + {\text{ p}}_{ 2 1. 5. 1 6} + {\text{ p}}_{ 4 1. 1 7} {\text{p}}_{ 2 4} } \right)]\} \hfill \\ N_{3}^{HRp} = \mathop W\nolimits_{4}^{*} p_{24} [p_{01} (1 - p_{33.10} - {\text{ p}}_{ 7 3} {\text{p}}_{ 3 7} )p_{12.6} + p_{02} \{ (1 - p_{33.10} - {\text{ p}}_{ 7 3} {\text{p}}_{ 3 7} )(1 - p_{11.13} ) - p_{13.8} p_{31.9} )\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, + p_{03} p_{12.6} p_{31.9} ]\,\,{\text{and D2 is already mentioned}} .\hfill \\ \end{gathered} $$

6 Expected number of h/w replacements and s/w up-gradations

Let $R_{i}^{H} (t)\,\,{\text{and}}$ $R_{i}^{S} (t)$the expected number of h/w replacements and software up-gradations by the server in (0, t] given that the system entered the regenerative state i at t = 0. The recursive relations for $R_{i}^{H} (t)\,\,{\text{and}}$ $R_{i}^{S} (t)$ are given as

$$ R_{i}^{H} (t) = \sum\limits_{j} {q_{i,j}^{(n)} (t)\circledS \left[{\delta_{j} + R_{j}^{H} (t)} \right],\;R_{i}^{S} (t) = \sum\limits_{j} {q_{i,j}^{(n)} (t)\circledS \left[ {\delta_{j} + R_{j}^{S}(t)} \right]^{{}} } } $$

(13)

where j is any regenerative state to which the given regenerative state i transits and $\delta j$ = 1, if j is the regenerative state where the server does job afresh, otherwise $\delta j$ = 0.

Taking LST of relations and, solving for $\tilde{R}_{0}^{H} (s)$ and $\tilde{R}_{0}^{S} (s)$. The expected numbers of h/w replacements per unit time and software up-gradations per unit time are respectively given by

$$ R_{0}^{H} (\infty ) = \mathop {\lim }\limits_{s \to 0} s {R}_{0}^{H} (s) = \frac{{N_{4}^{H} }}{{D_{2} }}\,{\text{and}} \;\tilde{R}_{0}^{S} (\infty ) = \mathop {\lim }\limits_{s \to 0} s\tilde{R}_{0}^{S} (s) = \frac{{N_{4}^{S} }}{{D_{2} }} $$

(14)

$$ \begin{gathered} N_{4}^{H} = (p_{24} + p_{21.5,16} + p_{22,12,15} + p_{23,11.14} )\{ p_{01} (1 - p_{33.10} - {\text{p}}_{ 7 3} {\text{p}}_{ 3 7} )p_{12.6} + p_{02} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,[(1 - p_{11.13} )(1 - p_{33.10} - {\text{p}}_{ 7 3} {\text{p}}_{ 3 7} ) - p_{31.9} p_{13.8} ] + p_{03} p_{31.9} p_{12.6} \} \,\,\,\,\,\,\,\,\,\,\, \hfill \\ N_{4}^{S} = (p_{30} + p_{33,10} + p_{31.9} )\{ {\text{p}}_{0 1} \left[ \begin{gathered} {\text{p}}_{ 1 2. 6} \left( {{\text{p}}_{ 2 3. 1 1} + {\text{ p}}_{ 2 3. 1 1, 1 4} + {\text{ p}}_{ 4 3. 1 8} {\text{p}}_{ 2 4} } \right) + \hfill \\ \, \left( { 1- {\text{ p}}_{ 2 2. 1 2} - {\text{ p}}_{ 2 2. 1 2. 1 5} - {\text{ p}}_{ 2 4} {\text{p}}_{ 4 2. 1 9} } \right){\text{p}}_{ 1 3. 8} \hfill \\ \end{gathered} \right] \hfill \\ \,\,\,\,\,\,\,\, + {\text{ p}}_{0 2} \left[ {\left( { 1-_{{}} {\text{p}}_{ 1 1. 1 3} } \right) \, \left( {{\text{p}}_{ 2 3. 1 1} + {\text{ p}}_{ 2 3. 1 1, 1 4} + {\text{ p}}_{ 4 3. 1 8} {\text{p}}_{ 2 4} } \right) + {\text{ p}}_{ 1 3. 8} \left( {{\text{p}}_{ 2 1. 5} + {\text{ p}}_{ 2 1. 5. 1 6} + {\text{ p}}_{ 4 1. 1 7} {\text{p}}_{ 2 4} } \right)} \right] \hfill \\ \,\,\,\,\,\,\,\, + {\text{p}}_{0 3} \left[ {\left( { 1-_{{}} {\text{p}}_{ 1 1. 1 3} } \right) \, \left( { 1- {\text{ p}}_{ 2 2. 1 2} - {\text{ p}}_{ 2 2. 1 2. 1 5} - {\text{ p}}_{ 2 4} {\text{p}}_{ 4 2. 1 9} } \right) - {\text{ p}}_{ 1 2. 6} \left( {{\text{p}}_{ 2 1. 5} + {\text{ p}}_{ 2 1. 5. 1 6} + {\text{ p}}_{ 4 1. 1 7} {\text{p}}_{ 2 4} } \right)} \right]\} \hfill \\ \end{gathered} $$

where D₂ is already mentioned.

7 Expected number of visits by the server

Let N_i(t) be the expected number of visits by the server in (0, t] given that the system entered the regenerative state i at t = 0. The recursive relations for N_i(t) are given as

$$ N_{i}^{{}} (t) = \sum\limits_{j} {q_{i,j}^{(n)} (t)\circledS \left[{\delta_{j} + N_{j}^{{}} (t)} \right]^{{}} } $$

(15)

where j is any regenerative state to which the given regenerative state i transits and $\delta j$ = 1, if j is the regenerative state where the server does job afresh, otherwise $\delta j$ = 0. Taking LST of relation (15) and solving for $\tilde{N}_{0} (s)$. The expected number of visit per unit time by the server are given by

$$ N_{0} (\infty ) = \mathop {\lim }\limits_{s \to 0} s \tilde{N}_{0} (s)\; = \;\frac{{N_{5} }}{{D_{2} }},\;{\text{where}} $$

(16)

N₅ = (p₀₁ + p₀₂ + p₀₃){(1 − p_11.13) [(1 − p_33.10 − p₇₃ p₃₇) (1 − p_22.12 − p_22.12.15 − p₂₄p_42.19)] − p_12.6 [(1 − p_33.10 − p₇₃ p₃₇) (p_22.5 + p_21.5.16 + p_41.17p₂₄) + p_31.9(p_23.11 + p_23.11,14 + p_43.18p₂₄)] − p_13.8[(1 − p_22.12 − p_22.12.15 − p₂₄p_42.19)p_31.9]}

8 Profit analysis

The profit incurred to the system model in steady state can be obtained as

$$ P = K0A0 - K1\mathop B\nolimits_{0}^{P} - \,K2\mathop B\nolimits_{0}^{R} -\, K3\mathop B\nolimits_{0}^{S} -\, K4\mathop B\nolimits_{0}^{HRp} - \,K5\mathop R\nolimits_{0}^{H} - K6\mathop R\nolimits_{0}^{S} - \,K7\mathop N\nolimits_{0}^{{}} $$

(17)

K₀ :

Revenue per unit up-time of the system

K₁ :

Cost per unit time for which server is busy due preventive maintenance

K₂ :

Cost per unit time for which server is busy due to hardware failure

K₃ :

Cost per unit time for which server is busy in software up-gradation

K₄ :

Cost per unit time for which server is busy in h/w replacement

K₅ :

Cost per unit time h/w replacement

K₆ :

Cost per unit time s/w up-gradation

K₇ :

Cost per unit time visit by the server

9 Conclusion

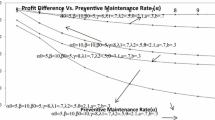
In the present study, the numerical results for mean time to system failure (MTSF) and profit are obtained giving some particular values to various parameters and costs taking $g(t) = \theta e^{ - \theta t}$, $h(t) = \beta e^{ - \beta t}$, $f(t) = \alpha e^{ - \alpha t}$ and $m(t) = \gamma e^{ - \gamma t}$. The graphs for MTSF and profit are drawn with respect to preventive maintenance rate (α) for fixed values of other parameters including a = 0.7 and b = 0.3 as shown respectively in Figs. 2 and 3. These figures indicate that MTSF and profit increase with the increase of preventive maintenance rate (α), maximum repair time (β₀), and h/w repair rate (θ). But the values of these measures decrease with the increase of maximum operation time (α₀). Thus finally it is concluded that a computer system in which chances of h/w failure are high can be made more reliable and profitable to use

Fig. 2

.

Fig. 3

.

• (i) By taking one more unit (computer system) in cold standby.

• (ii) By conducting preventive maintenance of the system after a specific period of operation.

• (iii) By giving maximum repair time to the server for h/w repair in case priority is given to the h/w repair over s/w up-gradation.

• (iv) By making s/w up-gradation immediately as per requirements in case s/w fails to execute the desired functions properly