1 Introduction

Complex systems generally tend to be considered by high diversity and high interconnectedness. Multiple adaptive pathways (known as redundancies) are apportioned with high interconnectedness. This prevents flop from crushing the device. However, because of the high level of interconnectedness, septicemia can spread more easily, ending in system collapse. How do naturally developed complex systems in nature (e.g. rainforests, ecologies, etc.) maintain high connectedness, but limit contagion and thereby prevent system collapse?

In this fast-moving world, the roles of technology in our day-to-day operations, ranging from social, economic, and industrial technology or otherwise cannot be overstressed. The computer network system has become quite a necessity and a critical need of human life. The computer communication network system is made up of many comprehensive and local area computer network systems joined by peripherals. Because new computer network systems are being added at a quick pace, giving an accurate structure of the computer network system is a difficult undertaking. The performance of a computer network system can be predicted in a variety of ways, including transfer time, response time, and the number of users, as well as the transmission media, power supply, hardware, and software that make up the computer network system. Furthermore, the frequency of failure and the time it takes to recover from failure in the event of a disaster are used to assess computer network system reliability. Over the decades, researchers have worked hard to develop an appropriate mechanism. Researchers have concentrated on creating structures that can be repaired due to various configurations, as well as assessing dependability, availability, operating costs, and other factors, to satisfy manufacturing businesses' specific demands. Similarly, to come up with a system that has high system availability and low maintenance costs while satisfying the consumers, many researchers have investigated various aspects of the complicated repairable system's reliability for this aim. In 1990, most of the researchers studied system performances of different types of repairable systems, and using one repair policy with general repair distribution. To explore the study of several investigators, Vanderperre (1990) premeditated on the reliability features of a parallel system and used general repair distribution. Gupta and Sharma (1993) studied a model for a two-duplex unit standby system using a general repair policy. Singh et al. (2001) studied complex standby redundant systems involving multi-failure—human failure using general repair policy. Ram and Singh (2008) studied a complex system using (1-out-of-2: F) and (1-out-of-n: F) subsystems and using general repair distributions policy. Ram and Singh (2010) also studied mutually exclusive complex systems and used a general repair policy. In a repairable system, two types of failures are observed i.e., partial failure and complete failure. As a due cause of complete failure, the entire system stops functioning, resulting in a huge loss of the output of the system. Consequently, it needs fast repair to get ready for work. In a realistic situation, a failed system can be repaired in a couple of ways using multi-repair approach. Hence whenever the system experiences a complete shutdown mode, it should be repaired using the copula repair approach.

Copulas are functions that connect the one-dimensional margins of multivariate distribution functions to their one-dimensional margins. Copula research and its application in statistics are a relatively recent, yet rapidly expanding area. To explore the utility of copula in the study of repairability, Singh and Rawal (2014) applied copula distribution, to examine the availability, MTTF, and cost analysis of a complex system with a preemptive resume repair policy. Kumar et al. (2017) conducted studies on the availability and cost analysis of an engineering system containing series subsystems. Ghosh et al. (2017) studied how to reduce the life cycle costs of a modern helicopter by improving the stability and maintainability variables. Gahlot et al. (2018) employed a copula linguistics approach, the premeditated performance of a repairable system under different types of failure, and two types of repair policies. Singh and Ayagi (2018) analyzed complex repairable systems using a preemptive resume repair policy together with a copula approach. Lado and Singh (2019) used Gumbel–Hougaard family copula distribution, to evaluate the profit valuation of a complex repairable system comprising two subsystems in a series configuration. Together with the series and parallel configuration, a specific type of configuration in which out-of-n identical k units are essential for functioning is defined as a k-out-of-n: G/F type of configuration and is found in almost all industrial systems. For the system to be operative, at least k of its units out of n need to be operational. The remaining (n−k) units are considered redundant units, while the first k units are known as fundamental units. Further, a k-out-of-n: G system is equivalent to (k + 1)-out-of-n: F, and the (n-out-of-n: G) system has a purely parallel configuration, while (1-out-of-n: F) is a purely series system. To confine the study of the k-out-of-n: G/F types of configuration, Tamegai (1980) studied the k-out-of-n: F repairable systems that have one or two servers and constant failure rates and use general repair policy. Dhillon and Anude's (1994) dynamic structure was examined for the failure of a k-out-of-n: G system.  Malik and Bhardwaj (2007) studied the reliability and cost of the 2-out-of-3 redundant system using general repair distribution and waiting time. Singh et al. (2012) studied a system consisting of two subsystems and using k-out of n: G policy and copula. Gulati et al. (2014) studied a reliability system having two units in a parallel configuration and using repairs, general repair and Gumbel–Hougaard family copula distribution. Gahlot et al. (2020) analyzed a system consisting of three identical units under the k-out-of-n: G scheme with copula repair approach. Cost–benefit analysis of a k-out-of-n: G kind of warm standby system under catastrophic failure via copula repair approach was performed by Poonia and Sirohi (2020). A multi-state computer network with five web servers and three database servers system in a series configuration with the implication of copula repair approach was studied by Poonia (2021) via supplementary variable and Laplace transforms. Sirohi et al. (2021) used the Gumbel–Hougaard copula to estimate reliability indices for a complex repairable system in a series configuration with switch and catastrophic failure. A system concerning five clients and two servers as subsystem 1 and subsystem 2 under the k-out-of-n: G scheme was analyzed by Yusuf et al. (2021) with implications of copula repair. Poonia et al. (2021) analyzed the performance of a warm standby k-out-of-n: G, and 2-out-of-4: G system in a series configuration using copula repair strategy. The reliability performance prediction of a solar photovoltaic system for rural consumption using Gumbel–Hougaard family copula has been addressed stochastically by Maihulla and Yusuf (2021). Recently, the performance of a complex system consisting of three subsystems in series configuration has been stochastically analyzed by Jibril et al. (2022).

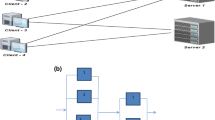
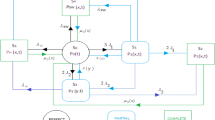
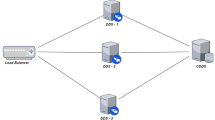
In the present model, system performance was evaluated through reliability measures; the system description consisted of four subsystems in series arrangement. The first subsystem is the client's server which consists n clients and the work policy is the k-out-of-n: G to perform aptly. The second subsystem is a load balancer (LB) which balances the load to distributed servers DDS1 and DDS2 which are placed in a parallel configuration and at least one database server is essential to be operative for the system operational mode. Subsystem 3 has two identical distributed database servers (DDS) I and II connected in a parallel configuration. In subsystem 4, CDDS is a centralized distributed database server that manages all of the application data in DDS. The system architecture and state transition diagram in Fig. 1a, b explain the system structure and state conversions from one state to another. The states S0, S1, S2, and S3 are the states for subsystem 1 operations, S4 is the state for load balance failure, S5, S6 represent states for DDS1 and DDS2 and S7 indicates CDDS failure (Table 1).

Fig. 1
figure 1

a System architecture of the model. b State transition diagram of the model from (a)

Full size image

2 Notations, expectations, and assumptions of the system

2.1 Notations

See Table 1.

Table 1 Nomenclature of symbolic terminology
Full size table

2.2 Assumption

S0: Perfect working state, all subsystems are satisfactory.

S1: Minor degraded state due to failure of one client in subsystem 1. It is a working state as minor partial failure raised and working policy is k-out-of-n: G for subsystem 1.

S2: Major degraded state after failure of (n–k) clients in subsystem 1 and further failure of a single client would lead to state S3.

S3: Complete failed state due to the failure of (k + 1) clients in subsystem 1.

S4: Complete failed state due to the failure of load balancer (LB) system not working.

S5: Major degraded and working state due to the failure of DDS1 in subsystem 3.

S6: Complete failed state due to the failure of whole subsystem 3.

S7: Complete failed state due to failure of database distributed centralized server CDDS server.

3 Formulation of the mathematical model

By a probability of considerations and continuity arguments, we can obtain the following set of differential equations governing the present mathematical model.

$$\begin{aligned} \left[ {\frac{\partial }{\partial t} + n\lambda_{1} + \lambda_{2} + 2\lambda_{3} + \lambda_{4} } \right]P_{0} (t)& = \left[ {\int\limits_{0}^{\infty } {\varphi_{1} (x)P_{1} (x,t)} {\text{d}}x + \int\limits_{0}^{\infty } {\varphi (y)P_{5} } (y,t){\text{d}}y} \right. \\ & \quad + \int\limits_{0}^{\infty } {\mu_{0} (x)\;P_{4} (x,t)} {\text{d}}x + \int\limits_{0}^{\infty } {\mu_{0} (x)\;P_{3} (x,t)} {\text{d}}x + \int\limits_{0}^{\infty } {\mu_{0} (z)\;P_{7} (z,t)} {\text{d}}z + \int\limits_{0}^{\infty } {\mu_{0} (y)\;P_{6} (y,t)} {\text{d}}y, \\ \end{aligned}$$
(1)
$$\left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + (n - k)\lambda_{1} + \lambda_{2} + \lambda_{4} + 2\lambda_{3} + \varphi_{1} (x)} \right]P_{1} (x,t) = 0,$$
(2)
$$\left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + (n - k - 1)\lambda_{1} + \lambda_{2} + \lambda_{4} + \varphi_{1} (x)} \right]P_{2} (x,t) = 0,$$
(3)
$$\left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + \mu_{0} (x)} \right]P_{3} (x,t) = 0,$$
(4)
$$\left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + \mu_{0} (x)} \right]P_{4} (x,t) = 0,$$
(5)
$$\left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial y} + \lambda_{3} + \lambda_{2} + \lambda_{4} + \varphi (y)} \right]P_{5} (y,t) = 0,$$
(6)
$$\left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial y} + \mu_{0} (y)} \right]P_{6} (y,t) = 0,$$
(7)
$$\left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial z} + \mu_{0} (z)} \right]P_{7} (z,t) = 0.$$
(8)

Boundary conditions

$$P_{1} (0,t) = n\lambda_{1} P_{0} (t),$$
(9)
$$P_{2} (0,t) = n(n - k)\lambda_{1}^{2} P_{0} (t),$$
(10)
$$P_{3} (0,t) = n(n - k)(n - k - 1)\lambda_{1}^{3} P_{0} (t),$$
(11)
$$P_{4} (0,t) = \lambda_{2} \left[ {1 + n\lambda_{1} + n(n - k)\lambda_{1}^{2} + 2\lambda_{3} (1 + n\lambda_{1} )} \right]P_{0} (t),$$
(12)
$$P_{5} (0,t) = 2\lambda_{3} (1 + n\lambda_{1} )P_{0} (t),$$
(13)
$$P_{6} (0,t) = 2\lambda_{3}^{2} (1 + n\lambda_{1} )P_{0} (t),$$
(14)
$$P_{7} (0,t) = \lambda_{4} \left[ {1 + n\lambda_{1} + n(n - k)\lambda_{1}^{2} + 2\lambda_{3}^{2} (1 + n\lambda_{1} )} \right]P_{0} (t).$$
(15)

Initials conditions

$$P_{0} (0) = 1\,{\text{and}}\,{\text{other}}\,{\text{state}}\,{\text{probabilities}}\,{\text{are}}\,{\text{zero}}\,{\text{at}}\,t \, = \, 0$$
(16)

4 Solution of the model

Taking Laplace transformation of Eqs. (1)–(15) and using Eq. (16), we obtain

$$\begin{aligned} \left[ {s + n\lambda_{1} + \lambda_{2} + 2\lambda_{3} + \lambda_{4} } \right]\overline{P}_{0} (s) &= \left[ {\int\limits_{0}^{\infty } {\varphi_{1} (x)\overline{P}_{1} (x,s)} {\text{d}}x + \int\limits_{0}^{\infty } {\varphi (y)\overline{P}_{5} } (y,s){\text{d}}y} \right. \\ & \quad + \int\limits_{0}^{\infty } {\mu_{0} (x)\;\overline{P}_{4} (x,s)} {\text{d}}x + \int\limits_{0}^{\infty } {\mu_{0} (x)\;\overline{P}_{3} (x,s)} {\text{d}}x\; + \;\int\limits_{0}^{\infty } {\mu_{0} (z)\;\overline{P}_{7} (z,s)} {\text{d}}z + \;\int\limits_{0}^{\infty } {\mu_{0} (y)\;\overline{P}_{6} (y,s)} {\text{d}}y, \\ \end{aligned}$$
(17)
$$\left[ {s + \frac{\partial }{\partial x} + (n - k)\lambda_{1} + \lambda_{2} + \lambda_{4} + 2\lambda_{3} + \varphi_{1} (x)} \right]\overline{P}_{1} (x,s) = 0,$$
(18)
$$\left[ {s + \frac{\partial }{\partial x} + (n - k - 1)\lambda_{1} + \lambda_{2} + \lambda_{4} + \varphi_{1} (x)} \right]\overline{P}_{2} (x,s) = 0,$$
(19)
$$\left[ {s + \frac{\partial }{\partial x} + \mu_{0} (x)} \right]\overline{P}_{3} (x,s) = 0,$$
(20)
$$\left[ {s + \frac{\partial }{\partial x} + \mu_{0} (x)} \right]\overline{P}_{4} (x,s) = 0,$$
(21)
$$\left[ {s + \frac{\partial }{\partial y} + \lambda_{3} + \lambda_{2} + \lambda_{4} + \varphi (y)} \right]\overline{P}_{5} (y,s) = 0,$$
(22)
$$\left[ {s + \frac{\partial }{\partial y} + \mu_{0} (y)} \right]\overline{P}_{6} (y,s) = 0,$$
(23)
$$\left[ {s + \frac{\partial }{\partial z} + \mu_{0} (z)} \right]\overline{P}_{7} (z,s) = 0,$$
(24)
$$\overline{P}_{1} (0,s) = n\lambda_{1} \overline{P}_{0} (s),$$
(25)
$$\overline{P}_{2} (0,s) = n(n - k)\lambda_{1}^{2} \overline{P}_{0} (s),$$
(26)
$$\overline{P}_{3} (0,s) = n(n - k)(n - k - 1)\lambda_{1}^{3} \overline{P}_{0} (s),$$
(27)
$$\overline{P}_{4} (0,s) = \lambda_{2} \left[ {1 + n\lambda_{1} + n(n - k)\lambda_{1}^{2} + 2\lambda_{3} (1 + n\lambda_{1} )} \right]\;\overline{p}_{0} (s),$$
(28)
$$\overline{P}_{5} (0,s) = 2\lambda_{3} (1 + n\lambda_{1} )\overline{P}_{0} (s),$$
(29)
$$\overline{P}_{6} (0,s) = 2\lambda_{3}^{2} (1 + n\lambda_{1} )\overline{P}_{0} (s),$$
(30)
$$\overline{P}_{7} (0,s) = \lambda_{4} \left[ {1 + n\lambda_{1} + n(n - k)\lambda_{1}^{2} + 2\lambda_{3}^{2} (1 + n\lambda_{1} )} \right]\;\overline{P}_{0} (s).$$
(31)

Solving (25)–(36) with the help of (37)–(46), one may get

$$\, \overline{P}_{0} (s) = \frac{1}{D(s)},$$
(32)
$$\, \overline{P}_{1} (s) = \frac{{n\lambda_{1} }}{D(s)}\frac{{(1 - S_{{\varphi_{1} }} (s + (n - k)\lambda_{1} + \lambda_{2} + \lambda_{4} + 2\lambda_{3} ))}}{{(s + (n - k)\lambda_{1} + \lambda_{2} + \lambda_{4} + 2\lambda_{3} )}},$$
(33)
$$\, \overline{P}_{2} (s) = \frac{{n(n - k)\lambda_{1}^{2} }}{D(s)}\frac{{(1 - S_{{\varphi_{1} }} (s + (n - k - 1)\lambda_{1} + \lambda_{2} + \lambda_{4} ))}}{{(s + (n - k - 1)\lambda_{1} + \lambda_{2} + \lambda_{4} )}},$$
(34)
$$\, \overline{P}_{3} (s) = \frac{{n(n - k)(n - k - 1)\lambda_{1}^{3} }}{D(s)}\frac{{(1 - S_{{\mu_{0} }} (s))}}{(s)},$$
(35)
$$\, \overline{P}_{4} (s) = \frac{{\lambda_{2} \left[ {1 + n\lambda_{1} + n(n - k)\lambda_{1}^{2} + 2\lambda_{3} (1 + n\lambda_{1} )} \right]}}{D(s)}\frac{{(1 - S_{{\mu_{0} }} (s))}}{(s)},$$
(36)
$$\, \overline{P}_{5} (s) = \frac{{2\lambda_{3} (1 + n\lambda_{1} )}}{D(s)}\frac{{(1 - S_{\varphi } (s + \lambda_{3} + \lambda_{2} + \lambda_{4} ))}}{{s + \lambda_{3} + \lambda_{2} + \lambda_{4} }},$$
(37)
$$\, \overline{P}_{6} (s) = \frac{{2\lambda_{3}^{2} (1 + n\lambda_{1} )}}{D(s)}\frac{{(1 - S_{{\mu_{0} }} (s))}}{s},$$
(38)
$$\, \overline{P}_{7} (s) = \frac{{\lambda_{4} \left[ {1 + n\lambda_{1} + n(n - k)\lambda_{1}^{2} + 2\lambda_{3}^{2} (1 + n\lambda_{1} )} \right]}}{D(s)}\frac{{(1 - S_{{\mu_{0} }} (s))}}{s},$$
(39)
$$\begin{aligned} D(s) & = s + n\lambda _{1} + \lambda _{2} + 2\lambda _{3} + \lambda _{4} - \{ n\lambda _{1} \bar{S}_{{\varphi _{1} }} (s + (n - k)\lambda _{1} + \lambda _{2} + \lambda _{4} + 2\lambda _{3} ) \\ & \quad + 2\lambda _{3} \left( {1 + n\lambda _{1} } \right)S_{\varphi } (s + \lambda _{3} + \lambda _{2} + \lambda _{4} ) \\ & \quad + \lambda _{2} \left[ {1 + n\lambda _{1} + n(n - k)\lambda _{1}^{2} + 2\lambda _{3} (1 + n\lambda _{1} )} \right]\;\overline{S} _{{\mu _{0} }} (s). \\ \end{aligned}$$
(40)

The Laplace transformations of the probabilities that the system is in up (i.e., either good or degraded state) and failed state at any time are as follows:

$$\, \overline{P}_{up} (s) = \overline{P}_{0} (s) + \overline{P}_{1} (s) + \overline{P}_{2} (s) + \overline{P}_{5} (s)$$
(41)
$$\, = \frac{1}{D(s)}\left[ \begin{gathered} 1 + n\lambda_{1} \frac{{(1 - \overline{S}_{{\varphi_{1} }} (s + (n - k)\lambda_{1} + \lambda_{2} + \lambda_{4} + 2\lambda_{3} ))}}{{(s + (n - k)\lambda_{1} + \lambda_{2} + \lambda_{4} + 2\lambda_{3} )}} + n(n - k)\lambda_{1}^{2} \frac{{(1 - \overline{S}_{\varphi } (s + (n - k - 1)\lambda_{1} + \lambda_{4} + \lambda_{2} ))}}{{(s + (n - k - 1)\lambda_{1} + \lambda_{4} + \lambda_{2} )}} \hfill \\ \quad + 2 \lambda_{3} (1 + n\lambda_{1} )\frac{{(1 - \overline{S}_{\varphi } (s + \lambda_{3} + \lambda_{2} + \lambda_{4} ))}}{{(s + \lambda_{3} + \lambda_{2} + \lambda_{4} )}} \hfill \\ \end{gathered} \right],$$
(42)
$$\, \overline{P}_{{{\text{failed}}}} (s) = \overline{P}_{3} (s) + \overline{P}_{4} (s) + \overline{P}_{6} (s) + \overline{P}_{7} (s).$$
(43)

5 Analytical study of model

5.1 Availability analysis

When repair follows exponential and general distribution.

Setting \(\overline{S}_{{\mu_{0} }} \left( s \right) = \frac{{\mu_{0} \left( x \right)}}{{s + \mu_{0} \left( x \right)}},\;\mu_{0} (x) = \exp \left[ {x^{\theta } + \left\{ {\log \phi \left( x \right)} \right\}^{\theta } } \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \theta }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\theta $}}}} ,\) \(\overline{S}_{{\phi_{1} }} \left( s \right) = \frac{{\phi_{1} }}{{s + \phi_{1} }}\) in Eq. (42) and setting the values of different parameters as \(\lambda_{1}\) = 0.002, \(\lambda_{2}\) = 0.02, \(\lambda_{3}\) = 0.01, \(\lambda_{4}\) = 0.022, \(\varphi\) = 1, θ = 1, x = 1, n = 50, k = 30 and then taking inverse Laplace transform, one can obtain

$$\begin{aligned} \, (a) & = - 0.004370691056e^{ - 1.080000000t} + 0.01834516992e^{ - 2.769791233t} - 0.1610502486e^{ - 1.234748565t} \\ & \quad + 0.003732471750e^{ - 1.075979702t} \;\;\;n = 50,\;k = 30, \\ \end{aligned}$$
$$\begin{aligned} \, (b) & = - 0.002698837430e^{ - 1.100000000t} + 0.01841727178e^{ - 2.770103895t} - 0.01828462046e^{ - 1.250152916t} \\ & \quad + 0.001753932297e^{ - 1.079128739t} + 1.000812254e^{ - 0.002914450451t} \;\;\;n = 50,\;k = 20, \\ \end{aligned}$$
$$\begin{aligned} \, (c) & = 0.01851717582e^{ - 2.770502055t} - 0.02034819216e^{ - 1.266111943t} + 0.001759207778e^{ - 1.081751282t} \\ & \quad + 1.003097449e^{ - 0.003934719794t} - 0.003025640352e^{ - 1.120000000t} \;\;\;n = 50,\;k = 10, \\ \end{aligned}$$
$$\begin{aligned} \, (d) & = 0.01857747171e^{ - 2.770733200t} - 0.02133520386e^{ - 1.274265936t} + 0.001817831986e^{ - 1.082898227t} \\ & \quad + 1.004193103e^{ - 0.004402637530t} - 0.003253202999e^{ - 1.130000000t} \;\;\;n = 50,\;k = 5. \\ \end{aligned}$$

For, t = 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100 units of time, one may get different values of Pup(t) as shown in Table 2. If there are n identical units in subsystem 1 in a parallel configuration, then the computations for different values of k, n, are presented in Table 2 and the graphical representation of the availability is given in Fig. 2.

Table 2 Availability analysis for copula repair
Full size table
Fig. 2
figure 2

Variation of availability when repair follows copula distribution

Full size image

Figure 2 provides the material of availability of the system changes (when repair follows copula distribution) concerning the time when failure rates are fixed at different values. We have analyzed four cases for different values n and k as:

(a) n = 50, k = 30, (b) n = 50, k = 20, (c) n = 50, k = 10 and (d) n = 50, k = 5. It can be noticed that the availability decreases; hence, it can be concluded that the availability of the system (when repair follows copula distribution) decreases as the value of the parameters increases, and after a sufficiently long time it converges to zero.

5.2 Availability analysis when the system follows general repair

When the repair follows general distribution, for different values of time variable t = 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100 units of time and \(\varphi\)1(x) = \(\varphi\)(y) = 1 and µ0(x) = 1, we get different values of Pup(t) after taking inverse Laplace transform, as shown in Table 3 and corresponding Fig. 3. For similar configuration, (a) n = 50, k = 30, (b) n = 50, k = 20, (c) n = 50, k = 10 and (d) n = 50, k = 5, the given expressions are obtained as in (a), (b), (c) and (d).

$$\begin{aligned} \, (a) & = - 0.01640918357e^{ - 1.080000000t} + 0.009339395761e^{ - 1.266318299t} + 0.01898355262e^{ - 1.078833057t} \\ & \quad + 0.01546340219e^{ - 1.017114012t} + 0.9726228329e^{ - 0.001734632698t} \;\;\;n = 50,\;k = 30, \\ \end{aligned}$$
$$\begin{aligned} \, (b) & = - 0.003601302136e^{ - 1.100000000t} + 0.004807265361e^{ - 1.279593433t} + 0.007820210534e^{ - 1.083536788t} \\ & \quad + 0.01627627655e^{ - 1.018031108t} + 0.9746975497e^{ - 0.002838670822t} \;\;n = 50,\;k = 20, \\ \end{aligned}$$
$$\begin{aligned} \, (c) & = - 0.003700556475e^{ - 1.120000000t} + 0.0004924485519e^{ - 1.293593998t} + 0.009690064558e^{ - 1.087770412t} \\ & \quad + 0.01690739010e^{ - 1.018804271t} + 0.9766106536e^{ - 0.003831320084t} \;\;n = 50,\;k = 10. \\ \end{aligned}$$
Table 3 Time vs. availability
Full size table
Fig. 3
figure 3

Variation of availability when repair follows the general distribution

Full size image

For different values of time variable t = 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100 units of time, we get different values of Pup (t) as shown in Table 2 and Fig. 3

Figure 3 presents the availability variation (when repair follows general distribution) for the time when failure rates are fixed at different values. We have analyzed four cases for different values of n and k,

(a) n = 50, k = 30, (b) n = 50, k = 20, (c) n = 50, k = 10 and (d) n = 50, k = 5. It can be seen that the availability decreases; hence, it can be concluded that the availability of the system (when repair follows general distribution) decreases as the value of the parameters increases, and after a sufficiently long time converges to zero.

6 Reliability analysis

The system performance of a non-repairable system is known as reliability. Therefore, treating all repairs of the system to zero in (43) and the inverse Laplace transform of the resulting expression give us the reliability of the system, and one can obtain the expression (a), (b), (c), and (d) given as (Table 4):

$$\begin{aligned} \, (a) & = 1.724137931e^{ - 0.1220000000t} - 1.137019287e^{ - 0.1800000000t} + 0.04000000000e^{ - 0.08000000000t} \\ & \quad + 0.3728813559e^{ - 0.06200000000t} \;\;n = 50,\;k = 30, \\ \end{aligned}$$
$$\begin{aligned} \, (b) & = 0.07500000000e^{ - 0.1000000000t} + 2.631578947e^{ - 0.14200000000t} - 2.079460303e^{ - 0.18000000000t} \\ & \quad + 0.3728813559e^{ - 0.06200000000t} \;\;n = 50,\;k = 20, \\ \end{aligned}$$
$$\begin{aligned} \, (c) & = - 5.061770245e^{ - 0.1800000000t} + 5.555555556e^{ - 0.1620000000t} + 0.3728813559e^{ - 0.06200000000t} \\ & \quad + 0.1333333333e^{ - 0.12000000000t} \;\;n = 50,\;k = 10, \\ \end{aligned}$$
$$\begin{aligned} \, (d) & = - 12.05288136e^{ - 0.1800000000t} + 12.50000000e^{ - 0.1720000000t} + 0.18000000000e^{ - 0.13000000000t} \\ & \quad + 0.3728813559e^{ - 0.06200000000t} \;\;n = 50,\;k = 5. \\ \end{aligned}$$
Fig. 4
figure 4

Variation of reliability for different configurations

Full size image
Table 4 Time vs. reliability for different configurations
Full size table

Figure 4 as indicated shows the reliability of the system when the repair is not present. By taking all the repairs in an expression of availability as zero, we obtained the expression (a), (b), (c), and (d) of reliability as a function of time and it can be seen that the reliability of the system decreases.

7 Mean time to failure (MTTF) analysis

Setting \(\phi_{1} (x),\;\phi (y)\;{\text{and}}\;\mu_{0} (x)\;{\text{to}}\;{\text{zero}}\), Eq. (42) and taking the limit of the expression, as s tends to zero one can achieve the MTTF expression as:

$${\text{M}}.{\text{T}}.{\text{T}}.{\text{F}}. = \mathop {\lim }\limits_{s \to 0} \overline{P}_{{{\text{up}}}} (s) = \frac{{1 + \frac{{n\lambda_{1} }}{{(n - k)\lambda_{1} + \lambda_{2} + \lambda_{4} + 2\lambda_{3} }} + \frac{{n(n - k)\lambda_{1}^{2} (1 + \lambda_{1} )}}{{(n - k - 1)\lambda_{1} + \lambda_{4} + \lambda_{2} }} + \frac{{2\lambda_{3} (n\lambda_{1} + 1)}}{{\left( {2\lambda_{3} + \lambda_{2} + \lambda_{4} } \right)}}}}{{\left( {n\lambda_{1} + \lambda_{2} + 2\lambda_{3} + \lambda_{4} } \right)}}.$$
(44)

Setting \(\lambda_{2} = \, 0.02, \quad \lambda_{3} = \, 0.02,\,\,\lambda_{4} = 0.022\) and varying λ1 as 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09 and 0.10 in (44), one may obtain Table 5 whose column 2 demonstrates variation of MTTF with respect to λ1.

Table 5 Failure rate vs. MTTF
Full size table

Setting \(\lambda_{1} = \, 0.002,\,\,\,\,\lambda_{3} = \, 0.02,\,\,\lambda_{4} \, = \, 0.022\;\) and varying λ2 as 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, and 0.09 in (44), one may obtain Table 5 whose column 3 demonstrates variation of MTTF with respect to λ2.

Setting \(\lambda_{1} = \, 0.002,\,\,\,\,\lambda_{2} = \, 0.02,\,\,\lambda_{4} \, = \, 0.022\;\) and varying λ3 as 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, and 0.09 in (44), one may obtain Table 5, whose column 4 shows variation of MTTF with respect to λ3.

Setting \(\lambda_{1} = \, 0.002,\,\,\,\,\lambda_{2} = \, 0.02,\,\,\lambda_{3} \, = \, 0.02\;\) and varying λ4 as 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, and 0.09 in (44), one may obtain Table 5, which reveals variation of MTTF with respect to λ4.

Figure 5 provides the mean time to system failure (MTTF) of the system concerning variations in λ1, λ2, λ3, and λ4, respectively, when the other parameters have been taken as constants. The variation in MTTF corresponding to failure rate λ1 decreases slowly, but the variation corresponding to λ2, λ3, and λ4 decreases faster, while the variation of MTTF concerning λ1, λ2, λ3 and λ4 seem to be closely related and decreasing slowly.

Fig. 5
figure 5

Failure rate vs. MTTF

Full size image

8 Cost/profit analysis

Let the failure rates of the system be λ1 = 0.002, λ2 = 0.02, λ3 = 0.02, and λ4 = 0.022, mean time to repair be \(\varphi (x) = 1\) and \(x = 1,\;\theta = 1,\;\varphi (x) = 1\) setting in Eq. (42) and taking inverse Laplace transform, one can obtain the availability expression.

Let the service facility be always available, then the expected profit during the interval [0, t) is

$$E_{p} (t) = K_{1} \int\limits_{0}^{t} {P_{{{\text{up}}}} (t)} {\text{d}}t - K_{2} t,$$
(45)

where K1 and K2 are revenue service costs per unit time. Hence,

$$\begin{aligned} E_{p} (t) & = \, 0.006861404561e^{ - 1.245189414t} \\ & \quad - 0.4251585799e^{ - 0.3127453416t} - 560.3151582e^{ - 0.001563144460t} \\ & \quad - 0.004272451862e^{ - 1.076332100t} + 0.004513638618e^{ - 1.080000000t} \\ & \quad + 560.7332140\;n = 50,\;k = 30. \\ \end{aligned}$$
(46)

Setting K\(_{1}\) = 1 and K\(_{2}\) = 0.6, 0.5, 0.4, 0.3, 0.2 and 0.1, respectively, and varying t = 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100 units of time, one gets Table 6.

Table 6 Time vs. expected profit copula repair approach for n = 50, k = 30
Full size table

Figure 6 finally shows the expected profit increases concerning the time when the service cost K2 = 0.6, 0.5, 0.4, 0.3, 0.2, and 0.1, respectively; one can see that as the service cost decreases, the profit increases. Finally, one can observe that when the service cost is low, the expected profit is increased.

Fig. 6
figure 6

Time vs. expected profit copula repair approach n = 40, k = 30

Full size image

9 Result and conclusion

Tables 2 and 3 and Figs. 2 and 3 provide information on how the availability of the complex repairable system changes with regard to the time when failure rates are fixed at different values. Fixing the failure rates as λ1 = 0.002, λ2 = 0.02, λ3 = 0.02, λ4 = 0.022, the system availability decreases and the probability of failure increases, with varying time t and ultimately becomes steady to the value zero after a sufficiently long interval of time. As a result, one may confidently forecast the future behavior of a complex system at any time for any given set of parametric values, as evidenced by the model's graphical representation. It has also been found for a fixed value of n, the system availability decreases for lower values of k = 20, 10, and 5. Table 3 and the corresponding figure present that general repair was not recommendable when the system was in a complete failed state.

Table 4 presents the reliability of the system for different values of time t. It is clear from Table 4 and Fig. 4 that the system efficiency of the non-repairable system is very low, compared to the repairable one. As higher values of time t are approached, the reliability approaches zero. It has also been seen that for reliability computations for fixed values of n and varying k, there is not much variation.

Table 5 yields the mean time to failure (MTTF) of the system for variation in λ1, λ2, λ3, and λ4, respectively, when the other parameters have been taken as constant.

When revenue cost per unit time K1 is fixed at 1, service costs K2 = 0.6, 0.5, 0.4, 0.3, 0.2, 0.01, profit was calculated and the results are demonstrated by graphs in Fig. 6. One can observe that as service costs decrease, the profit increases. Whenever the service cost increases the net profit starts decreasing for a high value of time.

The present study is focused on performance evaluations for four state repairable systems. The study can also be extended for the k state working system under (k − 1) minor degraded and kth major degraded state. Another interesting model can be also developed with more than two DDS servers and switching devices and another essential component of networking.