Introduction

In the process of natural disaster risk analysis and assessment, the sample size is an important part which can affect the precision of assessment results. If the sample size is too small, it will lead to inaccurate and meaningless evaluation results (Kong et al. 2015; Myint et al. 2008; Parsons et al. 2016; Wang et al. 2015a, b). However, in some cases, it is difficult to extract sufficient information from incomplete data from a few samples (Hao et al. 2014; Li et al. 2013). To solve the problem of lack of information caused by small sample sizes, Professor Chong-fu Huang proposed the information distribution and diffusion method in 1995 (Kazama et al. 2012; Nagata and Shirayama 2012). The method is now widely applied to the risk analysis of a variety of disasters including earthquakes, floods, hailstorms, city fires, loess collapsibility, and rainstorms (Levitan and Wronski 2013; Xue and Gencay 2012; Li et al. 2012; Bai et al. 2014; Mundahl and Hunt 2011). The method is recognized by the industry as the most effective way to manage information incompleteness (Feng and Luo 2008; Lin 2015; Maillé and Saint-Charles 2014).

But what is information incompleteness? The mathematical expressions of information completeness are derived from its rigorous theory (Xu et al. 2013). The theoretical definition of information completeness is too abstract and it is difficult to guide the practical activities based on the theory. A sample size smaller than 30 is statistically considered to cause information incompleteness (Sun and Zhang 2008; Huang 2005; Gamboa et al. 2015; Malterud et al. 2015; Perneger et al. 2015). Although 30 is given as the threshold for a small sample, the concept of the small sample itself is very vague (Baio et al. 2015; de Bekker-Grob et al. 2015; Dembkowski et al. 2012; Engblom et al. 2016; Schorr et al. 2014).

In the field of environmental geosciences, when studying the natural factors such as precipitation, temperature and number of earthquakes, the size of the sample is directly related to the accuracy of the final result. Therefore, from a statistical point of view, we attempt to collect data of 3050 weather stations in China as the experimental raw data. The Monte Carlo method is used to resample the original experimental data to build a probability distribution interval with a certain confidence. By comparing the information diffusion method with the traditional hard histogram method, a method can be found that can better reflect the actual state under the condition of small sample, so that an intuitive understanding can be provided when the related scientific workers deal with incomplete information. (Andreotti et al. 2014; Dehghani et al. 2014; Elanique et al. 2012; Haar et al. 2017; Medhat et al. 2017; Newhauser et al. 2007).

Data and methods

Data and processing

Considering the amount of data have a great impact on the experimental results, it requires a large amount of data as the basic data source to test which method can be used to obtain better results in different sample sizes and find out what is the minimum sample size if we want to make the data results good enough. This study selected China as the study area. Its topography is high in the west and low in the east. The climate in China is complex and diverse but distributed in an orderly manner from south to north. China locates in the northern hemisphere, spans six temperature zones. The temperature rises from north to south and also has an obvious change with season. There are many meteorological stations in the country, which are densely populated in the south and sparsely in the north. The overall temperature conditions meet the requirements of the experiment. We collect all the weather data in June 2016 from weather stations across the country in the database of China Weather Network (http://www.weather.com.cn/). First, the weather site data of extreme weather or abnormal temperature was removed through the screening method, and then averaging the remaining data, finally we got a total of 3050 temperature data of the weather stations (Fig. 1).

Fig. 1
figure 1

Study area map

Full size image

Regarding the selected temperature data as the parent Ω, the Monte Carlo method is used to resample data in the parent data. Collect n samples (n = 5, 6, 7,…, 1000) randomly, and then collect each of these NTH samples we got just now. In the case of different pseudo-random numbers, repeat the experiment m times (m = 100) [11,17]. We count all the sample data generated by re-sampling (we can name it data set A for distinction) using the traditional histogram statistics method (hard histogram) and the improved histogram method under the information allocation (soft histogram) separately to get dataset B. In the next step, we estimate data set B and calculate the expected and standard deviations of the two histogram estimates separately. By comparing the correlation coefficient and the average value (expectation value) of the correlation coefficient between the actual value and the theoretical value of the traditional hard histogram and information diffusion model, the experimental conclusion can be obtained. The core of the experimental design consists of two parts: (1) the histogram estimate and (2) the impact of sample size on normality information diffusion measure design (Fig. 2):

Fig. 2
figure 2

Monte Carlo simulation flowchart

Full size image

Monte Carlo simulation method

The Monte Carlo (MC) method, also known as the random sampling method, belongs to a branch of computational mathematics. It was developed in the 1940s for the field of atomic energy. The traditional method could not produce results close to the actual values; thus, it was difficult to obtain satisfactory results. However, since the Monte Carlo method is able to simulate the actual physical processes, it is capable of getting reasonable results. Currently, the Monte Carlo method is widely used in various subjects (Andreotti et al 2014; Dehghani et al. 2014; Elanique et al. 2012; Gamboa et al. 2015; Gregory and Graves 2004).

The Monte Carlo (MC) method is very different from general calculation methods. The general calculation method for solving multi-dimensional complex problems is very difficult, unlike the Monte Carlo method. Monte Carlo analysis is based on direct tracing of the particles and thus the physical aspect is relatively clear and easy to understand. It uses the random sampling method that simulates the particle transport process reflecting the statistical fluctuation of the law without the complexity of multidimensional, multi-factor models. The limit is a good way to solve complex particle transport problems with a clear and simple MC program structure. It is easier to obtain intermediate results with MC models and they can be applied with great flexibility to a variety of problems (Del Moral et al. 2011; Haar et al. 2017; Medhat et al. 2017; Tang et al. 2016; Vadapalli et al. 2014).

Besides the advantages, the MC method has a few shortcomings: one of them is the slow convergence speed problem and error in models of probabilistic nature. Increasing the number of simulations to reduce the sampling error greatly increases the computational intensity of the model (Ableidinger et al. 2017; Dornheim et al. 2015; Newhauser et al. 2007; Wang et al. 2015a, b).

If experimental calculations are performed directly on the basis of existing data, there are some interference conditions that cannot be avoided which can lead to errors in the experimental results. Based on the advantages of the MC method, many limitations can be avoided early in the experiment, and real-world sample data can be simulated more realistically. Especially in the case of a small sample state, the MC method is very suitable to resample the existing data again so that we can get accurate experimental results.

The principle of information diffusion and diffusion estimation

According to the principle of information diffusion, the maternal probability density function estimation is defined as diffusion estimation, n > 0, is a constant, so (Bai et al. 2015; Hao et al. 2014; Li et al. 2013; Liang et al. 2012; Lin 2015; Maillé and Saint-Charles 2014; Shin 2009):

$$\hat {f}\left( y \right)=\frac{1}{{n{\Delta _n}}}\sum\limits_{{i=1}}^{n} {\mu \left( {\frac{{y - {y_i}}}{{{\Delta _{{n_{}}}}}}} \right)} .$$
(1)

Type (1) is a diffusion estimation of maternal probability density function f(y), µ(x) is called the diffusion function and n is the window width,

$$x=\frac{{y - {y_i}}}{{{\Delta _n}}}.$$
(2)

The concrete forms of diffusion µ(x) are the key to the diffusion estimation. For different µ(x) values, the results can predict different diffusion values. According to the theory of molecular diffusion, the function of normal diffusion can be deduced as:

$$\mu \left( x \right)=\frac{1}{{\sigma \sqrt {2\pi } }}\sum\limits_{{i=1}}^{n} {\exp \left[ { - \frac{{{{\left( {y - {y_i}} \right)}^2}}}{{2{h^2}}}} \right]} .$$
(3)

Therefore, substituting type (3) in type (1), the normal diffusion estimation of the maternal probability density function can be deduced as:

$$\hat {f}\left( y \right)=\frac{1}{{nh\sqrt {2\pi } }}\sum\limits_{{i=1}}^{n} {\exp \left[ { - \frac{{{{\left( {y - {y_i}} \right)}^2}}}{{2{h^2}}}} \right]} ,$$
(4)

where h = σΔn was considered as the window width of the standard normal diffusion. From type (4), the normal diffusion estimation f(y) of the parent probability density is not only related to the observed values yi and the numbers of the observed values n, but also related to the window width H of the standard normal diffusion.

When the observations are completed, the observed values and the number of observed values n are known, and the window width h is unknown. For confirming the window width H, a simple calculation method is adapted for checking the width of the window. According to the close principle, the empirical formula of window width h can be deduced as:

$$h=\left\{ {\begin{array}{*{20}{l}} {0.8146(b - a),}&{n=5} \\ {0.5690(b - a),}&{n=6} \\ {0.4560(b - a),}&{n=7} \\ {0.3860(b - a),}&{n=8} \\ {0.3362(b - a),}&{n=9} \\ {0.2986(b - a),}&{n=10} \\ {2.6851(b - a)/(n - 1),}&{n \geqslant 11} \end{array}} \right.,$$

where \(b=\hbox{max} \left\{ {{x_i}} \right\},a=\hbox{min} \left\{ {{x_i}} \right\};\quad i \in (1,n).\)

Histogram estimation

The hard histogram model is a traditional histogram model. To construct a traditional histogram model, it needs to be divided into N intervals of width h, then set the midpoint of each interval and select the control point interval. The soft histogram estimation is based on the traditional histogram model through the distribution of information obtained by improving the histogram model. According to the below equation, we calculate the probability of each random sample point that falls within each section:

$$\mu ({x_i})=\frac{1}{{{h_x}\sqrt {2\pi } }}\exp \left[ { - \frac{{{{({u_j} - {u_i})}^2}}}{{2{h_x}^{2}}}} \right].$$
(5)

The following equation calculates the cumulative probability:

$${q_j}=\sum\limits_{{i=1}}^{n} {\frac{1}{{{h_x}\sqrt {2\pi } }}} \exp \left[ { - \frac{{{{({u_j} - {u_i})}^2}}}{{2{h_x}^{2}}}} \right],$$
(6)

where xi is the ITH sample point, hx = 0.5, uj is the midpoint of the interval for J.

Normalization of different interval probabilities is presented in the following equation:

$${q_j}={q_j}/\sum {{q_i}} .$$
(7)

To investigate the influence of the sample size on information diffusion, this experiment uses two indicators: the correlation coefficient and root mean square error [Eqs. (8), (9)]. The correlation coefficient (r) is a measure of the degree of correlation between variables. Its value lies between − 1 and 1. For |r| close to 1, the correlation between two variables is stronger.

$$r=\frac{{\sum\nolimits_{{i=1}}^{n} {({x_i} - \overline {x} )({y_i} - \overline {y} )} }}{{\sum\nolimits_{{i=1}}^{n} {{{({x_i} - \overline {x} )}^2}{{({y_i} - \overline {y} )}^2}} }},$$
(8)

where \(\bar {x},\bar {y}\) are the mean values of the variables.

The root mean square error is a measure of the difference between two variables and is defined by:

$$rmse=\sqrt {\sum\limits_{{i=1}}^{n} {{{({x_i} - {y_i})}^2}/(n - 1)} } .$$
(9)

Conclusions

To make the experimental procedure simply and select the subsequent impact indicators conveniently in the experiment, first of all, based on the understanding of normal probability density function, this paper divides this curve into nine intervals on [0,54], the midpoint of normal distribution interval is [3,9,15,21,27,33,39,45,51], and then the function is integrated in each interval to get the normal distribution probability under each interval, corresponding to the midpoint of the normal distribution one by one, which is [0.0401,0.0655,0.121,0.1747,0.1974,0.1747,0.121,0.0655,0.0401]. The results are shown in Table 1. Then the resulting probability density values are subjected to a hard histogram density estimation operation (Table 1).

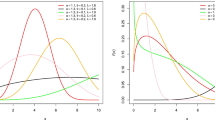
Table 1 Normal probability density function value in the cumulative probability under each section
Full size table

According to the above experimental scheme, the data are compiled and implemented using Python. Using Monte Carlo simulation results, the influence of the sample size on the diffusion of normal information is shown in Figs. 3 and 4, respectively.

Fig. 3
figure 3

Sample size estimation for normal diffusion (coefficient of correlation)

Full size image
Fig. 4
figure 4

Effect of sample size on normal diffusion estimation (RMSE)

Full size image

Figure 3 shows the results of 100 Monte Carlo simulations for the soft histogram coefficient of the correlation between the theoretical and simulated value and hard histogram coefficient of the correlation between the theoretical and simulated value of the mean (expected). It can be obviously seen that the correlation coefficient of the theoretical value of the soft histogram estimation is much better than that of the traditional hard histogram, which shows that the soft histogram estimation method can get better experimental results.

Figure 4 shows the results of 100 Monte Carlo simulations for the soft RMSE and hard histogram coefficient of the correlation between the theoretical and simulated value of the mean (expected). The conclusions can be drawn from the Fig. 3 and Fig. 4 that (1) with the increase in sample size, for both the traditional and soft histogram estimation method. This is in line with the statistics of the large numbers theorem; hard and soft histogram estimation methods are more likely to converge compared to the histogram method. (2) With the increase in the sample size, for both soft and hard estimation methods, the sample variance converges. (3) To achieve the same RMSE or correlation coefficient value, the required sample size is far less when the soft approach is used (45 or more) as the sample estimation method than when the hard approach is used (85 or more).

Discussion

Figures 3 and 4 reveal the unique advantages of the soft estimation methods in solving the problem of small sample sizes (incomplete samples). Small samples can be used with the traditional histogram method for the large sample estimation of the effect of the same law; this is also the main reason why the current method mentioned in the paper is for complete samples under non-extensive applications.

After processing the air temperature data, we found that if the traditional hard histogram estimation method is used, the ideal convergence state will be achieved when the sample size is above 85, while the soft histogram estimation method, can obtain good results when the sample size reaches 45; so, to get the best sample capture, use a sample size of at least 45. Although the soft histogram method requires fewer samples than the traditional hard histogram method, the data obtained are far superior to the traditional hard histogram method. However, with very few sample data, both the traditional hard histogram estimation method and the soft histogram estimation method cannot get good results, resulting in a large final result error. The sample size is still a key factor.

The experimental results show that when the sample size reaches the best capture value, the histogram will achieve the best convergence. After that, the trend is stable and the fluctuation is very slow. Even if the sample volume is increased, there will be no obvious change. Therefore, to reduce the consumption of calculation time, when the sample size reaches the best capture, that is to say, when the sample size of the soft histogram method is 45, stop the sample size increase and complete the simulation of the sample size.

For small samples, neither soft nor hard estimation methods can effectively solve the problem of incomplete information from the process under the inversion of reality. In current research efforts, scientists mostly use soft estimation methods for the analysis and evaluation of natural disaster risks. They use smaller samples to analyze the potential uncertainties associated with these analyses and to determine whether they could satisfy users’ production practice needs. This could be a future research topic.

The traditional sample size for the community to determine whether the information is complete is 30, which is considered unreasonable. Since the sample size is small, the points are relatively large and, therefore, they may be blurry between the complete and incomplete information regions. Therefore, the soft estimation method is in fact not a good solution to the problem of incomplete information. A better solution to this problem is needed to increase the model accuracy.