1 Introduction

The study of traversable wormholes plays a fundamental role in the pioneering work of Morris and Thorn [1]. Traversable wormholes are a solution of the Einstein equations that join two regions of different spacetimes or of the same spacetime through a throat [1]. The construction of wormholes required the existence of exotic matter to violate energy conditions, Morris et al. [2]. However, Visser [3] investigated the idea of thin shell wormholes (TSWs) by using the cut-and-paste scheme and minimizing the existence of exotic matter by assuming that this exotic matter is concentrated at the throat of a wormhole. Poisson and Visser [4] studied the stability of TSWs by pasting together two identical copies of the Schwarzschild metric. In addition, Israel [5] introduced a set of invariant junction conditions that connect the matter of the shell and the extrinsic curvature of the shell in both its regions.

Moreover, several authors analyzed the stability of TSWs by using a linear radial perturbation of a static solution and by choosing specific equations of state. For instance, Eiroa and Romero [6] discussed the stability and construction of Ressiner-Nordstrom (RN) black holes (BHs) TSWs. Eiroa [7] discussed the stability analysis of TSWs. Bronnikov et al. [8] analyzed the stability of wormholes in general relativity. Varela [9] discussed Schwarzschild TSW with variable equations of state. Eiroa and Simeone [10] studied the stability of cylindrical TSW. Rahaman et al. [11] discussed the stability of TSW in the context of heterotic string theory. Eiroa and Simeon [12] studied the stability of TSW with Chaplygin gas. Eid [13] studied the stability of TSWs in the Einstein–Hoffman–Born–Infeld theory. Eid [14] discussed the stability of TSW in the f(R) theory of gravity. Mehdizadeh et al. [15] studied higher-dimensional TSWs in third-order Lovelock gravity. Kokubu and Harada [16] studied the TSWs in the Einstein-Gauss-Bonnet theory of gravity. Moreover, Mustafa et al. [17] discussed the possibility of stable TSWs within string clouds and quintessential fields via van der Waals and the polytropic equation of state. Debnath et al. [18]. studied the modified cosmic chaplygin AdS BHs. Waseem et al. [19]. analyzed the stability constraints of d-dimensional charged TSWs via quintessence and a cloud of strings. Also, Bambi and Stojkovic [20] studied astrophysical wormholes.

Recently, within the context of string theory, Garfinkle et al. [21] investigated a new kind of charged TSW by gluing two copies of a statically charged black hole (BH) solution, called GMGHS (Gibbons–Maeda–Garfinkle–Horowitz–Strominger) [22, 23]. Also, Bhadra [24] studied gravitational lensing by a charged BH (GMGHS) in string theory. Afterward, Alam et al. [25] discussed the stability analysis of TSW in string theory with a perfect fluid equation of state. Chan et al. [26] studied charged dilaton black holes with unusual asymptotic. In addition, Ovgun and Jusufi [27] discussed stable dyonic TSWs in low-energy string theory. Chernicoff et al. [28] studied TSWs in AdS and string dioptric.

In the present work, the stability analysis of charged (GMGHS) TSWs in string theory is supported by a modified generalized Chaplygin gas (MGCG) equation of state (EoS) under a linear fluctuation around a static solution. In Sect. 2, the dynamics of a charged BH GMGHS TSW in string theory with MGCG EoS are briefly reviewed. The stability analysis under linear perturbation around the static solution is discussed in Sect. 3. Finally, a remarkable conclusion is presented in Sect. 4.

2 Dynamics of charged BH GMGHS in string theory

The action of four-dimensional low energy in string theory is described by Garfinkle et al. [21],

$$I = \smallint \left( { - R + \frac{1}{12}C_{\mu \nu \rho } C^{\mu \nu \rho } + \frac{1}{8}F_{\mu \nu } F^{\mu \nu } - G^{\mu \nu } \partial_{\mu } \phi \partial_{\upsilon } \phi } \right)e^{ - \phi } \sqrt { - g} d^{4} x,$$
(1)

where \(R,\) \({G}_{\mu \nu }\) and \({F}_{\mu \nu }\) are the Ricci scalar curvature, the metric in \(\sigma\) model, and the electromagnetic field tensor \({F}_{\mu \nu }= {\partial }_{\mu }{A}_{\upsilon }-{\partial }_{\upsilon }{A}_{\mu }\), while \(\phi\) is the dilaton field and \({A}_{\mu }\) is the potential 4-vector. The action (1), when \({C}_{\mu \nu \rho }=0,\) in the conformal Einstein frame becomes

$$I=\int \left(-R+ {e}^{-\upphi }{F}^{2}+2{\left(\nabla \phi \right)}^{2}\right)\sqrt{-g}{d}^{4}x$$
(2)

with \({g}_{\mu \nu }={e}^{-\upphi }{G}_{\mu \nu }\), where \({g}_{\mu \nu }\) is the Einstein frame metric.

The line element of the charged static BH solution (called GMGHS) obtained from action (2) is defined by [22]:

$$d{s}_{\pm }^{2}=-{H}_{\pm } d{t}_{\pm }^{2}+{H}_{\pm }^{-1} d{r}_{\pm }^{2}+{G}_{\pm } \left(d{\theta }_{\pm }^{2}+{\mathit{sin}}^{2}{\theta }_{\pm }d{\varphi }_{\pm }^{2}\right),$$
(3)

and

$$H_{ \pm } \left( {r_{ \pm } } \right) = 1 - \frac{{2m_{ \pm } }}{{r_{ \pm } }} ,\,\,G_{ \pm } \left( {r_{ \pm } } \right) = r_{ \pm }^{2} - \frac{{r_{ \pm } q_{ \pm }^{2} }}{{m_{ \pm } }}e^{{ - 2\phi_{^\circ } }} \,\,{\text{and}}\,\,e^{ - 2\phi } = e^{{ - 2\phi_{^\circ } }} \left( {1 - \frac{{ q_{ \pm }^{2} }}{{r_{ \pm } m_{ \pm } }}e^{{ - 2\phi_{^\circ } }} } \right).$$
(4)

where \(m_{ \pm }\) and \(q_{ \pm }\) are the black hole masses and magnetic charges of both sides, while \({\phi }_{^\circ }\) is the asymptotic constant value of the dilaton field; where \({q}_{\pm }^{2}=2{m}_{\pm }^{2}{e}^{2{\phi }_{^\circ }}\) is the external black hole; and also (−) denotes the interior, while (+) denotes the exterior region, respectively. Assuming that: \({m}_{-}={m}_{+}=m\) and \({q}_{+}={q}_{-}=q\). The Schwarzschild metric BH is recovered when the area \(G\) goes to zero by \(r=\frac{{q}^{2}}{m} {e}^{-2{\phi }_{^\circ }}\).

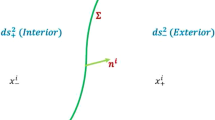
Afterward, the cut-and-paste method develops the geometry of TS surrounding wormhole spacetime. This method is based on minimizing and concentrating the use of exotic matter at the throat, which is treated as a hypersurface between two manifolds.

The single manifold \(M\), bounded by hypersurface \(\Sigma ,\) is obtained by gluing together the two regions \({M}^{+}\) and \({M}^{-}\) at their boundaries, \(M={M}^{+}\cup {M}^{-},\) with natural identification of the boundaries (hypersurface) \(\Sigma \equiv {\Sigma }^{+}={\Sigma }^{-}.\) For the time-like hypersurface \(\Sigma \equiv {\Sigma }^{\pm }=\left\{{r}^{\pm }=R|R>{r}_{h}\right\}\). We set the values of \(R\) (radius of the throat) greater than the event horizon radius \({r}_{h}\) to avoid the presence of horizons and singularities in the line element (3).

Moreover, the time evolution \(R(\tau )\) is described by the throat radius \({r}_{\pm }=R(\tau )\), with the proper time \(\tau\) along the hypersurface \(\Sigma\). Consequently, on the hypersurface \(\Sigma ,\) the induced (intrinsic) metric is defined by

$$ds^{2} = - d\tau^{2} + G\left( {R\left( \tau \right)} \right)\left( {d\theta^{2} + \sin^{2} \theta d\varphi^{2} } \right).$$
(5)

Furthermore, according to the Darmois-Israel formalism, the second fundamental form (extrinsic curvature) across the hypersurface Σ, Israel [5], is defined by

$${K}_{ij}^{\pm }=-{n}_{\mu }^{\pm }{\left.\left(\frac{{\partial }^{2}{\chi }_{\pm }^{\mu }}{\partial {\xi }^{i}\partial {\xi }^{j}}+{\Gamma }_{\alpha \beta }^{\mu }\frac{\partial {\chi }_{\pm }^{\alpha }}{\partial {\xi }^{i}}\frac{\partial {\chi }_{\pm }^{\beta }}{\partial {\xi }^{j}}\right)\right|}_{\Sigma },$$
(6)

where \(n_{\mu }^{ \pm }\) are the 4-unit normal vector, while \(\xi^{i}\) and \(\chi_{ \pm }^{\mu }\) are the coordinates on Σ and the coordinates in \({M}^{\pm }\), and \(\Gamma_{\alpha \beta }^{\mu }\) corresponds to the Christoffel symbols. Consequently, from metric (3), the extrinsic curvatures are defined by

$$K_{\theta \theta }^{ \pm } = \pm \frac{{G^{\prime}}}{2}\sqrt {H\left( R \right) + \dot{R}^{2} } \equiv K_{\varphi \varphi }^{ \pm } ,\,\,K_{\tau \tau }^{ \pm } = \mp \frac{1}{{H^{2} \sqrt {\dot{R}^{2} + H} }}\left[ { - H^{2} \ddot{R} - {\acute{H}}\left( {\dot{R}^{4} + H\dot{R}^{2} + \frac{1}{2 } H^{2} } \right)} \right],$$
(7)

where a prime and dot are derivatives concerning \(a\) and \(\tau\), respectively.

Accordingly, the discontinuity of \({K}_{ij}^{\pm }\) at Σ related to the surface stress-energy tensor \({S}_{ij}\), is given by the Lanczos equation [4],

$${S}_{ij}=\frac{-1}{8\pi }\left(\left[{K}_{ij}\right]-\left[K\right]{g}_{ij}\right),$$
(8)

where \(\left[ K \right]\) represents the trace of \(\left[ {K_{ij} } \right] = K_{ij}^{ + } - K_{ij}^{ - }\), and \({S}_{j}^{i}=diag(-\sigma ,{p}_{\theta },{p}_{\varphi })\), with pressure \(p\) and surface energy density \(\sigma\). Thus, Lanczos Eqs. (8) become

$$\sigma = \frac{ - 1}{{4\pi }}\left[ {K_{\theta }^{\theta } } \right],\,\,p = p_{\theta } = p_{\varphi } = \frac{1}{8\pi }\left( { \left[ {K_{\tau }^{\tau } } \right] + \left[ {K_{\theta }^{\theta } } \right] } \right).$$
(9)

Therefore, inserting (7) into (9) to obtain

$$\sigma = \frac{ - 1}{{4\pi }}\frac{{\mathop G^{\prime} }}{G}\sqrt {\dot{R}^{2} + H\left( R \right)} ,$$
(10)
$$p = \frac{1}{{8\pi \sqrt {H + \dot{R}^{2} } }} \left[ {\ddot{R} + \frac{1}{2}H^{\prime} + H^{\prime}\dot{R}^{2} H^{ - 2} \left( {H + \dot{R}^{2} } \right) + \frac{{G^{\prime}}}{2G} \left( {H + \dot{R}^{2} } \right)} \right].$$
(11)

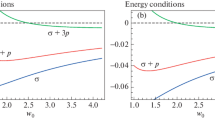
It is observed that the negative sign \(\sigma <0\) of Eq. (10) indicates the presence of exotic matter, and \(\sigma + p \ge 0\) means that the distribution of matter at the throat violates the weak energy condition (\(\sigma \ge 0\),\(\sigma + p \ge 0\)) because \(\sigma\) is negative and violates the null energy condition, which requires only that (\(\sigma + p \ge 0\)). Also, it may satisfy the strong energy condition that requires that (\(\sigma +3p\ge 0\) and \(\sigma + p \ge 0\)).

From this perspective, to study the stability and dynamics of TSW, we assume an exotic EoS, such as a modified generalized Chaplygin gas (MGCG), which is described by [29],

$$p = \omega \sigma - \frac{\beta }{{\sigma^{\gamma } }},\,\omega < 0,\,\beta > 0,$$
(12)

where \(0<\gamma \le 1\) is the parameter.

Also, Eq. (12) is reduced to Chaplygin gas with \(\omega =0\),\(\gamma =1,\) and when \(\beta =0,\) the phantom energy, is recovered, the generalized Chaplygin gas is recovered with \(\omega =0\).

Moreover, by plugging the Eqs. (10) and (11) into (12), the dynamical evolution becomes.

$$\begin{aligned} & \left( {\frac{{ - G^{\prime} }}{4\pi G}\sqrt {H + \dot{R}^{2} } } \right)^{\gamma } \left( {\ddot{R} + \frac{1}{2 } H^{\prime}} \right) + \left( {H + \dot{R}^{2} } \right)\left( {\frac{{ - G^{\prime} }}{4\pi G}\sqrt {H + \dot{R}^{2} } } \right)^{\gamma } \left( {\frac{{\dot{R}^{2} }}{{H^{2} }} H^{\prime} + \frac{{G^{\prime}}}{2G} } \right) \\ & \quad - 8\pi \omega \left( {\frac{{ - G^{\prime} }}{4\pi G}\sqrt {H + \dot{R}^{2} } } \right)^{\gamma + 1} \sqrt {H + \dot{R}^{2} } + 8\pi \beta \sqrt {H + \dot{R}^{2} } = 0. \\ \end{aligned}$$
(13)

3 Stability of the charged GMGHS TSW

Furthermore, the surface energy density \(\sigma\) and pressure \(p\) satisfy the energy conservation equation

$$\frac{d}{d\tau }(\text{A}\sigma )+p\frac{d}{d\tau }\text{A}=\Phi ,$$
(14)

with \(\text{A}=4\pi G\left(R\right)\) being the area at the location of the throat and

$$\Phi =\left({\left[{G}^{\prime}\right]}^{2}-2G{G}^{{\prime}{\prime}}\right) \frac{\dot{R}}{2G}\sqrt{H+{\dot{R}}^{2}},$$

being the momentum flux, and \(\Phi =0\) for \(\text{p}=-\upsigma\) [30]. Thus, Eq. (14) with \(\Phi =0\), will be written in the form:

$$\sigma^{\prime} = - \frac{{G^{\prime}}}{G}\left( {\sigma + p} \right).$$
(15)

Moreover, plugging Eq. (12) into (15) to obtain

$${\sigma }^{\prime}=-\frac{{G}^{\prime}}{G}\left[\sigma (1+\omega )-\frac{\beta }{{\sigma }^{\gamma }}\right].$$
(16)

And also, the second derivative of (16) becomes

$$\sigma^{\prime\prime} = \left( {\frac{{G^{\prime}}}{G}} \right)^{2} \left\{ {\left( {\sigma + p} \right)\left[ {\left( {2 + \chi^{2} } \right) - \frac{{GG^{\prime\prime}}}{{G^{{\prime}{2}} }}} \right]} \right\}.$$
(17)

Therefore, the solution of Eq. (16) becomes

$${\sigma }^{\gamma +1}=\frac{\beta }{(\omega +1)}\left(1-{\left(\frac{{G}_{^\circ }}{G}\right)}^{c}\right)+{{\left(\frac{{G}_{^\circ }}{G}\right)}^{c}{\sigma}} _{^\circ }^{\gamma +1} ,$$
(18)

where \(c=(\omega +1)(\gamma +1)\).

Consequently, from (10), the dynamical equation becomes

$$\dot{R}^{2} + {\Psi }\left( R \right) = 0,$$
(19)

where \(\Psi (R)\) represents the effective potential and is defined by

$$\Psi (R)=H(R)-{\left(\frac{4\pi G}{{G}{^\prime}}\right)}^{2}{\sigma }^{2}.$$
(20)

To study the stability analysis under linear perturbation, one uses the Taylor series of potential \(\Psi (R)\) up to the second order around \({R}_{\circ }\),

$$\Psi (R)=\Psi ({R}_{\circ })+{\Psi }{\prime}({R}_{\circ })(R-{R}_{\circ })+\frac{1}{2}{\Psi }^{^{\prime\prime} }({R}_{\circ })(R-{R}_{\circ }{)}^{2}+O\left[(R-{R}_{\circ }{)}^{3}\right] .$$
(21)

Moreover, the first and second derivatives of Eq. (20) become

$${\Psi }{^\prime}\left(R\right)={H}{^\prime}-32\sigma {\left(\frac{\pi G}{{G}{^\prime}}\right)}^{2}\left[{\sigma }{^\prime}+\sigma \left( \frac{{G}{^\prime}}{G} -\frac{{G}^{{\prime}{\prime}}}{{G}{^\prime}}\right)\right],$$
(22)
$${{\Psi ^{\prime\prime}}}\left( R \right) = H^{\prime\prime} - 2\left( {\frac{4\pi G}{{G^{\prime}}}} \right)^{2} \left\{ {\sigma^{2} \left( {\frac{{G^{^{\prime}2} }}{{G^{2} }} - 3\frac{{G^{\prime\prime}}}{G} + 3\frac{{G^{^{\prime\prime}2} }}{{G^{^{\prime}2} }} - \frac{{G^{\prime\prime\prime}}}{{G^{^{\prime}2} }}} \right) + 4\sigma \sigma{^\prime}\left( {\frac{{G^{\prime}}}{G} - \frac{{G^{\prime\prime}}}{{G^{\prime}}}} \right) + \sigma \sigma^{\prime\prime} + \sigma^{^{\prime}2} } \right\}.$$
(23)

Meanwhile, rewrite Eq. (23) in terms of Eqs. (16) and (17) to get

$${{\Psi ^{\prime\prime}}}\left( R \right) = H^{\prime\prime} - 2\left( {4\pi } \right)^{2} \left\{ {\sigma^{2} \frac{{G^{2} }}{{G^{^{\prime}2} }}\left( {3\frac{{G^{^{\prime\prime}2} }}{{G^{^{\prime}2} }} - \frac{{G^{\prime\prime\prime}}}{{G^{^{\prime}2} }}} \right) + \sigma \left( {\sigma + p} \right)\chi^{2} + \sigma p\left( {\frac{{3GG^{\prime \prime } }}{{G^{^{\prime}2} }}} \right) + p^{2} } \right\}.$$
(24)

where \({\upchi }^{2}\) represents the squared speed of sound.

In addition, the Eqs. (10) and (11) for the static solution (\(\ddot{R}=\dot{R}=0\)) at \(R={R}_{\circ }\) become.

$$\sigma \left( {R_{^\circ } } \right) = \frac{ - 1}{{4\pi }}\frac{{\mathop G\limits^{`}_{^\circ } }}{{G_{^\circ } }}\sqrt {H_{^\circ } } ,$$
(25)
$$p\left( {R_{^\circ } }\right) = \frac{1}{{8\pi \sqrt {H_{^\circ } } }} \left[ {\frac{1}{2}H{^\prime}_{^\circ} + \frac{{\mathop G{^\prime}_{^\circ }}}{{2G_{^\circ}}} H_{^\circ } } \right].$$
(26)

Moreover, the effective potential \(\Psi\) is approximated as a linear function about \(R={R}_{\circ }\). Consequently, the necessary conditions for the presence and stability of a static solution require \(\Psi ({R}_{\circ })=0\) and \({\Psi }{^\prime}({R}_{\circ })=0\).

It is observed that in the case of static solutions \(R={R}_{\circ }\), these conditions \(\Psi ({R}_{\circ })=0\) and \({\Psi }{^\prime}({R}_{\circ })=0\) are satisfied by inserting Eq. (25) into the right-hand side of Eqs. (20) and (22). Therefore, the dynamical equation in this order of approximation becomes: \({\dot{R}}^{2}\left(\tau \right)=-\Psi \left(R\right)=-\frac{1}{2}{\Psi }^{^{\prime\prime} }({R}_{\circ })(R-{R}_{\circ }{)}^{2}+O\left[(R-{R}_{\circ }{)}^{3}\right]\).

Moreover, the stability condition of a linear perturbation depends on the sign of \({\Psi }^{^{\prime\prime} }({R}_{\circ })\) across the throat radius. Therefore, the TSW is stable for \({\Psi }^{^{\prime\prime} }({R}_{\circ })>0\) and unstable for \({\Psi }^{^{\prime\prime} }({R}_{\circ })<0\).

Consequently, from Eq. (24), by assuming \({\Psi }^{^{\prime\prime} }(R)=0\), the speed of sound \({\upchi }^{2}\) becomes

$$\chi^{2} = \frac{{H^{\prime\prime}}}{{2\left( {4\pi } \right)^{2} \sigma \left( {\sigma + p} \right) }} - \frac{1}{{\sigma \left( {\sigma + p} \right)}}\left\{ {\sigma^{2} \frac{{G^{2} }}{{G^{{\prime}{2}} }}\left( {3\frac{{G^{{\prime\prime}{2}} }}{{G^{{\prime}{2}} }} - \frac{{G^{\prime\prime\prime}}}{{G^{{\prime}{2}} }}} \right) + \sigma p\left( {\frac{{3GG^{\prime \prime } }}{{G^{{\prime}{2}} }}} \right) + p^{2} } \right\}.$$
(27)

Afterward, the static solution of dynamical evolution (13) becomes

$${8\pi \beta \sqrt{H}+\left(\frac{{-G}{^\prime}}{4\pi G}\sqrt{H}\right)}^{\gamma }\left(\frac{1}{2 } {H}{^\prime}+H\frac{{G}{^\prime}}{2G}\right)-8\pi \omega {\left(\frac{{-G}{^\prime}}{4\pi G}\sqrt{H}\right)}^{\gamma +1}\sqrt{H}=0.$$
(28)

Meanwhile, rearranging Eqs. (25) and (26) in terms of (3) to get

$${\sigma (R}_{\circ })=\frac{-\sqrt{{R}_{\circ }-2m}}{4\pi {\left(\sqrt{{R}_{\circ }}\right)}^{3}}\left(\frac{2m{R}_{\circ }-{q}^{2} {e}^{-2{\phi }_{^\circ }}}{m{R}_{\circ }-{q}^{2} {e}^{-2{\phi }_{^\circ }}}\right),$$
(29)
$${p(R}_{\circ })=\frac{1}{16\pi {\left(\sqrt{{R}_{\circ }}\right)}^{3}\sqrt{{R}_{\circ }-2m}}\left[ 2m+ \left({R}_{\circ }-2m\right) \left(\frac{2m{R}_{\circ }-{q}^{2} {e}^{-2{\phi }_{^\circ }}}{m{R}_{\circ }-{q}^{2} {e}^{-2{\phi }_{^\circ }}}\right)\right].$$
(30)

Moreover, Eq. (20), as expressed in terms of (3), is described by

$${\Psi }\left( R \right) = \frac{{\left( {R - 2m} \right)}}{R} - \left( {4\pi R} \right)^{2} \left( {\frac{{mR - q^{2} e^{{ - 2\phi_{^\circ } }} }}{{2mR - q^{2} e^{{ - 2\phi_{^\circ } }} }}} \right)^{2} \sigma^{2} .$$
(31)

Afterward, rewrite Eq. (27) in terms of (3) to obtain

$$\chi^{2} = \frac{{W^{2} }}{h J }\left\{ { - \frac{2m}{R} - \frac{{R^{3} }}{{4\left( {R - 2m} \right)}}L^{2} + \frac{3R}{{2h}}L - \frac{{3\left( {R - 2m} \right)}}{{Rh^{2} }}} \right\},$$
(32)

where

$$\begin{aligned} J & \equiv 3R^{2} - 7mR + \frac{{\left( {8m - 3R} \right)}}{2m}q^{2} e^{{ - 2\phi_{^\circ } }} ,\,W \equiv \frac{{mR - q^{2} e^{{ - 2\phi_{^\circ } }} }}{m} , \\ L & \equiv \frac{m}{{R^{2} }} + \frac{{\left( {R - 2m} \right)}}{{2R^{2} }} \left( {\frac{{2mR - q^{2} e^{{ - 2\phi_{^\circ } }} }}{{mR - q^{2} e^{{ - 2\phi_{^\circ } }} }}} \right),\,h \equiv \frac{{2mR - q^{2} e^{{ - 2\phi_{^\circ } }} }}{2mR} . \\ \end{aligned}$$

The variation of \({{\varvec{\chi}}}^{2}\) versus \(R\) is plotted in Fig. 1 with different values of the free parameters \(m,q,\) and \({\phi }_{^\circ }\).

Fig.1
figure 1

The graph of \({\chi }^{2}\) versus \(R\) corresponds to: (a) \(m=0.5, {\phi }_{\circ }=0.01, q=0, 0.2, 0.5, 1,\) (b) \(m=0.5, {\phi }_{\circ }=0.1, q=0, 0.2, 0.5, 1,\) (c) \(m=1, {\phi }_{\circ }=0.01, q=0, 0.2, 0.5, 1,\) (d) \(m=1, {\phi }_{\circ }=0.1, q=0, 0.2, 0.5, 1,\) (e) \(m=1, q=1{, \phi }_{\circ }=0.01, 0.1, 0.5, 1\)

Full size image

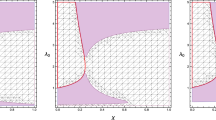
From Eqs. (31) and (18), the variation of \(\Psi (R)\) versus \(R\) is plotted in Fig. 2, taking different values of free parameters \(m,{R}_{\circ },{\phi }_{^\circ },{\sigma }_{^\circ },\omega ,\gamma ,\beta ,\) and \(q\).

Fig. 2
figure 2figure 2

The stability regions of \(\Psi (R)\) against \(R\) corresponding to \({\sigma }_{\circ }=1, {R}_{\circ }=1\) and different values of: (a) \(m=0.5, \gamma =1, \beta =1, \omega =-0.9, {\phi }_{\circ }=0.01, q=0, 0.2, 0.5, 1,\) (b) \(m=0.5, \gamma =1, \beta =1, \omega =-0.9, {\phi }_{\circ }=0.1, q=0, 0.2, 0.5, 1,\) (c) \(m=0.5, \gamma =1, \beta =1, \omega =-0.9, {\phi }_{\circ }=0.5, q=0, 0.2, 0.5, 1,\) (d) \(m=1, \gamma =1, \beta =1, \omega =-0.9, {\phi }_{\circ }=0.01, q=0, 0.2, 0.5, 1,\) (e) \(m=1, \gamma =1, \beta =1, \omega =-0.9, {\phi }_{\circ }=0.1, q=0, 0.2, 0.5, 1,\) (f) \(m=0.5, \gamma =1, \beta =1, \omega =-0.9, q=1, {\phi }_{\circ }=0.01, 0.1, 0.5, 1,\) (g) \(m=0.5, \gamma =1, \beta =1, {\phi }_{\circ }=0.01, q=1, \omega =-0.1, -0.5, -0.9, -1.2,\) (h) \(m=0.5, \gamma =1,q=1, \omega =-0.9, {\phi }_{\circ }=0.01, \beta =0.1, \text{0.5,1}, 2,\) (i) \(m=0.5, q=1, \beta =1, \omega =-0.9, {\phi }_{\circ }=0.01,\gamma =0.1, 0.5, 1, 2,\) (j) \(m=1, \gamma =1, \beta =1, \omega =-0.9, q=1, {\phi }_{\circ }=0.01, 0.1, 0.5, 1,\) (k) \(m=1, q=1, \beta =1, \gamma =1, {\phi }_{\circ }=0.01,\omega =-0.1, -0.5, -0.9, -1.2,\) (l) \(m=1, q=1,\gamma =1, \omega =-0.9, {\phi }_{\circ }=0.01, \beta =0.1, 0.5, 1, 2\)

Full size image

The graph of \({\chi }^{2}\) against \(R\) is given in Fig. 1. The stability configuration increases due to decreasing the asymptotic constant value of the dilaton field \({\phi }_{\circ }.\) Similarly, it happens by decreasing \(m\), and a drastic change occurs by changing \(q\).

Moreover, the variation of \(\Psi (R)\) versus \(R\) is given in Fig. 2. The stable regions can be slightly extended by decreasing \(m\) and also by decreasing the dilaton field \({\phi }_{\circ }.\) It is observed that stable regions can be extended by changing the values of the parameters \(\beta ,\upgamma ,\) and\(\upomega\). Furthermore, it is observed that the stable regions in all figures can be extended by decreasing the values of \(m, q,\) and\({\phi }_{\circ }\).

4 Conclusion

The dynamics of charged TSWs in the context of dilaton gravity by connecting two identical copies of GMGHS black hole spacetime through the cut and paste scheme are studied. The mechanical stability of CTSW is analyzed under linear radial perturbation around the static solution and through the modified generalized Chaplygin gas EoS.

By plotting their stability diagrams, we found that the existence of stability configurations depends on choosing the suitable values of different parameters included in the metric space–time (\(\text{m},\text{q},\) \({\phi }_{\circ }\)) and MGCG EoS (\({\chi }^{2},\upgamma ,\upbeta ,\upomega\)).

The stability configurations are affected to a great extent by the speed-like sound parameter \({\chi }^{2}\). The numerical configurations have been plotted in Figs. 1 and 2 in the form of parameters \({\chi }^{2}\) against \(\text{R}\), and \(\Psi\) against \(R.\)

It is observed that the influence of charge, mass, and speed of sound parameters enhances the stability of regions. The stability configurations increase by decreasing the asymptotic constant value of the dilaton field, and similarly, they increase by decreasing charge and mass.