Stability of thin shell wormholes with a modified Chaplygin gas in Einstein–Hoffman–Born–Infeld theory

Abstract

In the framework of Darmois–Israel formalism, the dynamics of motion equations of spherically symmetric thin shell wormholes that are supported by a modified Chaplygin gas in Einstein–Hoffman–Born–Infeld theory are constructed. The stability analysis of a thin shell wormhole is also discussed using a linearized radial perturbation around static solutions at the wormhole throat. The existence of stable static solutions depends on the value of some parameters of dynamical shell.

1 Introduction

Within the context of general relativity, the accelerated expansion of the universe during the matter dominated period requires the manifestation of dark energy. Several models to represent the dark energy have been proposed, namely, Cosmological constant [1], Quintessence [2], Dissipative matter fluid [3], Chaplygin gas [4], Phantom energy [5], Tracker field [6], K-essence [7].

On the other hand, the stability analysis of thin shell wormholes was reported by several authors. Further, the stability of static wormholes has been investigated, either using specific equation of state (EoS) or linearized radial perturbations around a static solution. Poisson and Visser [8] have discussed a thin shell wormhole (TSW) by pasting together two copies of the Schwarzschild solution. Garcia et al. [9] have analyzed generic spherically symmetric dynamic thin shell traversable wormholes in standard general relativity. Thibeault et al. [10] have studied the stability of TSW in Einstein Maxwell theory with a Gauss-Bonnet term. Rahaman et al. [11] have analyzed the stability of TSW in Heterotic string theory. Hoffmann [12] have studied the spherically symmetric solution in Einstein gravity with a Born–Infeld electrodynamics. Breton [13] has also investigated the spherically symmetric black holes in Born–Infeld electrodynamics coupled to Einstein gravity. Eiroa and Simeone [14] have explodes the mechanical stability of spherical shells in the framework of Einstein–Born–Infeld theory.

In this work, we will investigate the mechanical stability of spherically symmetric thin shell wormholes with a modified Chaplygin gas in the frameworks of Einstein–Hoffman–Born–Infeld (EHBI) theories.

2 The Darmois–Israel formalism

In the following we adopt the unit system (c = G = 1). We consider two distinct spacetime manifolds $M_{ + }$ and $M_{ - }$ of given metrics $g_{\mu \nu }^{ + } (x_{ + }^{\mu } )$ and $g_{\mu \nu }^{ - } (x_{ - }^{\mu } )$, in terms of independent defined coordinate systems $x_{ \pm }^{\mu }$. We assume that the manifolds are bounded by hypersurfaces $\varSigma_{ + }$ and $\varSigma_{ - }$, respectively. The hypersurfaces are isometric, i.e., $g_{ij}^{ + } (\xi ) = g_{ij}^{ - } (\xi ) = g_{ij} (\xi )$, in terms of the intrinsic coordinates, invariant under the isometric. A single manifold $M$ can be obtained by joining together $M_{ + }$ and $M_{ - }$ at their boundaries, i.e., $M = M_{ + } \cup M_{ - }$, with the natural identification of the boundaries $\varSigma = \varSigma_{ + } = \varSigma_{ - }$. The second fundamental forms (extrinsic curvature) associated with the two sides of the shell are:

$$K_{ij}^{ \pm } = - n_{\gamma }^{ \pm } \left( {\frac{{\partial^{2} x^{\gamma } }}{{\partial \xi^{i} \partial \xi^{j} }} + \varGamma_{\alpha \beta }^{\gamma } \frac{{\partial x^{\alpha } }}{{\partial \xi^{i} }}\frac{{\partial x^{\beta } }}{{\partial \xi^{j} }}} \right) \vdots_{\varSigma }$$

(1)

where $n_{\gamma }^{ \pm }$ are the unit normal 4-vector to $\varSigma$ in $M$, with $n_{\mu } n^{\mu } = 1$ and $n_{\mu } e_{i}^{\mu } = 0$. The Israel formalism requires that the normal point is from $M_{ - }$ to $M_{ + }$. In the case of a thin shell $K_{ij}$ is not continuous across $\varSigma$, thus, the discontinuity in the second fundamental form is defined as $\left[ {K_{ij} } \right] = K_{ij}^{ + } - K_{ij}^{ - }$. The Einstein equation determines the relations between the extrinsic curvature and the three dimensional intrinsic energy momentum tensor are given by Lanczos’s equations,

$$t_{ij} = \frac{ - 1}{8\pi }\left( {\left[ {K_{ij} } \right] - \left[ K \right]g_{ij} } \right)$$

(2)

where $\left[ K \right]$ is the trace of $\left[ {K_{ij} } \right]$, and $t_{ij}$ is the surface stress-energy tensor on $\varSigma$. The first contracted Gauss–Kodazzi equation or the “Hamiltonian” constraint is given by:

$$G_{\mu \nu } n^{\mu } n^{\nu } = \frac{1}{2}(K^{2} - K_{ij} K^{ij} - {}^{3}R),$$

(3)

with the Einstein equations provide the evolution identity as,

$$t^{ij} \bar{K}_{ij} = \left[ { - T_{\mu \nu } n^{\mu } n^{\nu } - \frac{\varLambda }{8\pi }} \right]_{ - }^{ + } .$$

(4)

We introduce the following convention, $[X] = X^{ + } - X^{ - }$, $\bar{X} = \frac{1}{2}(X^{ + } + X^{ - } )$, and the second contracted Gauss–Kodazzi equation or the “ADM” constraint is given as

$$G_{\mu \nu } e_{i}^{\mu } n^{\nu } = K_{i;j}^{j} - K_{,i}$$

(5)

Taking in consideration that the Lanczos equations gives the conservation identity

$$t_{j;i}^{i} = \left[ {T_{\mu \nu } e_{j}^{\mu } n^{\nu } } \right]_{ - }^{ + } .$$

(6)

The surface stress-energy tensor may be written in terms of the surface energy density $\sigma$, and surface pressure $p$: $t_{j}^{i} = diag( - \sigma ,p,p)$. For spherically symmetric thin shell, the Lanczos equations are then reduced to:

$$\sigma = \frac{ - 1}{4\pi }\left[ {K_{\theta }^{\theta } } \right]$$

(7)

$$p = \frac{1}{8\pi }\left( {\left[ {K_{\tau }^{\tau } } \right] + \left[ {K_{\theta }^{\theta } } \right]} \right).$$

(8)

If the surface stress-energy terms are zero, the junction is denoted as a boundary surface. In the presence of the surface stress terms, the junction is called a thin shell.

3 Dynamics of thin shell wormhole in Einstein– Hoffman –Born–Infeld theory

The Einstein–Hoffman–Born–Infeld electrodynamics is derived from an action of the gravitational electromagnetic field and given by [15],

$$S = \tfrac{1}{2}\int {\sqrt { - g} } (R + L(F))d^{4} x$$

(9)

where $R$ is the scalar of curvature, $g = \det \left| {g_{\mu \nu } } \right|$, and $L(F)$ is the non-linear electrodynamics Lagrangian. The Einstein nonlinear electrodynamics equations can be written as

$$G_{\mu }^{\nu } = T_{\mu }^{\nu } = \tfrac{1}{2}(L(F)\delta_{\mu }^{\nu } - 4L_{F} F_{\mu \sigma } F^{\upsilon \sigma } ),$$

(10)

with $F_{\sigma \upsilon } = \partial_{\sigma } A_{\upsilon } - \partial_{\upsilon } A_{\sigma }$ the electromagnetic tensor and $L_{F} = \tfrac{\partial L}{\partial F}$. The parameter $b$ (is the electric field at the origin, $r = 0$) indicates how much Hoffman–Born–Infeld and Maxwell electrodynamics differs; $b^{ - 1}$ is the maximum of the electric field. In the limit $b \to 0$, the Maxwell–Lagrangian is recovered. From Eq. (9), we can obtain the field equations, which they have a spherically symmetric for a pure electrically charged particle described by the line element [16]:

$$ds^{2} = - f(r)dt^{2} + f^{ - 1} (r)dr^{2} + r^{2} (d\theta^{2} + \sin^{2} \theta d\varphi^{2} ),$$

(11)

where $r \succ 0$ is the radial coordinate, $0 \le \theta \le \pi$ and $0 \le \varphi \prec 2\pi$ are the angular coordinates, and $f(r)$ has the form:

$$\begin{aligned} f(r) & = 1 - \frac{2m}{r} - \frac{{q^{2} }}{{3r_{ \circ }^{4} }}r^{2} \ln \left( {\frac{{r^{4} }}{{r^{4} + r_{ \circ }^{4} }}} \right) - \frac{{\sqrt 2 q^{2} }}{{3rr_{ \circ } }}\left\{ {\tan^{ - 1} \left( {\frac{\sqrt 2 r}{{r_{ \circ } }} + 1} \right)} \right. \\ & \left. { + \tan^{ - 1} \left( {\frac{\sqrt 2 r}{{r_{ \circ } }} - 1} \right)} \right\} - \frac{{\sqrt 2 q^{2} }}{{6rr_{ \circ } }}\ln \left\{ {\frac{{r^{2} + r_{ \circ }^{2} - \sqrt 2 rr_{ \circ } }}{{r^{2} + r_{ \circ }^{2} + \sqrt 2 rr_{ \circ } }}} \right\} + \frac{{\sqrt 2 \pi q^{2} }}{{3rr_{ \circ } }}, \\ \end{aligned}$$

(12)

with $r \succ r_{ \circ }$, $r_{ \circ } = \sqrt {qb}$, where $m$ is the mass, $q$ is the charge. The Schwarzschild metric is recovered by taking the limit $b \to \infty$, and the Reissner–Nordstrom geometry is obtained by taking the limit $b \to 0$. Let the equation of the shell be $r = a(\tau )$, the throat radius $a(\tau )$ describes the time evolution of the shell. The intrinsic metric on $\varSigma$ is written as:

$$ds^{2} = - d\tau^{2} + a^{2} (\tau )\left( {d\theta^{2} + \sin^{2} \theta d\varphi^{2} } \right)$$

(13)

where $\tau$ is the proper time of the shell. The Lanczos Eqs. (7) and (8) become,

$$\sigma = \frac{ - 1}{2\pi a}\sqrt {\dot{a}^{2} + f(a)}$$

(14)

$$p = \frac{1}{8\pi a}\frac{{2a\ddot{a} + 2\dot{a}^{2} + 2f(a) + af^{\prime}(a)}}{{\sqrt {f(a) + \dot{a}^{2} } }}$$

(15)

where dot and prime mean derivatives with respect to $\tau$ and $a$, respectively. From Eq. (14), $\sigma \prec 0$ indicates the presence of exotic matter, with a modified Chaplygin gas on the shell $\varSigma$. In this gas, the pressure has opposite sign to the energy density. Then, the equation of state at the throat can be written in the following form,

$$p = B\sigma - \frac{A}{{\left| \sigma \right|^{\alpha } }}$$

(16)

where $A \succ 0$, $0 \prec \alpha \le 1$ and $B \prec 0$ are constants, this equation can be reduced to generalized Chaplygin gas in the limit $B \to 0$. When $\alpha = 1$, the ordinary Chaplygin gas equation of state $p = {{ - A} \mathord{\left/ {\vphantom {{ - A} \sigma }} \right. \kern-0pt} \sigma }$ is recovered. Now, the dynamical evolution of the wormhole throat can be obtained by substituting Eqs. (14) and (15) into Eq. (16):

$$\begin{aligned} (2a)^{\alpha } \left\{ {a^{2} \left( {2\ddot{a} + f^{{\prime }} (a)} \right) + 2a\left( {f(a) + \dot{a}^{2} } \right)} \right\} + 2A\left( {4\pi a^{2} } \right)^{1 + \alpha } \hfill \\ \left[ {f(a) + \dot{a}^{2} } \right]^{{\tfrac{1}{2}(1 - \alpha )}} + 2B(2a)^{1 + \alpha } \left( {f(a) + \dot{a}^{2} } \right) = 0 \hfill \\ \end{aligned}$$

(17)

This differential equation should be satisfied by the throat radius of thin shell wormholes in Einstein–Hoffman–Born–Infeld theory that is treated by exotic matter with the state equation of a modified Chaplygin gas. It is convenient to define the parameter space of the problem using $A,\alpha ,B,m,q,b$ and $a$ as free parameters.

4 Stability analysis

The dynamical Eq. (17) for the static solution (where $\ddot{a} = \dot{a} = 0$), becomes

$$(2a_{ \circ } )^{\alpha } \left\{ {a_{ \circ }^{2} f^{{\prime }} (a_{ \circ } ) + 2(f(a_{ \circ } )} \right\} + 2A\left( {4\pi a_{ \circ }^{2} } \right)^{1 + \alpha } [f(a_{ \circ } )]^{{\tfrac{1}{2}(1 - \alpha )}} + 2B(2a_{ \circ } )^{1 + \alpha } f(a_{ \circ } ) = 0$$

(18)

The surface energy density and pressure in the static case are given by:

$$\sigma_{ \circ } = \frac{ - 1}{{2\pi a_{ \circ } }}\sqrt {f(a_{ \circ } )} ,\quad p_{ \circ } = \frac{1}{{8\pi a_{ \circ } }}\frac{{2f(a_{ \circ } ) + a_{ \circ } f^{{\prime }} (a_{ \circ } )}}{{\sqrt {f(a_{ \circ } )} }},$$

(19)

The surface energy density and pressure satisfy the conservation equation

$$\frac{d}{d\tau }\sigma H + p\frac{dH}{d\tau } = 0$$

(20)

where $H = 4\pi a^{2}$ is the area of the wormhole throat. This equation describes the continuity equation for the energy–momentum tensor (i.e. the change in internal energy of the throat plus the work done by the throat’s internal forces), and it can be written in the form

$$\frac{d}{d\tau }\sigma = - \frac{2}{a}(\sigma + p)\frac{da}{d\tau }$$

(21)

which can rewritten as

$$a\sigma^{{\prime }} = - 2(\sigma + p).$$

(22)

Rearranging Eq. (14) in order to obtain the dynamical equation of motion of the thin shell wormhole,

$$\dot{a}^{2} + V(a) = 0$$

(23)

where $V(a)$ is known as potential function given by

$$V(a) = f(a) - 4\pi^{2} a^{2} \sigma^{2} (a)$$

(24)

The differentiation of Eq. (24) gives:

$$V^{{\prime }} (a) = f^{{\prime }} (a) + 8\pi^{2} a\sigma (a)(\sigma + 2p)$$

(25)

Also, the first derivative of Eq. (16) is given by

$$\sigma^{{\prime }} + 2p^{{\prime }} = \sigma^{{\prime }} \left\{ {2B(1 + \alpha ) + 1 - \tfrac{2\alpha p}{\left| \sigma \right|}} \right\}$$

(26)

The Taylor series expansion of $V(a)$ up to second order around $a_{ \circ }$, is given by

$$V(a) = \sum\limits_{n = 0}^{2} {c_{n} (a - a_{ \circ } )^{n} } ,\quad c_{n} = \frac{{V^{(n)} (a_{ \circ } )}}{n!}$$

(27)

The prime denotes a derivative with respect to $a$. The second derivative of $V(a)$ is given by

$$V^{{\prime \prime }} (a) = f^{{\prime \prime }} (a) - 8\pi^{2} \left\{ {(\sigma + 2p)^{2} + 2\sigma (\sigma + p)[1 - 2\alpha \beta^{2} + 2B(1 + \alpha )]} \right\}$$

(28)

where $\beta^{2} = \tfrac{p}{\sigma }$ is the squared of sound velocity. In the static solutions $a = a_{ \circ }$, $V(a_{ \circ } ) = 0$ and $V^{{\prime }} (a_{ \circ } ) = 0$, while $V^{{\prime \prime }} (a_{ \circ } )$ becomes,

$$\begin{aligned} V^{{\prime \prime }} (a_{ \circ } ) = f^{{\prime \prime }} (a_{ \circ } ) - \frac{{(\alpha + 1)f^{{{\prime }2}} (a_{ \circ } )}}{{2f(a_{ \circ } )}} + [1 + 2B(1 + \alpha )] \hfill \\ \frac{{f^{{\prime }} (a_{ \circ } )}}{{a_{ \circ } }} - \frac{{2f(a_{ \circ } )}}{{a_{ \circ }^{2} }}[1 - \alpha + 2B(1 + \alpha )] \hfill \\ \end{aligned}$$

(29)

So that, $\dot{a}^{2} = - \frac{1}{2}V^{{\prime \prime }} (a_{ \circ } )(a - a_{ \circ } )^{2} + O\left[ {(a - a_{ \circ } )^{3} } \right]$. The stability conditions $V^{{\prime \prime }} (a_{ \circ } ) \succ 0$ lead to

$$2f_{ \circ } > a_{ \circ } f_{ \circ }^{{\prime }}, \quad 1 + 2B(\alpha + 1) < \frac{{2a_{ \circ }^{2} f_{ \circ } f_{ \circ }^{{\prime \prime }} - (\alpha + 1)a_{ \circ }^{2} f_{ \circ }^{{{\prime }2}} + 4\alpha f_{ \circ }^{2} }}{{2f_{ \circ } (2f_{ \circ } - a_{ \circ } f_{ \circ }^{{\prime }} )}},$$

(30)

and

$$2f_{ \circ } < a_{ \circ } f_{ \circ }^{{\prime }} ,\quad 1 + 2B(\alpha + 1) > \frac{{2a_{ \circ }^{2} f_{ \circ } f_{ \circ }^{{\prime \prime }} - (\alpha + 1)a_{ \circ }^{2} f_{ \circ }^{{{\prime }2}} + 4\alpha f_{ \circ }^{2} }}{{2f_{ \circ } \left( {2f_{ \circ } - a_{ \circ } f_{ \circ }^{{\prime }} } \right)}},$$

(31)

where $f_{ \circ } = f(a_{ \circ } )$. The TSW is stable under radial perturbations if and only if $V^{{\prime \prime }} (a_{ \circ } ) \succ 0$, while for $V^{{\prime \prime }} (a_{ \circ } ) \prec 0$, the static solution is unstable.

From Eq. (28), let $V^{{\prime \prime }} (a_{ \circ } ) = 0$, the squared of sound velocity $\beta^{2}$ is given by

$$\beta^{2} = \frac{1}{2\alpha }[1 + 2B(1 + \beta )] + \frac{{a_{ \circ }^{2} }}{4\alpha }\frac{{f^{{\prime \prime }} (a_{ \circ } ) - \frac{{f^{{{\prime }2}} (a_{ \circ } )}}{{2f(a_{ \circ } )}}}}{{\tfrac{1}{2}a_{ \circ } f^{{\prime }} (a_{ \circ } ) - f(a_{ \circ } )}}$$

(32)

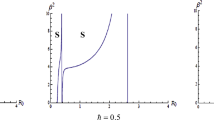
From Eq. (32), the plots of $\beta^{2}$ versus $a_{ \circ }$ with different values of the parameters ($m,q,b,B,\alpha$) are shown in Figs. (1, 2, 3 and 4).

Fig. 1

Stability regions for thin-shell wormholes corresponding to $b = 1,\alpha = 1$ and a fixed value of $m = 2$: (a) B = 1, q = 0.5, (b) B = 1, q = 1, (c) B = 1, q = 2

Fig. 2

Stability regions for thin-shell wormholes corresponding to $b = 1$ and a fixed value of $m = 2$: (a) B = −1, q = 0.5, α = 1, (b) B = −0.1, q = 2, α = 1, (c) B = 0.1, q = 1, α = 1, (d) B = −1, q = 1, α = 0.1

Fig. 3

Stability regions for thin-shell wormholes corresponding to $q = 1,B = 1$ and a fixed value of $m = 2$: (a) b = 3, α = 1, (b) b = 0.1, α = 1, (c) b = 1, α = 2, (d) b = 1, α = 0.5

Fig. 4

Stability regions for thin-shell wormholes corresponding to the different value of $q,b,B,\alpha$ and a fixed value of $m = 1$: (a) b = 1, q = 1, B = 1, α = 1, (b) b = 1, q = 2, B = −1, α = 1, (c) b = 1, q = 2, B = −1, α = 2, (d) b = 0.5, q = 2, B = −0.1, α = 0.5

5 Conclusion

The spherically symmetric thin shell wormholes supported by a modified Chaplygin gas within the framework of Einstein–Hoffman–Born–Infeld theory is derived, using the usual cut and paste scheme (Darmois–Israel formalism). Such kind of exotic matter has been recently considered to be of particular interest in cosmology as it provides a possible explanation for the accelerated expansion of the universe.

The stability analysis of thin shell wormholes with the equation of state of modified Chaplygin gas, with linearized spherically symmetric perturbation about a static equilibrium solution, is obtained. The energy density and the pressure at the throat were obtained as functions of the throat radius. It seems that the presence of the charge increases the stability regions for shells around black holes. From the stability conditions (30–31), the TSW is stable under radial perturbations if and only if $V^{{\prime \prime }} (R_{ \circ } ) > 0$, while for $V^{{\prime \prime }} (R_{ \circ } ) < 0$, the static solution is unstable. The output of thin shell wormholes can be either stable or unstable, depending on the mass $m$, the parameters $q,b,B,\alpha$ and the initial position $a_{ \circ }$ of the dynamical shell.