1 Introduction

The interfacial instability of two superposed fluids has been investigated since the turn of the nineteenth century by Lord Rayleigh and Taylor [1, 2], who studied the linear regime. According to their names, the problem of interfacial instability under gravitational field is known as Rayleigh–Taylor instability (RTI). This instability is observed when a fluid is accelerated across a sharp interface into a second, heavier fluid. Such flows occur in the explosive detonation of type la supernova and in the ablation stage of the Inertial Confinement Fusion (ICF) process. In ICF, ablation and blow-off at an outer core results in the shell interface accelerated normally inward with a complex acceleration profile, so that, applied perturbations grows, dominated by a strong RTI [3].

There are three stages in the RTI process. In the linear regime, where the amplitude of perturbation becomes very small compared to the wave length, the perturbed amplitude \(\xi (t)\) is obtained from the dispersion relation [4]

$$\begin{aligned} \ddot{\xi }(t) -g(t) k A\xi (t)=0 \end{aligned}$$

where g(t) is the acceleration, k is perturbed wave number and A is the Atwood number defined by \(\frac{\rho _h-\rho _l}{\rho _h+\rho _l}\), \(\rho _{h(l)}\) is the density of the upper(lower) fluid. When g(t) is constant, the amplitude of the interface grows as \(\sim \exp (\sqrt{Akg}t) \). In the second stage, the small perturbation grows into non-linear structures in the form of a bubble (a part of lighter fluid that penetrates into heavier one) and spike (a part of heavier fluid that penetrates into lighter region) where the amplitude of perturbation becomes comparable with the wave length. Finally, turbulent mixing occurs and the motion is broken [5].

In the linear stage, the amplitude of the bubble is just opposite to the spike due to the sinusoidal shape of the interface [4]. However, in the non-linear regime, the shape of the interface is far from the sinusoidal structure. To described the evolution of the non-linear structures, several models have been proposed. One of them was proposed by Layzer [6], where the initial structure is assumed to be a parabola. Extending this model for arbitrary density ration, Goncharov [7] derived the asymptotic velocity of the bubble tip, which is \(\sqrt{\frac{2A}{1+A}\frac{g}{3k}}\). However, the observed simulation and experimental results [8,9,10,11,12] claim that nonlinear theory correctly describes the bubble’s behavior in the early nonlinear stage, but fails in the highly nonlinear phase. Betti and Sanz [9] established that this occurs due to vorticity accretion inside the bubble and the velocity of the bubble tip is slightly greater than the classical value derived by Goncharov [7]. A similar result was observed by Fu et al. [10] using localized perturbations described by a Gaussian mode. The overwhelming majority of RTI investigations have been done assuming the gravitational acceleration as constant. However, in most experimental configurations, astrophysical systems and ICF applications, this instability occurs under a variable acceleration. Depending upon the nature of the acceleration profile, it may even be possible to stabilize the growth of the instability.

For the purpose of the study of the dynamic stabilization of RTI, Kawata et al. [13] reported the stabilization of RTI mixing layer, subject to temporally varying acceleration histories of the form \(g(t)= g_0+\mu ^2a\sin (\mu t) \), where \(g_0\) is the constant acceleration, \(\mu \) is the frequency and a is the amplitude. Instead of \(\sin (\mu t)\), Piriz et al. [14, 15] considered \(g(t)= g_0+mu^2a[\delta (\mu t-2\,m\pi )-\delta (\mu t-\overline{2\,m+1}\pi )]\), where m is an integer. Piriz et al. [16] also analyzed the dynamic stabilization of RTI in an ablation front by considering a general square wave for modulating the vertical acceleration of the front. In nonlinear regime, Mikaelian [17] analyzed the same effect by considering \(g(t)=g_0+g_1\cos (\mu t)\). Mikaelian [18] also reported the effect of variable accelerations of the form \(g(1-e^{-\frac{t}{T}})\) and \(g(1-e^{-\frac{t}{T}})(1+\cos \mu t)\) on RTI without considering the ablation. Recently, Ramapraphu et al. [3] and Aslangil el al. [19] considered the acceleration of the form \(g_0t^n\), and studied the stabilizing effect on RTI.

The variable g(t) induced RTI mixing study proposed here will help to understand the effect of pulse shaping on improving the entropy profiles and fuel capsule performance in an ICF setting [20]. Here we will investigate the effect of two simplified time dependent accelerations such as \(g(t) = g(1-e^{-\frac{t}{T}})\) and \(g(1-e^{-\frac{t}{T}})(1+\cos \mu t)\) on the RTI bubble tip using extended Layzer’s model with vorticity accumulation inside the bubble. These two types of acceleration profiles are idealized forms simplified from a realistic laser-driven system such as ICF. By considering the vorticity inside the bubble, as proposed by Betti and Sanz [9], the effect of time-varying accelerations on the late time evolution of RTI will be investigated analytically and numerically.

2 Non-linear hydrodynamic model

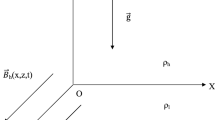
The x-y plane (\(z=0\)) is assumed to be the unperturbed interface between the denser fluid of density \(\rho _h\) (region \(z>0\)) and lighter fluid of density \(\rho _l\) (region \(z<0\)). Acceleration g(t) is taken to point along negative z-axis. According to Layzer [6], after perturbation the finger shape interface is assumed to take up a parabolic form, given by

$$\begin{aligned} z=\eta (x,t)=\eta _0(t)+\eta _2(t)x^2 \end{aligned}$$
(1)

where \(\eta _{0}>0\) and \(\eta _{2}<0\) respectively represents the amplitude and curvature of the bubble tip.

The evolution of the interface \(z=\eta (x,t)\) can be determined by the kinematical boundary conditions as [21]

$$\begin{aligned} \frac{\partial \eta }{\partial t}+v_{hx} \frac{\partial \eta }{\partial x}=v_{hz} \end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial \eta }{\partial x}(v_{hx}-v_{lx})=v_{hz}-v_{lz} \end{aligned}$$
(3)

where \((v_{h})_{x,z}\) and \((v_{l})_{x,z}\) are the velocity components of the denser and lighter fluids respectively.

The velocity potential describing the irrotational motion for the denser fluid is assumed to be given by [7, 22]

$$\begin{aligned} \phi (x,z,t)=a(t) \cos (kx) e^{-k(z-\eta _{0}(t))} \end{aligned}$$
(4)

where k is the perturbed wave number and a(t) is the perturbed velocity amplitude of the denser fluid.

The equation of motion of the upper incompressible fluid leads to the following Bernoulli’s equation [23]:

$$\begin{aligned} \rho _{h}[-\frac{\partial \phi }{\partial t}+ \frac{1}{2}(\vec {\nabla } \phi )^{2}+ g(t) z]+p_{h}=f_{h}(t) \end{aligned}$$
(5)

The motion of the lighter fluid inside the bubble is assumed to be rotational with vorticity \(\vec {\omega }=(\frac{\partial v_{lz}}{\partial x}-\frac{\partial v_{lx}}{\partial z}){{\hat{y}}}\). This motion is described by the stream function \(\Psi (x,z,t)\), given by [9]

$$\begin{aligned} \Psi (x,z,t)= \,& {} b_{0}(t)x+[b_{1}(t)e^{k(z-\eta _{0})}\nonumber \\{} & {} +\omega _{0}(t)/k^2] \sin {(k x)} \end{aligned}$$
(6)

with \(v_{lx}=-\frac{\partial \Psi }{\partial z}\) and \(v_{lz}=\frac{\partial \Psi }{\partial x}\).

Hence

$$\begin{aligned} \nabla ^2 \Psi =-\omega \end{aligned}$$
(7)

Now consider a function \(\chi (x,z,t)\), such that

$$\begin{aligned} \nabla ^2 \chi =-\omega \end{aligned}$$
(8)

clearly \((\Psi -\chi )\) is a harmonic function as \(\nabla ^2 (\Psi -\chi )=0\). Let \(\Phi (x,z,t)\) be the conjugate function of \((\Psi -\chi )\), then

$$\begin{aligned} \frac{\partial \Phi }{\partial x}=\frac{\partial \Psi }{\partial z}-\frac{\partial \chi }{\partial z} \end{aligned}$$
$$\begin{aligned} \frac{\partial \Phi }{\partial z}=-\frac{\partial \Psi }{\partial x}+\frac{\partial \chi }{\partial x} \end{aligned}$$
(9)

Hence the velocity components of the lighter fluid are

$$\begin{aligned} v_{lx}=-\frac{\partial \Psi }{\partial z}=-\frac{\partial \Phi }{\partial x}-\frac{\partial \chi }{\partial z} \end{aligned}$$
$$\begin{aligned} v_{lz}=\frac{\partial \Psi }{\partial x}=-\frac{\partial \Phi }{\partial z}+\frac{\partial \chi }{\partial x} \end{aligned}$$
(10)

Starting from the equation of motion of the lighter fluid

$$\begin{aligned} \rho _{l}\left[ \frac{\partial \vec {v}}{\partial t}+ \frac{1}{2}\vec {\nabla }(\vec {v}_{l} ){^2}+\omega {\widehat{y}}\times \vec {v}_{l}\right] +\vec {\nabla }(p_1+\rho _l g(t)z)=0 \end{aligned}$$
(11)

and using Eqs. (7)–(10), we get

$$\begin{aligned}{} & {} \rho _{l}[-\frac{\partial \Phi }{\partial t}+ \frac{1}{2}(\vec {v}_{l} ){^2}-\omega \Psi +g(t) z]\nonumber \\{} & {} \quad +\int \rho _{l}[(\Psi \frac{\partial \omega }{\partial z}-\frac{\partial {\dot{\chi }}}{\partial z})dx +(\Psi \frac{\partial \omega }{\partial x}+\frac{\partial {\dot{\chi }}}{\partial x})dz] + p_{l}=f_{l}(t) \end{aligned}$$
(12)

The following choices are made according to Ref. [12]

$$\begin{aligned} \Phi (x,z,t)=-b_0(t)y+b_1(t)\cos {(k x)} e^{k(z-\eta _0)} \end{aligned}$$
(13)

and

$$\begin{aligned} \chi (x,z,t)=\omega _{0}(t)\sin {(k x)}/k^2 \end{aligned}$$
(14)

Plugging the dynamical boundary condition \(p_h=p_l\) [21] at the interface \(z=\eta (x,t)\) in Eqs. (5) and (12), we obtained the following equation:

$$\begin{aligned}{} & {} \rho _{h}[-\frac{\partial \phi }{\partial t}+ \frac{1}{2}(\vec {\nabla } \phi )^{2}+ g z]- \rho _{l}[-\frac{\partial \Phi }{\partial t}\nonumber \\{} & {} \qquad + \frac{1}{2}(\vec {\nabla } \Phi ){^2}-\omega \Psi +g z]-\int \rho _{l}[(\Psi \frac{\partial \omega }{\partial z}-\frac{\partial {\dot{\chi }}}{\partial z})dx \nonumber \\{} & {} \qquad +(\Psi \frac{\partial \omega }{\partial x}+\frac{\partial {\dot{\chi }}}{\partial x})dz] =f_{h}(t)-f_l(t) \end{aligned}$$
(15)

satisfied at the interface \(z=\eta (x,t)\).

Substituting \(\eta \), \((v_{h})_{x,z}\), \((v_{l})_{x,z}\) in Eqs. (2) and (3) and expanding in powers of the transverse coordinate x, neglecting terms O(\(x^{i}\))(\(i\ge 3\)), we obtain the following equations:

$$\begin{aligned} \frac{\textrm{d}\xi _{1}}{\textrm{d}\tau }=\xi _{3} \end{aligned}$$
(16)
$$\begin{aligned} \frac{\textrm{d}\xi _{2}}{\textrm{d}\tau }=-\frac{1}{2}(6\xi _{2}+1)\xi _{3} \end{aligned}$$
(17)
$$\begin{aligned} \frac{kb_{0}}{\sqrt{kg_0}}=\frac{6\xi _{2}(2\xi _{3}-\Omega )}{(6\xi _{2}-1)} \end{aligned}$$
(18)
$$\begin{aligned} \frac{k^2b_{1}}{\sqrt{kg_0}}=-\frac{(6\xi _{2}+1)\xi _{3}-\Omega }{(6\xi _{2}-1)} \end{aligned}$$
(19)

where \(\xi _1=k\eta _0\), \(\xi _2=\frac{\eta _2}{k}\) and \(\xi _3=\frac{k^2a_1}{\sqrt{kg_0}}\) are respectively the dimensionless amplitude, curvature and velocity of the tip of the nonlinear bubble structure, \(\tau =t\sqrt{kg_0}\) is the dimensionless time, \(\Omega =\frac{\omega _{0}}{\sqrt{kg_0}}\) is the dimensionless vorticity and \(g_0\) is the constant acceleration due to gravity. Equations (16) and (17) are the first two of the three time development equations needed to describe the time evaluation of the nonlinear bubble structure.

Now, substituting \(\phi _h\), \(\Psi \), \(\chi \), \(\Phi \) and \(\eta \) in Eq. (15), using Eqs. (16)–(20) and equating coefficient of \(x^2\), we obtain the following time development equation for \(\xi _3\):

$$\begin{aligned} \frac{d\xi _3}{d\tau }= & {} \frac{1}{D(\xi _2,r)}[-N(\xi _2,r)\frac{\xi _3^2}{(6\xi _2-1)}+2(r-1)(6\xi _2-1)\xi _2G(\tau )\nonumber \\{} & {} +\frac{\Omega ^2-5(6\xi _{2}+1)\Omega \xi _3}{(1-6\xi _2)}+{\dot{\Omega }}] \end{aligned}$$
(20)

where \(r=\frac{\rho _h}{\rho _l}\), \(G(\tau )=\frac{g(t)}{g_0}\), \( D(\xi _2,r)=12(1-r)\xi _{2}^{2}+4(1-r)\xi _{2}+(r+1)\) and \( N(\xi _2,r)=36(1-r)\xi _{2}^{2}+12(4+r)\xi _{2}+(7-r)\)

Equations (16), (17) and (20) describe the time behavior of the bubble tip driven by variable acceleration profiles.

3 Results and discussions

The time evolution of the bubble structure of the interface is described by the Eqs. (16), (17) and (20). Before integrating the equations numerically, it is necessary to understand the dependence of the vorticity \(\Omega (\tau )\) on \(\tau \). As suggested by Snaz and Betti [9], we consider \(\Omega (\tau )\) in the following form so that the time dependence of \(\Omega (\tau )\) has similarities with the simulation results:

$$\begin{aligned} \Omega (\tau )=\frac{\Omega _{c}}{1+2\tanh (\tau _{0})}[\tanh (\tau _{0})(1+\tanh (\tau ))+\tanh (\tau -\tau _{0})] \end{aligned}$$
(21)

Here \(\Omega _c\) is the asymptotic value of the dimensionless vorticity and \(\tau _{0}\) is a dimensionless time parameter. Note that, \(\Omega (\tau )\) increases from 0 and tends to an asymptotic value \(\Omega _c\) as \(\tau \rightarrow \infty \). The constants \(\tau _0\) and \(\Omega _c\) are considered according to simulation results given by Snaz and Betti [9]. \(\tau _0=8\) and \(\Omega _c=2\) gives a good approximation of the simulation and experimental results. The plot for \(\Omega (\tau )\) is shown in Fig. 1.

Fig. 1
figure 1

Vorticity \(\Omega (\tau )\) plotted against \(\tau \) with \(\Omega _{c}\) = 2 and parameter \(\tau _{0}\)= 8

Full size image

To obtain the initial conditions of the numerical integration, it is assumed that the initial interface is given by \(z=\eta _{0}(t=0) cos(k x)\). The expansion of the cosine function gives \((\xi _{2})_\textrm{initial}= -\frac{1}{2}(\xi _{1})_\textrm{initial}\), where \((\xi _{1})_\textrm{initial}\) is the arbitrary initial amplitude. Since the perturbation starts from rest, we may often choose \((\xi _{3})_\textrm{initial}=0\).

Fig. 2
figure 2

The time evolution of the bubble amplitude (\(\xi _1\)), curvature (\(\xi _2\)) and velocity (\(\xi _3\)) under the acceleration profile \(G(\tau )=1-e^{-\frac{\tau }{\zeta }}\), where \(r=2\) and \(\zeta =0\) (Solid line), \(\zeta =1\) (Dot-dash line), \(\zeta =2\) (Dash line), \(\zeta =5\) (Dotted)

Full size image

The dimensionless time development of bubble parameters \(\xi _1\), \(\xi _2\) and \(\xi _3\) is shown in Figs. 2 and 3. In Fig. 2, we consider \(G(\tau )=(1-e^{-\frac{\tau }{\zeta }})\), where \(\zeta =T\sqrt{kg_0}\). For \(\zeta =0\), the result coincide with constant gravitational acceleration case, in which the asymptotic value of the curvature of the bubble tip and bubble velocity are obtained by setting \(\frac{\textrm{d}\xi _2}{\textrm{d}\tau }=0\) and \(\frac{\textrm{d}\xi _3}{\textrm{d}\tau }=0\).

$$\begin{aligned} \xi _2|_\textrm{asymptotic} = -\frac{1}{6} \end{aligned}$$
(22)
$$\begin{aligned} \xi _3|_\textrm{asymptotic}=\sqrt{\frac{2}{3}\frac{A}{1+A}+\frac{\Omega _{c}^2}{4}\frac{1-A}{1+A}} \end{aligned}$$
(23)

Figure 2 describes that, in early nonlinear stage the amplitude (\(\xi _1\)), curvature (\(\xi _2\)) and velocity (\(\xi _3\)) of the bubble tip depend on \(\zeta \). The growth and velocity of the bubble tip reduces for large \(\zeta \) and formation of the bubble slows down. This happens as \(G(\tau )<1\) for \(\zeta >0\). However, the asymptotic values of the velocity and curvature coincide with the classical asymptotic values given by Eqs. (22) and (23).

Fig. 3
figure 3

The time evolution of the bubble amplitude (\(\xi _1\)), curvature (\(\xi _2\)) and velocity (\(\xi _3\)) under the acceleration profile \(G(\tau )=(1-e^{-\frac{\tau }{\zeta }})(1+\cos \kappa \tau )\), where \(\kappa =10\), \(r=2\) and \(\zeta =0\) (Solid line), \(\zeta =1\) (Dotted line), \(\zeta =2\) (Dash line), \(\zeta =5\) (Dot-dash line)

Full size image

Next we consider another acceleration profile \(G(\tau )=(1-e^{-\frac{\tau }{\zeta }})(1+\cos \kappa \tau )\), where \(\kappa =\frac{\mu }{\sqrt{kg_0}}\). Figure 3 shows the temporal development of the parameters \(\xi _1\), \(\xi _2\) and \(\xi _3\) of bubbles with a given \(\kappa \) but with different values of \(\zeta \). It is found that the dynamical behavior of the bubble is oscillating about the classical value due to the term \(\cos \kappa \tau \). However, for \(\zeta =0\), we get the particular result obtained by Mikaelian [17]. As \(\kappa \) denote the dimensionless frequency, oscillation becomes more rapid with increasing \(\kappa \) and growth and velocity of the bubble tip reduces with increasing \(\zeta \). It is also observed that the asymptotic value of the curvature do not depend on \(\zeta \) and \(\kappa \) and always coincides with the classical value given by Eq. (22). In early nonlinear stage, the dynamics of the bubble are quite similar with the results obtained by Mikaelian [18] and in latter phase, the observation agrees with the MOBILE simulation results [3]. However, in asymptotic stage, the amplitude and velocity of the bubble tip is quite large due to vorticity accumulation.

4 Conclusions

In this article, a two dimensional nonlinear potential flow model of ablative Rayleigh–Taylor Instability with two different variable acceleration profiles \(g(t) = g(1-e^{-\frac{t}{T}})\) and \(g(1-e^{-\frac{t}{T}})(1+\cos \mu t)\) has been described. This model can be applied to investigate the evolution of the Rayleigh–Taylor Instability in Inertial Confinement Fusion where different gravitational profiles have been considered. It is found that, for \(g(t) = g(1-e^{-\frac{t}{T}})\), in the early nonlinear stage, the structure of the bubble is affected by T, but, as time increases, the effect reduces and coincides with the case \(T=0\). On the other hand, for \(g(t)=g(1-e^{-\frac{t}{T}})(1+\cos \mu t)\), the structure of the bubble is affected by both parameters T and \(\mu \). With increasing value of T, the growth and velocity of the bubble tip reduces with an oscillation due to the frequency term \(\mu \), but curvature of the bubble tip is always independent. This model can help to understand the RTI process in astrophysical and experimental laser-driven system under the variable acceleration profiles.