1 Introduction

The Rayleigh–Taylor instability occurs when a lighter density fluid pushes the heavier one against the gravitational force field. This instability appears in many physical and astrophysical situations [1,2,3,4,5], such as Inertial Confinement Fusion, where the magnetic field provides a stabilizing effect of the two fluid instability [6, 7], overturn of the outer portion of the collapsed core of massive stars, etc [8]. In the linear regime, the perturbation grows exponentially with the growth rate \(\sqrt{Akg}\), where \(A=\frac{\rho _{\mathrm{h}}-\rho _{\mathrm{l}}}{\rho _{\mathrm{h}}+\rho _{\mathrm{l}}}\) is the Atwood number, \(\rho _{\mathrm{h}}\) and \(\rho _{\mathrm{l}}\) are the densities of heavier and lighter fluid, respectively, k is the perturbation wave number and g is the interfacial acceleration [9]. In the nonlinear stage [10, 11], the interface can be divided into the bubble of the lighter fluid rising into the heavier fluid and spike of the heavier fluid penetrating into the lighter fluid. There are several methods for describing the nonlinear effect on this instability. Among them, Layzer [12] describes a formulation where the interface near the tip of the bubble is approximated by a parabola and determined the position, curvature and velocity of the bubble tip. Extending this model, Goncharov [13] derived the asymptotic velocity of the bubble tip, which is \(\sqrt{\frac{2A}{1+A}\frac{g}{3k}}\). However, the observed simulation and experimental results [14,15,16] indicate that nonlinear theory correctly captures the bubble behavior in the early nonlinear phase, but fails in the highly nonlinear stage. Betti and Sanz [15] showed that this occurs due to vorticity accretion inside the bubble, and the velocity of the bubble tip is slightly higher than the classical value obtained by Goncharov [13].

In an Inertial Confinement Fusion situation or in the astrophysical situation, the fluid may be ionized or may get ionized through laser irradiation in laboratory condition. In this case, the study of magnetic field effects on Rayleigh–Taylor instability is needed [17,18,19,20]. Under the linear theory, the influence of magnetic field on Rayleigh–Taylor instability has been studied in detail by Chandrasekhar [9]. He observed that, when the magnetic field is parallel to the interface separating of two fluids, the growth rate of the Rayleigh–Taylor instability is unaffected by magnetic field. However, using Layzer’s model, Gupta et al. [6] pointed that the parallel magnetic field becomes a stabilizing factor of the instability.

The asymptotic growth, curvature and growth rate of the bubble tip in Rayleigh–Taylor instability, which is one of the main factors in Inertial Confinement Fusion or in laboratory experiments, have been discussed by analytical and numerical approaches. In the presence of magnetic field, the dynamics of the bubble tip has been analyzed by considering the vorticity accumulation inside the bubble. The magnetic field is assumed to be parallel to the plane of the two fluid interface and acts in a direction perpendicular to the wave vector. The basic model is based on the Layzer’s theory.

The structure of this paper is as follows. Section 2 describes the kinematical and dynamical boundary conditions for the temporal nonlinear evolution of the bubble tip in Rayleigh–Taylor instability for incompressible, inviscid fluids. Here, the heavier fluid is assumed to be irrotational where the lower one is rotational. The results and discussions are presented in Sect. 3. Finally, we have concluded the results in Sect. 4.

2 Basic equations and boundary conditions

We suppose that a fluid of density \(\rho _{\mathrm{h}}\) lies in the region \(z>0\) and that a second fluid of density \(\rho _{\mathrm{l}}\) lies in the region \(z<0\). The system is subject to a uniform acceleration g in the negative direction of z axis (see Fig. 1). The magnetic field is taken along the direction of y axis, i.e, parallel to the surface of separation.

$$\begin{aligned} \vec {B} = \left\{ \begin{array}{lr} \widehat{y} B_{\mathrm{h}}(x,z,t) &{} : z>0\\ \widehat{y} B_{\mathrm{l}}(x,z,t) &{} : z<0 \end{array} \right. \end{aligned}$$
(1)

According to the chosen magnetic field \(\vec {\nabla }.\vec {B}=0\) everywhere.

Here, we are considering two-dimensional problem. Therefore, we approximate the perturbed interface by a parabola, given by

$$\begin{aligned} z=\eta (x,t)=\eta _{0}(t)+\eta _{2}(t)x^2 \end{aligned}$$
(2)

where, for a bubble, \(\eta _{0}(t)>0\) and \(\eta _{2}(t)<0\).

The kinematical boundary conditions satisfied by the interfacial surface \(z=\eta (x,t)\) are

$$\begin{aligned}&\frac{\partial \eta }{\partial t}+v_{{\mathrm{h}}x} \frac{\partial \eta }{\partial x}=v_{{\mathrm{h}}z} \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\partial \eta }{\partial x}(v_{{\mathrm{h}}x}-v_{{\mathrm{l}}x})=v_{{\mathrm{h}}z}-v_{{\mathrm{l}}z} \end{aligned}$$
(4)

where \((v_{{\mathrm{h}},l})_{x,z}\) are the velocity components of the heavier and lighter fluids, respectively.

The fluid motion is governed by the ideal magnetohydrodynamic equations

$$\begin{aligned}&\rho \left[ \frac{\partial \vec {v}}{\partial t}+(\vec {v}\cdot \vec {\nabla })\vec {v}\right] +\vec {\nabla }(p+g\rho z)\nonumber \\&\quad =\frac{1}{\mu }(\vec {\nabla }\times \vec {B})\times \vec {B}\nonumber \\&\quad =\frac{1}{\mu }(\vec {B}\cdot \vec {\nabla })\vec {B}-\frac{1}{2\mu }\vec {\nabla }(B^2)=-\frac{1}{2\mu }\vec {\nabla }(B^2) \end{aligned}$$
(5)

[\(\frac{1}{\mu }(\vec {B}\cdot \vec {\nabla })\vec {B}=0\), as \(\vec {B}(x,z,t)\) is taken along the y axis]

$$\begin{aligned} \frac{\partial \vec {B}}{\partial t}= \vec {\nabla }\times (\vec {v}\times \vec {B}) \end{aligned}$$
(6)

Under the Layzer-type approximation [12, 21], the velocity potential \(\phi _{\mathrm{h}}(x,z,t)\) of the heavier fluid can be written as

$$\begin{aligned} \phi _{\mathrm{h}}(x,z,t)=a(t) \cos (kx) e^{-k(z-\eta _{0}(t))} \end{aligned}$$
(7)

with \(\vec {v_{\mathrm{h}}}=-\vec {\nabla }\phi _{\mathrm{h}}\).

Since \(\vec {\nabla }\cdot \vec {v_{\mathrm{h}}}=0\), the equation of motion of the upper incompressible fluid leads to the following integral [16]:

$$\begin{aligned} \rho _{\mathrm{h}}\left[ -\frac{\partial \phi _{\mathrm{h}}}{\partial t}+ \frac{1}{2}\left( \vec {\nabla } \phi _{\mathrm{h}}\right) ^{2}+ g z\right] +p_{\mathrm{h}}+\frac{1}{2\mu _{\mathrm{h}}}B_{\mathrm{h}}^2=f_{\mathrm{h}}(t) \end{aligned}$$
(8)

For the lighter fluid, the motion inside the bubble is assumed rotational [15] with vorticity \(\vec {\omega }=(\frac{\partial v_{{\mathrm{l}}z}}{\partial x}-\frac{\partial v_{{\mathrm{l}}x}}{\partial z}){\hat{y}}\). The motion is described by the stream function \(\varPsi (x,z,t)\), given by

$$\begin{aligned} \varPsi (x,z,t)=b_{0}(t)x+[b_{1}(t)e^{k(z-\eta _{0})}+\omega _{0}(t)/k^2] \sin {(k x)} \end{aligned}$$
(9)

with \(v_{{\mathrm{l}}x}=-\frac{\partial \varPsi }{\partial z}\) and \(v_{{\mathrm{l}}z}=\frac{\partial \varPsi }{\partial x}\).

Hence

$$\begin{aligned} \nabla ^2 \varPsi =-\omega \end{aligned}$$
(10)

Let \(\chi (x,z,t)\) be a function such that

$$\begin{aligned} \nabla ^2 \chi =-\omega \end{aligned}$$
(11)

Hence \((\varPsi -\chi )\) is a harmonic function as \(\nabla ^2 (\varPsi -\chi )=0\). Let \(\varPhi (x,z,t)\) be its conjugate function

$$\begin{aligned} \frac{\partial \varPhi }{\partial x}= & {} \frac{\partial \varPsi }{\partial z}-\frac{\partial \chi }{\partial z}\nonumber \\ \frac{\partial \varPhi }{\partial z}= & {} -\frac{\partial \varPsi }{\partial x}+\frac{\partial \chi }{\partial x} \end{aligned}$$
(12)

Thus, the velocity components of the lighter fluid are

$$\begin{aligned} v_{{\mathrm{l}}x}= & {} -\frac{\partial \varPsi }{\partial z}=-\frac{\partial \varPhi }{\partial x}-\frac{\partial \chi }{\partial z}\nonumber \\ v_{{\mathrm{l}}z}= & {} \frac{\partial \varPsi }{\partial x}=-\frac{\partial \varPhi }{\partial z}+\frac{\partial \chi }{\partial x} \end{aligned}$$
(13)

Using Eqs. (10)–(13), the first integral of the equation of motion of the lighter fluid is given by

$$\begin{aligned}&\rho _{\mathrm{l}}\left[ -\frac{\partial \varPhi }{\partial t}+ \frac{1}{2}(\vec {v}_{\mathrm{l}}){^2}-\omega \varPsi +g z\right] \nonumber \\&\quad +\int \rho _{\mathrm{l}}\left[ \left( \varPsi \frac{\partial \omega }{\partial z}-\frac{\partial \dot{\chi }}{\partial z}\right) {\mathrm{d}}x +\left( \varPsi \frac{\partial \omega }{\partial x}+\frac{\partial \dot{\chi }}{\partial x}\right) {\mathrm{d}}z\right] \nonumber \\&\quad + p_{\mathrm{l}}+\frac{1}{2\mu _{\mathrm{l}}}B_{\mathrm{l}}^2=f_{\mathrm{l}}(t) \end{aligned}$$
(14)

Here, we set

$$\begin{aligned} \chi (x,z,t)=\omega _{0}(t)\sin {(k x)}/k^2 \end{aligned}$$
(15)

Therefore, Eq. (13) gives

$$\begin{aligned} \varPhi (x,z,t)=-b_0(t)y+b_1(t)\cos {(k x)} e^{k(z-\eta _0)} \end{aligned}$$
(16)

From Eqs. (8) and (14), we obtain our dynamical boundary condition:

$$\begin{aligned}&\rho _{\mathrm{h}}\left[ -\frac{\partial \phi _{\mathrm{h}}}{\partial t}+ \frac{1}{2}(\vec {\nabla } \phi _{\mathrm{h}})^{2}+ g z\right] \nonumber \\&\quad - \rho _{\mathrm{l}}\left[ -\frac{\partial \varPhi }{\partial t}+ \frac{1}{2}(\vec {\nabla } \varPhi ){^2}-\omega \varPsi +g z\right] \nonumber \\&\quad -\int \rho _{\mathrm{l}}\left[ \left( \varPsi \frac{\partial \omega }{\partial z}-\frac{\partial \dot{\chi }}{\partial z}\right) {\mathrm{d}}x \right. \nonumber \\&\quad \left. +\,\left( \varPsi \frac{\partial \omega }{\partial x}+\frac{\partial \dot{\chi }}{\partial x}\right) {\mathrm{d}}z\right] \nonumber \\&\quad +(p_{\mathrm{h}}-p_{\mathrm{l}})+\left( \frac{1}{2\mu _{\mathrm{h}}}B_{\mathrm{h}}^2-\frac{1}{2\mu _{\mathrm{l}}}B_{\mathrm{l}}^2\right) \nonumber \\&=f_{\mathrm{h}}(t)-f_{\mathrm{l}}(t) \end{aligned}$$
(17)

satisfied at the interface \(z=\eta (x,t)\).

Now, we turn to our magnetic field equations. In virtue of Eqs. (1) and (6), the magnetic fields are assumed to be

$$\begin{aligned} B_{\mathrm{h}}(x,z,t)=\beta _{{\mathrm{h}}0}(t)+\beta _{{\mathrm{h}}1}(t)e^{-k(z-\eta _{0})} \cos {(k x)} \end{aligned}$$
(18)
$$\begin{aligned} B_{\mathrm{l}}(x,z,t)=\beta _{{\mathrm{l}}0}(t)+\beta _{{\mathrm{l}}1}(t)e^{k(z-\eta _{0})} \cos {(k x)} \end{aligned}$$
(19)

Substituting \(\eta (x,t)\), \(v_{{\mathrm{h}}x}\), \(v_{{\mathrm{h}}z}\), \(v_{{\mathrm{l}}x}\) and \(v_{{\mathrm{l}}z}\) in Eqs. (3) and (4) and expanding in powers of the transverse coordinate x and neglecting terms \(O(x^i)\) (\(i\ge 3\)), we obtain the following equations [21]

$$\begin{aligned} \frac{{\mathrm{d}}\xi _{1}}{{\mathrm{d}}\tau }= & {} \xi _{3} \end{aligned}$$
(20)
$$\begin{aligned} \frac{{\mathrm{d}}\xi _{2}}{{\mathrm{d}}\tau }= & {} -\frac{1}{2}(6\xi _{2}+1)\xi _{3} \end{aligned}$$
(21)
$$\begin{aligned} \frac{kb_{0}}{\sqrt{kg}}= & {} \frac{6\xi _{2}(2\xi _{3}-\varOmega )}{(6\xi _{2}-1)} \end{aligned}$$
(22)
$$\begin{aligned} \frac{k^2b_{1}}{\sqrt{kg}}= & {} -\frac{(6\xi _{2}+1)\xi _{3}-\varOmega }{(6\xi _{2}-1)} \end{aligned}$$
(23)

where \( \xi _{1}=k\eta _{0}\), \(\xi _{2}=\frac{\eta _{2}}{ k}\) and \(\xi _{3}=\frac{k^2a}{\sqrt{kg}}\) are the nondimensionalized bubble height, curvature and velocity, respectively, \(\tau =t\sqrt{kg}\) is the nondimensionalized time and \(\varOmega =\frac{\omega _{0}}{\sqrt{kg}}\) is the nondimensionalized vorticity.

Next, substituting for the velocity components \(v_{{\mathrm{h}}x}\), \(v_{{\mathrm{h}}z}\), \(v_{{\mathrm{l}}x}\), \(v_{{\mathrm{l}}z}\) and \(B_{\mathrm{h}}(x,z,t)\), \(B_{\mathrm{l}}(x,z,t)\) in the Eq. (6) and equating coefficients of \(x^i\) for \(i=0\) and 2 we obtain the following four equations

$$\begin{aligned}&\dot{\beta }_{{\mathrm{h}}0}+\dot{\beta }_{{\mathrm{h}}1}=0\,\,\hbox {i.e, }\beta _{{\mathrm{h}}0}+\beta _{{\mathrm{h}}1}=B_{{\mathrm{h}}0}\,\,\hbox {(say)} \end{aligned}$$
(24)
$$\begin{aligned}&\frac{{\mathrm{d}}\xi _{4}}{{\mathrm{d}}\tau }=\xi _3\xi _4\frac{2\xi _2-1}{2\xi _2+1} \end{aligned}$$
(25)

and

$$\begin{aligned}&\dot{\beta }_{{\mathrm{l}}0}+\dot{\beta }_{{\mathrm{l}}1}=0\,\,\hbox {i.e, }\beta _{{\mathrm{l}}0}+\beta _{{\mathrm{l}}1}=B_{{\mathrm{l}}0}\,\,\hbox {(say)} \end{aligned}$$
(26)
$$\begin{aligned}&\frac{{\mathrm{d}}\xi _{5}}{{\mathrm{d}}\tau }=\xi _5\frac{\xi _3(2\xi _2+1)(6\xi _2+1)+2\varOmega (2\xi _2-1)}{(2\xi _2-1)(6\xi _2-1)} \end{aligned}$$
(27)

where \(\xi _4=\frac{\beta _{{\mathrm{h}}1}}{B_{{\mathrm{h}}0}}\) and \(\xi _5=\frac{\beta _{{\mathrm{l}}1}}{B_{{\mathrm{l}}0}}\).

Again, the fluid pressures together with the magnetic pressures on both sides of the interface are equal [6], i.e.,

$$\begin{aligned} p_{\mathrm{h}}+\frac{B_{{\mathrm{h}}0}^2}{2\mu _{\mathrm{h}}}=p_{\mathrm{l}}+\frac{B_{{\mathrm{l}}0}^2}{2\mu _{\mathrm{l}}} \end{aligned}$$
(28)

Using Eqs. (28) in (17), the coefficient of \(x^2\) of Eq. (17) gives the following equation for \(\xi _3\).

$$\begin{aligned} \frac{{\mathrm{d}}\xi _3}{{\mathrm{d}}\tau }= & {} \frac{1}{D(\xi _2,r)}\left[ -N(\xi _2,r)\frac{\xi _3^2}{(6\xi _2-1)}+2(r-1)(6\xi _2-1)\xi _2\right. \nonumber \\&\quad \left. +\frac{\varOmega ^2-5(6\xi _{2}+1)\varOmega \xi _3}{(1-6\xi _2)}+\dot{\varOmega }\right] \nonumber \\&\quad -\frac{6\xi _2-1}{D(\xi _2,r)}\left[ rV_{\mathrm{h}}^2\xi _4(2\xi _2+1)+V_{\mathrm{l}}^2\xi _5(2\xi _2-1)\right] \end{aligned}$$
(29)

where

$$\begin{aligned} N(\xi _2,r)= & {} 36(1-r)\xi _{2}^{2}+12(4+r)\xi _{2}+(7-r) \end{aligned}$$
(30)
$$\begin{aligned} D(\xi _2,r)= & {} 12(1-r)\xi _{2}^{2}+4(1-r)\xi _{2}+(r+1) \end{aligned}$$
(31)

\(r=\frac{\rho _{\mathrm{h}}}{\rho _{\mathrm{l}}}\) and \(V_{{\mathrm{h}}(l)}=\frac{k B_{{\mathrm{h}}0(l0)}^2 }{\rho _{{\mathrm{h}}(l)}\mu _{{\mathrm{h}}(l)}g}\) is the normalized Alfven velocity.

Thus, the magnetic field-affected Rayleigh–Taylor instability-induced growth of the bubble tip is determined by the parameters \(\xi _1(t)\), \(\xi _2(t)\), \(\xi _3(t)\) as also the magnetic induction perturbation \(\xi _4(t)\) and \(\xi _5(t)\) given by Eqs. (20), (21), (29), (25) and (27).

3 Results and discussions

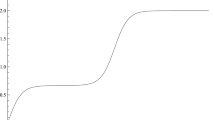
The system of equations given by Eqs. (20), (21), (29), (25) and (27) for the fluid parameters shows that the complete understanding of the Rayleigh–Taylor instability is not possible without knowing the dependence of the vorticity \(\varOmega (\tau )\) on \(\tau \). According to the simulation results obtained by Snaz and Betti [15], we chose the \(\varOmega (\tau )\) in the following form so that the time dependence of \(\varOmega (\tau )\) has approximate qualitative agrement with the simulation results.

$$\begin{aligned} \varOmega (\tau )= & {} \frac{\varOmega _{c}}{1+2\tanh (\tau _{0})}\left[ \tanh (\tau _{0})(1+\tanh (\tau ))\right. \nonumber \\&\quad \left. +\tanh (\tau -\tau _{0})\right] \end{aligned}$$
(32)

Here, \(\varOmega _c\) is the asymptotic value of the nondimensionalized vorticity and \(\tau _{0}\) is a nondimensionalized time parameter. Clearly, \(\varOmega (\tau )\) increases from 0 and tends to an asymptotic value \(\varOmega _c\) as \(\tau \rightarrow \infty \). The constants \(\tau _0\) and \(\varOmega _c\) are adjusted accordingly to Ref. [15]. The plot for \(\varOmega (\tau )\) is shown in Fig. 2. It is clear from the figure that the \(\tau _0=8\) and \(\varOmega _c=2\) give a good approximation of the simulation results.

To integrate the system of equations numerically, it is necessary to know the initial value of the parameters. The initial interface is assumed to be \(z=\eta _0(t=0)\cos (kx)\). The expansion of the interfacial function gives \((\xi _2)_{\mathrm{initial}}\)\(=-\frac{1}{2}(\xi _1)_{\mathrm{initial}}\) where \((\xi _1)_{\mathrm{initial}}\) is the arbitrary perturbation amplitude. As the perturbation starts from rest, we may consider \((\xi _3)_{\mathrm{initial}}=0\). The initial values of \((\xi _4)_{\mathrm{initial}}\) and \((\xi _5)_{\mathrm{initial}}\) depend upon the initial magnetic induction perturbation.

To describe the steady flow in Rayleigh–Taylor instability, we first consider \(B_{{\mathrm{h}}0}\ne 0\), \(B_{{\mathrm{l}}0}=0\). This situation may happen when the heavier fluid is magnetized and the lighter is nonmagnetic. In this case, \(\xi _5=0\) and \(V_{\mathrm{l}}=0\). The numerical results of the bubble dynamics are presented in Fig. 3. Figure 3 demonstrates that, in early nonlinear stage the growth (\(\xi _1\)), curvature (\(\xi _2\)) and velocity (\(\xi _3\)) depend on the magnetic field and initial magnetic induction perturbation. More precisely, the growth of the bubble tip reduces for large \(B_{{\mathrm{h}}0}\) and \((\xi _4)_{\mathrm{initial}}<0\). These observations are supported by blue (\(V_{\mathrm{h}}=1\), \((\xi _4)_{\mathrm{initial}}=-0.1\)) and dot-dash (\(V_{\mathrm{h}}=1.5\), \((\xi _4)_{\mathrm{initial}}=-0.1\)) lines in Fig. 3. This happens as the instability driving pressure differences term \(2(r-1)(6\xi _2-1)\xi _2\) together with the vorticity term \(\frac{\varOmega ^2-5(6\xi _{2}+1)\varOmega \xi _3}{(1-6\xi _2)}+ \dot{\varOmega }\) is lowered or enhanced by \(rV_{\mathrm{h}}^2\xi _4(2\xi _2+1)(6\xi _2-1)\) according to \(\xi _4<\) or \(>0\). However, the asymptotic values of the growth rate and curvature are unaffected by the magnetic field as \(\xi _4 \rightarrow 0\) as \(\tau \rightarrow \infty \). The asymptotic values are given by setting \(\frac{{\mathrm{d}}\xi _2}{{\mathrm{d}}\tau }=0\) and \(\frac{{\mathrm{d}}\xi _3}{{\mathrm{d}}\tau }=0\).

$$\begin{aligned} \xi _2|_{{\mathrm{asymptotic}}}= & {} -\frac{1}{6} \end{aligned}$$
(33)
$$\begin{aligned} \xi _3|_{{\mathrm{asymptotic}}}= & {} \sqrt{\frac{2}{3}\frac{A}{1+A}+\frac{\varOmega _{c}^2}{4}\frac{1-A}{1+A}} \end{aligned}$$
(34)

Thus, the asymptotic growth rate and curvature become the same as in the nonmagnetic case [15, 16]. This result agrees the nonlinear result obtained by Gupta et al. [6].

Next, we consider the reverse situation of the above case, i.e., \(B_{{\mathrm{h}}0}= 0\), \(B_{{\mathrm{l}}0}\ne 0\). This circumstance may happen when the heavier fluid is nonmagnetic and the lighter is ionized. It is clear from the Eq. (29) that the instability driving pressure difference term \(2(r-1)(6\xi _2-1)\xi _2\) together with the vorticity term \(\frac{\varOmega ^2-5(6\xi _{2}+1)\varOmega \xi _3}{(1-6\xi _2)}+ \dot{\varOmega }\) is now lowered or enhanced by \(V_{\mathrm{l}}^2\xi _5(2\xi _2-1)(6\xi _2-1)\) (note that \(-\frac{1}{6}\le \xi _2<0\)) according to \(\xi _4>\) or \(<0\). This conclusion is supported by the Fig. 4, where the growth of the bubble tip reduces for large \(V_{\mathrm{l}}\) with \((\xi _5)_{\mathrm{initial}}>0\). It is clear from Fig. 4 that bubble parameters depend on the magnetic field and initial magnetic perturbation. However, in asymptotic stage, i.e., as \(\tau \rightarrow \infty \), \(\xi _5\rightarrow 0\) and the dependency reduce strongly. This has the consequence that the asymptotic growth rate of the bubble tip becomes the same as in the nonmagnetic case.

Finally, we consider the situation when both liquids are magnetic, i.e., \(B_{{\mathrm{l}}0}\ne 0\) and \(B_{{\mathrm{h}}0}\ne 0\). Figure 5 shows that in early nonlinear stage, the growth of the bubble tip (\(\xi _1\)) strongly reduces due to both magnetic fields for \((\xi _4)_{\mathrm{initial}}<0\) and \((\xi _5)_{\mathrm{initial}}>0\). This happens as the pressure difference term \(2(r-1)(6\xi _2-1)\xi _2\) in Eq. (29) together with the vorticity effect \(\frac{\varOmega ^2-5(6\xi _{2}+1)\varOmega \xi _3}{(1-6\xi _2)}+ \dot{\varOmega }\) is suppressed by the magnetic effect \((6\xi _2-1)[rV_{\mathrm{h}}^2\xi _4(2\xi _2+1)+V_{\mathrm{l}}^2\xi _5(2\xi _2-1)]\) for \((\xi _4)_{\mathrm{initial}}<0\) and \((\xi _5)_{\mathrm{initial}}>0\) (as \(-\frac{1}{6}\le \xi _2<0\)). In asymptotic stage, growth rate (\(\xi _3\)) and curvature (\(\xi _2\)) of the bubble tip do not depend on the magnetic field and magnetic perturbation.

Thus, in the presence of horizontal magnetic field, which is perpendicular to the plane of motion, the parameters of the bubble tip such as growth, curvature and growth rate depend on the strength of the magnetic filed and the initial magnetic perturbation at the early nonlinear stage. However, the asymptotic values coincide with the nonmagnetic case. Previously, [6] nonlinear results show that the asymptotic growth rate depends upon Alfven velocity of the lower fluid only by considering irrotational motion in both fluids. However, due to vorticity accretion inside the bubble, here we observed that the asymptotic growth rate does not depend upon the Alfven velocity of the both fluids.

4 Conclusions

Fig. 1
figure 1

Schematic diagram of the model

Full size image
Fig. 2
figure 2

Vorticity \(\varOmega (\tau )\) plotted against \(\tau \) with asymptotic value \(\varOmega _{c}=2\) and parameter \(\tau _{0}=8\)

Full size image
Fig. 3
figure 3

Variation of \(\xi _1\), \(\xi _2\), \(\xi _3\), \(\xi _4\) with \(\tau \) for \(r=1.5\), \(V_{\mathrm{l}}=0\), \(\varOmega _{c}=2\), \((\xi _1)_{\mathrm{initial}}=0.1\), \((\xi _2)_{\mathrm{initial}}=-0.05\) and \((\xi _3)_{\mathrm{initial}}=0\); \(V_{\mathrm{h}}=0\), \((\xi _4)_{\mathrm{initial}}=0\) (Solid line); \(V_{\mathrm{h}}=1\), \((\xi _4)_{\mathrm{initial}}=0.1\) (Dotted line); \(V_{\mathrm{h}}=1\), \((\xi _4)_{\mathrm{initial}}=-0.1\) (Large dash line); \(V_{\mathrm{h}}=1.5\), \((\xi _4)_{\mathrm{initial}}=0.1\) (Dash line); \(V_{\mathrm{h}}=1.5\), \((\xi _4)_{\mathrm{initial}}=-0.1\) (Dot-dash line)

Full size image
Fig. 4
figure 4

Variation of \(\xi _1\), \(\xi _2\), \(\xi _3\), \(\xi _5\) with \(\tau \) for \(r=1.5\), \(V_{\mathrm{h}}=0\), \(\varOmega _{c}=2\), \((\xi _1)_{\mathrm{initial}}=0.1\), \((\xi _2)_{\mathrm{initial}}=-0.05\) and \((\xi _3)_{\mathrm{initial}}=0\); \(V_{\mathrm{h}}=1\), \((\xi _5)_{\mathrm{initial}}=0\) (Solid line); \(V_{\mathrm{l}}=1\), \((\xi _5)_{\mathrm{initial}}=0.1\) (Dotted line); \(V_{\mathrm{l}}=1\), \((\xi _5)_{\mathrm{initial}}=-0.1\) (Large dash line); \(V_{\mathrm{l}}=1.5\), \((\xi _5)_{\mathrm{initial}}=0.1\) (Dash line); \(V_{\mathrm{l}}=1.5\), \((\xi _5)_{\mathrm{initial}}=-0.1\) (Dot-dash line)

Full size image
Fig. 5
figure 5

Variation of \(\xi _1\), \(\xi _2\), \(\xi _3\), \(\xi _5\) with \(\tau \) for \(r=1.5\), \(\varOmega _{c}=2\), \((\xi _1)_{\mathrm{initial}}=0.1\), \((\xi _2)_{\mathrm{initial}}=-0.05\) and \((\xi _3)_{\mathrm{initial}}=0\); \(V_{\mathrm{h}}=0\), \(V_{\mathrm{l}}=0\), \((\xi _4)_{\mathrm{initial}}=0\)\((\xi _5)_{\mathrm{initial}}=0\) (Solid line); \(V_{\mathrm{h}}=0.5\), \(V_{\mathrm{l}}=0.5\), \((\xi _4)_{\mathrm{initial}}=-0.1\), \((\xi _5)_{\mathrm{initial}}=0.1\) (Dotted line); \(V_{\mathrm{h}}=1\), \(V_{\mathrm{l}}=1\), \((\xi _4)_{\mathrm{initial}}=-0.1\)\((\xi _5)_{\mathrm{initial}}=0.1\) (Large dash line); \(V_{\mathrm{h}}=0.5\), \(V_{\mathrm{l}}=0.5\), \((\xi _4)_{\mathrm{initial}}=0.1\), \((\xi _5)_{\mathrm{initial}}=-0.1\) (Dash line); \(V_{\mathrm{h}}=1\), \(V_{\mathrm{l}}=1\), \((\xi _4)_{\mathrm{initial}}=0.1\)\((\xi _5)_{\mathrm{initial}}=-0.1\) (Dot-dash Dash);

Full size image

We have described a two-dimensional nonlinear model of the Rayleigh–Taylor Instability in the presence of horizontal magnetic field with vorticity accretion inside the bubble. This model can be applied to investigate the nonlinear evolution of the Rayleigh–Taylor Instability in Inertial Confinement Fusion or in formation of core collapsed supernova. The effect of upper magnetic field (\(B_{{\mathrm{h}}0}\ne 0\), \(B_{{\mathrm{l}}0}=0\)), lower magnetic filed (\(B_{{\mathrm{h}}0}= 0\), \(B_{{\mathrm{l}}0}\ne 0\)) and total magnetic field (\(B_{{\mathrm{h}}0}\ne 0\), \(B_{{\mathrm{l}}0}\ne 0\)) has been discussed separately. It is found that, in the early nonlinear stage, the structure of the bubble is effected by the magnetic field, but, as time goes, the effect is reduced and coincides with the nonmagnetic case. Furthermore, the nonlinear growth of the bubble saturates when the bubble reaches a constant velocity and this stage does not depend upon the Alfven velocity.

Our results agree with the results observed by Gupta et al. [6] for irrotational motion. But the obtained simulation and experimental results [14,15,16] note that results for irrotational motion fail in highly nonlinear stage due to vorticity accumulation inside the bubble. We hope our theoretical model will help the experimental research in future.