Three-layered relativistic hybrid star with distinct equation of states

Abstract

In this paper, we are proposing a three-layered hybrid compact star model with a distinct equation of states (EOSs) in the realm of general relativity. The core is assumed to be quark matter described by the MIT-bag model, an intermediate layer filled with neutron liquid and a thin envelope of matter satisfying a quadratic EoS. Three pairs of interfaces are matched by using Darmois–Israel conditions. For better and easier tuning, we have chosen $\alpha$ as a free parameter for core, k for intermediate layer and g and t for envelope, while the rest of the constant parameters are linked with mass and radius. Most of the physical parameters such as density, pressures and EoS parameters are continuous in all the three regions; however, $v_t^2$ and stability factor are discontinuous. This is because of the non-differentiability of $p_t$’s at the interfaces. Hence, stability is not defined at the interfaces. Further, matching of $p_t$’s can be performed by tuning suitable values of the free parameters $\alpha , ~k, ~g$ and t. Further, the most prevailing aspect of this method is that we can arbitrarily choose the radii of each region. As per Buchler and Barkat (PRL 27: 48, 1971) and Baym et al.(PRL 175: 225, 1971) , there exists a smooth transition density between quark core and intermediate neutron-liquid layer at about $\rho > 10^{14}~{\mathrm{g/cc}}$. Our calculation shows that the smooth transition density is at about $\rho _I=4.16 \times 10^{14}~ {\mathrm{g/cc}}$ which is in good agreement with the above prediction.

1 Introduction

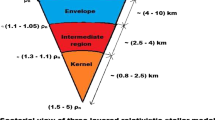
Since the discovery of pulsars, scientists are still investigating the possible structure of such highly dense, fast rotating compact stars. The lack of detailed observational evidence and very limited theoretical knowledge makes it very difficult to determine the exact structure and matter compositions at high-density regime. However, many researchers have suggested various models on the possible equation of state (EoS) and interior structure. As per Ginzberg’s [1] perception, the structure of neutron star consists of several layers:

(1):

Thin gaseous plasma envelope and solid crust The external layer ($\rho \le 10^{12} ~{\mathrm{g/cc}}$) consists of nuclei and electrons in gaseous plasma state. However, the main part of this plasma envelope is a solid crust made up of neutron-rich nuclei with degenerate electron gas. The formation of solid crust is due to rapid cooling down via emission of neutrino and electromagnetic radiation below $1-5 \times 10^8 \mathrm{K}$ just after its formation. The thickness of the solid crust is about $10-100$ m [2].

(2):

Intermediate layer of neutron liquid Under the solid crust there is $^3P_2-$liquid neutron where the density is greater than $3-5\times 10^{13} ~{\mathrm{g/cc}}$ while the concentration of protons and electrons are of the order of one or several percent [3]. The electrons remain as normal Fermi liquid, while neutrons and protons undergo Bose–Einstein condensation (BEC). Therefore, neutrons will be in the state of $^3P_2-$superfluid and protons are in $^1S_0-$superconductor [4,5,6,7,8,9,10].

(3):

Dense core The core is also sufficiently massive however, non-superfluid and non-superconducting.

Nowadays, many researchers have suggested various possible matter compositions at the interior of compact stars. At the core, strange particles like hyperons and BEC pions and/or kaons may be abundant. It is also possible that a mixed phase transition exists between hadrons and deconfined quarks [11]. Various suggestions have been made that quarks are in color-superconducting phase with [12] and without mesons condensation [13]. The deconfinement transition is a first-order phase transition at low temperature and high density [14, 15]. Other exotic matters such as $\mu ^-,~\Sigma ^-,~\Lambda , ~\Delta ^-(1236 ~{\mathrm{MeV/c^2}})$ most likely appear at the core [16].

Using extended semi-empirical mass formula, Langer et al. [17], Bethe et al. [18] and Cameron [19] predicted a sharp transition in density of about $4-5\times 10^{14} ~{\mathrm{g/cc}}$ at the core–intermediate layer interface. However, using more fundamental nuclear matter theories ensures a smooth and continuous transition density at $\rho > 10^{14} ~{\mathrm{g/cc}}$ [20, 21]. Many investigations also suggested the possible existence of quark-gluon plasma (QGP) at the core of neutron stars. Study of Jacobsen et al. [22] on QGP in neutron stars reveals that the maximum mass and radius decrease with the increase in the baryon density of phase transition.

Fig. 1

Variation of metric potentials for PSR J1614−2230

Existence of a quark phase at the interior of compact star is more stable as compared to hadronic phases, and therefore, quark core is highly possible [23, 24]. This opened up a completely new possible variety of compact star known as quark/strange star. Researchers already suggested few strange star candidate, e.g., 4U 1820-30 [25], Her X-1 [26], SAX J 1808.4-3658 [27], 4U 1728-34 [28], PSR 0943+10 [29], RX J 185635-3754 [30]. Cheng et al. [31], Kettner et al. [32] and Phukon [33] suggested that strange stars have low-density nuclear crust with a thin electron layer between crust and core. The electron content ensures the charge neutrality. Predictions have been made for Her X-1 in the presence of quark–diquark matter [34] where a complex scalar field was used to describe the bosonic diquarks with a $\Phi$-four interaction potential. This method was first suggested by Colpi et al. [35] and Kastor and Traschen [36] where the quark–diquark core is wrapped by a low density nucleon envelope. A modified model, i.e., deconfined quark core inside a low-density mixed phase envelope, was also put forwarded by Drago and Lavagno [37].

Due to these layered structures of neutron stars, many researchers have been inspired to further explore within the framework of general relativity by considering core–envelope model [38,39,40]. This method is sometimes troublesome while matching the interface boundaries and thereby the realistic model of star could not be developed. In this method, core and envelope are designed separately either by considering separate equation of states and/or metric potentials. Then the interfaces are matches with Darmois–Israel condition to ensure the continuity of the physical quantities.

Core–envelope model was in fact first proposed by Bondi [41] assuming an EoS $p=\rho /3$. Das and Narlikar [42] forwarded the Bondi method with $p=k\rho$ and therefore a constant sound speed model however, discontinuous at the CE interface. The continuity of density and sound speed in CE model was presented by Durgapal et al. [43, 44]. Vaidya and Tikekar [45] designed a core–envelope model with an anisotropic core. Soon later, Negi et al. [46, 47] successfully followed the path of CE model where Tolman IV and Tolman V were used to design the core and envelope, respectively. Sharma and Mukherjee [48] used ansatz Vaidya–Tikekar metric potential to develop a CE model. However, the physical parameters such as density and pressure, etc., are discontinuous at the CE interface. CE model by considering anisotropic core wrapped by an isotropic envelope was also reported by several authors [49,50,51]. Very recently, Hansraj et al. have presented a CE model satisfying Einstein–Maxwell field equations [52]. A partially continuous CE model in few of the physical parameters was also reported very recently [53]. Very recently, two papers on core–envelop models are also presented by Pant et al. [54] and Gedela et al. [55]. The most generalized Vaidya–Tikekar and Buchdahl solutions were also used by Gupta & Jasim [56, 57] to model physically acceptable compact stellar systems. In a similar manner, Maurya et al. [58] have also extensively discussed the Buchdahl solution for different cases and model many compact stellar system.

Fig. 2

Variation of density for PSR J1614−2230

Fig. 3

Variation of pressure for PSR J1614−2230

In the current paper, we are developing a three-layered hybrid compact star in the background of general relativity. We will be considering a quark core with MIT-bag EoS, an intermediate neutron fluid layer with modified BEC EoS and a quadratic EoS envelope. We will use Darmois–Israeli conditions at the interfaces in order to determine the constants of integration. Some of the constants will be treated as free parameters for tuning purposes. Several authors [59,60,61,62,63] have suggested that during gravitational collapse many exotic phase transitions may occur, out of which pion condensation is also one of the possible phase transitions that soften the equation of state [64]. This phase transition may lead to anisotropy in pressure as well [65]. The possibility that protons inside compact stars condensate into type-II superconductor was discussed by Jones [66] and Easson and Pethick [67]. Here, the flux lines originate from the anisotropic part of the stress tensor. The existence of solid core [68, 69] and presence of type P superfluid are few possible origins of anisotropy. Gleiser [70] presented a model of spherically symmetric anisotropic boson star bounded by gravity which was in equilibrium by considering a free or complex scalar field. To check the stability of such system, he considered charge conserving small radial perturbation for both free and self-interacting $\phi ^4$-theory. Another very promising source of anisotropy is the two-fluid model. Letelier [71] has shown that anisotropy can arise if two different types of fluids are contained in the system. He thoroughly examined the nature of anisotropy by considering two perfect fluids, one perfect fluid and a null fluid, and two null fluids. Viscosity is also a source of local anisotropy at very high density. Cores of compact stars are usually highly dense, and therefore, neutrino trapping may occur at a density of about $10^{11}-10^{12}{\mathrm{g/cc}}$. Such trapped neutrinos have long mean free path and small Reynolds number [72] which leads to a viscous core [73, 74]. Herrera and Santos [75] have shown that the classical Jeans equation for collisionless gas is equivalent to the anisotropic TOV equation. They have also shown that the first-order slow rotation approximation is equivalent to the anisotropic one. Herrera [76] has also shown that any initially isotropic configuration may end up as anisotropic due to dissipative fluxes, inhomogeneities in density and shear fluid flow during dissipative collapse. Therefore, anisotropy is an inevitable component of this present paper.

The paper will be organized as follows: Sect. 2 will be devoted to field equations, in sect. 3 we will elaborate our work on three-layered stellar systems, while Sect. 4 will be presenting the non-singular nature of the solution. The matching of interior and exterior spacetimes using Darmois–Israel condition will be discussed extensively in Sect. 5, and the non-exotic nature of the fluid applying energy condition will be given in Sect. 6. The stability analysis of the system will be extensively discussed using several techniques in Sect. 7. Section  8 presents slow rotation of the model, while all the results are accumulated and discussed in Sect. 9.

2 Einstein field equations in core–intermediate layer–envelope model

Consider the interior of compact star that satisfies the same spacetime which is of the form

$$\begin{aligned} \mathrm{d}s^{2}=e^{\nu (r)}\mathrm{d}t^{2}-e^{\lambda (r)}\mathrm{d}r^{2}-r^{2}(\mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\phi ^{2}). \end{aligned}$$

(1)

Henceforth, the subscripts “c”, “i” and ‘e” represent core, intermediate layer and envelope, respectively.

Assuming the matter distribution inside the compact star is anisotropic both at the core and envelope given as

$$\begin{aligned} T_{{\mathrm{\nu }}}^{\mu }=(\rho +p_{\mathrm{t}})u^{\mu }u_{{\mathrm{\nu }}}-p_{\mathrm{t}} g_{\mathrm{\nu }}^{\mu }+(p_{\mathrm{r}}-p_{\mathrm{t}})\eta ^{\mu }\eta _{\mathrm{\nu }} \end{aligned}$$

(2)

with $u^\mu u_\mu = -\eta^\mu \eta_\mu = 1$ and $u^{i}\eta _{\mathrm{j}}= 0$. Here, the vector $u_{\mathrm{i}}$ is the fluid 4-velocity and $\eta ^{i}$ is the spacelike vector which is orthogonal to $u_{\mathrm{i}}$, $\rho$ is the matter density, $p_{\mathrm{r}}$ and $p_{\mathrm{t}}$ are, respectively, the radial and the transversal pressure of the fluid.

Taking $G = 1 = C$ the Einstein’s field equations are

$$\begin{aligned} 8\pi \rho= & {} \frac{1}{r^{2}}\left[ r(1-e^{-\lambda })\right] ' \end{aligned}$$

(3)

$$\begin{aligned} 8\pi p_{\mathrm{r}}= & {} -\frac{1}{r^{2}}(1-e^{-\lambda })+\frac{\nu '}{r}e^{-\lambda } \end{aligned}$$

(4)

$$\begin{aligned} 8\pi p_{\mathrm{t}}= & {} \frac{e^{-\lambda }}{4}\left( 2\nu ''+\nu '^2+\frac{2\nu ^\prime }{r}-\nu ^\prime \lambda ^\prime -\frac{2\lambda '}{r}\right) \end{aligned}$$

(5)

where ‘$\prime$’ represents differentiation with respect to the radial co-ordinate ‘r’.

Using the variable transformations $x=r^2, ~z(x) = e^{-\lambda }$ and $y(x) = e^\nu$, we can rewrite the field equations as

$$\begin{aligned} 8\pi \rho= & {} {1-z \over x}-2\dot{z}, \end{aligned}$$

(6)

$$\begin{aligned} 8\pi p_{\mathrm{r}}= & {} 2z~{\dot{y} \over y}-{1-z \over x}, \end{aligned}$$

(7)

$$\begin{aligned} 8\pi p_{\mathrm{t}}= & {} zx\left( {2\ddot{y} \over y}-{\dot{y}^2 \over y^2}\right) +\dot{z}\left( 1+ {x\dot{y} \over y}\right) +{1-z \over x}, \end{aligned}$$

(8)

here $\dot{y} = \mathrm{d}y/\mathrm{d}x$ and so on. The measure of anisotropy can be given as $\Delta = p_{\mathrm{t}}-p_{\mathrm{r}}$.

Fig. 4

Variation of anisotropy for PSR J1614−2230

3 Development of core, intermediate layer and envelope

In this section, we will develop three-layered model by assuming Vaidya–Tikekar type $-g_{\mathrm{rr}}$ along with MIT-bag equation of state (EoS) for core, modified Bose–Einstein condensate (BEC) EoS for intermediate layer and a quadratic EoS for envelope. For continuity of the graphs, we need to match the metric functions, density and pressure at the interfaces. The constant parameters can be expressed in terms of mass and radius of the configuration along with some free parameters. This can be achieved only when the spacetime of the envelope is matched with the exterior vacuum solution.

Fig. 5

Variation of pressure to density ratio for PSR J1614−2230

Fig. 6

Variation of red-shift for PSR J1614−2230

3.1 Core: quark matter

Assuming the MIT-bag EoS and Vaidya–Tikekar type$-g_{rr}$ are given as

$$\begin{aligned} z_{\mathrm{c}}(x) = {1+ax \over 1+bx}~~;~~ p_{\mathrm{rc}} = \alpha \rho _{\mathrm{c}} -\beta , \end{aligned}$$

(9)

one can solve the field equations for $g_{\mathrm{tt}}-$metric potential. Here, $a ~ \& ~b$ are constants, $\alpha$ ensures the satisfaction of causality condition and $\beta$ links with the bag constant and interface density. By using the field Eqs. (6) and (7) with (9), we get

$$\begin{aligned} y_{\mathrm{c}}(x)= & {} A (a x+1)^{\xi } ~e^{-4 \pi b \beta x/a} \end{aligned}$$

(10)

where A is constant of integration and

$$\begin{aligned} \xi = \frac{8 \pi b \beta -a^2 (3 \alpha +1)+a (\alpha b+b-8 \pi \beta )}{2 a^2} . \end{aligned}$$

Fig. 7

Variation of mass and compactness parameter ratio for PSR J1614−2230

Fig. 8

Variation of density and pressure gradients for PSR J1614−2230

Now the physical parameters become

$$\begin{aligned} \rho _{\mathrm{c}}(x)= & {} \frac{(b-a) (b x+3)}{8 \pi (b x+1)^2} \end{aligned}$$

(11)

$$\begin{aligned} p_{\mathrm{rc}}(x)= & {} \alpha \rho _c(x) -\beta \end{aligned}$$

(12)

$$\begin{aligned} \Delta _{\mathrm{c}}(x)\,= \,& {} \frac{x}{32 (\pi a x+\pi ) (b x+1)^2} \nonumber \\ \times \,&\Big [a^2 \left\{ 9 \alpha ^2+12 \alpha +\left( 9 \alpha ^2+18 \alpha +1\right) b x+3\right\}\nonumber \\& + \big \{\alpha ^2-2 a f_1(x)+b^3 x (\alpha -8 \pi \beta x+1)^2\nonumber \\&+b^2 32 \pi \alpha \beta x+3 (1-8 \pi \beta x)^2\big \}+64 \pi ^2 \beta ^2\nonumber \\&+16 \pi \beta b (12 \pi \beta x-\alpha -2) \Big ] \end{aligned}$$

(13)

$$\begin{aligned} p_{\mathrm{tc}}= & {} \Delta _{\mathrm{c}}(x)+p_{\mathrm{rc}}(x), \end{aligned}$$

(14)

where

$$\begin{aligned} f_1(x)= & {} 8 \pi (3 \alpha +2) \beta +b^2 x \big (24 \pi \alpha \beta x+8 \pi \beta x-6 \alpha -1 \\&-3 \alpha ^2\big )+b \left( 48 \pi \alpha \beta x-3 \alpha ^2-2 \alpha +24 \pi \beta x-3\right) . \end{aligned}$$

Equation of state parameter ($\omega$), redshift (Z), mass function (m) and compactness parameter (u) can be determined as

$$\begin{aligned} \omega _{\mathrm{rc}}= & {} {p_{\mathrm{rc}} \over \rho _{\mathrm{c}}}~~,~~\omega _{\mathrm{tc}} = {p_{\mathrm{tc}} \over \rho _{\mathrm{c}}} \end{aligned}$$

(15)

$$\begin{aligned} Z_{\mathrm{c}}(x)= & {} y_{\mathrm{c}}(x)^{-1/2}-1 \end{aligned}$$

(16)

$$\begin{aligned} m_{\mathrm{c}}(x)= & {} \int _0^{x_{\mathrm{c}}} 2\pi \rho (x) \sqrt{x}~\mathrm{d}x = \frac{x_{\mathrm{c}}^{3/2} (b-a)}{2 b x_{\mathrm{c}}+2} \end{aligned}$$

(17)

$$\begin{aligned} u_{\mathrm{c}}(x)= & {} {2m_{\mathrm{c}}(x) \over \sqrt{x}}. \end{aligned}$$

(18)

Here, $x_{\mathrm{c}}=r_{\mathrm{c}}^2$.

Fig. 9

Variation of energy conditions for PSR J1614−2230

Fig. 10

Variation of forces in TOV-equation for PSR J1614−2230

3.2 Intermediate layer: BEC matter

Since classical BEC EoS has the form $p \propto \rho ^2$ [77], we have modified by adding a constant term to obtain a free parameter for the purpose of matching. In addition to quadratic EoS, we are still assuming Vaidya–Tikekar type$-g_{\mathrm{rr}}$. This is because the matching at the interface is much easier.

$$\begin{aligned} z_{\mathrm{i}}(x) = \frac{1+a x}{1+b x}~~;~~ p_{\mathrm{ri}} = k \rho _{\mathrm{i}}^2 -q, \end{aligned}$$

(19)

here k and q constants. On using the field Eqs. (6) and (7) with (19), we get

$$\begin{aligned} y_{\mathrm{i}}(x)= & {} B \exp \bigg [\frac{1}{16 \pi } \bigg \{\frac{f_2 \ln (a x+1)}{a^2 (a-b)}+\frac{8 a k-4 b k}{b x+1}\nonumber \\&+ \frac{2 k (a-b)}{(b x+1)^2}-\frac{k \ln (b x+1)}{ (b-3 a)^{-2}(a-b)}-\frac{64 \pi ^2 b q x}{a} \bigg \} \bigg ] \nonumber \\ \end{aligned}$$

(20)

where B is constant of integration and

$$\begin{aligned} f_2= & {} 9 a^4 k-2 a^3 (3 b k+4 \pi )+a^2 t(b^2 k+16 \pi b \\&-64 \pi ^2 q)-8 \pi a b (b-16 \pi q)-64 \pi ^2 b^2 q. \end{aligned}$$

Now the physical parameters become

$$\begin{aligned} \rho _{\mathrm{i}}(x)= & {} \frac{(b-a) (b x+3)}{8 \pi (b x+1)^2} \end{aligned}$$

(21)

$$\begin{aligned} p_{\mathrm{ri}}(x)= & {} k \rho _i^2(x) -q \end{aligned}$$

(22)

$$\begin{aligned} \Delta _{\mathrm{i}}(x)=\, & {} \frac{x}{2048 \pi ^3 (a x+1) (b x+1)^7}\, \Big [f_3(x)\nonumber \\&-4 a^3 k (b x+3) f_4(x)+b^8 x^4 \{k\nonumber \\&+8 \pi x (1-8 \pi q x)\}^2+f_5(x)+f_6(x)+2 b^6 x^2 f_7(x) \nonumber \\&+2 a^2 (b x+3) \left\{ f_8(x)+f_9(x)\right\} -4 a \Big \{b^3 \big [81 k^2\nonumber \\&- 4 \pi k x (1264 \pi q x+73)-160 \pi ^2 x^2 (88 \pi q x-7)\big ] \nonumber \\&-8 \pi b^2 \big \{k (336 \pi q x+33)+64 \pi x (18 \pi q x-1)\big \} \nonumber \\&+f_{10}(x)+f_{11}(x)\Big \} \Big ] \end{aligned}$$

(23)

$$\begin{aligned} p_{\mathrm{ti}}= & {} \Delta _{\mathrm{i}}(x)+p_{\mathrm{ri}}(x), \end{aligned}$$

(24)

where

$$\begin{aligned} f_3(x)= & {} a^4 k^2 (b x+3)^4+64 \pi ^2 b^2 \big (1792 \pi ^2 q^2 x^2-18 k q \\&-208 \pi q x+3\big )+{2048 \pi ^3 b q \over (16 \pi q x-1)^{-1}}+4096 \pi ^{4} q^{2} \\ f_4(x)= & {} b^4 x^3 (k+20 \pi x)+b^3 x^2 (9 k+140 \pi x)+b^2 x \\&(27 k+244 \pi x)+b (27 +148 \pi x)+24 \pi \\ f_5(x)= & {} 4 b^7 x^3 \big [3 k^2-8 \pi k x (40 \pi q x-3)+128 \pi ^2 x^2 (1 \\&-8 \pi q x)^2\big ]+32 \pi b^3 \big [32 \pi x \big (224 \pi ^2 q^2 x^2-36 \pi q x \\&+1\big )-21 k (8 \pi q x+1)\big ] \\ f_6(x)= & {} 4 b^5 x \Big [27 k^2-16 \pi k x (152 \pi q x+15)+128 \pi ^2 x^2 \\&\big \{448 \pi ^2 q^2 x^2-100 \pi q x+5\big \}\big ]+b^4 \big [81 k^2-16 \pi \\&k x (632 \pi q x+95)+320 \pi ^2 x^2 \big (896 \pi ^2 q^2 x^2-176\\&\pi q x+7\big )\big ] \\ f_7(x)= & {} 27 k^2-16 \pi k x (156 \pi q x+1)+32 \pi ^2 x^2 \big (1792 \pi ^2 \\&q^2 x^2-432 \pi q x+25\big ) \\ f_8(x)= & {} b^5 x^3 \big (3 k^2+8 \pi k x (11-8 \pi q x)+32 \pi ^2 x^2\big ) \\&-16 \pi b (52 \pi k q x+k-10 \pi x)+32 \pi ^2 (1-6 k q) \\ f_9(x)= & {} b^4 x^2 \big [27 k^2-8 \pi k x (56 \pi q x-73)+160 \pi ^2 x^2\big ]\nonumber \\&+ b^3 x \left[ 81 k^2-24 \pi k x (48 \pi q x-37)+320 \pi ^2 x^2\right] \\&+b^2 \left[ 81 k^2-8 \pi k x (176 \pi q x-47)+320 \pi ^2 x^2\right] \\ f_{10}(x)= & {} b^7 x^4 \big [k^2+4 \pi k x (7-16 \pi q x)+32 \pi ^2 x^2 (1- 8 \pi q x)\big ] \nonumber \\&+2 b^5 x^2 \big [27 k^2+12 \pi k x (27-104 \pi q x) \\&+16 \pi ^2 x^2 (25-216 \pi q x)\big ]-32 \pi ^2 b (18 k q+104 \\&\pi q x-3)-512 \pi ^3 q \\ f_{11}(x)= & {} 4 b^6 x^3 \big [3 k^2+2 \pi k x (31-80 \pi q x)\nonumber\\&+64 \pi ^2 x^2 (1- 8 \pi q x)\big ] +4 b^4 x \big [27 k^2-4 \pi k x (304 \pi q x-25)\nonumber\\&+ 320 \pi ^2 x^2 (1-10 \pi q x)\big ]. \end{aligned}$$

The rest of the physical parameters can be determined as

$$\begin{aligned} \omega _{ri}= & {} {p_{ri} \over \rho _i}~~,~~\omega _{ti} = {p_{ti} \over \rho _i} \end{aligned}$$

(25)

$$\begin{aligned} Z_i(x)= & {} y_i(x)^{-1/2}-1 \end{aligned}$$

(26)

$$\begin{aligned} m_i(x)= & {} \int _{x_c}^{x_i} 2\pi \rho _i(x) \sqrt{x}~dx = \bigg [\frac{x^{3/2} (b-a)}{2 b x+2}\bigg ]_{x_c}^{x_i} \end{aligned}$$

(27)

$$\begin{aligned} u_i(x)= & {} {2m_i(x) \over \sqrt{x}}. \end{aligned}$$

(28)

3.3 Envelope: quadratic EoS

For the envelope, we have assumed a quadratic EoS along with Vaidya–Tikekar type$-g_{\mathrm{rr}}$, i.e.,

$$\begin{aligned} z_{\mathrm{e}}(x) = \frac{1+a x}{1+b x}~~;~~ p_{\mathrm{re}} = g \rho _e^2+ t \rho _e-\gamma , \end{aligned}$$

(29)

here g,  t and $\gamma$ are constants. By using the field Eqs. (6) and (7) with (29), we get

$$\begin{aligned} y_e(x)= & {} F \exp \bigg [\frac{1}{16 \pi } \bigg \{\frac{w_1 \ln (a x+1)}{a^2 (a-b)}+\frac{2 g (a-b)}{(b x+1)^2} \nonumber \\&+\frac{8 a g-4 b g}{b x+1}-\frac{64 \pi ^2 b \gamma x}{a}+\frac{\chi \ln (b x+1)}{b-a} \bigg \} \bigg ] \end{aligned}$$

(30)

where B is constant of integration and

$$\begin{aligned} w_1= & {} 9 a^4 g-2 a^3 (3 b g+4 (3 \pi t+\pi ))+a^2 \big [b^2 g+16 b \\&(2 \pi t+\pi )-64 \pi ^2 \gamma \big ]-8 \pi a b (b t+b-16 \pi \gamma ) \\&-64 \pi ^2 b^2 \gamma \\ \chi= & {} 9 a^2 g-2 a (3 b g+8 \pi t)+b (b g+16 \pi t). \end{aligned}$$

Now the physical parameters become

$$\begin{aligned} \rho _e(x)= & {} \frac{(b-a) (b x+3)}{8 \pi (b x+1)^2} \end{aligned}$$

(31)

$$\begin{aligned} p_{\mathrm{re}}(x)= & {} g \rho _e^2(x)+t \rho _e(x) -\gamma \end{aligned}$$

(32)

$$\begin{aligned} \Delta _e(x)= & {} \frac{x}{2048 \pi ^3 (a x+1) (b x+1)^7} \Big [a^4 g^2 (b x+3)^4 \nonumber \\&-4 a^3 g (b x+3) w_2(x)+2 a^2 \big (b^2 w_{11}(x)+w_8(x) \nonumber \\&+w_9(x)+w_{10}(x)\big )-4 a \big (b^3 w_{16}(x)+w_{12}(x) \nonumber \\&+w_{13}(x)-w_{14}(x)+w_{15}(x)\big )+4 b^7 x^3 w_7(x) \nonumber \\&+2 b^6 x^2 w_5(x)+4 b^5 x w_6(x)+b^4 w_{17}(x)\nonumber \\&+ 16 \pi b^3 w_4(x)+w_3(x) \Big ] \end{aligned}$$

(33)

$$\begin{aligned} p_{te}= & {} \Delta _e(x)+p_{re}(x), \end{aligned}$$

(34)

where

$$\begin{aligned} w_2(x)= & {} b^4 x^3 \{g+4 \pi (t+5) x)+b^3 x^2 [9 g+4 \pi (8 t+35) \\&x]+b^2 x (27 g+4 \pi (22 t+61) x\}+b \{27 g+4 \pi \\&(24 t+37) x\}+12 \pi (3 t+2) \\ w_3(x)= & {} b^8 x^4 \{g+8 \pi x (t-8 \pi \gamma x+1)\}^2+64 \pi ^2 b^2 \big [9 t^2 \\&-18 \gamma g-8 t (38 \pi \gamma x+1)+1792 \pi ^2 \gamma ^2 x^2-208 \\&\pi \gamma x+3\big ]+1024 \pi ^3 b \gamma (32 \pi \gamma x-3 t-2) \\&+4096 \pi ^4 \gamma ^2 \\ w_4(x)= & {} 27 g t-42 g (8 \pi \gamma x+1)+8 \pi x \big (21 t^2-408 \pi \gamma \\&t x-13 t+1792 \pi ^2 \gamma ^2 x^2-288 \pi \gamma x+8\big ) \\ w_5(x)= & {} 27 g^2-16 \pi g x (1-23 t+156 \pi \gamma x)+32 \pi ^2 x^2 \\&\big [39 t^2+t (28-528 \pi \gamma x)+1792 \pi ^2 \gamma ^2 x^2\nonumber \\&- 432 \pi \gamma x+25\big ] \\ w_6(x)= & {} 27 g^2-8 \pi g x (30-45 t+304 \pi \gamma x)+64 \pi ^2 x^2 \\&\big [19 t^2+t (3-260 \pi \gamma x)+896 \pi ^2 \gamma ^2 x^2-200 \pi \\&\gamma x+10\big ] \\ w_7(x)= & {} 3 g^2+4 \pi g x (11 t-80 \pi \gamma x+6)+32 \pi ^2 x^2 \big [5 t^2 \\&+t (7-72 \pi \gamma x)+4 (1-8 \pi \gamma x)^2\big ] \\ w_8(x)= & {} 4 b^3 x \big [81 g^2+4 \pi g x (135 t-304 \pi \gamma x+190)\nonumber\\&+32 \pi ^2 \big (19 t^2+63 t+10\big ) x^2\big ]\nonumber\\&+96 \pi ^2 \big (3 t^2-6 \gamma g +4 t+1\big ) \\ w_9(x)= & {} b^6 x^4 \big [3 g^2+8 \pi g x (3 t-8 \pi \gamma x+11)\nonumber\\&+32 \pi ^2 (t^2+6 t+1) x^2\big ]+4 b^5 x^3 \big [9 g^2\nonumber\\&+2 \pi g x (33 t- 80 \pi \gamma x+106)\nonumber\\&+16 \pi ^2 \left( 5 t^2+27 t+4\right) x^2\big ] \\ w_{10}(x)= & {} 2 b^4 x^2 \big [81 g^2-24 \pi g x (52 \pi \gamma x-55-23 t)\nonumber\\&+16 \pi ^2 (39 t^2+168 t+25) x^2\big ]-8 \pi b \big [g (6- 81 t\nonumber\\&+336 \pi \gamma x)-8 \pi (21 t^2+39 t+8) x\big ]\\ w_{11}(x)= & {} 243 g^2-8 \pi g x (632 \pi \gamma x-243 t-139) \\&+32 \pi ^2\left( 79 t^2+198 t+35\right) x^2 \\ w_{12}(x)= & {} 4 b^6 x^3 \big [3 g^2+\pi g x (33 t-160 \pi \gamma x+62)+16 \pi ^2 \\&x^2 \left( 5 t^2-36 \pi \gamma t x+17 t-32 \pi \gamma x+4\right) \big ]-32 \\&\pi ^2 b \big [18 \gamma g-9 t^2+2 t (76 \pi \gamma x-1)+104 \pi \gamma x\nonumber\\&- 3\big ]-256 \pi ^3 \gamma (3 t+2) \\ w_{13}(x)= & {} b^7 x^4 \big [g^2+4 \pi g x (3 t-16 \pi \gamma x+7)-32 \pi ^2 x^2 \\&\left( 8 \pi \gamma t x-t^2-4 t+8 \pi \gamma x-1\right) \big ]+4 b^4 x \big [27 g^2 \\&+2 \pi g x (135 t-608 \pi \gamma x+50)-32 \pi ^2 x^2 \big (130 \pi \\&\gamma t x-19 t^2-33 t+100 \pi \gamma x-10\big )\big ] \\ w_{14}(x)= & {} 4 \pi b^2 \big [g (672 \pi \gamma x-81 t+66)+16 \pi x \big (204 \pi \\&\gamma t x-21 t^2-13 t+144 \pi \gamma x-8\big )\big ] \\ w_{15}(x)= & {} 2 b^5 x^2 \big [27 g^2+12 \pi g x (23 t-104 \pi \gamma x+27)- 16 \\&\pi ^2 x^2 \big (264 \pi \gamma t x-39 t^2-98 t+216 \pi \gamma x-25\big )\big ] \\ w_{16}(x)= & {} 81 g^2-4 \pi g x (1264 \pi \gamma x-243 t+73)-32 \pi ^2 \\&x^2 \left( 600 \pi \gamma t x-79 t^2-88 t+440 \pi \gamma x-35\right) \\ w_{17}(x)= & {} 81 g^2-16 \pi g x (632 \pi \gamma x-81 t+95)+64 \pi ^2 x^2 \\&\big [79 t^2-2 t (600 \pi \gamma x+11)+5 \big (896 \pi ^2 \gamma ^2 x^2\nonumber\\&- 176 \pi \gamma x+7\big )\big ]. \end{aligned}$$

The rest of the physical parameters can be determined as

$$\begin{aligned} \omega _{re}= & {} {p_{re} \over \rho _e}~~,~~\omega _{te} = {p_{te} \over \rho _e} \end{aligned}$$

(35)

$$\begin{aligned} Z_e(x)= & {} y_e(x)^{-1/2}-1 \end{aligned}$$

(36)

$$\begin{aligned} m_e(x)= & {} \int _{x_i}^{x_e} 2\pi \rho _e(x) \sqrt{x}~dx = \bigg [\frac{x^{3/2} (b-a)}{2 b x+2}\bigg ]_{x_i}^{x_e} \end{aligned}$$

(37)

$$\begin{aligned} u_e(x)= & {} {2m_e(x) \over \sqrt{x}}. \end{aligned}$$

(38)

4 Regularity of the solution

The finiteness in the central values of the physical parameters will ensure a regular solution, i.e.,

$$\begin{aligned} \rho _{c0}= & {} {3(b-a) \over 8\pi }> 0 ~~,~~\forall ~~b>a, \end{aligned}$$

(39)

$$\begin{aligned} p_{rc0}= & {} p_{tc0} = {3(b-a) \alpha \over 8\pi }-\beta >0 \end{aligned}$$

(40)

and for rest of the parameters can be seen from graphs.

Fig. 11

Variation of sound speed for PSR J1614−2230

Zeldovich’s criterion is also needed to fulfill by any physical solutions, i.e.,

$$\begin{aligned} {p_{rc0} \over \rho _{c0}} = \alpha -{8\pi \beta \over 3(b-a)} \le 1. \end{aligned}$$

(41)

In the view of (40) and (41), we get

$$\begin{aligned} {3(b-a) (\alpha -1) \over 8\pi } \le \beta < {3(b-a) \alpha \over 8\pi }. \end{aligned}$$

(42)

5 Boundary conditions

The three boundaries, i.e., core–intermediate layer interface, intermediate layer–envelope interface and envelope–vacuum interface, match for the continuity of the physical parameters using Darmois–Israel conditions.

5.1 Envelope-vacuum boundary

Assuming the exterior vacuum solution to be Schwarzschild’s solution, i.e.,

$$\begin{aligned} \mathrm{d}s^2_+= & {} \left( 1-{2m_{Sch} \over R} \right) dt^2 - \left( 1-{2m_{Sch} \over R} \right) ^{-1} \mathrm{d}R^2 -\mathrm{R}^2(d\theta ^2+\sin ^2 \theta ~\mathrm{d}\phi ^2) \end{aligned}$$

(43)

the boundary matching at $R=r_{\mathrm{e}}$ and $M=m_{{\mathrm{Sch}}}(r_{\mathrm{e}})$ yields

$$\begin{aligned} 1-{2M \over r_{\mathrm{e}}}= & {} {1+b r_e^2 \over 1+a r_e^2} \end{aligned}$$

(44)

$$\begin{aligned} 1-{2M \over r_{\mathrm{e}}}= & {} F \exp \bigg [\frac{1}{16 \pi } \bigg \{\frac{w_1(r_{\mathrm{e}}) \ln (a r_e^2+1)}{a^2 (a-b)}\nonumber \\&+ \frac{2 g (a-b)}{(b r_e^2+1)^2} + \frac{8 a g-4 b g}{b r_e^2+1}-\frac{64 \pi ^2 b \gamma r_e^2}{a} \nonumber \\&+\frac{\chi \ln (b r_e^2+1)}{b-a} \bigg \} \bigg ] \end{aligned}$$

(45)

$$\begin{aligned} p_{\mathrm{re}}(r_{\mathrm{e}})= & {} g \rho _e^2(r_{\mathrm{e}})+t \rho _e(r_{\mathrm{e}}) -\gamma = 0. \end{aligned}$$

(46)

In the view of (44, 45, 46). we get

$$\begin{aligned} a= & {} -\frac{2 b M}{r_e}+b-\frac{2 M}{r_e^3} \end{aligned}$$

(47)

$$\begin{aligned} \gamma= & {} \frac{(b-a) \left( b r_e^2+3\right) }{64 \pi ^2 \left( b r_e^2+1\right) ^4} \times \nonumber \\&\left[ g (b-a) \left( b r_e^2+3\right) +8 \pi t \left( b r_e^2+1\right) ^2\right] , \end{aligned}$$

(48)

$$\begin{aligned} F= & {} \frac{r_e-2 M}{r_e} \left( a r_e^2+1\right) ^{\delta } \left( b r_e^2+1\right) ^{\eta } ~\exp \Big [\frac{1}{8 \pi } \Big \{\frac{32 \pi ^2}{a} \nonumber \\&b \gamma r_e^2-\frac{a g \left( 4 b r_e^2+5\right) }{\left( b r_e^2+1\right) ^2}+\frac{b g \left( 2 b r_e^2+3\right) }{\left( b r_e^2+1\right) ^2} \Big \} \Big ] \end{aligned}$$

(49)

where

$$\begin{aligned} \delta= & {} \frac{1}{16 \pi a^2 (a-b)} \Big [a^3 (6 b g+8 (3 \pi t+\pi ))-a^2 \big (b^2 g \\&+16 b (2 \pi t+\pi )-64 \pi ^2 \gamma \big )+8 \pi a b (b t+b-16 \pi \gamma ) \\&+ 64 \pi ^2 b^2 \gamma -9 a^4 g \Big ] \\ \eta= & {} \frac{9 a^2 g-6 a b g-16 \pi a t+b^2 g+16 \pi b t}{16 \pi a-16 \pi b} . \end{aligned}$$

Fig. 12

Variation of stability for PSR J1614−2230

5.2 Intermediate layer–envelope boundary

The boundary conditions at intermediate layer–envelope interface can be written as

$$\begin{aligned} z_{\mathrm{i}}(r_{\mathrm{i}})= & {} z_e(r_{\mathrm{i}}) \end{aligned}$$

(50)

$$\begin{aligned} y_{\mathrm{i}}(r_{\mathrm{i}})= & {} y_e(r_{\mathrm{i}}) \end{aligned}$$

(51)

$$\begin{aligned} p_{\mathrm{ri}}(r_{\mathrm{i}})= & {} p_{ri}(r_{\mathrm{i}}) . \end{aligned}$$

(52)

Here, $r_{\mathrm{i}}$ is the radius at intermediate layer–envelope interface. Since $z_{\mathrm{i}}(r_{\mathrm{i}})$ and $z_e(r_{\mathrm{i}})$ are assumed to be of same metric function, the densities at intermediate layer $\rho _{\mathrm{i}}$ and at envelope $\rho _{\mathrm{e}}$ are continuous by itself.

Now using the boundary conditions (50, 51, 52), we get

$$\begin{aligned} a_i= & {} a_e = a = b-\frac{2 b M}{r_e}-\frac{2 M}{r_e^3} \end{aligned}$$

(53)

$$\begin{aligned} B= & {} F \left( a r_i^2+1\right) {}^{\omega } \left( b r_i^2+1\right) {}^{\sigma } \exp \Big [{1 \over 8\pi } \Big \{\frac{a (g-k) }{\left( b r_i^2+1\right) {}^2} \nonumber \\&\left( 4 b r_i^2+5\right) +\frac{32 \pi ^2 b r_i^2 (q-\gamma )}{a}-\frac{b (g-k) }{\left( b r_i^2+1\right) ^2} \nonumber \\&\left( 2 b r_i^2+3\right) \Big \}\Big ] \end{aligned}$$

(54)

$$\begin{aligned} q= & {} \frac{1}{64 \pi ^2 (b r_i^2+1)^4} \Big [k (a-b)^2 (b r_i^2+3t)^2-g (a-b)^2 \nonumber \\&(b r_i^2+3t)^2+8 \pi t (a-b) \left( b r_i^2+3\right) \left( b r_i^2+1\right) ^2 \nonumber \\&+64 \pi ^2 \gamma \left( b r_i^2+1\right) ^4 \Big ], \end{aligned}$$

(55)

where,

$$\begin{aligned} \omega= & {} \frac{1}{16 \pi a^2 (a-b)} \Big [ 9 a^4 (g-k)-6 a^3 \{b (g-k)+4 \pi t\}\nonumber\\&+ a^2 \left\{ b^2 (g-k)+32 \pi b t+64 \pi ^2 (q-\gamma )\right\} -8 \pi a b \{b t\nonumber\\&+16 \pi (q-\gamma )\}+64 \pi ^2 b^2 (q-\gamma )\Big ] \\ \sigma= & {} \frac{1}{16 \pi (a-b)} \Big [6 a b (g-k)-9 a^2 (g-k)+16 \pi a t\nonumber\\&+b^2 (k-g)-16 \pi b t\Big ] . \end{aligned}$$

5.3 Core–intermediate layer boundary

The boundary conditions at outer core–intermediate layer interface can be written as

$$\begin{aligned} z_{\mathrm{i}}(r_{\mathrm{c}})= & {} z_{\mathrm{c}}(r_{\mathrm{c}}) \end{aligned}$$

(56)

$$\begin{aligned} y_{\mathrm{i}}(r_{\mathrm{c}})= & {} y_{\mathrm{c}}(r_{\mathrm{c}}) \end{aligned}$$

(57)

$$\begin{aligned} p_{\mathrm{ri}}(r_{\mathrm{c}})= & {} p_{\mathrm{rc}}(r_{\mathrm{c}}) . \end{aligned}$$

(58)

Here, $r_{\mathrm{c}}$ is the radius at core–intermediate layer interface. Again, since $z_{\mathrm{i}}(r_{\mathrm{c}})$ and $z_{\mathrm{c}}(r_{\mathrm{c}})$ are assumed to be same metric function, the densities at outer core $\rho _{\mathrm{i}}$ and at core $\rho _{\mathrm{c}}$ are continuous by itself. After using (56)-(58), we get,

$$\begin{aligned} a_{\mathrm{c}}= & {} a_{\mathrm{i}} = a_{\mathrm{e}} = a = b-\frac{2 b M}{r_{\mathrm{e}}}-\frac{2 M}{r_e^3} \end{aligned}$$

(59)

$$\begin{aligned} A= & {} B \left( a r_c^2+1\right) ^{\mu } \left( b r_c^2+1\right) ^{-\frac{k (b-3 a)^2}{16 \pi (a-b)}} \exp \Big [-{1 \over 8\pi } \nonumber \\&\Big \{\frac{32 \pi ^2 b r_c^2 (q-\beta )}{a}-\frac{a k \left( 4 b r_c^2+5\right) }{\left( b r_c^2+1\right) ^2}+ \nonumber \\&\frac{b k \left( 2 b r_c^2+3\right) }{\left( b r_c^2+1\right) {}^2} \Big \} \Big ] \end{aligned}$$

(60)

$$\begin{aligned} \beta= & {} \frac{\alpha (b-a) \left( b r_c^2+3\right) }{8 \pi \left( b r_c^2+1\right) ^2}-\frac{k (a-b)^2 \left( b r_c^2+3\right) ^2}{64 \pi ^2 \left( b r_c^2+1\right) ^4} \nonumber \\&+q, \end{aligned}$$

(61)

where

$$\begin{aligned} \mu= & {} \frac{1}{16 \pi a^2 (a-b)} \Big [ 9 a^4 k-6 a^3 (b k-4 \pi \alpha )+a^2 \big \{b^2 k \\&-32 \pi \alpha b+64 \pi ^2 (\beta -q)\big \}+8 \pi a b \{\alpha b+16 \pi (q-\beta )\} \\&+64 \pi ^2 b^2 (\beta -q) \Big ]. \end{aligned}$$

Fig. 13

Variation of adiabatic index for PSR J1614−2230

6 Energy conditions

Energy conditions are required to be satisfy by any solutions of field equations if they represent physical matter distributions. There are four energy conditions (EC):

$$\begin{aligned} \text{ weak }&:&\rho >0 ,~\rho +p_j \ge 0, \end{aligned}$$

(62)

$$\begin{aligned} \text{ null }&:\rho +p_j \ge 0, \end{aligned}$$

(63)

$$\begin{aligned} \text{ dominant }&:\rho \ge |p_j|, \end{aligned}$$

(64)

$$\begin{aligned} \text{ strong }&:\rho +\sum _i p_j \ge 0 \end{aligned}$$

(65)

where $j \equiv (r,t)$ for radial and transverse components. These conditions must be satisfied in each region.

Fig. 14

Variation of mass with central density for $a=0.01327$

7 Stability and equilibrium analysis

7.1 TOV equation and equilibrium

All the forces acting of a stellar system are at equilibrium for a stable star which is represented by TOV equation. The following equations are needed to satisfy at the respective regions:

$$\begin{aligned} -{\nu _c' \over 2} (\rho _{\mathrm{c}}+p_{\mathrm{rc}})-{\mathrm{d}p_{\mathrm{rc}} \over \mathrm{d}r}+{2\Delta _\mathrm{c} \over r}= & {} 0 \end{aligned}$$

(66)

$$\begin{aligned} -{\nu _i' \over 2} (\rho _i+p_{\mathrm{ri}})-{dp_{\mathrm{ri}} \over \mathrm{d}r}+{2\Delta _{\mathrm{i}} \over r}= & {} 0 \end{aligned}$$

(67)

$$\begin{aligned} \underbrace{-{\nu _e' \over 2} (\rho _\mathrm{e}+p_{\mathrm{re}})}_{F_\mathrm{g}}\underbrace{-{\mathrm{d}p_{\mathrm{re}} \over dr}}_{F_\mathrm{h}}+\underbrace{{2\Delta _e \over r}}_{F_\mathrm{a}}= & {} 0. \end{aligned}$$

(68)

The TOV equation not only satisfies separately but also requires the continuity of the graph at the interfaces.

7.2 Causality and stability

Any physical solution must obey causality condition, i.e., the speed of sound must be subluminal. The speed of sound can be determined as

$$\begin{aligned} v_{\mathrm{re}}= & {} \sqrt{{dp_{\mathrm{re}} \over d\rho _\mathrm{e}}} ~~;~~v_{\mathrm{te}} = \sqrt{{\mathrm{d}p_{\mathrm{te}} \over d\rho _\mathrm{e}}} \end{aligned}$$

(69)

$$\begin{aligned} v_{\mathrm{ri}}= & {} \sqrt{{dp_{\mathrm{ri}} \over d\rho _\mathrm{i}}} ~~;~~v_{\mathrm{ti}} = \sqrt{{\mathrm{d}p_{\mathrm{ti}} \over d\rho _\mathrm{i}}} \end{aligned}$$

(70)

$$\begin{aligned} v_{\mathrm{rc}}= & {} \sqrt{{dp_{\mathrm{rc}} \over d\rho _\mathrm{c}}} ~~;~~v_{\mathrm{tc}} = \sqrt{{\mathrm{d}p_{\mathrm{tc}} \over d\rho _c}}. \end{aligned}$$

(71)

Since the radial pressures at the interfaces were matched, the radial sound speeds will be continuous; however, continuation of tangential sound speed may not be possible. Therefore, the stability factor $v_{\mathrm{t}}^2-v_{\mathrm{r}}^2$ also may not be continuous, however must lie within 0 and $-1$ [85, 86].

Fig. 15

Determination of maximum mass on assuming $a = 0.01,~b = 0.075$

Fig. 16

Determination of maximum moment of inertia on assuming $a = 0.01,~b = 0.075$

Fig. 17

Equation of state for PSR J1614−2230

7.3 Adiabatic index and stability

Bondi [41] has clearly mentioned that the adiabatic index must be greater than 4/3 in Newtonian case. However, this condition is modified for relativistic fluid and if anisotropy, depends on nature of anisotropy [78]. For positive anisotropy $\Gamma _r > 4/3$ and vice versa. The adiabatic indices can be found as

$$\begin{aligned} \Gamma _{\mathrm{rc}}= & {} {p_{\mathrm{rc}}+\rho _c \over p_{\mathrm{rc}}}~ v_{\mathrm{rc}}^2~~, \Gamma _{\mathrm{ri}} = {p_{\mathrm{ri}}+\rho _\mathrm{i} \over p_{\mathrm{ri}}}~ v_{\mathrm{ri}}^2 \nonumber \\ \Gamma _{\mathrm{re}}= & {} {p_{\mathrm{re}}+\rho _e \over p_{\mathrm{re}}}~ v_{\mathrm{re}}.^2 \end{aligned}$$

(72)

A more accurate limit on the critical value of $\Gamma$ that depends on compactness parameter M/R was derived by Moustakidis [79] as

$$\begin{aligned} \Gamma _{\mathrm{crit}} = {4 \over 3} + {19 \over 42} ~2\beta . \end{aligned}$$

(73)

Hence, for a stable stellar solution one requires $\Gamma > \Gamma _{\mathrm{crit}}$.

7.4 Static stability criterion

The stability analysis adopted by Harrison et al. [80] and Zeldovich & Novikov [81] implied that for static stable configuration the mass of the star must be increasing with central density, i.e., $\partial m(\rho _0) /\partial \rho _0>0$. For the solution, we get

$$\begin{aligned} m(\rho _0)= & {} \frac{4 \pi R^3 \rho _0}{3 a R^2+8 \pi R^2 \rho _0+3} \end{aligned}$$

(74)

$$\begin{aligned} {\partial m(\rho _0) \over \partial \rho _0}= & {} \frac{12 \pi R^3 \left( a R^2+1\right) }{\left( 3 a R^2+8 \pi R^2 \rho _0+3\right) ^2} \end{aligned}$$

(75)

Fig. 18

Visualization of the three-layered compact object

8 Slow rotation model

Since the EoS is more sensitive to moment of inertia (I) and mass M graph as compare to $M-R$ graph. Therefore, plotting $M-I$ graph will enlighten more insight on the nature of EoS. The moment of inertia is defined as [82]

$$\begin{aligned} I = {8\pi \over 3} \int _0^R r^4 (\rho +p_r) e^{(\lambda -\nu )/2} ~{\bar{\omega } \over \Omega }~dr \end{aligned}$$

(76)

where $\Omega$ is the angular velocity, $\bar{\omega }$ the rotational drag satisfying the Hartle’s equation [83]

$$\begin{aligned} {d \over dr} \left( r^4 j ~{d\bar{\omega } \over dr} \right) = -4r^3\bar{\omega }~ {dj \over dr} . \end{aligned}$$

(77)

with $j=e^{-(\lambda +\nu )/2}$ which has boundary value $j(R)=1$. An approximate moment of inertia I up to the maximum mass $M_{\mathrm{max}}$ was given by Bejger and Haensel [84] as

$$\begin{aligned} I = {2 \over 5} \Big (1+{M/R \over M_\odot }\Big ) \cdot {MR^2}. \end{aligned}$$

(78)

9 Discussion and conclusion

We have successfully presented for the first time a three-layered compact star model consisting of a quark core, an intermediate layer of neutron liquid and a thin envelope satisfying quadratic EoS. All the interfaces are matched using Darmois–Israel conditions. Further, matching of $p_{\mathrm{t}}$’s cannot be preformed analytically due to their complex and lengthy expressions. Indeed, it can be performed by tuning proper values of a few free parameters, i.e., g,  t,  k,   and $\alpha$ for a chosen values of M and R.

We have completely analyzed the solution for a chosen compact star, i.e., PSR J1614−2230. To plot the graphs, we have taken $M=1.97 M_\odot , ~r_{\mathrm{e}}=R=9.69 \mathrm{km}, ~k = 400, ~r_c=3.5 \mathrm{km}, ~r_i=8.59 \mathrm{km}, ~\alpha =0.752, ~b=0.004,~ g=140$ and $t=0.345$. With these values, we found that the physical parameters, i.e., metric potentials, density, pressures, anisotropy, equation of state parameters, red-shift, energy conditions, TOV equation, adiabatic index, $v_r^2$, mass function and compactness parameter are well behaved and continuous at the interfaces (see Figs. 1, 2, 3, 4, 5,6, 7, 8, 9, 10, 11, 13); however, $\mathrm{d}p_{\mathrm{t}}/\mathrm{d}r, ~v_{\mathrm{t}}^2$ and stability factor are discontinuous at the interfaces (see Figs. 8, 11, 12). This is because $p_t$ is continuous throughout within the star but not differentiable at the interfaces; thereby, $v_t^2$ and stability factor are discontinuous at the interfaces. In our model, the $c^2 = \alpha = 0.752$ at the core. As we have discussed in section at the quark core, there may exist many hadrons, which will lead to a mixed phase hybrid EoS. Such quark–hadron hybrid phase includes two vector-coupling parameters $\eta _2$ and $\eta _4$ that may arise the sound speed even up to light speed [87].

The variations of the EoSs within stellar interior are shown in Fig. 17, and we can see that there exist smooth transitions from quark matter to neutron liquid at a density of about $\rho _I=4.16 \times 10^{14}~ \mathrm{g/cc}$ and neutron liquid to crustal matter obeying quadratic EoS at a density of about $\rho _{II}=2.934 \times 10^{14}~ \mathrm{g/cc}$. A smooth transition density between quark core and neutron liquid intermediate layer as predicted by Buchler & Barkat [20] and Baym et al. [21] was at $\rho > 10^{14}~\mathrm{g/cc}$ which is in quite agreement with our prediction (i.e., $\rho _I$). Further, we predicted that the transition density at the neutron liquid-quadratic EoS envelope happens around $\rho _{II}$. Since the stability factor is not defined as the tangential pressure is discontinuous at the junctions, one cannot define the stability using the stability factor. However, we can determine its stability using the static stability criterion. From Fig. 14, it is confirmed that the solution is stable under radial perturbations.

The $M-R$ shown in Fig. 15 is in good agreement with the observed values of masses and radii. Here, we have shown for 4U 1538-52 ($M=0.87\pm 0.07 M_\odot$, $R=7.866 \pm 0.21 ~\mathrm{km}$, [88]), LMC X-4 ($M=1.04\pm 0.09 M_\odot$, $R=8.301 \pm 0.2 ~\mathrm{km}$, [88]), 4U 1820-30 ($M=1.58\pm 0.06 M_\odot$, $R=9.1 \pm 0.4 ~\mathrm{km}$, [89]) and 4U 1608-52 ($M=1.74\pm 0.14 M_\odot$, $R=9.3 \pm 1.0 ~\mathrm{km}$, [89]). Therefore, we have also predicted the ranges of moment of inertia for the above stars as $(48.998 \pm 5.824) \times 10^{43} \mathrm{g~cm^2}$, $(124.173 \pm 7.599) \times 10^{43} \mathrm{g~cm^2}$, $(143.24 \pm 16.83) \times 10^{43} \mathrm{g~cm^2}$ and $(65.044 \pm 8.447) \times 10^{43} \mathrm{g~cm^2},$ respectively (see Fig. 16). The complete profile of the EoSs inside the compact can be seen in Fig. 17, and the visualization of the model is given in Fig. 18.

All the three solutions of the three layers can be generated from two generating functions. As per Herrera et al. [90], any spherically symmetric anisotropic static solutions can be generated by using two generators; one generator links with the metric potential $g_{\mathrm{tt}}$ and the other with pressure anisotropy. These generators $\zeta (r)$ and $\Pi (r)$ are defined via the following equations:

$$\begin{aligned} e^\nu= & {} \exp \left[ \int \left( 2\zeta (r)-{2 \over r} \right) \right] \end{aligned}$$

(79)

$$\begin{aligned} \Pi (r)= & {} 8\pi (p_\mathrm{r}-p_\mathrm{t}). \end{aligned}$$

(80)

For the core, the two generators are

$$\begin{aligned} \zeta _\mathrm{c}(r)= & {} \frac{1}{\sqrt{x}}+ \frac{\sqrt{x} (a x+1)^{-\xi } e^{\frac{4 \pi b \beta x}{a}}}{A} \bigg [a A \xi (a x+1)^{\xi -1} \nonumber \\&e^{-\frac{4 \pi b \beta x}{a}}-\frac{4 \pi A b \beta (a x+1)^{\xi } e^{-\frac{4 \pi b \beta x}{a}}}{a} \bigg ] \end{aligned}$$

(81)

$$\begin{aligned} \Pi _\mathrm{c} (r)= & {} -8\pi \Delta _\mathrm{c}(r), \end{aligned}$$

(82)

for intermediate layer,

$$\begin{aligned} \zeta _\mathrm{i}(r)= & {} \frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{16 \pi } \bigg [\frac{f_2}{a (a-b) (a x+1)}-\frac{b k (b-3 a)^2}{(a-b) (b x+1)} \nonumber \\&-\frac{b (8 a k-4 b k)}{(b x+1)^2}-\frac{4 b k (a-b)}{(b x+1)^3}-\frac{64 \pi ^2 b q}{a} \bigg ] \end{aligned}$$

(83)

$$\begin{aligned} \Pi _\mathrm{i} (r)= & {} -8\pi \Delta _i(r), \end{aligned}$$

(84)

and for envelope are

$$\begin{aligned} \zeta _\mathrm{e}(r)= & {} \frac{\sqrt{x}}{16 \pi }\bigg [-\frac{64 \pi ^2 b \gamma }{a}-\frac{4 b g (a-b)}{(b x+1)^3}-\frac{b (8 a g-4 b g)}{(b x+1)^2} \nonumber \\&+\frac{w_1}{a (a-b) (a x+1)}+\frac{b \chi }{(b-a) (b x+1)} \bigg ]+\frac{1}{\sqrt{x}} \end{aligned}$$

(85)

$$\begin{aligned} \Pi _\mathrm{e} (r)= & {} -8\pi \Delta _\mathrm{e}(r). \end{aligned}$$

(86)