Three-layered star comprising polytropic, quark and gaseous matter

Abstract

We construct a new exact model for a dense stellar object utilising the Einstein–Maxwell system of equations. The model comprises three interior regions with distinct equations of state (EoS): the polytropic EoS at the core region, linear EoS at the intermediate region and Chaplygin EoS at the envelope region. Our model can regain earlier solutions. A physical analysis reveals that the matter variables, metric functions and other physical conditions are well behaved and consistent in the study of dense stellar objects. Matching of the boundary layers is done with help of the Reissner–Nordstrom exterior space–time. An interesting feature is that the innermost region is outfitted with a polytropic EoS, and this study extends a core–envelope model developed by Mardan, Noureen and Khalid into a three-layered model.

1 Introduction

Construction of stellar models in a multilayered setting has drawn the attention of many researchers. It has been noted that the interior structure of a massive stellar object has several layers leading to an interior structure which is complex. In the past, several models have been formulated to demonstrate a variety of physical features in the interior of dense stellar objects. Treatment of the interior structure of the stellar sphere with multilayers yields interesting physical features related to the matter variables and metric functions. Stellar objects with concentric interior layers are massive and possess strong magnetic and gravitational fields (Durgapal and Bannerji [1], Itoh [2]). Gravitating stellar objects with such properties include white dwarfs, quark stars, pulsars, neutron stars, quasars and gravastars. These dense stellar objects have a unique interior structure which need further gravitational investigation. According to Pant et al [3], the total mass and density of the compact objects are approximately 1.0–2.0 $M_{\odot }$ and $10^{15}$ g cm$^{-3}$ respectively. Jasim et al [4] considered dense objects with masses 1.4–$2.0M_{\odot }$ and radii 11.0–15.0 km. A thorough investigation of the multilayered stellar object is required with these values.

The idea of establishing a multilayered stellar model is possible in the Einstein general theory of relativity which relies on the space–time curvature (Mardan et al [5]). A variety of stellar models are known showing importance of the field equations in the study of gravitating objects. This includes the works of Das et al [6] and Herrera [7] who developed stellar models to describe the stability in the interior. The presence of electromagnetic field in the stellar object increases stability, and slows gravitational collapse (Rahaman et al [8]). According to Bhatia et al [9], electric charges are created as a result of the electrons shifting from the inner layer of the stellar object. Many papers show that the charge affects masses, red-shifts, luminosities and causal signals. The effects of electric charge have been discussed in the works of Bonnor [10], Sharma and Maharaj [11], Rao et al [12], Jape et al [13], Sharma and Mukherjee [14], Lighuda et al [15], Ray et al [16], Sunzu and Danford [17], Mathias et al [18] and Thirukannesh and Maharaj [19, 20]. Modelling of relativistic anisotropic stellar objects requires an EoS according to the composition in the interior of the star. Researchers choose a suitable EoS for a particular layer depending on the density of the matter contained (Mardan et al [5]). Most studies use linear EoS, quadratic EoS, polytropic EoS, Chaplygin EoS and Van der Waal EoS. Linear EoS are contained in the treatments of Sharma and Maharaj [11], Sunzu and Danford [17], Thirukannesh and Maharaj [19, 20], Maharaj et al [21], Sunzu et al [22, 23], Varela et al [24], Chaisi and Maharaj [25, 26]. Some stellar models with polytropic EoS are contained in Maharaj and Mafa Takisa [27], Freitas and Goncalves [28], Sunzu [29], Tooper [30] and Chavanis [31]. Models developed with Chaplygin EoS include Rahaman et al [8], Lighuda et al [15], Gorini and Moschella [32], Singh and Baruah [33], Bhar [34, 35] and Bhar et al [36].

Two-layered models describing an inner region and the envelope region have been constructed utilising the Einstein–Maxwell field equations with EoS. Recently, Mardan et al [5] utilised a polytropic EoS in the core region, and the envelope region has a linear EoS. Stellar models with linear EoS at the core and quadratic EoS at the envelope demonstrate, that the envelope region consists of less dense material, were established by Mafa Takisa and Maharaj [37] and Mafa Takisa et al [38]. Thomas et al [39] described an isotropic fluid at the core region and anisotropic fluid at the envelope region. In the treatment by Paul and Tikekar [40], the core layer is considered anisotropic and the corresponding envelope is assumed to be isotropic. The model developed by Metcalfe et al [41] discusses the physical characteristics of white dwarf stars. The studies of Pant et al [42] and Gedela et al [43] describe the physical behaviour of dense objects utilising linear EoS at the core and quadratic EoS at the envelope. Other stellar models describing the physical properties of the dense object comprising two regions are the works of Sharma and Mukherjee [14], Hansraj et al [44], Montgomery et al [45], Tikekar and Jotania [46] and Ramesh and Thomas [47].

Three-layered models describing the interior regions of dense stellar objects are now being considered by many researchers. The interior structure of the stellar object comprises three layers which are determined by their density profiles. Realistically, one layer is not sufficient to describe the whole interior of the stellar object. The recent models developed by Pant et al [3] and Bisht et al [48] demonstrate that there exists a subregion between the core and the envelope regions. In their study, the analysis is done by using linear EoS for the quark matter at the core region, the particular quadratic EoS convenient for Bose–Einstein condensate matter in the intermediate region, and the general quadratic EoS in the envelope region. The charged model established by Lighuda et al [15] describes the core region utilising linear EoS, the intermediate region with quadratic EoS and the envelope with Chaplygin EoS. Another charged stellar model comprising three regions, linear EoS, the Bose–Einstein EoS and quadratic EoS at the core region, intermediate region and the envelope region, respectively, was developed by Lighuda et al [49].

In the current work, we formulate a three-layered model following the approach in a two-layered model generated by Mardan et al [5]. A notable feature in our three-layered model is the existence of a polytropic EoS at the core region and Chaplygin EoS in the third layer. In this paper, we develop a three-layered model with a linear EoS in the intermediate layer. We construct a new charged model with three interior regions. In our study, we specify one of the metric functions and electric field which makes a detailed physical analysis possible .

2 Field equations

The interior of the stellar object is described by a static spherically symmetric space–time utilising Schwarzschild coordinates $(x^{\iota }= t, r, \theta , \phi )$ as

$$\begin{aligned} \textrm{d}s^{2}=-\textrm{e}^{2\nu (r)}\textrm{d}t^{2}+\textrm{e}^{2\lambda (r)}\textrm{d}r^{2}+r^2(\mathrm {\textrm{d}}\theta ^2+\sin ^2\theta \mathrm {\textrm{d}}\phi ^2).\nonumber \\ \end{aligned}$$

(1)

The exterior space–time is represented by a line element described in Reissner–Nordstrom geometry given in the form

$$\begin{aligned} \textrm{d}s^{2}= & {} -\,\left( \begin{array}{c} 1-\dfrac{2\epsilon }{r}+\dfrac{q^2}{r^2}\end{array}\right) \textrm{d}t^{2}+\left( \begin{array}{c} 1-\dfrac{2\epsilon }{r}+\dfrac{q^2}{r^2}\end{array}\right) ^{-1}\textrm{d}r^{2}\nonumber \\{} & {} +\,r^2(\textrm{d}\theta ^2+\sin ^2\theta \textrm{d}\phi ^2), \end{aligned}$$

(2)

where $\nu (r)$ and $\lambda (r)$ are the metric functions, q stands for the total charge and $\epsilon$ represents the total mass of the sphere.

We take the energy–momentum tensor for the charged stellar object as

$$\begin{aligned} T_{ij}= & {} \text{ diag } \left( -\,\rho -\dfrac{1}{2}E^2, p_{r}-\dfrac{1}{2}E^2,p_{t}+\dfrac{1}{2}E^2,\right. \nonumber \\{} & {} \left. p_{t}+\dfrac{1}{2}E^2 \right) , \end{aligned}$$

(3)

where $\rho$ is the energy density, E is the electric field, $p_{r}$ and $p_{t}$ are the radial and tangential pressures, respectively. With $G=c=1$ in the Einstein–Maxwell field equations, we get

$$\begin{aligned}{} & {} 8\pi \rho +\dfrac{1}{2}E^2 =\dfrac{1}{r^2}(1-\textrm{e}^{-2\lambda })+\dfrac{2\lambda ^{\prime }}{r}\textrm{e}^{-2\lambda }, \end{aligned}$$

(4a)

$$\begin{aligned}{} & {} 8\pi p_{r}-\dfrac{1}{2}E^2 = -\,\dfrac{1}{r^2}(1-\textrm{e}^{-2\lambda })+\dfrac{2\nu ^{\prime }}{r}\textrm{e}^{-2\lambda }, \end{aligned}$$

(4b)

$$\begin{aligned}{} & {} 8\pi p_{t}+\dfrac{1}{2}E^2 = \textrm{e}^{-2\lambda }\left( \begin{array}{c} \nu ^{\prime \prime }+\nu ^{\prime ^2}-\nu ^{\prime }\lambda ^{\prime }+\dfrac{\nu ^{\prime }}{r}-\dfrac{\lambda ^{\prime }}{r}\end{array}\right) \nonumber \\{} & {} +\,\dfrac{2\lambda ^{\prime }}{r}\textrm{e}^{-2\lambda }, \end{aligned}$$

(4c)

$$\begin{aligned}{} & {} \sigma =\dfrac{1}{r^2}\textrm{e}^{-\lambda }(r^2E)^{\prime }, \end{aligned}$$

(4d)

where primes ($\prime$) denote derivatives.

We utilise new variables, as given in Durgapal and Bannerji [50] in the form

$$\begin{aligned} x=r^2,\quad Z(x)=\textrm{e}^{-2\lambda },\quad \textrm{e}^{2\nu }=A^2y^2(x). \end{aligned}$$

(5)

Substituting eq. (5) into (4), the field equations become

$$\begin{aligned}{} & {} 8\pi \rho = \dfrac{1-Z}{x}-2\dot{Z}-\dfrac{1}{2}E^2, \end{aligned}$$

(6a)

$$\begin{aligned}{} & {} 8\pi p_{r}=-\dfrac{1}{x}(1-Z)+4Z\dfrac{\dot{y}}{y}+\dfrac{1}{2}E^2, \end{aligned}$$

(6b)

$$\begin{aligned}{} & {} 8\pi p_{t}=4xZ\dfrac{\ddot{y}}{y}+\left( \begin{array}{c}4Z+2x\dot{Z}\end{array}\right) \dfrac{\dot{y}}{y}+\dot{Z}-\dfrac{1}{2}E^2, \end{aligned}$$

(6c)

$$\begin{aligned}{} & {} \Delta =8\pi ( p_{t}- p_{r})\nonumber \\{} & {} =4xZ\dfrac{\ddot{y}}{y}+\left( \begin{array}{c}4xZ+2x\dot{Z}-4Z\end{array}\right) \dfrac{\dot{y}}{y}+\dot{Z}\nonumber \\{} & {} +\dfrac{1}{x}(1-Z)-E^2, \end{aligned}$$

(6d)

$$\begin{aligned}{} & {} \sigma =2\left( \begin{array}{c}x{\dot{E}}+E\end{array}\right) \sqrt{\dfrac{Z}{x}}. \end{aligned}$$

(6e)

System (6) has eight variables ($\rho$, $p_{t}$, $p_{r}$, $\Delta$, Z, y, $\sigma$, E). From system (6), two physical variables may be specified to find the solution for the others.

In our model, we assume one of the metric functions in the form

$$\begin{aligned} Z(x)=\textrm{e}^{-2\lambda }=1-\alpha x+\beta x^2 +\eta x^3, \end{aligned}$$

(7)

where $\alpha , \beta$ and $\eta$ are the arbitrary real constants. The specified metric function Z is finite and continuous everywhere at the interior. The choice of Z in eq. (7) implies that no singularity assists at the centre. Inserting $\eta =0$ from (7), we regain the metric function utilised in the models by Mardan et al [5], Pant et al [3, 42] and Lighuda et al [49]. In this study, we choose the electric field in the form

$$\begin{aligned} E^2= \kappa xZ=\kappa x(1-\alpha x+\beta x^2 +\eta x^3), \end{aligned}$$

(8)

where $\kappa$ is an arbitrary real constant. The assumed electric field $E^2$ in eq. (8) is physically reasonable and vanishes at the centre. It ensures continuity from the centre towards the surface. If we choose electric field with $\kappa =0$, then we may recover the earlier uncharged models.

3 Classification of the interior regions

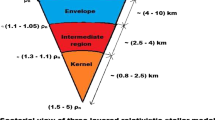
Interior layers of the dense stellar object are classified in terms of three regions: the core (I), the intermediate (II) and the envelope (III). These regions are given by the core layer (Region I): $0\le r\le R_{\textrm{I}}$, the intermediate layer (Region II): $R_{\textrm{I}}\le r \le R_{\textrm{II}}$, and the envelope layer (Region III): $R_{\textrm{II}} \le r \le R_{\textrm{III}}$. For the three regions, line element (1) becomes

$$\begin{aligned} \textrm{d}s^{2}|_{\textrm{I}}= & {} -\textrm{e}^{2\nu _{\textrm{I}}} \textrm{d}t^{2}+\textrm{e}^{2\lambda _{\textrm{I}}}\textrm{d}r^{2}+r^2(\textrm{d}\theta ^2\nonumber \\{} & {} +\sin ^2\theta \textrm{d}\phi ^2), \end{aligned}$$

(9a)

$$\begin{aligned} \textrm{d}s^{2}|_{\textrm{II}}= & {} -\textrm{e}^{2\nu _{\textrm{II}}} \textrm{d}t^{2}+\textrm{e}^{2\lambda _{\textrm{II}}}\textrm{d}r^{2}+r^2(\textrm{d}\theta ^2\nonumber \\{} & {} +\sin ^2\theta \textrm{d}\phi ^2), \end{aligned}$$

(9b)

$$\begin{aligned} \textrm{d}s^{2}|_{\textrm{III}}= & {} -\textrm{e}^{2\nu _{\textrm{III}}} \textrm{d}t^{2}+\textrm{e}^{2\lambda _{\textrm{III}}}\textrm{d}r^{2}+r^2(\textrm{d}\theta ^2\nonumber \\{} & {} +\sin ^2\theta \textrm{d}\phi ^2). \end{aligned}$$

(9c)

3.1 Layer I (core)

The basic postulate in the theory of polytropes indicates that the pressure forces of the gravitating sources rely upon the density profile (Mardan et al [5]). We choose to utilise the polytropic EoS to investigate the dynamical properties of polytropes in the core layer. The polytropic EoS has also been shown to be relevant in the core region in the stellar distributions of Maharaj and Matondo [51]. This is given in the form

$$\begin{aligned} p_{r_{\textrm{I}}}=\mu \rho _{\textrm{I}}^{1+1/n}, \end{aligned}$$

(10)

where $\mu$ and n are the arbitrary real constants for $n>0$. Combining (6a) and (10) yields

$$\begin{aligned} p_{r_{\textrm{I}}}=\mu \left( \begin{array}{c}\dfrac{1-Z}{8\pi x}-\dfrac{\dot{Z}}{4\pi }-\dfrac{1}{16\pi }E^2\end{array}\right) ^{1+1/n}. \end{aligned}$$

(11)

Equating (6b) and (11) gives

$$\begin{aligned} \dfrac{\dot{y}}{y}= & {} \dfrac{\mu }{4Z}\left( \begin{array}{c}\dfrac{1-Z}{8\pi x}-\dfrac{\dot{Z}}{4\pi }-\dfrac{1}{16\pi }E^2\end{array}\right) ^{1+1/n}\nonumber \\{} & {} +\,\dfrac{1-Z}{4Zx}-\dfrac{E^2}{8Z}. \end{aligned}$$

(12)

Substituting (7) and (8) into eq. (12) yields

$$\begin{aligned} \dfrac{\dot{y}}{y}= & {} [2\alpha +x^2(\alpha -x(\beta +x\eta ))\kappa -x(2\beta +2x\eta +\kappa )\nonumber \\{} & {} +\,2^{-3-\frac{4}{n}}\pi ^{-\frac{1+n}{n}}(-2\alpha +x(6\beta +10x\eta -\kappa )\nonumber \\{} & {} +\,x^2(\alpha -x(\beta +x\eta ))\kappa )^{1+\frac{1}{n}}\mu ][8(1+x(-\alpha \nonumber \\{} & {} +\,x(\beta +x\eta )))]^{-1}. \end{aligned}$$

(13)

Then with the help of (7), (8) and (13) and system (6), we obtain the following gravitational and matter variables in the core layer:

$$\begin{aligned}{} & {} \textrm{e}^{2\lambda _{\textrm{I}}}= [1-\alpha x+\beta x^2+\eta x^3]^{-1}, \end{aligned}$$

(14a)

$$\begin{aligned}{} & {} \textrm{e}^{2\nu _{\textrm{I}}}= A^2 [\exp (H_{0}(x))]^2, \end{aligned}$$

(14b)

$$\begin{aligned}{} & {} \rho _{\textrm{I}}=[-2\alpha +x(6\beta +10x\eta -\kappa )+x^2(\alpha \nonumber \\{} & {} \qquad \quad -\,x(\beta +x\eta ))\kappa ][16\pi ]^{-1}, \end{aligned}$$

(14c)

$$\begin{aligned}{} & {} p_{r_{\textrm{I}}}=\mu [[-2\alpha +x(6\beta +10x\eta -\kappa )+x^2(\alpha \nonumber \\{} & {} \qquad \quad -\,x(\beta +x\eta ))\kappa ][16\pi ]^{-1}]^{(1+1/n)) },\end{aligned}$$

(14d)

$$\begin{aligned}{} & {} p_{t_{\textrm{I}}}=1/128 (-((16 (\alpha - x (2 \beta + 3 x \eta )))/\pi ) \nonumber \\{} & {} \qquad \quad -\, (8 x (1- x \alpha + x^2 \beta + x^3 \eta ) \kappa )/\pi \nonumber \\{} & {} \qquad \quad +\, (16 (4 (1 - x \alpha + x^2 \beta + x^3 \eta ) + (x (-\alpha \nonumber \\{} & {} \qquad \quad +\, x (2 \beta + 3 x \eta )))/(4 \pi )) (2 \alpha - 2 x (\beta + x \eta ) \nonumber \\{} & {} \qquad \quad - \,x (1- x \alpha + x^2 \beta + x^3 \eta ) \kappa + 2^{-3 - 4/n} \nonumber \\{} & {} \qquad \quad \times \,\pi ^{-((1 + n)/n)}(\alpha (-2 + x^2 \kappa ) - x (-10 x \eta + \kappa \nonumber \\{} & {} \qquad \quad +\, x^3 \eta \kappa + \beta (-6 + x^2 \kappa )))^{1 + 1/n} \mu ))/(1 - x \alpha \nonumber \\{} & {} \qquad \quad +\, x^2 \beta + x^3 \eta ) + 1/(\pi (1 + x (-\alpha + x (\beta \nonumber \\{} & {} \qquad \quad +\, x \eta )))^2)(1 x \alpha + x^2 \beta + x^3 \eta ) (-8 (-\alpha \nonumber \\{} & {} \qquad \quad +\, x (2 \beta + 3 x \eta ))(2 \alpha + x^2 (\alpha - x (\beta + x \eta )) \kappa \nonumber \\{} & {} \qquad \quad - \,x (2 \beta + 2 x \eta + \kappa )+ 2^{-3 - 4/n} \pi ^{-((1 + n)/n)} (-2 \alpha \nonumber \\{} & {} \qquad \quad +\, x (6 \beta + 10 x \eta - \kappa )+ x^2 (\alpha - x (\beta + x \eta ))\nonumber \\{} & {} \qquad \quad \times \,\kappa )^{1 + 1/n} \mu )+ (2 \alpha + x^2 (\alpha - x (\beta + x \eta )) \kappa \nonumber \\{} & {} \qquad \quad - \,x (2 \beta + 2 x\eta + \kappa ) + 2^{-3 - 4/n}\pi ^{-((1 + n)/n)} (-2 \alpha \nonumber \\{} & {} \qquad \quad +\, x (6 \beta + 10 x \eta - \kappa ) +x^2 (\alpha - x (\beta + x \eta ))\nonumber \\{} & {} \qquad \quad \times \,\kappa )^{1 + 1/n} \mu )^2 + (1+ x (-\alpha + x (\beta + x \eta ))) \nonumber \\{} & {} \qquad \quad \times \,(-8 (2 \beta + 4 x\eta + \kappa - 2 x \alpha \kappa + x^2 (3\beta \nonumber \\{} & {} \qquad \quad + \,4x\eta ) \kappa ) -(2^{-4/n} (1+ n) \pi ^{-((1 + n)/n)} (-2 \alpha \nonumber \\{} & {} \qquad \quad +\, x (6 \beta + 10 x\eta -\kappa )+x^2(\alpha - x(\beta \nonumber \\{} & {} \qquad \quad +\, x\eta ))\kappa )^{1/n}(-6\beta +\kappa +x^2 (3\beta + 4x\eta ) \kappa \nonumber \\{} & {} \qquad \quad -\,2 x (10 \eta + \alpha \kappa )) \mu )/n))),\end{aligned}$$

(14e)

$$\begin{aligned}{} & {} \Delta _{\textrm{I}}=p_{t_{\textrm{I}}}-p_{r_{\textrm{I}}},\end{aligned}$$

(14f)

$$\begin{aligned}{} & {} \sigma _{\textrm{I}}=(2 (2 - 3 x \alpha +4x^2\beta +5 x^3 \eta ))((x \kappa ))^{-1/2} ,\end{aligned}$$

(14g)

$$\begin{aligned}{} & {} E^2_{\textrm{I}}=\kappa x(1-\alpha x+\beta x^2+\eta x^3), \end{aligned}$$

(14h)

where for simplicity, we have defined

$$\begin{aligned} H_{0}(x)= & {} \dfrac{1}{8} \int _{0}^{2.5}{(2 \alpha +x^2(\alpha -x(\beta +x\eta )) \kappa }\\{} & {} {-\,x(2\beta +2x\eta +\kappa )+2^{-3 - 4/n} \pi ^{-((1 + n)/n)}}\\{} & {} {\times (-2\alpha +x(6\beta +0x \eta -\kappa )+x^2(\alpha }\\{} & {} {-\,x(\beta +x\eta ))\kappa )^{1 + 1/n} \mu )1+x(-\alpha }\\{} & {} {+\,x(\beta +x\eta )))^{-1}} \textrm{d}x. \end{aligned}$$

The mass of the stellar object in the core region is given in the form

$$\begin{aligned}{} & {} \epsilon _{\textrm{I}}(r)=4\pi \int _{0}^{2.5}{r^2\rho _{\textrm{I}}\textrm{d}r}, \quad r^2=x\nonumber \\{} & {} \epsilon _{\textrm{I}}=\int _{0}^{2.5}[x(-2\alpha +x(6\beta +10x\eta -\kappa )\nonumber \\{} & {} \qquad +\,x^2(\alpha -x(\beta +x\eta )))\kappa ][8x^{1/2}]^{-1}\textrm{d}x\nonumber \\{} & {} \qquad =-0.658808 ( \alpha - 5.83929 \beta \nonumber \\{} & {} \qquad \quad \, - \,15.997 \eta + 0.75 \kappa ) \kappa . \end{aligned}$$

(15)

3.2 Layer II (intermediate)

In this subsection, we present the intermediate layer utilising the linear EoS which is convenient to describe the quark matter satisfying the MIT-bag model. In the recent work [51], the linear EoS was shown to be relevant, away from the core region. This is written in the form

$$\begin{aligned} p_{r_{\textrm{II}}}={d}\rho _{\textrm{II}}- b, \end{aligned}$$

(16)

where d and b are arbitrary real constants. Using eqs (6a) and (16) we obtain

$$\begin{aligned} p_{r_{\textrm{II}}}=d\left( \dfrac{1-Z}{8\pi x}-\dfrac{\dot{Z}}{4\pi }-\dfrac{1}{16\pi }E^2\right) -b. \end{aligned}$$

(17)

Equating (6b) and (17), and using (7) and (8) we obtain a differential equation in the form

$$\begin{aligned} \dfrac{\dot{y}}{y}= & {} -\,(16b\pi +2(x\alpha ^2+x(\beta (1-3d+x^2\beta )+x(1\nonumber \\{} & {} -\,5d+2x^2\beta )\eta +x^4\eta ^2)+\alpha (-1+d-2x^2(\beta \nonumber \\{} & {} +\,x\eta )))+(d+8\pi )x(1-x\alpha +x^2\beta )\kappa )( 64(\pi \nonumber \\{} & {} +\,\pi x(-\alpha +x(\beta +x\eta ))))^{-1}. \end{aligned}$$

(18)

Substituting (7), (8) and (18) into system (6), the gravitational and matter variables at the intermediate layer become

$$\begin{aligned}{} & {} \textrm{e}^{2\nu _{\textrm{II}}}=A^2y^2(x)= A^2 [\exp (\tau _{0}(x))]^2,\end{aligned}$$

(19a)

$$\begin{aligned}{} & {} \rho _{\textrm{II}}=[-2\alpha +x(6\beta +10x\eta -\kappa )+x^2(\alpha -x(\beta \nonumber \\{} & {} \qquad \quad +\,x\eta ))\kappa ][16\pi ]^{-1},\end{aligned}$$

(19b)

$$\begin{aligned}{} & {} p_{r_{\textrm{II}}}= d[-2\alpha +x(6\beta +10x\eta -\kappa )+x^2(\alpha -x(\beta \nonumber \\{} & {} \qquad \quad +\,x\eta ))\kappa ][16\pi ]^{-1}-b,\end{aligned}$$

(19c)

$$\begin{aligned}{} & {} p_{t_{\textrm{II}}}=1/(8192 \pi ) (-1024 (\alpha - x (2 \beta + 3 x \eta )) \nonumber \\{} & {} \qquad \quad -\, 512 x (1 +\, x (-\alpha + x (\beta + x \eta ))) \kappa \nonumber \\{} & {} \qquad \quad -\, (32 (2 - 3 x \alpha + 4 x^2 \beta \nonumber \\{} & {} \qquad \quad +\, 5 x^3 \eta ) (2 (8 b \pi + x \alpha ^2 + x (\beta (1 - 3 d + x^2 \beta )\nonumber \\{} & {} \qquad \quad +\, x (1 - 5 d + 2 x^2 \beta ) \eta + x^4 \eta ^2) + \alpha (-1 + d \nonumber \\{} & {} \qquad \quad -\, 2 x^2 (\beta + x \eta ))) + (d + 8 \pi ) x (1-x \alpha +x^2 \beta )\nonumber \\{} & {} \qquad \quad \times \, \kappa ))/(\pi + \pi x (-\alpha + x (\beta + x \eta ))) + 1/(\pi \nonumber \\{} & {} \qquad \quad +\, \pi x (-\alpha + x (\beta + x \eta )))^2 x (1 + x (-\alpha + x (\beta \nonumber \\{} & {} \qquad \quad +\, x \eta ))) (64 \pi (-\alpha + x (2 \beta + 3 x \eta )) (16 b \pi \nonumber \\{} & {} \qquad \quad +\, 2 (x \alpha ^2 +\, x (\beta (1 - 3 d + x^2 \beta )\nonumber \\{} & {} \qquad \quad +\, x (1 - 5 d + 2 x^2 \beta ) \eta \nonumber \\{} & {} \qquad \quad +\,x^4 \eta ^2) + \alpha (-1 + d-2 x^2 (\beta + x \eta ))) + (d \nonumber \\{} & {} \qquad \quad +\, 8 \pi ) x (1 -x \alpha + x^2 \beta ) \kappa ) + (16 b \pi \nonumber \\{} & {} \qquad \quad +\, 2 (x \alpha ^2 +\, x (\beta (1- 3 d + x^2 \beta )\nonumber \\{} & {} \qquad \quad +\, x (1 - 5 d + 2 x^2 \beta ) \eta \nonumber \\{} & {} \qquad \quad +\, x^4 \eta ^2) + \alpha (-1 + d - 2 x^2 (\beta + x \eta ))) + (d \nonumber \\{} & {} \qquad \quad +\, 8 \pi ) x (1-x\alpha +x^2\beta ) \kappa )^2-64\pi (1 +x (-\alpha \nonumber \\{} & {} \qquad \quad +\, x (\beta + x \eta ))) (2 (\alpha ^2+\beta -3d\beta - 2 x \alpha (2\beta \nonumber \\{} & {} \qquad \quad +\,3x\eta )+x(2(1-5d)\eta + x(\beta +x\eta )(3\beta \nonumber \\{} & {} \qquad \quad +\,5x\eta )))+(d+8\pi ) (1-2x\alpha \nonumber \\{} & {} \qquad \quad +\,3x^2\beta ) \kappa ))),\end{aligned}$$

(19d)

$$\begin{aligned}{} & {} \Delta _{\textrm{II}}=p_{t_{\textrm{II}}}-p_{r_{\textrm{II}}}, \end{aligned}$$

(19e)

where for simplicity we have set

$$\begin{aligned} \tau _{0}(x)= & {} -\,\int _{2.5}^{4}{((16b\pi +2(x\alpha ^2+x(\beta (1-3d}\\{} & {} +\,{x^2\beta )+x(1-5d}+{2x^2\beta )\eta +x^4\eta ^2}\\{} & {} {+\,\alpha (-1+d-2x^2(\beta +x\eta )))+(d}\\{} & {} {+\,8\pi )x(1-x\alpha +x^2\beta )\kappa )(64(\pi }\\{} & {} {+\,\pi x(-\alpha +x(\beta +x \eta ))))^{-1}\textrm{d}x.} \end{aligned}$$

We present the mass of the stellar object in the intermediate region in the form

$$\begin{aligned}{} & {} \epsilon _{\textrm{II}}(r)=4\pi \int _{2.5}^{4}{r^2\rho _{\textrm{II}}\textrm{d}r}, \quad r^2=x\nonumber \\{} & {} \epsilon _{\textrm{II}}=\int _{2.5}^{4}[x(-2\alpha +x(6\beta +10x\eta -\kappa )\nonumber \\{} & {} ~+\,x^2(\alpha -x(\beta +x\eta )))\kappa ][8x^{1/2}]^{-1}\textrm{d}x\nonumber \\{} & {} =-1.10589 \kappa (0.609937 \alpha - 9.33585 \beta \nonumber \\{} & {} ~-\, 44.6675 \eta + \kappa ). \end{aligned}$$

(20)

3.3 Layer III (envelope)

Following the density profile in the interior of the star, the envelope layer should be less compact than the core and the intermediate layers: consisting of neutron fluids and Coulomb liquids (Bisht et al [48]). The Chaplygin EoS is chosen which is suitable for describing gaseous matter with less compaction so as to examine the radial pressure forces in the envelope (Lighuda et al [15, 49]). This is given by

$$\begin{aligned} p_{r_{\textrm{III}}}=s\rho _{\textrm{III}}-\dfrac{w}{\rho _{\textrm{III}}}, \end{aligned}$$

(21)

where s and w are the arbitrary real constants. From (6a) and (21) we have

$$\begin{aligned} p_{r_{\textrm{III}}}= & {} s \left( \begin{array}{c}\dfrac{1-Z}{8\pi x}-\dfrac{\dot{Z}}{4\pi }-\dfrac{1}{16\pi }E^2\end{array}\right) \nonumber \\{} & {} -w\left( \begin{array}{c}\dfrac{1-Z}{8\pi x}-\dfrac{\dot{Z}}{4\pi }-\dfrac{1}{16\pi }E^2\end{array}\right) ^{-1}. \end{aligned}$$

(22)

Equating (6b) and (22) gives

$$\begin{aligned} \dfrac{\dot{y}}{y}= & {} \dfrac{s}{4Z} \left( \begin{array}{c}\dfrac{1-Z}{8\pi x}-\dfrac{\dot{Z}}{4\pi }-\dfrac{1}{16\pi }E^2\end{array}\right) \nonumber \\{} & {} +\dfrac{w}{4Z}\left( \begin{array}{c}\dfrac{1-Z}{8\pi x}-\dfrac{\dot{Z}}{4\pi }-\dfrac{1}{16\pi }E^2\end{array}\right) ^{-1}\nonumber \\{} & {} +\dfrac{1-Z}{32\pi Z}-\dfrac{1}{16\pi }E^2. \end{aligned}$$

(23)

Substituting (7) and (8) into (23), we obtain a first-order differential equation in the form

$$\begin{aligned} \dfrac{\dot{y}}{y}= & {} (2x(\alpha -x(\beta +x\eta ))-4x(1-x\alpha +x^2\beta )\kappa \nonumber \\{} & {} +(s(-2\alpha +x(6\beta +10x\eta -\kappa )+x^2(\alpha \nonumber \\{} & {} -x\beta )\kappa ))(1+x(-\alpha +x(\beta +x\eta )))^{-1}\nonumber \\{} & {} +(256\pi ^2w)((1+x(-\alpha +x(\beta +x\eta )))^{-1}(2\alpha \nonumber \\{} & {} +x^2(-\alpha +x\beta )\kappa +x(-6\beta -10x\eta \nonumber \\{} & {} +\kappa ))))^2(4096\pi ^2)^{-1}. \end{aligned}$$

(24)

Solving eq. (24), the envelope variables for the third layer become

$$\begin{aligned} \textrm{e}^{2\nu _{\textrm{III}}}&=A^2y^2(x)= A^2 [\exp (G_{0}(x))]^2, \end{aligned}$$

(25a)

$$\begin{aligned} \rho _{\textrm{III}}&=[-2\alpha +x(6\beta +10x\eta -\kappa )+x^2(\alpha \nonumber \\&\quad - x(\beta +x\eta ))\kappa ][16\pi ]^{-1}, \end{aligned}$$

(25b)

$$\begin{aligned} p_{r_{\textrm{III}}}&=s [-2\alpha +x(6\beta +10x\eta -\kappa )+x^2(\alpha -x(\beta \nonumber \\&\quad + x\eta ))\kappa ][16\pi ]^{-1}-w([-2\alpha +x(6\beta +10x\eta \nonumber \\&\quad - \kappa )+x^2(\alpha -x(\beta +x\eta ))\kappa ][16\pi ]^{-1})^{-1},\end{aligned}$$

(25c)

$$\begin{aligned} p_{t_{\textrm{III}}}&=\dfrac{1}{8192 \pi ^3} (-1024 \pi ^2 (\alpha - x (2 \beta + 3 x \eta )) \nonumber \\&\quad - 512 \pi ^2 x (1 + x (-\alpha + x (\beta + x \eta ))) \kappa + 16 \pi \nonumber \\&\quad \times (4 - 6 x \alpha + 8 x^2 \beta +10 x^3 \eta ) (2 x (\alpha - x (\beta + x \eta ))\nonumber \\&\quad - 4 x (1 - x \alpha + x^2 \beta ) \kappa + (s (-2 \alpha + x (6 \beta \nonumber \\&\quad + 10 x \eta -\, \kappa ) + x^2 (\alpha - x \beta ) \kappa ))( 1 \nonumber \\&\quad + x (-\alpha + x (\beta + x \eta )))^{-1} \nonumber \\&\quad + (256 \pi ^2 w)((1 + x (-\alpha + x (\beta + x \eta )))^{-1} (2 \alpha \nonumber \\&\quad + x^2 (-\alpha + x \beta ) \kappa + x (-6 \beta - 10 x \eta + \kappa )))) \nonumber \\&\quad + x (1 + \,x (-\alpha + x (\beta + x \eta ))) ((2 x (\alpha - x (\beta \nonumber \\&\quad + x \eta ))- \,4 x (1 - x \alpha + x^2 \beta ) \kappa + (s(-2 \alpha \nonumber \\&\quad + x (6 \beta + 10 x \eta - \kappa ) + x^2 (\alpha - x \beta ) \kappa ))(1 \nonumber \\&\quad + x (-\alpha + x (\beta + x \eta )))^{-1}+ (256 \pi ^2 w)((1 + x (-\alpha \nonumber \\&\quad + x (\beta + x \eta ))) (2 \alpha +x^2 (-\alpha + x \beta ) \kappa + x (-\beta \nonumber \\&\quad - 10 x \eta + \kappa )))^{-1})^2 + 64 \pi (2 \alpha - 4 x \beta - 6 x^2 \eta \nonumber \\&\quad - 4 \kappa + 8 x \alpha \kappa -12 x^2 \beta \kappa + (s (\alpha - x (2 \beta \nonumber \\&\quad + 3 x \eta )) (-2 \alpha +x (6 \beta + 10 x \eta - \kappa ) + x^2 (\alpha \nonumber \\&\quad - x \beta ) \kappa ))(1 + x (-\alpha + x (\beta + x \eta )))^{-2}\nonumber \\&\quad + (256 \pi ^2 w (\alpha - x (2 \beta + 3 x \eta )))\nonumber \\&\quad \times ((1 + x (-\alpha + x (\beta + \,x \eta )))^2\nonumber \\&\quad (2 \alpha + x^2 (-\alpha + x \beta ) \kappa + x (-6 \beta - 10 x \eta \nonumber \\&\quad + \kappa )))^{-1} + (s (20 x \eta - \kappa + 2 x \alpha \kappa \nonumber \\&\quad + \beta (6 - 3 x^2 \kappa )))\nonumber \\&\quad \times (1 + x (-\alpha + x (\beta + x \eta )))^{-1} - ( 256 \pi ^2 w (\kappa \nonumber \\&\quad + 3 \beta (-2 + x^2 \kappa ) - 2 x (10 \eta + \alpha \kappa )))((1 + x (-\alpha \nonumber \\&\quad + x (\beta + x \eta ))) (2 \alpha + x^2 (-\alpha + x \beta ) \kappa \nonumber \\&\quad + x (-6 \beta - 10 x \eta + \kappa ))^2)^{-1}))), \end{aligned}$$

(25d)

$$\begin{aligned} \Delta _{\textrm{III}}&=p_{t_{\textrm{III}}}-p_{r_{\textrm{III}}}, \end{aligned}$$

(25e)

where for simplicity we have set

$$\begin{aligned} G_{0}(x)= & {} \int _{4}^{10}{(2x(\alpha -x(\beta +x\eta ))-4x(1-x\alpha }\\{} & {} {+\,x^2\beta )\kappa +(s(-2\alpha +x(6\beta +10x\eta -\kappa )}\\{} & {} +\,{(x^2(\alpha -x\beta )\kappa ))(1+x(-\alpha +x(\beta }\\{} & {} {+\,x\eta )))^{-1}+(256\pi ^2w)((1+x(-\alpha }\\{} & {} {+\,x(\beta }+{x\eta )))^{-1}(2\alpha +x^2(-\alpha }+x\beta )\kappa \\{} & {} {+x(-6\beta -10x\eta }{+\,\kappa ))))^2(4096\pi ^2)^{-1}}\textrm{d}x. \end{aligned}$$

The mass of the stellar sphere in the envelope region is given in the form

$$\begin{aligned} \epsilon _{\textrm{III}}(r)= & {} 4\pi \int _{4}^{10}{r^2\rho _{\textrm{III}}\textrm{d}r}, \quad r^2=x \end{aligned}$$

$$\begin{aligned} \epsilon _{\textrm{III}}= & {} \int _{4}^{10}[x(-2\alpha +x(6\beta +10x\eta -\kappa )\nonumber \\{} & {} +\,x^2(\alpha -x(\beta +x\eta )))\kappa ][8x^{1/2}]^{-1}\textrm{d}x\nonumber \\= & {} \frac{1}{315} \kappa \left( 420\alpha -8(558\beta +2360\eta \right. \nonumber \\{} & {} -\,\left. 63\kappa )-25 \sqrt{10} (21 \alpha - 828 \beta \right. \nonumber \\{} & {} \left. -\, 8000 \eta + 63 \kappa )\right) . \end{aligned}$$

(26)

4 Matching of the layers

The matching of the radial pressure ($p_{r}$) and gravitational potentials ($\textrm{e}^{-2\lambda }, \textrm{e}^{-2\nu }$) at the interfaces are done to ensure continuity of the physical variables utilising the Darmois–Israel junction conditions. This is presented as follows:

(a) Continuity of region I–region II interface at $r=R_{\textrm{I}}$:

This is given by

$$\begin{aligned}{} & {} \textrm{e}^{-2\lambda _{\textrm{I}}}(R_{\textrm{I}})=\textrm{e}^{-2\lambda _{\textrm{II}}}(R_{\textrm{I}}), \end{aligned}$$

(27a)

$$\begin{aligned}{} & {} \textrm{e}^{2\nu _{\textrm{I}}}(R_{\textrm{I}})=\textrm{e}^{2\nu _{II}}(R_{\textrm{I}}), \end{aligned}$$

(27b)

$$\begin{aligned}{} & {} p_{r_{\textrm{I}}}(R_{\textrm{I}})=p_{r_{\textrm{II}}}(R_{\textrm{I}}). \end{aligned}$$

(27c)

It follows that

$$\begin{aligned} \mu \rho (R_{\textrm{I}})^{1+1/n}=d\rho {(R_{\textrm{I}})}-b. \end{aligned}$$

(28)

(b) Continuity of region II–region III interface at $r=R_{\textrm{II}}$:

This is given in the form

$$\begin{aligned}{} & {} \textrm{e}^{-2\lambda _{\textrm{II}}}(R_{\textrm{II}})=\textrm{e}^{-2\lambda _{\textrm{III}}}(R_{\textrm{II}}), \end{aligned}$$

(29a)

$$\begin{aligned}{} & {} \textrm{e}^{2\nu _{\textrm{II}}}(R_{\textrm{II}})=\textrm{e}^{2\nu _{\textrm{III}}}(R_{\textrm{II}}), \end{aligned}$$

(29b)

$$\begin{aligned}{} & {} p_{r_{\textrm{II}}}(R_{\textrm{II}})=p_{r_{\textrm{III}}}(R_{\textrm{II}}). \end{aligned}$$

(29c)

It follows that

$$\begin{aligned} d\rho {(R_{\textrm{I}})}-b=s\rho (R_{\textrm{II}})-\frac{w}{\rho (R_{\textrm{II}})}. \end{aligned}$$

(30)

(c) Continuity of region III–boundary interface:

The interior line element (1) is matched to the Schwarzschild exterior line element (2) at the surface boundary $r=R_{\textrm{III}}$.

$$\begin{aligned} \textrm{d}s^{2}|_{\textrm{III}}= & {} -\,\left( \begin{array}{c} 1-\dfrac{2\epsilon }{R_{\textrm{III}}}+\dfrac{q^2}{R_{\textrm{III}}^2}\end{array}\right) \textrm{d}t^{2}\nonumber \\ {}{} & {} +\left( \begin{array}{c} 1-\dfrac{2\epsilon }{R_{\textrm{III}}}+\dfrac{q^2}{R_{\textrm{III}}^2}\end{array}\right) ^{-1}\textrm{d}r^{2}\nonumber \\{} & {} +\,r^2(\textrm{d}\theta ^2+\sin ^2\theta \textrm{d}\phi ^2). \end{aligned}$$

(31)

The continuity of $\textrm{e}^{-2\lambda }$ and $\textrm{e}^{-2\nu }$ via the surface is called the first fundamental form of the Dormois–Israel junction condition $[\textrm{d}s^2]_{\Sigma }=0$, producing

$$\begin{aligned} \textrm{e}^{2\lambda _{\textrm{III}}}(R_{\textrm{III}})= & {} \left( \begin{array}{c}1-\dfrac{2\epsilon }{R_{\textrm{III}}}+\dfrac{q^2}{R^2_{\textrm{III}}}\end{array}\right) ^{-1}, \end{aligned}$$

(32a)

$$\begin{aligned} \textrm{e}^{2\nu _{\textrm{III}}}(R_{\textrm{III}})= & {} \left( \begin{array}{c}1-\dfrac{2\epsilon }{R_{\textrm{III}}}+\dfrac{q^2}{R^2_{\textrm{III}}}\end{array}\right) , \end{aligned}$$

(32b)

$$\begin{aligned} p_{r_{\textrm{III}}}(R_{\textrm{III}})= & {} 0. \end{aligned}$$

(32c)

The radial pressure vanishes at the boundary. Equation (32c) represents the second fundamental form $[G_{\delta \psi }x^{\psi }]_{\Sigma }=0$ where $x^{\psi }$ stands for unit vector following the radial direction. These give the conditions

$$\begin{aligned}{} & {} (1-\alpha R_{\textrm{III}}+\beta R_{\textrm{III}}^2+\eta R_{\textrm{III}}^3)=F_{1}(x), \end{aligned}$$

(33a)

$$\begin{aligned}{} & {} A^2 [\exp (G_{0}(x))]^2=F_{2}(x), \end{aligned}$$

(33b)

$$\begin{aligned}{} & {} sN_{1}(x)-w(N_{1}(x))^{-1}=0, \end{aligned}$$

(33c)

where for simplicity we have set

$$\begin{aligned} F_{1}(x)= & {} (1+(2N_{0}(x))(R_{\textrm{III}})^{-1}+(\kappa x(1-\alpha R_{\textrm{III}}\\{} & {} +\,\beta R_{\textrm{III}}^2+\eta R_{\textrm{III}}^3))(R_{\textrm{III}}^3)^{-1})^{-1},\\ F_{2}(x)= & {} (1+(2N_{0}(x))(R_{\textrm{III}})^{-1}+(\kappa x(1-\alpha R_{\textrm{III}}\\{} & {} +\,\beta R_{\textrm{III}}^2+\eta R_{\textrm{III}}^3))(R_{\textrm{III}}^3)^{-1}),\\ N_{0}(x)= & {} (-x^2(-15\alpha (-4+x^2\kappa )-2x (60\beta -75x\eta \\{} & {} +\,10\kappa +6x^2\beta +5x^3\eta \kappa )))(240)^{-1},\\ N_{1}(x)= & {} [-2\alpha +x(6\beta +10x\eta -\kappa )+x^2(\alpha -x(\beta \\{} & {} +\,x\eta ))\kappa ][16\pi ]^{-1}. \end{aligned}$$

We observe from systems (27)–(33) that there are sufficient number of free parameters $\alpha$, $\beta$, $\mu$, $\kappa$, $\eta$, $\epsilon$, b, d, n, q, s, w, A, $R_{\textrm{I}}$, $R_{\textrm{II}}$, $R_{\textrm{III}}$, yielding an undetermined number of equations. This indicates that the matching conditions have a real solution.

5 Conditions for a well-behaved model

The interior matter variables and other physical features should meet the following physical conditions:

• (i) The energy density, radial and tangential pressures should be non-negative, continuous, regular and finite throughout the interior.

• (ii) The metric functions $\textrm{e}^{2\lambda }$ and $\textrm{e}^{2\nu }$ should be positive and continuous.

• (iii) The radial sound speed should be less than the speed of light so as to satisfy the causality criterion $\dfrac{\textrm{d}p_{r}}{\textrm{d}\rho }<1$. In our model, these criteria in each region are given by

  $$\begin{aligned} \nu _{\textrm{I}}= & {} (\mu (1+n)(16\pi )^{-1/n}(-2\alpha +x(6\beta \nonumber \\{} & {} +\,10x\eta -\kappa )+x^2(\alpha -x(\beta \nonumber \\{} & {} +\,x\eta ))\kappa )^{1/n})/n, \end{aligned}$$

  (34a)
  $$\begin{aligned} \nu _{\textrm{II}}= & {} d, \end{aligned}$$

  (34b)
  $$\begin{aligned} \nu _{\textrm{III}}= & {} s+(256\pi ^2w)(-2\alpha +x(6\beta \nonumber \\{} & {} +\,10x\eta -\kappa )+x^2(\alpha -x(\beta \nonumber \\{} & {} +\,x\eta ))\kappa )^{-2}. \end{aligned}$$

  (34c)

• (iv) The energy conditions should be continuous, greater or equal to zero to satisfy the strong energy condition (SEC), the weak energy condition (WEC) and the null energy condition (NEC), i.e., SEC: $\rho -p_{r}-2p_{t}\ge 0$, WEC: $\rho -3p_{t}\ge 0$, $\rho -3p_{r}\ge 0$, NEC: $\rho -p_{r}\ge 0$, $\rho -p_{t}\ge 0$.

• (v) The stellar model should satisfy the stability condition

  $$\begin{aligned}{} & {} \Gamma =\dfrac{\rho +p_{r}}{p_{r}}\dfrac{\textrm{d}p_{r}}{\textrm{d}\rho } \ge \dfrac{4}{3}. \end{aligned}$$

  In our model, the condition in each layer is given by

  $$\begin{aligned} \Gamma _{\textrm{I}}= & {} ((1+n)(1+\mu (16\pi )^{-1/n}(-2\alpha \nonumber \\{} & {} +\,x(6\beta +10x\eta -\kappa )+x^2(\alpha \nonumber \\{} & {} -\,x(\beta +x\eta ))\kappa )^{1/n}))/n, \end{aligned}$$

  (35)
  $$\begin{aligned} \Gamma _{\textrm{II}}= & {} 1+d-(16b\pi )(16b\pi +2d(\alpha \nonumber \\{} & {} -\,3x\beta -5x^2\eta )+dx(1+x(-\alpha \nonumber \\{} & {} +\,x(\beta +x\eta )))\kappa )^{-1},\end{aligned}$$

  (36)
  $$\begin{aligned} \Gamma _{\textrm{III}}= & {} ((s +(256\pi ^2 w)(-2 \alpha + x (6 \beta \nonumber \\{} & {} +\, 10 x \eta - \kappa ) + x^2 (\alpha - x (\beta \nonumber \\{} & {} +\, x \eta )) \kappa )^{-2}) (-256 \pi ^2 w + (1 + s) \nonumber \\{} & {} \times \,(-2 \alpha + x (6 \beta + 10 x \eta - \kappa )+ x^2 (\alpha \nonumber \\{} & {} - \,x (\beta + x \eta )) \kappa )^2))(16 \pi (-2 \alpha + x (6 \beta \nonumber \\{} & {} +\, 10 x \eta - \kappa )+ x^2 (\alpha - x (\beta + x \eta )) \kappa ) \nonumber \\{} & {} \times \,(-((16 \pi w)(-2 \alpha + x (6 \beta + 10 x \eta \nonumber \\{} & {} -\, \kappa ) + x^2 (\alpha - x (\beta + x \eta )) \kappa )^{-1})\nonumber \\{} & {} + \,(s (-2 \alpha + x (6 \beta + 10 x \eta - \kappa ) \nonumber \\{} & {} +\, x^2 (\alpha - x (\beta + x \eta )) \kappa ))\nonumber \\{} & {} \times \,(16\pi )^{-1}))^{-1}. \end{aligned}$$

  (37)

• (vi) It has been pointed out by researchers that the surface red-shift of the stellar sphere must not exceed 5.211 for anisotropic fluids in general relativity (Ivanov [52, 53]; Baraco and Hamity [54]). The formula for the surface red-shift is written as

  $$\begin{aligned}{} & {} z_{s}=\dfrac{1}{\sqrt{1-\dfrac{2\epsilon (r)}{r}}}-1, \end{aligned}$$

  (38)

  where $\epsilon (x)$ defines the total mass. In our model we obtain the red-shift as

  $$\begin{aligned} z_{s}= & {} -1+(1-(8c_{1}\pi )x{-1}+1/30\pi ^2x(60\alpha \nonumber \\{} & {} -\,30x(4\beta +5x\eta )+x(20+x(-15\alpha \nonumber \\{} & {} +\,2x(6\beta +5x\eta )))\kappa ))^{-1/2}. \end{aligned}$$

  (39)

• (vii) The compactification factor for the stellar object has been discussed by Jasim et al [4, 56]. This factor in general relativity is determined by the mass-radius ratio given in the form

  $$\begin{aligned}{} & {} \Omega (r)=\dfrac{2\epsilon (r)}{r}. \end{aligned}$$

  In our study, we obtain

  $$\begin{aligned} \Omega (x)= & {} (8c_{1}\pi )x^{-1}+1/30\pi ^2x(30x(4\beta +5x\eta )\nonumber \\{} & {} -\,2x(10+6x^2\beta +5x^3\eta )\kappa \nonumber \\{} & {} +\,15\alpha (-4+x^2\kappa )). \end{aligned}$$

  (40)

• (viii) Study of the interior equilibrium forces is examined by utilising the Tolman– Oppenheimer–Volkoff equation (TOV). For an electrically charged object, we infer four interior forces: gravitational force ($F_{g}$), anisotropic force ($F_{a}$), hydrostatic force ($F_{h}$) and electromagnetic force ($F_{e}$). The resultant of the equilibrium forces must be zero: $F_{g} +F_{a} + F_{h} + F_{e}=0$. This equation is satisfied in the model of Jape et al [13], Lighuda et al [15], Mathias et al [18], Maurya and Ortiz [55] and Jasim et al [56]. The TOV equation is presented in the form

  $$\begin{aligned} 0= & {} -\,\dfrac{\nu ^{\prime }}{2}(\rho +p_{r})-\dfrac{\textrm{d}p_{r}}{\textrm{d}r} +\dfrac{2}{r}(p_{t}-p_{r})\nonumber \\{} & {} +\,\sigma E \textrm{e}^{-2\lambda }. \end{aligned}$$

  (41)

  In our study, we find that

  $$\begin{aligned} F_{g}= & {} -\,\dfrac{\nu ^{\prime }}{2}(\rho +p_{r}),\end{aligned}$$

  (42)
  $$\begin{aligned} F_{h}= & {} -\,\dfrac{\textrm{d}p_{r}}{\textrm{d}r}\nonumber \\= & {} (1 + 1/n) (16 \pi )^{(-1 - 1/n)} (6 \beta + 20 x \eta \nonumber \\{} & {} -\, \kappa + x^2 (-\beta - 2 x \eta ) \kappa + 2 x (\alpha - x (\beta \nonumber \\{} & {} +\, x \eta )) \kappa ) (-2 \alpha + x (6 \beta + 10 x \eta - \kappa )\nonumber \\{} & {} +\, x^2 (\alpha - x (\beta + x \eta )) \kappa )^{(1/n)} \mu ,\end{aligned}$$

  (43)
  $$\begin{aligned} F_{a}= & {} \dfrac{2}{r}(p_{t}-p_{r})=\dfrac{2}{r}\Delta ,\end{aligned}$$

  (44)
  $$\begin{aligned} F_{e}= & {} \sigma E e^{-2\lambda }\nonumber \\= & {} 2 (2 - 3 x \alpha + 4 x^2 \beta + 5 x^3 \eta ) (1 \nonumber \\{} & {} +\,x (-\alpha + x (\beta + x \eta )))^2 \sqrt{x \kappa }. \end{aligned}$$

  (45)

Fig. 1

Energy density vs. radial distance r.

Fig. 2

Radial pressure vs. radial distance r.

6 Discussion

In this section, we discuss the behaviour of the geometrical variables and the matter variables, and other physical conditions. We use the Python programming language. In our model we plot graphs for the energy density (figure 1), the radial pressure (figure 2), the tangential pressure (figure 3), the gravitational potentials (figure 4), mass (figure 5), the energy conditions (figures 6–10), the measure of anisotropy (figure 11), adiabatic index (figure 12), radial sound speed (figure 13), charge density (figure 14), electric field (figure 15), mass–radius ratio (figure 16), surface red-shift (figure 17) and equilibrium forces (figure 18). The graphs were generated by utilising the following values of the constants: $A=0.05, b=0.0005, d=\pm 12.4, n=1, s=0.00042, w=\pm 655, \alpha =\pm 183, \beta =\pm 0.5, \eta =3 \times 10^{-6}, \mu =1.8$ and $\kappa =\pm 5 \times 10^{-5}$. All graphs for the radial coordinate r use the domain of radius r, as in Pant et al [3] and Lighuda et al [15, 49].

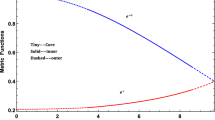
We observe in figures 1 and 2 that the energy density and the radial pressure are continuous, and monotonically decreasing functions away from the centre. In figure 3, the tangential pressure shows an increasing behaviour from the centre towards the surface. Figure 4 indicates that the metric function e$^{-2\lambda }$ is an increasing function and e$^{2\nu }$ is a decreasing function. It is interesting to see that the metric functions merge at the boundary of the star. We observe from figure 5 that the mass function is a monotonically increasing function with the radial distance r. Figures 6–10 show that the energy conditions are positive and monotonically increasing towards the surface. The measure of anisotropy in figure 11 is a continuous and positive increasing function. This implies that the tangential pressure may be greater than the radial pressure and the star experiences repulsive force. We observe in figure 12 that the adiabatic index obtained satisfies stability criteria in the interior of the stellar sphere $( \Gamma \ge 4/3 )$. In our study, the minimum adiabatic index at $x=0$ is $\Gamma _{0}=6.7245$, verifying that the object is stable from gravitational instabilities. Figure 13 indicates that the speed of sound is less than the speed of light. It is found to be in the range $0.00188 \le \nu \le 0.55418$. Figures 14 and 15 illustrate that the charge density and electric field are monotonically increasing functions. In figure 16, we demonstrate the behaviour of the mass–radius ratio as an increasing function, reaching the maximum value $\Omega (x)=0.251$ which is consistent for an utradense compact star. In figure 17 we see that the surface red-shift is a continuous, monotonically increasing function with radial coordinate (r), reaching the maximum point at $z_{s}=1.97856$ which is consistent with the astrophysical objects. In figure 18, we observe that all equilibrium forces are balanced in the stellar interior.

Fig. 3

Tangential pressure vs. radial distance r.

Fig. 4

Gravitational potential vs. radial distance r.

Fig. 5

Mass vs. radial distance r.

Fig. 6

Energy conditions vs. radial distance r.

Fig. 7

Energy conditions vs. radial distance r.

Fig. 8

Energy conditions vs. radial distance r.

Fig. 9

Energy conditions vs. radial distance r.

Fig. 10

Energy conditions vs. radial distance r.

Fig. 11

Measure of anisotropy vs. radial distance r.

Fig. 12

Adiabatic index vs. radial distance r.

Fig. 13

Radial sound speed vs. radial distance r.

Fig. 14

Charge density vs. radial distance r.

Fig. 15

Electric field vs. radial distance r.

Fig. 16

Mass–radius ratio vs. radial distance r.

Fig. 17

Surface red-shift vs. radial distance r.

Fig. 18

Equilibrium forces vs. radial distance r.

In our model we presented the geometrical features for the gravitational potentials and matter variables. We are pleased to note that the profile of the features in our model are also similar to the works of Pant et al [3, 42], Jasim et al [4, 56], Mardan et al [5], Das et al [6], Jape et al [13], Lighuda et al [15, 49], Sunzu and Danford [17], Mathias et al [18], Maharaj et al [21], Mafa Takisa and Maharaj [27], Bhar et al [35], Gedela et al [43], Bisht et al [48], Thirukkanesh and Ragel [57], Ngubelanga and Maharaj [58], Murad [59], Maharaj and Mafa Takisa [60], Maurya et al [61], and Fulara and Sah [62].

7 Conclusion

In this article, we have developed a new class of exact solutions utilising the Einstein–Maxwell field equations. We constructed a stellar model comprising three interior layers: the core layer with polytropic EoS, the intermediate layer which satisfies a linear EoS and the envelope layer described by a Chaplygin EoS. In our study, we have chosen the electric field and one of the metric functions. Our model comprises a new feature, a third layer with gaseous matter which is absent in Mardan et al [5]. The physical analysis demonstrates that the metric functions, matter variables and other physical conditions are relevant and compatible with the study of astrophysical objects. The physical discussion reveals that our model is well behaved. The results found in this paper are required to investigate the physical structures, features and properties of charged anisotropic superdense stellar objects with three layers in general relativity. For future work, the approach of three interior layers can be extended to include layers with different equations of state for each layer to obtain a deeper understanding of gravitational interactions for a star with composite matter distributions.