1 Introduction

The theory of thermoelasticity is well established [1]. To explain and remove the paradox of infinite velocity of heat propagation, Lord and Shulman [2], Green and Lindsay [3], Green and Naghdi (GN) [4,5,6], and many more have derived and formulated generalized theories of thermoelasticity. Later, to incorporate the effects of microscopic interactions in the fast-transient process of heat transport mechanism in a macroscopic, Tzou [7] and Chandrasekharaiah [8] introduced a dual-phase-lag (DPL) heat conduction model. Recently, Roychoudhuri [9] introduced another model of generalized thermoelasticity theory with three-phase-lag. All these models predict the finite speed of propagation of the elastic as well as the thermal waves. In several research works [10,11,12,13,14,15,16,17], the generalized thermoelasticity theory was used to investigate the coupled generalized thermoelastic problems.

Scott Blair’s model [18], which is basically a material model, includes a formula for memory phenomena in various disciplines. The model takes the form

$$\begin{aligned} {^0{\mathcal {D}}}_t^\alpha \epsilon (t)=\kappa \sigma (t), \end{aligned}$$
(1)

where \({^0{\mathcal {D}}}_t^\alpha \epsilon (t)\) denotes the fractional-order derivative which depends on the strain history from 0 to t. For integral value of \(\alpha =n\), \({^0{\mathcal {D}}}_t^\alpha \epsilon (t)={\mathrm{d}}^n\epsilon (t)/{\mathrm{d}}t^n\), \(\kappa (>0)\) is a constant and \(\sigma\) is the stress.

A fractional-order derivative is a generalization of an integer order derivative and integral. It originated from a letter of L’Hopital to Leibnitz in 1695 regarding the meaning of the half-order derivative. It is a promising tool for describing memory phenomena [19]. The kernel function of a fractional derivative is termed the memory function, but it does not replicate any physical process. Imprecise physical meaning has been a big obstacle that keeps fractional derivatives lagging far behind the integer-order calculus. There are several definitions of a fractional derivative. The Riemann–Liouville [18] derivative is one of the most standard definitions

$$\begin{aligned} {^0{\mathcal {D}}}_t^\alpha \epsilon (t)=\frac{1}{\Gamma (n-\alpha )}\frac{\mathrm{d}^n}{\mathrm{d}t^n}\int _0^t\frac{\epsilon (s)}{(t-s)^{1+\alpha -n}}\mathrm{d}s,\quad m-1\le \alpha <m, \end{aligned}$$

where \(\Gamma (\cdot )\) is the Euler’s gamma function and m is an integer. A memory process generally consists of two stages: the first is short, with permanent retention at the beginning, and it cannot be neglected in general, and the second is governed by the fractional model Eq. (1). The critical point between the fresh stage and the working stage is usually not the origin. This is quite different from the traditional fractional models of one stage. The key point is that the order of a fractional derivative is an index of memory. The dimensionless form of the solution of Eq. (1) is

$$\begin{aligned} E(\eta )=\eta ^\alpha -(\eta -1)^\alpha , \end{aligned}$$
(2)

where \(\eta =t/t_M\) and \(E(\eta )=\epsilon (t)/\epsilon _M\), where \(\epsilon _M\) is the strain at the end of time of creeping \(t=t_M\). Equation (2) reveals that \(E(\eta )\) increases with an increase in \(\alpha\). The higher the value of the index \(\alpha\), the slower is the forgetting during the process. In particular, at \(\alpha =0,~E=0\), meaning that ‘nothing is memorized’, and \(E=1\) for \(\alpha =1\) which means that ‘nothing is forgotten’. Therefore, the fractional order \(\alpha\) is basically termed as the index of the memory effect.

For a standard creep and recovery process, the specimen is usually loaded under a constant stress \(\sigma (t)=\sigma _0\) from 0 to \(t_M\), and the load is removed at the instant \(t=t_M\), then \(\sigma (t)=0\) for \(t\ge t_M\). If H(t) is the Heaviside function, Eq. (1) takes the following form:

$$\begin{aligned} {^0{\mathcal {D}}}_t^\alpha \epsilon (t)=\kappa \sigma _0\left( H(t)-H(t-t_M)\right) , \end{aligned}$$
(3)

where \({^0{\mathcal {D}}}_t^\alpha \epsilon (t)\) is the Riemann–Liouville fractional-order derivative with zero initial condition. The superposition method gives the solution of Eq. (3) as follows:

$$\begin{aligned} \epsilon (t)=\frac{\kappa \sigma _0}{\Gamma (1+\alpha )}\left[ t^\alpha H(t)-(t-t_M)^\alpha H(t-t_M)\right] . \end{aligned}$$

This is in agreement with the early observation of the behavior of some viscoelastic materials. Equation (1) works not only in modeling viscoelastic materials, but also in modeling biological kinetics with memory.

During recent years, fractional calculus has also been introduced in the field of thermoelasticity. Povstenko [20] has constructed the theory of thermoelasticity based on the space-time-fractional heat conduction equation. Sherief et al. [21] formulated a model in generalized thermoelasticity. Another theory of fractional order generalized thermoelasticity was proposed by Youssef [22]. Yu et al. [23] studied fractional order generalized electro-magneto-thermo-elasticity problem.

Memory-dependent derivatives (MDDs) were first introduced by Wang and Li [24]. They proposed a fractional derivative with arbitrary kernel \(K(t-\xi )\) (can be chosen freely) over a slipping interval \([t-\tau , t]\) as follows:

$$\begin{aligned} {\mathcal {D}}^{(1)}_\tau f(t)=\frac{1}{\tau } \int_{t-\tau }^t K(t-\xi ) f'(\xi ) {\mathrm{d}}\xi , \end{aligned}$$
(4)

where \(\tau ~(>0)\) is called the delay time, which can be chosen freely. The kernel function \(K(t\cdot \xi )\) must be a differentiable function with respect to its arguments. The kernel function and the memory scales must be chosen in such a way that they are compatible with the physical problem, so this type of derivative provides more possibilities to capture the material response. Generally, the memory effect needs weight \(0\le K(t-\xi ) \le 1\) for \(\xi \in [t -\tau , t]\) so that the magnitude of \(D_\tau f(t)\) is usually smaller than that of the common derivative \(f'(t)\). As \(\xi \in [t -\tau , t]\), one can easily understand that the function \(f(\xi )\) takes value from different points on the time interval \([t -\tau , t]\). Considering our present time as t, we can say \([t -\tau , t)\) is the past time interval. Thus we conclude the main feature of MDD that is the functional value in real time depends on the past time also. That is why \(D_\tau\) is called the non-local operator whereas integer order derivative or integration) is a local operator (i.e., it does not depend on the past time). The kernel function \(K(t- \xi )\) can be chosen freely, such as \(1, [1-(t-\xi )], [1-(t-\xi )/\tau ]^p\) for any positive real number p which may be more practical. They are a monotonic increasing function from 0 to 1 in the interval \([t -\tau , t]\). According to the nature of the problem, one can select a suitable kernel function of his/her choice. The preceding modifications of fractional-ordered derivatives are termed memory-dependent derivatives.

Yu et al. [25] introduced memory-dependent derivatives in the Fourier’s law of heat conduction in the following way:

$$\begin{aligned} \left( 1+ \tau {\mathcal {D}}_a\right) q_i= -K_T\varTheta _{,i}, \end{aligned}$$

where \(D_a f(t)=D^{(1)}_a f(t)\), \(q_i\) are the heat flux components, \(\varTheta =T-T_0\) is the temperature increment above the uniform reference temperature \(T_0\) of the medium, T is the absolute temperature of the medium and \(K_T\) is the thermal conductivity. This new generalization of hyperbolic-type heat conduction models is accepted as the modified heat conduction law with measuring memory. Later, Ezzat et al. [26, 27] introduced the first order MDD, instead of fractional calculus, into the rate of heat flux in Lord–Shulman theory [2] of generalized thermoelasticity to denote memory-dependence as:

$$\begin{aligned} \left( 1+\tau _0 {\mathcal {D}}_{\tau _0}\right) q_i= -K_T\varTheta _{,i}, \end{aligned}$$

where \(\tau _0\) is introduced as the time delay parameter. The above equation provides the following advantages compared with the aforementioned amendments of Fourier’s law by using fractional derivatives: (1) the influence of memory dependency claims it’s superiority in terms of memory scale parameter; (2) in a limiting sense, this simplification develops the Lord–Shulman model of generalized thermoelasticity; and (3) because the kernel function and the memory scale parameters may be chosen subjectively, it is more malleable in many practical applications. Some applications of MDDs model in generalized thermoelasticity can be found in the literature [24,25,26,27,28,29,30,31,32].

Wave propagation and wave reflection phenomena are applicable in various fields like geophysical exploration, mineral and oil exploration, seismology, etc. The body wave propagation in thermoelastic solids is applicable in various fields of engineering. Several problems on plane harmonic wave propagation in coupled and generalized thermoelasticities have been investigated by many authors during the last five decades. Some of the notable among them are found in the literature [33,34,35,36,37,38,39,40,41,42,43]. In this paper, a two-dimensional generalized thermoelastic model of the problem of reflection of plane waves on a stress-free thermally insulated half-space of thermally conducting isotropic homogeneous elastic material has been considered based on the Lord–Shulman model under the heat transfer with MDD [27]. The case of total reflection is taken into account to calculate the critical angle. Phase velocities and the corresponding attenuation factors of the coupled dilatational elastic-thermal waves and the reflection coefficients have been calculated and illustrated graphically for copper-like material and highlight the effect of various parameters of interest.

2 Basic governing equations and formulation of the problem

We consider a homogeneous, isotropic and thermally conducting elastic half-space defined by:

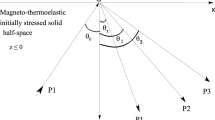
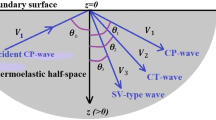
$$\begin{aligned} M=\left\{ (x,y,z);-\infty<x, y<\infty ,~0\le z<\infty \right\} , \end{aligned}$$

at an uniform reference temperature \(T_0\) in the undisturbed state and discuss the thermoelastic plane wave motion of small amplitude. Let the origin O of a fixed rectangular Cartesian coordinate system Oxyz be fixed at a point on the plane boundary \(z=0\) with z-axis pointing vertically downward into M and x-axis is directed along the horizontal direction (see Fig. 1). The y-axis is taken in the direction of the line of intersection of the plane wavefront with the plane surface. The boundary surface \(z=0\) is assumed to be thermally insulated and free from the mechanical stresses.

Fig. 1
figure 1

Schematic of the present problem: incident and reflected thermoelastic waves at the surface \(z=0\)

Full size image

If we restrict our analysis to a plane strain problem parallel to the xz-plane with the displacement vector \(\vec {u}(x,z,t)=(u,0,w)\) and the temperature change \(\varTheta (x,z,t)\), then the fundamental equations of motion, heat conduction equation and the stress–strain–temperature relation in the absence of body force and the heat source in generalized thermoelasticity with memory-dependent heat transfer as developed by Ezzat et al. [26, 27] can be written in vector form as

$$\begin{aligned} \mu \nabla ^2\vec {u}+(\lambda +\mu )\vec {\nabla }\vec {\nabla }\cdot \vec {u}-\gamma \vec {\nabla }\varTheta =\rho \ddot{\vec {u}}, \end{aligned}$$
(5)
$$\begin{aligned} K_T\nabla ^2\varTheta =\frac{\partial }{\partial t}\left( 1+\tau {\mathcal {D}}_\tau \right) \left( \rho C_E\varTheta +\gamma T_0\vec {\nabla }\cdot \vec {u}\right) , \end{aligned}$$
(6)
$$\begin{aligned} \vec {\sigma }=\lambda \vec {\nabla }\cdot \vec {u}\vec {I}+\mu \left[ {\nabla }\vec {u}+{\nabla }\vec {u}^T\right] -\gamma \varTheta \vec {I}, \end{aligned}$$
(7)

where \(\nabla ^2\equiv (\partial ^2/\partial x^2+\partial ^2/\partial z^2)\), \(\lambda ,~\mu\) are Lame’s constants, \(\gamma =(3\lambda +2\mu )\alpha _T\) is the thermoelastic coupling parameter, \(\alpha _T\) is the coefficient of linear thermal expansion, \(\rho\) is the mass density, \(C_E\) is the specific heat at constant strain, \(\vec {\sigma }\) is the stress tensor, and \(\vec {I}\) is the identity tensor of order 3. All the considered physical quantities are assumed to be bounded as \(x\rightarrow \infty\). The comma notation is used for the spatial derivatives, and the superposed dot represents a time differentiation.

In our present study, we shall deal with the following kernel function in the definition (4):

$$\begin{aligned} K(t-\xi )=A+B(t-\xi )=\left\{ \begin{array}{ll} \frac{1}{2} &{}\quad \text{ if }\,\,A=\frac{1}{2},~B=0,\\ \frac{1}{2}-\left( \frac{t-\xi }{\tau }\right) &{}\quad \text{ if }\,\,A=\frac{1}{2}, B=-\frac{1}{\tau },\\ 1-(t-\xi ) &{}\quad \text{ if }\,\,A=1,~B=-1, \end{array}\right. \end{aligned}$$
(8)

where A and B are constants.

Equations (5) and (6) together represent a fully hyperbolic system that permits finite speed for both the elastic and the thermal disturbances. We now define the following dimensionless quantities

$$\begin{aligned}&(x',z')=\frac{\omega ^*}{C_L}(x,z),~(u',w')=\frac{\rho \omega ^*C_L}{\gamma T_0}(u,w),~t'=\omega ^* t,\\&\varTheta '=\frac{\varTheta }{T_0},~\tau _{ij}'=\frac{\tau _{ij}}{\gamma T_0}, \end{aligned}$$

where \(C_L^2=(\lambda +2\mu )/\rho\) is the speed of the classical P-wave and \(\omega ^*=C_E(\lambda +2\mu )/K_T\) is the characteristic frequency. Upon using the above quantities into Eqs. (5)–(7), we have (suppressing the primes for convenience)

$$\begin{aligned} \beta ^2\nabla ^2\vec {u}+(1-\beta ^2)\vec {\nabla }\vec {\nabla }\cdot \vec {u}-\vec {\nabla \varTheta }=\ddot{\vec {u}}, \end{aligned}$$
(9)
$$\begin{aligned} \nabla ^2\varTheta =\frac{\partial }{\partial t}\left( 1+\tau {\mathcal {D}}_\tau \right) \left( \varTheta +{\varepsilon }\vec {\nabla }\cdot \vec {u}\right) , \end{aligned}$$
(10)
$$\begin{aligned} \vec {\sigma }=(1-2\beta ^2)\vec {\nabla }\cdot \vec {u}\vec {I}+\beta ^2\left[ {\nabla }\vec {u}+{\nabla }\vec {u}^T\right] -\varTheta \vec {I}, \end{aligned}$$
(11)

where \(\beta ^2=\mu /(\lambda +2\mu )\) is the ratio of the classical SV-wave speed to the classical P-wave speed and \(\varepsilon =\gamma ^2T_0/[\rho C_E(\lambda +2\mu )]\) is the dimensionless thermoelastic coupling constant. Introducing the displacement potentials \(\phi\) (corresponds to dilatational wave) and \(\psi\) (corresponds to shear wave) through the Helmholtz vector representation,

$$\begin{aligned} u=\vec {\nabla }\phi +\vec {\nabla }\times \vec {\psi },\quad \vec {\nabla }\cdot \vec {\psi }=0, \end{aligned}$$
(12)

into Eqs. (9)–(11), we can write

$$\begin{aligned} \nabla ^2\phi -\ddot{\phi }-\varTheta =0, \end{aligned}$$
(13)
$$\begin{aligned} \beta ^2\nabla ^2{\vec \psi }-\ddot{\vec \psi }=0, \end{aligned}$$
(14)
$$\begin{aligned} \nabla ^2\varTheta -\left( 1+\tau D_\tau \right) \dot{\varTheta }=\varepsilon \left( 1+\tau D_\tau \right) \nabla ^2\dot{\phi }. \end{aligned}$$
(15)

Equations (13) and (15) reveal that the thermal field \(\varTheta\) is coupled with the potential \(\phi\) only and so creates two coupled longitudinal waves, namely a coupled dilatational elastic wave (CP-wave) and a coupled thermal wave (CT-wave). Eliminating \(\varTheta\) between Eqs. (13) and (15), we arrive at

$$\begin{aligned} \nabla ^4\phi -\left[ (1+\varepsilon )\left( 1+\tau D_\tau \right) \nabla ^2\dot{\phi }+\nabla ^2\ddot{\phi }\right] +\left( 1+\tau D_\tau \right) \dddot{\phi }=0. \end{aligned}$$
(16)

Considering (12), we may choose \({\vec \psi }=(0,\psi ,0)\), and hence Eq. (14) takes the form

$$\begin{aligned} \beta ^2\nabla ^2\psi =\ddot{\psi }. \end{aligned}$$
(17)

Thus, the potential \(\psi\) corresponds to the displacement motion in the xz-plane due to a SV-type wave.

3 Dispersion equation and its solutions

For a harmonic plane wave propagating in the direction where the wave normal vector lies in the xz-plane making an angle \(\theta _0\) with the positive z-axis, the solutions of Eqs. (16) and (17) may be assumed as

$$\begin{aligned} (\phi , \psi )=(\phi ^0, \psi ^0)\exp \{\iota k(x\sin \theta _0-z\cos \theta _0)-\iota \omega t\}, \end{aligned}$$
(18)

where \(\phi ^0,~\psi ^0\) are the constants (possibly complex) representing the coefficients of the wave amplitudes, \(\iota =\sqrt{-1}\), k is the dimensionless wavenumber (possibly complex) to be determined, and \(\omega\) is the dimensionless assigned real angular frequency. If we set \(k=\mathfrak {R}(k)+\iota \mathfrak {I}(k)\), (where \(\mathfrak {R}(\cdot )\) and \(\mathfrak {I}(\cdot )\) denote the real and imaginary parts of a complex number, respectively), it may be verified that for the waves to be physically realistic, we should have \(\mathfrak {R}(k)>0\) and \(\mathfrak {I}(k)\ge 0\) and that only the real parts of the solution (18) are physically relevant [43]. Also note that x and z in (18) are both non-negative (\(x,z\ge 0\)). Then on the surface \(z=0\), the term \(\exp [-x\mathfrak {I}(k)\sin \theta _0]\rightarrow 0\) as \(x\rightarrow +\infty\) which in turn means that the energy represented by the wave solutions (18) is bounded (Billingham and King [44]). Further, the solution (18) corresponds to waves for which \(\omega /\mathfrak {R}(k)\) is the phase speed and \(\mathfrak {I}(k)\) is the decay (attenuation) coefficient.

Substituting Eq. (18) into Eqs. (16) and (17), we get

$$\begin{aligned} k^4-L_1k^2+L_2=0, \end{aligned}$$
(19)
$$\begin{aligned} \beta ^2k^2-\omega ^2=0, \end{aligned}$$
(20)

where \(L_1=\iota \omega (1+G)(1+\varepsilon )+\omega ^2,~L_2=i\omega ^3(1+G),~ G\equiv G(\tau ,\omega )=(A\omega +\iota B)[1-\exp (\iota \tau \omega )]/\omega -B\tau \exp (\iota \tau \omega ).\)

The quadratic Eq. (19) in \(k^2\) is the general dispersion relation for the wave propagation in generalized thermoelasticity with MDD. Clearly, the coefficients \(L_1\) and \(L_2\) are complex for \(\omega >0\). Hence the roots of Eq. (19) are complex in general.

We now seek the perturbation solutions of the dispersion relation (19). The perturbation method was widely used to study the wave propagation problems in classical (coupled) and non-classical (generalized) thermoelastic continua. Here, our aim is to derive the perturbation solution for the roots of the dispersion relation (19). Following Sharma et al. [36], the dispersion relation (19) can be expressed as

$$\begin{aligned} f(k^2)-\varepsilon g(k^2)=0, \end{aligned}$$
(21)

where \(f(k^2)=k^4-k^2\left[ \iota \omega (1+G)+\omega ^2\right] +i\omega ^3(1+G),~~~g(k^2)=\iota \omega (1+G)k^2.\)

For most of the thermoelastic materials, \(\varepsilon \ll 1\) and therefore, we develop series expansions in terms of \(\varepsilon\) for the roots \(k_j^2~(j=1,2)\) in order to explore the effect of various interacting fields on the waves. Thus, for \(\varepsilon \ll 1\), we obtain the perturbation solutions for the roots as

$$\begin{aligned}&k_1^2(\varepsilon )=\omega ^2\left[ 1-\frac{(1+G)}{(1+G+\iota \omega )}\varepsilon +\cdots \right] ,\nonumber \\&k_2^2(\varepsilon )=\iota \omega (1+G)\left[ 1+\frac{(1+G)}{(1+G+\iota \omega )}\varepsilon +\cdots \right] . \end{aligned}$$
(22)

Equation (19) indicates that there are two distinct traveling coupled longitudinal waves, namely a CP-wave and a CT-wave of wavenumber \(k_1\) and \(k_2\), respectively. Both of the waves are influenced by the elastic as well as the thermal fields. This result agrees with that in the conventional coupled as well as the L–S theories [2] of thermoelasticity. In these theories, it has also been observed that one of the longitudinal waves is a CP-wave and the other is a CT-wave. The phase speeds of the CP-wave and the CT-wave are given by \(V_1=\omega /\mathfrak {R}(k_1)\) and \(V_2=\omega /\mathfrak {R}(k_2)\), respectively. It is clear that the attenuation coefficients \(\mathfrak {I}(k_{1,2})\) and the phase speeds \(V_{1,2}\) are (nonlinear) functions of \(\omega\), which in turn means that the coupled dilatational elastic-thermal waves experience attenuation as well as dispersion due to the thermoelastic character of the medium considered. Besides, since the wavenumbers of both the waves are complex, so they are inhomogeneous waves. A look at Eq. (20) reveals that there exists one SV-type wave of wavenumber \(k_3=\omega /\beta\) whose phase speed is

$$\begin{aligned} V_3=\beta . \end{aligned}$$
(23)

The expression (23) indicates that the SV-type wave remains unaffected by the presence of the thermal wave effect. It is also noted that this wave is non-dispersive and propagates in the medium considered without being attenuated.

4 Reflection problem

Let a train of SV-type wave having amplitude \(A_0\) and phase speed \(V_3\) is made incident on \(z=0\) by making an angle \(\theta _0\) with the normal to the free surface \(z=0\) as shown in Fig. 1. Assuming that the radiation in vacuum is neglected, when the SV-type wave impinges the boundary \(z=0\), three reflected waves are created in the medium. Suppose the reflected CP-, CT- and the SV-type waves make angles \(\theta _1,~\theta _2\) and \(\theta _3\), respectively, with the positive z-axis. Then the complete structure of the wave fields consisting of the incident and the reflected waves in the medium M may be expressed as

$$\begin{aligned} \phi= A_1\exp {\left\{ \iota k_1(x\sin \theta _1+z\cos \theta _1)-\iota \omega t\right\} }+A_2\exp {\left\{ \iota k_2(x\sin \theta _2+z\cos \theta _2)-\iota \omega t\right\} }, \end{aligned}$$
(24)
$$\begin{aligned} \varTheta =\zeta _1A_1\exp {\left\{ \iota k_1(x\sin \theta _1+z\cos \theta _1)-\iota \omega t\right\} }+\zeta _2A_2\exp {\left\{ \iota k_2(x\sin \theta _2+z\cos \theta _2)-\iota \omega t\right\} }, \end{aligned}$$
(25)
$$\begin{aligned} \psi =A_0\exp {\left\{ \iota k_3(x\sin \theta _0-z\cos \theta _0)-\iota \omega t\right\} }+B_1\exp {\left\{ \iota k_3(x\sin \theta _3+z\cos \theta _3)-\iota \omega t\right\} }, \end{aligned}$$
(26)

where \(\zeta _j=(\omega ^2-k_j^2)\) and \(A_1,~A_2,~B_1\) represent the coefficients of the amplitudes of the reflected CP-, CT- and the SV-type waves, respectively. The reflection coefficient is defined as the ratio of the amplitude of the reflected wave to the incident wave and is determined by the appropriate boundary conditions on the free surface \(z=0\).

We consider the surface \(z=0\) as stress-free and thermally insulated. These conditions can be written mathematically as follows:

$$\begin{aligned} \sigma _{zz}=\sigma _{xz}=\frac{\partial \varTheta }{\partial z}=0,~~~\text {at}\,\,z=0. \end{aligned}$$
(27)

In terms of the displacement potentials, the boundary conditions (27) are simplified to

$$\begin{aligned} \nabla ^2\phi +2\beta ^2\left( \psi _{,xz}-\phi _{,xx}\right) -\varTheta =0, \end{aligned}$$
(28)
$$\begin{aligned} 2\phi _{,xz}+\psi _{,xx}-\psi _{,zz}=0,\,\,\text {at}\,\,z=0. \end{aligned}$$
(29)

In order to satisfy the above boundary conditions at \(z=0\), the following relation must be hold on \(z=0\):

$$\begin{aligned} k_3\sin \theta _0=k_1\sin \theta _1=k_2\sin \theta _2=k_3\sin \theta _0. \end{aligned}$$
(30)

Relation (30) is also written as

$$\begin{aligned} \theta _0=\theta _3\, \text {and}\,\frac{\sin \theta _1}{V_1}=\frac{\sin \theta _2}{V_2}=\frac{\sin \theta _0}{V_3},\quad \text {at} \quad z=0, \end{aligned}$$
(31)

which is often referred to as extended Snell’s law.

Substituting from Eqs. (24)–(26) into the boundary conditions (27)–(29) and using either (30) or (31), we obtain the following expressions for the reflection coefficients, say \(R_{{\rm SP}}=A_1/A_0,~R_{{\rm ST}}=A_2/A_0,~R_{{\rm SS}}=B_1/A_0\):

$$\begin{aligned} R_{{\rm SP}}= \frac{\beta ^2 \zeta _2 k_2 k_3^2 \sin \left( 4 \theta _0\right) \cos \left( \theta _2\right) }{\begin{array}{c} -\zeta _1 k_1 \cos \left( \theta _1\right) \left( \omega ^2 \cos \left( 2 \theta _0\right) +2 \beta ^2 k_2^2 \sin \left( 2 \theta _0-\theta _2\right) \sin \left( \theta _2\right) \right) \\ +2 \beta ^2 \zeta _2 k_1^2 k_2 \sin \left( 2 \theta _0-\theta _1\right) \sin \left( \theta _1\right) \cos \left( \theta _2\right) +\zeta _2 k_2 \omega ^2 \cos \left( 2 \theta _0\right) \cos \left( \theta _2\right) \end{array}}, \end{aligned}$$
(32)
$$\begin{aligned} R_{{\rm ST}}= \frac{\beta ^2 \zeta _1 k_1 k_3^2 \sin \left( 4 \theta _0\right) \cos \left( \theta _1\right) }{\begin{array}{c} \zeta _1 k_1 \cos \left( \theta _1\right) \left( \omega ^2 \cos \left( 2 \theta _0\right) +2 \beta ^2 k_2^2 \sin \left( 2 \theta _0-\theta _2\right) \sin \left( \theta _2\right) \right) \\ -2 \beta ^2 \zeta _2 k_1^2 k_2 \sin \left( 2 \theta _0-\theta _1\right) \sin \left( \theta _1\right) \cos \left( \theta _2\right) +\zeta _2 k_2 \omega ^2 \left( -\cos \left( 2 \theta _0\right) \right) \cos \left( \theta _2\right) \end{array}}, \end{aligned}$$
(33)
$$\begin{aligned} R_{{\rm SS}}= \frac{\begin{array}{c} \zeta _1 k_1 \cos \left( \theta _1\right) \left( 2 \beta ^2 k_2^2 \sin \left( \theta _2\right) \sin \left( 2 \theta _0+\theta _2\right) -\omega ^2 \cos \left( 2 \theta _0\right) \right) \\ -2 \beta ^2 \zeta _2 k_1^2 k_2 \sin \left( \theta _1\right) \sin \left( 2 \theta _0+\theta _1\right) \cos \left( \theta _2\right) +\zeta _2 k_2 \omega ^2 \cos \left( 2 \theta _0\right) \cos \left( \theta _2\right) \end{array}}{\begin{array}{c} \zeta _1 k_1 \cos \left( \theta _1\right) \left( \omega ^2 \cos \left( 2 \theta _0\right) +2 \beta ^2 k_2^2 \sin \left( 2 \theta _0-\theta _2\right) \sin \left( \theta _2\right) \right) \\ -2 \beta ^2 \zeta _2 k_1^2 k_2 \sin \left( 2 \theta _0-\theta _1\right) \sin \left( \theta _1\right) \cos \left( \theta _2\right) +\zeta _2 k_2 \omega ^2 \left( -\cos \left( 2 \theta _0\right) \right) \cos \left( \theta _2\right) \end{array}}. \end{aligned}$$
(34)

We observe that the reflection coefficients in (32)–(34) are dependent on \(\theta _0\), time-delay of MDD and on the material properties of the medium M.

5 Total reflection

We now consider the most interesting case, namely the case of total reflection beyond the critical angle. By using the relation (31) into the solution (24), we get (after omitting the factor \(\exp {(-\iota \omega t)}\))

$$\begin{aligned} \phi& {}= A_1\exp {\left\{ \iota k_1(x\sin \theta _1+z\cos \theta _1)\right\} }+A_2\exp {\left\{ \iota k_2(x\sin \theta _2+z\cos \theta _2)\right\} },\nonumber \\& {} = \exp {\left\{ \frac{\iota \omega }{V_3}x\sin \theta _0\right\} }\left[ {\bar{A}}_1\exp {\left\{ \frac{\iota \omega z}{V_3}\sqrt{\frac{V_3^2}{V_1^2}-\sin ^2\theta _0}\right\} }\right. \nonumber \\&\left. \quad +\,{\bar{A}}_2\exp {\left\{ \frac{\iota \omega z}{V_3}\sqrt{\frac{V_3^2}{V_2^2}-\sin ^2\theta _0}\right\} }\right] , \end{aligned}$$
(35)

where \({\bar{A}}_j=A_j\exp {\left\{ -\mathfrak {I}(k_j)(x\sin \theta _j+z\cos \theta _j)\right\} },~~~\mathfrak {I}(k_j)\ge 0~~~(j=1,2).\)

Since \(V_1<V_2\), hence \(V_3/V_2<V_3/V_1\) and when \(\theta _0\) increases, \(\sin (\theta _0)\) increases to the value \(V_3/V_2\) first. If \(\sin \theta _0=V_3/V_2=\sin \theta _C\), then \(\theta _0=\theta _C\) is called the critical angle. For \(\theta _0>\theta _C\), the factor \(\sqrt{V_3^2/V_1^2-\sin ^2\theta _0}\) becomes purely imaginary. The critical angle \(\theta _C\) for the elastic case is given by \(\theta _C=\sin ^{-1}(\beta )\) [45]. When \(\sin \theta _0>V_3/V_2\), we obtain from (35) that

$$\begin{aligned} \phi & {}= \exp {\left\{ \frac{\iota \omega }{V_3}x\sin \theta _0\right\} }\left[ {\bar{A}}_1\exp {\left\{ -\frac{\omega z}{V_3}\sqrt{\sin ^2\theta _0-\frac{V_3^2}{V_1^2}}\right\} }\right. \nonumber \\&\left. \quad +\,{\bar{A}}_2\exp {\left\{ -\frac{\omega z}{V_3}\sqrt{\sin ^2\theta _0-\frac{V_3^2}{V_1^2}}\right\} }\right] . \end{aligned}$$
(36)

Thus the thermal part and the elastic part of the reflected coupled dilatational elastic-thermal wave propagate horizontally in the x-direction, whereas its amplitude decays exponentially with depth (z).

6 Results and discussion

In this section, we perform some numerical calculations in order to illustrate the analytical results obtained in the previous sections. For this purpose, we choose copper-like material whose physical data are [26]: \(\lambda =7.76\times 10^{10}\,\mathrm{N/m}^2\), \(\mu =3.86\times 10^{10}\,\mathrm{N/m}^2\), \(T_0=293\,\mathrm{K}\), \(\rho =8954\,\mathrm{kg/m}^3\), \(C_e=383.1\,\mathrm{m}^2/\mathrm{K}\), \(K_T=386\,\mathrm{N/K}\,\mathrm{s}\), \(\alpha _T=383.1\,\mathrm{K}^{-1}\), \(\varepsilon =0.0168\).

Using the above values of the material constants, the critical angle can be calculated as \(\theta _C\approx 20.6^\circ\).

Figure 2 expresses a comparison between the reflection coefficients \(|R_{\mathrm{SP}}|\), \(|R_{\mathrm{ST}}|\) and \(|R_{\mathrm{SS}}|\) within the range of the incident angle \(\theta _0\) (\(0^\circ \le \theta _0\le 90^\circ\)) of the incident SV-type wave. It is noticed that the reflection coefficient of the reflected CP-wave dominates, while the reflected CT- and SV-type waves are both smaller than the reflection coefficient of the CP-wave. The maximum value of \(|R_{\mathrm{SP}}|\) occurs at \(\theta _0=0^\circ\), while that of \(|R_{\mathrm{ST}}|\) and \(|R_{\mathrm{SS}}|\) occurs at the critical angle \(\theta _C=20.6^\circ\). The reflection coefficient of the SV-type wave attains its minimum value 0 at \(\theta _0=0^\circ\).

Fig. 2
figure 2

Comparison of the reflection coefficients with respect to \(\theta _0\)

Full size image

The influence of the Poison ratio \(\sigma\) upon the variations of the magnitudes of the reflection coefficients are also interesting. It is evident from Fig. 3 that the reflection coefficient of the CP-wave is most sensitive to the Poison ratio, while the reflection coefficient of the CT-wave is most insensitive to \(\sigma\). The increasing of the Poison ratio makes the reflected CT-wave weaken. The reflection coefficients \(|R_{\mathrm{SP}}|\) and \(|R_{\mathrm{ST}}|\) increase with an increase in the value of \(\sigma\). On the contrary, the reflection coefficient \(|R_{\mathrm{SS}}|\) decreases with an increase in \(\sigma\). The pattern of the curves in each of the reflection coefficient is similar apart from the magnitudes.

Fig. 3
figure 3

Variations of the reflection coefficients with respect to \(\theta _0\) for different \(\sigma\)

Full size image

Figure 4 is drawn to show the influence of the thermo-mechanical coupling parameter (\(\varepsilon\)) on the variations of \(|R_{\mathrm{SP}}|\), \(|R_{\mathrm{ST}}|\) and \(|R_{\mathrm{SS}}|\) at fixed \(K(t,\xi )=1/2-(t-\xi )/\tau ,~\tau =0.05,~\sigma =0.34\). Here, we take the three values of \(\varepsilon\) as 0.0168,  0.0336 and 0.0504. We can observe from these figures that the absolute values of the reflection coefficients \(R_{\mathrm{SP}}\) and \(R_{\mathrm{ST}}\) have large values for large \(\varepsilon\) meaning it has an increasing effect on \(|R_{\mathrm{SP}}|\) and \(|R_{\mathrm{ST}}|\) at each angle of incidence. On the other hand, it shows an decreasing effect on the variation of \(|R_{\mathrm{SS}}|\). We can also observe from these figures that the influence of the coupling parameter on \(|R_{\mathrm{SP}}|\) and \(|R_{\mathrm{SS}}|\) is greater as compared to the influence of the coupling parameter on \(|R_{\mathrm{SS}}|\).

Fig. 4
figure 4

Variations of the reflection coefficients with respect to \(\theta _0\) for different \(\varepsilon\)

Full size image

Finally, we observe from Figs. 2, 3 and 4 that the critical angle of incidence of the SV-type wave for thermoelastic case is \(\theta _C\approx 20.6^\circ\) which is exactly the same as the calculated value of the critical angle.

In Fig. 5, we plot the phase speeds of the CP-wave and the CT-wave with the non-dimensional angular frequency \((\omega )\). It can be noticed that the phase speeds of the CP-wave and the CT-wave have larger values for the L–S theory as compared to the MDD theory. If we compare the phase speeds for both the waves, we found that the CP-wave has larger magnitudes. From this set of figures, we can say that the memory effect is more sensitive for the phase speed of the CT-wave as compared to the CP-wave, i.e., the presence of memory plays a significant role for the phase speeds. Also, the significant changes in the profiles of the phase speeds of both of the CP- and CT-waves with respect to \(\omega\) indicates that these waves are dispersive in nature and experience attenuation.

Fig. 5
figure 5

Comparison of the phase speeds of the CP-wave and CT-wave versus non-dimensional angular frequency \(\omega\) for MDD and L–S theories

Full size image

7 Conclusions

The following points can be concluded according to our present study:

  1. 1.

    The reflection coefficients are functions of angle of incidence, Poison ratio, and the thermoelastic coupling parameter of the medium.

  2. 2.

    Poison ratio affects significantly the reflection coefficients of all the waves. It has no effect on phase speeds.

  3. 3.

    The phase speeds of the CP- and CT-wave are larger for L–S model as compared to MDD model. The CP- and CT-waves are dispersive and experience attenuation, whereas the SV-type wave is non-dispersive as well as experiences no attenuation as it does not depend on the angular frequency.

  4. 4.

    It is observed that the MDD model supports the finite speed of thermal wave (CT-wave) propagation through the medium considered. Hence, this theory is indeed a generalized theory of thermoelasticity.

  5. 5.

    The present work is of geophysical interest for investigations on earthquakes and similar phenomena in seismology and engineering where ‘MDD may play a significant role’.