1 Introduction

The dynamical theory of thermoelasticity is the study of the interaction between thermal and mechanical fields in solid bodies and is of considerable importance in various engineering fields, soil dynamics, aeronautics, nuclear reactors, high-speed aircraft, earthquake engineering, geophysical exploration, etc. Biot [1] developed the classical dynamical coupled thermoelasticity. Lord and Shulman [2] and Green and Lindsay [3] extended the classical dynamical coupled theory of thermoelasticity to the theory of generalized thermoelasticity which removed the paradox of infinite speed of thermal wave as in Biot [1] coupled thermoelasticity. These generalizations are explained in detail by Green and Naghdi [4, 5], Hetnarski and Ignaczak [6] and Ignaczak and Ostoja-Starzewski [7]. The study of the propagation of seismic waves in isotropic and anisotropic medium with additional parameters like rotation, magnetic field, thermal field, initial stress, etc., are of great practical importance, not only in seismology for investigating the internal structure of the earth but also in various fields like geophysical exploration, mineral and oil exploration, engineering materials, acoustics, etc. A significant number of problems on the reflection phenomenon of elastic waves at the free surface with additional parameters like rotation, magnetic field, thermal field, initial stress, and interfaces of different elastic media may be found in the literature. Some problems of interest in different elastic media are discussed by the following researchers. Gutenberg [8] studied the energy relation of reflected and refracted seismic waves. Willson [9] and Paria [10] studied the propagation of magneto-thermoelastic plane waves in a homogeneous isotropic elastic half-space. Biot [11] summarized that acoustic propagation under the initial stresses would be fundamentally different from that under a stress-free state. Achenbach [12] studied the wave propagation in elastic solids and derived the expression for energy ratio. Schoenberg and Censor [13] studied the effect of rotation on the propagation of elastic waves in rotating media. Sinha and Sinha [14] studied the reflection of thermoelastic waves at a solid half-space with thermal relaxation. Chattopadhyay et al. [15] studied the reflection and refraction phenomena of plane waves in an unbounded medium under initial stresses. Sidhu and Singh [16] studied the effect of initial stress on the reflection of elastic waves. Chandrasekharaiah and Srikantiah [17] investigated the effect of rotation on thermoelastic plane waves without energy dissipation. Dey et al. [18] studied the reflection and refraction of elastic waves under initial stress. Initial stresses in the medium are developed due to many reasons like the variation in temperature, a process of quenching, shot pinning and cold working, overburden layer, and slow process of creep, gravitation, weight, largeness, nitriding and so forth. Montanaro [19] studied the isotropic linear thermoelasticity with hydrostatic initial stress. Ahmad and Khan [20] studied thermoelastic plane waves in rotating isotropic medium. It has been shown that the rotation does not increase the number of waves in an isotropic medium, but it affects their speeds significantly. Ezzat et al. [21] studied a two-dimensional electro-magneto-thermoelastic plane wave problem with a medium of perfect conductivity. Abbas [22] studied the effect of natural frequencies of a poroelastic hollow cylinder. Palani and Abbas [23] studied free convection magneto-hydrodynamic flow with thermal radiation from an impulsively started vertical plate. Abbas and Youssef [24] studied temperature-dependent materials in nonlinear thermoelasticity. Singh and Yadav [25] studied the reflection of plane waves in a rotating transversely isotropic magneto-thermoelastic solid half-space. Naggar et al. [26] studied thermoelastic plane waves under the effect of initial stress, magnetic field, voids, and rotation. Kumar and Abbas [27] studied the thermoelastic deformation in micropolar thermoelastic media with thermal and conductive temperatures. Othman et al. [28] studied the effect of initial stress on a generalized thermoelastic medium with the three-phase-lag model under temperature-dependent properties. Othman and Mansour [29] studied the effect of two-temperature on the plane problem of the magneto-thermoelastic medium under 3PHL model thermoelasticity. Singh and Yadav [30] analyzed the propagation of plane waves in a rotating monoclinic magneto-thermoelastic medium. Mondal et al. [31] studied magneto-photo-thermoelastic wave propagation in an isotropic semiconducting medium. Alzahrani and Abbas [32] studied thermoelastic plane waves in a poroelastic medium without energy dissipations. Saeed et al. [33] investigated thermoelastic plane waves in a porous medium in the GL model of thermoelasticity using the finite element method.

Due to miniaturization of devices, wide application of ultrafast lasers, and the use of multi-layered structures, classical thermoelasticity may be challenged to give accurate results that gives the idea of elastic non-local parameter, mechanical relaxation time, and fractional-order parameter on the thermoelasticity. The fractional derivative has a history as long as that of classical calculus, but it is much less popular than classical calculus. But in recent years, fractional calculus has been applied in an increasing number of fields, such as electromagnetism, control engineering and signal processing, chemistry, astrophysics, quantum mechanics, nuclear physics, quantum field theory, etc. The memory process usually consists of two stages, one is short with permanent retention and the other is governed by a simple model of a fractional derivative. The fractional derivative analysis is useful in mechanics, biology, and psychology. Youssef [34] and Sherief et al. [35] formulated the fractional-order theory of thermoelasticity by using the methodology of fractional calculus. Youssef [36] formulated a new theory of generalized thermoelasticity with fractional-order strain in the context of one temperature type and two-temperature types in which 14 different models of thermoelasticity are formulated. Mainardi [37] studied the application of the calculus of fractional-order derivatives in elastic problems. Povstenko [38] investigated the fractional-order thermoelasticity heat conduction equation. Sarkar and Lahiri [39] studied the plane waves in a rotating thermoelastic medium under fractional-order generalized thermoelasticity. Du et al. [40] studied the measurement of memory with the order of the fractional derivative. Yu et al. [41] studied the problem of electro-magneto-thermoelasticity in fractional-order derivative. Povstenko [42] investigated thermal stress problems in a composite medium in solids in fractional-order thermoelasticity. Shaw [43] investigated the generalized theory of thermoelasticity with memory-dependent derivatives. Mittal and Kulkarni [44] studied the two-temperature fractional-order theory of thermoelasticity in a spherical domain. Bhoyar et al. [45] obtained an exact analytical solution for fractional-order thermoelasticity in a multi-stacked elliptic plate.

Impedance boundary conditions problems are used in various fields of physics like acoustics and electromagnetism and very important in the field of science and technology. Impedance boundary condition in electromagnetism is defined by linear conditions between tangential electric and magnetic field components at the boundary surface. Plane waves that satisfy the boundary conditions identically are called waves matched to the boundary. Familiar examples of matched waves include surface waves and leaky waves attached to certain boundaries. Impedance-like boundary conditions are successfully applied in different fields of physics and material science. However, they are not very well-known in seismology. Generally, the problems of Rayleigh waves are considered in a traction-free surface. From a mathematical point of view, a traction-free surface is described by Neumann boundary conditions. Another type of boundary condition is rarely considered in geophysics or seismology. In the study of Rayleigh waves propagation in a half-space coated with a thin layer, the researchers often replace the effect of the thin layer on the half-space by the effective boundary conditions on the surface of the half-space. Tiersten [46], while studying the wave propagation in an isotropic elastic solid coated with a thin film to simulate the effect of a thin layer of different materials over an elastic half-space, observed another type of boundary condition known as impedance boundary conditions. These boundary conditions specify traction in terms of displacement and its derivatives. Malischewsky [47] investigated Rayleigh waves with Tiersten's impedance boundary conditions. Godoy et al. [48] studied Rayleigh waves with impedance boundary conditions and defined impedance boundary conditions as a relation between the unknown functions and their derivatives which are prescribed on the boundary. Vinh and Hue [49] investigated the effect of anisotropy on the propagation of Rayleigh waves by studying the propagation in an orthotropic and monoclinic half-space with impedance boundary conditions. Singh et al. [50] investigated the effect of impedance boundary on reflection of plane waves from the free surface of a rotating thermoelastic solid half-space. Singh et al. [51] studied the reflection of plane waves from the free surface of a micropolar thermoelastic solid half-space with impedance boundary. Yadav [52] studied the effect of impedance and diffusion on the reflection of plane waves in a rotating magneto-thermoelastic solid half-space. Moreover, the literature on wave propagation phenomenon with impedance boundary conditions is at the incubating stage. Feverish attention has been given to study the effect of impedance boundary on the reflection of plane waves in an initially stressed perfectly conducting rotating thermoelastic solid in the presence of a magnetic field in fractional-order derivative.

2 Basic Equations

Following Lord and Shulman [2], Willson [9], Schoenberg and Censor [13] and Montanaro [19] the linear governing equations of rotating isotropic perfectly conducting generalized fractional-order derivative thermoelastic medium with impedance boundary in the presence of a magnetic field under hydrostatic initial stress in the absence of body forces and heat sources, are

Equations of motion:

$$\left(\mu - \frac{P}{2}\right)u_{i,jj} + \left(\lambda + \mu + \frac{P}{2}\right)u_{j,ij} - \beta_{T} T_{,i} + \mu_{e} ({\mathbf{J}} \times {\mathbf{H}})_{i} \, = \rho \{ {\mathbf{\ddot{u}}}_{i} + ({{\varvec{\Omega}}} \times { (}{{\varvec{\Omega}}} \times {\mathbf{u}}))_{i} + (2{{\varvec{\Omega}}} \times {\dot{\mathbf{u}}}\,)_{i} \} .$$
(1)

Sherief’s model of fractional-order generalized thermoelastic heat conduction equation [35]:

$$KT_{,ii} = \left( {1 + \tau_{0} \frac{{\partial^{\beta + 1} }}{{\partial t^{\beta + 1} }}} \right)\left( {\rho C_{E} \dot{T} + \beta_{T} T_{0} \dot{e}_{ii} } \right),$$
(2)

where \(\beta\) is constant of fractional-order \(0 < \,\beta \, < 1\).

$$\frac{{\partial^{\beta } }}{{\partial t^{\beta } }}f(x,t) = \left\{ \begin{gathered} f(x,t) - f(x,0),\,\,\,\,when,\,\,\beta \to 0, \hfill \\ I^{1 - \beta } \frac{\partial }{\partial t}f(x,t),\,\,\,\,\,\,\,\,\,when,\,\,0 < \beta < 1 \hfill \\ \frac{\partial }{\partial t}f(x,t)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,when,\,\,\beta = 1, \hfill \\ \end{gathered} \right.,$$

and \(I^{\beta }\) is Riemann–Liouville fractional integral operator defined as \(I^{\beta } f(t) = \frac{1}{\Gamma (\beta )}\int\limits_{0}^{t} {(t - s)^{\beta - 1} f(s)ds,}\) and \(\Gamma (\beta )\) is Gamma function, for the case \(\beta = 1\), it reduces to Lord and Shulman [2] with one relaxation time parameter.

Constitutive equations:

$$\sigma_{ij} = \lambda \delta_{ij} e_{kk} + 2\mu e_{ij} - P(\delta_{ij} + \omega_{ij} ) - \beta_{T} T\delta_{ij} ,$$
(3)
$$e_{ij} = \frac{1}{2}(u_{i,j} + u_{j,i} ),\,\,\,\,\,\,\,\,\,\,\,\omega_{ij} \, = \frac{1}{2}(u_{j,i} - u_{i,j} ).$$
(4)

Maxwell’s equations:

$$Curl\;{\mathbf{H}}\; = \;\,{\mathbf{J}},\;Curl\;{\mathbf{E}}\; = \; - \frac{{\partial {\mathbf{B}}}}{\partial t}, \;{\mathbf{B}} = \mu_{e} {\mathbf{H}},\;{\text{div}} \;{\mathbf{B}} = \,0.$$
(5)

Ohm’s law in generalized form is

$${\mathbf{J}}\; = \;\sigma \;[\,{\mathbf{E}} + (\,{\dot{\mathbf{u}}} \times {\mathbf{B}}\,)],$$
(6)

and magnetic stress is given by

$$\overline{\sigma }_{ij} = \mu_{e} \left[ {H_{i} h_{j} + H_{j} h_{i} - H_{k} h_{k} \delta_{ij} } \right]\,\,,i,j,k = 1,2,3,$$
(7)

where

$$\sigma_{zz} = (\lambda + 2\mu )\frac{\partial w}{{\partial z}} + \lambda \frac{\partial u}{{\partial x}} - \beta_{T} T - P,\sigma_{xx} = (\lambda + 2\mu )\frac{\partial u}{{\partial x}} + \lambda \frac{\partial w}{{\partial z}} - \beta_{T} T - P,$$
(8)
$$\sigma_{zx} = \left( {\mu + \frac{P}{2}} \right)\frac{\partial w}{{\partial x}} + \left( {\mu - \frac{P}{2}} \right)\frac{\partial u}{{\partial z}},\sigma_{xz} = \left( {\mu + \frac{P}{2}} \right)\frac{\partial u}{{\partial z}} + \left( {\mu - \frac{P}{2}} \right)\frac{\partial w}{{\partial x}},$$
(9)
$$\overline{\sigma }_{zz} = - \mu_{e} H_{0}^{2} \left( {\frac{\partial u}{{\partial x}} + \frac{\partial w}{{\partial z}}} \right)\,,\,\,\overline{\sigma }_{zx} = 0.$$
(10)

3 Formulation of the Problem and Solution

Considering a homogeneous isotropic thermoelastic perfectly conducting medium under hydrostatic initial stress P (initial pressure) which is permeated by a primary magnetic field B, such that B \(= \mu_{e}\) H with reference temperature T0. The medium is uniformly rotating with an angular velocity Ω \(= \Omega\) n, where n is the unit vector representing the direction of the axis of rotation such that Ω \(= (0,\Omega ,0).\) The magnetic field is taken as \({\mathbf{H}} = {\mathbf{H}}_{0} + {\mathbf{h}},\) \({\mathbf{H}}_{0} = \left( {0,H_{0} ,0} \right),\) \({\mathbf{h}}\left( {h_{x} ,\;h_{y} ,\;h_{z} } \right)\), is a change in the basic magnetic field, an induced magnetic field \({\mathbf{h}} = (0,h,0)\) and an induced electric field \({\mathbf{E}}\) are developed due to the application of initial magnetic field \({\mathbf{H}}\; = \;\left( {0,\;H_{0} ,\;0} \right)\) and rotation, Ω \(= (0,\Omega ,0)\) about y axis with centripetal acceleration \(({{\varvec{\Omega}}} \times { (}{{\varvec{\Omega}}} \times {\mathbf{u}}))\) due to time-varying motion only and \((2{{\varvec{\Omega}}} \times \frac{{\partial {\mathbf{u}}}}{\partial t}\,)\) is the Coriolis acceleration. The effect on the conduction current J due to thermal gradient is neglected and for perfectly conducting medium \(\sigma \to \infty .\) For linearizing the basic equations, the product terms of h, u, and their derivatives are neglected as the induced magnetic field \({\mathbf{h}}\) is very small. We take the origin on the plane surface and restrict our analysis to plane strain parallel to x–z plane represented by (z ≤  0) with displacement vector u \(= (u,\,\,0,\,\,w)\) and \(\frac{\partial }{\partial y} = 0.\)

From Eqs. 5 and 6 it follows that

$$\frac{1}{{\sigma \mu_{e} }}\nabla^{2} {\mathbf{H}} = \left[ {\frac{{\partial \;{\mathbf{H}}\;}}{\partial t} - \nabla \times \left( {\frac{{\partial {\mathbf{u}}}}{\partial t}\; \times {\mathbf{H}}} \right)} \right],\nabla \times \left( {\frac{{\partial {\mathbf{u}}}}{\partial t}\; \times \;{\mathbf{H}}} \right) = \left( {0, - H_{0} \left\{ {\frac{\partial }{\partial x}\left( {\frac{\partial u}{{\partial t}}} \right) + \frac{\partial }{\partial z}\left( {\frac{\partial w}{{\partial t}}} \right)} \right\},\,0\,} \right).$$
(11)

In component form, Eq. 11 can be written as

$$\frac{{\partial H_{x} }}{\partial t} = \frac{1}{{\sigma \mu_{e} }}\nabla^{2} H_{x} ,\,\frac{{\partial H_{y} }}{\partial t} = \frac{1}{{\sigma \mu_{e} }}\nabla^{2} H_{y} - H_{0} \left\{ {\frac{\partial }{\partial x}\left( {\frac{\partial u}{{\partial t}}} \right) + \frac{\partial }{\partial z}\left( {\frac{\partial w}{{\partial t}}} \right)} \right\},\frac{{\partial H_{z} }}{\partial t} = \frac{1}{{\sigma \mu_{e} }}\nabla^{2} H_{z} .$$
(12)

For perfectly conducting medium (\(\sigma \to \infty\)), Eq. 12 becomes

$$\left. {\frac{{\partial \;H_{x} \;}}{\partial t} = 0,\frac{{\partial \;H_{y} \;}}{\partial t} = - H_{0} \{ \,\,\frac{\partial }{\partial x}(\,\frac{\partial u}{{\partial t}}) + \,\,\,\,\frac{\partial }{\partial z}(\frac{\partial w}{{\partial t}})\,\} ,\,\frac{{\partial \;H_{z} \;}}{\partial t} = 0} \right\}.$$
(13)

We assume that the primary magnetic field is uniform throughout the space. It is clear from Eq. 13 that there is no perturbation in \(H_{x} ,\) \(H_{z}\) and there is perturbation in \(H_{y}\). Therefore, taking small perturbations \(\;h_{y}\) in \(H_{y}\) and integrating Eq. 13, we get

$$H_{x} = 0,\,H_{z} = 0,\,\,H_{y} = - H_{0} \left\{ {\frac{\partial u}{{\partial x}} + \frac{\partial w}{{\partial z}}} \right\}.$$
(14)

Therefore,

$$h_{x} \; = 0,\;h_{y} = - H_{0} \left\{ {\frac{\partial u}{{\partial x}} + \,\,\,\,\frac{\partial w}{{\partial z}}} \right\},\;\;h_{z} = 0.$$
(15)

From relation \(({\mathbf{J}} \times {\mathbf{B}})_{i} = \;\mu_{e} \left( {Curl\;{\mathbf{h}} \times \;{\mathbf{H}}} \right)\), using Eqs. 14 and 15, we obtain

$$\left. {({\mathbf{J}} \times {\mathbf{B}})_{1} = \mu_{e} H_{0}^{2} \{ \frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{\partial x\partial z}\} ,\,\,({\mathbf{J}} \times {\mathbf{B}})_{2} \; = \;0,\,({\mathbf{J}} \times {\mathbf{B}})_{3} \; = \;\mu_{e} H_{0}^{2} \{ \frac{{\partial^{2} u}}{\partial x\partial z} + \frac{{\partial^{2} w}}{{\partial z^{2} }}\} } \right\}.$$
(16)

Using Eq. 16 the governing field equations in x–z plane in absence of body forces and heat sources become

$$\begin{aligned} & (\lambda + 2\mu )\frac{{\partial^{2} u}}{{\partial x^{2} }} + \left( {\lambda + \mu + \frac{P}{2}} \right)\frac{{\partial^{2} w}}{\partial x\partial z} + \left( {\mu - \frac{P}{2}} \right)\frac{{\partial^{2} u}}{{\partial z^{2} }} + \mu_{e} H_{0}^{2} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{\partial x\partial z}} \right) \\ & \quad - \beta_{T} \frac{\partial T}{{\partial x}} = \rho \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }} - \Omega^{2} u + 2\Omega \frac{\partial w}{{\partial t}}} \right), \\ \end{aligned}$$
(17)
$$\begin{aligned} & (\lambda + 2\mu )\frac{{\partial^{2} w}}{{\partial z^{2} }} + \left( {\lambda + \mu + \frac{P}{2}} \right)\frac{{\partial^{2} u}}{\partial x\partial z} + \left( {\mu - \frac{P}{2}} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + \mu_{e} H_{0}^{2} \left( {\frac{{\partial^{2} u}}{\partial x\partial z} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right) \\ & \quad - \beta_{T} \frac{\partial T}{{\partial z}} = \rho \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} - \Omega^{2} w + 2\Omega \frac{\partial u}{{\partial t}}} \right). \\ \end{aligned}$$
(18)

Equation 2 is written in x–z plane as

$$\left( {1 + \tau_{0} \frac{{\partial^{\beta + 1} }}{{\partial t^{\beta + 1} }}} \right)\left[ {\beta_{T} T_{0} \left( {\frac{{\partial^{2} u}}{\partial x\partial t} + \frac{{\partial^{2} w}}{\partial z\partial t}} \right)\, + \,\,\rho C_{E} \frac{\partial T}{{\partial t}}\,\,} \right]\,\, = K\left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right).$$
(19)

Using the following Helmholtz’s representations

$$u = \,\frac{\partial q}{{\partial x}} - \frac{\partial \psi }{{\partial z}},\,\,\,w = \,\frac{\partial q}{{\partial z}} + \frac{\partial \psi }{{\partial x}}\,.\,$$
(20)

Using Eqs. 20 in Eqs. 17, 18 and 19, we get

$$\overline{C}_{1}^{2} \left( {\frac{{\partial^{2} q}}{{\partial x^{2} }} + \frac{{\partial^{2} q}}{{\partial z^{2} }}} \right) + \overline{\mu }_{e} H_{0}^{2} \left( {\frac{{\partial^{2} q}}{{\partial x^{2} }} + \frac{{\partial^{2} q}}{{\partial z^{2} }}} \right)\, - \overline{\beta }_{T} T - \ddot{q} + \Omega^{2} q - 2\Omega \dot{\psi } = 0,$$
(21)
$$(\overline{C}_{2}^{2} - \overline{P})\left( {\frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial z^{2} }}} \right) - \ddot{\psi } + \Omega^{2} \psi + \Omega \dot{q} = 0,$$
(22)
$$K\left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) = \left( {1 + \tau_{0} \frac{{\partial^{\beta + 1} }}{{\partial t^{\beta + 1} }}} \right)\left[ {\,\rho C_{E} \dot{T} + \beta_{T} T_{0} \left( {\frac{{\partial^{2} \dot{q}}}{{\partial x^{2} }} + \frac{{\partial^{2} \dot{q}}}{{\partial z^{2} }}} \right)} \right].$$
(23)

The solution of Eqs. 21–23 is sought in the following form

$$(q\,\,,\,\psi \,,T\,\,) = (\overline{q}\,,\,\overline{\psi }\,,\,\overline{T}\,)\,e^{ik(x\sin \theta + z\cos \theta - \,\,Vt)} ,$$
(24)

where \(\overline{q}\,,\,\overline{\psi }\,,\,\overline{T}\,\,\) are the constants, V is phase velocity and k is wave number. The existence of non-trivial solution of Eqs. 21–23 requires

$$\tilde{D}_{0} V^{6} \, + \tilde{D}_{1} \,V^{4} + \tilde{D}_{2} \,V^{2} \, + \,\tilde{D}_{3} \,\, = 0,$$
(25)

where

$$\tilde{D}_{0} = (1 - \tilde{\Omega }^{*} )^{2} ,\,\tilde{D}_{1} = - \,[\overline{\overline{K}}(1 - \tilde{\Omega }^{*} )^{2} + (1 + \tilde{\Omega }^{*} )(\overline{C}_{1}^{2} + \overline{C}_{2}^{2} + \tilde{\varepsilon } - \overline{P} + \overline{\mu }_{e} H_{0}^{2} )],$$
$$\tilde{D}_{2} = \,\left[ {\overline{\overline{K}}(1 + \tilde{\Omega }^{*} )(\overline{C}_{1}^{2} + \overline{C}_{2}^{2} - \overline{P} + \overline{\mu }_{e} H_{0}^{2} ) + (\overline{C}_{2}^{2} - \overline{P})(\tilde{\varepsilon } + \overline{C}_{1}^{2} + \overline{\mu }_{e} H_{0}^{2} )} \right],\,$$
$$\begin{gathered} \tilde{D}_{3} = - \overline{\overline{K}}(\overline{C}_{2}^{2} - \overline{P})(\overline{C}_{1}^{2} + \overline{\mu }_{e} H_{0}^{2} ),\,\,\,\tau_{0}^{*} = \tau_{0} ( - i\omega )^{\beta } + \frac{i}{\omega },\,\,\,\,\overline{K} = \frac{K}{{\tau_{0}^{*} }},\,\,\tilde{\Omega }^{*} = \left( {\frac{\Omega \,}{\omega }} \right)^{2} ,\,\,\overline{\overline{K}} = \frac{{\overline{K}\,}}{{\rho C_{E} }}\,, \hfill \\ \tilde{\varepsilon } = \frac{{\beta_{T}^{2} T_{0} }}{{\rho^{2} C_{E} }},\,\,\overline{C}_{1}^{2} = \frac{(\lambda + 2\mu )}{\rho },\,\,\overline{C}_{2}^{2} = \,\frac{\mu }{\rho },\overline{\beta }_{T} = \frac{{\beta_{T} }}{\rho }\,,\,\,\overline{\mu }_{e} = \frac{{\mu_{e} }}{\rho }\,,\,\,\,\overline{P} = \frac{P}{2\rho }\,, \hfill \\ \end{gathered}$$

ω = kV is circular frequency of wave. If \(V_{i}^{ - 1} \, = \;v_{i}^{ - 1} - i\,\omega^{ - 1} \,q_{i} ,\,i = 1,2,3,\) then the real parts \(v_{1} \,,v_{2} \,,v_{3} \,,\) of the three roots of Eq. 25 are the speed of three coupled plane waves namely \(P_{1} \,\), \(P_{2} \,\) and \(P_{3} \,\) wave. If waves are in x-direction then velocities take the form of \(v_{1} = \sqrt {\frac{\lambda + 2\mu + P}{\rho }} \,\,,\,\,v_{2} = \sqrt {\frac{\mu + P/2}{\rho }} .\)

4 Reflection from Free Surface

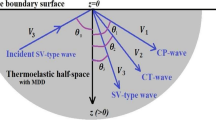
A homogenous rotating thermoelastic isotropic perfectly conducting elastic solid half-space in the undeformed state is considered with thermally insulated traction-free surface with impedance boundary. The displacement vector is \(\vec{u}\, = (\,u,\,0\,,w)\) and negative z-axis is taken along the increasing depth into the half-space. For incident \(P_{1} \,\) (or \(P_{2}\)) wave, there will be reflected \(P_{1} \,\), \(P_{2} \,\) and \(P_{3} \,\) wave in the half-space. The complete geometry showing the incident and reflected waves is shown in Fig. 1.

Fig. 1
figure 1

Geometry of the problem showing incident and reflected waves in an initially stressed rotating magneto-thermoelastic solid half-space

Full size image

The appropriate displacement, temperature, field potentials in the half-space are taken as

$$q = X_{0} \exp \left\{ {ik_{1} \left( {xsin\theta_{0} + z\cos \theta_{0} - v_{1} t} \right)} \right\} + \sum\limits_{s = 1}^{3} {X_{s} \exp \left\{ {ik_{s} \left( {xsin\theta_{s} - z\cos \theta_{s} - v_{s} t} \right)} \right\},}$$
(26)
$$T = F_{1} X_{0} \exp \left\{ {ik_{1} \left( {xsin\theta_{0} + z\cos \theta_{0} - v_{1} t} \right)} \right\} + \sum\limits_{s = 1}^{3} {F_{s} X_{s} \exp \left\{ {ik_{s} \left( {xsin\theta_{s} - z\cos \theta_{s} - v_{s} t} \right)} \right\},}$$
(27)
$$\psi = G_{1} X_{0} \exp \left\{ {ik_{1} \left( {xsin\theta_{0} + z\cos \theta_{0} - vt} \right)} \right\} + \sum\limits_{s = 1}^{3} {G_{s} X_{s} \exp \left\{ {ik_{s} \left( {xsin\theta_{s} - z\cos \theta_{s} - v_{s} t} \right)} \right\},}$$
(28)

where \((s = 1,2,3),v_{1} \,\) is the velocity of the incident and reflected \(P_{1} \,\), and \(v_{2} ,\,v_{3} ,\) are the velocities of reflected \(P_{2} \,\) and \(P_{3} \,\) waves, respectively, \(k_{s} ,\,(s = 1,\,2,3)\) are complex wave numbers, respectively, and the coupling coefficient \(\frac{{F_{s} }}{{k_{s}^{2} }},\) \(G_{s} ,\) \((s = 1,2,3)\) are given as

$$\frac{{F_{s} }}{{k_{s}^{2} }} = \;\frac{{2i\frac{\Omega \,}{\omega }v_{s}^{2} G_{s} + (1 + \tilde{\Omega }^{*} )v_{s}^{2} - \overline{C}_{1}^{2} - \overline{\mu }_{e} H_{0}^{2} }}{{\overline{\beta }_{T} }}\;,\,\,\,\,G_{s} = \frac{{2i\frac{\Omega \,}{\omega }v_{s}^{2} \;}}{{v_{s}^{2} (1 + \tilde{\Omega }^{*} ) + \overline{P} - \overline{C}_{2}^{2} }}\;,\,\,\,s = 1,2,3.$$
(29)

Malischewsky [47] modified Tiersten's impedance boundary conditions as \(\sigma_{ij} + \varepsilon_{i} u_{i} = 0,\) at \(x_{j} = 0,\) where \(\varepsilon_{i}\) is impedance parameter in terms of stresses and displacements having dimension of stress /length. Godoy et al. [48] further modified Tiersten's impedance boundary conditions as \(\sigma_{ij} + \omega Z_{i}^{/} u_{i} = 0,\) at \(x_{j} = 0,\) where \(Z_{i}^{/} ,\) is the impedance real-valued parameter having dimension of stress/velocity. Following Godoy et al. [48], the required boundary conditions at the surface z = 0 are vanishing of normal stresses, tangential stresses and normal component of the heat flux vector, i.e.,

$$\sigma_{zz} + \overline{\sigma }_{zz} + \omega Z_{3}^{*} w = - P,\,\,\,\,\sigma_{zx} + \overline{\sigma }_{zx} + \omega Z_{1}^{*} u = 0,\,\,\,\,\frac{\partial T}{{\partial z}} + h_{1} T = 0,$$
(30)

and \(h_{1} \to 0\) for thermally insulated and \(h_{1} \to \infty\) for isothermal case, \(Z_{1}^{*} ,Z_{3}^{*}\) are real-valued impedance parameters. In particular, \(Z_{1}^{*} = Z_{3}^{*} = 0,\) leads to traction-free boundary conditions. On the other hand, the limit \(\left| {Z_{3}^{*} } \right| \to + \infty\) is equivalent to a vanishing normal displacement and the limit \(\left| {Z_{1}^{*} } \right| \to + \infty\) is equivalent to a vanishing tangential displacement. The potentials 26–28 corresponding to the incident and reflected waves must satisfy the boundary conditions (30). Since the phases of the waves must be the same for each value of x. The wavenumber \(\,k_{1} \,,k_{2} \,,k_{3}\) and the angles \(\theta_{0} \,,\theta_{1} ,\theta_{2} ,\theta_{3}\) are connected by the relation, then we obtain the Snell’s law for the present problem at the surface z = 0, written as

$$\frac{{\sin \theta_{0} }}{{v_{1} }} = \frac{{\sin \theta_{i} }}{{v_{i} }},\,\,\,\,k_{i} v_{i} = \omega \left( {say} \right),\,\,\,\,\,(i = 1,2,3),$$
(31)

and using Eqs. 26–28 in Eq. 30 and with the help of Eq. 31, the following system of three non-homogeneous is obtained as

$$\sum\limits_{j = 1}^{3} {\overline{a}_{ij} } \overline{Z}_{j} = \overline{b}_{i} ,\;\left( {i = 1,2,3} \right),$$
(32)

where

$$\begin{aligned} \overline{a}_{1j} \; &= \;\left[ {\lambda + 2\mu \left\{ {1 - \left( {\frac{{v_{j} }}{{v_{1} }}} \right)^{2} \sin^{2} \theta_{0} } \right\} + \frac{{\beta_{T} F_{j} }}{{k_{j}^{2} }} - \mu_{e} H_{0}^{2} \,} \right]\left( {\frac{{v_{1} }}{{v_{j} }}} \right)^{2} \, - iZ_{3}^{*} G_{j} v_{1} \sin \theta_{0} \\ & \quad - \left( {2\mu G_{j} \;\sin \theta_{0} - iZ_{3}^{*} v_{1} } \right)\frac{{v_{1} }}{{v_{j} }}\sqrt {1 - \left( {\frac{{v_{j} }}{{v_{1} }}} \right)^{2} \sin^{2} \theta_{0} } \,, \\ \end{aligned}$$
$$\begin{aligned} \overline{a}_{2j} \; &= \;\left[ { - \mu G_{j} \left\{ {1 - \left( {\frac{{v_{j} }}{{v_{1} }}} \right)^{2} \sin^{2} \theta_{0} } \right\} - \frac{P}{2}G_{j} } \right]\,\left( {\frac{{v_{1} }}{{v_{j} }}} \right)^{2} - 2\mu \;\sin \theta_{0} \frac{{v_{1} }}{{v_{j} }}\sqrt {1 - \left( {\frac{{v_{j} }}{{v_{1} }}} \right)^{2} \sin^{2} \theta_{0} } \, \\ & \quad + \mu G_{j} \sin^{2} \theta_{0} \, - iZ_{1}^{*} v_{1} \;\sin \theta_{0} - iZ_{1}^{*} v_{1} G_{j} \left( {\frac{{v_{1} }}{{v_{j} }}} \right)\sqrt {1 - \left( {\frac{{v_{j} }}{{v_{1} }}} \right)^{2} \sin^{2} \theta_{0} } ,\,\,\,\,\,\,\,\,\,\,\,\,\,(j = 1,2,3\,), \\ \end{aligned}$$
$$\overline{b}_{1} = - [\lambda + 2\mu \;\cos^{2} \theta_{0} + 2\mu \;G_{1} \sin \theta_{0} \cos \theta_{0} + \frac{{\beta_{T} F_{1} }}{{k_{1}^{2} }} - \mu_{e} H_{0}^{2} \, - iZ_{3}^{*} v_{1} \cos \theta_{0} - iZ_{3}^{*} G_{1} v_{1} \sin \theta_{0} ],$$
$$\overline{b}_{2} \; = - \;[2\mu \;\sin \theta_{0} \cos \theta_{0} + \mu G_{1} \sin^{2} \theta_{0} - \mu G_{1} \cos^{2} \theta_{0} - \frac{P}{2}G_{1} - iZ_{1}^{*} v_{1} \;\sin \theta_{0} + iZ_{1}^{*} v_{1} G_{1} \cos \theta_{0} \,],$$

  • For thermally insulated

    $$\overline{a}_{3j} = \frac{{F_{j} }}{{k_{j}^{2} }}\left( {\frac{{v_{1} }}{{v_{j} }}} \right)^{3} \;\;\sqrt {1\; - \left( {\frac{{v_{j} }}{{v_{1} }}} \right)^{2} \sin^{2} \theta_{0} } ,\,\,\,(j = 1,2,3\,),\,\;\overline{b}_{3} = \frac{{F_{1} }}{{k_{1}^{2} }}\cos \theta_{0} \,,$$

  • For isothermal

    $$\overline{a}_{3j} = \frac{{F_{j} }}{{k_{j}^{2} }}\left( {\frac{{v_{1} }}{{v_{j} }}} \right)^{2} ,\quad \,(j = 1,2,3\,)\,,\,\,\,\overline{b}_{3} = - \frac{{F_{1} }}{{k_{1}^{2} }}\;,\,$$

\(\overline{Z}_{j} = \frac{{X_{j} }}{{X_{0} }}\,,\,(j = 1,2,3),\) are reflection coefficients of reflected \(P_{1} \,,P_{2} \,\) and \(P_{3} \,\) waves, respectively.

5 Particular Cases

  • Rotating isotropic thermoelastic solid with initial stress and magnetic field: taking \(Z_{1}^{*} = 0,Z_{3}^{*} = 0,\) \(\beta = 0,\) the above analysis reduces for rotating thermoelastic isotropic magneto-elastic solid with initial stress. Variations of the reflection coefficient of reflected P1, P2 and P3 waves against the angle of incidence of P1 wave at different values of the magnetic parameter \(H_{0}\) when Ω = 10 Hz, \(\beta = 0,\)\(Z_{1}^{*} = 0,\)\(Z_{3}^{*} = 0,\) \(P = 1.0 \times {1}0^{{{1}0}} {\text{N}} \cdot {\text{m}}^{{ - {2}}} ,\)\(\tau_{0} = 0.05,\) \(\omega = 50\,Hz\) are shown in Fig. 3a–c and variations of the reflection coefficient of reflected P1, P2 and P3 waves against the angle of incidence of P1 wave at different values of initial parameter P when Ω = 10 Hz, \(H_{0} = 6 \times 10^{5} Oe,\)\(\tau_{0} = 0.05,\)\(,\beta = 0,Z_{1}^{*} = Z_{3}^{*} = 0,\) \(\omega = 50\,Hz\) are shown in Fig. 4a–c. Variations of the energy ratios of reflected P1, P2 and P3 waves against the angle of incidence of P1 wave at different values of initial parameter P when Ω = 10 Hz, \(H_{0} = 6.0 \times 10^{5} Oe,\)\(\beta = 0,Z_{1}^{*} = Z_{3}^{*} = 0,\)\(\tau_{0} = 0.05,\) \(\omega = 50\,Hz\) are shown in Fig. 6a–c. Variations of the energy ratios of reflected P1, P2 and P3 waves against the angle of incidence of incident P1 wave at different values of rotation parameter Ω, when \(P = 1.0 \times {1}0^{{{1}0}} {\text{N}}.{\text{m}}^{{ - {2}}} ,\)\(\beta = 0, Z_{1}^{*} = Z_{3}^{*} = 0,\) \(H_{0} = 6.0 \times 10^{5} Oe,\) \(\tau_{0} = 0.05,\) \(\omega = 50\,Hz\) are shown in Fig. 7a–c.

  • Initially stressed thermoelastic solid with magnetic field: neglecting impedance boundary and rotation, i.e., \(Z_{1}^{*} = 0,Z_{3}^{*} = 0,\) \(\Omega = 0\,\) the above analysis reduces for initially stressed magneto-thermoelastic solid.

  • Isotropic magneto-thermoelastic solid: taking \(\Omega = 0\,,P = 0\,,\) the above analysis reduces for isotropic magneto-thermoelastic solid with impedance boundary surface.

  • Rotating thermoelastic isotropic solid: taking \(H_{0} = 0\,,P = 0\,,\) the above analysis reduces for rotating isotropic thermoelastic solid with impedance boundary surface.

6 Energy Partition

Following Achenbach [12], the instantaneous rate of work of surface traction is the scalar product of the surface traction and the particle velocity. This scalar product is called the power per unit area, denoted by <P*> represents the average energy transmission per unit surface area per unit time:

$$\langle P^{*} \rangle \, = \sigma_{zz} \dot{w} + \sigma_{zx} \dot{u}\,.$$
(33)

The expressions for energy ratios \(E_{1} ,E_{2}\) and \(E_{3}\) of reflected waves \(P_{1} \,,P_{2} \,\) and \(P_{3} \,\), respectively are

$$\begin{aligned} & E_{1} = \frac{{\langle P_{{ref.\,\,\,P_{1} }}^{*} \rangle }}{{\langle P_{{inc.\,\,P_{1} }}^{*} \rangle }} \\ & \quad = - \frac{{\left[ {\left( {\lambda + 2\mu + \mu G_{1}^{2} + \frac{P}{2}G_{1}^{2} + \beta_{T} \frac{{F_{1} }}{{k_{1}^{2} }}} \right)\cos \theta_{0} \, - \left( {\lambda + \mu + \beta_{T} \frac{{F_{1} }}{{k_{1}^{2} }} - \frac{P}{2}} \right)G_{1} \sin \theta_{0} \,} \right]}}{{\left[ {\left( {\lambda + 2\mu + \mu G_{1}^{2} + \frac{P}{2}G_{1}^{2} + \beta_{T} \frac{{F_{1} }}{{k_{1}^{2} }}} \right)\cos \theta_{0} \, + \left( {\lambda + \mu - \frac{P}{2} + \beta_{T} \frac{{F_{1} }}{{k_{1}^{2} }}} \right)G_{1} \sin \theta_{0} } \right]}}\left( {\frac{{X_{1} }}{{X_{0} }}} \right)^{2} \,, \\ \end{aligned}$$
(34)
$$\begin{aligned} & E_{2} = \frac{{\langle P_{{ref.\,\,\,P_{2} }}^{*} \rangle }}{{\langle P_{{inc.\,\,P_{1} }}^{*} \rangle }} \\ & \quad = - \frac{{\left[ {\left( {\lambda + 2\mu + \mu G_{2}^{2} + \frac{P}{2}G_{2}^{2} + \beta_{T} \frac{{F_{2} }}{{k_{2}^{2} }}} \right)\sqrt {1 - \left( {\frac{{v_{2} }}{{v_{1} }}} \right)^{2} \sin^{2} \theta_{0} } - \left( {\lambda + \mu + \beta_{T} \frac{{F_{2} }}{{k_{2}^{2} }} - \frac{P}{2}} \right)G_{2} \frac{{v_{2} }}{{v_{1} }}\sin \theta_{0} } \right]}}{{\left[ {\left( {\lambda + 2\mu + \mu G_{1}^{2} + \frac{P}{2}G_{1}^{2} + \beta_{T} \frac{{F_{1} }}{{k_{1}^{2} }}} \right)\cos \theta_{0} \, + \left( {\lambda + \mu - \frac{P}{2} + \beta_{T} \frac{{F_{1} }}{{k_{1}^{2} }}} \right)G_{1} \sin \theta_{0} \,} \right]}}\left( {\frac{{v_{1} }}{{v_{2} }}} \right)^{3} \left( {\frac{{X_{2} }}{{X_{0} }}} \right)^{2} \,, \\ \end{aligned}$$
(35)
$$\begin{aligned} & E_{3} = \frac{{\langle P_{{ref.\,\,\,P_{3} }}^{*} \rangle }}{{\langle P_{{inc.\,\,P_{1} }}^{*} \rangle }} \\ & \quad = - \frac{{\left[ {\left( {\lambda + 2\mu + \mu G_{3}^{2} + \frac{P}{2}G_{3}^{2} + \beta_{T} \frac{{F_{3} }}{{k_{3}^{2} }}} \right)\sqrt {1 - \left( {\frac{{v_{3} }}{{v_{1} }}} \right)^{2} \sin^{2} \theta_{0} } - \left( {\lambda + \mu + \beta_{T} \frac{{F_{3} }}{{k_{3}^{2} }} - \frac{P}{2}} \right)G_{3} \frac{{v_{3} }}{{v_{1} }}\sin \theta_{0} } \right]}}{{\left[ {\left( {\lambda + 2\mu + \mu G_{1}^{2} + \frac{P}{2}G_{1}^{2} + \beta_{T} \frac{{F_{1} }}{{k_{1}^{2} }}} \right)\cos \theta_{0} \, + \left( {\lambda + \mu - \frac{P}{2} + \beta_{T} \frac{{F_{1} }}{{k_{1}^{2} }}} \right)G_{1} \sin \theta_{0} \,} \right]}}\left( {\frac{{v_{1} }}{{v_{3} }}} \right)^{3} \left( {\frac{{X_{3} }}{{X_{0} }}} \right)^{2} \,. \\ \end{aligned}$$
(36)

7 Numerical Results and Discussion

Choosing copper material constants from Othman and Mansour [29] at T0 = 298 K, \(\lambda\) = 7.76 × 1010 N·m−2, \(\mu\) = 3.86 × 1010 N·m−2, \(\rho\) = 8.954 × 103 kg·m−3, \(\tau_{0}\) = 0.04 s, \(C_{E}\) = 0.3831 × 103 J·Kg−1·K−1, \(K\) = 0.386 × 103 N·K−1·s−1, \(P\) = 1.0 × 1010 N·m−2, \(\alpha_{0} = 1.78 \times 10^{ - 5} K^{ - 1} ,\) \(\beta = 0.5\) \(H_{0} = 6.0 \times 10^{5} Oe,\) \(\omega = 50Hz,\)

For the above numerical data, reflection coefficients \(\left| {Z_{1} } \right|,\left| {Z_{2} } \right|\) and \(\left| {Z_{3} } \right|\) from the system of Eq. 32 and energy ratios \(\left| {E_{1} } \right|,\left| {E_{2} } \right|\) and \(\left| {E_{1} } \right|\) of reflected \(P_{1} \,,P_{2} \,\) and \(P_{3} \,\) waves from the expressions 34–36 are computed numerically against the angle of incidence of \(P_{1}\) wave by using a Fortran program for thermally insulated case. The variations of the reflection coefficients and energy ratios of reflected \(P_{1} \,,P_{2} \,\) and \(P_{3} \,\) waves are shown graphically in Figs. 2a–c, 3, 4, 5, 6, 7, 8, 9a–c.

To observe the effect of magnetic field parameter on the variations of the reflection coefficients \(\left| {Z_{1} } \right|,\left| {Z_{2} } \right|\) and \(\left| {Z_{3} } \right|\) of reflected \(P_{1} \,,P_{2} \,\) and \(P_{3} \,\) waves, respectively, against angle of incidence of \(P_{1}\) wave are shown graphically in Fig. 2a–c for three different values of magnetic parameter \(H_{0}\) and fractional-order parameter \(\beta ,\) \(H_{0} = 6.0 \times 10^{5} Oe,\,\beta = 0.25\) (denoted by solid black line with solid square) \(H_{0} = 8.0 \times 10^{5} Oe,\;\beta = 0.5\) (denoted by solid black line with solid triangle) and \(H_{0} = 10.0 \times 10^{5} Oe,\;\beta = 0.75\) (denoted by solid black line with solid circle), when Ω = 10 Hz, \(Z_{1}^{*} = 10,\) \(Z_{3}^{*} = - 10,\)\(P = 1.0 \times {1}0^{{{1}0}} {\text{N}} \cdot {\text{m}}^{{ - {2}}} ,\)\(\tau_{0} = 0.05,\) \(\omega = 50\,Hz.\). The value of \(\left| {Z_{1} } \right|\) of reflected \(P_{1}\) wave is 1.001 792 at normal incidence and it increases to a maximum value 1.73 359 at θ0 = 79°. Thereafter, it decreases to value 1.166749 at grazing incidence at \(H_{0} = 6.0 \times 10^{5} Oe,\,\beta = 0.25\). It is 1.007 903 at normal incidence and it increases to a maximum value 1.127 151 at θ0 = 81°. It then decreases to a value 1.12 485 at grazing incidence at \(H_{0} = 8.0 \times 10^{5} Oe,\,\beta = 0.5\) and it is 1.00 700 at normal incidence and it increases to a maximum value 1.09 706 at grazing incidence at \(H_{0} = 10.0 \times 10^{5} Oe,\,\beta = 0.75\) denoted by solid black line with solid square, solid black line with solid triangle and solid black line with solid circle, respectively, as shown in Fig. 2a. The value of \(\left| {Z_{2} } \right|\) of reflected \(P_{2}\) wave is 0.00 034 at normal incidence and it decreases to a minimum value 0.0 013 at grazing incidence at \(H_{0} = 6.0 \times 10^{5} Oe,\,\beta = 0.25\) and similarly variations for \(H_{0} = 8.0 \times 10^{5} Oe,\,\beta = 0.5\) and \(H_{0} = 10.0 \times 10^{5} Oe,\,\beta = 0.75\) are denoted by solid black line with solid square, solid black line with solid triangle and solid black line with solid circle, respectively, as shown in Fig. 2b. The value of \(\left| {Z_{3} } \right|\) of reflected \(P_{3}\) wave is 0.0032 at normal incidence and it increases sharply to value 0.011 382 at grazing incidence at \(H_{0} = 6.0 \times 10^{5} Oe,\,\beta = 0.25\) and similarly variations for \(H_{0} = 8.0 \times 10^{5} Oe,\,\beta = 0.5\) and \(H_{0} = 10.0 \times 10^{5} Oe,\,\beta = 0.75\) are denoted by solid black line with solid square, solid black line with solid triangle and solid black line with solid circle, respectively, as shown in Fig. 2c. It is observed that as we increase the magnetic field, the reflection coefficients decrease.

Fig. 2
figure 2

a–c Variations of the reflection coefficient of reflected P1, P2 and P3 waves against angle of incidence of P1 wave at different values of magnetic parameter \(H_{0}\) and \(\beta\) when Ω = 10 Hz, \(Z_{1}^{*} = 10,\) \(Z_{3}^{*} = - 10,\)\(P = 1.0 \times {1}0^{{{1}0}} {\text{N}} \cdot {\text{m}}^{{ - {2}}} ,\)\(\tau_{0} = 0.05,\) \(\omega = 50\,Hz\)

Full size image

Similarly, the variations of the effect of magnetic field parameter for Lord and Shulman’s thermoelasticity without impedance parameter (\(\beta = 0,Z_{1}^{*} = Z_{3}^{*} = 0\)) on the reflection coefficients \(\left| {Z_{1} } \right|,\left| {Z_{2} } \right|\) and \(\left| {Z_{3} } \right|\) of reflected \(P_{1} \,,P_{2} \,\) and \(P_{3} \,\) waves, respectively, against angle of incidence of \(P_{1}\) wave are shown graphically in Fig. 3a–c for three different values of magnetic parameter \(H_{0}\) \(H_{0} = 6.0 \times 10^{5} Oe,\) (denoted by solid black line with solid square) \(H_{0} = 8.0 \times 10^{5} Oe,\) (denoted by solid black line with solid triangle) and \(H_{0} = 10.0 \times 10^{5} Oe,\) (denoted by solid black line with solid circle), when Ω = 10 Hz, \(Z_{1}^{*} = 0,\) \(Z_{3}^{*} = 0,\)\(P = 1.0 \times {1}0^{{{1}0}} {\text{N}} \cdot {\text{m}}^{{ - {2}}} ,\)\(\tau_{0} = 0.05,\) \(\omega = 50\,Hz.\)

Fig. 3
figure 3

a–c Variations of the reflection coefficient of reflected P1, P2 and P3 waves against angle of incidence of P1 wave at different values of magnetic parameter \(H_{0}\) when Ω = 10 Hz,\(\beta = 0,\)\(Z_{1}^{*} = 0,\)\(Z_{3}^{*} = 0,\)\(P = 1.0 \times {1}0^{{{1}0}} {\text{N}} \cdot {\text{m}}^{{ - {2}}} ,\)\(\tau_{0} = 0.05,\) \(\omega = 50\,Hz\)

Full size image

The variations of the reflection coefficients \(\left| {Z_{1} } \right|,\left| {Z_{2} } \right|\) and \(\left| {Z_{3} } \right|\) of reflected \(P_{1} \,,P_{2} \,\) and \(P_{3} \,\) waves, respectively, against angle of incidence of \(P_{1}\) wave are shown graphically in Fig. 4a–c for three different values of initial stress, P = 0.0 (denoted by solid black line with solid square), \(P\) = 0.5 × 1010 N·m−2 (denoted by solid black line with solid triangle), \(P\) = 1.0 × 1010 N·m−2 (denoted by solid black line with solid circle), when Ω = 10 Hz, \(\beta = 0,Z_{1}^{*} = Z_{3}^{*} = 0,\)\(H_{0} = 6.0 \times 10^{5} Oe,\)\(\tau_{0} = 0.05,\) \(\omega = 50\,Hz.\) The value of \(\left| {Z_{1} } \right|\) of reflected \(P_{1}\) wave is 0.97 625 at normal incidence and it increases to a maximum value 1.11 906 at θ0 = 54°. Thereafter, it decreases sharply to value one at grazing incidence for \(P\) = 0.0. It is 0.97 621 at normal incidence and it increases to a maximum value 1.11 378 at θ0 = 54°. Thereafter it decreases sharply to value one at grazing incidence for \(P\) = 0.5 × 1010 N·m−2 and is 0.97 618 at normal incidence and then increases to a maximum value 1.10 843 at θ0 = 54°. Thereafter, it decreases sharply to value one at grazing incidence for \(P\) = 1.0 × 1010 N·m−2 denoted by solid black line with solid square, solid black line with solid triangle and solid black line with solid circle, respectively, as shown in Fig. 4a. The value of \(\left| {Z_{2} } \right|\) of reflected \(P_{2}\) wave is 0.00 001 at normal incidence and it increases to a maximum value 0.00 432 at θ0 = 47°. Thereafter, it decreases sharply to value zero at grazing incidence at \(P\) = 0.0 and similar variations for \(P\) = 0.5 × 1010 N·m−2 and \(P\) = 1.0 × 1010 N·m−2 denoted by solid black line with solid square, solid black line with solid triangle and solid black line with solid circle, respectively, as shown in Fig. 4b. The value of \(\left| {Z_{3} } \right|\) of reflected \(P_{3}\) wave is 0.0025 at normal incidence and it decreases sharply to value zero at grazing incidence at \(P\) = 0.0 and similar variations for \(P\) = 0.5 × 1010 N·m−2 and \(P\) = 1.0 × 1010 N·m−2 are denoted by solid black line with solid square, solid black line with solid triangle and solid black line with solid circle, respectively, as shown in Fig. 4c.

Fig. 4
figure 4

a–c Variations of the reflection coefficient of reflected P1, P2 and P3 waves against angle of incidence of P1 wave at different values of initial parameter P when Ω = 10 Hz,\(H_{0} = 6 \times 10^{5} Oe,\)\(\tau_{0} = 0.05,\)\(\beta = 0,Z_{1}^{*} = Z_{3}^{*} = 0,\) \(\omega = 50\,Hz\)

Full size image

The variations of the reflection coefficients \(\left| {Z_{1} } \right|,\left| {Z_{2} } \right|\) and \(\left| {Z_{3} } \right|\) of reflected \(P_{1} ,\) \(P_{2}\) and \(P_{3}\) waves against rotation parameter Ω at an angle of incidence 450 for incidence \(P_{1}\) wave for \(\beta = 0.5,\) \(Z_{1}^{*} = 10,\) \(Z_{3}^{*} = - 10,\) when \(P = 1.0 \times {1}0^{{{1}0}} {\text{N}}.{\text{m}}^{{ - {2}}} ,\) \(H_{0} = 6.0 \times 10^{5} Oe,\)\(\tau_{0} = 0.05,\) \(\omega = 50\,Hz,\) are denoted by solid black line with solid square, while the variations for \(\beta = 0,\) \(Z_{1}^{*} = 0,\) \(Z_{3}^{*} = 0,\) when \(P = 1.0 \times {1}0^{{{1}0}} {\text{N}}.{\text{m}}^{{ - {2}}} ,\) \(H_{0} = 6.0 \times 10^{5} Oe,\)\(\tau_{0} = 0.05,\) \(\omega = 50\,Hz,\) are denoted by solid black line with solid triangle as shown graphically in Fig. 5a–c. Each value of \(\left| {Z_{2} } \right|\) and \(\left| {Z_{3} } \right|\) is observed multiplied by \(10^{2}\) and \(10\), respectively.

Fig. 5
figure 5

a–c Variations of the reflection coefficient of reflected \(P_{1} ,P_{2} ,\) and \(P_{3} ,\) waves for incidence of P1 wave against rotation parameter Ω, for \(\beta = 0.5,\) \(Z_{1}^{*} = 10,\) \(Z_{3}^{*} = - 10,\) and \(\beta = 0,\) \(Z_{1}^{*} = 0,\) \(Z_{3}^{*} = 0,\) when \(P = 1.0 \times {1}0^{{{1}0}} {\text{N}} \cdot {\text{m}}^{{ - {2}}} ,\) \(H_{0} = 6.0 \times 10^{5} Oe,\)\(\tau_{0} = 0.05,\) \(\omega = 50\,Hz\)

Full size image

The variations of the energy ratios \(\left| {E_{1} } \right|,\left| {E_{2} } \right|\) and \(\left| {E_{3} } \right|\) of reflected \(P_{1} \,,P_{2} \,\) and \(P_{3} \,\) waves, respectively, against angle of incidence of \(P_{1}\) wave are shown graphically in Fig. 6a–c for three different values of initial stress P = 0.0 (denoted by solid black line with solid square), P = 0.5 × 1010 N·m−2 (denoted by solid black line with solid triangle), P = 1.0 × 1010 N·m−2 (denoted by solid black line with solid circle), when Ω = 10 Hz, \(\beta = 0,Z_{1}^{*} = Z_{3}^{*} = 0,\)\(H_{0} = 6.0 \times 10^{5} Oe,\)\(\tau_{0} = 0.05,\) \(\omega = 50\,Hz.\) The energy ratio \(\left| {E_{1} } \right|\) of reflected \(P_{1} \,\) wave is 0.99469 at normal incidence, it increases to maximum value 0.99542 at θ0 = 48° and then decreases to 0.99470 at grazing incidence for P = 0.0. Similarly, the behavior of the energy ratios for P = 1.0 × 1010 N·m−2 are observed similar. The values of energy ratios at P = 0.5 × 1010 N·m−2 are more than the values at P = 0.0 and values decreases for P = 0.5 × 1010 N·m−2 denoted by solid black line with solid squares. Solid black line with solid triangle and solid black line with solid circle, respectively, as shown in Fig. 6a. The energy ratio \(\left| {E_{2} } \right|\) of reflected \(P_{2} \,\) wave is 0.0 at normal incidence and it increases to a maximum value 0.033 336 at θ0 = 51°. Thereafter, it decreases to value zero at grazing incidence for P = 0.0. Similarly, the behavior of the energy ratios for P = 0.5 × 1010 N·m−2 and P = 1.0 × 1010 N·m−2 are observed similar. However, the values of energy ratios are different at each angle of incidence except normal and grazing incidence denoted by solid black line with solid square, solid black line with solid triangle and solid black line with solid circle, respectively, as shown in Fig. 6b. Each value of \(\left| {E_{2} } \right|\) is observed multiplied by \(10^{3} .\) The value of \(\left| {E_{3} } \right|\) of reflected \(P_{3}\) wave is 0.0063 at normal incidence and it decreases sharply to value zero at grazing incidence at \(P\) = 0.0 and variations for \(P\) = 0.5 × 1010 N·m−2 and \(P\) = 1.0 × 1010 N·m−2 are denoted by solid black line with solid square, solid black line with solid triangle and solid black line with solid circle, respectively, as shown in Fig. 6c. Each value of \(\left| {E_{3} } \right|\) is observed multiplied by \(10^{3} .\)

Fig. 6
figure 6

a–c Variations of the energy ratios of reflected P1, P2 and P3 waves against angle of incidence of P1 wave at different values of initial parameter P when Ω = 10 Hz, \(H_{0} = 6.0 \times 10^{5} Oe,\)\(\beta = 0,Z_{1}^{*} = Z_{3}^{*} = 0,\)\(\tau_{0} = 0.05,\) \(\omega = 50\,Hz\)

Full size image

The variations of the energy ratios \(\left| {E_{1} } \right|,\left| {E_{2} } \right|\) and \(\left| {E_{3} } \right|\) of reflected \(P_{1} \,,P_{2} \,\) and \(P_{3} \,\) waves, respectively, against angle of incidence of \(P_{1}\) wave are shown graphically in Fig. 7a–c for two different values of rotation parameter \(\Omega = 20\) Hz (denoted by solid black line with solid square), and \(\Omega = 25\) Hz (denoted by solid black line with solid circle), when \(\beta = 0,Z_{1}^{*} = Z_{3}^{*} = 0,\) P = 1.0 × 1010 N·m−2, \(H_{0} = 6.0 \times 10^{5} Oe,\)\(\tau_{0} = 0.05,\) \(\omega = 50\,Hz.\) The energy ratio \(\left| {E_{1} } \right|\) of reflected \(P_{1}\) wave is 0.99 846 at normal incidence and it increases sharply to 0.9985 at grazing incidence at Ω = 20 Hz. It is 0.997 46 at normal incidence increases sharply to 0.9982 at grazing incidence Ω = 25 Hz. denoted by solid black line with solid square and solid black line with solid circle, respectively, as shown in Fig. 7a. The value of energy ratio \(\left| {E_{2} } \right|\) of reflected \(P_{2}\) wave is 0.0 at normal incidence and it increases to a maximum value 0.00 223 at θ0 = 49°. Thereafter, it decreases to value zero at grazing incidence at Ω = 20 Hz. and similar variations for Ω = 25 Hz. However, the values of energy ratios are different at each angle of incidence except normal and grazing incidence denoted by solid black line with solid square and solid black line with solid circle, respectively, as shown in Fig. 7b. Each value of \(\left| {E_{2} } \right|\) is observed multiplied by \(10^{2} .\) The value of \(\left| {E_{3} } \right|\) of reflected \(P_{3}\) wave is 0.00 007 at normal incidence and it decreases sharply to value zero at grazing incidence at Ω = 20 Hz and similar variations are observed for Ω = 25 Hz denoted by solid black line with solid square and solid black line with solid circle, respectively, as shown in Fig. 7c. Each value of \(\left| {E_{3} } \right|\) is observed multiplied by \(10.\)

Fig. 7
figure 7

a–c Variations of the energy ratios of reflected P1, P2 and P3 waves for incidence of P1 wave against angle of incidence of incident P1 wave at different values of parameter Ω, when \(P = 1.0 \times {1}0^{{{1}0}} {\text{N}} \cdot {\text{m}}^{{ - {2}}} ,\)\(\beta = 0,Z_{1}^{*} = Z_{3}^{*} = 0,\) \(H_{0} = 6.0 \times 10^{5} Oe,\)\(\tau_{0} = 0.05,\)\(\omega = 50\,Hz\)

Full size image

The variations of the energy ratios \(\left| {E_{1} } \right|,\left| {E_{2} } \right|\) and \(\left| {E_{3} } \right|\) of reflected \(P_{1} \,,P_{2} \,\) and \(P_{3} \,\) waves, respectively, against impedance parameter \(Z_{1}^{*}\) are shown graphically in Fig. 8a–c for two different values of initial stress parameter \(P = 0.5\,\, \times {1}0^{{{1}0}} {\text{N}} \cdot {\text{m}}^{{ - {2}}}\)(denoted by solid black line with solid square) and \(P = 0.75\,\, \times {1}0^{{{1}0}} {\text{N}} \cdot {\text{m}}^{{ - {2}}}\) (denoted by solid black line with solid circle), when Ω = 10 Hz, \(Z_{3}^{*} = 0,\) \(\beta = 0.0,\)\(\tau_{0} = 0.05,\) \(H_{0} = 6.0 \times 10^{5} Oe,\)\(\omega = 50\,Hz.\) Each value of \(\left| {E_{3} } \right|\) is observed multiplied by \(10^{4} .\) The variations of the energy ratios \(\left| {E_{1} } \right|,\left| {E_{2} } \right|\) and \(\left| {E_{3} } \right|\) of reflected \(P_{1} \,,P_{2} \,\) and \(P_{3} \,\) waves, respectively, against impedance parameter \(Z_{3}^{*}\) are shown graphically in Fig. 9a–c for two different values of initial stress parameter \(P = 0.5\,\, \times {1}0^{{{1}0}} {\text{N}} \cdot {\text{m}}^{{ - {2}}} ,\)(denoted by solid black line with solid square) and \(P = 1.0\,\, \times {1}0^{{{1}0}} {\text{N}} \cdot {\text{m}}^{{ - {2}}} ,\) (denoted by solid black line with solid circle), when Ω = 10 Hz, \(Z_{1}^{*} = 0,\) \(\beta = 0.25,\)\(\tau_{0} = 0.05,\) \(H_{0} = 6.0 \times 10^{5} Oe,\)\(\theta_{0} = 45^{ \circ } ,\)\(\omega = 50\,Hz.\) Each value of \(\left| {E_{2} } \right|\) and \(\left| {E_{3} } \right|\) is observed multiplied by \(10^{3}\) and \(10^{4}\), respectively.

Fig. 8
figure 8

a–c Variations of the energy ratios of reflected P1, P2 and P3 waves for incidence of P1 wave against impedance parameter \(Z_{1}^{*}\) at different values of initial stress parameter \(P,(P = 0.5,0.75)\), when \(\Omega = 10Hz,\)\(\beta = 0.25,Z_{3}^{*} = 0,\) \(H_{0} = 6.0 \times 10^{5} Oe,\)\(\tau_{0} = 0.05,\)\(\theta_{0} = 45^{ \circ } ,\)\(\omega = 50\,Hz\)

Full size image
Fig. 9
figure 9

a–c Variations of the energy ratios of reflected P1, P2 and P3 waves for incidence of P1 wave against impedance parameter \(Z_{3}^{*}\) at different values of initial stress parameter \(P,(P = 0.5,1.0)\), when \(\Omega = 10Hz,\)\(\beta = 0.25,Z_{1}^{*} = 0,\) \(H_{0} = 6.0 \times 10^{5} Oe,\)\(\tau_{0} = 0.05,\)\(\theta_{0} = 45^{ \circ } ,\)\(\omega = 50\,Hz\)

Full size image

8 Conclusions

The reflection of plane waves from a thermally insulated surface with impedance boundary of initially stressed magneto-thermoelastic rotating half-space in the context of fractional-order derivative thermoelasticity is studied. The relations between reflection coefficients of reflected waves are derived. The expressions for energy ratios of all reflected waves are also obtained. The significant effect of angle of incidence, initial stress parameters, magnetic field parameters, and rotation parameter on reflection coefficients and energy ratios of reflected waves is observed. From numerical illustrations the following conclusions can be drawn:

  1. 1.

    With the increase in the magnetic field parameter \(H_{0} (6,8,10),\) and fractional derivative parameter \(\beta = (0.25,\,0.50,0.75),\) the reflection coefficient of reflected \(P_{1}\), \(P_{2}\) and \(P_{3}\) waves decreases with an increase in incident angle \(\theta_{0}\) \((0^{ \circ } \le \theta_{0} \le 90^{ \circ } )\) for \(P = 1.0,\,\,\Omega = 10,\;Z_{1}^{*} = 10,\;Z_{3}^{*} = - 10.\)

  2. 2.

    With the increase in the magnetic field parameter \(H_{0} (6,8,10),\) the reflection coefficient of reflected \(P_{1}\), \(P_{2}\) and \(P_{3}\) waves decreases with an increase in incident angle \(\theta_{0}\) \((0^{ \circ } \le \theta_{0} \le 90^{ \circ } )\) for \(P = 1.0,\,\,\Omega = 10,\,\,\beta = 0,Z_{1}^{*} = Z_{3}^{*} = 0.\)

  3. 3.

    With the increase of initial stress parameter \(P(0.0,\,0.5,1.0),\) the reflection coefficient of reflected \(P_{1} ,\) and \(P_{2}\) waves decreases while there is no significant change in the reflection coefficient of \(P_{3}\) wave with an increase in incident angle \(\theta_{0}\) \((0^{ \circ } \le \theta_{0} \le 90^{ \circ } )\) for \(\beta = 0,\Omega \, = 10,\,H_{0} = 6,\,Z_{1}^{*} = Z_{3}^{*} = 0.\)

  4. 4.

    With the increase of rotation parameter \(\Omega \,\,(20,\,25)\), the energy ratio of reflected \(P_{1} ,\)\(P_{2}\) and \(P_{3}\) waves increases with an increase in incident angle \(\theta_{0}\) \((0^{ \circ } \le \theta_{0} \le 90^{ \circ } )\) for \(\beta = 0,P\, = 1.0,\,H_{0} \, = \,6,\,Z_{1}^{*} = Z_{3}^{*} = 0.\)

  5. 5.

    With the increase of initial stress parameter \(P(0.5,0.75),\) the energy ratio of reflected \(P_{1}\) wave, decreases while the energy ratio of \(P_{2}\) and \(P_{3}\) waves increases for the increase in the impedance parameter \(Z_{1}^{*} ,\) \((1.0 \le Z_{1}^{*} \le 10.0)\) for \(\beta = 0.0,\)\(\Omega \, = \,10,\)\(Z_{3}^{*} = 0,\)\(H_{0} = 6.\)

  6. 6.

    With the increase of initial stress parameter \(P(0.5,1.0)\), the energy ratio of reflected \(P_{1}\) wave, decreases while the energy ratio of \(P_{2}\) and \(P_{3}\) waves increases for the increase in the impedance parameter \(Z_{3}^{*} ,\) \((1.0 \le Z_{3}^{*} \le 10.0)\) for \(\beta = 0.25,\)\(\Omega \, = \,10,\)\(Z_{1}^{*} = 0,\)\(H_{0} = 6.\)